为满足地质井位部署和后期储层改造要求,提高单井产量和油田效益,以水平井为主的井型逐渐增多,并出现了水平井“井工厂”模式[1],原二维水平井已不能满足需要,三维水平井显得越来越重要。三维水平井设计的重要内容之一就是井眼轨道设计,目前,轨道设计模型主要包括空间圆弧模型、圆柱螺线模型、自然参数模型和恒工具面角模型,其中空间圆弧设计模型研究比较广泛[2-9],而恒工具面角模型应用非常少,轨道设计行业标准也未将其列入其中[4],但该模型独有的特点非常适合采用常规装备施工,对于致力于低成本开发的油气田来说非常适用。为此,笔者对这几种主要设计模型进行了对比分析,根据其优点与不足,优选恒工具面角模型进行三维水平井轨道设计,并应用到泾河油田JH17P36轨道设计中,该井采用常规钻井装备与“螺杆+MWD系统”定向工具,实钻井深2 604 m,钻井周期21.21 d。目前,该轨道设计方法已推广应用到多口三维平水平井中,取得了良好的应用效果。
1 轨道设计模型优选空间圆弧法是研究与应用最广泛的三维轨道设计模型之一,轨迹是位于空间斜平面内的圆弧,井眼曲率保持不变,但井斜变化率、方位变化率、工具面角随井斜角变化[4-10],给现场定向施工工艺都带来了一些困难。
圆柱螺线模型也是常用的三维井眼轨道设计模型,轨迹是一条等变螺旋角的圆柱螺线,在垂直剖面图和水平投影图上井眼轨道均为圆弧,井斜变化率是常数,但井眼曲率、方位变化率和工具面角不是常数[11-18],且井眼曲率随井斜变化幅度较大,这种特点不利于井眼轨迹控制。
自然参数模型假设曲线是一条自然参数曲线,其井斜变化率和方位变化率均为常数,但井眼曲率和工具面角却不是常数[19-20],这给定向施工也带来不小的困难,但对于设计具有方位漂移特性的井眼轨道具有优势。
恒工具面角模型是近来出现的新设计方法,最显著的特点是工具面角、井眼曲率是及井斜变化率均是常数,与上述三种设计模型不同,其参数计算模型不是解析式,需要数值求解,计算复杂[14-17],现场应用非常少见,但对于现场定向施工非常有优势。4种模型优缺点见表 1。
| 表1 4种轨道设计模型评价 Table 1 Evaluation of four wellpath models |
根据不同设计模型的优缺点,经过充分调研论证,因恒工具面角轨道设计模型具有明显的优势,优选恒工具面角设计模型。
2 三维水平井井眼轨道设计 2.1 井眼轨道类型三维水平井轨道特点是井口、
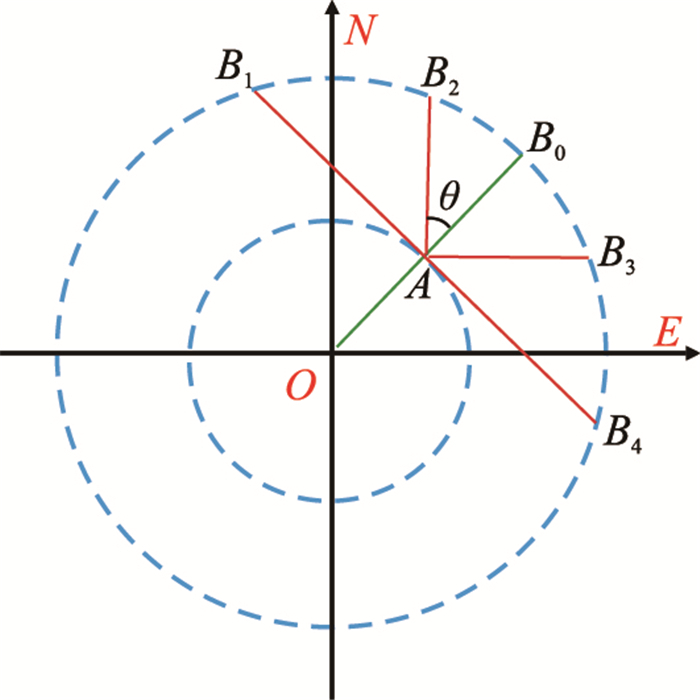 |
| 图1 三维水平井基本类型 Fig. 1 Basic types of 3D horizontal well |
三维水平井井眼轨道自造斜点至
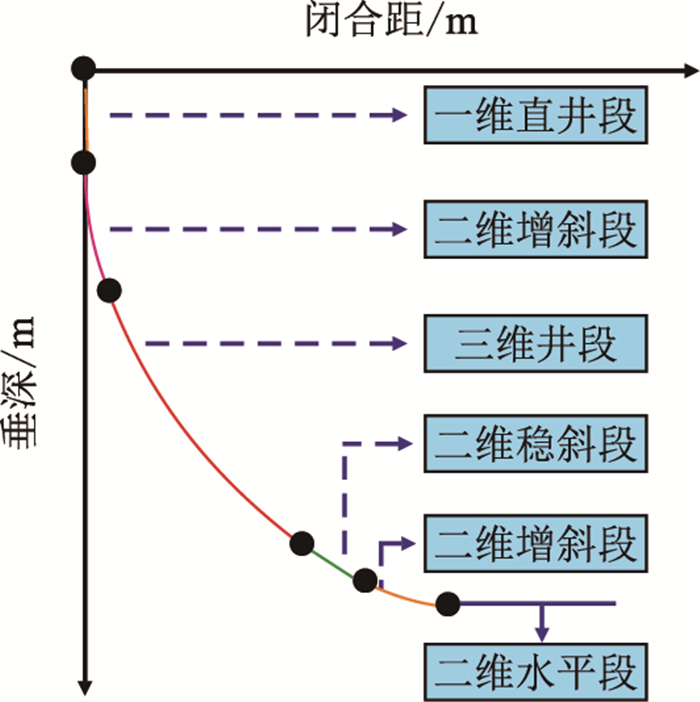 |
| 图2 六段制三维水平井轨道 Fig. 2 Six section 3D horizontal well trajectory |
采用恒工具面角模型设计的三维井段上任意点,恒工具面模型基本方程为[16-20]
| $ K\left( {{L}_{2}}-{{L}_{1}} \right)\cos \omega +{{\alpha }_{1}}={{\alpha }_{2}} $ | (1) |
| $ \tan \omega \ln \dfrac{\tan (0.5{{\alpha }_{2}})}{\tan (0.5{{\alpha }_{1}})}+{{\phi }_{1}}={{\phi }_{2}} $ | (2) |
| $ {\int}_{{{\alpha }_{1}}}^{{{\alpha }_{2}}}{\sin \alpha \sin }\left[\tan \omega \ln \dfrac{\tan (0.5\alpha )}{\tan (0.5{{\alpha }_{1}})}+{{\phi }_{1}} \right]{\rm d}\alpha \cdot \\{\kern 40pt} \dfrac{1}{K\cos \omega }=\Delta {{E}_{\rm H}} $ | (3) |
| $ {\int}_{{{\alpha }_{1}}}^{{{\alpha }_{2}}}{\sin \alpha \cos }\left[\tan \omega \ln \dfrac{\tan (0.5\alpha )}{\tan (0.5{{\alpha }_{1}})}+{{\phi }_{1}} \right]{\rm d}\alpha \cdot \\{\kern 40pt} \dfrac{1}{K\cos \omega }=\Delta {{N}_{\rm H}} $ | (4) |
式中:
为简化说明,仅考虑
根据
| $ \sum\limits_{i=1}^{4}{\Delta {{E}_{i}}=}\Delta E $ | (5) |
| $ \sum\limits_{i=1}^{4}{\Delta {{N}_{i}}=}\Delta N $ | (6) |
式中:
在钻井实践中,为减少起下钻次数,保持施工连续性,提高钻井效率,通常在二维造斜段和三维扭方位段使用同一钻具组合,因此,钻具造斜率是一样的。因此,根据式(2)
| $ \dfrac{1-\cos {{\alpha }_{1}}}{K}\sin {{\phi }_{1}} +\Delta L\sin {{\alpha }_{2}}\sin {{\phi }_{2}}+\\ \frac{\int_{{{\alpha }_{1}}}^{{{\alpha }_{2}}}{\sin \alpha \sin }\left[\tan \omega \ln \dfrac{\tan (0.5\alpha )}{\tan (0.5{{\alpha }_{1}})}+{{\phi }_{1}} \right]}{K\cos \omega }{\rm d}\alpha+ \\ \dfrac{\cos {{\alpha }_{2}}-\cos {{\alpha }_{A}}}{K}\sin {{\phi }_{2}}=\Delta E $ | (7) |
| $ \dfrac{1-\cos {{\alpha }_{1}}}{K}\cos {{\phi }_{1}}+\Delta L\sin {{\alpha }_{2}}\cos {{\phi }_{2}}+\\ \frac{{\int}_{{{\alpha }_{1}}}^{{{\alpha }_{2}}}{\sin \alpha \cos }\left( \tan \omega \ln \dfrac{\tan (0.5\alpha )}{\tan (0.5{{\alpha }_{1}})}+{{\phi }_{1}} \right){\rm d}\alpha} {K\cos \omega }+ \\ \dfrac{\cos {{\alpha }_{2}}-\cos {{\alpha }_{A}}}{K}\cos {{\phi }_{2}}=\Delta N $ | (8) |
式中:
通过联立式(7),式(8),化简,得到关于
| $ \left( 1-\cos {{\alpha }_{1}} \right)\cos {{\phi }_{1}}\cos \omega \left( {{\phi }_{1}} \right)+N\left( {{\phi }_{1}} \right)+\left( \cos {{\alpha }_{2}}-\cos {{\alpha }_{A}} \right)\cos {{\phi }_{2}}\cos \omega \left( {{\phi }_{1}} \right)+ \\{\kern 40pt}K\left( {{\phi }_{1}} \right)\cos \omega \left( {{\phi }_{1}} \right)\left( \Delta L\sin {{\alpha }_{2}}\cos {{\phi }_{2}}-\Delta N \right)=0 $ | (9) |
| $ K\left( {{\phi }_{1}} \right)=\dfrac{E({{\phi }_{1}})+\left( 1-\cos {{\alpha }_{1}} \right)\sin {{\phi }_{1}}\cos \omega \left( {{\phi }_{1}} \right)+\left( \cos {{\alpha }_{2}}-\cos {{\alpha }_{A}} \right)\sin {{\phi }_{2}}\cos \omega \left( {{\phi }_{1}} \right)}{\left( \Delta E-\Delta L\sin {{\alpha }_{2}}\sin {{\phi }_{2}} \right)\cos \omega \left( {{\phi }_{1}} \right)} $ | (10) |
| $ N\left( {{\phi }_{1}} \right)\!=\!{\int}_{{{\alpha }_{1}}}^{{{\alpha }_{2}}}{\sin \alpha \cos }\left[\tan \omega \left( {{\phi }_{1}} \right)\ln \dfrac{\tan (0.5\alpha )}{\tan (0.5{{\alpha }_{1}})}+{{\phi }_{1}} \right]{\rm d}\alpha $ | (11) |
| $ E\left( {{\phi }_{1}} \right)={\int}_{{{\alpha }_{1}}}^{{{\alpha }_{2}}}{\sin \alpha \sin }\left[\tan \omega \left( {{\phi }_{1}} \right)\ln \dfrac{\tan (0.5\alpha )}{\tan (0.5{{\alpha }_{1}})}+{{\phi }_{1}} \right]{\rm d}\alpha $ | (12) |
| $ \omega \left( {{\phi }_{1}} \right)=\arctan \dfrac{{{\phi }_{2}}-{{\phi }_{1}}}{\ln \dfrac{\tan (0.5{{\alpha }_{2}})}{\tan (0.5{{\alpha }_{1}})}} $ | (13) |
通过方程(9)可求解出参数
大量数据模拟表明,式(9)的函数特性是关于初始定向方位角的一元非线性函数,在求解区间上具有单调性,可通过二分法、黄金分割法和Fibonacci法等一维搜索法求解。
2.4 其他参数计算模型根据参数
井深计算公式为
| $ L={{L}_{1}}+\dfrac{\alpha -{{\alpha }_{1}}}{K\left( {{\phi }_{1}} \right)\cos \omega \left( {{\phi }_{1}} \right)} $ | (14) |
式中:
垂深计算公式为
| $ D={{D}_{1}}+\dfrac{\sin \alpha -\sin {{\alpha }_{1}}}{K\left( {{\phi }_{1}} \right)\cos \omega \left( {{\phi }_{1}} \right)} $ | (15) |
式中:
方位计算公式为
| $ \phi ={{\phi }_{1}}+\tan \omega \left( {{\phi }_{1}} \right)\ln \dfrac{\tan 0.5\alpha }{\tan 0.5{{\alpha }_{1}}} $ | (16) |
式中:
水平投影长度计算公式为
| $ S={{S}_{1}}+\dfrac{\cos {{\alpha }_{1}}-\cos \alpha }{K\left( {{\phi }_{1}} \right)\cos \omega \left( {{\phi }_{1}} \right)} $ | (17) |
式中:
井眼轨道设计数据来源分为两部分,一部分是根据地质设计的井口坐标、
根据这两部分数据,通过初始定向方位角计算模型,基于一维搜索法求解出初始定向方位角,然后计算造斜率和工具面角,据此计算井深、垂深和方位等其他轨道参数,进而完成整个井眼轨道设计。如果进行了坐标变换,解出各参数后,需要进行逆变换。具体设计与计算步骤框图,见图 3。
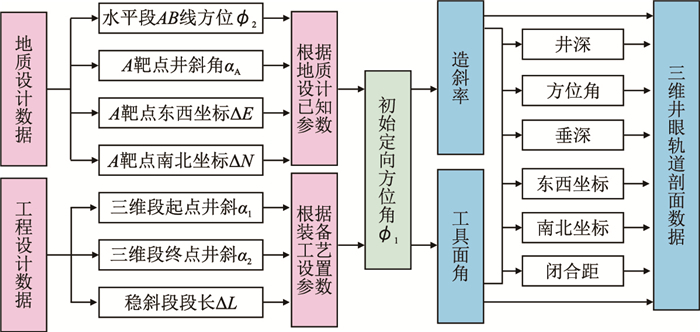 |
| 图3 井眼轨道设计 Fig. 3 Design and calculation of wellpath |
基于恒工具面角模型的轨道设计方法已成功应用于泾河油田和洛河油田多口井,表现出了良好的优势,与同区块其他方法相比,具有易于钻井施工的特点。为节约篇幅,以泾河油田第一口三维水平井为例说明。泾河油田位于鄂尔多斯盆地,属于“低孔、低渗、低压”油藏,单井产量低,一直采用低成本开发[22]。地表沟壑纵横,平整井场和修建道路受限;水平井均采用压裂建产模式,为产生垂直缝水平段井眼方向需沿最小主应力方向。为实现泾河油田经济有效开发,部署了首口三维水平井JH17P36试验井,该井目的层为长812层段,采用二级井身结构,二开
JH17P36井地质设计水平段长750.00 m,
由于泾河油田长8层属于河流道沉积,储层非均质性强,根据邻井实钻数据,
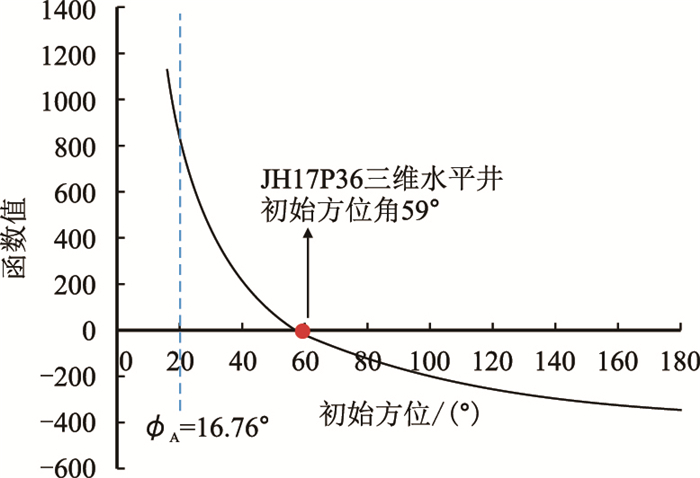 |
| 图4 JH17P36井初始定向方位角 Fig. 4 Initial azimuth angle of JH17P36 |
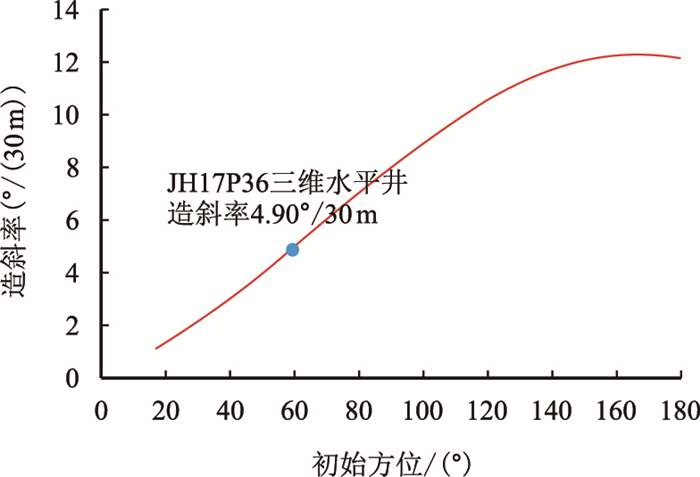 |
| 图5 JH17P36井造斜率 Fig. 5 Build-up rate of JH17P36 |
根据初始定向方位角、造斜率和工具面角,计算出其他轨道参数。
JH17P36井眼轨道设计三维坐标图见图 6;轨道设计与实钻对比见图 7,井眼轨道参数见表 2。
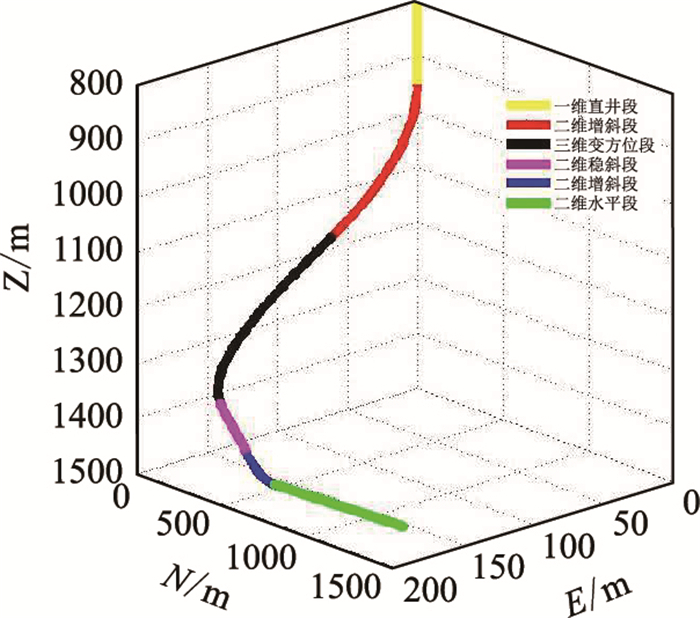 |
| 图6 三维井眼轨迹图 Fig. 6 3D well trajectory |
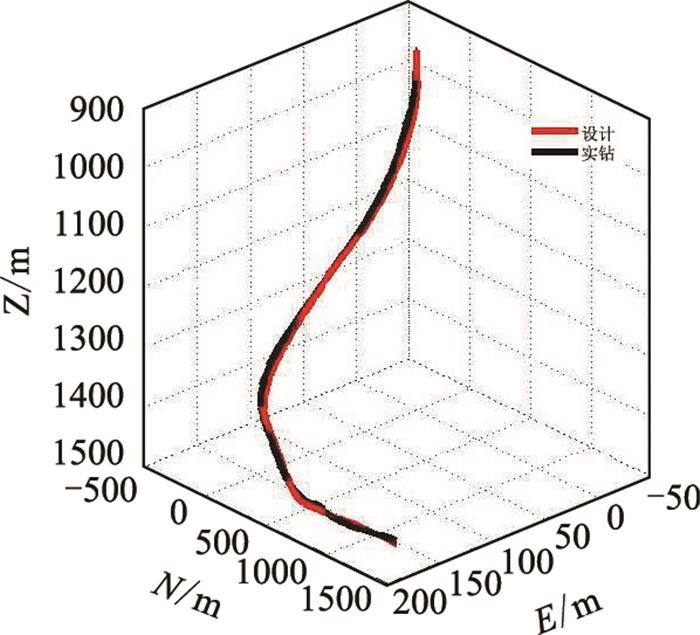 |
| 图7 实钻轨迹与设计对比三维坐标图 Fig. 7 Comparison of 3D drilling trajectory and design |
| 表2 JH17P36井眼轨道参数 Table 2 Wellpath parameter of JH17P36 |
采用ZJ40钻机和F-1300钻井泵,不配备顶驱和旋转导向系统[23],通过“螺杆+MWD测量系统”进行定向施工,基于常规录井进行地质导向,主要包括岩屑录井、气测录井、钻时录井和荧光录井。为了使工具面稳定和易于定向施工,优选三牙轮钻头和单弯柔性倒装钻具组合,三维井段钻具组合为
通过井眼轨迹精细化控制,该井顺利着陆
JH17P36井
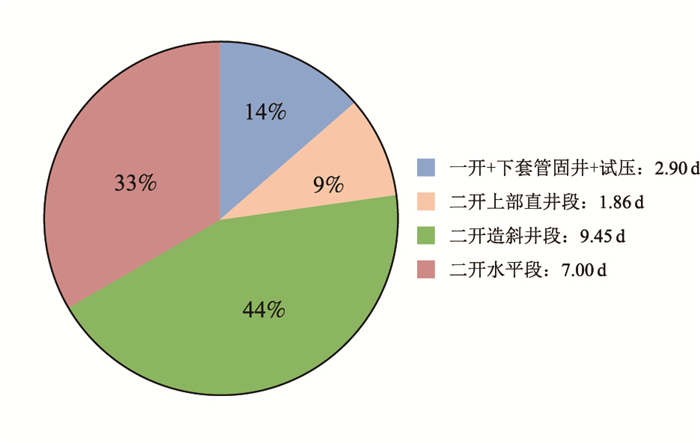 |
| 图8 JH17P36井各井段施工时间 Fig. 8 Construction time of each section in JH17P36 |
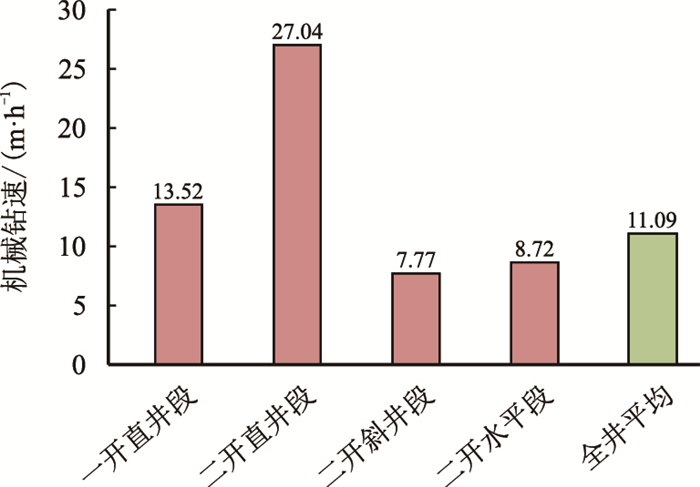 |
| 图9 JH17P36井各井段机械钻速 Fig. 9 ROP of each section in JH17P36 |
|
表3 JH17P36井 |
JH17P36井完钻井深2 604 m,水平段长750 m,钻井周期21.20 d(图 8),平均机械钻速11.09 m/h(图 9);其钻井周期较该油田二维水平井平均值缩短29.53%,机械钻速提高11.23%。完钻后电测顺利,油层套管一次性安全下入到底,固井质量良好,投产后日产油8.3 t,地质效果显著。
4 结论(1) 基于典型六段制轨道和恒工具面角模型,给出了初始定向方位角计算模型,其函数特性是关于初始定向方位角的一元非线性函数,易于编程实现。
(2) 根据初始定向方位角、造斜率和工具面角,求取其他轨道参数,形成了比较完整的三维水平井轨道设计方法和步骤,可广泛应用于各三维水平井道设计中。
(3) 利用恒工具面角模型设计的井眼轨道,井眼曲率和工具面角是常数,适合采用常规钻井装备施工,现场易于定向操作,减少了起下钻更换钻具组合次数,提高了效率。
(4) JH17P36井的现场应用表明,通过“螺杆+MWD测量系统”进行定向施工,实钻井眼轨迹与设计符合率高,各技术指标优秀,表明计算模型和设计方法是正确、合理和可行的,也验证了恒工具面角模型具有的优越性,对其他油田进行类似三维水平井设计与施工具有借鉴意义。
| [1] |
闫吉曾, 邓红琳. "井工厂"模式在大牛地气田的应用[C]//中国石化油气开采技术论坛秘书处. 中国石化油气开采技术论坛论文集: 2013. 北京: 中国石化出版社, 2013: 191-197.
YAN Jizeng, DENG Honglin. Application of multi-well pad in Daniudi Gas Field[C]//Sinopec Oil and Gas Technology Forum Secretariat. Sinopec oil and gas technology forum: 2013. Beijing: China Petrochemical Press, 2013: 191-197. http://www.wanfangdata.com.cn/details/detail.do?_type=conference&id=8705909 |
| [2] |
刘修善, 何树山. 井眼轨道的软着陆设计模型及其应用[J].
天然气工业, 2002, 22(2): 43–45.
LIU Xiushan, HE Shushan. Well-path soft landing design model and its application[J]. Natural Gas Industry, 2002, 22(2): 43–45. doi: 10.3321/j.issn:1000-0976.2002.02.013 |
| [3] |
刘修善. 三维侧钻绕障井的设计方法[J].
石油学报, 2009, 30(6): 916–922.
LIU Xiushan. Planning technique of 3D sidetrack wells for bypassing obstacles[J]. Acta Petrolei Sinica, 2009, 30(6): 916–922. doi: 10.7623/syxb200906022 |
| [4] |
国家能源局. SY/T 5435-2012定向井轨道设计与轨迹计算[S]. 北京: 石油工业出版社, 2012.
NATIONAL Energy Administration. SY/T 5435-2012 Wellpath planning & trajectory calculation for directional wells[S]. Beijing: Petroleum Industry Press, 2012. |
| [5] |
刘修善, 郭钧. 空间圆弧轨道的描述与计算[J].
天然气工业, 2000, 20(5): 44–47.
LIU Xiushan, GUO Jun. Description and calculation of the well path with spatial arc model[J]. Natural Gas Industry, 2000, 20(5): 44–47. doi: 10.3321/j.issn:1000-0976.2000.-05.013 |
| [6] |
刘修善, 王超. 空间圆弧轨迹的解析描述技术[J].
石油学报, 2014, 35(1): 134–140.
Liu Xiushan, Wang Chao. Analytic description of spatialarc wellbore trajectory[J]. Acta Petrolei Sinica, 2014, 35(1): 134–140. doi: 10.7623/syxb201401016 |
| [7] |
韩志勇. 斜面圆弧形井眼的轨迹控制新模式[J].
石油钻探技术, 2004, 32(2): 1–3.
HAN Zhiyong. New control mode for well trajectoty on circular arc with inclined planes[J]. Petroleum Drilling Techniques, 2004, 32(2): 1–3. doi: 10.3969/j.issn.1001-0890.2004.02.001 |
| [8] |
韩志勇. 三维定向井轨道设计和轨迹控制的新技术[J].
石油钻探技术, 2003, 31(5): 1–3.
HAN Zhiyong. The new techniques of well trajectory design and well path control fit for 3D directional wells[J]. Petroleum Drilling Techniques, 2003, 31(5): 1–3. doi: 10.-3969/j.issn.1001-0890.2003.05.001 |
| [9] |
鲁港, 佟长海, 夏泊洢, 等. 空间圆弧轨迹的矢量描述技术[J].
石油学报, 2014, 35(4): 759–764.
LU Gang, TONG Changhai, XIA Boyi, et al. Vector description of spatial-arc wellbore trajectory[J]. Acta Petrolei Sinica, 2014, 35(4): 759–764. doi: 10.7623/syxb-201404019 |
| [10] |
鲁港, 王刚, 邢玉德, 等. 定向井钻井空间圆弧轨道计算的两个问题[J].
石油地质与工程, 2006, 20(6): 53–55.
LU Gang, WANG Gang, XING Yude, et al. Two questions of space circular arc orbit calculation during drilling directional well[J]. Petroleum Geology and Engineering, 2006, 20(6): 53–55. doi: 10.3969/j.issn.1673-8217.2006.06.018 |
| [11] |
刘修善, 石在虹. 给定井眼方向的修正轨道设计方法[J].
石油学报, 2002, 23(2): 72–76.
LIU Xiushan, SHI Zaihong. A new method of pathcorrection planning with the desired direction[J]. Acta Petrolei Sinica, 2002, 23(2): 72–76. doi: 10.7623/syxb-200202016 |
| [12] |
唐雪平, 苏义脑, 陈祖锡. 三维井眼轨道设计模型及其精确解[J].
石油学报, 2003, 24(4): 1–4.
TANG Xueping, SU Yinao, CHEN Zuxi. Three dimensional well-path planning model and its exact solution[J]. Acta Petrolei Sinica, 2003, 24(4): 1–4. doi: 10.7623/syxb-200304021 |
| [13] |
谢国民, 张良万, 杜远洋, 等. 定向井实用三维设计——方位比较法[J].
石油学报, 2000, 21(3): 77–82.
XIE Guomin, ZHANG Liangwan, DU Yuanyang, et al. Azimuthal comparison method:Practical 3D design of directional well[J]. Acta Petrolei Sinica, 2000, 21(3): 77–82. doi: 10.7623/syxb200003016 |
| [14] | SCHUH F J. Trajectory equations for constant tool face angle deflections[C]. SPE 23853-MS 1992. doi: 10.2118/-23853-MS. http://www.researchgate.net/publication/254523212_Trajectory_Equations_for_Constant_Tool_Face_Angle_Deflections |
| [15] | GUO Boyun, MISKA Stefan, LEE R L. Constant curvature method for planning a 3D directional well[C]. SPE 24381-MS, 1992. doi: 10.2523/24381-MS https://www.researchgate.net/publication/254523989_Constant_Curvature_Method_for_Planning_a_3-D_Directional_Well |
| [16] |
鲁港, 吴俊林, 张海明, 等. 恒装置角曲线钻井轨道计算的方法研究初步[C]. 2006年钻井基础理论与前沿技术开发新进展学术研讨会论文集. 北京: 石油工业出版社, 2007: 195-204.
LU Gang, WU Junlin, ZHANG Haiming, et al. Calculational methods of well trajectory by constant tool-fac angle curves[C]. 2006 Symposium on new progress of drilling basic theory and cutting-edge technology. Beijing: Petroleum Industry Press, 2007: 195-204. http://www.wanfangdata.com.cn/details/detail.do?_type=conference&id=6461969 |
| [17] |
方敏, 鲁港, 王立波. 恒装置角曲线的半解析计算[J].
同济大学学报(自然科学版), 2008, 36(3): 844–848.
FANG Min, LU Gang, WANG Libo. Semi-analytic computing of constant tool face angle curves[J]. Journal of Tongji University (Natural Science), 2008, 36(3): 844–848. doi: 10.3321/j.issn:0253-374X.2008.06.028 |
| [18] |
刘修善, 苏义脑. 井斜控制方案设计方法[J].
石油学报, 2015, 36(7): 890–896.
LIU Xiushan, SU Yinao. A design method of borehole deviation control scheme[J]. Acta Petrolei Sinica, 2015, 36(7): 890–896. doi: 10.7623/syxb201507014 |
| [19] |
刘修善.
井眼轨道几何学[M]. 北京: 石油工业出版社, 2006: 287-289.
LIU Xiushan. The geometry of wellbore trajectory[M]. Beijing: Petroleum Industry Press, 2006: 287-289. |
| [20] |
韩志勇.
定向钻井设计与计算[M]. 2版. 东营: 中国石油大学出版社, 2007: 304-308.
HAN Zhiyong. Design and calculation of directional drilling[M]. 2nd Edition. Dongying: China University of Petroleum Press, 2007: 304-308. |
| [21] |
王勇茗, 余世福, 周文军, 等. 长庆致密油三维水平井钻井技术研究与应用[J].
西南石油大学学报(自然科学版), 2015, 37(6): 79–84.
WANG Yongming, YU Shifu, ZHOU Wenjun, et al. Research and application of the 3D horizontal well drilling technology in Changqing Tight Oilfield[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2015, 37(6): 79–84. doi: 10.11885/j.issn.1674-5086.2013.07.19.03 |
| [22] |
姚昌宇, 王迁伟, 高志军, 等. 连续油管带底封分段压裂技术在泾河油田的应用[J].
石油钻采工艺, 2014, 36(1): 94–96.
YAO Changyu, WANG Qianwei, GAO Zhijun, et al. Application of sectional fracturing technique with coiled tubing and bottompacker in Jinghe Oilfield[J]. Oil Drilling & Production Technology, 2014, 36(1): 94–96. doi: 10.-13639/j.odpt.2014.01.025 |
| [23] |
赵金海, 施太和, 张云连, 等. 导向钻井系统导向钻进水平井段的理论与实践[J].
西南石油大学学报(自然科学版), 2001, 23(3): 30–33.
ZHAO Jinhai, SHI Taihe, ZHANG Yunlian, et al. Theoretic research and practice of steerable drilling in horizontal section[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2001, 23(3): 30–33. doi: 10.3863/j.issn.1674-5086.2001.03.009 |
| [24] |
何世明, 汤明, 熊继有, 等. 小井眼长水平段水平井摩阻扭矩控制技术[J].
西南石油大学学报(自然科学版), 2015, 37(6): 85–92.
HE Shiming, TANG Ming, XIONG Jiyou, et al. Friction and torque control technology for slim and long horizontal well[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2015, 37(6): 85–92. doi: 10.-11885/j.issn.1674-5086.2013.10.04.02 |
 2018, Vol. 40
2018, Vol. 40


