2. “油气藏地质及开发工程”国家重点实验室·西南石油大学, 四川 成都 610500;
3. 西南石油大学材料科学与工程学院, 四川 成都 610500
2. State Key Laboratary of Oil and Gas Reservoir Geology and Exploration, Southwest Petroleum University, Chengdu, Sichuan 610500, China;
3. School of Materials Science and Engineering, Southwest Petroleum University, Chengdu, Sichuan 610500, China
随着中国天然气事业及储运配套设施建设的步伐推进,盐岩储气库逐渐引起业界关注,其建设进度不断加快[1-3]。但由于盐岩本身所具有的层状分布、多泥质夹层、不溶杂质含量高等物性特征,腔体建成后在底部会堆积有一定厚度的不溶物[4-7]。相较国内,国外盐层纯度高,产生堆积物数量小,其研究也多集中在水溶建腔方面,对于堆积物的提及较少[8-9]。而国内盐层该问题较为突出,部分地区不溶物含量甚至可达50%,由此产生的影响也较为明显[10-12]。堆积物的存在,不仅浪费了相当一部分库容体积,同时也为后续注气排卤及井下作业带来了安全隐患。因此有必要对堆积物分布特征及空隙体积进行研究,以为科学评价腔体库容体积、合理布置施工处理措施及提升储库整体建设质量提供理论基础与技术借鉴。
1 堆积物样品制备与测定 1.1 样品制备由于腔底堆积物蓬松且浸满卤水,加之各方面条件限制,实现对其取样较为困难。根据相似性原理及现场工艺流程,自主设计模拟实验装置,利用腔体不同层位岩芯分别进行相同条件下的室内水溶试验以获取堆积物样品。
实验装置见图 1c,对岩芯进行中部钻孔(模拟井眼),分别下入同心圆管(模拟溶腔内、外管),在外管与孔壁间加注防护液(模拟溶腔油垫),控制溶蚀高度。在实验过程中,通过控制流量、调整油垫与管柱相对位置、改变循环方式,控制溶腔形态发展。
 |
| 图1 建腔模拟试验图 Fig. 1 Simulation test of cavity construction |
结合现场盐层与不溶物含量数据以及溶腔阶段发展动态,选用典型层位岩芯进行试验。以金坛矿区某井为例,试验选用岩芯截面约10 cm,对其进行处理打磨,使重量相等,为1.17 kg(以最小者为基准),层位及描述如表 1。
| 表1 岩芯层位及描述 Table 1 The Formation of core and its description |
水溶实验后,对形成的不溶堆积物烘干、分析,并进行分布测定。
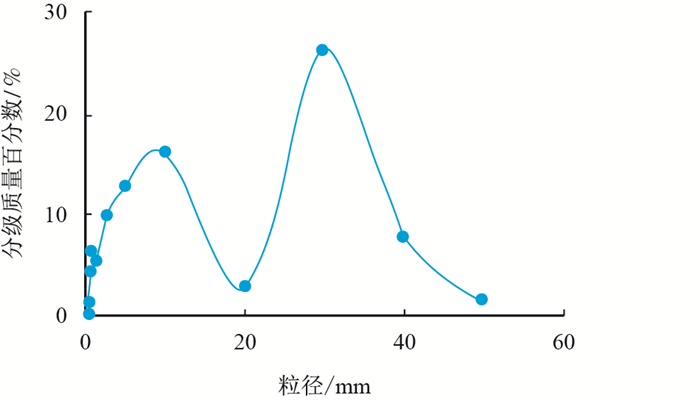
1.2 粒度分布测定粒度分布测定方法较多,其中利用筛分法既可测定粒度,还可以绘制累积粒度分布曲线[13]。对各组岩芯所获取堆积物岩样分别采用筛分法进行测定,进而累加,得到堆积物样品总体粒径数据及各分组数据(以3#岩芯样品为例)如图 2、图 3。
 |
|
图2
样品总体粒径分级质量图
Fig. 2
Quality classification of all the samples |
 |
|
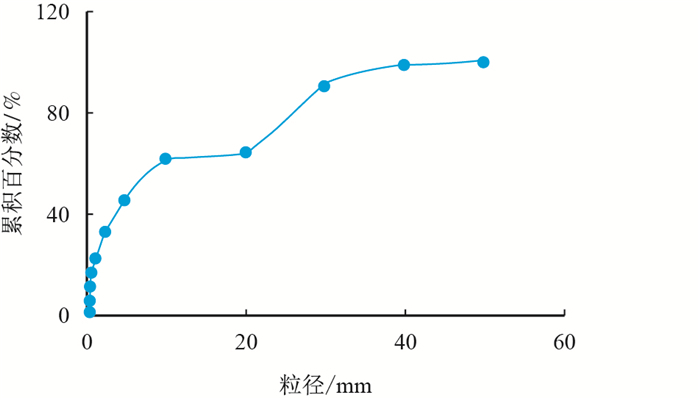
图3
样品总体粒径累积质量图
Fig. 3
Quality cumulation of all the samples |
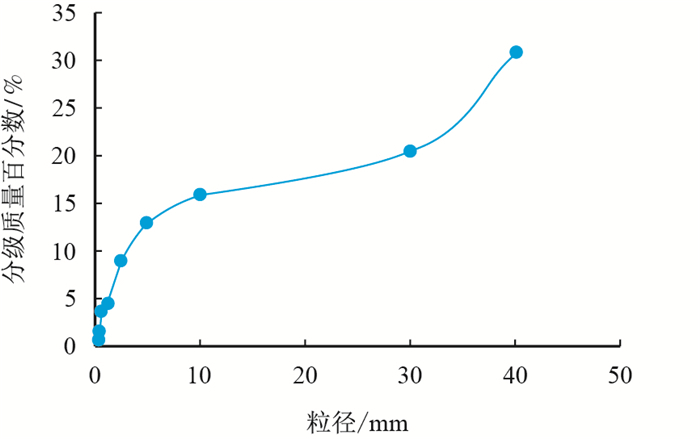
各分组所获取的堆积物样品粒度测定数据,其粒径范围及分级、累积质量百分数有所区别但差距有限,限于篇幅及数据重复性考虑,不将各组数据全部列出,仅以3#岩芯获取的不溶物岩样为例(下文处理同),测定结果如图 4、图 5。由图 4、图 5可知,样品粒径多集中在30~40 mm及10~20 mm,而各分组粒径集中范围有所差异,如3#样品粒径相对较大,有30.8%部分大于40 mm。
 |
|
图4
3#岩芯不溶物岩样粒径分级质量图
Fig. 4
Quality classification of 3# sample |
 |
|
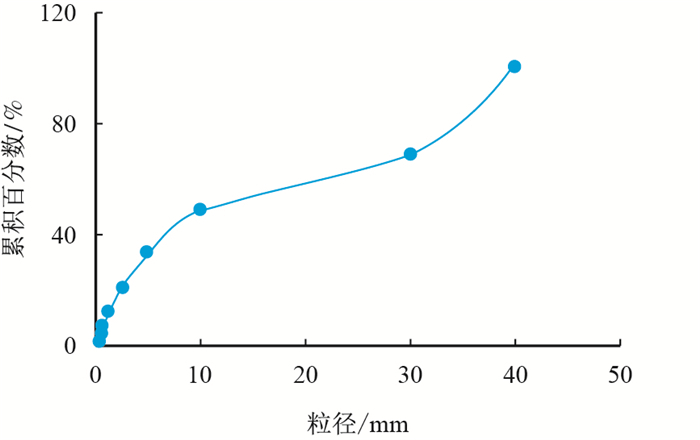
图5
3#岩芯不溶物岩样粒径累积质量图
Fig. 5
Quality cumulation of 3# sample |
为进行后续特征描述、评价,研究与之相符的分布函数。
由粒径分级质量图(图 4、图 5)可看出,样品总体符合双正态分布,但分组粒径却各有差别。鉴于分形理论近年来的发展创新及独特优势[14-16],采用分形函数对堆积物粒度特征进行描述分析。
根据Mandelbrot分形理论,多分散颗粒系统若符合分形分布,应满足[17]
| $ n_{(>x)}=C\cdot x^{-D} $ | (1) |
式中:
定义粒度
| $ m(x)=\lim {\dfrac{{ - \Delta n_{(>x)}}}{{\Delta x}}} = - \dfrac{{\textrm{d}n_{(>x)}}}{{\textrm{d}x}} $ | (2) |
整理,得
| $ m(x)=CD{x^{ - (D + 1)}} $ | (3) |
根据分布矩概念,将累积分布与分形维数联系起来,累积质量为
| $ w_{(>x)}=\int_x^{{x_{\max }}} {\rho {C_{\textrm{V}}}{x^3}} m(x)\textrm{d}x \\~~~~~~~~ = \rho {C_{\textrm{V}}}C\dfrac{D}{{3 -D}}\left (x_{\max }^{3 -D} -{x^{3 -D}}\right) $ | (4) |
式中:
注意到总累积质量
| $ {w_{\textrm{T}}}=\int_0^{{x_{\max }}} {\rho {C_{\textrm{V}}}{x^3}} m(x)\textrm{d}x = \rho {C_{\textrm{V}}}C\dfrac{D}{{3 - D}}x_{\max }^{3 - D} $ |
式中:
则大于特定粒径值的累积质量,即粒度上累积分布,可用函数表示为
| $ N(x)=\dfrac{{w_{(>x)}}}{{{w_{\textrm{T}}}}} \times 100 = 100\left[{1-{{\left (\dfrac{x}{{{x_{\max }}}}\right )}^{3-D}}} \right] $ | (6) |
式中:
令
| $ M(x){\textrm{ = 100}}{\left( {\dfrac{x}{{{x_{\max }}}}} \right)^T} $ | (7) |
式中:
将粒度值和累积颗粒数分别取对数,进行分布拟合。3#岩芯不溶物岩样及样品总体拟合结果图如图 6、图 7。
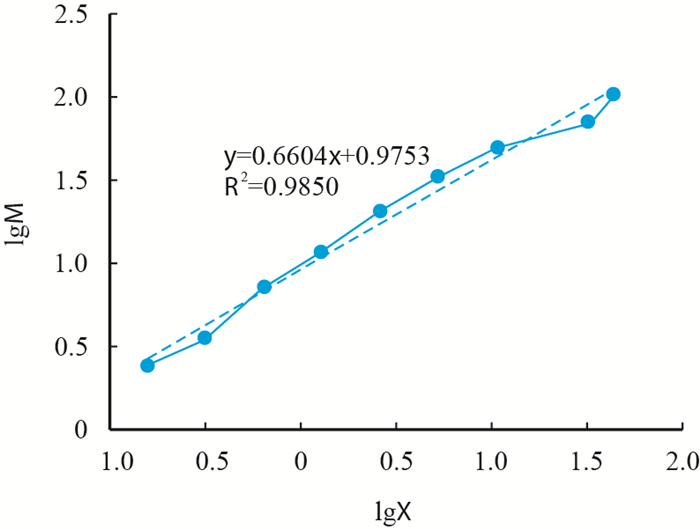 |
| 图6 3#岩芯不溶物岩样分布拟合图 Fig. 6 The fitting figure of of 3# sample |
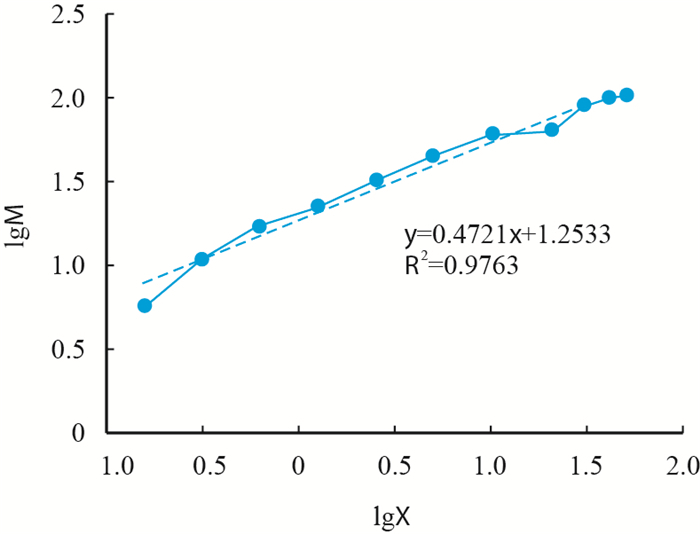 |
| 图7 样品总体分布拟合图 Fig. 7 The fitting figure of all the samples |
对比实际数据线(实线)与拟合趋势线(虚线)可知,拟合偏差
| 表2 各组拟合分形维数计算数据表 Table 2 Calculation data on fractal dimension of each group fitting |
根据计算结果,对比样品粒径数据可知,分形维数越大,颗粒集中性和均匀程度越差;相反,分形维数越小时,颗粒均匀性越好,颗粒尺寸也越集中。
2.3 分形维数与溶解度关系由于腔底堆积物是各岩层段不溶物沉积累加的结果,为避免采用某单一特征参数表征其分布特性,并考虑颗粒级配产生的协同效应[18],分析分形维数与溶解度数据之间关系。岩芯各层分形维数和溶解度数据如表 3。
| 表3 各组拟合分形维数计算数据表 Table 3 Calculation data on fractal dimension of each group fitting |
对分形维数与溶解度进行拟合,结果如图 8。由图 8可知,不溶物分形维数与溶解度呈线性相关。
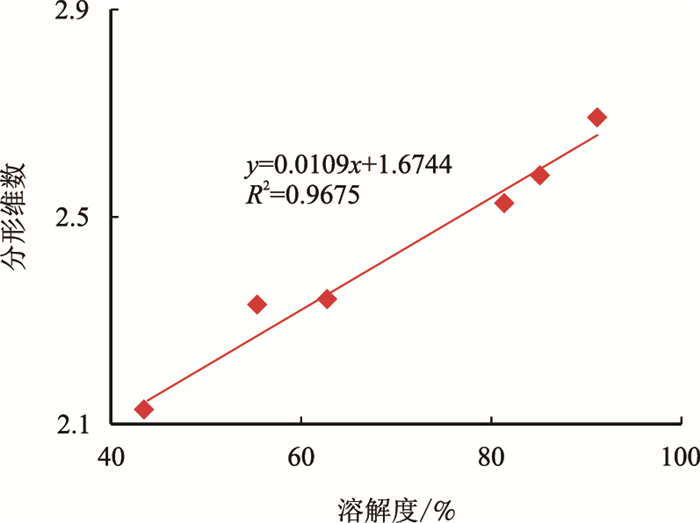 |
| 图8 不溶物岩样分形维数与溶解度关系图 Fig. 8 Relationship between the fractal dimension and the solubility of sample |
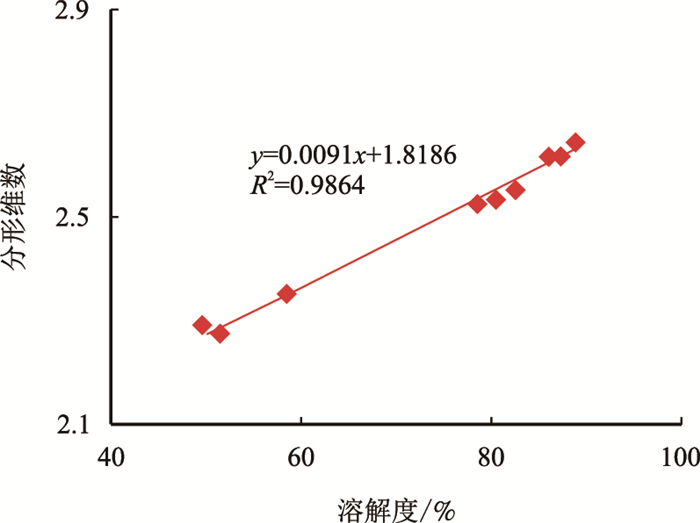
为对两者关系的独立性做进一步分析研究,并验证与粒径组别范围的无关性,将5组样品不溶物中任意两组进行质量组合累加,得到10个新的组合,计算各组分形维数及溶解度并进行拟合(图 9)。
 |
|
图9
岩样累加组合分形维数与溶解度关系图
Fig. 9
Relationship between the fractal dimension and solubility of samples |
由图 9可看出,不溶物分形维数与溶解度成线性关系,且关系曲线可描述为
| $ y=0.0091x+1.8186 $ |
式中:
相关度在0.98以上。由此,堆积物分布分形维数可由其溶解度数据计算得到,且不溶物溶解度越大,形成的堆积物分形维数越大,亦即颗粒尺寸越不均匀,即堆积物分布特征可用分形函数进行表征。
3 空隙体积数值研究 3.1 空隙率数值模拟受实验条件及因素限制,采用离散元仿真软件模拟不溶物堆积过程,并计算堆积空隙率。根据前述实验测定的堆积物分布结果,利用Origin拟合得出其分布特征参数,采用三维离散元方法模拟其堆积过程,并对模拟结果进行数值分析,从而得到各组不溶物岩样及总体堆积空隙率,结果如表 4。
| 表4 不溶物岩样及总体堆积空隙率模拟数据表 Table 4 Simulated data on pore volume of sample |
根据相关研究[19],随着颗粒粒度分形维数增加,其堆积空隙率线性减小,即其堆积结构越好,填充能力增强。据此对不溶物岩样数据进行空隙率与分形维数关系验证,验证结果如图 10。
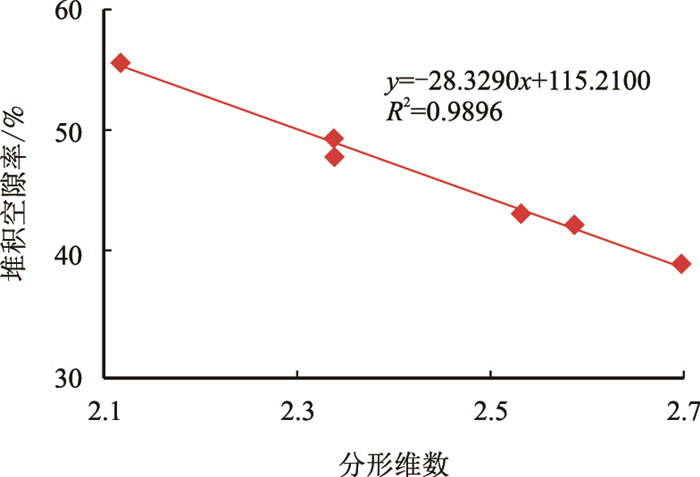 |
| 图10 不溶物岩样分形维数与空隙率关系图 Fig. 10 Relationship between the fractal dimension and pore volume of sample |
由图 10可知,堆积物空隙率与其粒度分形维数成线性关系,且随分形维数增加,堆积空隙率下降。分形维数越大即颗粒越分散,粒级越多,这时颗粒间会互相填隙,空隙率从而变小。
为进一步探索堆积空隙率与分形维数间线性关系的独立性,研究相同分形维数不同粒度范围的颗粒堆积空隙率变化。所用各组样品颗粒分布如表 5。
| 表5 同分形维数、不同粒度范围的样品组数据(D=2.558 4) Table 5 Data of combination with same fractal dimension and the different particle size range (D=2.558 4) |
采用同样处理方法,模拟得到各组堆积空隙率值,如表 6。
| 表6 空隙率模拟数据表 Table 6 Simulated data on pore volume of sample |
由表 6可知,分形维数相同粒度范围不同时,空隙率值也基本一致,即堆积空隙率与粒度范围无关,取决于其分形维数即颗粒分布特征。
4 空隙体积模型 4.1 可压缩堆积模型腔底堆积物在形成过程中,颗粒间是相互影响的,小颗粒的存在会使大颗粒无法达到最紧密堆积,即松动效应;而大颗粒的存在会使小颗粒在靠近大颗粒壁面附近堆积,不能最密实,即附壁效应。同时,颗粒与颗粒间还存在互相压实的作用。
de Larrard等在考虑上述影响的基础上,为克服一般模型单一粒径假设的局限性,提出了可压缩堆积模型[20-22]。根据该研究,在多粒级颗粒堆积系统中,假设第
| $ \left\{ \begin{array}{l} {\gamma _i} = {\beta _i}/\left[ {1 - \sum\limits_{j = 1}^{i - 1} {\left[ {1 - {\beta _i} + {b_{ij}}{\beta _i}\left( {1 - 1/{\beta _j}} \right)} \right]{y_j} - \sum\limits_{j = i + 1}^n {\left( {1 - {a_{ij}}{\beta _i}/{\beta _j}} \right){y_j}} } } \right]\\ \gamma {\rm{ = }}\min \left( {{\gamma _i}} \right)\\ k = \frac{{{u_i}/{\beta _i}}}{{1/\mathit{\Phi - 1/}\gamma }} \end{array} \right. $ | (8) |
式中:
应用时,剩余堆积密实度可采用相关文献[23-24]所得数据。根据Larrard的试验校准研究,压实指数在简单倾倒形式堆积时可取4.1,盐岩不溶物在堆积过程中主要受重力沉降作用并在此基础上压实形成[25-27],故按该情况处理。
由此,在确定堆积物各粒级尺寸及质量分数后,通过为各粒级剩余堆积密实度取值,求出系统虚拟堆积密实度,进而根据压实指数公式求得系统实际堆积密实度,最终确定堆积空隙率。
4.3 计算模型上述堆积空隙率计算方法所针对的是盐岩溶腔各层位,要计算整个腔体的堆积物空隙率,需对各分层数据进行累加求解。假设共
| $ {D_m}{\textrm{ = }}\sum\nolimits_{i = 1}^n {(1 - {x_i}) \cdot {h_i} \cdot \pi } {l_i}^2 $ | (9) |
对于溶腔各层位,溶解度可通过岩性测井数据转换求解,进而求得各层位堆积物空隙率,再进行累加求解,即可得到腔体总体空隙率,表达式如下
| $ \phi {\textrm{ = }}\dfrac{{\sum\nolimits_{i = 1}^n {{\phi _i} \cdot \lambda \cdot (1 - {x_i}){h_i} \cdot \pi } {l_i}^2}}{{{D_m} \cdot \lambda }}\\~~~~~= \dfrac{{\sum\nolimits_{i = 1}^n {{\phi _i} \cdot (1 - {x_i}){h_i} \cdot \pi } {l_i}^2}}{{{D_m}}} $ | (10) |
式中:
由此,利用相关数据可对溶腔现场腔底堆积物空隙体积进行计算。
4.4 应用实例实例井某溶腔段腔体测井解释数据如表 7。
| 表7 实例井某溶腔阶段腔体层位测井解释数据表 Table 7 Logging data of cavity layers in sample well of certain stage |
采用可压缩堆积模型计算堆积空隙率,需首先确定堆积物各粒级组成,受条件限制,无法获取盐岩储库腔底不溶物具体颗粒组成。但根据前述分形研究结论,在分形维数相同时,空隙率值与粒度范围关系很小。故可根据上述基础数据,确定各层堆积后的分形维数,并选定50 mm(此时筛下累积质量为100%)作为最大粒径,以此确定各盐岩层位溶解后粒径分布,具体数据如表 8。
| 表8 各盐岩层位堆积粒度分布推导数据表 Table 8 Derived data of size distribution of all the layers |
采用前述计算方法,对以上数据进行实例井计算,该溶腔阶段腔体堆积物空隙率计算结果如表 9。
| 表9 实例井某溶腔阶段堆积物空隙率计算数据表 Table 9 alculation data on pore volume of deposits in sample well of certain stage |
根据计算结果,实例井某溶腔阶段堆积物总体空隙率为48.23%,现场通过后续声纳测腔分析得出的空隙率44.26%,本计算方法结果值稍大,但偏差不超过8.97%,故计算方法可行。
5 结论(1) 通过室内溶腔实验获取了盐岩储气库腔底堆积物样品,采用筛分法对其粒度分布进行了实验测定,从而得到了样品粒径分级质量数据及总体累积质量数据。
(2) 腔底堆积物粒度分布可用分形函数进行表征,且分形维数作为特征参量能很好地描述颗粒分布的集中性与均匀程度。
| [1] |
杨春和, 梁卫国, 魏东吼. 中国盐岩能源地下储存可行性研究[J].
岩石力学与工程学报, 2005, 24(24): 4409–4417.
YANG Chunhe, LIANG Weiguo, WEI Donghou. Investigation on possibility of energy storage in salt rock in China[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(24): 4409–4417. doi: 10.3321/j.issn:1000-6915.2005.24.002 |
| [2] |
丁国生, 李春, 王皆明, 等. 中国地下储气库现状及技术发展方向[J].
天然气工业, 2015, 35(11): 107–112.
DING Guosheng, LI Chun, WANG Jieming, et al. The status quo and technical development direction of underground gas storages in China[J]. Natural Gas Industry, 2015, 35(11): 107–112. doi: 10.3387/j.issn.1000-0976.-2015.11.017 |
| [3] |
徐博, 张刚雄, 张愉, 等. 我国地下储气库市场化运作模式的基本构想[J].
天然气工业, 2015, 35(11): 102–106.
XU Bo, ZHANG Gangxiong, ZHANG Yu, et al. The basic conception of UGS market driven operation modes in China[J]. Natural Gas Industry, 2015, 35(11): 102–106. doi: 10.3387/j.issn.1000-0976.2015.11.016 |
| [4] |
完颜祺琪, 冉莉娜, 韩冰洁, 等. 盐穴地下储气库库址地质评价与建库区优选[J].
西南石油大学学报(自然科学版), 2015, 37(1): 57–64.
WANYAN Qiqi, RAN Lina, HAN Bingjie, et al. Study on site selection and evaluation of underground gas storage in salt cavern[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2015, 37(1): 57–64. doi: 10.11885/j.issn.1674-5086.2013.05.29.02 |
| [5] |
李银平, 葛鑫博, 王兵武, 等. 盐穴地下储气库水溶造腔管柱的动力稳定性试验研究[J].
天然气工业, 2016, 36(7): 81–87.
LI Yinping, GE Xinbo, WANG Bingwu, et al. Dynamic stability tests on tubing string for solution mining of a salt cavern UGS[J]. Natural Gas Industry, 2016, 36(7): 81–87. doi: 10.3787/j.issn.1000-0976.2016.07.012 |
| [6] |
王东旭, 马小明, 伍勇, 等. 气藏型地下储气库的库存量曲线特征与达容规律[J].
天然气工业, 2015, 35(1): 115–119.
WANG Dongxu, MA Xiaoming, WU Yong, et al. Curve characteristics and rules of the storage capacity establishment of a reservoir-type underground gas storage (UGS)[J]. Natural Gas Industry, 2015, 35(1): 115–119. doi: 10.3787/j.issn.1000-0976.2015.01.016 |
| [7] |
胥洪成, 王皆明, 屈平, 等. 复杂地质条件气藏储气库库容参数的预测方法[J].
天然气工业, 2015, 35(1): 103–108.
XU Hongcheng, WANG Jieming, QU Ping, et al. A prediction model of storage capacity parameters of a geologically-complicated reservoir-type underground gas storage (UGS)[J]. Natural Gas Industry, 2015, 35(1): 103–108. doi: 10.3787/j.issn.1000-0976.2015.01.014 |
| [8] | YU L, LIU J. Stability of interbed for salt cavern gas storage in solution mining considering cusp displacement catastrophe theory[J]. Petroleum, 2015, 1(1): 82–90. doi: 10.1016/j.petlm.2015.03.006 |
| [9] | XIONG J, HUANG X, MA H. Gas leakage mechanism in bedded salt rock storage cavern considering damaged interface[J]. Petroleum, 2015, 1(4): 366–372. doi: 10.-1016/j.petlm.2015.10.008 |
| [10] |
魏东吼. 金坛盐穴地下储气库造腔工程技术研究[D]. 青岛: 中国石油大学(华东), 2008.
WEI Donghou. Engineering technology of cavity making in Jintan salt caverns underground gas storage[D]. Qingdao: China University of Petroleum (East China), 2008. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1363268 |
| [11] |
李银平, 杨春和, 罗超文, 等. 湖北省云应地区盐岩溶腔型地下能源储库密闭性研究[J].
岩石力学与工程学报, 2007, 26(12): 2430–2436.
LI Yinping, YANG Chunhe, LUO Chaowen, et al. Study on sealability of underground energy storage in deep salt formation in YunYing area, HuBei Province[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(12): 2430–2436. doi: 10.3321/j.issn:1000-6915.2007.12.007 |
| [12] |
施锡林, 李银平, 杨春和, 等. 盐穴储气库水溶造腔夹层垮塌力学机制研究[J].
岩土力学, 2009, 30(12): 3615–3620.
SHI Xilin, LI Yinping, YANG Chunhe, et al. Research on mechanical mechanism of interlayer collapse in solution mining for salt cavern gas storage[J]. Rock and Soil Mechanics, 2009, 30(12): 3615–3620. doi: 10.16285/j.rsm.-2009.12.006 |
| [13] |
王元磊. 粒度趋势分析方法的研究进展[J].
山东师范大学学报(自然科学版), 2008, 23(2): 81–84.
WANG Yuanlei. Research progress on analysis of grain size trends[J]. Journal of Shandong Normal University (Natural Science), 2008, 23(2): 81–84. |
| [14] |
蔡建超, 胡祥云.
多孔介质分形理论与应用[M]. 北京: 科学出版社, 2016.
CAI Jianchao, HU Xiangyun. Fractal theory in porous media and its applications[M]. Beijing: Science Press, 2016. |
| [15] |
朱华, 姬翠翠.
分形理论及其应用[M]. 北京: 科学出版社, 2011.
ZHU Hua, JI Cuicui. Fractal theory and its applications[M]. Beijing: Science Press, 2011. |
| [16] |
舒志乐, 刘新荣, 刘保县, 等. 基于分形理论的土石混合体强度特征研究[J].
岩石力学与工程学报, 2009, 28(S1): 2652–2656.
SHU Zhile, LIU Xinrong, LIU Baoxian, et al. Study of strength properties of earth-rock aggregate based on fractures[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(S1): 2652–2656. |
| [17] | MANDELBROT B. The Fractal Geometry of Nature[M]. San Francisco: W. H. Freeman, 1982. |
| [18] |
韩涛. 矿渣粉粒度分布特征及其对水泥强度的影响[D]. 西安: 西安建筑科技大学, 2004.
HAN Tao. The distribute characteristic of slag powder and the influence on strength of cement[D]. Xi'an: Xi'an University of Architecture and Technology, 2004 http://cdmd.cnki.com.cn/Article/CDMD-10703-2004072607.htm |
| [19] |
吴成宝, 段百涛. 中空玻璃微珠粒度分布分形特征及其与空隙率关系的研究[J].
中国粉体技术, 2008, 14(1): 16–19.
WU Chengbao, DUAN Baitao. Study on relationship between fractal character of particle size distribution and voidage of hollow glass beads[J]. China Powder Science and Technology, 2008, 14(1): 16–19. doi: 10.13732/j.issn.-1008-5548.2008.01.003 |
| [20] | de LARRARD F, SEDRAN T. Optimization of ultra-highperformance concrete by the use of a packing model[J]. Cement and Concrete Research, 1994, 24(6): 997–1009. doi: 10.1016/0008-8846(94)90022-1 |
| [21] |
陈瑾祥. 基于可压缩堆积模型的绿色混凝土材料性能研究[D]. 深圳: 深圳大学, 2015.
CHEN Jinxiang. Compressible packing model based study of green concrete[D]. Shenzhen: Shenzhen University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10590-1015413843.htm |
| [22] |
聂晶. 基于可压缩堆积模型的水泥基复合材料性能研究[D]. 长沙: 湖南大学, 2008.
NIE Jing. Study on performance of cement-based composite materials based on compressible packing model[D]. Changsha: Hunan University, 2008. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1260820 |
| [23] |
弗朗索瓦·德拉拉尔. 混凝土混合料的配合[M]. 廖欣, 叶枝荣译. 北京: 化学工业出版社, 2004.
de LARRARD F. Concrete mixture proportioning[M]. translated by LIAO Xin, YE Zhirong. Beijing: Chemical Industry Press, 2004. |
| [24] |
周卫峰, 赵可, 王德群, 等. 水泥稳定碎石混合料配合比的优化[J].
长安大学学报(自然科学版), 2006, 26(1): 24–28.
ZHOU Weifeng, ZHAO Ke, WANG Dequn, et al. Mix ratio optimization design of cement stabilized macadam based on static pressure method and vibration method[J]. Journal of Chang'an University (Natural Science Edition), 2006, 26(1): 24–28. |
| [25] |
班凡生. 盐穴储气库水溶建腔优化设计研究[D]. 廊坊: 中国科学院渗流流体力学研究所, 2008.
BAN Fansheng. Study on optimization design of solution mining cavern for underground gas storage[D]. Langfang: Institute of Porous Flow and Fluid Mechanics, Chinese Academy of Sciences, 2008. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1622979 |
| [26] |
汪蓬勃. 基于巨厚盐膏层以及碳酸盐储层的钻井技术研究[D]. 成都: 西南石油大学, 2015.
WANG Pengbo. Research on the drilling technique based on the layer of thick salt paste and carbonate reservoir[D]. Chengdu: Southwest Petroleum University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10615-1016098399.htm |
| [27] |
赵志成. 盐岩储气库水溶建腔流体输运理论及溶腔形态变化规律研究[D]. 廊坊: 中国科学院渗流流体力学研究所, 2008.
ZHAO Zhicheng. Theory of fluid transportation and configuration development in solution mining cavern for underground gas storage[D]. Langfang: Institute of Porous Flow and Fluid Mechanics, Chinese Academy of Sciences, 2008. http://cdmd.cnki.com.cn/Article/CDMD-80027-2003112374.htm |
 2018, Vol. 40
2018, Vol. 40


