对于注水开发油田开发指标预测,水驱曲线被国内外广泛应用,相关理论日臻完善,经典水驱曲线已列入石油行业计算标准。但对于注气驱油藏的动态还没有成熟的油藏工程方法进行评价[1],常用油藏数值模拟或实验测试来评价油藏开发效果[2-5],而且注气混相驱的研究重点在驱替机理和混相压力方面[6-7]。在借鉴甲型水驱特征曲线基础上,杨国绪、顾乔元、袁士宝、童凯军等[8-11]提出了累积产气与累积产油量关系的气驱曲线,并用于气顶油藏、凝析气藏和稠油油藏的开发指标预测。李菊花等[12]建立了水气交替驱特征曲线关系式。孙雷等[13]建立了混相驱拟含气率与采出程度图版。但是,上述研究存在以下缺陷:(1)未对混相驱渗流特征进行描述;(2)气驱特征曲线为累积产气和累积产油关系,而地层中实际渗流的流体为注入气和被驱替原油;(3)水驱特征曲线是累积产水和累积产油关系且在含水率达到50%以后才适用[14],类比建立的气驱特征曲线在注气开发中后期才能使用;(4)不便用于阶段产量预测。
本文在分析油藏注气开发驱替过程基础上,分别描述混相驱替和非混相驱替油气渗流特征。在稳定渗流理论基础上,推导出地层中实际渗流流体注入气和被驱替原油关系式,命名为新型气驱特征曲线,并说明了该曲线的适用条件。应用实例,研究了注采井网和驱替机理变化对气驱曲线形态特征的影响,同时该曲线在已知注气量条件下,可实现长期以及阶段产量预测且在注气开发较早阶段便可应用。该曲线计算简便可行,对注气驱油藏的开发指标预测具有一定的指导意义。
1 新型气驱特征曲线推导 1.1 假设条件(1) 地层温度恒定;(2)忽略毛管力作用;(3)注气保压开发油藏;(4)注入气无漏失或漏失量可忽略不计;(5)天然水体能量较弱油藏;(6)在半对数坐标系中
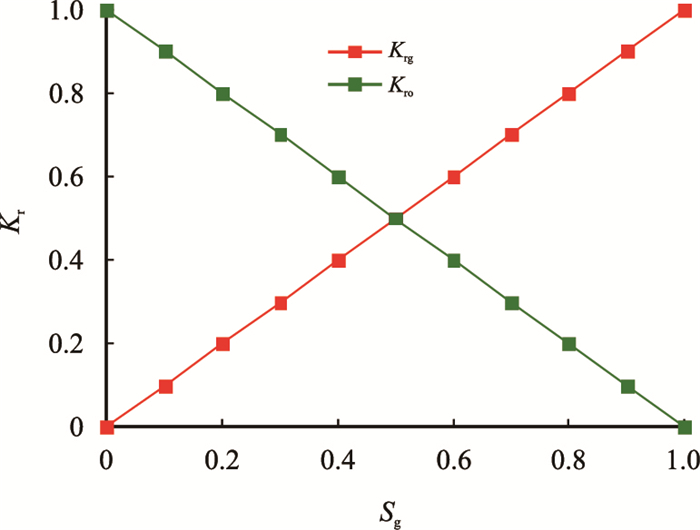
注气驱油藏开发过程中,地层中实际参与渗流的流体为注入气和被驱替地层油,因此将描述注入气和地层油的渗流规律。分析注气驱替过程发现,混相驱替过程中同时存在注入气与被驱替原油的混相驱和非混相驱渗流。对于混相驱替,油气相对渗透率与其饱和度成正比关系[15],见式(1),关系曲线见图 1。
| $ \begin{equation} \dfrac{{{K_{\rm{o}}}}}{{{K_{\rm{g}}}}} = \dfrac{{{S_{\rm{o}}}}}{{{S_{\rm{g}}}}} \end{equation} $ | (1) |
 |
|
图1
混相驱油气相对渗透率与含气饱和度关系曲线
Fig. 1
Gas and oil relative permeability curves as a function of |
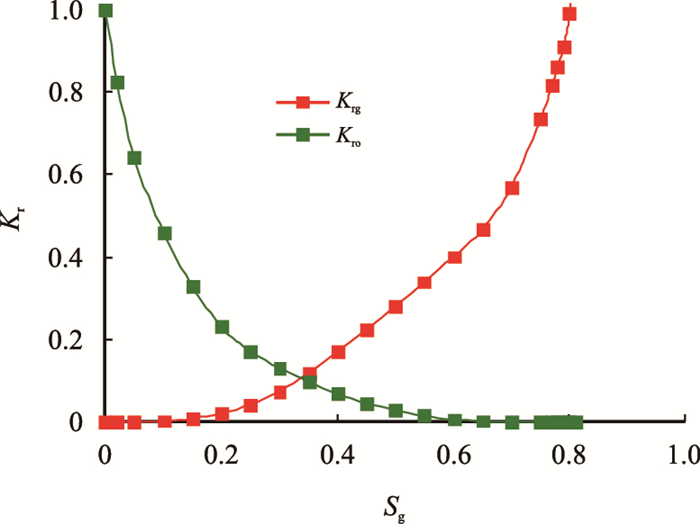
对于非混相驱替,在油、气两相渗流的条件下,油、气相对渗透率比与含气饱和度关系,采用常规指数形式表示,见式(2)[16]。选取西非深水M油藏岩芯,测试油气在非混相条件下(实验压力小于最小混相压力)相渗数据,油气相渗曲线见图 2。
| $ \begin{equation} \dfrac{{{K_{{\rm{rg}}}}}}{{{K_{{\rm{ro}}}}}} = d{{\rm{e}}^{ - c{S_{\rm{g}}}}} \end{equation} $ | (2) |
 |
|
图2
非混相驱油气相对渗透率与含气饱和度关系曲线
Fig. 2
Gas and oil relative permeability curves as a function of |
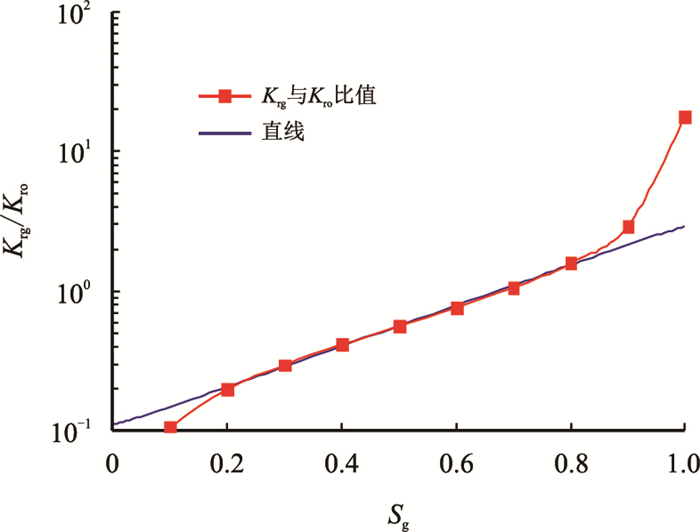
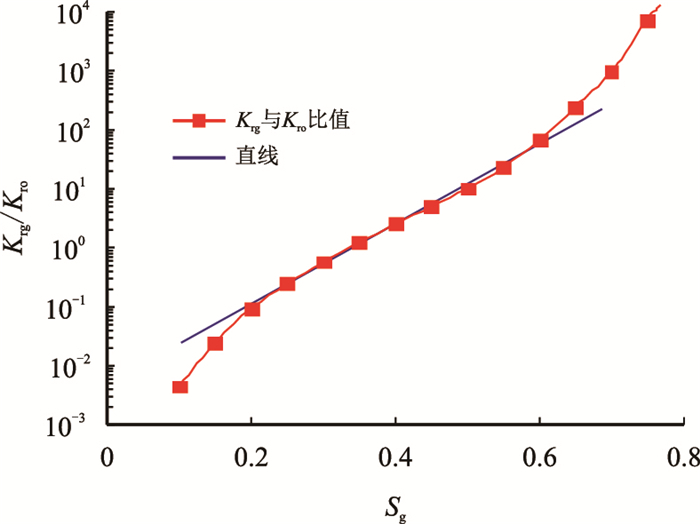
分别作出混相驱和非混相油、气渗相对透率比与含气饱和度半对数关系曲线(见图 3~图 4),从图中可以看出,在混相驱替过程中,含气饱和度在0.2~0.8时,油、气相对渗透率比对数与含气饱和度存在线性关系;在非混相驱驱替过程中,含气饱和度在0.2~0.6时,油、气相对渗透率比的对数与含气饱和度存在线性关系[16]。因此,当注气到一定阶段,油、气相对渗透率比与含气饱和度关系可用式(2)统一描述。
 |
|
图3
混相驱油气渗透率比与含气饱和度半对数关系曲线
Fig. 3
Gas/oil relative permeability ratio plotted as a function of |
 |
|
图4
非混相驱油气渗透率比与含气饱和度半对数关系曲线
Fig. 4
Gas/oil relative permeability ratio plotted as a function of |
现取油藏中与注入气接触的原油微单元,微单元总气量包括在油藏原油溶解气和以注入气形式流到储层中的气体,可以用式(3)表示。
| $ \begin{equation} {Q_{\rm{g}}} = {Q_{{\rm{sg}}}} + {Q_{{\rm{injg}}}} \end{equation} $ | (3) |
当注气量远大于溶解气量时,总气量近似等于注气量。在忽略毛管力影响时,储层出现气驱的稳定渗流条件下,由平面径向流公式,日产油量、日注气量与流体黏度、体积系数和相对渗透率之间存在如下关系[17]
| $ \begin{equation} \dfrac{{{Q_{{\rm{injg}}}}}}{{{Q_{\rm{o}}}}} = \dfrac{{{\mu _{\rm{o}}}{B_{\rm{o}}}}}{{{\mu _{\rm{g}}}{B_{\rm{g}}}}}\dfrac{{{K_{{\rm{rg}}}}}}{{{K_{{\rm{ro}}}}}} \end{equation} $ | (4) |
油田的累积注气量,可由下式来表示
| $ \begin{equation} {G_{\rm{i}}} = \int_0^t {{Q_{{\rm{injg}}}}} {\rm{d}}t \end{equation} $ | (5) |
由式(2)~式(5)得
| $\begin{equation} {G_{\rm{i}}} = \dfrac{{{\mu _{\rm{o}}}{B_{\rm{o}}}}}{{d{\mu _{\rm{g}}}{B_{\rm{g}}}}}\int_0^t {{Q_{\rm{o}}}{{\rm{e}}^{c{S_{\rm{g}}}}}} {\rm{d}}t \end{equation} $ | (6) |
油田累积产油量可表示为
| $ \begin{equation} {N_{\rm{p}}} = \dfrac{{100Ah\phi {S_{\rm{g}}}}}{{{B_{\rm{o}}}}} \text{,其中:}{S_{\rm{g}}} = \dfrac{{{N_{\rm{p}}}{B_{\rm{o}}}}}{{100Ah\phi }} \end{equation} $ | (7) |
由油田瞬时产油量与累积产油量的关系可得
| $ \begin{equation} {Q_{\rm{o}}} = \dfrac{{{\rm{d}}{N_{\rm{p}}}}}{{{\rm{d}}t}} = 100Ah\phi \dfrac{1}{{{B_{\rm{o}}}}}\dfrac{{{\rm{d}}{S_{\rm{g}}}}}{{{\rm{d}}t}} \end{equation} $ | (8) |
将式(8)代入式(6)积分整理可得
| $ \begin{equation} {G_{\rm{i}}} = \dfrac{N}{{1 - {S_{{\rm{wc}}}}}}\dfrac{{{\mu _{\rm{o}}}{B_{\rm{o}}}}}{{dc{\mu _{\rm{g}}}{B_{\rm{g}}}}}({{\rm{e}}^{c{S_{\rm{g}}}}} - c) \end{equation} $ | (9) |
将式(9)两边取常用对数可得新型气驱特征曲线方程为
| $ \begin{equation} \ln ({G_{\rm{i}}} + cD) = a + b{N_{\rm{p}}} \end{equation} $ | (10) |
式中:
| $ D = \dfrac{{N{\mu _{\rm{o}}}{B_{\rm{o}}}}}{{dc{\mu _{\rm{g}}}{B_{\rm{g}}}(1 - {S_{{\rm{wc}}}})}}, a = \ln D, b = \dfrac{{c{B_{\rm{o}}}}}{{100Ah\phi }} $ |
由式(10)可以看出,累积产气量必须加上一个常数,才能与累积产油量在半对数坐标上成一完整的直线关系。但是,随着油田的持续生产,累积注气量的连续增加,
| $ \begin{equation} \ln {G_{\rm{i}}} = a + b{N_{\rm{p}}} \end{equation} $ | (11) |
建立的新型气驱特征曲线适用于天然水体能量较弱、注气保压开发的油藏,并且要求油藏基于一套井网、一套工作制度和一种驱替机理,但在实际开发过程中,油藏一般不会采用一套模式一成不变的生产,大多数都需要调整井网和工作制度以改善油藏的开发效果,同时也可能伴随着驱替机理的变化,上述因素都会影响气驱特征曲线的形态。因此,在生产早期阶段,气驱特征曲线开始适用后,可用于阶段短期预测;对于中长期的产量预测要待注气达到均一稳定状态后才可使用。以下将结合实例分别进行分析。
2 实例分析 2.1 实例1M油藏为西非深水A油田的主力油藏之一,水深1 300~1 450 m,储层发育为深水海底扇朵叶复合沉积,为层状构造边水油藏。流体为纵向具有明显组分梯度的高挥发性油。原油地面密度平均为0.797 g/cm
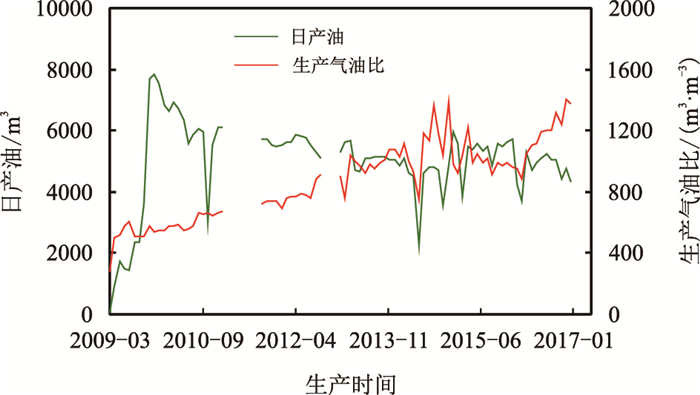 |
| 图5 M油藏日产油、气油比动态曲线(2009-2017) Fig. 5 Daily oil production and gas oil ratio curve of M reservoir(2009-2017) |
用M油藏实际生产动态数据绘制气驱特征曲线,见图 6。依据驱替机理、井网以及工作制度是否发生变化,将M油藏2009—2017年生产历程分为3个阶段,各阶段气驱特征曲线拟合系数见表 1。从图 6可以看出,当油藏采出程度达到一定阶段后,累注气量与累产油半对数呈现线性关系,即阶段Ⅰ;当油藏中有生产井注气突破或增加生产井,气驱特征曲线的系数会发生一定程度的变化,见阶段Ⅱ,Ⅲ。从气驱曲线拟合系数来看,阶段Ⅰ与Ⅱ、Ⅲ阶段斜率
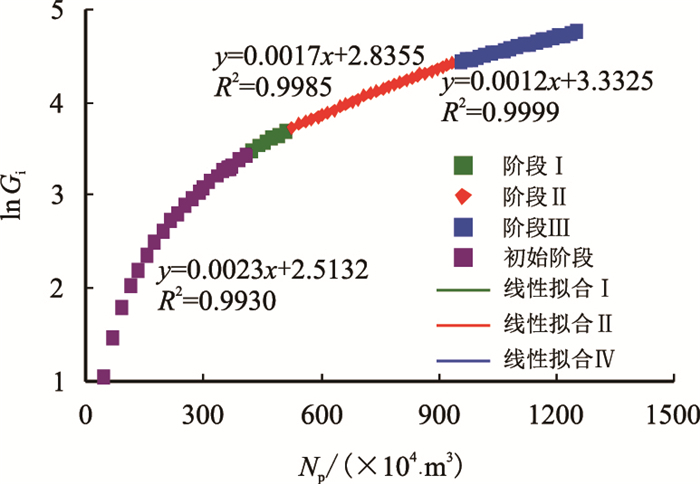 |
| 图6 M油藏累注气量-累产油半对数关系曲线 Fig. 6 Semi-logarithmic relationship curve between cumulative oil production and cumulative gas injection in M reservoir |
| 表1 M油藏气驱特征曲线拟合统计表 Table 1 Fit effect statistic of gas drive characteristics curve in M reservoir |
应用新型气驱特征曲线,阶段Ⅱ内2012年6月—2013年1月拟合结果,应用公式(11)对后续两年累产油指标进行预测,实际累积产油与理论计算结果见图 7,可以看出,2013年2月—2014年10月预测累产油量与实际累产油平均相对误差为0.66%,最大的相对误差为1.86%。总体上看,新型气驱特征曲线利用阶段历史数据拟合,预测同阶段累积产油精度高,具有较高的应用价值。
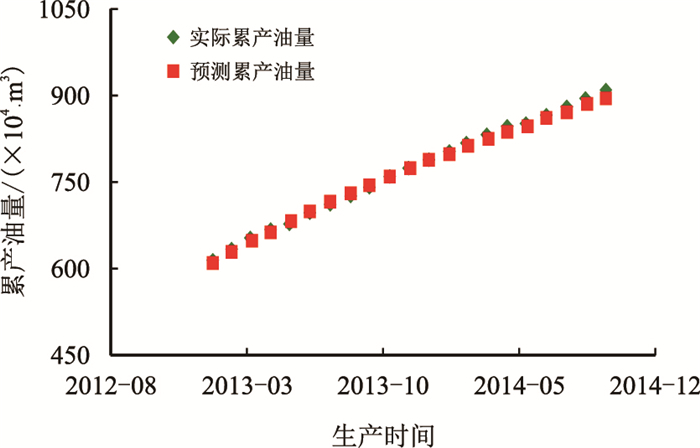 |
| 图7 M油藏实际累产油量与预测累产油量对比曲线 Fig. 7 Cumulative oil production comparison curve between actual and forecasting in M reservoir |
Pickton油田[18-20]位于美国东德克萨斯盆地,储层顶深为2 220 m,净油柱高度为69 m,海相碳酸盐构造岩性油藏,流体为挥发油,纵向流体性质有差异,原油地面密度为0.797 g/cm
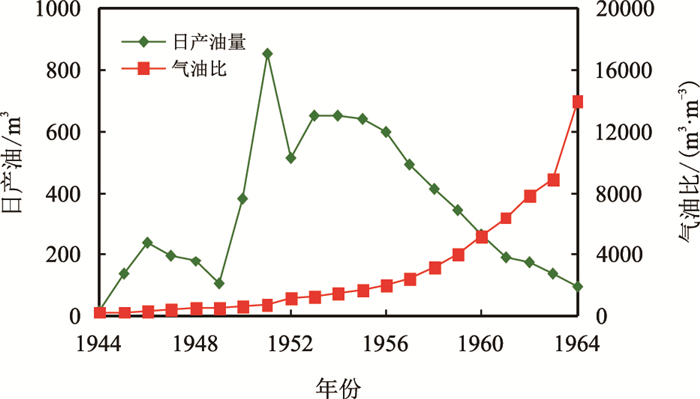 |
| 图8 Pickton油田日产油与气油比曲线(1944—1964) Fig. 8 Dailyoil production and gas oil ratio curve of Pickton Oilfield(1944-1964) |
现选取1954—1957年实际生产数据,用新型气驱特征曲线进行拟合,拟合参数
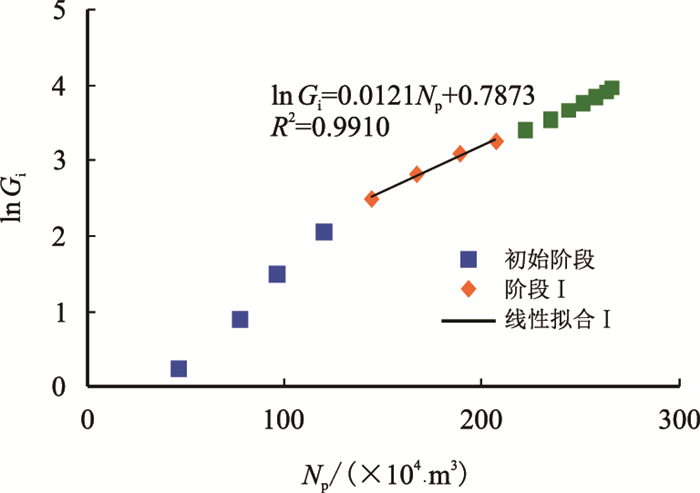 |
| 图9 Pickton油田累注气量-累产油半对数关系曲线 Fig. 9 Semi-logarithmic relationship curve between cumulative oil production and cumulative gas injection in Pickton Oilfield |
应用新型气驱特征曲线,1954—1957年实际生产数据拟合结果对1957—1964年累产油指标进行预测,累积产油的实际数据与理论计算结果见图 10,可以看出,1957—1964年预测结果的平均相对误差为1.70%,最大的相对误差为2.27%。总体上看,新型气驱特征曲线利用历史数据拟合后,预测油田累积产油精度高,具有较高的应用价值。
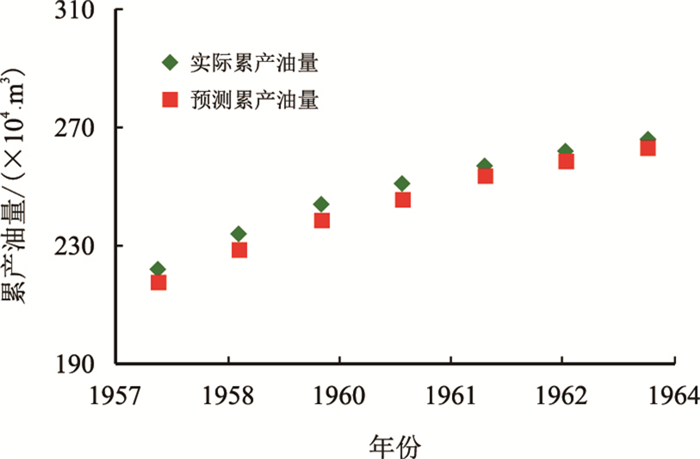 |
| 图10 Pickton油田实际累产油量与预测累产油量对比曲线 Fig. 10 Cumulative oil production comparison curve between actual and forecasting in Pickton Oilfield |
(1) 注气混相驱油藏,含气饱和度在0.2
(2) 注气驱油藏地层中实际参与渗流的流体为注入气和被驱替地层油,而不是传统认为的产出气和被驱替地层油。
(3) 基于稳定渗流理论,建立了新型气驱特征曲线关系式,即累积注气量和累积产油半对数关系式。实例分析表明,井网加密、驱替机理变化等因素都会影响气驱特征曲线形态,调整效果的不同,曲线的斜率也会呈现不同的变化特征,可用于评价调整效果。
(4) 新型气驱特征曲线在已知注气量条件下,可用于长期以及阶段产量预测且在注气开发较早阶段便可应用。实例计算表明,该特征曲线使用简便可靠,对注气驱油藏的动态分析及开发指标预测具有一定的指导意义。
符号说明
| [1] |
郭平, 李士伦, 杜志敏, 等. 低渗透油藏注气提高采收率评价[J].
西南石油学院学报, 2002, 24(5): 46–50.
GUO Ping, LI Shilun, DU Zhimin, et al. Evaluation on IOR by gas injection in low permeability oil reservoir[J]. Journal of Southwest Petroleum Institute, 2002, 24(5): 46–50. doi: 10.3863/j.issn.1674-5086.2002.05.015 |
| [2] | WARNER H R. An Evaluation of miscible CO2 flooding in waterflooded sandstone reservoirs[J]. Journal of Petroleum Technology, 1977, 29(10): 1339–1347. doi: 10.-2118/6117-PA |
| [3] | CUI M, DING Y, YANG Z, et al. Numerical simulation study on CO2, flooding in ultra-low permeability reservoirs[J]. Procedia Environmental Sciences, 2011, 11(1): 1469–1472. doi: 10.2118/949055-G |
| [4] |
杜建芬, 陈静, 李秋, 等. CO2微观驱油实验研究[J].
西南石油大学学报(自然科学版), 2012, 34(6): 131–135.
DU Jianfen, CHEN Jing, LI Qiu, et al. Experimental study on micro-displacement oil for different CO2 displacement mechanism[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2012, 34(6): 131–135. doi: 10.3863/j.issn.1674-5086.2012.06.019 |
| [5] |
郝永卯, 薄启炜, 陈月明. CO2驱油实验研究[J].
石油勘探与开发, 2005, 32(2): 110–112.
HAO Yongmao, BO Qiwei, CHEN Yueming. Laboratory investigation of CO2 flooding[J]. Petroleum Exploration and Development, 2005, 32(2): 110–112. doi: 10.3321/j.-issn:1000-0747.2005.02.027 |
| [6] | 克林斯M A. 二氧化碳驱油机理及工程设计[M]. 程绍进, 译. 北京: 石油工业出版社, 1989. |
| [7] |
苏畅, 孙雷, 李士伦. CO2混相驱多级接触过程机理研究[J].
西南石油学院学报, 2001, 23(2): 33–36.
SU Chang, SUN Lei, LI Shilun. Mechanism of CO2 miscible flooding during multiple contact procedure[J]. Journal of Southwest Petroleum Institute, 2001, 23(2): 33–36. doi: 10.3863/j.issn.1674-5086.2001.02.009 |
| [8] |
杨国绪, 甄鹏, 赵爱婷. 气驱特征曲线在油田开发中的应用[J].
石油勘探与开发, 1994, 21(1): 71–74.
YANG Guoxu, ZHEN Peng, ZHAO Aiting. Application of gas drive characteristics curve in oilfield development[J]. Petroleum Exploration and Development, 1994, 21(1): 71–74. |
| [9] |
顾乔元, 唐兆青, 鲜波, 等. 气驱特征曲线在凝析气藏开发中的应用[J].
新疆石油地质, 2014, 35(6): 724–727.
GU Qiaoyuan, TANG Zhaoqing, XIAN Bo, et al. Application of gas-drive characteristic curve in condensate gas reservoir by dry gas injection development process[J]. Xinjiang Petroleum Geology, 2014, 35(6): 724–727. |
| [10] |
袁士宝, 杨凤祥, 师耀利, 等. 气驱特征曲线在稠油油藏火驱开发中的应用[J].
新疆石油地质, 2016, 37(3): 318–320.
YUAN Shibao, YANG Fengxiang, SHI Yaoli, et al. Application of gas-drive type curves to fire-flooding development of heavy oil reservoirs[J]. Xinjiang Petroleum Geology, 2016, 37(3): 318–320. doi: 10.7657/XJPG20160314 |
| [11] |
童凯军, 张迎春, 戴卫华, 等. 天然气驱油藏开发动态评价及可采储量预测新方法[J].
石油学报, 2015, 36(6): 740–747.
TONG Kaijun, ZHANG Yingchun, DAI Weihua, et al. A new method for evaluation of development performance and recoverable reserves estimates in natural gas flooding reservoirs[J]. Acta Petrolei Sinica, 2015, 36(6): 740–747. doi: 10.7623/syxb201506011 |
| [12] |
李菊花, 康凯锋, 高文君, 等. 水气交替驱特征曲线关系式的理论推导及应用[J].
石油天然气学报, 2010, 32(5): 139–142.
LI Juhua, KANG Kaifeng, GAO Wenjun, et al. Application and derivation of water-alternating gas drive characteristic curves[J]. Journal of Oil and Gas Technology, 2010, 32(5): 139–142. doi: 10.3969/j.issn.1000-9752.-2010.05.032 |
| [13] |
孙雷, 冯乔, 陈国利, 等. CO2混相驱拟含气率与采出程度图版的建立[J].
西南石油大学学报(自然科学版), 2014, 36(1): 83–88.
SUN Lei, FENG Qiao, CHEN Guoli, et al. Establishment of the chart of equivalent gas ratio-recovery degree for CO2 miscible flooding[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2014, 36(1): 83–88. doi: 10.11885/j.issn.1674-5086.2013.10.14.06 |
| [14] |
陈元千, 杜霞. 水驱曲线关系式的对比以及直线段出现时间的判断[J].
石油勘探与开发, 1986, 13(6): 55–63.
CHEN Yuanqian, DU Xia. A comparison between the different forms of displacement characteristic curves and the criterion for the appearance of straight line section[J]. Petroleum Exploration and Development, 1986, 13(6): 55–63. |
| [15] | 桑德拉R, 尼尔森R F. 油藏注气开采动力学[M]. 北京: 石油工业出版社, 1987: 150-152. |
| [16] | JR H R W, MCGREGOR D S, LAIEB K, et al. Analysis of gasfloods using semilog graphs of free-gas gas/oil ratio vs. cumulative oil production[J]. Journal of Petroleum Technology, 2010, 62(9): 85–91. doi: 10.2118/129301-JPT |
| [17] | 陈军斌, 王冰, 张国强. 渗流力学与渗流物理[M]. 北京: 石油工业出版社, 2013: 47-49. |
| [18] | BARTON H B, JR F R D. Performance of the Pickton Field[J]. Journal of Petroleum Technology, 1958, 10(2): 27–31. doi: 10.2118/908-G |
| [19] | MCGRAW J H, LOHEC R E. The Pickton field-review of a successful gas injection project[J]. Journal of Petroleum Technology, 1964, 16(4): 399–405. doi: 10.2118/667-PA |
| [20] | WELSH J R, SIMPSON R E, SMITH J W, et al. A study of oil and gas conservation in the Pickton Field:petroleum Transactions[J]. American Institute of Mining Engineers, 1949, 1(3): 55–65. doi: 10.2118/949055-G |
 2018, Vol. 40
2018, Vol. 40


