2. "油气藏地质及开发工程"国家重点实验室·西南石油大学, 四川成地 质及开发工程, 四川 成都 610500
2. State Key Laboratory of Oil & Gas Reservoirs Geology and Exploitation, Southwest Petroleum University, Chengdu, Sichuan 610500, China
为解决高温高压气井、稠油热采井等复杂井筒安全问题,具备金属对金属密封结构的特殊螺纹目前被广泛使用[1-3]。特殊螺纹常见的密封结构主要有锥面对锥面、球面对锥面、球面对柱面以及球面对球面共4种结构。由于特殊螺纹种类繁多、结构复杂,目前主要采用实验法[4-7]和有限元法[9-11]研究其气密封性能,关于其理论研究相对较少[12-15]。同时,现有的研究几乎都集中在通过分析特殊螺纹密封面接触应力分布来定性描述螺纹气密封性能,而缺乏能够直接计算特殊螺纹气密封压力的理论模型。为此,%作者在前期研究基础上,针对球面对锥面密封结构,结合Hertz接触力学理论和密封接触能机理建立了考虑密封面作用扭矩的特殊螺纹气密封压力计算理论模型,研究了球面半径、锥面锥度和密封面作用扭矩对螺纹气密封性能影响规律,以期为特殊螺纹密封参数优化设计和上扣扭矩控制提供理论依据。
1 特殊螺纹气密封压力理论模型 1.1 球面对锥面密封接触应力球面对锥面密封结构是一种典型的非协调径向过盈接触密封,如图 1所示。
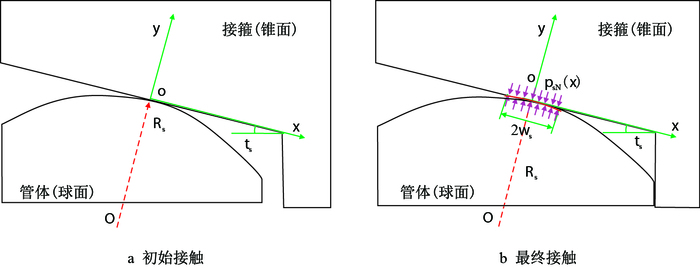 |
| 图1 特殊螺纹球面对锥面径向过盈接触密封示意图 Fig. 1 The schematic diagram of radial interference sealing contact |
根据Hertz接触力学理论,密封面法向接触应力可表达为[14]
| ${p_{{\rm{sN}}}}\left( x \right) = \dfrac{{{E^*}}}{{4{R_{\rm{s}}}}}\sqrt {w_{\rm{s}}^2 - {x^2}} \\ {\kern 40pt}\left( { - {w_{\rm{s}}} \leqslant x \leqslant {w_{\rm{s}}}, 0 < 2{w_{\rm{s}}} \ll {R_{\rm{s}}}} \right)$ | (1) |
式中:
式(1)中,当量弹性模量满足
| $\dfrac{1}{{{E^*}}} = \dfrac{1}{2}\left( {\dfrac{{1 - \nu _{\rm{p}}^2}}{{{E_{\rm{p}}}}} + \dfrac{{1 - \nu _{\rm{c}}^2}}{{{E_{\rm{c}}}}}} \right)$ | (2) |
式中:
密封面接触半宽可通过密封面附加上扣扭矩确定[16]
| ${w_{\rm{s}}} = \dfrac{{20}}{\pi }\sqrt {\dfrac{{10{R_{\rm{s}}}{T_{{\rm{se}}}}}}{{{E^*}{r_{\rm{s}}}\left\{ {\dfrac{{{t_s}}}{{\sqrt {4 + t_{\rm{s}}^2} }}\left[{\dfrac{P}{{2\pi }} + \dfrac{{{\mu _{\rm{t}}}}}{{\cos \alpha }} {\dfrac{{2{E_7} + \left( {g-{L_7}} \right){t_{\rm{t}}}}}{4}} } \right] + {\mu _{\rm s}}{r_{\rm s}}} \right\}}}}$ | (3) |
式中:
由式(1)~式(3)可知,当密封参数和其他参数一定时,密封面接触应力由密封面附加上扣扭矩直接决定。对于球面对锥面密封结构,为防止高接触应力导致密封面屈服黏结,规定密封面最大接触应力应小于材料屈服强度
| $\dfrac{{{E^*}{w_{\rm{s}}}}}{{4{R_{\rm{s}}}}} \leqslant {\sigma _{\rm{s}}}$ | (4) |
将式(3)代入式(4),整理可得密封面允许最大附加上扣扭矩
| ${T_{{\rm{sem}}}} \!=\! \dfrac{{{R_{\rm{s}}}{r_{\rm{s}}}\sigma _{\rm{s}}^2{\pi ^2}}}{{250{E^*}}}\left[{\dfrac{{{t_{\rm{s}}}}}{{\sqrt {4 \!+\! t_{\mathop{\rm s}\nolimits} ^2} }}\left( {\dfrac{P}{{2\pi }} \!+\! \dfrac{{{\mu _{\rm{t}}}}}{{\cos \alpha }}\cdot{\dfrac{{2{E_7} + g{t_{\rm t}}-{L_7} {t_{\rm t}}}}{4}}} \right) \!+\! {\mu _{\rm{s}}}{r_{\rm{s}}}} \right]$ | (5) |
式中:
密封接触能理论认为,阻止气体通过金属对金属密封结构的流动阻力可由密封接触应力在有效密封长度上的某种积分值表征。根据Murtagian[6]的研究,球面对锥面密封结构在高温高压(忽略螺纹脂)环境中的气密封指数可表示为
| ${W_{\rm{a}}} = \int_{ - {w_{\rm{s}}}}^{{w_{\rm{s}}}} {p_{_{{\rm{sN}}}}^{1.4}} \left( x \right){\rm{d}}x$ | (6) |
式中:
当密封结构的气密封指数
| ${W_{{\rm{ac}}}} = 10 \times {\left( {\dfrac{{{p_{\rm{g}}}}}{{{p_{\rm{a}}}}}} \right)^{0.838}}$ | (7) |
式中:
当已知密封面接触应力分布时,由式(6)、式(7)可得高温高压环境下球面对锥面密封结构的最大气密封压力为
| ${p_{{\rm{gm}}}} = {p_{\rm a}}{\left[{\dfrac{{\int_{-{w_{\rm{s}}}}^{{w_{\rm{s}}}} {p_{_{{\rm{sN}}}}^{1.4}\left( x \right){\rm{d}}x} }}{{10}}} \right]^{\frac{1}{{0.838}}}}$ | (8) |
式中:
由式(8)可知,特殊螺纹球面对锥面密封的最大气密封压力与密封接触应力分布密切相关,而由式(1)~(3)可知密封面接触应力主要与金属对金属密封结构参数(
| 表1 某套管特殊螺纹基本参数 Table 1 The basic parameters for a casing premium connection |
假设锥面锥度ts为1:16,密封面附加上扣扭矩Tse为500 N·m,计算了球面半径Rs为10~200 mm时螺纹最大气密封压力,结果如图 2所示。
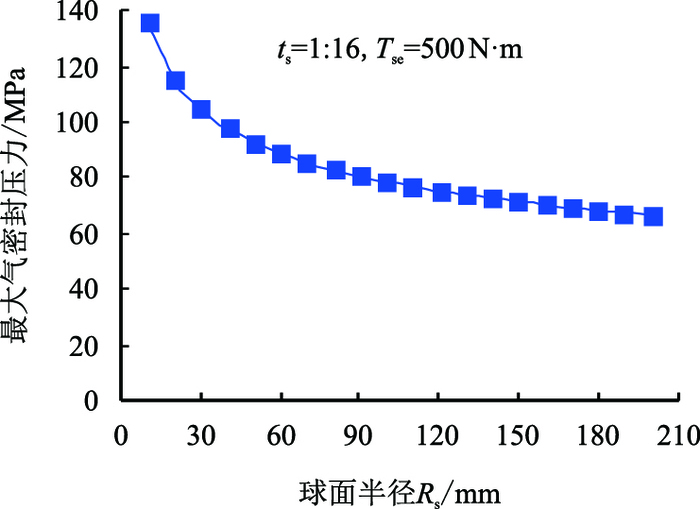 |
| 图2 球面半径对螺纹最大气密封压力的影响 Fig. 2 The effect of spherical radius on the maximum gas sealing pressure |
由图 2可知,当锥面锥度和密封面附加上扣扭矩一定时,随球面半径增大,特殊螺纹的最大气密封压力呈幂指数规律降低,且降低的速度越来越小,当球面半径从10 mm增加到100 mm时,螺纹最大气密封压力从136.37 MPa下降到78.72 MPa,下降了42.3%。因此,实际中在保证密封面不发生屈服的情况下可尽量减小球面半径。
2.2 锥面锥度的影响假设球面半径Rs为100 mm,密封面附加上扣扭矩Tse为500 N·m,计算了锥面锥度ts为1/64、1/32、1/16、1/8和1/4(对应密封面平均半径rs依次为59.85,59.77,59.62,59.30,58.68 mm)时螺纹最大气密封压力,结果如图 3所示。
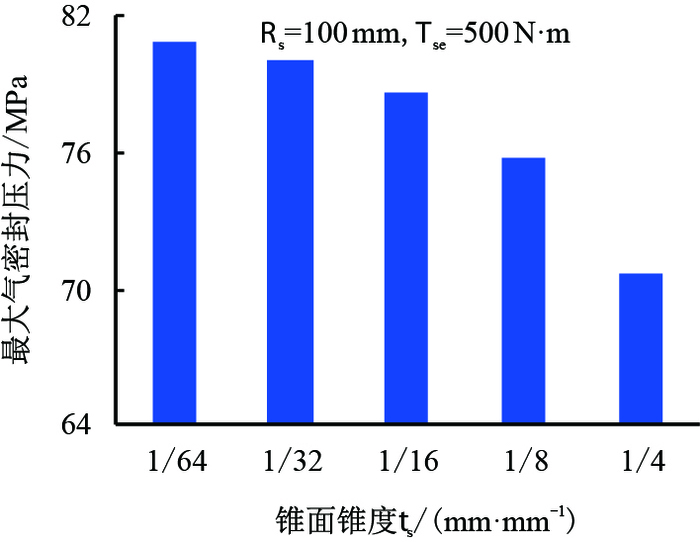 |
| 图3 锥面锥度对螺纹最大气密封压力的影响 Fig. 3 The effect of cone taper on the maximum gas sealing pressure |
由图 3可知,当球面半径和密封面附加上扣扭矩一定时,随锥面锥度增大,特殊螺纹的最大气密封压力逐渐降低,但降低的幅度均较小,当锥面锥度从1/64增加到1/4时,螺纹最大气密封压力从80.97 MPa下降到70.69 MPa,仅下降了12.7%。由于锥度越小,螺纹密封性能受轴向载荷影响越小,因此实际中应尽量降低锥面锥度。
2.3 密封面附加上扣扭矩的影响根据前文分析可知,密封结构参数中球面半径对螺纹气密封压力影响显著,且在满足密封面不屈服的情况下应尽量降低球面半径。为此,假设锥面锥度ts为1:16,球面半径Rs分别为10,20,30 mm,计算了密封面附加上扣扭矩Tse为0~1000 N·m时螺纹最大气密封压力,结果如图 4所示。
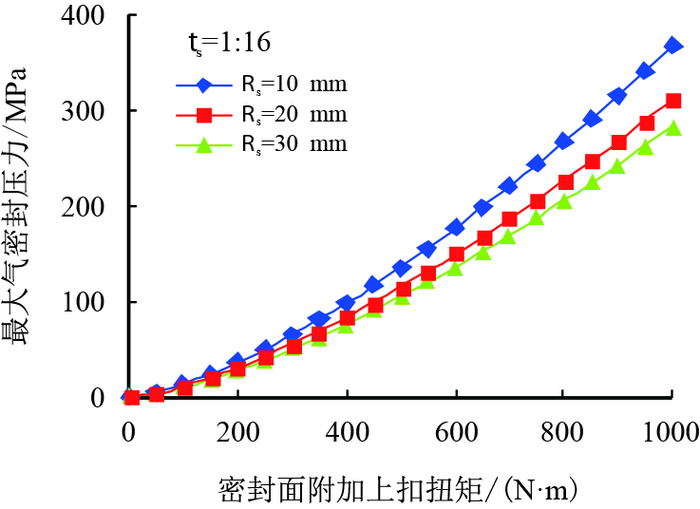 |
| 图4 密封面附加上扣扭矩对螺纹最大气密封压力的影响 Fig. 4 The effect of additional sealing torque on the maximum gas sealing pressure |
由图 4可知,当锥面锥度和球面半径一定时,随密封面附加上扣扭矩增加,特殊螺纹的最大气密封压力呈抛物线型增大,当密封面附加上扣扭矩从50 N·m增大到500 N·m时,最大气密封压力均增大约26倍,这表明密封面附加上扣扭矩对螺纹密封性能影响显著。对于拟密封的气体压力,存在一个最小的密封面附加上扣扭矩使得螺纹满足气密封要求。例如,拟密封的气体压力为100 MPa,则对于球面半径为20 mm的密封结构,密封面附加上扣扭矩至少应为452 N·m;同时,为防止密封面发生屈服黏结,由式(5)确定此时密封面的最大附加上扣扭矩为599 N·m。因此,当球面半径为20 mm时,特殊螺纹满足100 MPa可靠气密封的密封面附加上扣扭矩应为452~599 N·m。实际上扣时应密切关注上扣扭矩曲线,尽量控制密封面附加上扣扭矩在该范围内。
3 结论(1) 针对球面对锥面密封结构,基于密封接触能机理建立了特殊螺纹气密封压力理论模型,为定量评价特殊螺纹气密封性能提供了一种较可靠的方法。
(2) 随球面半径增大,螺纹气密封压力呈幂指数规律降低,且降低的速度越来越小;随锥面锥度增大,螺纹气密封压力逐渐降低,但降幅较小;随密封面附加上扣扭矩增加,螺纹气密封压力呈抛物线型增大。
(3) 为提高特殊螺纹气密封性能,一方面应优化球面半径,另一方面应控制密封面作用扭矩在合理范围,既根据拟密封的气体压力确定密封面最小附加上扣扭矩,同时根据密封面极限屈服条件确定密封面最大附加上扣扭矩。
| [1] | CARCAGNO G E. The design of tubing and casing premium connections for hthp wells[C]. SPE 97584, 2005. doi:10.2118/97584-MS |
| [2] | BRADLEY A B, NAGASAKU S, Verger E. Premium connection design, testing, and installation for hpht sour wells[C]. SPE 97585, 2005. doi:10.2118/97585-MS |
| [3] | SUGINO M, NAKAMURA K, YAMAGUCHI S, et al. Development of an innovative high-performance premium threaded connection for OCTG[C]. SPE 20734, 2010. doi:10.4043/20734-MS |
| [4] | International Organization for Standardization(ISO). Petroleum and natural gas industries-procedures for testing casing and tubing connections[S]. ISO 13679:2002(E), 2002. |
| [5] |
王新虎, 申照熙, 王建东, 等. 特殊螺纹油管与套管的上扣扭矩构成与密封性能研究[J].
石油矿场机械, 2010, 39(12): 45–50.
WANG Xinhu, SHEN Zhaoxi, WANG Jiandong, et al. Study on the makeup torque constitutes and seal integrity of tubing and casing premium connection[J]. Oil Field Equipment, 2010, 39(12): 45–50. doi: 10.3969/j.issn.1001-3482.2010.12.014 |
| [6] | MURTAGIAN G R, FANELLI V, VILLASANTE J A, et al. Sealability of stationary metal-to metal seal[J]. Journal of Tribology, 2004, 126(3): 591–596. doi: 10.1115/1.1715103 |
| [7] |
许志倩, 闫相祯, 杨秀娟, 等. 非API套管接头主密封结构气密性能试验分析[J].
压力容器, 2014, 4: 7–12.
XU Zhiqian, YAN Xiangzhen, YANG Xiujuan, et al. Analysis of gas sealing performance test for non-api casing connection with radial cone sealing structure[J]. Pressure Vessel Technology, 2014, 4: 7–12. doi: 10.3969/j.issn.10014837.2014.04.002 |
| [8] | TAKANO J, YAMAGUCHI M, KUNISHIGE H. Development of premium connection "KSBEAR"for withstanding high compression, high external pressure, and severe bending[R]. Kawasaki steel technical report No. 47, 2002. |
| [9] |
杨智春, 李斌, 史交齐. 特殊扣套管接头的应力及密封特性分析[J].
机械科学与技术, 2004, 23(7): 771–776.
YANG Zhichun, LI Bin, SHI Jiaoqi. Stress and sealing property analysis of premium threaded connection[J]. Mechanical Science and Technology, 2004, 23(7): 771–776. doi: 10.3321/j.issn:1003-8728.2004.07.005 |
| [10] | XIE J, TAO G. Analysis of casing connections subjected to thermal cycle loading[C]. 2010 Simulia Customer Conference, 2010. |
| [11] | XIE J. Numerical evaluation of tubular connections for HPHT applicants[C]. Baosteel BAC, 2013:F6-F14. |
| [12] |
许志倩, 闫相祯, 杨秀娟, 等. 微观泄漏机理在非API套管接头密封性能评估中的应用[J].
石油学报, 2014, 35(5): 963–971.
XU Zhiqian, YAN Xiangzhen, YANG Xiujuan, et al. Aplication of micro-leakage mechanism for evaluating the sealing performance of non-API casing connections[J]. Acta Petrolei Sinica, 2014, 35(5): 963–971. doi: 10.7623/syxb201405018 |
| [13] |
许志倩, 闫相祯, 杨秀娟. 非API套管接头完整性评估计算方法[J].
工程力学, 2016, 33(2): 188–199.
XU Zhiqian, YAN Xiangzhen, YANG Xiujuan. Integrity evaluation method for non-api casing connections[J]. Engineering Mechanics, 2016, 33(2): 188–199. |
| [14] |
许红林, 李天雷, 杨斌, 等. 油套管特殊螺纹球面对锥面密封性能理论分析[J].
西南石油大学学报(自然科学版), 2016, 38(5): 1–8.
XU Honglin, LI Tianlei, YANG Bin, et al. Theoretical analysis on sphere to cone sealing performance for tubing and casing premium connection[J]. Journal of Southwest Petroleum University(Science & Technology Edition), 2016, 38(5): 1–8. doi: 10.11885/j.issn.16745086.2014.07.28.01 |
| [15] | 许红林. 油套管特殊螺纹连接强度和密封理论研究[D]. 成都: 西南石油大学, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10615-1016005920.htm |
| [16] |
许红林, 施太和, 张智. 油套管特殊螺纹接头上扣扭矩理论分析[J].
西南石油大学学报(自然科学版), 2014, 36(5): 160–168.
XU Honglin, SHI Taihe, ZHANG Zhi. Theoretical analysis on makeup torque in tubing and casing premium threaded connections[J]. Journal of Southwest Petroleum University(Science & Technology Edition), 2014, 36(5): 160–168. doi: 10.11885/j.issn.1674-5086.2014.04.30.03 |
| [17] | American Petroleum Institute(API). Specification for threading, gauging, and thread inspection of casing, tubing, and line pipe Threads[S]. API Spec 5B:15(E), 2008. |
 2017, Vol. 39
2017, Vol. 39


