2. 中海石油(中国)有限公司北京研究中心, 北京 朝阳 100027;
3. 中国石油大庆油田第三采油厂, 黑龙江 大庆 163113
2. Beijing Research Center, CNOOC(China) Co. Ltd., Chaoyang, Beijing, 100027, China;
3. The No.3 Oil Recovery Plant, Daqing Oilfield, Daqing, Heilongjiang 163113, China
油藏往往存在较为严重的层间非均质性,如果采用多层合采的开发方式开发油藏,可能会发生层间干扰,降低开发效果[1-2]。国内外诸多学者长期以来对层间干扰的问题进行了大量的研究,他们一般采用矿场试验、室内实验以及数值模拟等方法[3-6]研究层间干扰的渗流机理、影响因素及评价方法[7-10]。鲜波等[11]从压力系统与渗透率之间的组合方式出发,研究了层间干扰规律;余华杰等[12]从流度的角度出发,得到了不同油田的层间干扰规律;李大建等[13]建立了两层的低渗透油藏模型,并研究了其合采时的层间干扰规律。屈亚光等[14]综合考虑了合采层数、油层厚度、层间非均质程度等诸多因素,在此基础上,研究了层间干扰机理及其开发效果。王渊等[15]根据气井多层合采物理模型,利用气井二项式产能公式及井筒压力计算模型,建立了气井层间干扰系数的计算方法。
层间干扰问题的研究采用了多种方式:从实验研究到公式推导,从公式推导到数值模拟等,这些研究成果由浅入深地剖析了层间干扰的机理。随着层间干扰问题研究的不断深入,评价层间干扰的影响因素逐渐增多,层间干扰系数的计算方法也得到了改进。但这些研究大多数着眼于层间干扰的静态影响因素,并且计算的是静态的指标,鲜有动态的层间干扰规律研究,并且各影响因素之间综合性不强,有待进一步完善[16-17]。
利用渗流力学知识,结合层间干扰主控因素分析结果[18],建立了多层合采油井层间干扰现象模拟数学模型,并对数学模型进行数值求解。并利用所建立的数学模型分别分析了无水期以及见水期的层间干扰机理与规律,为油田实施层系细分、分注分采等提供依据。
1 模型的建立 1.1 物理模型建立n层物理模型,为表示方便,n=3时地质模型和对应的油藏模型分别见图 1和图 2(
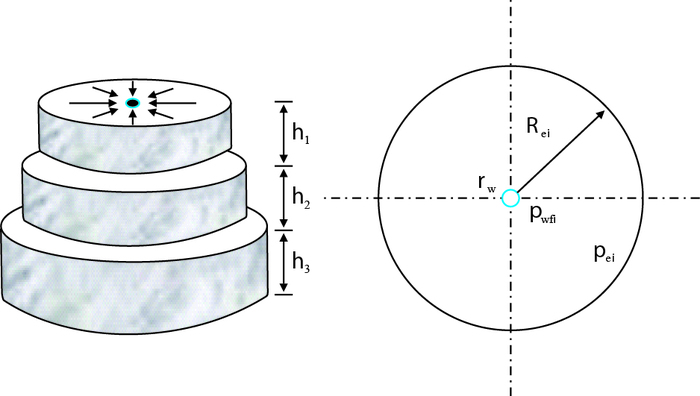 |
| 图1 n层地质模型平面径向流示意图(n=3) Fig. 1 Diagram of n plane radial flow n=3 |
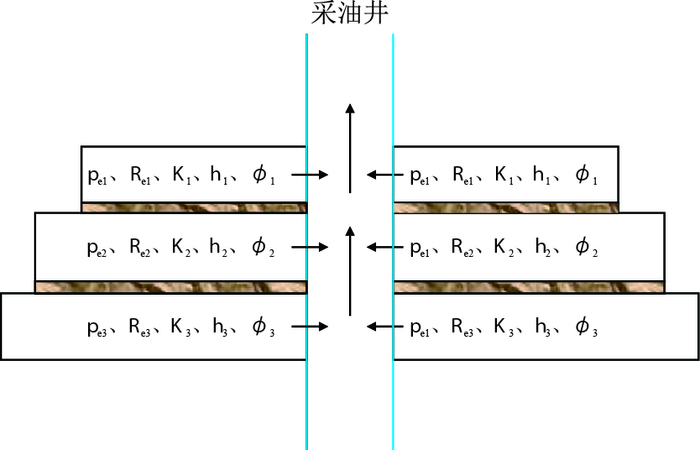 |
| 图2 n层油藏示意图(n=3) Fig. 2 Diagram of multi-layer n reservoir(n=3) |
假设条件:多层油藏;各产层只在井筒连通,层间无窜流;层间非均质;不封闭油藏。
1.2 数学模型模型中,流体流动分为3个时期,包括压力降波及到含油外边界前(单相油流);未见水时期(油水两相流+单相油流);见水时期(油水两相流)。
1.2.1 压力降波及到含油外边界前(单相油流)压力降波及到含油外边界前水驱油示意图见图 3(
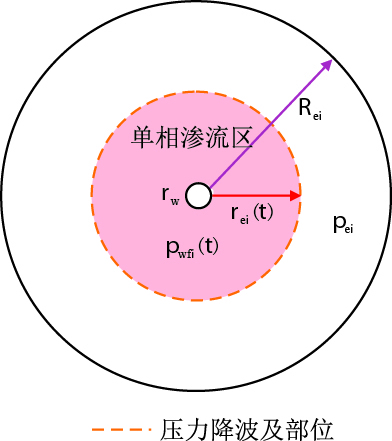 |
| 图3 压力降波及到含油外边界之前水驱油示意图 Fig. 3 Diagram of water/oil displacement before productive limit is swept by producing pressure difference |
| ${{p}_{\text{wf}i}}\left( {t} \right)={{p}_{\text{e}i}}-\dfrac{{{Q}_{\text{L}i}}\left( {t} \right){{\mu }_{\text{o}i}}}{\text{4 }\!\!{\rm{\pi }}\!\!\text{ }{{K}_{{i}}}{{h}_{{i}}}}\ln\dfrac{\text{2.25}{{\eta }_{{i}}}t}{r_{\text{w}}^{\text{2}}}$ | (1) |
| ${{f}_{{\text w}i}}\left( t \right)=0$ | (2) |
| ${{Q}_{\text{o}i}}\left( t \right)={{Q}_{\text{L}i}}\left( t \right)$ | (3) |
式中:
未见水时期地层水驱油示意图见图 4(
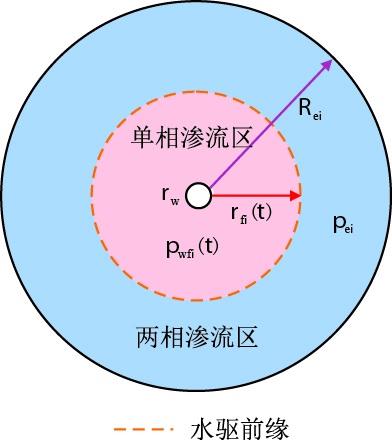 |
| 图4 未见水时期地层水驱油示意图 Fig. 4 Diagram of water/oil displacement in water free producing period |
(1) 渗流阻力
| $\left\{ {\begin{array}{*{20}{l}} {{R_i}\left( t \right){\rm{ = }}\frac{{{\rm{100}}}}{{{\rm{8}}.{\rm{64}}}}\frac{{{\mu _{{\rm{o}}i}}}}{{{\rm{2}}\pi {h_i}{K_i}{K_{{\rm{ro}}i}}\left( {{S_{{\rm{wc}}i}}} \right)}} \cdot }\\ {\quad \left[ {\frac{{{K_{{\rm{ro}}i}}({S_{{\rm{wc}}i}})}}{{\rm{2}}}\int_{{S_{{\rm{wm}}i}}}^{{S_{{\rm{wf}}i}}} {\frac{{\varphi _i^\prime \left( {{S_{\rm{w}}}} \right){\rm{d}}{S_{\rm{w}}}}}{{\xi \left( t \right)}}} {\rm{ + ln}}\frac{{{r_{{\rm{fi}}}}\left( t \right)}}{{{r_{\rm{w}}}}}} \right]}\\ {\xi \left( t \right){\rm{ = }}\left[ {{K_{{\rm{ro}}i}}\left( {{S_{\rm{w}}}} \right){\rm{ + }}{\mu _{{\rm{ow}}i}}{K_{{\rm{rw}}i}}\left( {{S_{\rm{w}}}} \right)} \right] \cdot }\\ {\quad \left[ {\frac{{{\varphi _{\rm{i}}}\left( {{S_{{\rm{wf}}i}}} \right)}}{{{\rm{1 - }}{{\left( {{r_{\rm{w}}}{\rm{/}}{r_{{\rm{ei}}}}} \right)}^{\rm{2}}}}} - {\varphi _i}\left( {{S_{\rm{w}}}} \right)} \right]} \end{array}} \right.$ | (4) |
式中:
(2) 井底流压
| ${{p}_{\text{wf}i}}\left( t \right)\text{=}{{p}_{\text{e}i}}-{{R}_{{i}}}\left( t \right)\cdot {{Q}_{\text{L}i}}\left( t \right)$ | (5) |
(3) 含水率
| ${{f}_{\text{w}i}}\left( t \right)=0$ | (6) |
(4) 产油量
| ${{Q}_{\text{o}i}}\left( t \right)={{Q}_{\text{L}i}}\left( t \right)$ | (7) |
见水时期(油水两相流)地层水驱油示意图见图 5。
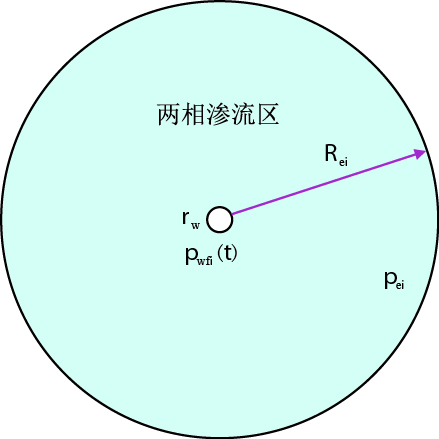 |
| 图5 见水期地层流动区域示意图 Fig. 5 Diagram of water/oil displacement after water breakthrough |
(1) 渗流阻力
| $\left\{ \begin{array}{l} {R_i}\left( t \right) = \dfrac{{100}}{{8.64}}\dfrac{{{\mu _{{\rm{o}}i}}}}{{2\pi {h_i}{K_i}}}\int_{\, {s_{{\rm{wf}}i}}}^{\, {s_{{\rm{we}}i}}} {\dfrac{{{\varphi _i}'\left( {{S_{\rm{w}}}} \right){\rm{d}}{S_{\rm w}}}}{{2\xi \left( t \right)}}} \\[6pt] \xi \left( t \right) = \left[{{K_{{\rm{ro}}i}}\left( {{S_{\rm{w}}}} \right) + {\mu _{{\rm{ow}}i}}{K_{{\rm{rw}}i}}\left( {{S_{\rm{w}}}} \right)} \right] \cdot \\{\kern 40pt}\left[{\dfrac{{{\varphi _i}\left( {{S_{{\rm{wf}}i}}} \right)}}{{1-{{\left( {\dfrac{{{r_{\rm{w}}}}}{{{R_{{\rm{e}}i}}}}} \right)}^2}}}-{\varphi _i}\left( {{S_{\rm{w}}}} \right)} \right] \end{array} \right.$ | (8) |
式中:
(2) 井底流压
| ${{p}_{\text{wf}i}}\left( t \right)={{p}_{\text{e}i}}-{{R}_{{i}}}\left( t \right)\cdot {{Q}_{\text{L}i}}\left( t \right)$ | (9) |
(3) 产油量
| ${{Q}_{\text{o}i}}\left( t \right)={{Q}_{\text{L}i}}\left( t \right)\left( 1-{{f}_{\text{w}i}}\left( t \right) \right)$ | (10) |
(4) 含水率
累积注水倍数的计算公式为
| ${{W}_{\text{D}}}_{{i}}\left( t \right)=\dfrac{{{w}_{{i}}}\left( t \right)}{\pi \left( {{r}_{\text{e}i}}^{2}-{{r}_{\text{w}}}^{2} \right){{h}_{{i}}}{{\phi }_{{i}}}}$ | (11) |
式中:
累积注水倍数与含水率一阶导数关系为
| ${{\varphi }_{i}}\left( {{S}_{\text{w}}} \right)=\dfrac{1}{{{W}_{\text{D}}}_{{i}}\left( t \right)}$ | (12) |
通过对含水率
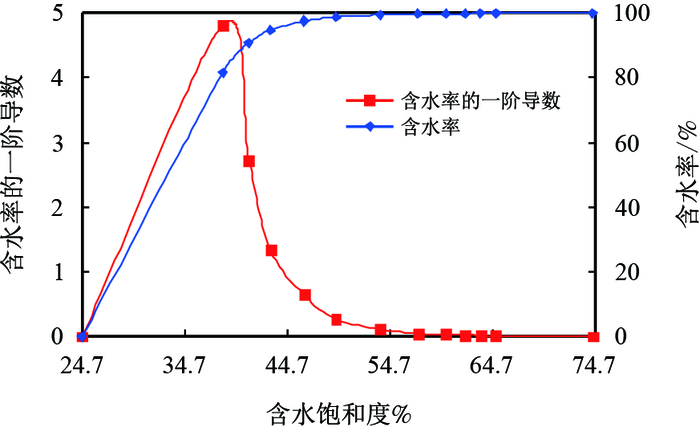 |
| 图6 含水率计算方法图 Fig. 6 Calculation of water cut |
(1) 合采采油指数
| ${{J}_{}}\left( t \right)=\sum\limits_{i=1}^{n}{\dfrac{{{Q}_{{\rm o}i}}\left( t \right)}{{p}_{{\rm e}i}-{{p}_{\rm wf}}\left( t \right)}}$ | (13) |
式中:
(2) 分采采油指数
| ${{J}_{i}}\left( t \right)\text{=}\dfrac{{{Q}_{{\rm o}i}}\left( t \right)}{{{p}_{{\rm e}i}}-{{p}_{{\rm wf}i}}\left( t \right)}$ | (14) |
式中:
多层合采层间干扰系数定义为油井各小层分别生产的生产指数之和,与这些小层合采的生产指数的差值,再除以各小层分别生产的生产指数之和。
| $\eta(t)=\dfrac{\sum\limits_{i=1}^{n}{{{J}_{i}}(t)} -{{J}_{}}(t)}{\sum\limits_{i=1}^{n}{{{J}_{i}}(t)}}$ | (15) |
式中:
产能预测模型在任意时间点都可进行测试,合采分测连续进行,计算合采产能、分采产能以及层间干扰系数。
模型考虑的主要因素如下:
(1) 层间非均质性
模型考虑的主控因素有:渗透率、相对渗透率曲线、油层厚度、孔隙度、黏度、供给半径、原始地层压力以及启动压力梯度。各层这些参数均可不同。
(2) 启动压力梯度
若压力梯度大于启动压力梯度,则该层参与流动;若压力梯度小于或等于启动压力梯度,则该层不参与流动。其中,通过室内实验研究得到启动压力梯度与渗透率存在如下关系
| ${{G}_{i}}=0.6989{{\left( \dfrac{{{K}_{i}}}{{{\mu }_{\text{o}i}}} \right)}^{-1.1147}}$ | (16) |
式中:
(3) 井筒连通
各层原始地层压力及其他物性参数不同。多层油藏合采油井生产过程中,层间无窜流,只通过井筒连通。流体的流动压力受物性较好层控制,而使得物性较差层受到抑制。
(4) 液量转移
合采模式下,不同小层产液量随时间而变化,剩余油多、阻力大的小层的产液量比例越来越小,而含水饱和度高、阻力小的小层的产液量比例越来越大,分采模式下,没有这种现象,导致合采与分采模式开发效果存在差异。
短时间内,各小层间的液量转移不可能很大。
2 无水期层间干扰机理与规律利用所建立的数学模型,结合收集到的海上油田相关静态资料,计算不同控制因素下无水期的层间干扰系数,从层间非均质性、启动压力梯度以及测试工作制度3个方面揭示无水期层间干扰机理与规律。
2.1 层间非均质性(1) 出液厚度比例
利用所建立的数学模型,模拟不同生产压差下,油井出液厚度比例的变化(图 7)。
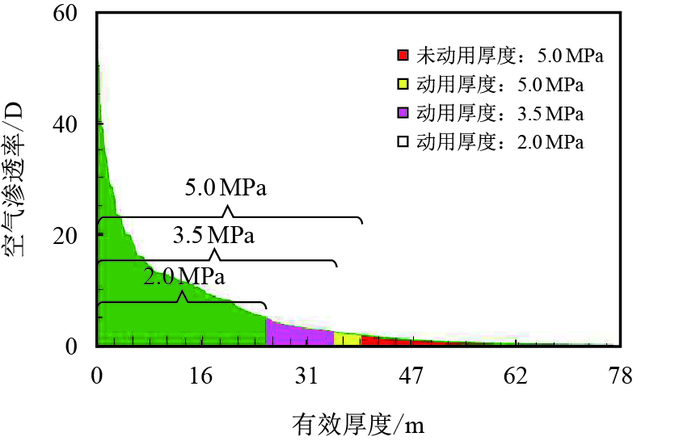 |
| 图7 出液厚度比例变化曲线 Fig. 7 The change of thickness of outputting liquid in water free producing period |
由图 7可以看出,无水期,随着生产压差的增加,油井出液厚度逐渐增大,并且渗透率越大的层越容易动用。
在其他物性参数相同的情况下,当层数分别被细分为3层和13层时,利用所建立的数学模型,模拟同一测试时间的层间干扰系数,分析层间干扰系数与层数的关系(图 8)。由图 8可见,合采段层数越多,层间干扰越严重。原因是合采层段层数越多,纵向非均质性越严重,导致层间干扰越严重。但是层数并不是造成层间干扰的根本原因,根本原因是储层及流体物性参数的差异,即层间非均质性。
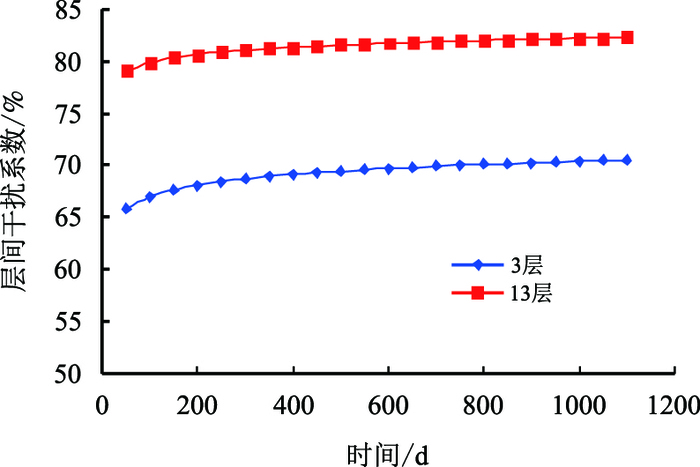 |
| 图8 层间干扰系数与层数的关系曲线 Fig. 8 Relationship between interlayer interference coefficient and number of layers |
(2) 渗透率级差
以海上某油田典型的7口井为例,利用已有的统计资料,分别计算了各口井的渗透率级差。然后利用所建立的数学模型,在无其他因素影响的情况下,分别对5口井进行产能预测,计算层间干扰系数。最后分别选取同一测试时间点的层间干扰系数,绘制层间干扰系数与渗透率级差的关系曲线,对曲线进行回归,得到层间干扰系数与渗透率级差的关系式。计算结果见图 9。
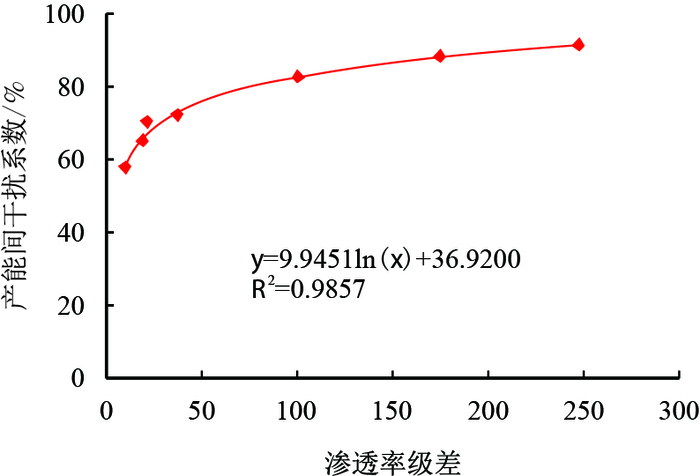 |
| 图9 典型井层间干扰系数与渗透率级差关系曲线 Fig. 9 Relationship between interlayer interference coefficient and permeability contrast |
由图 9可以看出,渗透率级差越大,层间非均质性越严重,层间干扰越严重。利用层间干扰系数与渗透率级差的关系式进行相关计算,计算结果表明,在进行层系组合时,若渗透率级差小于4,则可保证层间干扰系数小于50%;若渗透率级差小于10,则可保证层间干扰系数小于60%。
2.2 启动压力梯度利用所建立的数学模型,模拟不同拟启动压力情况下的层间干扰系数,计算结果见图 10。
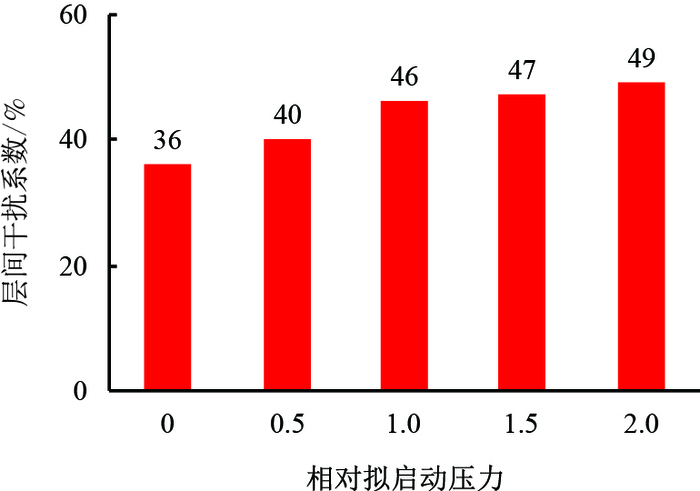 |
| 图10 层间干扰系数与启动压力梯度的关系图 Fig. 10 Relationship between interlayer interference coefficient and threshold pressure gradient |
由图 10可以看出,相对拟启动压力越大,层间干扰越严重。原因是油井合采过程中各层按照启动压力大小依次启动,无水期,合采时启动压力梯度越大,油井克服启动压力动用厚度比例越少,层间干扰越严重。
2.3 测试工作制度(1) 生产压差利用所建立的数学模型,在无其他因素影响的情况下,计算不同合采生产压差下的层间干扰系数,绘制了无水期层间干扰系数随生产压差的变化曲线,计算结果见图 11。
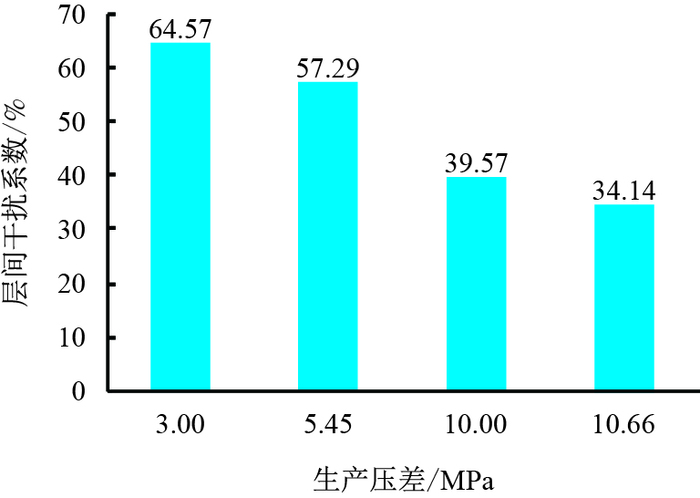 |
| 图11 层间干扰系数与合采生产压差关系曲线 Fig. 11 Relationship between interlayer interference coefficient and producing pressure difference of commingled production |
由图 11可见,无水期,合采生产压差越大,层间干扰程度越弱。原因是无水期合采生产压差越大,油井克服启动压力动用厚度比例越大,层间干扰程度越弱。
(2) 产液量
利用所建立的数学模型,各方案分别给定不同的合采产液量,计算不同合采产液量情况下的层间干扰系数,计算结果见图 12。
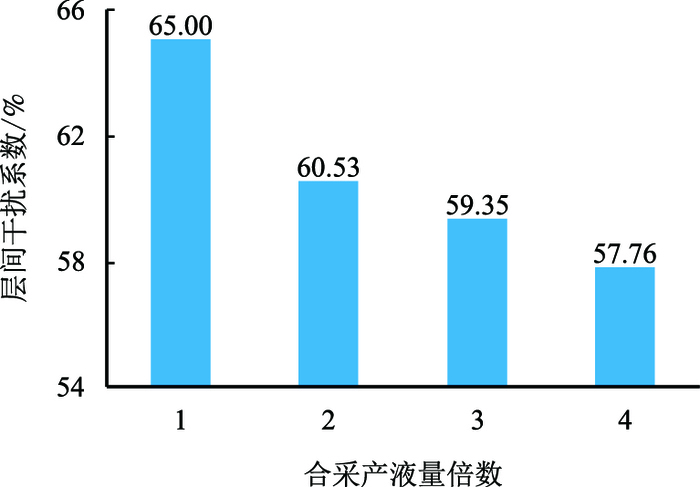 |
| 图12 层间干扰系数与合采产液量关系曲线 Fig. 12 Relationship between interlayer interference coefficient and liquid production of commingled production |
由图 12可以看出,随着合采产液量的增加,干扰系数逐渐减小。原因是合采产量较大时,对应的井底流压相对较低,因此生产压差相对较大,油井克服启动压力参与流动的厚度比例增加,层间干扰程度减弱。但是在实际生产过程中,不能无限地增加产液量,要符合油田生产实际。
综合以上研究结果,无水期,层间干扰程度主要受出液厚度的影响。因此,在无水期,可以不划分层系,在合理生产范围内尽可能放大生产压差,提高产液量,提高油层动用厚度,减小层间干扰。
3 见水期层间干扰机理与规律利用所建立的数学模型,结合收集到的海上油田相关静态资料,计算不同控制因素下见水期的层间干扰系数,从合采含水率以及测试工作制度两个方面揭示见水期层间干扰机理与规律。
3.1 合采含水率利用所建立的数学模型,计算不同含水率阶段的层间干扰系数,绘制层间干扰系数与合采含水率的关系曲线,计算结果见图 13。
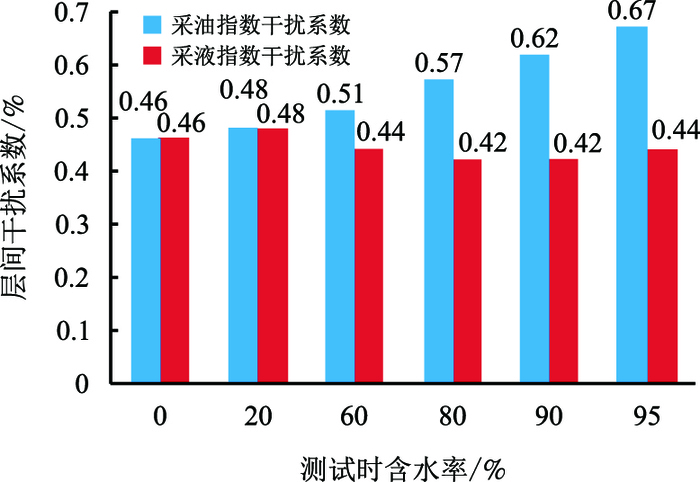 |
| 图13 层间干扰系数与合采含水率的关系曲线 Fig. 13 Relationship between interlayer interference coefficient and water cut of commingled production |
由图 13可以看出,当合采含水率达到90%时,层间干扰系数为92%,含水率越高,层间干扰越严重。原因是含水率越高,低阻力层的产液量比例越大,高阻力层(产油量多)产液量比例越小,低阻力层对高阻力层形成抑制作用,加剧层间干扰。
3.2 生产压差利用所建立的数学模型,计算见水期不同合采生产压差下的层间干扰系数,分析见水期合采生产压差对层间干扰的影响,计算结果见图 14。
 |
| 图14 层间干扰系数与合采生产压差关系曲线 Fig. 14 Relationship between interlayer interference coefficient and producing pressure difference of commingled production |
由图 14可以看出,见水期,层间干扰主要受高含水层产液比例的影响,增加生产压差层间干扰加剧的概率将会增加。
综合以上研究结果,见水期,层间干扰主要受高含水层产液比例的影响,增加生产压差层间干扰加剧的概率将会增加,因此应控制生产压差。可以在这一时期采取划分层系、对薄差层实施压裂或者调剖堵水等增产措施。
4 结语(1) 基于渗流力学知识,结合层间干扰主控因素分析结果,建立了层间干扰评价模拟模型,模型考虑了层间非均质性、启动压力梯度、井筒连通以及液量转移。
(2) 层间干扰的主控因素包括储层及流体物性、启动压力梯度、含水阶段以及测试工作指数。无水期,各主控因素通过控制流体渗流阻力,影响油井出液厚度比例,最终形成层间干扰。见水期,各主控因素通过控制流体渗流阻力,影响高含水层产液比例,最终形成层间干扰。
(3) 无水采油期,合采段层数越多,层间干扰越严重;渗透率级差越大,层间非均质性越严重;启动压力梯度越大,低渗透层越难参与流动,层间干扰越严重;随着合采产液量的增加,干扰系数逐渐减小;分采与合采产液量比值越大,层间干扰越严重。见水期,合采含水率越大,层间干扰越严重,高含水层干扰低含水层,由于含水率越高,则低阻力层的液量比例越大,高阻力层(产油量多)液量比例越小,低阻力层对高阻力层形成抑制作用,加剧层间干扰;并且层间干扰主要受高含水层产液比例的影响。增大生产压差,层间干扰加剧的概率将会增加。
(4) 按照测试层段的厚度进行配产,可以减小由于测试工作制度造成的层间干扰;应避免射开厚度小,渗透率大的小层产油量少,以免在见水期形成低效或者无效循环,影响采收率;在无水期,层间干扰程度主要受出液厚度的影响,故可以不划分层系,在合理生产范围内尽可能放大生产压差,提高产液量,增加油层动用厚度,减小层间干扰;见水期,应控制生产压差以减少层间干扰,可以在这一时期采取划分层系、对薄差层实施压裂或者调剖堵水等增产措施。
| [1] |
刘洪杰. 常规油藏多层合采层间干扰系数确定新方法[J].
石油地质与工程, 2013, 27(5): 47–50.
LIU Hongjie. New determination method of interlayer interference coefficient among commingling production layers in conventional reservoirs[J]. Petroleum Geology and Engineering, 2013, 27(5): 47–50. doi: 10.3969/j.issn.1673-8217.2013.05.022 |
| [2] |
马奎前, 刘英宪, 苏彦春. 渤海S油田高含水期加密井产能评价[J].
断块油气田, 2013, 20(1): 71–73.
MA Kuiqian, LIU Yingxian, SU Yanchun. Productivity evaluation of infill well at high water cut stage in S Oilfield, Bohai Bay[J]. Fault-Block Oil & Gas Field, 2013, 20(1): 71–73. doi: 10.6056/dkyqt201301017 |
| [3] |
张浩, 李廷礼, 贾晓飞, 等. 海上稠油油田层间干扰变化研究[J].
断块油气田, 2015, 22(5): 656–659.
ZHANG Hao, LI Tingli, JIA Xiaofei, et al. Study on interlayer interference changes in offshore heavy oil reservoirs[J]. Fault-Block Oil & Gas Field, 2015, 22(5): 656–659. doi: 10.6056/dkyqt201505024 |
| [4] |
黄世军, 康博韬, 程林松, 等. 海上普通稠油油藏多层合采层间干扰定量表征与定向井产能预测[J].
石油勘探与开发, 2015, 42(4): 488–495.
HUANG Shijun, KANG Botao, CHENG Linsong, et al. Quantitative characterization of interlayer interference and productivity prediction of directional wells in the multilayer commingled production of ordinary offshore heavy oil reservoirs[J]. Petroleum Exploration and Development, 2015, 42(4): 488–495. doi: 10.11698/PED.2015.04.10 |
| [5] |
张臣. 海上多层常规稠油油藏层间干扰影响因素研究[D]. 成都: 西南石油大学, 2015.
ZHANG Chen. Research on affecting factor of interlayer interference among commingling production layers in conventional offshore oilfield[D]. Chengdu:Southwest Petroleum University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10615-1015605851.htm |
| [6] |
安伟煜. 特高含水期多层非均质油藏层间干扰因素分析[J].
东北石油大学学报, 2012, 36(5): 76–82.
AN Weiyu. Interference mechanism of multilayer heterogeneous reservoir in high water-cut stage[J]. Journal of Northeast Petroleum University, 2012, 36(5): 76–82. doi: 10.3969/j.issn.2095-4107.2012.05.015 |
| [7] |
罗宪波, 赵春明, 刘英. 海上稠油油田投产初期产能评价研究[J].
断块油气田, 2011, 18(5): 630–633.
LUO Xianbo, ZHAO Chunming, LIU Ying. Study on deliverability evaluation of offshore heavy oil field at initial stage of production[J]. Fault-Block Oil & Gas Field, 2011, 18(5): 630–633. |
| [8] |
王峙博, 黄爱先, 魏进峰. 薄互层油藏层间干扰数值模拟研究[J].
石油天然气学报, 2012, 34(9): 247–250.
WANG Shibo, HUANG Aixian, WEI Jinfeng. Numerical simulation on interlayer interference of thin and interbed reservoirs[J]. Journal of Oil and Gas Technology, 2012, 34(9): 247–250. |
| [9] |
姚帅, 吴财芳, 李腾. 潘庄区块煤层气井间层间干扰数值模拟研究[J].
煤炭工程, 2014, 46(3): 80–83.
YAO Shuai, WU Caifang, LI Teng. Study on numerical simulation of interferences between stratum interfaces of coal bed methane well in Panzhuang Block[J]. Coal Engineering, 2014, 46(3): 80–83. doi: 10.11799/ce201403025 |
| [10] |
耿站立, 孙福街, 田冀, 等. 海上油田开发生产系统整体优化决策技术[J].
石油天然气学报, 2012, 34(3): 132–135.
GENG Zhanli, SUN Fujie, TIAN Ji, et al. Technology for optimization and decision of development-production system in offshore oilfields[J]. Journal of Oil and Gas Technology, 2012, 34(3): 132–135. doi: 10.3969/j.issn.10009752.2012.03.027 |
| [11] |
鲜波, 熊钰, 石国新, 等. 薄层油藏合采层间干扰分析及技术对策研究[J].
特种油气藏, 2007, 14(3): 51–54.
XIAN Bo, XIONG Yu, SHI Guoxin, et al. Interlayer interference analysis of commingled production in thin reservoirs and its technical countermeasures[J]. Special Oil & Gas Reservoirs, 2007, 14(3): 51–54. doi: 10.3969/j.issn.1006-6535.2007.03.014 |
| [12] |
余华杰, 朱国金, 谭先红. 砂岩油藏多层合采层间干扰及开发策略研究[J].
西南石油大学学报(自然科学版), 2014, 36(1): 101–106.
YU Huajie, ZHU Guojin, TAN Xianhong. Study on interlayer interference caused by commingling production and development strategy in sandstone reservoir[J]. Journal of Southwest Petroleum University(Science & Technology Edition), 2014, 36(1): 101–106. doi: 10.11885/j.issn.16745086.2012.06.06.01 |
| [13] |
李大建, 牛彩云, 吕亿明, 等. 低渗透油藏两层合采油井层间干扰分析[J].
西部探矿工程, 2012(12): 20–23.
LI Dajian, NIU Caiyun, LÜ Yiming, et al. Analysis on interlayer interference in low permeability reservoir two laminated production wells[J]. West-China Exploration Engineering, 2012(12): 20–23. doi: 10.3969/j.issn.10045716.2012.12.008 |
| [14] |
屈亚光, 刘月田, 汪国辉, 等. 高尚堡复杂断块油藏合理开发层系研究[J].
断块油气田, 2010, 17(6): 741–744.
QU Yaguang, LIU Yuetian, WANG Guohui, et al. Study on reasonable development layer series for complicated faultblock reservoir of Gaoshangpu Oilfield[J]. Fault-Block Oil & Gas Field, 2010, 17(6): 741–744. |
| [15] |
王渊, 何志雄, 李嘉瑞, 等. 低渗气藏多层合采层间干扰系数的确定[J].
科学技术与工程, 2012, 12(34): 9163–9166.
WANG Yuan, HE Zhixiong, LI Jiarui, et al. Determination of interlayer interference coefficient for commingling production in low permeability gas reservoir[J]. Science Technology and Engineering, 2012, 12(34): 9163–9166. doi: 10.3969/j.issn.1671-1815.2012.34.007 |
| [16] | BARRI A, ALNUAIM S. A graphical method to evaluate multi-reservoir commingling[C]. SPE 172194, 2014. doi:10.2118/172194-MS |
| [17] | RADLER M. Worldwide look at reserves and production[J]. Oil Gas Journal, 2011, 109: 26–29. |
| [18] |
张继成, 何晓茹, 周文胜, 等. 大段合采油井层间干扰主控因素研究[J].
西南石油大学学报(自然科学版), 2015, 37(4): 101–106.
ZHANG Jicheng, HE Xiaoru, ZHOU Wensheng, et al. Main controlling factors of interlayer interference in big intervals commingled production oil wells[J]. Journal of Southwest Petroleum University(Science & Technology Edition), 2015, 37(4): 101–106. doi: 10.11885/j.issn.16745086.2015.03.12.02 |
 2017, Vol. 39
2017, Vol. 39


