2. 中国地质大学(北京)能源学院, 北京 海淀 100083;
3. 山东新汶矿业集团有限责任公司, 山东 新汶 271219;
4. 西南石油大学地球科学与技术学院, 四川 成都 610500
2. School of Energy Resources, China University of Geosciences(Beijing), Haidian, Beijing 100083, China;
3. Shandong Xinwen Mining Group Co. Ltd., Xintai, Shandong 271219, China;
4. School of Geoscience and Technology, Southwest Petroleum University, Chengdu, Sichuan 610500, China
储层流体在地下的赋存及活动状态受地层现今应力及孔隙压力的综合影响[1],储层岩石现今应力场特征对油气运聚成藏、压裂增产措施及井壁稳定等方面的研究均具有重要指导意义[2-4]。现今应力场的研究内容包括现今地应力大小及方向,研究方法主要有实验测试法、测井解释法及模拟法[5],其中,测井及模拟方法依然需要实验测试的应力结果进行校正。具有强非均质性及各向异性的煤储层同时具有极强的应力敏感性[6]。因此,煤层中应力场特征的准确预测与否,将直接关系到煤层气排采方案(如生产压差、生产周期、水平井定向及压裂层段优选等)的制定[6-7]。同时,对于煤层而言,其埋深往往较浅,因而各主应力值通常较小[8]。因此,精确预测煤储层应力场分布特征尤为重要。
本文利用沁南樊庄区块北部煤层气井区二维地震资料,对区内石炭系—二叠系的构造样式及断层特征进行精细解释,在此基础上,对研究区山西组3号煤层现今应力场特征进行单井分析及平面模拟研究。研究结果可以为下一步制定合理煤层气开发方案提供合理依据。
1 研究区断裂构造解释研究区位于沁南樊庄区块北部的固县煤层气井区内,该区目前以开采煤层气为主,主采煤层为山西组3号煤层。研究区3号煤层埋深一般在300 800 m,区内分布稳定,厚度在5~8 m,含气量普遍高于15~m3/t。3号煤储层压力系数普遍小于1,具有负压、低渗及强非均质性特征。研究区具有背斜、向斜相间发育的构造特征,断层规模往往较小,地层产状总体有由西北向东南逐渐抬升的趋势。樊庄区块沉积地层单元划分、地层厚度及岩性统计见表 1,其中,3号煤层所属山西组厚39~79 m,平均厚度约50 m。
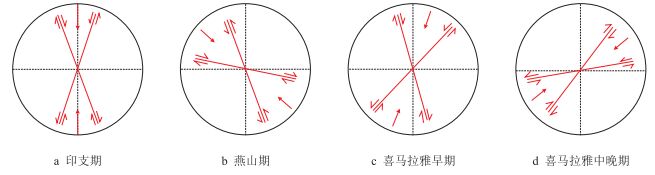
研究区经历了复杂的构造演化,褶曲及断裂的形成主要受以下4个期次的水平构造挤压运动影响[10](图 1):(1) 印支期,近SN向挤压;(2) 燕山期,NWW—SEE向挤压;(3) 喜马拉雅早期,NEE—SSW向挤压;(4) 喜马拉雅中晚期,NE—SW向挤压。樊庄区块的褶皱构造以NNE、近SN及NW向为主,这些褶皱的形成主要受控于燕山期及喜马拉雅期构造活动及相互叠加作用[10-12]。
利用研究区二维地震资料,对工区内石炭系—二叠系的构造样式及断层特征进行精细解释。研究区构造较为复杂,主控断层均为高角度正断层(图 2)。区内地层构造样式可划分为两大类:Ⅰ类为基底卷入式构造样式;Ⅱ类为断层滑脱式构造样式。其中,基底卷入式构造样式(Ⅰ类)又可细分为高角度断展褶皱(图 2a)及花状构造(图 2b)两种样式;断层滑脱式构造样式(Ⅱ类)主要为中—低角度断展褶皱(图 2c,图 2d)。
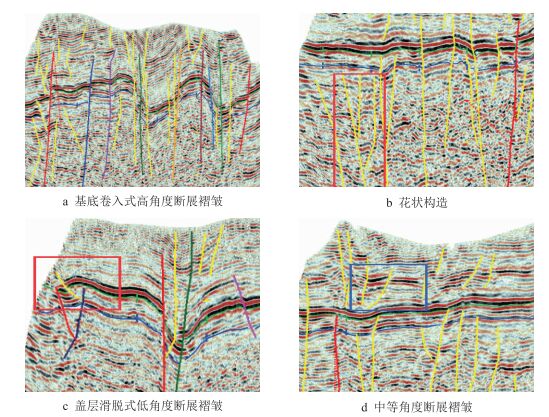 |
| 图2 研究区构造样式分类图 Fig. 2 Structure style division diagram in the studied area |
高角度断展褶皱在区内发育普遍,单条断层产状稳定,往往直插基底且穿透3号煤层(绿轴),但也有部分高角度正断层未穿透煤层。区内同时存在大量“花状断裂”,但其规模往往较小。从南向北,工区内切穿煤层的高角度断层越来越多,但花状断裂数量逐渐变少,且规模也越来越小。工区西部发育的高角度断层及少量花状断裂往往不切穿煤层;东部部分高角度断层及花状断裂往往切穿煤层。
2 单井现今应力特征地层现今应力的确定方法有很多,但只有差应变分析(DSA)和水力压裂测试能准确反映地层现今应力大小[13],其他方法如声发射及FMI法等测试或计算结果只能为地层现今应力的确定提供对比和参考[14-15]。
差应变分析的基本原理为:岩芯应力释放后微裂缝随之张开,通过对岩芯进行静水加压,加载过程中微裂缝首先闭合,其次为岩石骨架的变形,通过进行不同方向的差应变分析,确定各主应力的大小及方向。
水力压裂法则通过对压裂测试曲线数据进行分析计算,从而确定各主应力。该方法认为,地层的初始破裂发生在井壁切向应力最小的位置[16],若地层存在天然裂缝或节理等弱面,则初始破裂位置很可能出现在弱面处,而不一定发生在井壁切向应力最小的位置。因此,在应用该方法时,应选择地层完整的压裂井段,即选择在压裂施工曲线中能明显识别出破裂点的压裂井[17]。
在完整压裂过程中,压裂曲线清晰地记录了地层破裂压力、瞬时停泵压力及裂缝重张压力等参数值[18]。水平最小主应力(
| $\begin{equation} {\sigma _{\rm{H}}} = {\rm{3}}{p_{\rm{s}}} - {p_{\rm{r}}} - {p_{\rm{o}}} \end{equation}$ | (1) |
式中:
研究区煤层气井所压裂层段均位于3号煤层段,选取研究区压裂曲线具有明显破裂点的57口垂直井进行地应力分析,结果见图 3。
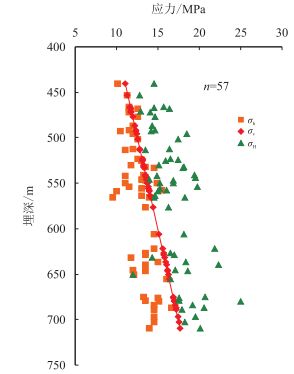 |
| 图3 压裂测试获得的研究区山西组3号煤各主应力大小随深度变化关系图 Fig. 3 Relationship of the value of the Shanxi Formation No.3 coal seam main stress obtained with the fracture tests and the buried depth |
从图 3可以看出,除少量异常(
研究中还发现,3号煤层的
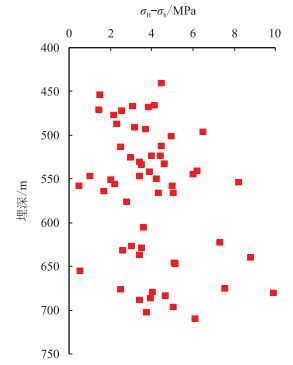
同时,水平方向主应力差(
 |
|
图4
3号煤层 |
地层破裂压力是指井筒内液柱压力升高到足以使无宏观裂缝地层产生新的破裂时所对应的压力值[23]。该压力的确定能为合理确定井深结构、安全钻井及压裂施工提供重要依据。压裂测试结果表明,3号煤层的破裂压力主要分布在12.0~30.0~MPa,该压力与
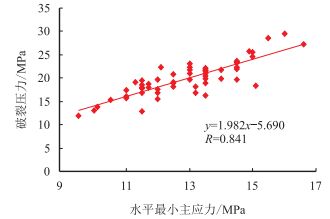 |
| 图5 3号煤层破裂压力与水平最小主应力关系图 Fig. 5 Relationship of the burst pressure and the minimum horizontal stress of No.3 coal seam |
对于研究区3号煤层的现今应力方向,可根据成像测井诱导缝分析方法确定[14-15]。钻井诱导缝是钻井过程中产生的裂缝,其优势分布方向代表现今水平最大主应力方向,根据该方法确定了研究区3口井水平最大主应力方向,见图 6。从图中可以看出,该地区应力方向整体上位于SN及NNE之间,与喜马拉雅中晚期构造挤压运动相关[10]。同时,该地区复杂构造特征及断裂的存在也会对地应力方向造成一定影响。如加拿大地下实验室(URL)的一竖井切过了两条逆断层[24],应力测试结果表明,断层两侧的应力方向最大可偏转近90°。复杂构造特征及断裂的存在对应力转向的具体影响机制目前来说尚未彻底解决,但普遍认为构造越复杂,同时断裂越发育,地应力方向越分散。
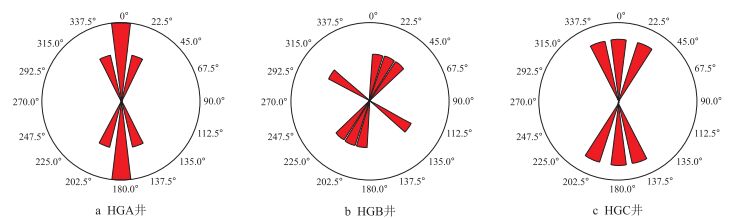 |
| 图6 钻井诱导缝优势方向分布玫瑰图 Fig. 6 The rose diagram of drilling induced fractures directions |
采用有限元法[3]对研究区3号煤层现今应力场进行了模拟。有限元网格划分的总体原则为细分网格以满足计算精度、粗分网格以减少计算工作量。考虑到研究区域内的各背斜、向斜构造及主要断裂对地应力场分布有较为重要的影响作用[25],在这些区域进行网格剖分时,网格间距尽量小一些;而在平缓构造带,为了减少计算工作量,这些区域的网格距离可以稍微取大一点。最终选择四边行网格进行剖分,同时,在褶皱及断层位置将单元细分,划分出14 996个单元,参与运算的节点14 992个。
在对不同单元体进行赋值时,考虑了断层及褶皱的影响。断层一般被认为是被弱化的区域,其弹性模量往往比地层岩石略低,而泊松比则比地层岩石略高[26, 27]。文献[26]认为,断层区域的弹性模量应为正常地层的50.0%~70.0%,而泊松比与正常地层的差值在0.02~0.10;文献[27]在对河西务构造带孔店期—沙四期进行应力场模拟时,认为断层区的弹性模量为正常地层的85.0%,泊松比与正常地层相差0.05,而密度则为正常地层的95.8%。对于褶皱,通常认为是被强化的区域,因此其弹性模量往往比正常地层略高,而泊松比则比正常地层略低。文献[26]认为,褶皱区地层弹性模量应为正常地层的1.5~3.0倍;而泊松比则比正常地层小0.01~0.15。考虑到研究区3号煤层的应力状态及所处挤压背景条件,根据岩石力学实验测试结果,最终定义各单元体力学参数赋值方案如表 2所示。其中,3号煤层弹性模量和泊松比根据三轴力学测试获得;抗张强度通过巴西劈裂实验获得;内聚力和内摩擦角则通过Mohr-Columb准则由岩样破坏时轴向应力
| 表2 应力场模拟力学参数取值表 Table 2 Mechanical parameter value in stress field simulation |
从表 2可以看出,3号煤层具有密度较小、弹性模量较低及泊松比较大的物理力学特征。由于3号煤层处于挤压环境,因而,研究区断层的物理力学参数赋值结果与3号煤层相差不大;其密度和弹性模量略小于煤层,而泊松比略高于煤层。对于褶皱区,其密度和弹性模量显著大于3号煤层,而泊松比则显著小于3号煤层;褶皱区弹性模量赋值约为3号煤层的1.85倍,泊松比与3号煤层差值为0.074。
对单元体赋值完成之后,对研究区3号煤层进行应力场模拟。根据前述研究区现今应力方向分析结果,设定
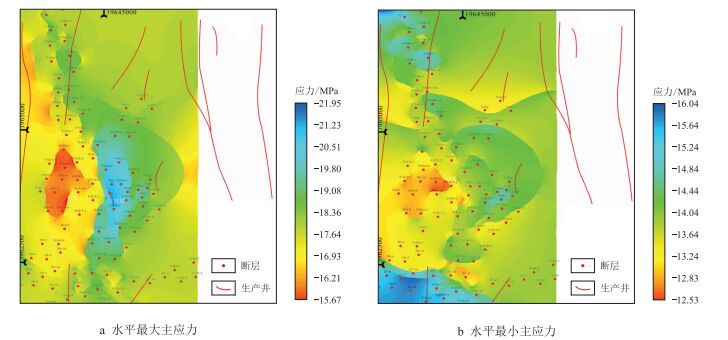 |
| 图7 研究区山西组3号煤层主应力平面分布图 Fig. 7 The plane distribution diagram of main stress of Shanxi formation No.3 coal seam in the studied area |
图中负号代表挤压应力[10, 25],研究区3号煤层
3号煤层的
图 8为加拿大URL竖井切过的两条逆断层[24](2号断层及3号断层,其中,1.9号断层和2.5号断层为2号断层的分支断层),从3种方法测试的
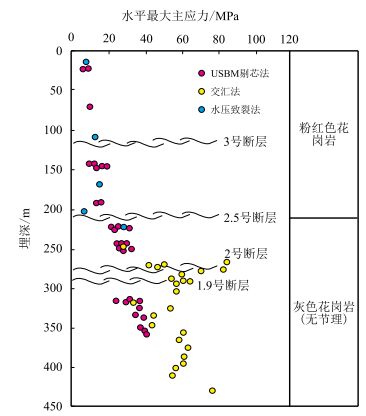 |
| 图8 加拿大URL水平最大主应力测试结果与埋深关系图[24] Fig. 8 Relationship of the tested Canada URL maximum horizontal stress results and the buried depth[24] |
对于本文研究区而言,模拟结果(图 7)显示,中部地区应力集中现象较为明显,
为了验证所模拟结果的可靠性,将研究区3号煤层的
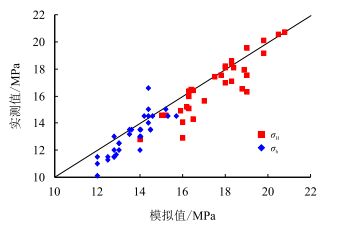 |
| 图9 3号煤层水平方向主应力模拟值与实测值对比图 Fig. 9 Compare of the simulated and measured results of No.3 coal seam horizontal main stress |
(1) 研究区主控断层为高角度(近垂直)正断层;地层构造样式可划分为基底卷入式及断层滑脱式两大类,可进一步细分为高角度断展褶皱、花状构造、中—低角度断展褶皱3小类。
(2) 研究区3号煤层主应力满足
(3) 研究区现今地应力在SN和NNE之间,与喜马拉雅中晚期的构造挤压运动相关;复杂的局部构造特征及断裂的存在会使地应力发生转向。
(4) 3号煤层
| [1] |
张跃磊, 李大华, 王青华, 等. 修正的页岩气等温吸附模型[J].
西南石油大学学报(自然科学版), 2016, 38(1): 107–112.
ZHANG Yuelei, LI Dahua, WANG Qinghua, et al. Modified isothermal adsorption model of shale gas[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2016, 38(1): 107–112. doi: 10.11885/j.issn.-1674-5086.2013.11.05.05 |
| [2] | PAUL S, CHATTERJEE R. Determination of in-situ stress direction from cleat orientation mapping for coal bed methane exploration in south-eastern part of Jharia Coalfield, India[J]. International Journal of Coal Geology, 2011, 87(2): 87–96. doi: 10.1016/j.coal.2011.05.003 |
| [3] | DING W, FAN T, YU B, et al. Ordovician carbonate reservoir fracture characteristics and fracture distribution forecasting in the Tazhong area of Tarim Basin, Northwest China[J]. Journal of Petroleum Science & Engineering, 2012, s86-87(3): 62–70. doi: 10.1016/j.petrol.2012.03.-006 |
| [4] |
尹帅, 单钰铭, 周文, 等. Hoek-Brown准则在致密砂岩弹性参数测井解释中的应用[J].
石油钻探技术, 2015, 43(1): 88–95.
YIN Shuai, SHAN Yuming, ZHOU Wen, et al. Appli-cation of Hoek-Brown criterion for tight sandstone elastic parameters in log interpretation[J]. Petroleum Drilling Techniques, 2015, 43(1): 88–95. doi: 10.11911/syztjs.-201501015 |
| [5] | KANG H, ZHANG X, SI L, et al. In-situ stress measurements and stress distribution characteristics in underground coal mines in China[J]. Engineering Geology, 2010, 116(3-4): 333–345. doi: 10.1016/j.enggeo.2010.-09.015 |
| [6] |
王建, 孔庆明, 董雄英. 二连盆地致密油形成特征及勘探潜力[J].
西南石油大学学报(自然科学版), 2016, 38(2): 11–19.
WANG Jian, KONG Qingming, DONG Xiongying. The formation characteristics and exploration potential of tight oil in Erlian Basin[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2016, 38(2): 11–19. doi: 10.11885/j.issn.1674-5086.2014.04.15.05 |
| [7] | WANG S, ELSWORTH D, LIU J. Mechanical behavior of methane infiltrated coal:The roles of gas desorption, stress level and loading rate[J]. Rock Mechanics and Rock Engineering, 2013, 46(5): 945–958. doi: 10.1016/j.ijrmms.-2015.08.022 |
| [8] | GUO Z, JIANG Y, PANG J, et al. Distribution of ground stress on Puhe Coal Mine[J]. International Journal of Mining Science and Technology, 2013, 23(1): 139–143. doi: 10.1016/j.ijmst.2013.03.004 |
| [9] |
秦勇, 梁建设, 申建, 等. 沁水盆地南部致密砂岩和页岩的气测显示与气藏类型[J].
煤炭学报, 2014, 39(8): 1559–1565.
QIN Yong, LIANG Jianshe, SHEN Jian, et al. Gas logging shows and gas reservoir types in tight sandstones and shales from southern Qinshui Basin[J]. Journal of China Coal Society, 2014, 39(8): 1559–1565. |
| [10] |
李月, 林玉祥, 于腾飞. 沁水盆地构造演化及其对游离气藏的控制作用[J].
桂林理工大学学报, 2011, 31(4): 481–487.
LI Yue, LIN Yuxiang, YU Tengfei. Tectonic evolution of Qinshui Basin and free gas reservoir control[J]. Journal of Guilin University of Technology, 2011, 31(4): 481–487. doi: 10.3969/j.issn.1674-9057.2011.04.002 |
| [11] |
林玉祥, 刘虎, 郭凤霞, 等. 沁水盆地地层剥蚀量研究[J].
地质与勘探, 2014, 50(1): 114–120.
LIN Yuxiang, LIU Hu, GUO Fengxia, et al. Strata erosion amount of the Qinshui Basin[J]. Geology and Exploration, 2014, 50(1): 114–120. |
| [12] |
王莹, 张庆龙, 朱文斌, 等. 沁水盆地北端中生代构造变形与构造应力场特征[J].
煤田地质与勘探, 2014, 42(1): 8–18.
WANG Ying, ZHANG Qinglong, ZHU Wenbin, et al. Mesozoic structural deformation and tectonic stress field characteristics in the north of Qinshui Basin[J]. Coal Geology & Exploration, 2014, 42(1): 8–18. doi: 10.3969/j.-issn.1001-1986.2014.01.002 |
| [13] | ZOBACK M D, BARTON C A, BRUDY M, et al. Determination of stress orientation and magnitude in deep wells[J]. International Journal of Rock Mechanics & Mining Sciences, 2003, 40(7): 1049–1076. |
| [14] | NELSON E J, MEYER J J, HILLIS R R, et al. Transverse drilling-induced tensile fractures in the West Tuna Area, Gippsland Basin, Australia:Implications for the in situ stress regime[J]. International Journal of Rock Mechanics & Mining Sciences, 2005, 42(3): 361–371. doi: 10.1016/j.ijrmms.2004.12.001 |
| [15] |
刘平礼, 兰夕堂, 李年银, 等. 酸预处理在水力压裂中降低伤害机理研究[J].
西南石油大学学报(自然科学版), 2016, 38(3): 150–155.
LIU Pingli, LAN Xitang, LI Nianyin, et al. A study on damage reduction mechanism of acid preflushing during hydraulic fracturing[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2016, 38(3): 150–155. doi: 10.11885/j.issn.1674-5086.2014.03.28.01 |
| [16] | DENG J, ZHU W, MA Q. A new seepage model for shale gas reservoir and productivity analysis of fractured well[J]. Fuel, 2014, 124(15): 232–240. doi: 10.1016/j.fuel.2014.-02.001 |
| [17] | LIU Chaoru. Distribution laws of in-situ stress in deep underground coal mines[J]. Procedia Engineering, 2011, 26: 909–917. doi: 10.1016/j.proeng.2011.11.2255 |
| [18] |
孟文, 陈群策, 吴满路, 等. 龙门山断裂带现今构造应力场特征及分段性研究[J].
地球物理学进展, 2013, 28(3): 1150–1160.
MENG Wen, CHEN Qunce, WU Manlu, et al. Research on segmentation and characteristic of tectonic stress field of Longmenshan fault zone[J]. Progress in Geophysics, 2013, 28(3): 1150–1160. doi: 10.6038/pg20130306 |
| [19] |
雍世和, 张超谟.
测井数据处理与综合解释[M]. 东营: 中国石油大学出版社, 2007.
YONG Shihe, ZHANG Chaomo. Logging data processing and comprehensive interpretation[M]. Dongying: China University of Petroleum Press, 2007. |
| [20] |
张立松, 闫相祯, 田中兰, 等. 基于可靠性方法的储层钻井坍塌压力分析[J].
石油学报, 2012, 33(3): 477–481.
ZHANG Lisong, YAN Xiangzhen, TIAN Zhonglan, et al. A collapse pressure analysis in reservoir drilling based on the reliability method[J]. Acta Petrolei Sinica, 2012, 33(3): 477–481. doi: 10.7623/syxb201203020 |
| [21] |
申瑞臣, 屈平, 杨恒林. 煤层井壁稳定技术研究进展与发展趋势[J].
石油钻探技术, 2010, 38(3): 1–6.
SHEN Ruichen, QU Ping, YANG Henglin. Advancement and development of coal bed wellbore stability technology[J]. Petroleum Drilling Techniques, 2010, 38(3): 1–6. doi: 10.3969/j.issn.1001-0890.2010.03.001 |
| [22] | GUO B, SHAN J, FENG Y. Productivity of blast-fractured wells in liquid-rich shale gas formations[J]. Journal of Natural Gas Science & Engineering, 2014, 18(18): 360–367. doi: 10.1016/j.jngse.2014.03.018 |
| [23] | ALKAN H, CINAR Y, PUSCH G. Rock salt dilatancy boundary from combined acoustic emission and triaxial compression tests[J]. International Journal of Rock Mechanics & Mining Sciences, 2007, 44(1): 108–119. doi: 10.1016/j.ijrmms.2006.05.003 |
| [24] | MARTIN C D. Characterizing in situ stress domains at the AECL underground research laboratory[J]. Canadian Geotechnical Journal, 1990, 27(27): 631–646. doi: 10.-1016/0148-9062(91)91035-P |
| [25] | KAI J, DING W L, HUANG W H, et al. Simulation of paleotectonic stress fields within Paleogene shale reservoirs and prediction of favorable zones for fracture development within the Zhanhua Depression, Bohai Bay Basin, east China[J]. Journal of Petroleum Science & Engineering, 2013, 110(7): 119–131. doi: 10.1016/j.petrol.2013.-09.002 |
| [26] | ZENG W, DING W, ZHANG J, et al. Fracture development in Paleozoic shale of Chongqing Area (South China). Part two:Numerical simulation of tectonic stress field and prediction of fractures distribution[J]. Journal of Asian Earth Sciences, 2013, 75(8): 267–279. doi: 10.1016/j.-jseaes.2013.07.014 |
| [27] |
戴俊生, 邹娟, 赵贤正, 等. 基于应力场模拟解释河西务构造带孔店沙四期断层特征[J].
天然气地球科学, 2014, 25(10): 1529–1535.
DAI Junsheng, ZOU Juan, ZHAO Xianzheng, et al. Fault characteristics interpretation of Ek-Es4 sedimentary period in Hexiwu tectonic belt through stress field simulation[J]. Natural Gas Geoscience, 2014, 25(10): 1529–1535. doi: 10.11764/j.issn.1672-1926.2014.10.1529 |
| [28] | COLMENARES L B, ZOBACK M D. A statistical evaluation of rock failure criteria constrained by polyaxial test data for five different rocks[J]. International Journal of Rock Mechanics & Mining Sciences, 2002, 39(6): 695–729. doi: 10.1016/S1365-1609(02)00048-5 |
| [29] | ZOBACK M D, ROLLER J C. Magnitude of shear stress on the San andress fault:Implications of a stress measurement profile at shallow depth[J]. Science, 1979, 206(4417): 445. doi: 10.1126/science.206.4417.445 |
| [30] |
高建理, 丁建民, 梁国平, 等. 龙羊峡水电站水压致裂应力测量[J].
岩石力学与工程学报, 1990, 9(2): 134–145.
GAO Jianli, DING Jianmin, LIANG Guoping, et al. Hydraulic fracturing stress measurement in Longyangxia water power stations[J]. Chinese Journal of Rock Mechanics and Engineering, 1990, 9(2): 134–145. |
 2017, Vol. 39
2017, Vol. 39