2. 中国石油塔里木油田分公司天然气事业部, 新疆 库尔勒 841000
2. Department of Gas, Tarim Oilfield Company, CNPC, Korla, Xinjiang 841000, China
地层中的油气资源是基于一定的钻采工艺,通过钻井系统在地层中形成井眼开采出来的。该钻井系统包括井架与顶驱等地面设备以及钻杆与钻头等井下设备,其中简要的钻柱系统主要包括转盘、钻柱以及钻头[1]。井口能量由持续转动的转盘输入钻柱系统,该能量通过钻柱由井口传至井底的钻头,钻头在下部钻具的重量及钻柱传递的扭矩下与地层直接作用,刮切岩石并形成井眼,钻头破碎的岩屑由钻井液带出井筒完成钻井过程[2]。
由于钻柱具有大长径比(其数值通常大于10 000,深井往往大于25 000) 的特性,其刚度很小,在地层的阻碍作用下,钻柱系统极易产生黏滑振动[3]。钻柱的黏滑振动是指在钻进过程中,转盘接受井口的能量输入并将其由钻柱传往井底,而钻头却因无法克服地层阻力而保持黏滞状态,待钻柱积蓄的能量足以打破黏滞状态后,钻头便在巨大的驱动力下高速运转[4]。钻柱系统的黏滑振动表现为钻头黏滞与滑脱状态不断地交替,钻头在滑脱阶段的速度及加速度通常都较高,这种振动造成钻头处能量的浪费,还容易引起下部钻具的提前失效并影响井身质量,进一步影响钻井效率与开发成本[5-7]。
随着油气勘探开发的不断进行,深井超深井数量逐步增大[8]。一方面,随井深的增加,岩石强度通常增大且可钻性变差,钻头打破岩石阻碍所需能量增加;另一方面,钻柱刚度随井深的增加而减小,钻柱系统更易于产生或加剧黏滑振动[9]。深部地层较高的岩石强度及剧烈的振动是深井段平均机械钻速普遍较低的原因。文献[10]报道了中国元坝地区深井钻进的研究,结果表明,深井段的平均机械钻速仅为上部井段平均机械钻速的15%~30%,部分地区该比例甚至低于8%。图 1所示为文献[11]给出的通过随钻测量得到的地面、随钻测量仪以及钻头处的角速度时程响应,表明下部钻具产生了明显的黏滑振动。
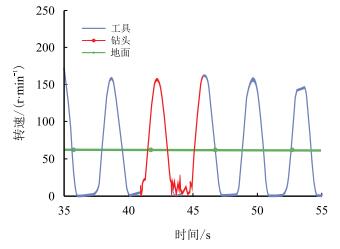 |
| 图1 现场的实钻数据[11] Fig. 1 Real time drilling data |
国外关于钻柱系统黏滑振动的研究已有数十年的历史,大量文献报道了钻井现场的黏滑振动现象,但黏滑振动方面的理论研究进展却相当缓慢[12]。随着深井钻进的不断增加,钻柱黏滑振动产生的影响也逐渐增大,引起学者与钻井人员的注意。近年来,针对黏滑振动的研究多集中于对黏滑现象的揭示以及通过测量井下参数判断井下的振动情况,然后根据振动情况进行钻井参数的主动控制[13-16]。然而,关于黏滑振动的产生机理及其振动特性的研究却鲜见报道[17]。研究黏滑振动的最终目的是进行振动控制,而掌握黏滑振动的产生机理及其振动特性却是实现黏滑振动控制的基础。从这一点出发,开展黏滑振动特性的研究具有重要的理论与应用价值。
1 钻柱黏滑振动力学模型 1.1 基本假设研究重点为钻柱系统的黏滑振动,为抓住主要矛盾,忽略次要因素,根据钻柱系统的工作特性建立基本假设:(1) 将钻柱系统简化为具有扭转刚度和集中质量的弹簧;(2) 忽略其他振动的影响,仅研究钻柱的黏滑振动;(3) 将钻头与井底岩石的互作用视为库仑摩擦。
1.2 建立黏滑振动力学模型黏滑振动发生时系统中的弹性元件周期性地储存和释放能量,在驱动力、摩擦力以及阻尼力等外力作用下,表现为振动物体周期性地停止和运动。随着能量持续不断地供给,物体形成稳定的周期运动。实际中的黏滑振动都较为复杂,现有关于黏滑振动的研究普遍使用经典的质量-弹簧-轮带模型[18-19]。该模型将工程系统简化为包含能量输入元件、振动器和转换装置的力学系统,可较好地解释许多实际工程中出现的黏滑振动现象。然而,对于该质量-弹簧-轮带模型,将其用于描述钻柱系统的黏滑振动将存在偏差,其主要原因在于该模型中能量输入来源于摩擦,而实际钻柱系统的能量由转盘输入。为此,建立如图 2所示的钻柱系统的黏滑振动力学模型。
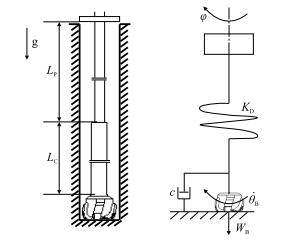 |
| 图2 钻柱系统黏滑振动力学模型 Fig. 2 Mechanical model of the stick-slip vibration |
图中:
g—重力加速度,g=9.8 m·s−2;
c—等效阻尼系数,N·m·rad−1;
对于产生黏滑振动的钻柱系统,钻头在黏滞阶段与滑脱阶段的运动方程不同。由于钻头所受的摩擦扭矩与其运动方向相反,摩擦扭矩具有分段特性。
对应黏滞阶段,钻头的速度为零,其运动方程可写为
| $\dot \theta _{\rm{B}} = 0$ | (1) |
该阶段钻头受力包括钻柱的驱动扭矩以及地层的静摩擦力,钻头所受钻柱施加的扭矩即弹簧的恢复力为
| $K_{\rm{D}} \varphi t = \dfrac{{{\rm{d}}V}}{{{\rm{d}}\theta _{\rm{B}} }}$ | (2) |
式中:
t—时间,s;
V—系统的势能,J;
对于所分析的钻柱系统,V的表达式可写为
| $V = \dfrac{1}{2}K_{\rm{D}} \left( {\theta _{\rm{B}} - \varphi t} \right)^2$ | (3) |
黏滞阶段钻头的约束力与恢复力大小相等方向相反,使钻头保持受力平衡,且约束力(静摩擦力)小于最大静摩擦力数值,即有
| $\left| {\dfrac{{{\rm{d}}V}}{{{\rm{d}}\theta _{\rm{B}} }}} \right| \leqslant \mu _{\rm{S}} W_{\rm{B}} \bar R_{\rm{B}}$ | (4) |
式中:
若式(4) 不满足,对应钻头处于滑脱状,即
| $\left| {\dot \theta _{\rm{B}} } \right| > 0$ | (5) |
滑脱阶段钻头的运动方程可由Euler-Lagrange方程表示,有
| $\dfrac{{\rm{d}}}{{{\rm{d}}t}}\left( {\dfrac{{ \partial T}}{{ \partial \dot \theta _{\rm{B}} }}} \right) = \dfrac{{ \partial T}}{{ \partial \theta _{\rm{B}} }} + Q$ | (6) |
式中:
T—系统的动能,J,
J—转动惯量,N·m·s2·rad−1;
Q—作用于系统的外载,N·m,其表达式可写为
| $Q = - \dfrac{{{\rm{d}}V}}{{{\rm{d}}\theta _{\rm{B}} }} + {\mathop{\rm sgn}} \left( {\dot \theta _{\rm{B}} } \right)\mu _{\rm{K}} W_{\rm{B}} \bar R_{\rm{B}} + c\dot \theta _{\rm{B}}$ | (7) |
式中:
结合式(6) 与式(7),得到滑脱阶段钻头的运动方程为
| $J\ddot \theta _{\rm{B}}\!+\!c\dot \theta _{\rm{B}}\!+\!K_{\rm{D}} \left( {\theta _{\rm{B}}\!-\!\varphi t} \right) + \mu _{\rm{K}} W_{\rm{B}} \bar R_{\rm{B}} {\mathop{\rm sgn}} \left( {\dot \theta _{\rm{B}} } \right) = 0$ | (8) |
式中:
假设井口转盘转速方向为顺时针,钻头打破黏滞后将形成顺时针转动,则方程(8) 可改写为
| $J\ddot \theta _{\rm{B}} + c\dot \theta _{\rm{B}} + K_{\rm{D}} \left( {\theta _{\rm{B}} - \varphi t} \right) + \mu _{\rm{K}} W_{\rm{B}} \bar R_{\rm{B}} = 0$ | (9) |
式(9) 为二阶非齐次常微分方程,根据微分方程理论,其解应由该式对应齐次方程的通解及其非齐次方程的一个特解叠加而成。假设产生黏滑振动的钻柱系统为欠阻尼系统(实际系统多为欠阻尼系统,且一般有阻尼比
| $\theta _{\rm{B}} = A{\rm{e}}^{ - \xi \omega _n t} \sin \left( {\sqrt {1 - \xi ^2 } \omega _n t + \psi } \right) + \varphi t -\\ \hspace{4em}\dfrac{{\mu _{\rm{K}} W_{\rm{B}} \bar R_{\rm{B}} }}{{K_{\rm{D}} }}$ | (10) |
式中:
A—由初始条件确定的振幅,rad;
4个参数的表达式为
| $\omega _n = \sqrt {\dfrac{{K_{\rm{D}} }}{J}}$ | (11) |
| $\xi = \dfrac{c}{{2J}}/\sqrt {\dfrac{{K_{\rm{D}} }}{J}}$ | (12) |
| $A=\sqrt {\left( {\theta _{{\rm{B0}}}\!+\!\dfrac{{\mu _{\rm{K}} W_{\rm{B}} \bar R_{\rm{B}} }}{{K_{\rm{D}} }}} \right)^2+\left[{\dfrac{{\varphi-\dot \theta _{{\rm{B0}}}+\xi \omega _n \left( {\theta _{{\rm{B0}}}+\dfrac{{\mu _{\rm{K}} W_{\rm{B}} \bar R_{\rm{B}} }}{{K_{\rm{D}} }}} \right)}}{{\sqrt {1-\xi ^2 } \omega _n }}} \right]^2 }$ | (13) |
| $\psi = \arctan \dfrac{{\sqrt {1 - \xi ^2 } \omega _n \left( {\theta _{{\rm{B0}}} + \dfrac{{\mu _{\rm{K}} W_{\rm{B}} \bar R_{\rm{B}} }}{{K_{\rm{D}} }}} \right)}}{{\varphi - \dot \theta _{{\rm{B0}}} + \xi \omega _n \left( {\theta _{{\rm{B0}}} + \dfrac{{\mu _{\rm{K}} W_{\rm{B}} \bar R_{\rm{B}} }}{{K_{\rm{D}} }}} \right)}}$ | (14) |
式中:
对于产生黏滑振动的系统,当系统进入滑脱阶段时钻头的角位移滞后于转盘。设
| $\theta _{{\rm{B0}}} = - \dfrac{{\mu _{\rm{K}} W_{\rm{B}} \bar R_{\rm{B}} }}{{K_{\rm{D}} }}$ | (15) |
为形象地描述钻头的振动响应,分析如表 1所示参数系统的振动,部分参数请参考文献[20]。黏滑阶段的钻头处于静止状态,结合式(15) 便可确定钻头进入滑脱阶段的初始条件,由式(10)~式(14) 可进一步得到钻头的振动响应。
| 表1 系统参数表 Table 1 Parameters of the drilling system |
图 3所示为表 1所给参数的钻柱系统中钻头的绝对角位移时程响应。由图可知,系统产生了黏滑振动,表现为钻头的运动为周期运动,且黏滞与滑脱状态交替出现。由于转盘持续地顺时针转动,钻头在钻柱驱动下其角位移总体上呈不断增大的趋势,且角位移的平均增速与转盘转速的数值相当。
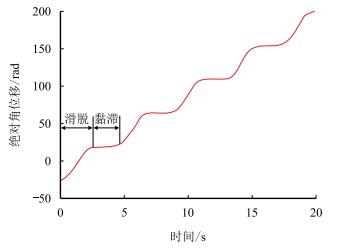 |
| 图3 钻头绝对角位移时程响应 Fig. 3 Time history of the absolute angular displacement of drill bit |
分析钻柱系统中钻头的绝对角速度时程响应,见图 4。
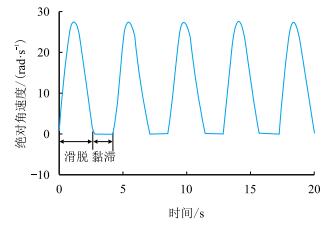 |
| 图4 钻头绝对角速度时程响应 Fig. 4 Time history of the absolute angular velocity of drill bit |
根据该响应可确定钻头的绝对角速度,还可得到钻头黏滑振动的周期特性。由图 4可知,对于产生黏滑振动的该钻柱系统,钻头在滑脱阶段的运动为类似简谐的运动,钻头在滑脱阶段的最大角速度是其常规转速(转盘转速)的2.8倍,这一结果与现场实测结果相吻合[21-22]。钻头滑脱阶段较大的转速将使下部钻具产生较大的应力,同时黏滞与滑脱的不断交替将使钻具受力交替循环,由此容易导致下部钻具的失效。
由于钻头的绝对角位移随时间的增加不断增大,因此,由钻头绝对角位移和绝对角速度所得的钻头绝对运动相轨迹将随绝对角位移坐标不断延伸。而钻头相对转盘的角位移与角速度均维持在一定范围,为考察钻头相对转盘运动的相轨迹,在得到钻头的绝对角位移及绝对角速度后,通过计算式
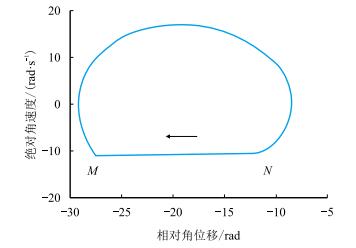 |
| 图5 钻头相对转盘运动相轨迹 Fig. 5 Phase trajectory of the relative motion between the drill bit and the rotary table |
工程中的自激振动表现为系统以自身的运动状态作为调节器以控制能量的输入,系统能自主地从定常的能量输入单元中吸收能量。对于钻进中的钻柱而言,钻头与地层间的摩擦作用构成耗散的振动单元,转盘的转动构成稳定的能量输入单元,而连接转盘与钻头的弹性钻柱便构成调节器,因此钻柱系统具备形成自激振动的条件。
自激振动在相平面内的相轨迹通常是唯一的孤立封闭曲线,称为极限环。当相点由于扰动而偏离极限环后,系统将沿新的相轨迹运动。若扰动后的相轨迹仍渐近地贴近极限环,那么认为该极限环是稳定的,对应于物理上可实现的自激振动。当系统产生自激振动时,其振幅和频率由系统的物理参数唯一确定,与初始条件无关。
在前述钻头振动响应的分析中,钻头相对转盘运动的相轨迹形成孤立封闭的相轨迹。那么,对于确定系统参数的可形成黏滑振动的钻柱系统,是否也具有与初始条件无关的极限环呢?为了解答这一问题,下面研究不同钻头初相点对应的相轨迹。
对于所选参数的钻柱系统,当钻头转速为零且其相对转盘的角位移位于
在钻井过程中,由于钻井环境的复杂性,钻头处可能具有不同的初始条件,例如钻头卡钻可能使其形成初始角位移大于由静摩擦扭矩形成的初始角位移,井下冲击可能使钻头在克服最大静摩擦扭矩的时刻具有初速度。前面已得到钻头黏滑振动的黏滞区间,下面研究位于黏滞区间外的初始条件。分析钻头初相点远离极限环的情形,以
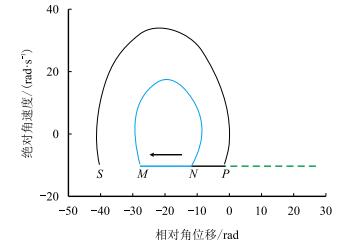 |
| 图6 初相点远离极限环时的相轨迹 Fig. 6 Phase trajectory of initial phase point far away from the loop |
图 6中,绿色、黑色以及蓝色直线共同组成钻头的黏滞区间。钻头在经历初始阶段的滑脱后便进入黏滞区间(由S点运动至P点),随后相点沿黑色相轨迹由P点运动至N点并继续直线运动至M点。由于钻头在初始滑脱后便进入黏滞区间,随后钻头将形成稳定的黏滑振动,其运动相轨迹如图中的蓝色相轨迹所示(即图 5)。由此说明,当钻头初相点远离极限环时,钻头在经历初始阶段的滑脱将产生稳定的黏滑振动,相点的运动收敛于唯一孤立的封闭相轨迹。
对于表 1所给参数,分析钻头初相点靠近极限环的情形,以
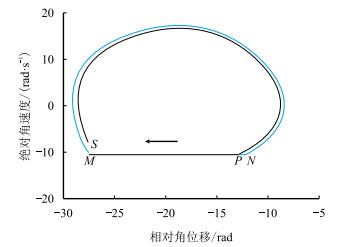 |
| 图7 初相点靠近极限环时的相轨迹 Fig. 7 Phase trajectory of initial phase point close to the loop |
对于上面所分析的两种情形,钻头最终都将产生稳定的黏滑振动,表现为相轨迹收敛于同一封闭相轨迹,即系统在初始扰动下都将收敛于唯一孤立的封闭相轨迹。由此说明,系统的黏滑振动为自激振动,振动形成了稳定的极限环。除上述所选初始条件的参数外,其他参数组合也可证明该结论。
4 自激振动产生的原因当钻头处于黏滞状态时,其
| $T_{{\rm{BS}}} \leqslant T_{{\rm{BS}}\max } = \mu _{\rm{S}} W_{\rm{B}} \bar R_{\rm{B}}$ | (16) |
钻头处于黏滞阶段时其运动方程可写为
| $J\ddot \theta _{\rm{B}} + c\dot \theta _{\rm{B}} + K_{\rm{D}} \left( {\theta _{\rm{B}} - \varphi t} \right) + T_{{\rm{BS}}} = 0$ | (17) |
对应于黏滞向滑脱状态转变的临界状态,有
| $J\ddot \theta _{\rm{B}} + c\dot \theta _{\rm{B}} + K_{\rm{D}} \left( {\theta _{\rm{B}} - \varphi t} \right) + T_{{\rm{BS}}\max } = 0$ | (18) |
当钻头处于滑脱状态时,所受动摩擦扭矩与钻头相对转盘角位移无关,摩擦扭矩维持常值且与动摩擦系数成正比
| $T_{{\rm{BK}}} = \mu _{\rm{K}} W_{\rm{B}} \bar R_{\rm{B}}$ | (19) |
对应滑脱阶段钻头的运动方程为
| $J\ddot \theta _{\rm{B}} + c\dot \theta _{\rm{B}} + K_{\rm{D}} \left( {\theta _{\rm{B}} - \varphi t} \right) + T_{{\rm{BK}}} = 0$ | (20) |
考察钻头的临界平衡状态,即黏滞转变为滑脱状态的临界点。当钻头处于黏滞状态时其运动方程由式(17) 表示,当钻头进入滑脱状态时其运动方程则由式(20) 表示。对于该临界状态,钻头的运动方程既满足式(18) 又满足式(20)。不难发现,两个方程左端前3项均相同,而最后一项存在差异
| $\Delta T_{\rm{B}} = T_{{\rm{BS}}\max } - T_{{\rm{BK}}} = \Delta \mu W_{\rm{B}} \bar R_{\rm{B}} \ne 0$ | (21) |
式中:
对于钻头的另一个平衡状态,即滑脱转变为黏滞的临界点,钻头在滑脱阶段和黏滞阶段的运动方程分别为式(20) 和式(17)。当钻头在进入黏滞状态时式(17) 中的静摩擦扭矩
| $T_{{\rm{BS}}} = K_{\rm{D}} \left( {\theta _{\rm{B}} - \varphi t} \right)$ | (22) |
方程(16)~(22) 便构成钻柱系统黏滑振动的数学模型。为便于分析,给出表 1所示参数的钻柱系统中钻头所受地层的摩擦扭矩时程响应(图 8)。
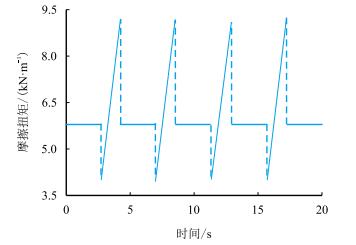 |
| 图8 钻头所受地层的摩擦扭矩 Fig. 8 Time history of the frictional on the drill bit |
对于产生黏滑振动的系统,钻头由黏滞状态转变为滑脱状态时其所受的摩擦扭矩由最大静摩擦扭矩降到动摩擦扭矩水平。这个力使钻头受力不平衡从而打破黏滞状态并使钻头加速运动。在此过程中钻头角速度增加而摩擦扭矩减小,可认为摩擦扭矩对钻头角速度的导数为负值且该数值的绝对值相当大,相当于出现了负阻尼力。这种负阻尼力破坏了系统平衡点的稳定性(对应平衡运动为与转盘相同转速的匀速运动),从而使系统发生软激励的自激振动。当然,对于所采用的库仑摩擦模型,如果不考虑静动摩擦扭矩间的差值,该负阻尼力也就不存在。
滑脱状态的钻头在滑脱阶段的后期处于衰减振动状态,对应钻柱的驱动扭矩小于摩擦扭矩。与上述分析类似,当钻头由滑脱状态转变为黏滞状态时,钻头所受的摩擦扭矩由动摩擦扭矩突然变为静摩擦扭矩,而且该静摩擦扭矩数值小于动摩擦扭矩。相当在由滑脱状态转变至黏滞状态的瞬间,钻头上作用了负阻尼力,这种负阻尼力打破钻头原来的运动状态,迫使其进入稳定的黏滞状态。当钻头进入黏滞状态后,钻头所受摩擦扭矩不断增加,其数值大小与钻柱驱动扭矩相等,钻柱的势能也不断增大,直至摩擦扭矩的数值增至最大静摩擦扭矩后进入下一个滑脱状态。
因此,钻头在临界状态转变时均存在负阻尼效应,由此将钻柱的振动调节为自激振动。
5 结论(1) 对于产生黏滑振动的系统(例如表 1所给参数的系统),钻头在滑脱阶段呈类似简谐的运动,黏滞与滑脱状态周期性地交替。在转盘的作用下,钻头的绝对角位移总体上具有与转盘转速相当的增速,钻头相对转盘的运动在相平面上表现为封闭的相轨迹。
(2) 钻头的运动存在由最大静摩擦扭矩与钻柱刚度确定的黏滞区间,若转速减至零的钻头相对转盘的角位移位于该区间内,钻头将进入稳定的黏滑振动状态且该振动的振幅与频率由系统的物理参数唯一确定。当存在初始扰动时,钻头在经历初始阶段的波动后均将迅速进入黏滑振动状态,表现为其相轨迹均收敛于稳定的极限环。
(3) 分析系统处于黏滞与滑脱状态转变的临界状态,结果表明钻头在状态转变时其所受的摩擦扭矩均存在降落,相当于沿钻头转动方向存在外载,即产生了负阻尼效应。这种负阻尼效应对系统动能与势能进行调节,将钻柱的振动调节为自激振动。
| [1] | LIAO C M. Experimental and numerical studies of drillstring dynamics[D]. Maryland, University of Maryland, 2011. http://drum.lib.umd.edu/handle/1903/12269 |
| [2] | ALBDIRY M T, ALMENSORY M F. Failure analysis of drillstring in petroleum industry:a review[J]. Engineering Failure Analysis, 2016, 65: 74–85. doi: 10.1016/j.engfailanal.2016.03.014 |
| [3] | BAUMGART A. Stick-slip and bit-bounce of deep-hole drillstrings[J]. ASME Journal of Energy Resources Technology, 2000, 122(2): 78–82. doi: 10.1115/1.483168 |
| [4] |
祝效华, 汤历平, 童华. 高频扭转冲击钻进的减振与提速机理研究[J].
振动与冲击, 2012, 31(20): 75–78.
ZHU Xiaohua, TANG Liping, TONG Hua. Rock breaking mechanism of a high frequency torsional impact drilling[J]. Journal of Vibration and Shock, 2012, 31(20): 75–78. |
| [5] | PUEBLA H, RAMIREZ J A. Suppression of stick-slip in drillstrings:a control approach based on modelling error compensation[J]. Journal of Sound and Vibration, 2008, 310(4): 881–901. doi: 10.1016/j.jsv.2007.08.020 |
| [6] | LEINE R I, CAMPEN D H, KEULFJES W J G. Stick slip whirl interaction in drillstring dynamics[J]. ASME Journal of Vibration and Acoustics, 2002, 124(2): 209–220. doi: 10.1115/1.1452745 |
| [7] | ZHU X H, TANG L P, TONG H. Effects of high-frequency torsional impacts on rock drilling[J]. Rock Mechanics and Rock Engineering, 2014, 47(4): 1345–1354. doi: 10.-1007/s00603-013-0461-0 |
| [8] | GULYAEV I, SOLOV'EV I L, GORBUNOVICH I V. Stability of drillstrings in ultradeep wells:an integrated design model[J]. International Applied Mechanics, 2009, 45(7): 772–779. doi: 10.1007/s10778-009-0219-2 |
| [9] |
王大勋, 刘洪, 韩松, 等. 深部岩石力学与深井钻井技术研究[J].
钻采工艺, 2006, 29(3): 6–10.
WANG Daxun, LIU Hong, HAN Song, et al. Deep rock mechanics and deep or ultra-deep well drilling technology[J]. Drilling & Production Technology, 2006, 29(3): 6–10. doi: 10.3969/j.issn.1006-768X.2006.03.003 |
| [10] |
张克勤. 元坝地区钻井难题分析与技术对策探讨[J].
石油钻探技术, 2010, 38(3): 27–31.
ZHANG Keqin. Problems arising from drilling operations in Yuanba Area and its solutions[J]. Petroleum Drilling Techniques, 2010, 38(3): 27–31. doi: 10.3969/j.issn.1001-0890.2010.03.006 |
| [11] | LEDGERWOOD L W, JAIN J R, HOFFMANN O J, et al. Downhole measurement and monitoring lead to an enhanced understanding of drilling vibrations and polycrystalline diamond compact bit damage[J]. SPE Drilling & Completion, 2013, 28(3): 254–262. doi: 10.2118/134488-PA |
| [12] | ZHU X H, TANG L P, YANG Q M. A literature review of approaches for stick-slip vibration suppression in oilwell drillstring[J]. Adcances in Mechanical Engineering, 2014, 2014(6): 1–17. doi: 10.1155/2014/967952 |
| [13] | LAI S W, WOOD M J, EDDY A J, et al. Stick-slip detection and friction factor testing using surface-based torque and tension measurements[C]. SPE 170624, 2016. doi:10.2118/170624-PA |
| [14] | SUAREZ R H, PUEBLA H, LOPEZ RA, et al. An integral high order sliding mode control approach for stickslip suppression in oil drillstrings[J]. Journal of Petroleum Science and Technology, 2009, 27(8): 788–800. doi: 10.-1080/10916460802455483 |
| [15] | ZRIBI M, KARKOUB M, HUANG C C. Control of stick slip oscillations in oil well drillstrings using the back stepping technique[J]. International Journal of Acoustics and Vibration, 2011, 16(3): 134–143. doi: 10.20855/ijav.2011.-16.3289 |
| [16] | LIU H, GIRSANG I P, DHUPIA J S. Identification and control of stick-slip vibrations using Kalman estimator in oil-well drill strings[J]. Journal of Petroleum Science and Engineering, 2016, 140: 119–127. doi: 10.1016/j.petrol.2016.01.017 |
| [17] | GHASEMLOONIA A, RIDEOUT D G, BUTT SD. A review of drillstring vibration modeling and suppression methods[J]. Journal of Petroleum Science and Engineering, 2015, 131: 150–164. doi: 10.1016/j.petrol.2015.04.030 |
| [18] | VAN DE VRANDE B L, VAN CAMPEN D H, DE KRAKER A. An approximate analysis of dry-frictioninduced stick-slip vibrations by a smoothing procedure[J]. Nonlinear Dynamics, 1999, 19(2): 157–169. doi: 10.1023/A:1008306327781 |
| [19] | ABDO J, ABOUELSOUD A A. Analytical approach to estimate amplitude of stick-slip oscillations[J]. Journal of Theoretical and Applied Mechanics, 2011, 49(4): 971–986. |
| [20] | NAVARRO-LÓPEZ E M, LICÉAGA-CASTRO E. Nondesired transitions and sliding-mode control of a multiDOF mechanical system with stick-slip oscillations[J]. Chaos Solitons & Fractals, 2009, 41(4): 2035–2044. doi: 10.1016/j.chaos.2008.08.008 |
| [21] | RICHARD T, GERMAY C, DETOURNAY E. A simplified model to explore the root cause of stick slip vibrations in drilling systems with drag bits[J]. Journal of Sound and Vibration, 2007, 305(3): 432–456. doi: 10.1016/j.jsv.-2007.04.015 |
| [22] | PELFRENE G, SELLAMI H, GERBAUD L. Mitigating stick-slip in deep drilling based on optimization of PDC bit design[C]. SPE 139839, 2011. doi:10.2118/139839-MS |
 2017, Vol. 39
2017, Vol. 39


