西南石油大学学报(自然科学版)  2017, Vol. 39 Issue (4): 159-167
引用本文
赵广慧, 梁政, 李毅平, 等. 海洋浮式平台钻机井架动态响应的试验研究[J]. 西南石油大学学报(自然科学版), 2017, 39(4): 159-167.
ZHAO Guanghui, LIANG Zheng, LI Yiping, et al. Experimental Research on Dynamic Responses of Derrick of Offshore Floating Drilling Platform[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2017, 39(4): 159-167.
海洋浮式平台钻机井架动态响应的试验研究    [PDF全文]
赵广慧1 , 梁政1, 李毅平2, 蒋发光1, 叶哲伟1    
1. 西南石油大学机电工程学院, 四川 成都 610500;
2. 中国石油宝鸡石油机械有限责任公司, 陕西 宝鸡 721002
收稿日期: 2015-04-28; 网络出版时间: 2017-11-24
基金项目: 国家高技术研究发展计划（863计划）（2012AA09A20301）。
作者简介: 赵广慧, 1971年生, 女, 汉族, 河北石家庄人, 教授, 博士(后), 主要从事与石油天然气装备相关的力学问题研究。E-mail:wy_zgh@126.com;
梁政, 1960年生, 男, 汉族, 四川广安人, 教授, 博士生导师, 主要从事石油天然气装备设计与制造方面的研究。E-mail:liangz_2242@126.com;
李毅平, 1973年生, 男, 汉族, 四川巴中人, 工程师, 主要从事钻井装备的国际市场销售。E-mail:lyp@bomco.cn;
蒋发光, 1975年生, 男, 汉族, 四川大英人, 讲师, 博士, 主要从事石油天然气装备设计与仿真的教学与研究工作。E-mail:jiangfg@126.com;
叶哲伟, 1981年生, 男, 汉族, 湖北孝感人, 讲师, 主要从事油气地面装备及井下工具方面的研究工作。E-mail:yzw0135@126.com。
通信作者: 赵广慧, E-mail:wy_zgh@126.com
摘要: 深水浮式平台钻机井架在海洋环境载荷和平台运动条件下会受到较大的动态载荷。为评价浮式平台运动对井架动力响应的影响，以某海洋浮式平台及其配套的塔型井架为依据，按照相似原理设计了井架模型及其平台的6自由度运动条件，利用大型地震模拟试验台阵系统实施了动态井架试验。对振动台沿6个自由度方向单独激励以及模拟作业工况、生存工况和设计生存工况的6自由度耦合激励条件下井架各测点的加速度和动态应变进行测试。发现井架对于纵摇和垂荡激励最敏感，而对艏摇激励不敏感；钩载的变化对井架动态响应的影响不大；基于平台在风浪流沿不同方向入射的运动响应，发现在迎风迎浪迎流条件下井架的动态响应幅值最大，受力状况最恶劣。
关键词: 深水浮式平台     钻机井架     试验研究     单自由度激励     6自由度耦合激励    
Experimental Research on Dynamic Responses of Derrick of Offshore Floating Drilling Platform
ZHAO Guanghui1 , LIANG Zheng1, LI Yiping2, JIANG Faguang1, YE Zhewei1    
1. School of Mechanical Engineering, Southwest Petroleum University, Chengdu, Sichuan 610500, China;
2. CNPC Baoji Oilfield Machinery Co. LTD, Baoji, Shaanxi 721002, China
Abstract: The drilling rig derrick of floating platform is often subjected to big dynamic loadings from marine environmental pressure and platform movement. In order to evaluate the influence of platform movement on dynamic responses of derrick, a derrick model and six-degree-of-freedom (6-DOF) moving boundaries, which were based on one offshore floating platform and the matching tower-shaped derrick, were designed according to similarity principle and test of the dynamic derrick was carried out by means of large-scale seism simulation test-tables. Acceleration and dynamic strain were measured under vibrational excitations with each single DOF and coupling 6-DOF, which modeled platform movement under operating condition, survival condition and design survival condition. It's found that the derrick is the most impressible to pitch and heave driving, and relatively insensitive to yaw driving. Hook load has little effect on derrick's dynamic responses. Based on the movement of the platform under the combined loads of the wave, current and wind that are from different directions, we find that the dynamic response of the derrick is the strongest with the incidence angle of 180 degree. Experimental results would provide reference for design of the matching derrick for drilling rig of deep-water floating platform.
Key words: deep-water floating platform     drilling rig derrick     experimental research     single DOF driving     coupling 6-DOF driving    
引言

随着石油勘探开发力度日益加大，陆地石油资源必将趋向枯竭，各国纷纷将勘探开发的目光转向海洋。目前中国油气勘探开发集中在浅海、近海区域，平台以固定式和自升式为主，近年来投运的“海洋石油981”开创了中国深水浮式钻井平台设计制造的先河，如何系统实现深水浮式平台钻井装备的研发具有重要的意义。

海洋深水浮式钻井平台在钻井作业时，平台始终处于6自由度运动状态(纵荡、垂荡、横荡、纵摇、横摇、艏摇)，钻机井架安装于平台上部，随平台的运动而运动，井架将承受较大的动态载荷，从而可能导致疲劳失效和稳定性问题。与陆地钻机或固定式平台钻机相比，浮式平台钻机的特别之处就在于平台动边界效应的影响，目前国内外尚无浮式平台钻机井架的设计标准，亦未见相关的理论与试验研究的报道。关于钻机井架的研究大多是针对固定基础的陆地钻机或固定式平台钻机[1-5]，对井架进行的试验研究主要是静载荷下的强度测试以及固有频率测试[6-8]。周国强等[9-11]通过测试在役井架的固有频率来确定井架的临界承载能力；胡军等[12]针对海洋自升式平台钻机井架测试了固有频率以及应变和加速度时程，其激振力来自于风载、起下钻柱和钻进作业载荷。对于浮式平台钻机井架动态性能的测试方面，中国目前只有胡鹏等[13, 14]自制了6自由度摇摆试验台，可以模拟纵摇、横摇及小幅度升沉运动，摇摆频率分别为10 s和7 s，摇摆角度为2°与5°，并按1:10尺寸比例设计了一套塔形模型井架，进行了动边界条件下井架动力响应的测试，其测试结果与仿真结果进行了对照验证[14]。

为了更真实地反映浮式平台运动对井架动态响应的影响，以某半潜式平台在南海海域的运动响应及其配套的10 000 m海洋钻机的塔型井架为依据，按照相似理论设计井架模型及其平台的6自由度运动条件，依托桥梁工程结构动力学国家重点实验室完成了针对各种单自由度激励和对应各种工况的6自由度耦合激励条件下井架的动态响应测试，为深水浮式钻井平台配套井架的设计提供依据。

1 井架试验模型设计

平台钻机的井架，在振动时其位移较小，忽略重力的影响，采用弹性力相似律[15-16]。以长度[L]、弹性模量[E]和密度[$\rho$]为基本物理量，综合考虑实验室的高度限制、加载设备条件和测量仪器的测试范围，选取模型井架与原型井架同材料，基本比例常数分别选为：长度比尺$\lambda_{\rm L}=7$、密度比尺${{\lambda }_{\rho }}=1$和弹性模量比尺${\lambda _{\rm E}}=1$，则原型井架与模型井架的主体尺寸如表 1所示。

表1 井架主体尺寸表 Table 1 The main dimensions of derrick

井架模型整体分为两个部分：上部尖劈和下部井架，每部分井架内部之间采用焊接连接，上、下部之间采用螺栓连接，同时在螺栓连接处加焊板进行加固；井架大腿与振动台之间采用螺栓连接，安装于振动台上的模型井架如图 1所示。

图1 安装在振动台上的井架模型 Fig. 1 Derrick model installed on shaking table

井架随平台摇摆时，其重力会产生横向分力，加之受到横向惯性力的作用，井架的变形以弯曲为主，因此在模型井架型钢选取时把截面惯性矩当作主要因素。原型井架主体使用了12种H型钢，考虑加工难度，把惯性矩相差不大以及作用相近的选为同一种类型。依据相似原理得到的模型惯性矩较小，没有对应型号的H型钢或工字钢，以模型关于两个形心轴惯性矩的比值尽量与原型接近、焊接方便且模型型钢的厚度不小于3 mm为原则，模型井架选用了5种矩形型钢，各种型钢的“长度×宽度×壁厚”及其在模型井架中的位置如图 2所示。

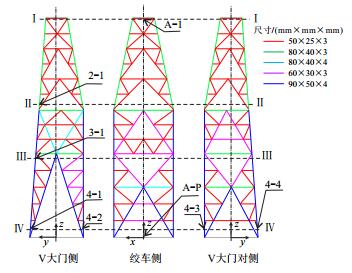图2 模型井架矩形型钢选用及其测点布置示意图 Fig. 2 Selected rectangular shape steel and sensor location of the derrick model
2 测试方案

平台钻机井架的模型试验是在“桥梁工程结构动力学国家重点实验室”的大型地震模拟试验台上进行的，如图 1所示。该系统采用了目前国际上最先进的数字控制系统和软件，输入波采用国际单位制的加速度时程，可以实现6个自由度耦合运动。

2.1 测点布置和测试原理

为了考察井架试验模型在不同运动状态下的动力响应，在井架上选取了Ⅰ~Ⅳ共4个截面，共布置56个应变测点：在截面Ⅰ-Ⅰ的4个大腿上共布4个测点；截面Ⅱ-Ⅱ和Ⅲ-Ⅲ的大腿、斜杆和横杆上共18个测点，其中第二层12个，第三层6个；截面Ⅳ-Ⅳ的大腿和斜杆上共32个测点，部分特征测点的位置如图 2所示。应变测点均布置在杆件横向尺寸的中间位置处，避开杆件端部复杂应力的影响，且均沿杆件轴向布设以测量相应杆件的轴向应变。应变测试采用电阻应变片以及Dewetron公司的DEWE-501型64通道动态信号采集系统，可同时记录64路电压和应变信号。

为了考察试验模型井架的运动响应情况，在模型井架顶端的4根横梁、V大门对侧和绞车侧的主要横梁上共布置14个加速度传感器，测试模型在两个水平方向(x向和y向)的动态响应；在振动台台面上布置3个加速度传感器，测量振动台沿3个坐标方向的加速度响应，对比振动台的输出运动与输入运动显示，振动台的激励时程与振动反馈基本重合，满足试验要求。

2.2 模型加载

模型加载通过以下两个方面实施：

(1) 在模型井架的顶端施加大钩载荷。钩载通过液压系统调节液压缸的拉力模拟(图 3)，此拉力通过上顶板移至井架顶端，平均施加在井架顶端的4个节点上。考虑井架的最大钩载、集中力比例尺以及液缸参数，施加于模型井架的最大钩载选为140 kN。

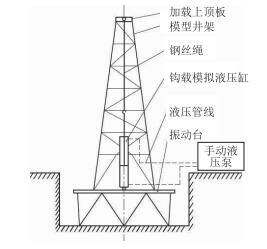图3 模型大钩载荷加载示意图 Fig. 3 Ketch of hook load

(2) 通过振动台的运动边界条件对井架进行加载。为尽可能准确地模拟井架在海洋浮式平台运动条件下的动态响应，基于某深海浮式平台在各种工况(一年一遇的作业工况、十年一遇的生存工况以及百年一遇的设计生存工况)、风浪流沿不同方向入射条件下的运动响应，通过移动平均法对位移时程数据进行光滑并求二阶导数得到其加速度时程，然后通过线加速度比例尺${\lambda _a}$=1/7和角加速度比例尺${\lambda _\alpha }$=1/49转换为振动台的加速度时程。振动台的加速度驱动边界条件在下面第3部分给出。

3 振动台驱动条件和测试结果

在振动台分别沿纵荡、横荡、垂荡、横摇、纵摇和艏摇方向的单自由度驱动以及振动台6自由度耦合驱动条件下，测量井架各个测点的加速度或应变随时间的变化。在每个试验工况前均进行一次清零处理，即应变测试结果中不包含静载荷成分，只有动态响应部分。

3.1 单自由度驱动

单自由度驱动试验是沿着每一个自由度方向单独驱动振动台，按比例改变激励强度，测取各个测点的加速度和应变时程，评价井架对各个方向激励的敏感程度。以纵荡方向的单独激励为例，在实际平台所有工况中提取纵荡加速度峰值最大工况对应的运动时程数据，依据相似关系转换为试验平台的纵荡加速度驱动数据，记作axmax（t）(amax—最大线加速度，m/s2；t—时间，s；下标x—沿纵荡方向)，坐标系选取如图 2所示。将此加速度时程所有时刻的值按比例因子0.2、0.4、0.6和0.8进行缩小，记为0.2axmax、0.4axmax、0.6axmax和0.8axmax，加之axmax激励条件共进行5组试验。井架动力响应对其他5个单自由度方向敏感性的评价与此类同，单自由度激励共进行了30组试验测试。

3.1.1 单自由度激励边界条件

振动台沿着纵荡、横荡和垂荡3个方向最大幅值的线加速度激励时程曲线如图 4a，图 4b，图 4c所示，沿着横摇、纵摇和艏摇3个方向最大幅值的角加速度激励时程曲线如4d，图 4e，图 4f所示。下面分别从模型井架的运动响应和动力响应两个方面进行研究。

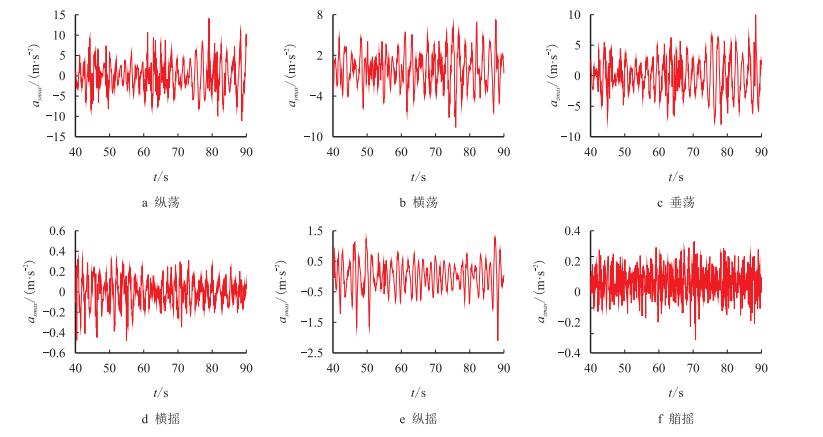图4 平台沿着6个单自由度方向激励的加速度时程曲线 Fig. 4 Time history of driving acceleration along the six DOFs
3.1.2 加速度响应

在纵荡最大幅值加速度的激励条件下(图 4a)，井架顶端A-1点与平台上A-P点(图 2)的x方向加速度时程对比见图 5($a_x$—x方向线加速度，m/s2)。

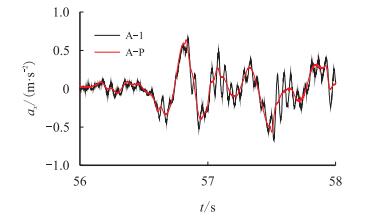图5 x方向的加速度时程对比 Fig. 5 Time history of x-axis acceleration

综合图 6所示平台及其顶端加速度的功率谱图可知，井架顶端较之于平台的加速度响应，在18.99 Hz处出现一个峰值，即多了高频成分，但低频成分是一致的。其他自由度方向激励的情况与之类似。

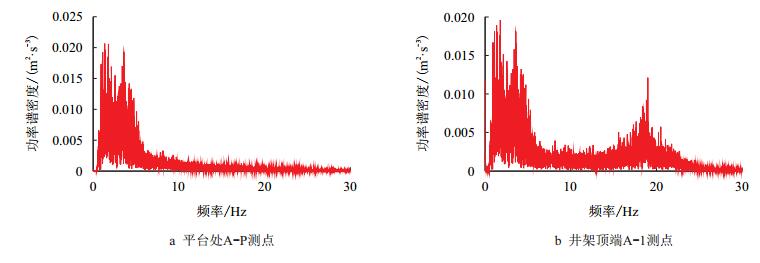图6 x方向加速度功率谱 Fig. 6 Power spectrum ofx-axis acceleration

由于井架的弹性以及结构不对称，在某一自由度方向激励时，其他自由度方向也会出现运动响应，但幅值很小。

3.1.3 应变响应

在各单自由度激励条件下，对比井架大腿上不同高度测点的动力响应，确定井架受力恶劣的位置。振动台以最大纵荡加速度幅值激励时(如图 4a)各层特征测点的应变时程如图 7所示，可见第2层测点2-1的幅值稍小，第3层测点3-1和第4层测点4-1的振荡时程基本重合。其他5个自由度方向单独激励条件下，各层测点应变时程对比有相似的规律。这样以第4层测点4-1作为特征点，研究井架对各个自由度方向激励强度的敏感度。

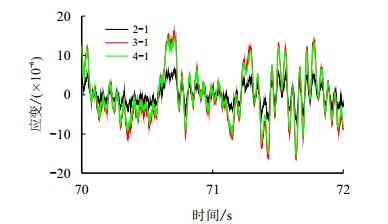图7 最大纵荡加速度激励下，不同高度测点的应变时程 Fig. 7 Time history of dynamic strain

图 8给出沿6个单自由度方向、大腿根部4-1点的应变幅值(应变幅值=最大应变-最小应变)随该方向加速度激励强度(用该方向最大加速度激励时程的比例因子表示)的变化曲线。

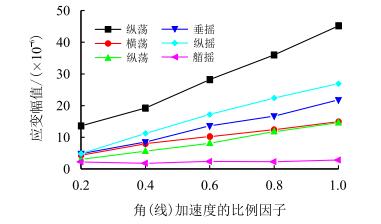图8 大腿根部4-1点应变幅值随激励强度的变化 Fig. 8 The amplitude of strain of the point 4-1 vs. driving strength

由图 8可见各单自由度方向的应变响应均随激励加速度幅值的增大而增大，表明平台运动强度决定了井架动载荷的大小，且井架在纵荡方向的动力响应最显著。动力响应对纵摇激励最敏感，最大y向角加速度激励下应变幅值是0.2倍y向角加速度${\alpha _{y\max }}$激励下的5.6倍，其次是垂荡方向的4.87倍和横摇方向的4.3倍；艏摇方向的动力响应最弱，且对激励强度变化最不敏感，激励幅值增大为5倍时，其应变幅值仅增大为1.27倍。

3.2 6自由度驱动

为真实评价井架在各种海况条件下的动态特性，试验模拟了一年一遇的作业工况、十年一遇的生存工况以及百年一遇的设计生存工况，对应每一种工况风浪流分别沿着90°、135°和180°入射，将各种工况条件下平台6自由度耦合的运动响应依据相似关系转换为振动台的6自由度耦合驱动时程。其中生存工况和设计生存工况不加钩载；作业工况的3种入射角度条件下，将最大钩载140 kN分成5个等级分别施加，即不加钩载以及钩载分别为40，80，120和140 kN，评价钩载对井架动力响应的影响。这样6自由度耦合的试验一共进行21组。

3.2.1 作业工况—钩载的影响

以风浪流沿135°入射的工况为例，说明井架的动力响应特征以及钩载对响应的影响。

模拟该工况的振动台加速度驱动时程如图 9所示。图 9a为纵荡、横荡和垂荡的线加速度驱动时程，图 9b为横摇、纵摇和艏摇的角加速度驱动时程。变换5组钩载，测得大腿根部4-1测点的应变时程如图 10a所示，该测点的应变幅值随钩载的变化如图 10b所示，可见应变幅值随着钩载的增大而减小，钩载从0增大到140 kN，其动应变幅值的相对减小率为13%，井架的动力响应主要为平台运动引起的动态载荷。

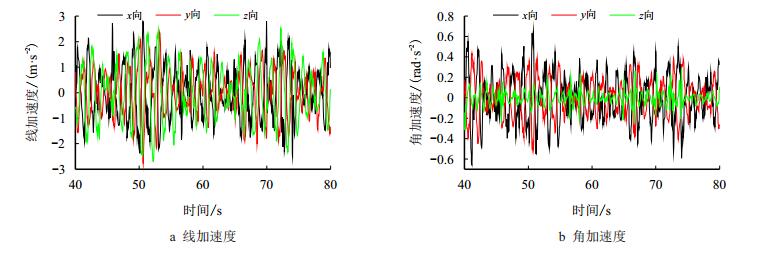图9 风浪流沿135°入射的作业工况下平台激励加速度时程 Fig. 9 Acceleration driving of shaking table under operating condition with incoming angle of wind-wave-current being 135°
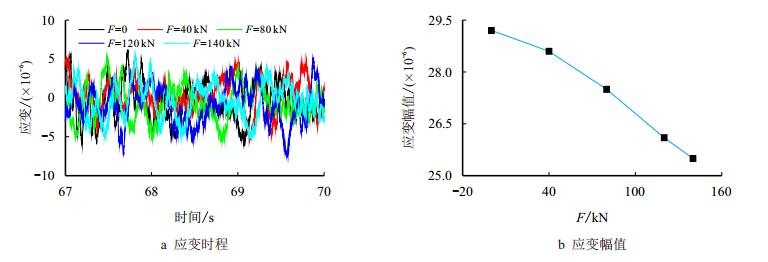图10 下4-1点的应变时程，应变幅值随钩载变化曲线 Fig. 10 For point 4-1, Time history of strain and the amplitude of strain vs. hook load
3.2.2 生存工况—入射角度的影响

模拟风浪流分别沿90°、135°和180°入射的十年一遇生存工况下振动台的驱动加速度如图 11~ 图 13所示，大腿根部测点4-1在以上3种激励条件下的动应变时程见图 14。4条大腿根部测点4-1、4-2、4-3和4-4的应变幅值随入射角度的变化见图 15，这4个测点在风浪流沿180°入射条件下的应变响应最强烈，近似为90°响应的3倍，因此井架在平台迎风迎浪迎流的条件下动力响应最强；4-4点的动态应变响应幅值高达98.2×10-6，为4个测点中的最大值，对应%折算为动态应力的的应力响应幅值为20.622 MPa。

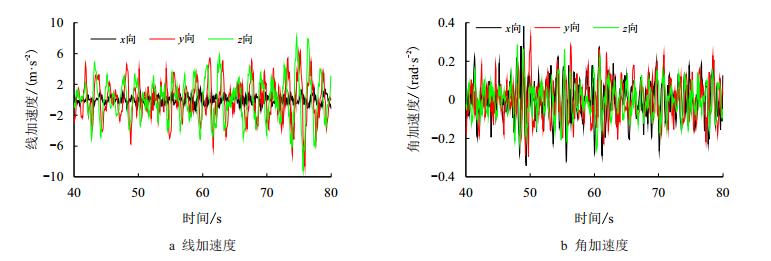图11 风浪流沿90°入射的生存工况下的平台激励加速度时程 Fig. 11 Acceleration driving of shaking table with incoming angle of 90°
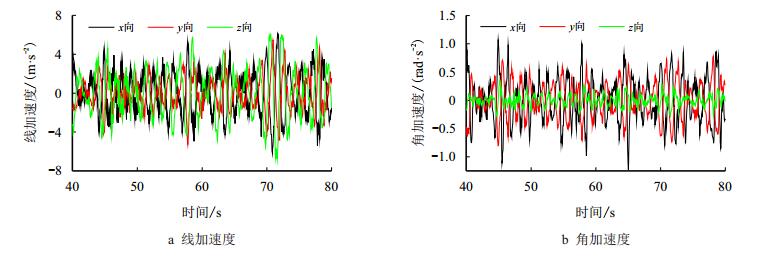图12 风浪流沿135°入射的生存工况下的平台激励加速度时程 Fig. 12 Acceleration driving of shaking table with incoming angle of 135°
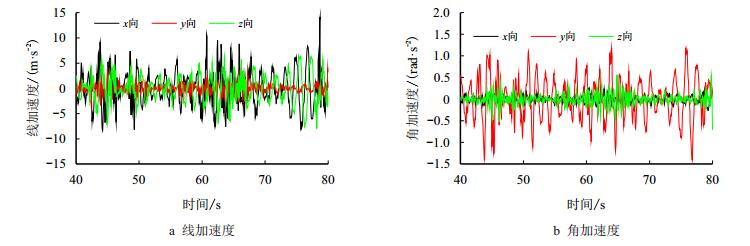图13 风浪流沿180°入射的生存工况下的平台激励加速度时程 Fig. 13 Acceleration driving of shaking table with incoming angle of 180°
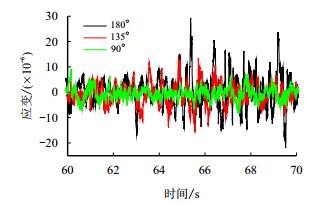图14 风浪流沿不同角度入射条件下4-1测点的应变 Fig. 14 Time history of strain at point 4-1
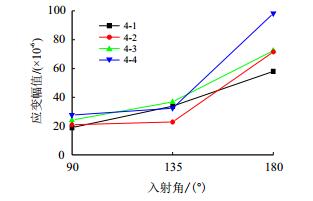图15 应变幅值随风浪流入射角度的变化 Fig. 15 The amplitude of strain vs. incoming angle
3.2.3 风浪流强度对井架动态响应的影响

风浪流沿135°入射、零钩载条件下，对应作业工况、生存工况以及设计生存工况的大腿根部测点4-1的动应变时程如图 16所示，振动台加速度驱动时程分别如图 9、图 12和图 17所示。

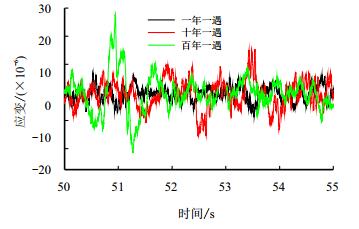图16 不同海况下4-1测点的动应变时程 Fig. 16 Time history of dynamic strain of point 4-1
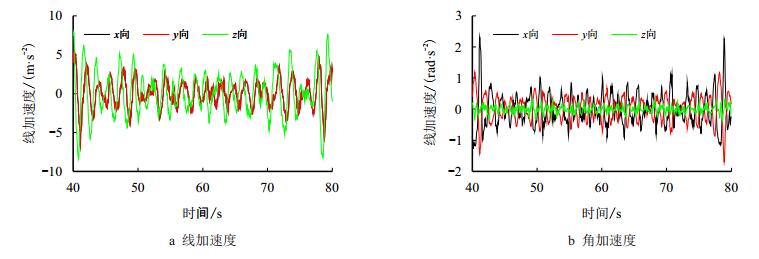图17 风浪流沿135°入射的设计生存工况下的平台激励加速度时程 Fig. 17 Acceleration driving of shaking table under design survival condition with incoming angle of wind-wave-current being 135°

3种工况下大腿根部动态应变幅值分别为29.2×10-6、33.9×10-6和49.2×10-6，随着海洋风、浪、流强度的加大，平台运动响应加剧，使得井架的动力响应加强。

4 结论

(1) 由于井架的弹性以及结构的不对称性，使得井架顶端的加速度响应较之于平台加速度出现高频成分，而两者的低频响应是一致的。

(2) 各个单自由度激励条件下，井架下段的动力响应幅值均大于上段，大腿根部的受力最为恶劣；且平台在纵荡方向激励时井架的动力响应最显著。

(3) 井架动力响应对平台纵摇激励的强度变化最敏感，对艏摇最不敏感。

(4) 井架动应变的幅值随钩载的增大而有所减小，但变化量不大。

(5) 相比于风浪流横向入射(90°)和斜向入射(135°)，平台在迎风迎浪迎流(180°)条件下运动时，井架的动力响应最强烈。

(6) 海洋环境载荷越恶劣，井架动力响应的振荡幅值越大。

参考文献
[1] GUAN F, DUAN M L, ZHOU C X, et al. Assessment of actual bearing capacity of offshore drilling and workover rig derrick[C]//Proceedings of the 20th international offshore and polar engineering conference, Beijing, June 20-25, 2010. Beijing, China:ISOPE, 2010.
[2] GUSELLA V, SPADACCINI O, VIGNOLI A. Dynamic identification of Vega platform drilling derrick[C]//Proceedings of the 2nd international offshore and polar engineering conference, San Francisco, USA, June 14-19, 1992. San Francisco, California, USA:ISOPE, 1992.
[3] GUSELLA V, SPADACCINI O, VIGNOLI A. In-service dynamic behavior of a drilling derrick on a jacket platform[J]. International Journal of Offshore and Polar Engineering, 1996, 6(3): 184–194.
[4] 刘清友, 何霞, 庞东晓, 等. 海洋修井机井架风洞实验方案设计[J]. 石油机械, 2003, 31(4): 12–12, 34.
LIU Qingyou, HE Xia, PANG Dongxiao, et al. Scheme design of wind tunnel test of ocean workover rig[J]. China Petroleum Machinery, 2003, 31(4): 12–12, 34. doi: 10.-3969/j.issn.1001-4578.2003.04.005
[5] 齐明侠, 胡朋, 许亮斌. 海洋钻机井架动态特性研究综述与展望[J]. 石油机械, 2011, 39(4): 80–83.
QI Mingxia, HU Peng, XU Liangbin. Reviews and future directions on dynamic features of offshore drilling derrick[J]. China Petroleum Machinery, 2011, 39(4): 80–83.
[6] 周国强, 韩东颖, 郭奕珊. 井架模型极限载荷试验[J]. 石油机械, 2005, 33(9): 9–11.
ZHOU Guoqiang, HAN Dongying, GUO Yishan. Ultimate load test of derrick model[J]. China Petroleum Machinery, 2005, 33(9): 9–11. doi: 10.3969/j.issn.1001-4578.2005.09.003
[7] 韩玉强. 钻井井架动力测试与综合性能评价[J]. 机械科学与技术, 2012, 31(10): 1649–1653.
HAN Yuqiang. Dynamic characteristics test and comprehensive performance evaluation of drilling derrick[J]. Mechanical Science and Technology for Aerospace Engineering, 2012, 31(10): 1649–1653. doi: 10.13433/j.cnki.1003-8728.2012.10.006
[8] 于广云, 葛新辉, 李宏波, 等. 钢结构井架动力特性测试分析与提高承载力研究[J]. 土木工程学报, 2006, 39(6): 61–65.
YU Guangyun, GE Xinhui, LI Hongbo, et al. Test and analysis of dynamic characteristics and enhanced bearing capacity of steel headframes[J]. China Civil Engineer-ing Journal, 2006, 39(6): 61–65. doi: 10.3321/j.issn:1000-131X.2006.06.011
[9] 周国强, 赵庆梅, 韩东颖. 实验室井架模型的动态测试研究[J]. 石油钻采工艺, 2006, 28(5): 10–12.
ZHOU Guoqiang, ZHAO Qingmei, HAN Dongying. Dynamic testing study of the lab derrick model[J]. Oil Drilling & Production Technology, 2006, 28(5): 10–12. doi: 10.3969/j.issn.1000-7393.2006.05.004
[10] 韩东颖, 周国强, 李子丰, 等. 基于振动测试参数的井架钢结构极限承载力预测[J]. 振动与冲击, 2011, 30(1): 106–110.
HAN Dongying, ZHOU Guoqiang, LI Zifeng, et al. Ultimate bearing capacity prediction of derrick steel structures based on dynamic measurement parameters[J]. Journal of Vibration and Shock, 2011, 30(1): 106–110. doi: 10.3969/-j.issn.1000-3835.2011.01.023
[11] 刘金梅, 周国强, 韩国有, 等. 波浪作用下海洋石油井架模态参数识别与承载力评价[J]. 海洋工程, 2009, 27(1): 22–27.
LIU Jinmei, ZHOU Guoqiang, HAN Guoyou, et al. Modal parameters identification and bearing capacity evaluation for ocean oil-derrick under wave excitation[J]. The Ocean Engineering, 2009, 27(1): 22–27. doi: 10.3969/j.-issn.1005-9865.2009.01.004
[12] 胡军, 唐友刚, 李士喜. 海洋钻机井架振动检测及评估——以ZJ50/3150DB钻机为例[J]. 石油勘探与开发, 2013, 40(1): 117–120.
HU Jun, TANG Yougang, LI Shixi. Vibration test and assessment for an ocean drilling rig derrick:Taking the ZJ50/3150DB drilling rig as an example[J]. Petroleum Exploration and Development, 2013, 40(1): 117–120.
[13] 胡朋. 浮式钻井平台塔形井架的动态特性研究[D]. 青岛: 中国石油大学, 2011.
HU Peng. Dynamic characteristic research of T-derrick on floating drilling platform[D]. Qingdao:China University of Petroleum, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10425-1011287424.htm
[14] 胡朋, 齐明侠. 半潜式钻井平台上钻机井架振动分析[J]. 石油机械, 2010, 38(11): 1–4.
HU Peng, QI Mingxia. An analysis of the derrick vibration of the drilling rig on the semi-submersible drilling platform[J]. China Petroleum Machinery, 2010, 38(11): 1–4.
[15] 林皋, 朱彤, 林蓓. 结构动力模型试验的相似技巧[J]. 大连理工大学学报, 2000, 40(1): 1–8.
LIN Gao, ZHU Tong, LIN Bei. Similarity technique for dynamic structural model test[J]. Journal of Dalian University of Technology, 2000, 40(1): 1–8. doi: 10.3321/j.-issn:1000-8608.2000.01.001
[16] 张曙光. 建筑结构试验[M]. 北京: 中国电力出版社, 2005.