2. 中国石油北京天然气管道有限公司, 北京 朝阳 100101
2. Beijing Natural Gas Pipeline Co. Ltd., PetroChina, Chaoyang, Beijing 100101, China
随着国民经济的发展,人们对天然气的需求量越来越大,天然气储存设施越来越多。储气库是天然气生产调峰和天然气资源储备的最佳选择[1-3]。储气库井的一个突出问题是生产管柱与套管密闭环空带压问题,并且难以判断问题来源[4-5]。对于高温高压天然气井测试和生产初期的环空带压问题,国内外做了一定的研究[6-10]。研究表明,对于充满液体的密闭环空,生产管柱内温度、压力的变化,均会引起环空压力的变化。这些研究所考虑的影响因素越来越多,计算方法越来越复杂,但没有对主要影响因素进行分析研究,现场应用困难;另外,对储气库环空带压研究较少。文献[11]对储气库油套环空进行了分析,建立了注入氮气柱的密闭环空压力变化计算模型,但没有考虑环空液体压缩问题。文献[12]对油气井密闭环空压力进行了分析,建立了计算密闭环空压力的数学模型,但是计算量大,没有对主要影响因素进行分析。
针对以上问题,本文基于管柱弹性力学平面应变理论、物质的热胀冷缩性质及流体PVT状态方程等,建立了储气库注采井在生产管柱内温度、压力变化时,密闭环空压力的计算模型,对储气库注采井、天然气井优化管柱设计和简化环空带压计算过程均具有较好的指导意义。
1 密闭环空分析模型根据储气库现场实际简化井身结构,采用如图 1所示的模型来进行分析。
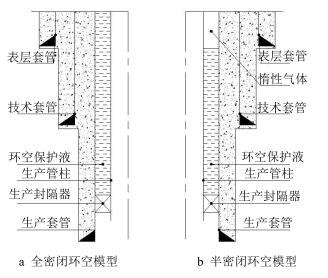 |
| 图1 简化的储气库井油管套管组合模型示意图 Fig. 1 Simplified model of tube-casing and casing string at gas storage well |
在注采油管外,利用下部封隔器和井口油管悬挂器,密封了封隔器上部的油套环空。图 1a是常规储气库井,完井后环空密闭了保护液,后续称为全密闭环空;图 1b是部分储气库井,完井后环空上部填充了预置一定压力的氮气[11],后续称为半密闭环空。
储气库井注采时,生产管柱(简称管柱)内部会发生压力、温度的变化,进而引起密闭环空的温度、压力变化,亦即表现为环空压力的变化。为简化分析计算,假设如下:
(1) 生产套管、外水泥环、技术套管及地层刚性,不会产生位移和变形;
(2) 管柱热传导性能良好,不考虑管壁的热量损失;
(3) 管柱壁厚均匀,封隔器和井口不移动。
2 数理解析模型的建立对于两端固定的管柱,内压力的增大将会使管柱外径增大,环空体积缩小,密闭环空压力增加;外压力的增大将会使管柱外径减小,环空体积增大[13-14]。对于两端密闭的环形空间,温度的升高,环空压力增加,将会使油管外径减小。此期间压力、温度、体积等相互耦合。
2.1 内外压力变化引起的管柱变形根据弹性力学平面应变状态下厚壁筒径向位移公式,得到管柱任一点r处的径向位移
| $u_{\rm{r}} = \dfrac{{\left( {1 + \mu } \right)r}}{{E\left( {b^2 - a^2 } \right)}}\left[{\left( {1-2\mu + \dfrac{{b^2 }}{{r^2 }}} \right)a^2 p_{\rm{i}}-\left( {1-2\mu + \dfrac{{a^2 }}{{r^2 }}} \right)b^2 p_{\rm{o}} } \right]$ | (1) |
式中:
E—管柱弹性模量,MPa;
a,b—管柱的内半径、外半径,m;
r—管柱管体上任一点至管柱圆心的距离,m;
对于图 1所示的管柱,主要研究在管柱内外压力变化情况下,引起的环空体积及压力变化。因此,只考虑压力引起外半径,即r=b的变化,式(1) 变为
| $u_{\rm{b}} = \dfrac{{\left( {1 + \mu } \right)b}}{{E\left( {b^2 - a^2 } \right)}}\left[{2\left( {1-\mu } \right)a^2 p_{\rm{i}}-\left( {1-2\mu + \dfrac{{a^2 }}{{b^2 }}} \right)b^2 p_{\rm{o}} } \right]$ | (2) |
如果管柱内压力变化为
| $\Delta u_{{\rm{b}}1} = 2\dfrac{{1 - \mu ^2 }}{E}\dfrac{{ba^2 }}{{b^2 - a^2 }}\Delta p_{\rm{i}}$ | (3) |
| $\Delta V_1 = π \left[{(b + \Delta u_{{\rm{b1}}} )^2-b^2 } \right]L$ | (4) |
式中:
L—分析管柱长度,m。
如果管柱外压力变化为
| $\Delta u_{{\rm{b2}}} = - \dfrac{{1 + \mu }}{E}\dfrac{b}{{b^2 - a^2 }}\left[{a^2 + (1-2\mu )b^2 } \right]\Delta p_{\rm{o}}$ | (5) |
| $\Delta V_2 = π \left[{(b + \Delta u_{{\rm{b2}}} )^2-b^2 } \right]L$ | (6) |
式中:
温度变化时,管柱将发生热膨胀或冷收缩。其体积变化将引起外环空的体积变化。假设管柱为各向同性固体,其体积膨胀系数为
| $\gamma = 3\alpha$ | (7) |
式中:
γ—管柱的热体积膨胀系数,1/℃;
α—管柱的热线膨胀系数,1/℃。
管柱热体积变化为
| $\Delta V_3 = \gamma π \left( {b^2 - a^2 } \right)\Delta TL$ | (8) |
式中:
温度升高,将引起环空保护液的热膨胀,其体积增大可按式(9) 计算
| $\Delta V_{\rm{m}} = \alpha _{\rm{m}} π \left( {c^2 - b^2 } \right)\Delta TL_{\rm{m}}$ | (9) |
式中:
c—生产套管的内半径,m;
如图 1a所示的全密闭环空。压力、温度引起的管柱、环空流体体积的增加,要依靠管柱、环空流体的压缩,即管柱外部环空的压力升高来抵消,即
| $\Delta V_1 + \Delta V_3 + \Delta V_{\rm{m}} = \Delta V_2 + \Delta p_{\rm{o}} k_{\rm{T}} V_{\rm{m}}$ | (10) |
式中:
利用迭代方式可以求出
如图 1b所示的半密闭环空。压力、温度引起的管柱、环空流体体积增加,要依靠环空惰性气体(简称气体)及管柱、环空流体的压缩,即管柱外部环空的压力升高来抵消。
温度升高引起环空气体体积的变化
| $\Delta V_4 = \alpha _{\rm{g}} V_{\rm{N}} \Delta T$ | (11) |
式中:
假设半密闭环空气体预置压力为
| $\dfrac{{p_{\rm{N}} V_{\rm{N}} }}{T} = \dfrac{{(p_{\rm{N}} + \Delta p_{\rm{N}} )(V_{\rm{N}} - \Delta V{}_{\rm{N}})}}{{T + \Delta T}}$ | (12) |
| $\Delta V_{\rm{N}} = \Delta V_1 + \Delta V_3 + \Delta V_{\rm{m}} + \Delta V_4 -\Delta V_2 - \\ \hspace{3em}\Delta p_{\rm{N}} k_{\rm{T}} V_{\rm{m}}$ | (13) |
式中:
T—环空气体初始绝对温度,K。
利用迭代方式可以求出
某井生产套管为ϕ177.8 mm×10.36 mm,油管为ϕ88.9 mm×6.45 mm;油管弹性模量为205~GPa、泊松比为0.3、热膨胀系数为1.29×10-5 ℃-1;环空保护液热膨胀系数为3.244×10-4 ℃-1,压缩系数为5.0×10-4 MPa-1。封隔器下入深度为3 100 m,图 1b情况初始气体长度为200 m,初始气体压力2.0 MPa,气体热膨胀系数3.67×10-3℃-1。
3.2 全密闭环空注采过程分析 3.2.1 注气时假设初始环空压力为0,管柱内的压力变化量为5~20 MPa(生产压力为15~35 MPa),温度从20 ℃增加到40 ℃。分别考虑管柱变形和不考虑管柱变形,计算不同生产阶段的环空压力。其中,只考虑了井筒的平均温度变化,井口温度取地表平均温度20 ℃。环空压力计算结果见表 1所示,表 1温度变化量△T=5 ℃。
| 表1 注气时全密闭环空压力计算结果(△T=5 ℃) Table 1 Calculation results of sealed annulus pressure in the process of gas injection (△T=5 ℃) |
如果不考虑管柱的温度、压力变化引起的变形,环空保护液的热膨胀就应该等于环空压力的压缩量,即:
| $\Delta p_{\rm{o}} = \dfrac{{\alpha _{\rm{m}} }}{{k_{\rm{T}} }}\Delta T$ | (14) |
以上作业过程,如果温度从15 ℃(地表平均温度)增加到55 ℃,环空压力计算结果见表 2,表 2温度变化量△T=10 ℃。
| 表2 注气时全密闭环空压力计算结果(△T=10 ℃) Table 2 Calculation results of sealed annulus pressure in the process of gas injection (△T=10 ℃) |
表 1和表 2认为考虑管柱变形是正确的,没有误差的。不考虑管柱变形是有误差的。由表 1、表 2可以看出:(1) 温度变化较压力变化影响大;(2) 温度变化小压力变化大时,不考虑管柱变形时误差大,但没有超过5%的工程精度。
3.2.2 采气时假设初始环空压力为0,管柱内的压力降变化量为5~20 MPa(生产压力为35~15 MPa),温度从20 ℃增加到60 ℃,环空压力计算结果如表 3所示。
| 表3 采气时全密闭环空压力计算结果 Table 3 Calculation results of sealed annulus pressure in the process of gas production |
由表 3可以看出,采气过程温度变化较大,不考虑管柱变形时误差较大,约为7.00%。
实际采气过程,井口温度会很快升高到55~60 ℃,采气井口压力逐步降低。为此,计算管柱内压力降低5 MPa,温度由20 ℃升高为45,50,55,60 ℃的环空压力计算结果见表 4。
| 表4 采气初期全密闭环空压力随温度变化计算结果 Table 4 Calculation results of sealed annulus pressure varies with temperature in the early process of gas production |
由表 3、表 4可以看出:温度变化大压力变化小时,不考虑管柱变化时误差没有超过5.00%的工程精度。密闭环空压力的计算,可以不考虑管柱的变形。
3.3 半密闭环空注气过程分析 3.3.1 注气时假设环空预置200 m、2 MPa气体,油管内的压力变化量为5~20 MPa(生产压力为15~35 MPa),温度从20 ℃增加到40 ℃,环空压力计算结果如表 5所示。
| 表5 注气时半密闭环空压力计算结果△T=5 ℃ Table 5 Calculation results of semi-sealed annulus pressure in the process of gas injection (△T=5 ℃) |
分别考虑管柱变形和不考虑管柱变形,计算不同生产压力阶段的环空压力。其中,只考虑了井筒的平均温度变化。
如果不考虑管柱的温度、压力变化引起的变形,环空保护液和环空气体的热膨胀就应该等于环空压力的压缩量,利用公式(15) 和公式(12) 迭代方式可以求出
| $\Delta V_{\rm{N}} + \Delta p_{\rm{N}} k_{\rm{T}} V_{\rm{m}} = \alpha _{\rm{m}} \Delta TV_{\rm{m}} + \Delta V_4$ | (15) |
以上作业过程,如果温度从15 ℃增加到55 ℃,环空压力计算结果见表 6所示。
| 表6 注气时半密闭环空压力计算结果(△T=10 ℃) Table 6 Calculation results of semi-sealed annulus pressure in the process of gas injection (△T=10 ℃) |
假设环空预置200 m、2 MPa气体,管柱内的压力降变化量为5~20 MPa(生产压力为35~15 MPa),温度从20 ℃增加到60 ℃,环空压力计算结果见表 7所示。
| 表7 采气时半密闭环空压力计算结果 Table 7 Calculation results of semi-sealed annulus pressure in the process of gas production |
由表 5、表 6、表 7可以看出:(1) 预置200 m、2 MPa气体后,压力、温度变化引起环空压力变化较小;(2) 考虑管柱变形和不考虑管柱变形计算结果基本一致,误差很小。
4 实例对比 4.1 全密闭对比实例1:井采气过程中,管柱内压力降低5.0 MPa,初始环空压力为11.300 MPa,井口温度由44.2 ℃很快升高到54.4 ℃,其他参数与某井基础数据相同。根据参考文献[15]计算出井口到井底各个位置对应的温度增量,可以计算出由44.2 ℃升高为50.0,52.1,54.4 ℃的环空压力值见表 8和图 2所示。
| 表8 采气初期全密闭环空压力随温度变化计算与监测结果对比 Table 8 Comparison of monitoring results and calculation results of sealed annulus pressure varies with temperature in the early process of gas production |
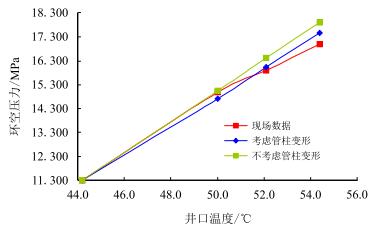 |
| 图2 采气初期全密闭环空压力随温度变化 Fig. 2 Calculation results of sealed annulus pressure varies with temperature in the early process of gas production |
由图 2可以看出,在一定温度下,现场数据与理论计算的数据吻合较好,现场数据较理论计算低一些,可能是环空保护液中有少量气泡引起。
4.2 半密闭对比实例2:井封隔器下入深度为2 900 m,环空氮气长度为150 m,其他参数与某井基础数据相同。采气过程中,管柱内压力降低5 MPa,初始环空压力为6.300 MPa,温度很快由14.9 ℃升高为28.4,32.1,44.7 ℃时,计算环空压力值见表 9和图 3所示。
| 表9 采气初期半密闭环空压力随温度变化计算与监测结果对比 Table 9 Comparison of monitoring results and calculation results of semi-sealed annulus pressure varies with temperature in the early process of gas production |
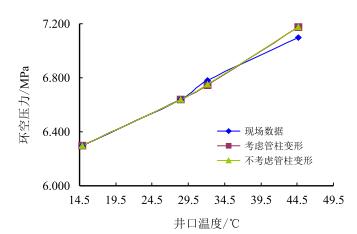 |
| 图3 采气初期半密闭环空压力随温度变化 Fig. 3 Calculation results of semi-sealed annulus pressure varies with temperature in the early process of gas production |
由图 3可以看出,现场数据与理论计算的数据吻合较好,现场数据较理论计算有一些误差,可能是环空氮气长度测量误差引起的。
5 结论(1) 温度变化是影响储气库注采井环空带压的主要因素。
(2) 储气库注采井在注采过程,通过理论计算与现场数据对比,环空压力值吻合较好。
(3) 对于全密闭环空,用式(14) 就可以计算环空压力;对于半密闭环空,用式(15) 和式(16) 可以计算环空压力。简化后的计算方法便于现场的环空压力快速预估。
| [1] |
李玥洋, 田园媛, 曹鹏, 等. 储气库建设条件筛选与优化[J].
西南石油大学学报(自然科学版), 2013, 35(5): 123–129.
LI Yueyang, TIAN Yuanyuan, CAO Peng, et al. Construction of underground gas storage conditions for screening and optimization[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2013, 35(5): 123–129. doi: 10.3863/j.issn.1674-5086.2013.05.017 |
| [2] |
袁进平, 李根生, 庄晓谦, 等. 地下盐穴储气库注气排卤及注采完井技术[J].
天然气工业, 2009, 29(2): 76–78.
YUAN Jinping, LI Gensheng, ZHUANG Xiaoqian, et al. Gas-injection production technology using underground gas-storage salt cavern to displace brine solution and contain injected gas[J]. Natural Gas Industry, 2009, 29(2): 76–78. doi: 10.3787/j.issn.1000-0976.2009.02.020 |
| [3] |
赵志成, 朱维耀, 单文文, 等. 盐穴储气库水溶建腔机理研究[J].
石油勘探与开发, 2003, 30(5): 107–109.
ZHAO Zhicheng, ZHU Weiyao, SHAN Wenwen, et al. Research on mechanism of solution mining for building underground gas storage in salt cavern[J]. Petroleum Exploration and Development, 2003, 30(5): 107–109. doi: 10.-3321/j.issn:1000-0747.2003.05.032 |
| [4] |
靳建州, 解文, 张华, 等. 大港板南储气库白6库1井尾管固井技术[J].
钻井液与完井液, 2014, 31(6): 58–61.
JIN Jianzhou, XIE Wen, ZHANG Hua, et al. Technology for liner cementing in Well 1 of storage Bai-6, Bannan, Dagang[J]. Drilling Fluid & Completion Fluid, 2014, 31(6): 58–61. doi: 10.3969/j.issn.1001-5620.2014.06.016 |
| [5] |
刘硕琼, 齐奉忠. 中国石油固井面临的挑战及攻关方向[J].
石油钻探技术, 2013, 41(6): 6–11.
LIU Shuoqiong, QI Fengzhong. Challenges and development trends of cementing technology in CNPC[J]. Petroleum Drilling Techniques, 2013, 41(6): 6–11. doi: 10.-3969/j.issn.1001-0890.2013.06.002 |
| [6] | ATTARD M. The occurence of annulus pressure in the northwest Hutton Field:Problems and solutions[C]. SPE 23136, 1991. doi:10.2118/23136-MS |
| [7] | ROGER W, WAYNE S. Control of contained-annulus fluid pressure buildup[C]. SPE/IADC 79875, 2003. doi:10.-2118/79875-MS |
| [8] | OUDEMAN P, KEREM M. Transient behavior of annular pressure build-up in HP/HT wells[C]. SPE 88735, 2004. doi:10.2118/88735-MS |
| [9] |
黎丽丽, 彭建云, 张宝, 等. 高压气井环空压力许可值确定方法及其应用[J].
天然气工业, 2013, 33(1): 101–104.
LI Lili, PENG Jianyun, ZHANG Bao, et al. A method determining the safety range of the annulus pressure for a high-pressure gas well and its application[J]. Natural Gas Industry, 2013, 33(1): 101–104. doi: 10.3787/j.issn.1000-0976.2013.01.017 |
| [10] |
赵鹏. 塔里木高压气井异常环空压力及安全生产方法研究[D]. 西安: 西安石油大学, 2012.
ZHAO Peng. A study of abnormal annulus pressure and methods of safe production for Tarim high pressure gas wells[D]. Xi'an:Xi'an Shiyou University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10705-1013156470.htm |
| [11] |
李勇, 王兆会, 陈俊, 等. 储气库井油套环空的合理氮气柱长度[J].
油气储运, 2011, 30(12): 923–926.
LI Yong, WANG Zhaohui, CHEN Jun, et al. Suitable length of the tube-casing annular nitrogen column of gas storage well[J]. Oil & Gas Storage and Transportation, 2011, 30(12): 923–926. |
| [12] |
邓元洲, 陈平, 张慧丽. 迭代法计算油气井密闭环空压力[J].
海洋石油, 2006, 26(2): 93–96.
DENG Yuanzhou, CHEN Ping, ZHANG Huili. Calculating the pressure in sealed annulus in oil well by iterative method[J]. Offshore Oil, 2006, 26(2): 93–96. doi: 10.-3969/j.issn.1008-2336.2006.02.019 |
| [13] | 郭小阳, 宋周成, 李早元, 等. SY/T 54672007套管柱试压规范[S]. 北京: 石油工业出版社, 2008. |
| [14] |
池英柳, 陈宪侃. 雁翎油田注入氮气沿微环隙窜流的可能性分析[J].
石油大学学报(自然科学版), 1994, 18(1): 10–16.
CHI Yingliu, CHEN Xiankan. Possibility of injected nitrogen channeling through microannulus in Yangling Oilfield[J]. Journal of University of Petroleum, China, 1994, 18(1): 10–16. |
| [15] |
田冷, 何顺利, 孙法胜. 大张坨地下储气库井口温度影响因素[J].
天然气工业, 2005, 25(8): 125–128.
TIAN Leng, HE Shunli, SUN Fasheng. Analysis on effecting factors of well-head temperature for Dazhangtuo underground gas storage[J]. Natural Gas Industry, 2005, 25(8): 125–128. doi: 10.3321/j.issn:1000-0976.2005.08.-040 |
 2017, Vol. 39
2017, Vol. 39


