2. 中国石油大学(北京)提高采收率研究院, 北京 昌平 102249
2. Research Institute of Enhanced Oil Recovering, China University of Petroleum, Changping, Beijing 102249, China
聚驱相对渗透率曲线是油田聚驱开发效果评价和预测的重要资料,对进一步认识聚驱具有重要意义。研究表明,聚驱相对渗透率与水驱相渗相比曲线明显右移,油相相渗相对增加,聚合物相相渗降低且变化幅度更明显。但大部分文献采用在管流情况下测定聚合物的弹性计算相渗曲线[1-6],难以符合多孔介质中的弹性,导致聚合物相相对渗透率被低估。
Schneider[7]利用稳态法测量了不同渗透率的露头和地层岩芯的聚驱相对渗透率曲线;Zaitoun等[8]认为聚合物吸附层对润湿相和非润湿相的流动都有影响,将渠道流态理论和两相流毛管束模型推出了两相渗流的相对渗透率计算公式;雷光伦等[9]利用非稳态法测定了聚驱相对渗透率曲线;汪伟英[10]通过黏度与剪切速率关系来计算聚驱相对渗透率曲线;Kamath等[11]用孔隙网络模型描述聚合物在非均质模型中的多相渗流规律;陈铁龙等[12]用稳态法测定聚驱的相对渗透率曲线,发现聚合物驱水相相对渗透率曲线的各点均存在右移;向开理等[13]用渗流力学和最优化理论,将瞬时界面张力和聚合物的影响引入相对渗透率模型;李俊键等[14]在油水两相网络孔隙模型的基础上,考虑了聚合物的流变特性、吸附特性及衰竭层效应,建立了油聚合物两相流的三维网络孔隙模型;周凤军等[15]采用非稳态法测量了聚合物相渗曲线,改进了J.B.N.实验中数据处理方法,并与水驱曲线进行对比;蒋莹等[16]绘制了聚驱相对渗透率曲线,并通过网络模型对实验结果进行拟合,见图 1a;周丛丛[17]利用孔隙网络模型计算聚驱相对渗透率曲线,用Carreau模型模拟聚合物黏弹性,并通过岩芯驱替实验验证了其所绘曲线,见图 1b,但Carreau模型模拟的是管流下聚合物黏弹性,并不适于多孔介质下的弹性。
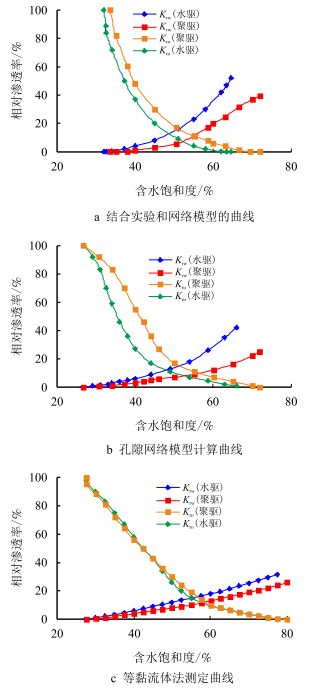 |
| 图1 聚驱相对渗透率曲线 Fig. 1 Polymer flooding relative permeability |
将剪切黏度及管流下的弹性黏度用于计算相对渗透率,得到了如图 1a和图 1b的结果,即聚合物相相对渗透率远小于水驱的水相相对渗透率。
李斌会[18]和杨清彦[19]通过纯黏流体甘油作为聚合物等黏流体,研究聚合物弹性对相对渗透率曲线的影响,发现弹性使聚合物相对渗透率曲线右移,降低残余油饱和度,提高驱油效率,实验结果见图 1c。
由于甘油和聚合物是等黏的,此时两种相对渗透率曲线中的油相相对渗透率几乎相等,而与等黏的甘油驱相比,聚驱的水相相对渗透率更低,说明弹性能够降低水相相对渗透率从而提高驱油效率。
1 聚合物的黏弹性作用机理 1.1 聚合物的流变性描述聚合物流变性的模型有幂律模型、Ellis模型、Meter模型、Cross模型[20]和Carreau模型[21]等。聚合物是一种典型的假塑性流体,其流变性可以用幂律模型表示。1939年Ostwald-de Waele等发现的非牛顿流体的幂律性质,并定义幂律本构方程为
| $\tau = k\gamma ^n$ | (1) |
式中:τ-流体所受的剪切应力,mPa;
k-聚合物的稠度系数或幂律系数,mPa·sn;
γ-剪切速率,s-1;
n-聚合物的流动特性指数或幂律指数,无因次。
幂律流体的表观黏度方程为
| $\mu _{\rm{a}} = k\gamma ^{n - 1}$ | (2) |
式中:
储能模量常被用来表征流体的弹性,但储能模量是在宏观振荡剪切条件下测定的,并不能完全反映流体在多孔介质渗流过程中弹性的大小。
Bird等[22]提出了弹性黏度的概念,并认为聚合物的表观黏度包含剪切黏度和弹性黏度两部分。
| $\mu _{\rm{a}} = \mu _{\rm{s}} + \mu _{\rm{e}}$ | (3) |
式中:
在聚驱油的过程中,实验测得的表观压力即是驱动油相的压力差,而对水相包含两部分:一部分用于克服聚合物的黏滞力及流体内部的弹性阻力驱动流体;另一部分是抵消因多孔介质剪切作用使聚合物发生弹性形变从而产生的弹性阻力。在多孔介质中的弹性力远大于流体内部的弹性力。
| $\Delta p_{\rm{a}} = \Delta p_{\rm{s}} + \Delta p_{\rm{e}}$ | (4) |
式中:
其实,只有剪切黏度遵循Darcy定律,弹性黏度是利用Darcy定律计算的等效黏度,其关系式如下
| $\dfrac{{f_{\rm{w}} qL}}{{K_{{\rm{rw}}} KA}} = \dfrac{{\Delta p_{\rm{s}} }}{{\mu _{\rm{s}} }} = \dfrac{{\Delta p_{\rm{a}} }}{{\mu _{\rm{a}} }} = \dfrac{{\Delta p_{\rm{s}} (q) + \Delta p_{\rm{e}} (q, t)}}{{\mu _{\rm{s}} (q) + \mu _{\rm{e}} (q, t)}}$ | (5) |
式中:
q-流量,mL/min;
L-岩芯长度,cm;
K-绝对渗透率,mD;
A-岩芯截面积,cm2。
聚合物在管流过程中受到剪切应力产生的弹性黏度和剪切黏度之间存在着一定的关系
| $\mu _{\rm{e}} = 2\gamma \lambda _{\rm{f}} \mu _{\rm{s}}$ | (6) |
式中:
基于ZR分子理论模型,松弛时间与聚合物的分子量、浓度以及黏度都有关。
| $\lambda _{\rm{f}} = 12\mu _{\rm{0}} M/π ^2 cN_{\rm{a}} k_0 T$ | (7) |
式中:
M-溶质的分子量,g/mol;
c-溶液浓度,g/L;
T-绝对温度,K。
根据非平衡分子动力学模拟研究结果,最长松弛时间
而聚合物溶液在多孔介质中渗流时受到的弹性阻力要远大于在流变仪中检测到的弹性阻力,聚合物的弹性恢复所需的时间也远长于松弛时间。
Marcus等[23]提出Deborah数来计算聚合物弹性恢复的观察时间
| $t_{\rm{r}} = \lambda _{\rm{f}} /De$ | (8) |
式中:
De-Deborah数;
Marhsall和Metnzer曾提出,用流体松弛时间和流体流过多孔介质孔道时拉伸和收缩速率的组合来表示Deboarh数
| $De\!=\!\dfrac{{\lambda _{\rm{f}} v}}{{L_1 }}\sqrt {\dfrac{3}{2}\!+\! \dfrac{1}{4}\left( {\dfrac{{L_1 }}{{L_2 }}} \right)^2 }\!=\!\dfrac{{\lambda _{\rm{f}} v}}{{L_1 }}\sqrt {\dfrac{3}{2}\!+\!\dfrac{1}{4}\left( {\dfrac{1}{{C^2 - 1}}} \right)}$ | (9) |
式中:
v-流速,cm/s;
L1-流动方向特征长度,cm;
L2-孔道截面方向特征长度,cm;
C-岩芯迂曲度,无因次。
一般认为
Hass等[24]提出的Deborah数经验公式为
| $De = a\dfrac{{[\mu]\mu _{\rm{a}} M}}{{N_{\rm{a}} k_0 T}}\dfrac{v}{d_{\rm{p}}}$ | (10) |
式中:
a-常数;
弹性恢复的观察时间实际上是流速的函数
| $De \approx 2.3\lambda _{\rm{f}} v/d_{\rm{p}}$ | (11) |
有学者设计了毛细管流变仪来研究多孔介质中的弹性黏度,但其模型结构简单,用于计算复杂孔隙结构中的弹性黏度存在一定问题。本文设计了一种弹性恢复实验来研究弹性对相对渗透率曲线的影响。
2 弹性恢复实验 2.1 实验材料实验所用水为大庆油田某三元复合驱区块的地层水。其矿化度为6 778 mg/L,密度为1.000 g/m3(25.35 ℃),水型为NaHCO3型,离子组成见表 1。
| 表1 大庆地层水离子组成 Table 1 Ion composition of the formation water in Daqing |
配制分子量800~2 900万,浓度1~2 g/L的聚合物,基本上涵盖了大庆油田所有聚合物分子量的范围。在室温(25.35 ℃)条件下,用HAAKE流变仪检测聚合物溶液的幂律特性;用Anton Paar MCR301测定聚合物松弛时间
| 表2 不同分子量聚合物的流变性(浓度为1.5 g/L) Table 2 Rheological property of polymer with molecular weights |
| 表3 不同浓度聚合物的流变性(分子量为2 900万) Table 3 Rheological property of polymer with concentrations |
所测数据在γ>0.8后,符合幂律流体模型,与趋势线的拟合度达99.9%。根据幂律方程可知幂律指数n为0.44。n<1也验证了聚合物溶液为假塑性流体。
实验所用的油相为液体石蜡,俗称白油,不溶于水、甘油、葡萄糖溶液等。因此甘油或葡萄糖溶液可作为等黏流体,来与聚合物做对比实验。
在25.35 ℃,101.325 kPa下,用Brookfield黏度计测定的白油黏度为24.3 mPa·s,用U型振动管流体密度计测定的白油密度为0.88 g/mL。
实验所用岩芯为取自大庆油田的天然岩芯。选择渗透率在1 000 mD左右,孔隙度在27%~29%的岩芯进行实验。岩芯中的X衍射方法测定黏土矿物相对含量小于5%,其速敏性、水敏性、酸敏性、碱敏性均较弱。石英和长石骨架点状胶结,应力敏为中等偏弱。自动渗吸法测定的岩石润湿性为弱油湿。
实验所用的黏均剪切速率γ的计算公式为
| $\gamma = \left( {\dfrac{{3n + 1}}{{4n}}} \right)^{\dfrac{n}{{n - 1}}} \dfrac{q}{{A\sqrt {0.5CK\phi } }}$ | (12) |
式中:
基于稳态法设计了一种弹性恢复实验来测定黏弹性流体的弹性黏度,其步骤如下:(1) 对钻取的岩样,测量尺寸,烘干后称其干重;(2) 抽真空,饱和地层水,称其湿重,并水测渗透率;(3) 流速从低到高饱和白油,以建立束缚水饱和度,用称重法和物质平衡法计算饱和度;(4) 注入地层水驱替岩芯,精确计量岩样进口的压力及采集装置中累计产水量,至不再产油或驱替20 PV后,用J.B.N.方法计算水驱相对渗透率以作参考;(5) 重复步骤(3),并将再次建立了束缚水饱和度的岩芯装入图 2所示的实验装置中;(6) 分别按照0.9 mL/min和0.1 mL/min的流速将油和聚合物注入岩样,稳定后记录岩样进口的压力,称量岩样质量,用称重法计算饱和度,计量油水采集装置中累计产油产水量,用物质平衡法计算饱和度;(7) 在驱替达到稳定时停泵5 min后继续驱替,计量此过程中的压力及产液变化情况;(8) 以1 mL/min总流速,将油和聚合物按8:2、7:3、…、1:9的比例依次注入岩样,并重复步骤(6) 和(7)。
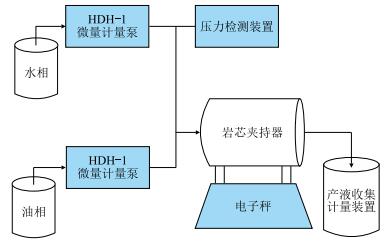 |
| 图2 稳态法实验装置示意图 Fig. 2 Schematic diagram of steady state method |
步骤(7) 中停顿的时间为5 min是根据公式(11) 估算得到的。薄片测定的大庆砂岩主粒径
按照9:1的油水注入速度比,驱替时的某一段压力曲线为例,见图 3。
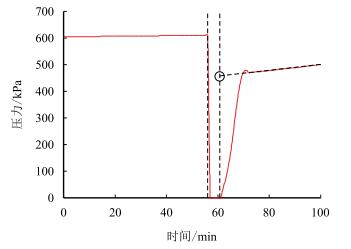 |
| 图3 压力曲线 Fig. 3 Pressure curves |
虚线处停泵5 min后继续驱替,发现压力并未立即恢复到停泵前的615 kPa,而是在压力达到471 kPa后,压力的增速明显放缓。
此外,在压力曲线的折点处之前注入速度大于采出速度,过了这点以后注、采速度基本达到一致。此现象具有较好的可重复性。
停泵后聚合物分子释放了弹性势能。而再次驱替至注采平衡时,黏滞力及流体内部弹力立即产生,但岩石表面的聚合物还处于松弛状态,恢复弹性需要一定时间的积累。因此,再次驱替的压力趋势线反向延长起泵时刻的交点近似等于黏滞力及流体内部弹性力产生的压差
图 3中在折点处还有一个压力的突起,这是由于在聚合物分子松弛后相互缠绕在一起,所以要额外做功来解开这种缠绕并达到一种平衡。平衡后聚合物的阻力减小,压力下降,因此压力曲线有一个突起。
3 实验结果与讨论 3.1 实验结果及分析测定浓度为1.5 g/mL、分子量为2 900万的聚合物溶液,在渗透率为1 000 mD的岩芯中的弹性黏度,结果见图 4。
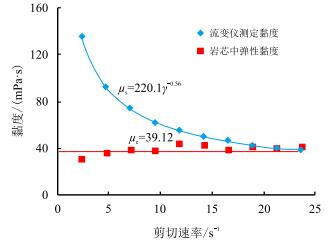 |
| 图4 黏度与剪切率的关系 Fig. 4 The relationship between viscosity and shear rate |
绘制的忽略弹性黏度的聚驱相对渗透率曲线和考虑弹性黏度的曲线,见图 5。
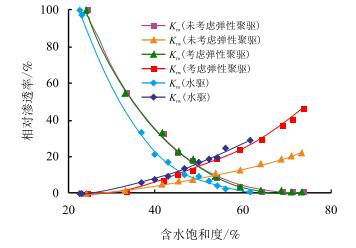 |
| 图5 稳态法相对渗透率 Fig. 5 Relative permeability of steady state method |
忽略弹性黏度的聚驱相对渗透率曲线,得到了与蒋莹等人[16]、周丛丛[17]计算相对渗透率相似的结果。采用本方法计算相对渗透率曲线,得到了与杨清彦等人[19]用等黏流体计算相对渗透率曲线相一致的结论。
单相油流区的范围由束缚水相饱和度
聚驱的等渗点与水驱相比向右侧发生了偏移,说明聚合物更倾向于滞留在岩芯中,也说明聚合物相的流动能力下降了,同时油相的流动能力增强了。
聚驱油相相对渗透率的下凹幅度小于水驱,由于油相黏度未发生变化,说明聚驱提高了油相的流动能力,所以聚驱的油相相对渗透率更高,且其下凹幅度比水驱小。聚驱水相相对渗透率曲线只是略低于水驱。聚驱降低了水相的渗流能力,但并不等于水相相对渗透率就会降低。因为和油相不同,水相的黏度也发生了变化,水相的渗流能力是水相相对渗透率和黏度共同作用的结果,可以用流度来表示。
3.2 方法对比与讨论本文方法将聚合物的弹性等效为弹性黏度,而传统方法将聚合物的弹性等效为聚合物相的渗流能力。传统方法存在一个致命的问题,即该方法计算的水相相对渗透率会随流速发生变化。当流量q发生变化时,流体受到的剪切速率γ也发生变化。
图 4表明聚合物的弹性黏度与聚合物的剪切黏度不同,不随聚合物的剪切速率增加而降低。而且弹性黏度对剪切速率并不敏感。根据珠簧模型,当“黏壶”的一端固定在岩壁上时,另一端的“黏壶”所受的黏滞力与流速成正比,岩壁上滞留的聚合物数量饱和时,弹性力与剪切数量成正比,即弹性黏度不变。
因此,用传统方法计算的相对渗透率曲线将随着注入流速增加而降低,与常识不符。
为证明此观点,用结合弹性恢复实验的J.B.N.方法测定岩芯的相对渗透率。实验之初饱和聚合物,并建立束缚聚合物相饱和度。用0.5 mL/min的流速和1.0 mL/min的流速进行实验,利用J.B.N.方法计算聚驱相对渗透率。实验结束用弹性恢复实验计算的聚合物的弹性黏度。假定在岩石表面的吸附的聚合物近似不变,绘制两种流速下的相对渗透率曲线,见图 6。
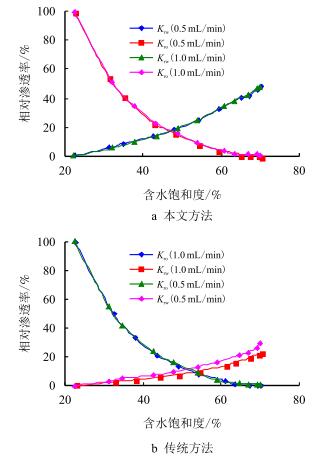 |
| 图6 黏度与剪切率的关系 Fig. 6 The relationship between viscosity and shear rate |
传统J.B.N.绘制的曲线,在较高流速下水相相对渗透率更高了。而本文方法绘制的曲线重合度更高,但并不是完全重合,油相相对渗透率在前期略降中期略高,这是由于流速较高使水窜的速度更快,中期流速较高的水冲刷油的能力更强。
3.3 弹性对相渗曲线的影响聚合物的弹性黏度主要受到聚合物分子量和浓度的影响。通过测定不同分子量和不同浓度的聚驱相对渗透率曲线来分析弹性对相对渗透率曲线的影响。
通过弹性恢复实验,测定5种分子量聚合物的弹性黏度,见表 4;计算聚驱相对渗透率曲线,见图 7。
| 表4 不同分子量聚合物的弹性黏度(浓度为1.5 g/L) Table 4 Elastic viscosity of polymer with molecular weights |
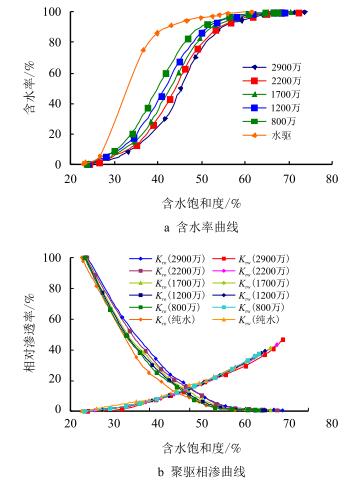 |
| 图7 不同分子量的聚驱相对渗透率 Fig. 7 Relative permeability with molecular weights |
结果表明,随着聚合物分子量的增加,聚合物分子在岩芯中的滞留能力增加,聚合物弹性黏度呈指数增加;含水率上升速度变缓;油相相对渗透率曲线有所增高;水相相对渗透率略有下降,对水相相对渗透率影响比油相较小;等渗点发生右移;油水两相渗流区间也逐渐增大;残余油饱和度随之降低。
通过弹性恢复实验,测定3种浓度的聚合物弹性黏度,见表 5;计算聚驱相对渗透率曲线,见图 8。
| 表5 不同浓度聚合物的弹性黏度(分子量为2 900万) Table 5 Elastic viscosity of polymer with concentrations |
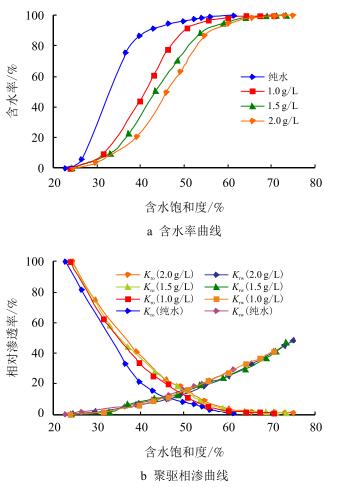 |
| 图8 不同浓度聚合物的相对渗透率 Fig. 8 Relative permeability with concentrations |
结果表明,随着聚合物浓度的增加,在岩芯中的聚合物弹性黏度随之增加;含水率上升速度变缓;油相相对渗透率增大;水相相对渗透率下降,但变化幅度小于油相;等渗点发生右移;油水两相渗流区间也逐渐增大;残余油饱和度随之降低。
通过增大聚合物分子量或浓度,可以增大聚合物的弹性黏度,而弹性黏度增加会使油相相对渗透率曲线增大;水相相对渗透率下降;等渗点发生右移等。实验所用岩芯为弱油湿性,因此实验结果与部分文献存在差异[13]。
4 结论(1) 设计了弹性恢复实验来计算稳态法中的弹性黏度,确定了弹性恢复观察时间等实验参数,并提出了相应的弹性黏度算法。
(2) 将弹性黏度用于修正相对渗透率曲线算法,得到了与文献中纯黏流体实验相似的结论。
(3) 传统的忽略弹性黏度方法存在相渗曲线受流速影响的缺陷。
(4) 通过测定不同分子量和浓度的聚合物在弱油湿岩芯中的弹性黏度和相渗曲线,发现聚合物分子量和浓度增加都会导致弹性黏度增大,而弹性黏度增大会使油相相渗提高,使聚合物相相渗降低。
| [1] | SANDENGEN K, MELHUUS K, KRISTOFFERSEN A. Polymer "viscoelastic effect"; does it reduce residual oil saturation[J]. Journal of Petroleum Science and Engineering, 2017, 153: 355–363. doi: 10.1016/j.petrol.2017.03.-029 |
| [2] | ZHANG R, HE X, CAI S, et al. Rheology of diluted and semi-diluted partially hydrolyzed polyacrylamide solutions under shear:experimental studies[J]. Petroleum, 2017, 3(2): 258–265. doi: 10.1016/j.petlm.2016.08.001 |
| [3] | ALI L, BARRUFET M A. Using centrifuge data to investigate the effects of polymer treatment on relative permeability[J]. Journal of Petroleum Science and Engineering, 2001, 29(1): 1–16. doi: 10.1016/S0920-4105(00)00086-3 |
| [4] | GRATTONI C A, LUCKHAM P F, JING X D, et al. Polymers as relative permeability modifiers:Adsorption and the dynamic formation of thick polyacrylamide layers[J]. Journal of Petroleum Science & Engineering, 2012, 45(3-4): 233–245. doi: 10.1016/j.petrol.2004.07.002 |
| [5] |
张红杰, 蔡振华, 李春, 等. 考虑剪切变稀和吸附滞留的聚合物驱相对渗透率研究[J].
科学技术与工程, 2015, 15(24): 61–65.
ZHANG Hongjie, CAI Zhenhua, LI Chun, et al. Considering shear-thinning, static adsorption and dynamic retention on polymer flooding relative permeability[J]. Science Technology and Engineering, 2015, 15(24): 61–65. doi: 10.3969/j.issn.1671-1815.2015.24.010 |
| [6] |
马东, 刘昌为, 徐海民, 等. 利用岩电参数计算聚合物驱相对渗透率[J].
中国石油大学学报(自然科学版), 2017, 41(1): 118–123.
MA Dong, LIU Changwei, XU Haimin, et al. A new method for calculating relative permeability of polymer flooding based on core-electrical parameters[J]. Journal of China University of Petroleum, 2017, 41(1): 118–123. doi: 10.3969/j.issn.1673-5005.2017.01.015 |
| [7] | SCHNEIDER F N, OWENS W W. Steady-state measurements of relative penneability for polymer/oil systems[C]. SPE 9408, 1982. doi:10.2118/9408-PA |
| [8] | ZAITOUN A, KOHLER N. Two-phase flow through porous media:effect of an adsorbed polymer layer[C]. SPE 18085, 1988. doi:10.2118/18085-MS |
| [9] |
雷光伦, 许震芳, 张铁林, 等. 聚合物驱相对渗透率曲线及影响因素试验研究[J].
水动力学研究与进展(A辑), 1994, 9(4): 469–476.
LEI Guanglun, XU Zhenfang, ZHANG Tielin, et al. Study on the curve of polymer displacement relative permeability and its influence factors[J]. Journal of Hydrodynamics, 1994, 9(4): 469–476. doi: 10.16076/j.cnki.cjhd.1994.04.-013 |
| [10] |
汪伟英. 确定聚合物/油体系相对渗透率曲线的新方法[J].
江汉石油学院学报, 1995, 17(2): 65–68.
WANG Weiying. A new method to determine polymer relative permeability curves[J]. Journal of Jianghan Petroleum Institute, 1995, 17(2): 65–68. |
| [11] | KAMATH J, XU B, LEE S H, et al. Pore network modeling of laboratory experiments on heterogeneous carbonates[C]. SPE 36681, 1996. doi:10.2118/36681-MS |
| [12] |
陈铁龙, 唐金星, 彭克宗, 等. 聚合物驱相对渗透率曲线的特征研究[J].
西南石油学院学报, 1996, 18(3): 51–56.
CHEN Tielong, TANG Jinxing, PENG Kezong, et al. Determination method of polymer flooding relative permeability curves[J]. Journal of Southwest Petroleum Institute, 1996, 18(3): 51–56. doi: 10.3863/j.issn.1000-2634.1996.-03.008 |
| [13] |
向开理, 江茂泽, 彭克琮. 确定ASP复合驱相对渗透率曲线的最优化方法[J].
石油学报, 1998, 19(2): 54–60.
XIANG Kaili, JIANG Maoze, PENG Kezong. The determination of relative permeability curves of ASP combination flooding by using optimization method[J]. Acta Petrolei Sinica, 1998, 19(2): 54–60. doi: 10.7623/-syxb199802011 |
| [14] |
李俊键, 姜汉桥, 陈民锋, 等. 聚合物驱相对渗透率曲线及影响因素微观模拟[J].
西南石油大学学报(自然科学版), 2009, 31(4): 122–126.
LI Junjian, JIANG Hanqiao, CHEN Minfeng, et al. Microscopic modelling of polymer flooding relative permeability curve and its influence factors[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2009, 31(4): 122–126. doi: 10.3863/j.issn.1674-5086.2009.04.026 |
| [15] |
周凤军, 张连锋, 王红娟. 聚合物驱相渗曲线特征[J].
石油地质与工程, 2010, 24(6): 117–119.
ZHOU Fengjun, ZHANG Lianfeng, WANG Hongjuan. Experiment study on relative permeability curve of polymer flooding[J]. Petroleum Geology and Engineering, 2010, 24(6): 117–119. doi: 10.3969/j.issn.1673-8217.-2010.06.036 |
| [16] |
蒋莹. 基于三维网络模型的聚驱相对渗透率及驱油效率研究[D]. 大庆: 大庆石油学院, 2010.
JIANG Ying. The research of relative permeability and oil displacement efficiency of polymer flooding based on three-dimensional network model[D]. Daqing:Daqing Petroleum Institute, 2010. |
| [17] |
周丛丛. 聚合物驱相对渗透率计算的微观模拟研究[J].
岩性油气藏, 2011, 23(3): 119–123.
ZHOU Congcong. Microscopic simulation of relative permeability curves in polymer flooding[J]. Lithologic Reservoirs, 2011, 23(3): 119–123. doi: 10.3969/j.issn.1673-8926.2011.03.023 |
| [18] |
李斌会. 聚驱相对渗透率曲线测定方法与应用研究[D]. 大庆: 大庆石油学院, 2009.
LI Binhui. Research of using and the experiment method for relative permeability curve of polymer flooding[D]. Daqing:Daqing Petroleum Institute, 2009. http://d.wanfangdata.com.cn/Periodical/dqsydzykf201204027 |
| [19] |
杨清彦. 两相驱替相对渗透率研究[D]. 北京: 中国地质大学(北京), 2012.
YANG Qingyan. Study on relative permeabilities in condition of two-phase flooding[D]. Beijing:China University of Geosciences, 2012. http://cdmd.cnki.com.cn/Article/CDMD-11415-1012364446.htm |
| [20] | CROSS M M. Rheology of non-Newtonian fluids:A new flow equation for pseudoplastic systems[J]. Journal of Colloid Science, 1965, 20(5): 417–437. doi: 10.1016/0095-8522(65)90022-X |
| [21] | CARREAU P J. Rheological equations from molecular network theories[J]. Journal of Rheology, 1972, 16(1): 99–127. doi: 10.1122/1.549276 |
| [22] | BIRD R B, ARMSTRONG R C, HASSAGER O. Dynamics of polymeric liquids[M]. New York: John Wiley and Sons Inc, 1987. |
| [23] | MARKUS R. The Deborah number[J]. Physics Today, 1964, 17(1): 62. doi: 10.1063/1.3051374 |
| [24] | HAAS R, DURST F. Viscoelastic flow of dilute polymer solutions in regularly packed beds[J]. Rheologica Acta, 1982, 21(4-5): 566–571. doi: 10.1007/BF01534349 |
 2017, Vol. 39
2017, Vol. 39 图1(Fig. 1)
图1(Fig. 1)



