2. 山东大学(威海)机电与信息工程学院, 山东 威海 264209
2. School of Mechanical, Electrical & Information Engineering, Shandong University, Weihai, Shandong 264209, China
中国西部地区蕴藏着丰富的浅层稠油资源,蒸汽辅助重力泄油(SAGD)是开发这类油藏的一项前沿技术。现场试验结果显示,SAGD蒸汽腔的形成、扩展与油藏中广泛发育的非渗透或低渗透泥岩密切相关。这些泥岩在稠油藏中多以盖层或隔夹层形式存在,如图 1所示。一方面,储层上覆泥岩盖层在高温高压蒸汽的连续注入过程中极易发生破裂,导致蒸汽外溢,污染上部含水层,甚至诱发安全事故[1];另一方面,储层内部泥岩隔夹层的存在将阻碍蒸汽腔的垂向扩展和重力泄油,严重制约SAGD的整体开发效果[2-4]。针对热采油藏的盖层完整性问题,油田的一般做法是通过小型压裂试验确定盖层的破裂压力,进而给出操作压力的安全值,即最大注汽压力[5-6]。然而,由于该方法仅考虑了岩层的拉伸破裂,且未考虑温度升高的影响,由此确定的注汽压力往往偏高,即使注汽压力低于安全操作压力时仍不能有效遏制盖层破裂问题的发生。研究泥岩层在稠油热采环境下的应力演化规律及破坏机理,有助于深入认识SAGD油藏中泥岩的破裂行为,从而制定合理的注汽方案,对于避免泥岩盖层的完整性破坏、打通泥岩隔夹层渗流通道,提高稠油藏开发效果具有重要意义。
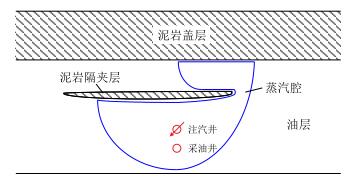 |
| 图1 双水平井SAGD开发油藏断面图 Fig. 1 Cross section of SAGD reservoir |
目前,相关研究多以盖层完整性问题为背景,研究方法主要包括数值模拟和物理试验。数值模拟方法大多通过油藏数值模拟软件与地质力学模拟软件的顺序迭代求解获得变温变压条件下岩层的应力和变形[7-12],但是岩层变形对温度及压力场的反作用往往无法准确模拟,因此无法实现温度场、压力场和应力场之间的完全耦合。物理试验方法大多通过高温三轴压缩试验研究泥岩在升温过程的变形和破坏特征,对其内在的应力演化规律缺少定量的评价[13-17]。目前,关于热采环境中温度、压力、应力耦合条件下泥岩层的破裂行为尚无系统深入的认识,泥岩层的应力演化规律及破坏机理尚不明确。本文采用理论分析与数值模拟相结合的方法,开展了热采环境泥岩层应力演化规律及破坏机理研究。首先基于连续介质力学理论建立了泥岩的热-水-应力全耦合数学模型,从理论上分析了泥岩的传热及增压机制;然后,针对温度、压力单独变化情况,推导了泥岩层应力增量的解析解,通过应力圆演化特征分析了其不同的破坏模式;最后针对加拿大Joslyn Creek SAGD项目的盖层破坏事件,采用热-水-应力全耦合数值模拟方法定量研究了SAGD开发过程中泥岩层温度场、压力场及应力场的分布、演化规律及相互作用机制,揭示了热采环境下泥岩层的破坏机理及关键影响因素。
1 理论分析 1.1 传热机制分析忽略孔隙水的黏性耗散和岩石骨架的应变能,同时假设孔隙水和岩石骨架瞬间达到热平衡,可建立泥岩层的能量守恒方程为[18]
| $\left\{ \begin{array}{*{35}{l}} {{C}_{\text{m}}}\frac{\partial T}{\partial t}={{\lambda }_{\text{m}}}{{\nabla }^{2}}T-{{\rho }_{\text{w}}}{{c}_{\text{pw}}}v\cdot \nabla T \\ {{C}_{\text{m}}}=\phi {{\rho }_{\text{w}}}{{c}_{\text{pw}}}\text{+}(\text{1}-\phi ){{\rho }_{\text{s}}}{{c}_{\text{ps}}} \\ {{\lambda }_{\text{m}}}=\phi {{\lambda }_{\text{w}}}+(1-\phi ){{\lambda }_{\text{s}}} \\ \end{array} \right.$ | (1) |
式中:
T—岩层温度,℃;
t—时间,s;
ρw—孔隙水的密度,kg/m3;
cpw—孔隙水的比热,J/(kg· ℃);
v—孔隙水的渗流速度矢量,m/s;
ϕ—岩石孔隙度,%;
式(1) 中,
| ${ P_{\rm e}}=\dfrac{\rho_{{\rm w}} c_{{\rm pw}} K\Delta p}{{\rm {\bf \lambda }}_{{\rm m}} \mu_{{\rm w}} }$ | (2) |
式中:Pe—Peclet数,无因次;
K—岩石渗透率,m2;
$\Delta p$—孔隙水渗流压差,Pa;
$\mu_{\rm w}$—孔隙水的黏度,Pa· s。
Peclet数反映了对流传热速率与导热传热速率的比值。令泥岩骨架的孔隙度为25%,导热率为2 W/(m·℃),上下边界孔隙水的渗流压差为1 MPa,计算得到Peclet数随泥岩渗透率的变化如图 2所示。
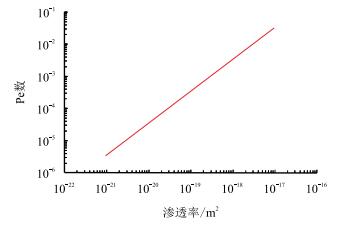 |
| 图2 Peclet数随泥岩渗透率的变化 Fig. 2 Variation of Peclet number with mudstone permeability |
可以看出,Peclet数随着渗透率的减小而减小,在泥岩渗透率范围内(10−21 ~10−17 m2),Peclet数远小于1,即泥岩层热量传递以热传导为主。此时,孔隙水热对流的影响可以忽略,能量守恒方程可简化为
| $C_{{\rm m}} \dfrac{ \partial T}{ \partial t}={\rm {\bf \lambda }}_{{\rm m}} \nabla^{2}T$ | (3) |
考虑孔隙水的PVT特性和岩石骨架的可压缩性,可建立泥岩层的孔隙水渗流方程为[18]
| $\rho_{{\rm w}} \phi c_{{\rm w}} \dfrac{ \partial p}{ \partial t}-\nabla \cdot \left[{\rho_{{\rm w}} \dfrac{K}{\mu_{{\rm w}} }(\nabla p+\rho_{{\rm w}} {\rm g}\nabla z)} \right]+ \\ {\kern 40pt}\rho_{{\rm w}} \dfrac{ \partial \varepsilon_{{\rm v}} }{ \partial t}-\rho _{{\rm w}} \phi \beta_{{\rm w}} \dfrac{ \partial T}{ \partial t}=0$ | (4) |
式中:cw—孔隙水的压缩系数,Pa-1;
p—孔隙水压力,Pa;
g—重力加速度,g=9.8 m/2;
z—水柱高度,m;
εv—岩石骨架的体应变;
βw—孔隙水的体积热膨胀系数,℃−1。
根据式(4) 可得到不排水条件下泥岩的增压速率公式
| $\frac{\partial p}{\partial t}=-\frac{1}{\phi {{c}_{\text{w}}}}\frac{\partial {{\varepsilon }_{\text{v}}}}{\partial t}+\frac{{{\beta }_{\text{w}}}}{{{c}_{\text{w}}}}\frac{\partial T}{\partial t}$ | (5) |
式(5) 中,等号右端第一项反映了岩石骨架体积变化引起的增压速率,负值表示岩石骨架体积膨胀将导致孔隙体积增大、孔隙水压力降低;等号右端第二项反映了温度升高引起的增压速率,正值表示温度升高将导致孔隙水体积膨胀、压力增大。温度对孔隙水压力的影响可用热压力系数,即单位温度变化引起的压力改变量∂p/∂T来表示。不排水条件下饱和水的热压力系数随温度的变化如图 3所示。
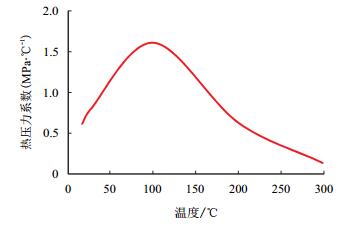 |
| 图3 不排水条件下饱和水的热压力系数随温度的变化 Fig. 3 Variation of thermal pressurization factor with temperature under undrained condition |
从图中可以看出,在0~300 ℃,水的热压力系数在0.13~1.56 MPa/℃,最大值出现在100 ℃附近。这意味着,在不排水条件下,水温每升高1 ℃,压力将增加0.13~1.56 MPa。可见,不排水条件下温度对水压的影响很大。由于岩石骨架的热膨胀作用及孔隙水的扩散作用,实际泥岩层的排水条件介于不排水和自由排水之间,孔隙水的热压力系数将小于上述值。
1.3 岩石骨架应力分析根据连续介质的动量守恒定律和饱和多孔介质的有效应力原理,可建立泥岩层的平衡方程[18]
| $\sigma _{ij,j}^{'}-\alpha {{p}_{,i}}+{{f}_{i}}=0$ | (6) |
式中:
α—Biot系数;
fi—岩石骨架的体积力,N/m3;
下标i, j—取值为直角坐标的x, y, z。
变温条件下,岩石骨架的本构方程为
| $\sigma _{ij}^{'}=2G{{\varepsilon }_{ij}}+\lambda {{\delta }_{ij}}{{\varepsilon }_{\text{v}}}-{{\beta }_{\text{s}}}{{K}_{\text{s}}}{{\delta }_{ij}}\left( T-{{T}_{0}} \right)$ | (7) |
式中:G—岩石骨架的切变模量,Pa;
T0—岩层的初始温度,℃。
鉴于岩层在SAGD开发过程中沿井筒长度方向的变形较小,因此可简化为平面应变问题。由式(6)、式(7) 可解得变温△T引起的应力增量
| $\Delta \sigma _{\text{H}}^{'}=\Delta \sigma _{\text{H}}^{'}=-\frac{E{{\beta }_{\text{s}}}\Delta T}{3(1-\nu )},~\Delta \sigma _{\text{v}}^{'}=0$ | (8) |
式中:
E—岩石骨架的弹性模量,Pa;
受水平约束限制,泥岩层受热后产生水平压应力增量,压应力增大,而垂向压应力不变。根据式(8),可绘制岩层内任一点的应力圆演化过程如图 4所示(
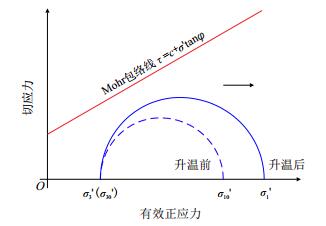 |
| 图4 温度升高引起的应力圆变化 Fig. 4 Changes of stresses caused by temperature rise |
同理,可求得孔隙压力增量
| $\Delta \sigma _{\text{H}}^{'}=\Delta \sigma _{\text{h}}^{'}=\frac{\nu \alpha \Delta p}{1-\nu },~~\Delta \sigma _{\text{z}}^{'}=\alpha \Delta p$ | (9) |
式中:
孔隙压力升高将导致岩层产生拉应力增量,岩层压应力减小。其中,垂向拉应力增量大于水平拉应力增量。压力升高时岩层内任一点的应力圆演化过程如图 5所示。压力升高后,应力圆整体向左移动、半径逐渐增大,有可能诱发岩层剪切破坏产生斜向裂缝或拉伸破坏产生水平裂缝。
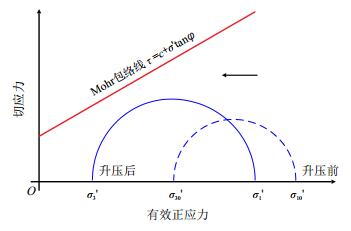 |
| 图5 压力升高引起的应力圆变化 Fig. 5 Changes of stresses caused by pressure rise |
热采环境中泥岩层的实际应力演化规律及破坏形式受蒸汽腔温度、压力以及泥岩层的孔渗、力学性能和原始地应力等因素共同影响。
2 工程实例分析加拿大艾伯塔省Joslyn Creek SAGD项目的204--I1P1井组在注汽过程中发生了严重的泥岩盖层破裂事故,导致储层蒸汽外溢,地表严重变形,给当地的生态环境和安全生产带来了严重的威胁[19]。目前,关于该事故产生的原因尚未形成确定性的结论[20]。本文将基于式(1)、式(4)、式(6),采用多物理场耦合分析软件COMSOL对SAGD开发过程中泥岩盖层的热-水-应力耦合进行数值模拟研究,分析其应力演化规律,揭示其失效的力学机理。
2.1 数值模型由于SAGD开发过程中泥岩盖层沿井筒长度方向变形较小,因此其热-水-应力耦合问题可简化为垂直于水平井的平面问题研究,力学模型见图 6。
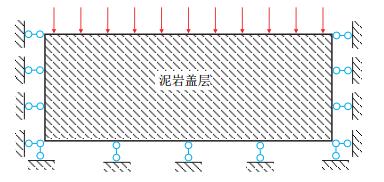 |
| 图6 泥岩盖层力学模型 Fig. 6 Mechanical model of mudstone caprock |
假设泥岩盖层水平最大地应力方向与水平井长度方向平行,顶部边界作用上覆岩层压力,为定外载荷、绝热、不渗透边界,左右两侧边界为无侧向位移、绝热、不渗透边界,泥岩盖层与油层的交界面即底部边界为无垂向位移、定温、定压边界,温度、压力与油层蒸汽腔相同,分别为212 ℃,2 MPa。模型所用参数主要参考已公开的相关文献[21, 22],取值如下:泥岩渗透率1×10-7 D,孔隙度25%,密度2 500 kg/m3,导热率2 W/(m·℃),比热2 000 J/(kg·℃),弹性模量300 MPa,泊松比0.25,热膨胀系数1×10−5/℃,黏聚力2.0 MPa,内摩擦角30°,抗拉强度0.5 MPa。盖层初始压力0.8 MPa,初始温度12 ℃,垂向地应力3.4 MPa,水平最小地应力3.4 MPa,水平最大地应力5.1 MPa。模拟注汽时间3 000 d。
2.2 数值解法SAGD开发过程中泥岩盖层的热-水-应力耦合模型属于不同类型的偏微分方程组,有限元刚度矩阵呈现不对称性。此外,渗流和传热方程中包含不同特征时间的一阶导数,对时间步长的选取非常困难。鉴于模型的复杂性,从计算精度、稳定性和计算效率等方面综合考量,确定采用迭代耦合方法求解SAGD开发过程中泥岩盖层的热-水-应力耦合模型。即在每一时间步内依次求解温度场、渗流场和变形场的控制方程,三场之间通过参数传递和系数更新实现耦合,通过循环迭代确保每一时间步的收敛性。
2.3 结果讨论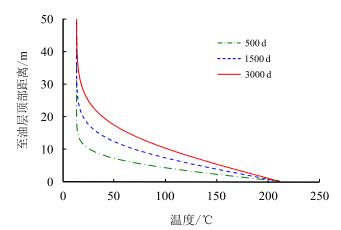 |
| 图7 泥岩层垂向温度演化 Fig. 7 Evolution of temperature along the thickness direction of mudstone caprock |
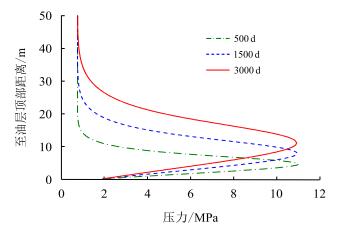 |
| 图8 泥岩层垂向孔隙压力演化 Fig. 8 Evolution of pore pressure along the thickness direction of mudstone caprock |
受油层高温蒸汽腔影响,泥岩层温度逐渐升高,加热厚度逐渐增大。泥岩层孔隙压力峰值并未出现在泥岩层与油层的界面处,而是位于界面之上的某一位置,并随时间逐渐上移。其数值约为11.2 MPa,超出注汽压力9.2 MPa,且整个开发过程中基本保持不变。与温度分布曲线对比发现,压力峰值处温度均约为95 ℃,该值与孔隙水最大热压力系数所对应的温度值(图 3)非常接近。
泥岩层垂向传热速率演化如图 9所示。
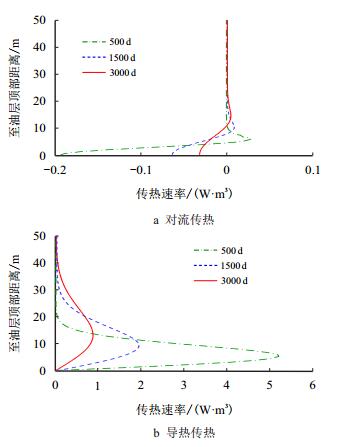 |
| 图9 泥岩层垂向传热速率演化 Fig. 9 Evolution of heat transfer rate along the thickness direction of mudstone |
沿泥岩层厚度方向,对流传热速率主要为负值,且越靠近油层区域数值越大,这说明孔隙水流动对泥岩层受热主要起反作用。而导热传热速率沿泥岩层厚度方向始终为正值,且除了靠近油层的局部区域外,大部分区域的导热传热速率远高于对流传热速率。通过两种传热速率的对比计算发现,在整个开发过程中远离油层的大部分区域Peclet数始终小于0.005。这一结果与前面的传热机制分析一致,即泥岩层热量传递以热传导为主。因此,在泥岩层的温度场模拟中可以用简化公式(3) 代替公式(1),在保证模拟精度的同时有助于提高计算效率。
泥岩层垂向增压速率演化如图 10所示。沿泥岩层厚度方向,岩石骨架变形引起的增压速率主要为负值,这说明岩石骨架变形主要引起泥岩层压力降低。而由孔隙水热膨胀引起的增压速率沿泥岩层整个厚度方向始终为正值,这说明孔隙水热增压是导致泥岩层压力大幅升高的主要原因。
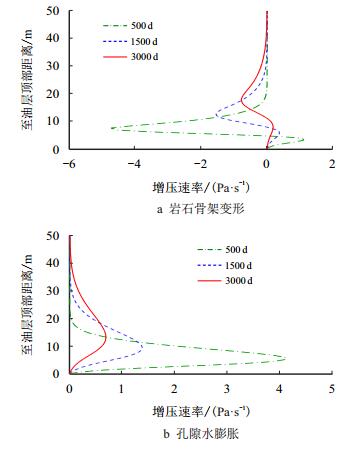 |
| 图10 泥岩层垂向增压速率演化 Fig. 10 Evolution of pressurization rate along the thickness direction of mudstone |
泥岩层垂向有效应力分布如图 11所示。在压力波及范围内,应力场出现扰动,有效应力曲线形态与孔隙压力曲线相似。除油层附近极小范围内水平有效压应力略有增加外,大部分区域有效压应力均呈减小趋势。可见,有效应力主要受孔隙压力影响。当孔隙压力峰值向上移动时,应力峰值也随之上移。除水平最大有效压应力外,其他两个有效应力曲线的峰值均为正,即有效压应力转变为有效拉应力。
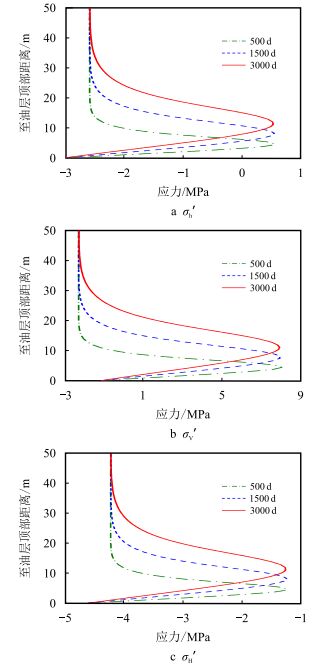 |
| 图11 泥岩层垂向有效应力分布 Fig. 11 Evolution of effective stress along the thickness direction of mudstone |
根据最大正应力强度准则和Mohr-Coulomb强度准则,建立泥岩层的破裂判据
| $f_{{\rm t}} ={\sigma }'_{1} -\sigma_{{\rm t}}$ | (10) |
| $f_{{\rm s}} =\dfrac{{\sigma }'_{1} -{\sigma }'_{3} }{2}-\dfrac{{\sigma }'_{1} +{\sigma }'_{3} }{2}\sin \phi -c\cos \phi$ | (11) |
式中:ft、fs—泥岩层的拉伸和剪切破裂因子;
泥岩层垂向破裂因子分布如图 12所示。当破裂因子
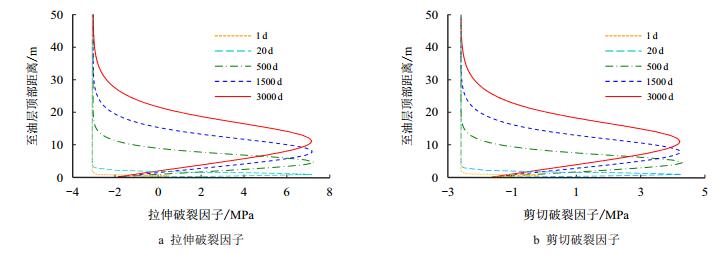 |
| 图12 泥岩层垂向破裂因子分布 Fig. 12 Evolution of failure factor along the thickness direction of mudstone |
破裂因子曲线形态与孔隙压力曲线相似。在孔隙压力扰动区内,泥岩层破裂因子均较初始值有所升高。注汽1 d后,位于泥岩层底部的拉伸破裂因子峰值首先达到正值,说明在此盖层破裂事故中泥岩层首先在其与油层的交界面处发生拉伸破坏。注汽20 d后,孔隙压力峰值处的破裂因子达到极值,且在后期开发过程中基本保持不变。在整个注汽过程中破裂因子峰值不断上移,说明泥岩层破裂区域逐渐向上扩展,随时间发展将贯穿整个盖层,从而诱发蒸汽外溢、地面变形等灾害性事故。
3 结论(1) 热采环境中,泥岩层的主要传热机制是热传导,主要增压机制是孔隙水受热后体积膨胀引起的热增压。受热增压影响,泥岩层孔隙压力远高于注汽压力,压力峰值位于孔隙水最大热压力系数所对应的温度附近。
(2) 温度升高仅导致泥岩层水平压应力增大,易诱发岩层剪切破坏,产生斜裂缝;孔隙压力升高将导致泥岩层三向压应力均减小,易诱发岩层拉伸或剪切破坏,产生水平裂缝或斜裂缝。
(3) 热采环境中,泥岩层应力状态主要受孔隙水的热增压影响。孔隙压力峰值附近岩层可能发生拉伸破坏和剪切破坏,具体破坏形式受泥岩层的孔渗、力学性能、原始地应力以及蒸汽腔温度、压力等因素共同影响。泥岩层破坏区域首先出现在其与油层的交界面处,随时间逐渐扩展并贯穿整个岩层。在热采油藏的受力分析以及注汽方案制定中必须充分考虑泥岩层的热-水-应力耦合效应。
| [1] | CARLSON M R M. A review of caprock issues in thermal recovery in Canada[C]. SPE 173854, 2015. doi:10.2118/173854-MS |
| [2] |
唐帅, 刘鹏程, 潘莉莉, 等. 稠油油藏井间泥岩夹层对双水平井SAGD开发效果的影响[J].
现代地质, 2016, 30(2): 388–393.
TANG Shuai, LIU Pengcheng, PAN Lili, et al. Effects of shale interlayers between injector-producer on SAGD performance with dual-horizontal wells for heavy oil reservoir[J]. Geoscience, 2016, 30(2): 388–393. doi: 10.3969/-j.issn.1000-8527.2016.02.014 |
| [3] |
石兰香, 李秀峦, 刘荣军, 等. 夹层对SAGD开发效果影响研究[J].
特种油气藏, 2015, 22(5): 133–136.
SHI Lanxiang, LI Xiuluan, LIU Rongjun, et al. Research on the effect of interlayers on SAGD development[J]. Special Oil and Gas Reservoirs, 2015, 22(5): 133–136. doi: 10.3969/j.issn.1006-6535.2015.05.030 |
| [4] |
鹿腾, 李兆敏, 韩继超, 等. 页岩夹层及压裂裂缝对蒸汽辅助重力泄油蒸汽腔扩展的影响[J].
石油钻采工艺, 2012, 34(1): 95–99.
LU Teng, LI Zhaomin, HAN Jichao, et al. The influence of shale interlayer and fracturing fracture on steam chamber expansion of SAGD[J]. Oil Drilling & Production Technology, 2012, 34(1): 95–99. doi: 10.3969/j.issn.1000-7393.-2012.01.027 |
| [5] | YUAN Y, XU B, YANG B. Geomechanics for the thermal stimulation of heavy oil reservoirs-Canadian experience[C]. SPE 150293, 2011. doi:10.2118/150293-MS |
| [6] | POWLESS, K R. The use of pressure transient analysis tools to interpret mini-frac data in alberta oilsands caprocks[C]. SPE 157843, 2012. doi:10.2118/157843-MS |
| [7] | LI P, CHALATURNYK R J. Gas-over-bitumen geometry and its SAGD performance analysis with coupled reservoir geomechanical simulation[J]. Journal of Canadian Petroleum Technology, 2007, 46(1): 42–49. doi: 10.2118/07-01-05 |
| [8] | KHAN S, HAN H, VISHTEH M, et al. Caprock integrity analysis in thermal operations:an integrated geomechanics approach[C]. WHOC 11-609, 2011. |
| [9] | HAN H, KHAN S, ANSARI S, et al. Prediction of injection induced formation shear[C]. SPE 151840, 2012. 10.-2118/151840-MS |
| [10] | YUAN Y, XU B, PALMGREN C. Design of caprock integrity in thermal stimulation of shallow oil-sands reservoirs[C]. SPE 149371, 2013. doi:10.2118/149371-MS |
| [11] | LI B, WONG R. Effect of thermally induced deformation of shale on wellbore and caprock integrity[C]. SPE 165393, 2013. doi:10.2118/165393-MS |
| [12] |
周大通, 李治平. 泥岩热弹塑性模型在SAGD中的应用[J].
岩土工程学报, 2015, 37(7): 1348–1352.
ZHOU Datong, LI Zhiping. Application of thermoplastic model for mudstone in SAGD[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(7): 1348–1352. doi: 10.11779/CJGE201507024 |
| [13] | MOUSTAFA M, MALEK S, JIANFU S. Experimental study of the thermomechanical behavior of the petroleum reservoir[C]. SPE 116953, 2008. doi:10.2118/116953-MS |
| [14] | XU B, YUAN Y G, WANG Z C. Thermal impact on shale deformation/failure behaviors-Laboratory studies[C]. ARMA 11-303, 2011. |
| [15] | XU B, YUAN Y, YANG B. Impact of thermal pore pressure on the caprock integrity during the SAGD operation[C]. SPE 165448, 2013. doi:10.2118/165448-MS |
| [16] | GHANNADI S, IRANI M, CHALATURNYK R. Understanding the thermo-hydromechanical pressurization in two-phase (steam/water) flow and its application in low-permeability caprock formations in steam-assistedgravity-drainage projects[J]. SPE Journal, 2014, 19(6): 1126–1150. doi: 10.2118/165544-PA |
| [17] | LI B, DIEDRO F, WONG R, et al. Experimental studies of thermally induced deformation and fracture generation in clay shale[C]. SPE 170133, 2014. doi:10.2118/170133-MS |
| [18] | 王海静. 水平井井筒油藏耦合问题的理论与试验研究[D]. 南京: 南京航空航天大学, 20-12. |
| [19] | CARLSON M R. A review of caprock issues in thermal recovery in Canada[C]. SPE 173854, 2015. doi:10.2118/-173854-MS |
| [20] | CARLSON M R. An analysis of the caprock failure at Joslyn[C]. SPE 156962, 2012. doi:10.2118/156962-MS |
| [21] | ONAISI A. Geo-mechanical insights into the may 18th 2006 joslyn steam release[C]. Summary of Investigation into the Joslyn May 18th, 2006. |
| [22] | HEIN F J, FAIRGRIEVE D B. Joslyn creek SAGD:Geologic factors related to a surface steam release incident, Athabasca oil sands area[C]. CSPG CSEG CWLS convention, 2011. |
 2017, Vol. 39
2017, Vol. 39


