2. 中国石油渤海钻探工程有限公司第二录井分公司, 河北 任丘 061000
2. The Second Mud Logging Branch, CNPC Bohai Drilling Engineering Co. Ltd., Renqiu, Hebei 061000, China
针对复合油气藏试井模型,国内外做了许多研究[1-5],早在1961年,Louck等就利用拉氏变换分析了两区径向复合油藏的压降特征并绘制了相应的压降图版。Carter[2]建立了圆形封闭外边界两区径向复合模型,通过解析解描述了复合油藏压力动态特征。Eggenchwiler等[3]利用拉氏变换得出了考虑井储和表皮效应的两区无限大复合油藏在拉氏空间的压力分布解。在中国,刘义坤等[4]针对具有不同流体性质的两区复合油藏模型进行了研究,建立了井筒储集和表皮效应影响的复合油藏试井模型,用拉氏变换方法求出了压力解,分析了压力及其导数典型曲线的特点。李顺初等建立了考虑井储和表皮效应以及3种外边界条件下的复合油藏试井分析模型[5-6],利用拉氏变换进行了求解,分析了井筒储集系数和表皮系数对井底压力的影响规律。
虽然国内外对复合油藏试井模型有一定研究[7-11],但目前对存在断层的复合油气藏试井模型研究不多,现有的文献[9]也只考虑了断层位于外区的情形,并且在现有的通用试井解释软件中,均只能对断层位于外区的情形进行计算分析,忽略了断层位于复合油气藏内区的情形。本文以无限大两区径向复合模型为基础,应用镜像反映法和叠加原理,研究了直线断层分别位于复合油气藏不同区域时的压力分布特征。
1 无限大地层复合油气藏试井模型 1.1 物理模型及假设条件两区无限大地层复合油气藏径向渗流物理模型[12-14]如图 1所示。
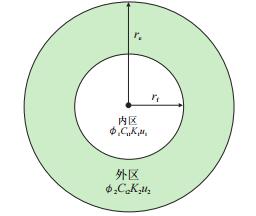 |
| 图1 两区径向复合油气藏示意图 Fig. 1 Schematic of 2-region radial composite reservoir |
其基本假设条件为:(1) 井位于两区径向复合油气藏的中心,地层水平等厚,各区物性参数不同,其流度比为M12,储容比为ω12、内区无因次半径为rfD;(2) 各区内流体均为单相微可压缩的流体,忽略重力和毛管力的影响;(3) 流体等温渗流且符合达西定律;(4) 测试前地层各处压力均为原始油气藏压力pi;(5) 油井以恒定的产量q从t=0时刻开始生产;(6) 考虑井筒储集效应和表皮效应的影响。
1.2 数学模型根据假设,应用渗流力学理论,可得到试井的无因次数学模型
| $\left\{ \begin{array}{l} \dfrac{1}{{{r_{\rm{D}}}}}\dfrac{ \partial }{{ \partial {r_{\rm{D}}}}}\left( {{r_{\rm D}}\dfrac{{ \partial {p_{1{\rm{D}}}}}}{{ \partial {r_D}}}} \right) = \dfrac{{ \partial {p_{1{\rm{D}}}}}}{{ \partial {t_{\rm{D}}}}}{, \kern 10pt}\left( {1 \leqslant {r_{\rm{D}}} \leqslant {r_{{\rm{fD}}}}} \right)\\[5pt] \dfrac{1}{{{r_{\rm{D}}}}}\dfrac{ \partial }{{ \partial {r_{\rm{D}}}}}\left( {{r_{\rm{D}}}\dfrac{{ \partial {p_{2{\rm{D}}}}}}{{ \partial {r_{\rm{D}}}}}} \right) = \dfrac{{{M_{12}}}}{{{\omega _{12}}}}\dfrac{{ \partial {p_{2{\rm{D}}}}}}{{ \partial {t_{\rm{D}}}}}{, \kern 10pt}\left( {{r_{{\rm{fD}}}} \leqslant {r_{\rm D}}} \right)\\[5pt] {p_{1{\rm{D}}}}\left( {{r_{\rm{D}}}, 0} \right) = {p_{2{\rm{D}}}}\left( {{r_{\rm{D}}}, 0} \right) = 0\\[5pt] {p_{2{\rm{D}}}}\left( {\infty, {t_{\rm{D}}}} \right) = 0\\[5pt] {C_{\rm{D}}}\dfrac{{{\rm d}{p_{{\rm{wD}}}}}}{{{\rm d}{t_{\rm{D}}}}} - {r_{\rm D}}\dfrac{{ \partial {p_{{\rm{1D}}}}}}{{ \partial {r_{\rm{D}}}}}\left| {_{{r_{\rm{D}}} = 1}} \right. = 1\\[5pt] {p_{{\rm{wD}}}} = \left( {{p_{{\rm{1D}}}} - S\dfrac{{ \partial {p_{{\rm{1D}}}}}}{{ \partial {r_{\rm{D}}}}}} \right)\left| {_{{r_{\rm{D}}}} =1} \right.\\[5pt] {p_{1{\rm{D}}}}\left( {{r_{{\rm{fD}}}}, {t_{\rm{D}}}} \right) = {p_{2{\rm{D}}}}\left( {{r_{{\rm{fD}}}}, {t_{\rm{D}}}} \right)\\[5pt] \dfrac{{ \partial {p_{1{\rm{D}}}}}}{{ \partial {r_{\rm{D}}}}}\left| {_{{r_{\rm D}} = {r_{{\rm{fD}}}}}} \right. = \dfrac{1}{{{M_{12}}}}\dfrac{{ \partial {p_{2{\rm{D}}}}}}{{ \partial {r_{\rm{D}}}}}\left| {_{{r_{\rm D}}} ={r_{{\rm{fD}}}}} \right. \end{array} \right.$ | (1) |
式(1) 中,各无因次变量的定义为
| ${p_{j{\rm{D}}}} = \left\{ \begin{array}{l} \dfrac{{{K_1}h}}{{1.842 \times {{10}^{ - 3}}qB{\mu _1}}}\left({p_{\rm{i}}} - {p_{{j}}}\right), \\[5pt]{\kern 10pt}\left( { 油藏, {{j}} = 1, 2, {\rm{w}}( 内区, 外区, 井底)} \right)\\[5pt] \dfrac{{{K_1}h}}{{0.01273qT}}\left({\psi _{\rm{i}}} - {\psi _{{j}}}\right), \\[5pt]{\kern 10pt}\left( { 气藏, {{j}} = 1, 2, {\rm{w}( 内区, 外区, 井底)}} \right) \end{array} \right.$ | (2) |
| ${C_{\rm{D}}} = \dfrac{{0.159C}}{{\phi {C_{\rm{t}}}hr_{\rm{w}}^2}}$ | (3) |
| ${{M}_{12}}=\frac{{{M}_{1}}}{{{M}_{2}}}=\frac{{{\left( K/\mu \right)}_{1}}}{{{\left( K/\mu \right)}_{2}}}$ | (4) |
| ${\omega _{12}} = \dfrac{{{\omega _1}}}{{{\omega _2}}} = \dfrac{{{{\left( {\phi {C_{\rm{t}}}} \right)}_1}}}{{{{\left( {\phi {C_{\rm{t}}}} \right)}_2}}}$ | (5) |
| ${r_{\rm{D}}} = \dfrac{r}{{{r_{\rm{w}}}}}$ | (6) |
| ${r_{{\rm{fD}}}} = \dfrac{{{r_{\rm{f}}}}}{{{r_{\rm{w}}}}}$ | (7) |
| ${t_{\rm{D}}} = \dfrac{{3.6{K_1}t}}{{\phi {C_{\rm{t}}}{\mu _1}r_{\rm{w}}^2}}$ | (8) |
对式(1) 进行Laplace变换求解[15-18],可以得到拉氏空间的无因次井底压力
| ${\overline p _{{\rm{wD}}}} = \dfrac{{{K_{\rm I}} \cdot {K_0}\left( {\sqrt u } \right) + {I_0}\left( {\sqrt u } \right)}}{\beta} + \dfrac{{\sqrt u S\left[{{K_{\rm I}}{K_1}\left( {\sqrt u } \right)-{I_1}\left( {\sqrt u } \right)} \right]}}{\beta}$ | (9) |
内区无因次压力、外区无因次压力和系数β分别为
| ${\overline p _{1{\rm{D}}}}\left( {{r_{\rm{D}}}, u} \right) = \dfrac{{{K_{\rm I}} \cdot {K_0}\left( {{r_{\rm{D}}}\sqrt u } \right) + {I_0}\left( {{r_{\rm{D}}}\sqrt u } \right)}}{\beta}$ | (10) |
| ${\overline p _{2{\rm{D}}}}\left( {{r_{\rm{D}}}, u} \right) \!=\! \dfrac{{{K_{\rm I}} \cdot \left[{{K_0}\left( a \right) + {K_1}\left( a \right)} \right] + \left[{{I_0}\left( a \right)-{I_1}\left( a \right)} \right]}}{{\beta \cdot \left[{{K_0}\left( b \right) + \sqrt {{\chi _{21}}} /{M_{12}}{K_1}\left( b \right)} \right]}}{K_0}\left( {{r_{\rm{D}}}\sqrt {{\chi _{21}}u} } \right)$ | (11) |
| $ \beta= \dfrac{1}{{{C_{\rm{D}}} \cdot {u^2}\left[{{K_{\rm I}} \cdot {K_0}\left( {\sqrt u } \right) + {I_0}\left( {\sqrt u } \right)} \right] + \sqrt u \left( {u + S \cdot {C_{\rm{D}}} \cdot {u^2}} \right)\left[{{K_{\rm I}} \cdot {K_1}\left( {\sqrt u } \right)-{I_1}\left( {\sqrt u } \right)} \right]}}$ | (12) |
其中:
| $\begin{align} &{{K}_{\text{I}}}=\frac{{{I}_{1}}\left( a \right){{K}_{0}}\left( b \right)+\frac{\sqrt{{{\chi }_{21}}}}{{{M}_{12}}}{{I}_{0}}\left( a \right){{K}_{1}}\left( b \right)}{{{K}_{1}}\left( a \right){{K}_{0}}\left( b \right)-\frac{\sqrt{{{\chi }_{21}}}}{{{M}_{12}}}{{K}_{0}}\left( a \right){{K}_{1}}\left( b \right)}; \\ &a={{r}_{\text{fD}}}\sqrt{u}; \\ &b={{r}_{\text{fD}}}\sqrt{{{\chi }_{21}}u}。\\ \end{align}$ |
与均质和双重介质油气藏一样,当对存在断层的复合油气藏油气井进行试井解释时,测试资料压力导数曲线会因为存在断层而变得很复杂,影响曲线的中期和晚期形状。断层对复合油气藏试井模型特征曲线的影响可以通过镜像反映和叠加原理来分析。因此,根据直线断层所处位置不同,可以将存在断层的复合油气藏分为两种情况讨论。
(1) 情况1
假设井到直线断层的距离rDd,当
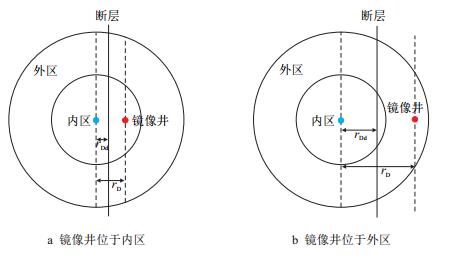 |
| 图2 镜像井分别位于复合内区、外区示意图 Fig. 2 Schematic of image well in the inner region or outer region |
| ${\overline p _{{\rm{1D}}}}\left( {{r_{{\rm{Dd}}}}, u} \right)\! =\! \dfrac{{K_{\rm I} \cdot {K_0}\left( {2{r_{{\rm{Dd}}}}\sqrt u } \right)\! +\! {I_0}\left( {2{r_{{\rm{Dd}}}}\sqrt u } \right)}}{B}$ | (13) |
此时(
| ${\overline p _{{\rm{wD}}1}} = {\overline p _{{\rm{wD}}}} + {\overline p _{1{\rm{D}}}}\left( {{r_{{\rm{Dd}}}}, u} \right)$ | (14) |
(2) 情况2
当井到直线断层的距离
| ${\overline p _{2{\rm{D}}}}\left( {{r_{{\rm{Dd}}}}, u} \right)\! =\! \dfrac{{{K_{\rm{I}}} \left[{{K_0}\left( a \right) \!+\! {K_1}\left( a \right)} \right] \!+\! \left[{{I_0}\left( a \right) \!-\! {I_1}\left( a \right)} \right]}}{{B \left[{{K_0}\left( b \right) \!+\! \sqrt {{\chi _{21}}} /{M_{12}}{K_1}\left( b \right)} \right]}}\cdot\\[2pt]{\kern 40pt}{K_0}\left( {2{r_{{\rm{Dd}}}}\sqrt {{\chi _{21}}u} } \right)$ | (15) |
此时(
| ${\overline p _{{\rm{wD}}2}} = {\overline p _{{\rm{wD}}}} + {\overline p _{{\rm{2D}}}}\left( {{r_{{\rm{Dd}}}}, u} \right)$ | (16) |
式(14) 和式(16) 分别为复合油气藏中镜像井分别位于内区和外区时,生产井井底压力的拉氏空间解。
3 试井曲线特征及影响因素分析根据前文的推导,利用Stehfest数值反演算法,可以求得对应条件下的井底无因次压力及其导数曲线[19-21]。所用基本参数为
当镜像井位于复合内区时,井到断层距离对试井曲线的影响如图 3所示。
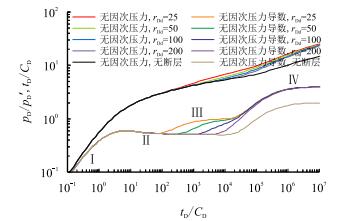 |
| 图3 镜像井位于复合油气藏内区时无因次压力及其导数曲线特征 Fig. 3 Characteristics of dimensionless pressure and pressure derivative curves when the image well in the inner region of composite reservoirs |
根据流动特征,可以将试井分析曲线划分为4个流动段:
(1) 第Ⅰ段为井筒储集阶段,在该阶段,无因次压力及压力导数曲线重合为斜率为1的直线。
(2) 第Ⅱ段为内区径向流阶段,在该阶段,井底附近流体向井筒径向流动,无因次压力导数曲线表现为值为0.5的水平线段。
(3) 第Ⅲ段为内区断层反映阶段,其压力导数曲线由内区径向流值为0.5的水平线上升为值为1.0的水平线。断层到生产井距离越近,压力波到达断层的时间越短,导致内区径向流动阶段结束时间越早,内区断层反映阶段持续时间越长;当井到断层的距离足够小时,内区径向流动阶段将可能被井筒储集效应所掩盖。反之,断层到生产井的距离越远,使得断层距复合油气藏交界面越近,导致断层反映阶段持续时间越短,表示内区断层反映的1.0水平线特征越不明显。
(4) 第Ⅳ段为外区流动阶段,由于断层对流体流动的阻挡作用,无因次导数曲线的值将由无断层时的M12/2水平线,上升为值为M12的水平线。
3.2 镜像井位于复合外区图 4为镜像井位于复合油气藏外区时,井到直线断层距离对双对数试井曲线的影响。根据流动特征,仍可以将试井分析曲线划分为4个流动段。
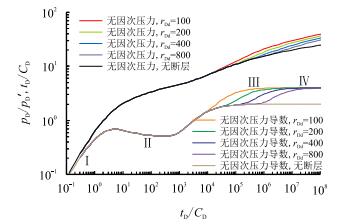 |
| 图4 镜像井位于复合油气藏外区时无因次压力及其导数曲线特征 Fig. 4 Characteristics of dimensionless pressure and pressure derivative curves when the image well in the outer region of composite reservoirs |
(1) 第Ⅰ段、第Ⅱ段特征与镜像井位于内区范围时的复合油气藏模型试井曲线一样。
(2) 第Ⅲ段为外区径向流阶段,在该阶段,复合外区的流体向井底径向流动,无因次压力导数曲线表现为值为M12/2的水平线段。
(3) 第Ⅳ段为外区断层反映阶段,在该阶段,压力波传播到位于复合外区的断层边界,无因次压力导数曲线表现为值为M12的水平线。由4图可知,断层到生产井距离越近,压力波到达断层的时间越早,因此,断层反映开始时间越早,而外区径向流持续时间越短;相反,断层距生产井越远,压力波到达断层时间越晚,断层反映开始时间越晚,而外区径向流持续时间越长。
4 结论(1) 断层的位置显著影响复合油气藏试井曲线特征。
(2) 镜像井位于内区时,呈现内区径向流阶段、内区断层反映阶段、外区流动阶段,无因次压力导数曲线依次表现为值为0.5,1.0,M12的水平线。
(3) 镜像井位于外区时,将呈现内区径向流阶段、外区径向流阶段、外区断层反映阶段,其无因次压力导数曲线值分别为0.5,M12/2,M12。
符号说明re—外区半径,m;
rf—内区半径,m;
ϕ1—内区孔隙度,%;
ϕ2—外区孔隙度,%;
Ct1—内区综合压缩系数,MPa-1;
Ct2—外区综合压缩系数,MPa-1;
K1—内区渗透率,D;
K2—外区渗透率,D;
µ1—内区流体黏度,mPa·s;
µ2—外区流体黏度,mPa·s;
M12—内外区流度比,无因次;
ω12—内外区储容比,无因次;
rfD—内区无因次半径;
pi —油藏原始地层压力,MPa;
q—生产井的产量,×104 m3/d;
t—生产时间,d;
rD—无因次径向距离;
p1D —内区无因次压力;
p2D—外区无因次压力;
tD—无因次时间;
CD—无因次井筒储集系数;
pwD—无因次井底压力;
S—表皮系数,无因次;
h—有效地层厚度,m;
B—地层体积系数,无因次;
ψi—气藏原始拟地层压力,MPa2/ mPa·s;
T—气藏温度,K;
C—井筒储集系数,m3/MPa;
Ct—综合压缩系数,MPa-1;
M1 —内区流度,D/(mPa·s);
M2—外区流度,D/(mPa·s);
ω1—内区储容系数,MPa-1;
ω2—外区储容系数,MPa-1;
K—渗透率,D;
r—径向距离,m;
u—Laplace变量;
| [1] | LOUCKS T L, GUERRERO E T. Pressure drop in a composite reservoir[J]. Society of Petroleum Engineers Journal, 1961, 1(3): 170–176. doi: 10.2118/19-PA |
| [2] | CARTER R D. Pressure behavior of a limited circular composite reservoir[J]. Society of Petroleum Engineers Journal, 1966, 6(4): 328–334. doi: 10.2118/1621-PA |
| [3] | EGGENSCHWILER M, RAMEY H J, SATMAN A. Interpretation of injection well pressure transient data in thermal oil recovery[C]. SPE 8908, 1980. doi:10.2118/8908-MS |
| [4] |
刘义坤, 阎宝珍, 翟云芳, 等. 均质复合油藏试井分析方法[J].
石油学报, 1994, 15(1): 92–100.
LIU Yikun, YAN Baozhen, ZHAI Yunfang, et al. Transient pressure behavior in a homogenous composite reservoir[J]. Acta Petrolei Sinica, 1994, 15(1): 92–100. doi: 10.-7623/syxb199401011 |
| [5] |
李顺初, 刘平礼, 赵立强. 复合油藏中不同边界条件下的井底压力分析[J].
西南石油学院学报, 2002, 24(5): 32–33.
LI Shunchu, LIU Pingli, ZHAO Liqiang. The analysis of bottom pressure in complex reservoir with different boundary conditions[J]. Journal of Southwest Petroleum Institute, 2002, 24(5): 32–33. doi: 10.3863/j.issn.1674-5086.2002.05.010 |
| [6] |
郑鹏社, 李顺初, 徐文昭. 基于解的相似结构的复合油藏试井分析方法[J].
钻采工艺, 2007, 30(3): 49–50.
ZHENG Pengshe, LI Shunchu, XU Wenzhao. Well analysis method based on the similar structure of pressure distribution in the composite reservoir[J]. Drilling & Production Technology, 2007, 30(3): 49–50. |
| [7] |
张烈辉, 张芮菡, 蒋和煦, 等. 低渗透复合油藏压力动态有限元理论分析[J].
西南石油大学学报(自然科学版), 2016, 38(4): 1–8.
ZHANG Liehui, ZHANG Ruihan, JIANG Hexu, et al. Theoretical analysis of low permeability composite reservoir using finite element method[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2016, 38(4): 1–8. doi: 10.11885/j.issn.1674-5086.2014.-09.26.02 |
| [8] |
姜瑞忠, 郜益华, 孙召勃, 等. 双重介质复合油藏偏心井试井分析[J].
新疆石油地质, 2016, 37(3): 327–331.
JIANG Ruizhong, GAO Yihua, SUN Zhaobo, et al. Off-center well test analysis for composite dual-porosity reservoirs[J]. Xinjiang Petroleum Geologs, 2016, 37(3): 327–331. doi: 10.7657/XJPG20160316 |
| [9] | 廖新维. 现代试井分析[M]. 北京: 石油工业出版社, 2002. |
| [10] |
孙贺东. 邻井干扰条件下的多井压力恢复试井分析方法[J].
天然气工业, 2016, 36(5): 62–68.
SUN Hedong. Pressure buildup analysis in multi-well systems under interferences from adjacent wells[J]. Natural Gas Industry, 2016, 36(5): 62–68. doi: 10.3787/j.issn.-1000-0976.2016.05.009 |
| [11] |
李顺初, 黄炳光, 李晓平, 等. 复合油藏压力分布研究[J].
断块油气田, 2001, 6(8): 29–31.
LI Shunchu, HUANG Bingguang, LI Xiaoping, et al. Research of composite reservoir pressure distribution[J]. Fault-block Oil & Gas Field, 2001, 6(8): 29–31. doi: 10.-3969/j.issn.1005-8907.2001.06.009 |
| [12] |
李顺初, 刘平礼, 赵立强. 复合油藏储层中压力分布的求解[J].
西南石油学院学报, 2000, 22(4): 76–79.
LI Shunchu, LIU Pingli, ZHAO Liqiang. Solution of composite reservoir pressure distribution model[J]. Journal of Southwest Petroleum Institute, 2000, 22(4): 76–79. doi: 10.3863/j.issn.1674-5086.2000.04.021 |
| [13] |
丘永新, 庄惠农. 复合油藏压力曲线在双对数综合图上的特征及实例分析[J].
油气井测试, 1992, 3(1): 16–20.
QIU Yongxin, ZHUANG Huinong. The characteristic on log-log plots for pressure curves of composite system and it's case study[J]. Well Testing, 1992, 3(1): 16–20. |
| [14] | SATMAN A. An analytical study of interference in composite reservoir[J]. Society of Petroleum Engineers Journal, 1985, 25(2): 281–290. doi: 10.2118/10902-PA |
| [15] | BROWN L P. Pressure transient behavior of the composite reservoir[C]. SPE Annual Technical Conference and Exhibition, 1985, (9):1-10. doi:10.2118/14316-MS |
| [16] | OLAREWAJU J S, LEE W J. A comprehensive application of a composite reservoir model to pressure transient analysis[C]. SPE California Regional Meeting, 1987(4):227-243.doi:https://doi.org/10.2118/16345-MS |
| [17] | OLAREWAJU J S, LEE W J. An analytical model for composite reservoirs produced at either constant bottomhole pressure or constant rate[C]. SPE Annual Technical Conference and Exhibition, 1987(9):217-231.doi:10.2118/16763-MS |
| [18] | ISSAKA M B, AMBASTHA A K. A generalized pressure derivative analysis for composite reservoirs[C]. Annual Technical Meeting, 1996, Calgary, Alberta.doi:10.2118/96-115 |
| [19] | MERRILL L S, KASSEMI H, GOGARTY W B. Pressure falloff analysis in reservoirs with fluid banks[J]. Journal of Petroleum Technology, 1974, 26(7): 809–818. doi: 10.2118/4528-PA |
| [20] | CLOSMANN P J, RATLIFF N W. Calculation of transient oil production in a radial composite reservoir[J]. Society of Petroleum Engineers Journal, 1967, 7(4): 623–629. doi: 10.2118/1675-PA |
| [21] | PRASAD R K. Pressure transient analysis in the presence of two intersecting boundaries[J]. Journal of Petroleum Technology, 1975, 27(1): 89–96. doi: 10.2118/4560-PA |
 2017, Vol. 39
2017, Vol. 39


