2. 中国石油新疆油田分公司采油一厂, 新疆 克拉玛依 834000;
3. 中国石油新疆油田分公司新疆技师学院, 新疆 克拉玛依 834000
2. NO.1 Oil Production Plant, Xinjing Oilfield Company, PetroChina, Karamay, Xinjiang 834000, China;
3. Institute of Xinjiang Technicians, Xinjing Oilfield Company, PetroChina, Karamay, Xinjiang 834000, China
地层封闭是异常高压形成的必要条件,开放的地层在任何情况下都不会出现异常高压,只有封闭的地层才可能在某些特定条件下出现异常高压[1-3]。封闭地层受挤压后孔隙体积变小,孔隙中的流体受到压缩却无法排出引起压力升高。基于这一理解,许多文献认为构造挤压作用是形成异常高压的主要原因之一[4-8]。从目前的文献来看,对挤压作用形成异常高压的研究均只是定性分析,未见定量研究的报道。因此,对挤压作用能否形成异常高压,以及能导致多大的压力异常,有必要进行定量研究。以双重有效应力理论和多孔介质弹性力学理论为基础,通过缜密的推导,对挤压作用导致的地层弹性压缩量进行了研究,得到了孔隙压力系数增量的理论计算公式。定量计算结果表明,挤压作用难以形成异常高压,一般不是异常高压形成的主要原因。
1 地层受挤压的可能情形以地层的当前状态作为研究的初始状态,其所受的现今地应力为最大水平主应力(σH)、最小水平主应力(σh)和垂向应力(σz)。假设经历若干时间后,水平方向产生挤压作用,根据安德森断层理论[9],地应力变化及地层破坏规律如表 1所示。
| 表1 挤压作用导致的地层破坏规律 Table 1 The law of formation damage caused by extrusion |
初始状态下由于σH > σh,水平方向已经存在一定的应力差,若挤压发生在σH方向上,则地层达到破坏所需的地应力增量小,相应地,地层破坏前其压缩量也小;若挤压发生在σh方向上,地层达到破坏所需的地应力增量大,相应地,地层破坏前其压缩量也大;若挤压发生在σH与σh方向之间,地应力增量与地层压缩量均介于前两种情况之间。
显然,对于封闭地层,受挤压后要使其孔隙压力增加幅度最大,必然要求地层压缩量最大,挤压作用应发生在σh方向上。以下针对初始地应力状态为σh < σz < σH,σh方向受挤压(即情形4)进行研究。
2 有效应力的选用由于岩石中孔隙流体的存在及其作用,在研究岩石变形与破坏时需使用有效应力。所谓有效应力,就是一种等效应力,它作用于多孔介质,与内、外应力同时作用于多孔介质所产生的力学行为是完全相同的。目前使用的有效应力理论主要有Terzaghi有效应力、Biot有效应力和双重有效应力理论。
Terzaghi于1923年针对疏松的土介质第一次提出了有效应力的概念,并在此基础上建立了第一门多孔介质力学土力学。Terzaghi有效应力公式为[10]
| $ \sigma _{\rm eff}^{\rm T} = \sigma {\rm{ - }}{p_{\rm{p}}} $ | (1) |
为了消除Terzaghi有效应力在工程应用中的不适应性,许多学者对其进行了修正,其中以Biot修正式应用最广。Biot于1941年提出的修正式为[11]
| $ \sigma _{{\rm{eff}}}^{\rm{B}} = \sigma {\rm{ - }}\alpha {p_{\rm{p}}} $ | (2) |
李传亮等于1999年提出了双重有效应力理论[12-13],认为岩石有两个有效应力:本体有效应力和结构有效应力。本体有效应力的计算公式为
| $ \sigma _{{\rm{eff}}}^{\rm{P}} = \sigma - \phi {p_{\rm{p}}} $ | (3) |
本体有效应力决定岩石的本体变形量,即岩石骨架颗粒本身的变形而导致的岩石总变形。
结构有效应力的计算公式为
| $ \sigma _{{\rm{eff}}}^{\rm{S}} = \sigma - {\phi _{\rm{c}}}{p_{\rm{p}}} $ | (4) |
结构有效应力决定岩石的结构变形量,即由岩石骨架颗粒之间的相对位移导致的岩石总变形,包括岩石的破坏和断裂。φc视岩石的胶结状况而定,其值为φ~1。胶结程度较低的点接触疏松土壤介质φc → 1;胶结程度较高的岩石φc → φ。
双重有效应力理论对Terzaghi有效应力和Biot有效应力进行了改进,在工程应用上适应性更强[14-16]。因此,以下在分析岩石的弹性变形力学行为时采用本体有效应力,在分析岩石破坏时采用结构有效应力。
3 挤压破坏前的弹性力学分析以某一渗透性地层为研究对象,对其进行弹性变形及破坏分析时做出如下假设:
(1) 地层受挤压之后破裂之前,只产生弹性变形,忽略临界破坏前的塑性变形;
(2) 该渗透性地层充满流体,被围岩绝对封闭,受挤压之后破裂之前流体无法排出;
(3) 该地层岩石为各向同性体;
(4) 地层破坏规律符合Mohr Coulomb准则。
地层初始地应力状态为σh < σz < σH,孔隙压力为pp,受力情况如图 1a所示。
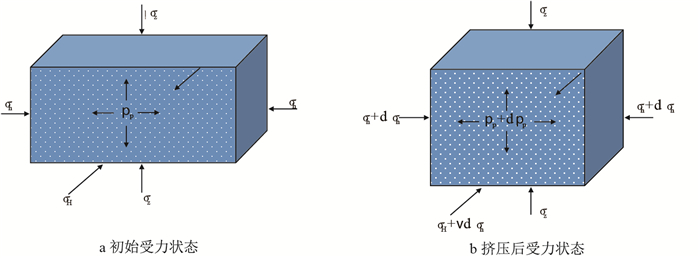 |
| 图1 σh方向挤压作用前、后地层受力状态 Fig. 1 The formation force state before and after the extrusion in σh direction |
地层受挤压后,在弹性变形阶段岩石的本体有效应力增量与应变之间符合Hooke定律
| $ {\rm{d}}\sigma _{{\rm{eff}}}^{\rm{P}} = E\varepsilon $ | (5) |
在最大、最小水平主应力和垂向应力方向上,式(5)的三维形式为
| $ \left\{ \begin{array}{l} {\varepsilon _{\rm{H}}} = \left[{{\rm{d}}\sigma _{{\rm{effH}}}^{\rm{P}}-\upsilon \left( {{\rm{d}}\sigma _{{\rm{effh}}}^{\rm{P}} + {\rm{d}}\sigma _{{\rm{effz}}}^{\rm{P}}} \right)} \right]/E\\[4pt] {\varepsilon _{\rm{h}}} = \left[{{\rm{d}}\sigma _{{\rm{effh}}}^{\rm{P}}-\upsilon \left( {{\rm{d}}\sigma _{{\rm{effH}}}^{\rm{P}} + {\rm{d}}\sigma _{{\rm{effz}}}^{\rm{P}}} \right)} \right]/E\\[4pt] {\varepsilon _{\rm{z}}} = \left[{{\rm{d}}\sigma _{{\rm{effz}}}^{\rm{P}}-\upsilon \left( {{\rm{d}}\sigma _{{\rm{effH}}}^{\rm{P}} + {\rm{d}}\sigma _{{\rm{effh}}}^{\rm{P}}} \right)} \right]/E \end{array} \right. $ | (6) |
若挤压作用发生在σh方向,该方向地应力增量为dσh(dσh > 0);由于垂直方向地层应变无约束,垂向应力将保持不变;根据弹性力学理论[17],σh方向地应力增加dσh,将在σH方向产生应力增量υdσh。因此,σh方向发生挤压后,地应力变化情况为
| $ \left\{ \begin{array}{l} {\rm{d}}{\sigma _{\rm H}} = \upsilon {\rm{d}}{\sigma _{\rm{h}}}\\ {\rm{d}}{\sigma _{\rm{h}}} = {\rm{d}}{\sigma _{\rm{h}}}\\ {\rm{d}}{\sigma _{\rm{z}}} = 0 \end{array} \right. $ | (7) |
设地层压缩导致的孔隙压力增量为dpp,受挤压之后地应力及孔隙压力的变化如图 1b所示。
地层压缩过程中,岩石外观体积与孔隙体积同步压缩,因此孔隙度保持不变[18-19]。根据式(7),并对式(3)微分,有
| $ \left\{ \begin{array}{l} {\rm{d}}\sigma _{{\rm{effH}}}^{\rm{P}} = {\rm{d}}{\sigma _{\rm{H}}} - \phi {\rm{d}}{p_{\rm{p}}} = \upsilon {\rm{d}}{\sigma _{\rm{h}}} - \phi {\rm{d}}{p_{\rm{p}}}\\ {\rm{d}}\sigma _{{\rm{effh}}}^{\rm{P}} = {\rm{d}}{\sigma _{\rm{h}}} - \phi {\rm{d}}{p_{\rm{p}}}\\ {\rm{d}}\sigma _{{\rm{effz}}}^{\rm{P}} = {\rm{d}}{\sigma _z} - \phi {\rm{d}}{p_{\rm{p}}} = - \phi {\rm{d}}{p_{\rm{p}}} \end{array} \right. $ | (8) |
将式(8)代入式(6),可得
| $ \left\{ \begin{array}{l} {\varepsilon _{\rm{H}}} = \left[{{\rm{-}}\left( {1{\rm{-}}2\upsilon } \right)\phi {\rm{d}}{p_{\rm{p}}}} \right]/E\\ {\varepsilon _{\rm{h}}} = \left[{\left( {1-{\upsilon ^2}} \right){\rm{d}}{\sigma _h}{\rm{-}}\left( {1{\rm{-}}2\upsilon } \right)\phi {\rm{d}}{p_{\rm{p}}}} \right]/E\\ {\varepsilon _{\rm{z}}} = \left[{-\upsilon \left( {1 + \upsilon } \right){\rm{d}}{\sigma _h}{\rm{-}}\left( {1{\rm{-}}2\upsilon } \right)\phi {\rm{d}}{p_{\rm{p}}}} \right]/E \end{array} \right. $ | (9) |
由式(9)可得岩石的总应变为
| $ {\varepsilon _{\rm v}} = {\varepsilon _{\rm{H}}} + {\varepsilon _{\rm{h}}} + {\varepsilon _{\rm{z}}} =\\{\kern 40pt} \left[{\left( {1 \!+\! \upsilon } \right)\left( {1 \!-\! 2\upsilon } \right){\rm d}{\sigma _h} \!-\! 3\left( {1\!-\!2\upsilon } \right)\phi {\rm{d}}{p_{\rm{p}}})} \right]/E $ | (10) |
地层受挤压后,弹性变形过程中岩石总应变(εv)与孔隙体积应变(εP)相等。由于地层封闭,孔隙体积应变等于孔隙中流体的体积应变(εL),因此,有
| $ {\varepsilon _{\rm v}} = {\varepsilon _{\rm{L}}} = \dfrac{{{\rm{ - d}}{V_{\rm L}}}}{{{V_{\rm L}}}} = \left( {{\rm{ - }}\dfrac{1}{{{V_{\rm L}}}}\dfrac{{{\rm{d}}{V_{\rm{L}}}}}{{{\rm{d}}{p_{\rm{p}}}}}} \right){\rm{d}}{p_{\rm{p}}} = {c_{\rm{L}}}{\rm{d}}{p_{\rm{p}}} $ | (11) |
联立式(10)式(11),有
| $ {\rm{d}}{\sigma _{\rm h}} = \dfrac{{{{\rm{c}}_{\rm{L}}}E + 3\left( {1 - 2\upsilon } \right)\phi }}{{\left( {1 + \upsilon } \right)\left( {1 - 2\upsilon } \right)}}{\rm{d}}{p_{\rm{p}}} $ | (12) |
式(12)即为地应力增量与孔隙压力增量之间的关系式。
4 挤压破坏分析初始地应力状态为σh < σz < σH,σh方向受挤压后地层破坏,根据Mohr Coulomb准则[20],地层破坏取决于σh和σz之间的应力差,而与σH无关。
根据式(4)、式(7),σh方向受挤压后,σh、σz方向上结构有效应力分别为
| $ \sigma _{_{{\rm{effh}}}}^{\rm{s}} = {\sigma _{\rm{h}}} + {\rm{d}}{\sigma _{\rm{h}}} - {\phi _{\rm{c}}}\left( {{p_{\rm{p}}} + {\rm{d}}{p_{\rm{p}}}} \right) $ | (13) |
| $ \sigma _{_{{\rm{effz}}}}^{\rm{s}} = {\sigma _{\rm{z}}} - {\phi _{\rm{c}}}\left( {{p_{\rm{p}}} + {\rm{d}}{p_{\rm{p}}}} \right) $ | (14) |
Mohr Coulomb准则表达式为[20]
| $ \left\{ \begin{array}{l} {\sigma _1} = {K^2}{\sigma _3} + 2CK \\ K = {\rm{ctg}}\left( {{{45}{°}} - \dfrac{\theta }{2}} \right) \\ \end{array} \right. $ | (15) |
由于σeffhs > σeffzs,令σ1 =σeffhs、σ3 = σeffzs,联立式(12)~式(15),化简,可得地层临界破坏时孔隙压力的增量极限
| $ {\Delta}{p_{{\rm{p}}\max }} \!=\! \dfrac{{{K^2}{\sigma _{\rm{z}}} \!+\! 2CK \!-\! {\sigma _{\rm{h}}} - \left( {{K^2} - 1} \right){\phi _{\rm{c}}}{p_{\rm{p}}}}}{{\left( {{K^2} - 1} \right){\phi _c} \!+\! \dfrac{{{{\rm{c}}_{\rm{L}}}E + 3\left( {1 - 2\upsilon } \right)\phi }}{{\left( {1 + \upsilon } \right)\left( {1 - 2\upsilon } \right)}}}} $ | (16) |
地层临界破坏时的孔隙压力系数的增量极限为
| $ \Delta {\alpha _{{\rm{p}}\max }} = \dfrac{{\Delta {p_{{\rm{pmax}}}}}\times 1000}{{{\rho _{\rm{w}}}{\rm{g}}D}} $ | (17) |
按照上面的过程,可推导出表 1中其他情形挤压作用发生后,地层达到临界破坏时孔隙压力系数的增量极限计算方法。
5 计算讨论假设某渗透性地层深度为4 500 m,初始孔隙压力为45.5 MPa(压力系数1.03),地层参数如表 2所示。改变地应力大小的初始取值(表 3),根据孔隙压力的增量极限计算公式和式(17),计算不同初始地应力状态下不同挤压方向孔隙压力系数的增量极限,结果如表 3所示。
| 表2 地层受挤压前的物理力学参数 Table 2 Physical and mechanical parameters of formation before extrusion |
| 表3 挤压作用导致的地层破坏规律 Table 3 The law of formation damage caused by extrusion |
计算结果表明,若初始地应力状态相同,相对于σH方向,挤压作用发生在σh方向时孔隙压力系数增量极限值更大。通过对比可知,相同地层参数条件下,情形4(初始地应力状态为σh < σH < σz,挤压作用发生在σh方向)的孔隙压力增量极限值最大。
在特定地质条件下,封闭地层受挤压作用后能使孔隙压力小幅度增大,产生轻微的压力异常,挤压作用导致的孔隙压力系数增量十分有限。只有当地层埋藏较深、强度足够大、围岩的密封性能好、挤压作用发生在最小水平主应力方向、且外挤压力足够大,这些条件同时满足时,才可能产生较大的异常高压。显然,同时满足这些条件的地层并不多。例如,挤压作用发生后,由于围岩的密封性能差导致孔隙压力释放,则不能形成异常高压;挤压作用发生在最大水平主应力方向,孔隙压力系数增大值一般不会超过0.35,难以形成较大的异常高压;外挤压力微弱,地层压缩量小,不能形成异常高压;地层强度较小,挤压作用导致地层破裂,孔隙压力释放,也不能形成异常高压。文献[3]研究表明,地层挤压破裂后,只要孔隙体积增大很小一部分(孔隙体积增量 < 0.5%地层总体积),即可达到异常低压的程度。由此可见,挤压作用形成异常高压的条件十分苛刻,一般不是异常高压形成的主要原因。
6 结论(1) 在特定地质条件下,封闭地层受挤压作用后能使孔隙压力小幅度增大,产生轻微的压力异常,挤压作用导致的孔隙压力系数增量十分有限。
(2) 挤压作用形成异常高压的条件十分苛刻,只有当地层埋藏较深、强度足够大、围岩的密封性能好、挤压作用发生在最小水平主应力方向、且外挤压力足够大,这些条件同时满足时,才可能产生较大的异常高压。
(3) 挤压作用难以形成异常高压,一般不是异常高压形成的主要原因。
符号说明
σH-最大水平主应力,MPa;
σh-最小水平主应力,MPa;
σz-垂向应力,MPa;
σeffT-Terzaghi有效应力,MPa;
σ-地应力,MPa;
pp-地层孔隙压力,MPa;
σeffB-Biot有效应力,MPa;
α-Biot系数,无因次;
σeffP-岩石的本体有效应力,MPa;
φ-岩石的孔隙度,%;
σeffS-岩石的结构有效应力,MPa;
φc-岩石的触点孔隙度,%;
E-岩石的杨氏模量,MPa;
ε-岩石的应变,无因次;
εH-岩石在最大水平主应力方向上的应变,无因次;
σeffHP-岩石在最大水平主应力方向上的本体有效应力,MPa;
υ-岩石的泊松比,无因次;
εh-岩石在最小水平主应力方向上的应变,无因次;
σeffHP-岩石在最小水平主应力方向上的本体有效应力,MPa;
εz-岩石在垂向应力方向上的应变,无因次;
σeffzP-岩石在垂向应力方向上的本体有效应力,MPa;
εv-岩石总应变,无因次;
εP-孔隙体积应变,无因次;
εL-孔隙中流体的体积应变,无因次;
VL-孔隙中流体体积,m3;
cL-孔隙中流体的压缩系数,MPa-1;
σeffhS-σh方向上岩石的结构有效应力,MPa;
σeffzS-σz方向上岩石的结构有效应力,MPa;
σ1-岩石破坏时所受的最大结构有效应力,MPa;
σ3-岩石破坏时所受的最小结构有效应力,MPa;
C-岩石的内聚力,MPa;
θ-岩石的内摩擦角,(°);
Δppmax-孔隙压力的增量极限,MPa;
Δαpmax-孔隙压力系数的增量极限,无因次;
ρw-地层水密度,g/cm3;
g-重力加速度,g=9.8 m/s2;
D-地层埋深,m。
| [1] | HUNT J M. Genneration and migration of petroleum from abnormally pressured fluid compartments[J]. AAPG Bulletin, 1990, 74(1): 1–12. |
| [2] | POWLEY D E. Presusures and hydrogeology in petroleum basins[J]. Earth Science Reviews, 1990, 29: 215–226. doi: 10.1016/0012-8252(0)90038-W |
| [3] |
李传亮. 地层异常压力原因分析[J].
新疆石油地质, 2004, 25(4): 443–445.
LI Chuanliang. Analysis of abnormal reservoir pressure[J]. Xinjiang Petroleum Geology, 2004, 25(4): 443–445. |
| [4] |
王江涛, 李育. 沉积盆地异常高压形成机制综述[J].
石油化工应用, 2014, 33(1): 5–9.
WANG Jiangtao, LI Yu. A summary of abnormal high pressure formation mechanism in sedimentary basin[J]. Petrochemical Industry Application, 2014, 33(1): 5–9. doi: 10.3969/j.issn.1673-5285.2014.01.002 |
| [5] |
高岗, 黄志龙, 王兆峰, 等. 地层异常高压形成机理的研究[J].
西安石油大学学报(自然科学版), 2005, 20(1): 15–5.
GAO Gang, HUANG Zhilong, WANG Zhaofeng, et al. Study on the mechanisms of the formation of f ormation abnormal high-pressure[J]. Journal of Xi'an Shiyou University(Natural Science Edition), 2005, 20(1): 15–5. |
| [6] |
曾联波, 周天伟, 吕休祥. 构造挤压对库车坳陷异常地层压力的影响[J].
地质论评, 2004, 50(5): 471–475.
ZENG Lianbo, ZHOU Tianwei, LÜ Xiuxiang. Influence of tectonic compression on the abnormal formation pressure in the Kuqa Depression[J]. Eological Review, 2004, 50(5): 471–475. |
| [7] |
熊建华, 施豫琴, 过敏. 构造挤压在川东北地区飞仙关组异常高压中的作用[J].
矿物岩石, 2010, 30(3): 83–88.
XIONG Jianhua, SHI Yuqin, GUO Min. Effectof tectonic compression on the abnormalpressure of the Feixianguan Formation in the northeast Sichuan[J]. Journal of Mineralogy and Petrology, 2010, 30(3): 83–88. |
| [8] |
王海芳, 杨辉, 陈培元, 等. 塔里木盆地柯克亚凝析气田异常高压成因分析[J].
新疆地质, 2014, 32(2): 231–234.
WANG Haifang, YANG Hui, CHEN Peiyuan, et al. Genesis analysis on abnormal high pressure in Kekeya Condensate Gas-Field, Tarim Basin[J]. Xinjiang Geology, 2014, 32(2): 231–234. |
| [9] | 马克D·佐白科. 储层地质力学[M]. 石林, 陈朝伟, 刘玉石, 译. 北京: 石油工业出版社, 2012. |
| [10] | 耶格J C, 库克N G W. 岩石力学基础[M]. 中国科学院力学研究所, 译. 北京: 科学出版社, 1981. |
| [11] | BIOT M A. General theory of three-dimensional consolidation[J]. Journal of Applied Physics, 1941, 12(2): 155–164. doi: 10.1063/1.1712886 |
| [12] |
李传亮, 孔祥言, 徐献芝, 等. 多孔介质的双重有效应力[J].
自然杂志, 1999, 21(5): 288–292.
LI Chuanliang, KONG Xiangyan, XU Xianzhi, et al. Dual effective stresses of porous media[J]. Chinese Journal of Nature, 1999, 21(5): 288–292. |
| [13] |
李传亮. 关于双重有效应力——回应洪亮博士[J].
新疆石油地质, 2015, 36(2): 238–243.
LI Chuanliang. Discussion on the dual effective stresses of porous media-Reply to Dr. HONG Liang[J]. Xinjiang Petroleum Geology, 2015, 36(2): 238–243. doi: 10.7657/XJPG20150222 |
| [14] |
李传亮. 岩石压缩系数与孔隙度的关系[J].
中国海上油气(地质), 2003, 17(5): 355–358.
LI Chuanliang. The relationship between rock compressibility and porosity[J]. China Offshore Oil and Gas(Geology), 2003, 17(5): 355–358. |
| [15] |
李传亮, 孔祥言. 岩石强度条件的理论研究[J].
应用科学学报, 2001, 19(2): 103–106.
LI Chuanliang, KONG Xiangyan. Theoretical study of rock strength conditions[J]. Journal of Applied Sciences, 2001, 19(2): 103–106. |
| [16] |
李传亮. 低渗透储层不存在强应力敏感[J].
石油钻采工艺, 2005, 27(4): 61–63.
LI Chuanliang. Low permeability rocks are less sensitive to stress[J]. Oil Drilling & Production Technology, 2005, 27(4): 61–63. |
| [17] | 徐芝纶. 弹性力学[M]. 第4版. 北京: 高等教育出版社, 2006. |
| [18] |
李传亮. 孔隙度校正缺乏理论依据[J].
新疆石油地质, 2003, 24(3): 254–256.
LI Chuanliang. The porosity correction is lack of theoretical basis[J]. Xinjiang Petroleum Geology, 2003, 24(3): 254–256. |
| [19] |
李传亮. 岩石本体变形过程中的孔隙度不变性原则[J].
新疆石油地质, 2005, 26(6): 732–734.
LI Chuanliang. The principle of rock porosity invar iability in pr imary deformation[J]. Xinjiang Petroleum Geology, 2005, 26(6): 732–734. |
| [20] |
陈勉, 金衍, 张广清.
石油工程岩石力学[M]. 北京: 科学出版社, 2008.
CHEN Mian, JIN Yan, ZHANG Guangqing. Petroleum Engineering and Rock mechanics[M]. Beijing: SciencePress, 2008. |
 2017, Vol. 39
2017, Vol. 39


