2. "油气藏地质及开发工程"国家重点实验室·西南石油大学, 四川 成都 610500
2. State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation, Southwest Petroleum University, Chengdu, Sichuan 610500, China
应力敏感评价早期主要用于岩土工程、地质工程等相关领域的研究,在石油工程领域,应力敏感评价主要是通过实验研究上覆地层压力(或称为围压)对渗透率的影响。相关学者通过研究发现,渗透率表现为有效应力的函数,且储层的孔隙形状[1]、骨架颗粒分选[1]、颗粒的粗糙程度[2]均对渗透率的应力敏感性存在一定影响。2014年,Jelmert等[3]通过研究发现,渗透率与有效应力间存在指数、乘幂和多项式等3种较为适用的函数关系。但是,对于不同孔隙结构的储层,渗透率与有效应力间的函数关系是存在差异的[4-10]。
岩石的电阻率性质是连接储层岩石岩性与物性及含油气性的桥梁。对岩石电阻率性质的研究与认识,直接影响储层含油气性的评价[11-20]。Bernabé等[21-22]基于逾渗网络模拟研究,得到了多孔介质渗透率和地层因素、孔喉连通性及孔隙结构参数间的关系,即BLM模型,研究发现,渗透率和地层因素、孔喉平均配位数(z)和临界配位数(zc)的差值(z-zc)服从乘幂关系,且只有当岩石的孔喉平均配位数z ≥ 1.5时,流体才能在多孔介质中流动,即临界配位数zc=1.5。基于Bernabé等[21-22]的研究成果,笔者发现,在孔隙流体与骨架颗粒间不发生任何化学反应且无环境因素影响时,渗透率和地层因素单纯表现为孔隙结构参数的函数。
本文首先研究了有效应力与多孔介质孔隙结构参数间的关系,根据Bernabé等[21-22]得到的地层因素和渗透率公式,推导出地层因素、渗透率与有效应力之间的函数关系,选取了不同物性不同地区的无黏土砂岩岩样的地层因素、渗透率随有效应力变化实验数据进行对比分析。最后,讨论了高孔隙度岩石与低孔隙度岩石应力敏感性差异,以及在双对数坐标下实验数据出现分段响应特征的原因。
1 理论模型推导有效应力(σeff)可表示为围压(pc)和孔隙流体压力(pp)(也称为内压)的函数
| $ {\sigma _{{\text{eff}}}} = {p_{\text{c}}}-\alpha {p_{\text{p}}} $ | (1) |
式中:σeff-有效应力,MPa;
α-有效应力系数,无因次;
pc-围压,MPa;
pp-内压,MPa。
当内压(pp)接近大气压时,内压可被忽略,则有
| $ {\sigma _{{\text{eff}}}} \approx {p_{\text{c}}} $ | (2) |
本文实验数据均为内压近似为大气压时所测,因此,围压可近似为有效应力。
1.1 孔隙结构与有效应力的关系Bernabé等[21-22]通过逾渗网络模拟建立了渗透率、地层因素与孔隙结构之间的关系,称为BLM模型。多孔介质的孔隙结构特征数用孔喉配位数(z)、孔喉分布变异系数(Vr)、水力半径(rH)、孔喉长度(l)和孔喉横截面纵横比(ε)等参数表征。其关系式为
| $ \frac{1}{F} = {C_{\text{F}}}{\left( {\frac{{{r_{\text{H}}}}}{l}} \right)^2}{\left( {z-{z_{\text{c}}}} \right)^\gamma } $ | (3) |
| $ K = {C_{\text{k}}}{\left( {\frac{{{r_{\text{H}}}}}{l}} \right)^2}{\left( {z-{z_{\text{c}}}} \right)^\beta }r_{\text{H}}^2 $ | (4) |
式中:F-地层因素,无因次;
rH-水力半径,μm,且rH=2Vp/Ap;
l-孔喉长度,μm;
z-孔喉配位数,无因次;
zc-孔喉临界配位数,无因次;
K-渗透率,mD;
Vp-孔隙体积,μm3;
Ap-孔隙内表面积,μm2。
参数γ、β、Ck和CF由孔喉形状和孔喉分布变异系数Vr决定,计算公式分别为
| $ {C_{\text{F}}} = \frac{{{{\left[{3\left( {1 + \varepsilon } \right)-\sqrt {3{\varepsilon ^2} + 10\varepsilon + 3} } \right]}^2}}}{{4\varepsilon }}{10^{ -\left( {0.32894 + 0.23339{V_r} + 1.1423V_r^2} \right)}} $ | (5) |
| $ {C_{\text{k}}} = \frac{{{{\left[{3\left( {1 + \varepsilon } \right)-\sqrt {3{\varepsilon ^2} + 10\varepsilon + 3} } \right]}^4}}}{{8\varepsilon \left( {1 + {\varepsilon ^2}} \right)}}{10^{ -\left( {1.195 + 0.8219{V_{\text{r}}} + 2.0459V_{\text{r}}^{\text{2}}} \right)}} $ | (6) |
| $ \gamma = 1.2903 + 0.045527{V_{\text{r}}} + 0.8239V_{\text{r}}^2 $ | (7) |
| $ \beta = 1.2343 + 0.93462{V_{\text{r}}} + 1.4755V_{\text{r}}^2 $ | (8) |
式中:ε-孔喉横截面纵横比,无因次,且ε=a/b;
a,b-孔喉横截面的短轴和长轴的长度,μm。
孔隙结构参数z、l、ε、rH和Vr是定量计算渗透率和地层因素的基础参数。Bernabé等[21-22]通过真实岩芯实验结果对比,发现式(3)、式(4) 对枫丹白露砂岩可以取得满意的计算结果。
Fredrich等[23-24]研究发现,无黏土砂岩的孔隙呈各种不规则形状。为方便研究岩石的输运属性,前人将岩石孔隙形状简化为圆形、椭圆形[25-27]、锥形[25-27]、星形[25]、三角形[25]和矩形[28]等。三角形、矩形等孔隙形状可进一步简化至圆形或椭圆形,此简化对研究岩石的宏观输运属性具有重要意义。
Bernabé等[21-22]在研究多孔介质孔隙结构时,采用了孔喉截面纵横比(ε)来表征岩石孔喉截面形状,ε越小,孔隙越扁;Dong等[26]采用孔隙形状因子(G,G = B/P2,B-孔喉横截面积,P-孔喉横截面的周长)表示孔喉截面形状。当多孔介质中存在类似椭圆或锥形的微裂缝时,孔喉横截面纵横比(ε)能更好地表征该类岩石渗流。当孔隙形状简化为椭圆形时,用孔喉横截面纵横比(ε)表征孔隙形状。在椭圆形孔喉中,认为长轴(b)基本上不随有效应力的变化而改变,椭圆的短轴长度随有效应力变化而发生变化,其变化关系服从[27]
| $ l\left( \sigma \right) = {l_0}\left[{1-\frac{{2\left( {1-{v^2}} \right)}}{{{\varepsilon _0}E}}{\sigma _{{\text{eff}}}}} \right] $ | (9) |
式中:l(σ)-有效应力为σeff时椭圆截面短轴长度,μm;
l0-零应力作用下椭圆截面短轴长度,μm;
v-泊松比,无因次;
E-弹性模量,GPa;
ε0-零应力作用下孔喉横截面的纵横比,无因次。
根据以往不同地区砂岩弹性参数的研究[29],砂岩弹性模量(E)为5~95 GPa,砂岩泊松比(v)为0.14~0.33。本文取砂岩的弹性模量为30 GPa,泊松比为0.25。
Bernabé等[21]通过二维图像分析及网络模拟,认为枫丹白露砂岩平均孔喉横截面的纵横比(ε)为0.02~0.40,通常情况下,孔隙度越高,ε越大。这里分别计算了初始孔喉横截面的纵横比(ε0)为0.400、0.300、0.200、0.100、0.010、0.005和0.001时,ε随有效应力的变化关系。
当孔隙形状简化为锥形时,锥形的短轴和长轴会随有效应力的变化而发生变化,其公式分别为[27]
| $ a\left( \sigma \right) = {a_0}{\left[{1-\frac{{4\left( {1-{v^2}} \right)}}{{3{\varepsilon _0}E}}{\sigma _{{\text{eff}}}}} \right]^{\frac{3}{2}}} $ | (10) |
| $ b\left( \sigma \right) = {b_0}{\left[{1-\frac{{4\left( {1-{v^2}} \right)}}{{3{\varepsilon _0}E}}{\sigma _{{\text{eff}}}}} \right]^{\frac{1}{2}}} $ | (11) |
式中:a(σ)-有效应力为σeff时锥形截面短轴长度,μm;
b(σ)-有效应力为σeff时锥形截面长轴长度,μm;
a0-零应力作用下锥形截面短轴长度,μm;
b0-零应力作用下锥形截面长轴长度,μm。
根据式(5) 和式(6),分别定义孔喉横截面纵横比函数fF(ε)和fk(ε)为
| $ {f_{\text{F}}}\left( \varepsilon \right) = \frac{{{{\left[{3\left( {1 + \varepsilon } \right)-\sqrt {3{\varepsilon ^2} + 10\varepsilon + 3} } \right]}^2}}}{{4\varepsilon }} $ | (12) |
| $ {f_{\text{k}}}\left( \varepsilon \right) = \frac{{{{\left[{3\left( {1 + \varepsilon } \right)-\sqrt {3{\varepsilon ^2} + 10\varepsilon + 3} } \right]}^4}}}{{8\varepsilon \left( {1 + {\varepsilon ^2}} \right)}} $ | (13) |
通过式(9)~式(11),得到不同有效应力下孔喉横截面纵横比(ε)的值,代入式(12) 和式(13),即得到不同有效应力下的fF(ε)、fk(ε)。不同有效应力下的fF(ε)、fk(ε)与初始的fF(ε0)、fk(ε0)比值关系见图 1、图 2。
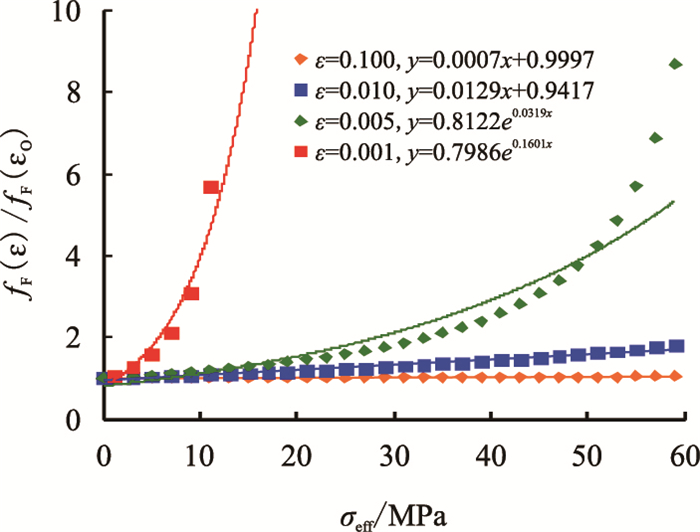 |
| 图1 椭圆形孔隙fF(ε)/fk(ε)随有效应力变化图 Fig. 1 Relationships between fF(ε)/fk(ε) and σeff for elliptical pores |
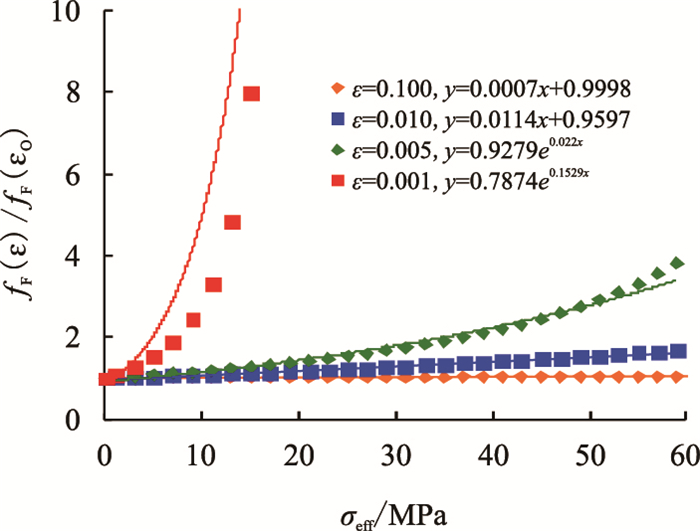 |
| 图2 锥形孔隙fF(ε)/fk(ε)随有效应力变化图 Fig. 2 Relationships between fF(ε)/fk(ε) and σeff for taper pores |
从图 1和图 2的拟合关系可以看到,椭圆形孔隙和锥形孔隙归一化孔喉横截面纵横比函数随有效应力的变化趋势一致,且拟合关系式基本相同。当孔喉横截面纵横比ε0)≥ 0.01时,归一化孔喉横截面纵横比函数(f(εp)/f(ε0))和有效应力之间满足线性关系
| $ \frac{{f\left( \varepsilon \right)}}{{f\left( {{\varepsilon _0}} \right)}} = f\left( {{\sigma _{{\text{eff}}}}} \right) = {a_{10}}{\sigma _{{\text{eff}}}} + {a_{11}} $ | (14) |
式中:a10、a11-拟合系数。
从图 1和图 2还可以看到,当孔喉的ε0 ≥0.100时,随有效应力的增加,ε基本不发生改变,可近似认为f(εp)/f(ε0) ≈ 1。
当ε0 ≤ 0.005时,有效应力增加会导致ε显著地减小,根据式(12) 和式(13) 的函数关系,fF(ε)、fk(ε)会显著增大,但此时孔隙水力半径已减小至零,因此,并不影响式(3) 和式(4) 中地层因素和渗透率随有效应力的变化趋势。归一化孔喉横截面纵横比函数(f(εp)/f(ε0))和有效应力间满足指数关系
| $ \frac{{f\left( \varepsilon \right)}}{{f\left( {{\varepsilon _0}} \right)}} = f\left( {{\sigma _{{\text{eff}}}}} \right) = {a_{20}}{e^{{a_{21}}{\sigma _{{\text{eff}}}}}} $ | (15) |
式中:a20、a21-拟合系数。
有效应力的作用会引起孔隙体积和孔隙表面积发生变化。当孔隙模型简化为椭圆模型和锥形模型时,通过式(9)、式(10) 和式(11),可以得到不同有效应力下的椭圆短轴(长轴视为不变)及锥形的长短轴,进而根据rH=2Vp/Ap,得到不同有效应力下孔隙的水力半径。归一化孔隙水力半径(rH)与有效应力的关系见图 3、图 4。
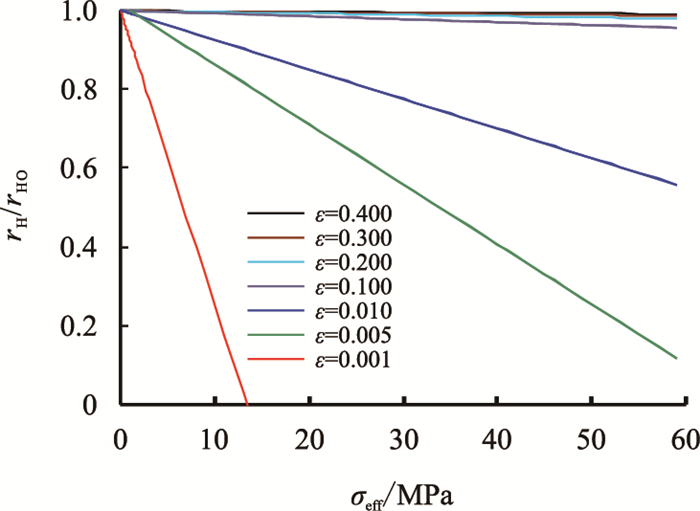 |
| 图3 椭圆形孔隙水力半径随有效应力变化关系图 Fig. 3 Changing of rH with σeff for elliptical pores |
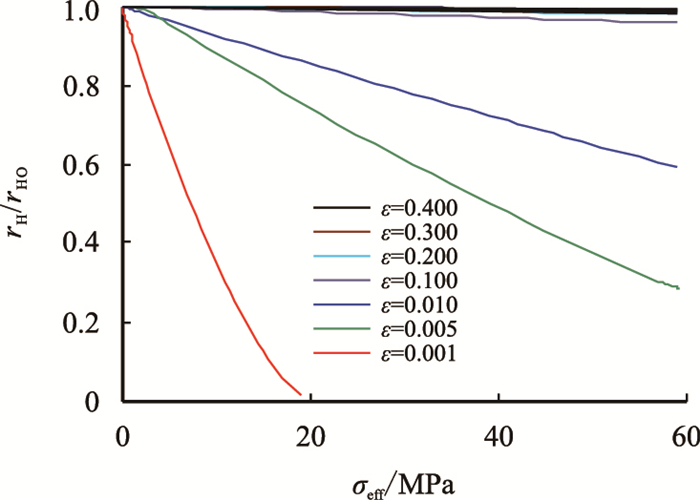 |
| 图4 锥形孔隙水力半径随有效应力变化关系图 Fig. 4 Changing of rH with σeff for taper pores |
从图 3、图 4可以看出,当孔喉的ε0≥0.1时,随有效应力的增加,rH基本上不会发生改变;而当ε0很小时,有效应力增加会导rH减小,甚至趋于零。
当孔隙模型简化为三角形模型,有效应力发生变化时,三角形中心到三角形的最远距离(即孔喉横截面纵横比中的长轴)随之发生变化[27],若将孔隙形状简化为正三角形,则得到水力半径的表达式
| $ {r_{\text{H}}} = c\left( {{\sigma _{{\text{eff}}}}} \right) = {c_0}\left[{1-{{\left( {\frac{{3\sqrt 2 \left( {1-{v^2}} \right)}}{{4\varepsilon 'E}}{\sigma _{{\text{eff}}}}} \right)}^{1/3}}} \right] $ | (16) |
式中:ε′-三角形孔喉横截面纵横比,且ε′ = a′=c0;
a′-零应力作用下三角形中心到三角形边界的最近距离,μm;
c0-零应力作用下三角形中心到三角形边界的最远距离,μm。
通过分析Bourbie和Zinszner[24]枫丹白露砂岩的岩石薄片图像,得到枫丹白露砂岩的三角形孔喉横截面纵横比的变化范围为0.2~0.5。因此,分别计算了ε= 0:2、0.3、0.4和0.5时,水力半径(rH)随有效应力的变化关系(图 5)。
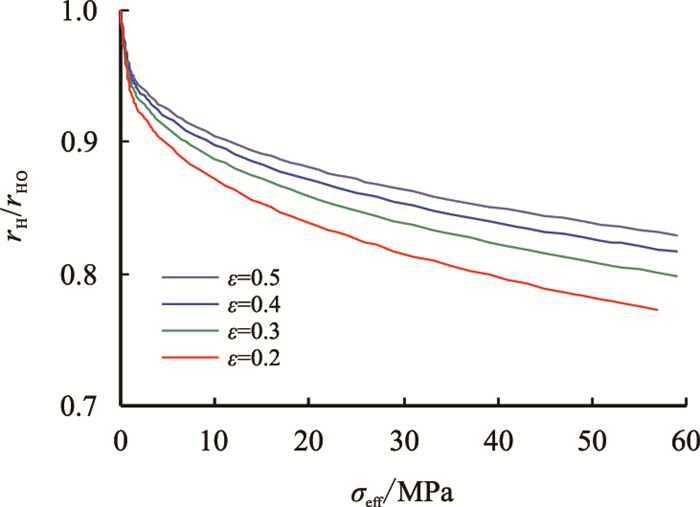 |
| 变化图(0.2 ≤ c ≤ 0.5) stress(0.2 ≤ c ≤ 0.5) 图5 三角形形模型孔隙水力半径随有效应力 Fig. 5 Triangle pore hydraulic radius model with effective |
图 3~图 5中的水力半径数值均进行了归一化处理。Yale[27]还模拟了星形孔隙的传导率随围压的变化情况,模拟显示,星形孔隙的传导率随围压的变化情况与三角形孔隙类似。
从上述3类孔隙模型的水力半径随有效应力的变化曲线可以得到:在有效应力发生变化时,孔隙的水力半径变化较小,且与有效应力呈现出一定函数关系。归一化水力半径(rHp/rH0)与有效应力(σeff)间具有函数关系
| $ \frac{{{r_{{\text{Hp}}}}}}{{{r_{{\text{H0}}}}}} = f\left( {{\sigma _{{\text{eff}}}}} \right) $ | (17) |
式中:rHp-有效应力为σeff时的水力半径,μm;
rH0-零应力作用下的水力半径,μm。
对于椭圆形和锥形孔隙,接近于线性关系
| $ \frac{{{r_{{\text{Hp}}}}}}{{{r_{{\text{H0}}}}}} = {a_{30}}{\sigma _{{\text{eff}}}} + {a_{31}} $ | (18a) |
对于三角形和星形孔隙,更接近于乘幂关系和对数线性关系
| $ \frac{{{r_{{\text{Hp}}}}}}{{{r_{{\text{H0}}}}}} = {a_{40}}\sigma _{{\text{eff}}}^{{a_{41}}} $ | (18b) |
| $ \frac{{{r_{{\text{Hp}}}}}}{{{r_{{\text{H0}}}}}} = {a_{50}}\ln {\sigma _{{\text{eff}}}} + {a_{51}} $ | (18c) |
式中:a30、a31、a40、a41、a50、a51-拟合系数。
从图 3~图 5还可以看到:当孔隙形状为较规则的锥形或椭圆形时,水力半径与有效应力关系服从直线关系;当孔隙形状为不规则的三角形或星形时,其水力半径与有效应力关系服从乘幂或对数线性关系。在研究多孔介质孔隙变形问题时,若仍然简单地假设为椭圆形孔隙,则会发现水力半径与有效应力呈直线关系,不规则孔隙形状的孔隙在有效应力作用下,其水力半径与有效应力之间偏离直线关系,而更接近于乘幂或对数线性关系。因此,本文认为,根据岩石孔隙形状的不同,归一化水力半径与有效应力之间具有直线、乘幂、对数线性等3种函数关系。
此外,从图 3和图 4中还可以看出,当ε很小时,有效应力增加会导致rH显著减小,甚至趋于零,孔隙形状发生明显改变,可以理解成非常扁的孔喉在很大的有效应力作用下会发生闭合。
当多孔介质中存在裂缝或者微裂缝时,在有效应力作用下,裂缝闭合会导致孔隙连通性发生变化。逾渗理论认为,孔隙连通性是影响多孔介质输运性质的重要因素[17]。配位数与有效应力间的函数关系如下
| $ \frac{{{z_{\text{p}}}-{z_{\text{c}}}}}{{{z_0}-{z_{\text{c}}}}} = f\left( {{\sigma _{{\text{eff}}}}} \right) $ | (19) |
式中:zp-有效应力为σeff时的孔喉配位数,无因次;
z0-零应力作用下的孔喉配位数,无因次;
zc-零应力作用下的孔喉临界配位数,无因次。
上述关系受孔隙形状及孔喉横截面纵横比分布的影响,只有当大量存在ε为10-3数量级的孔隙时,才会呈现出明显的函数关系。对于高孔隙度枫丹白露砂岩,孔隙或喉道不易被压缩至闭合,此时该关系式则为f(σeff)=1。
不同有效应力条件下,孔喉长度会发生伸长或缩短,同时,岩芯外观长度也随有效应力的变化而改变,本文研究中假设孔喉长度不发生变化。
康毅力等[28]对同一块岩样采用不同围压进行压汞实验。结果表明,随围压的变化,毛管压力曲线形态发生变化,孔隙大小分布非均质性略微变强。根据Chieric等[29]在地层压力下对储集层岩石物理特性的研究中,分别测试围压为0和40 MPa时的毛管压力曲线,并根据实验结果计算得围压为0和40 MPa时的孔喉大小分布变异系数Vr(表 1)。
| 表1 不同有效应力下孔喉大小分布变异系数 Table 1 Different effective stress coefficient of variation of pore size distribution |
根据式(5) 和式(6),分别定义预因子函数wF(Vr)和wk(Vr)为
| $ {w_{\text{k}}}\left( {{V_{\text{r}}}} \right) = {10^{-\left( {1.195 + 0.8219{V_{\text{r}}} + 2.0459V_{\text{r}}^2} \right)}} $ | (20) |
| $ {w_{\text{F}}}\left( {{V_{\text{r}}}} \right) = {10^{-\left( {0.32894 + 0.23339{V_{\text{r}}} + 1.1423V_{\text{r}}^2} \right)}} $ | (21) |
式中:wk(Vr)-渗透率预因子函数;
wF-(Vr)-地层因素预因子函数;
Vr-孔喉分布变异系数,无因次。
从表 1中可以看到,当有效应力从0增加到40 MPa时,孔喉分布变异系数(Vr)变化很小。因此,归一化预因子函数w(Vr)及归一化β、γ与有效应力间有如下关系
| $ \frac{{w\left( {{V_{{\text{rp}}}}} \right)}}{{w\left( {{V_{{\text{r0}}}}} \right)}} = \frac{{{\beta _{\text{p}}}}}{{{\beta _0}}} = \frac{{{\gamma _{\text{p}}}}}{{{\gamma _0}}} = f\left( {{\sigma _{{\text{eff}}}}} \right) \approx 1 $ | (22) |
根据上述关系,推导地层因素、渗透率与有效应力之间的关系。
1.2 地层因素与有效应力的关系假设有效应力为0时,地层因素的表达式为
| $ \frac{1}{{{F_0}}} = {C_{{\text{F0}}}}{\left( {\frac{{{r_{{\text{H0}}}}}}{{{l_0}}}} \right)^2}{\left( {{z_0}-{z_{\text{c}}}} \right)^{{\gamma _0}}} $ | (23) |
式中:F0-零应力作用下的地层因素,无因次;
| $ {C_{\text{F}}} = {f_{\text{F}}}\left( \varepsilon \right){w_{\text{F}}}\left( {{\sigma _{\text{r}}}} \right)。 $ |
当有效应力为σeff时
| $ \frac{1}{{{F_{\text{p}}}}} = {C_{{\text{Fp}}}}{\left( {\frac{{{r_{{\text{Hp}}}}}}{{{l_{\text{p}}}}}} \right)^2}{\left( {{z_{\text{p}}}-{z_{\text{c}}}} \right)^{{\gamma _{\text{p}}}}} $ | (24) |
根据式(5)、式(12)、式(21)、式(23) 和式(24),归一化地层因素(F0=Fp)的表达式为
| $ \frac{{{F_0}}}{{{F_{\text{p}}}}} = \frac{{{f_{\text{F}}}\left( {{\varepsilon _{\text{p}}}} \right){w_{\text{F}}}\left( {{\sigma _{{\text{rp}}}}} \right)}}{{{f_{\text{F}}}\left( {{\varepsilon _0}} \right){w_{\text{F}}}\left( {{\sigma _{{\text{r0}}}}} \right)}}{\left( {\frac{{{r_{{\text{Hp}}}}}}{{{r_{{\text{H0}}}}}}} \right)^2}{\left( {\frac{{{l_{\text{p}}}}}{{{l_0}}}} \right)^2}\frac{{{{\left( {{z_{\text{p}}}-{z_{\text{c}}}} \right)}^{{\gamma _{\text{p}}}}}}}{{{{\left( {{z_0}-{z_{\text{c}}}} \right)}^{{\gamma _0}}}}} $ | (25) |
根据1.1节研究结论,式(25) 可简化为
| $ \frac{{{F_0}}}{{{F_{\text{p}}}}} = \frac{{{f_{\text{F}}}\left( {{\varepsilon _{\text{p}}}} \right)}}{{{f_{\text{F}}}\left( {{\varepsilon _0}} \right)}}{\left( {\frac{{{r_{{\text{Hp}}}}}}{{{r_{{\text{H0}}}}}}} \right)^2}\frac{{{{\left( {{z_{\text{p}}}-{z_{\text{c}}}} \right)}^{{\gamma _{\text{p}}}}}}}{{{{\left( {{z_0}-{z_{\text{c}}}} \right)}^{{\gamma _0}}}}} $ | (26) |
式中:FP-有效应力为σeff时的地层因素,无因次;
lp-有效应力为σeff时的孔喉长度,μm;
l0-零应力作用下的孔喉长度,μm;
当岩石孔喉横截面纵横比ε≥0.1时,在有效应力作用下无(微)裂缝闭合现象。根据式(14) 和式(19),式(26) 可简化为
| $ \dfrac{{{F_0}}}{{{F_{\rm{p}}}}} = {\left({\dfrac{{{r_{{\rm{Hp}}}}}}{{{r_{{\rm{H0}}}}}}} \right)^2} $ | (27) |
根据式(18a)~式(18c)可得到地层因素与有效应力之间具有以下3种关系
| $ \sqrt {{F_0}/{F_{\rm{p}}}} = {{{r_{{\rm{Hp}}}}}}/{{{r_{{\rm{H0}}}}}} = {a_{30}}{{\sigma _{{\rm{eff}}}}}+ {a_{31}} $ | (28a) |
| $ \sqrt {{F_0}/{F_{\rm{p}}}} = {{{r_{{\rm{Hp}}}}}}/{{{r_{{\rm{H0}}}}}} = {a_{40}}{{{\sigma _{{\rm{eff}}}}} ^{{a_{41}}}} $ | (28b) |
| $ \sqrt {{F_0}/{F_{\rm{p}}}} = {{{r_{{\rm{Hp}}}}}}/{{{r_{{\rm{H0}}}}}} = {a_{50}}\ln {{\sigma _{{\rm{eff}}}}} + {a_{51}} $ | (28c) |
在低孔隙度岩石中,当岩石孔隙空间中不存在ε为10-3数量级的孔隙时,其孔隙连通性不会随有效应力发生改变,但是孔喉横截面纵横比函数随着有效应力改变,则地层因素与有效应力之间应具有如下关系
| $ \dfrac{{{F_0}}}{{{F_{\rm{p}}}}} = \dfrac{{{f_{\rm{F}}}({\varepsilon _{\rm{p}}})}}{{{f_{\rm{F}}}({\varepsilon _0})}}{\left({\dfrac{{{r_{{\rm{Hp}}}}}}{{{r_{{\rm{H0}}}}}}} \right)^2} $ | (29) |
| $ \sqrt {{F_0}/{F_{\rm{p}}}} = \sqrt {{a_{60}}{\sigma _{{\rm{eff}}}} + {a_{61}}} \left({{a_{30}}{\sigma _{{\rm{eff}}}} + {a_{31}}} \right) $ | (30a) |
| $ \sqrt {{F_0}/{F_{\rm{p}}}} = \sqrt {{a_{60}}{\sigma _{{\rm{eff}}}} + {a_{61}}} \left({{a_{40}}{\sigma _{{\rm{eff}}}}^{{a_{41}}}} \right) $ | (30b) |
| $ \sqrt {{F_0}/{F_{\rm{p}}}} = \sqrt {{a_{60}}{\sigma _{{\rm{eff}}}} + {a_{61}}} \left({{a_{50}}\ln {\sigma _{{\rm{eff}}}} + {a_{51}}} \right) $ | (30c) |
式中:a60、a61-拟合系数。
对于低孔隙度岩石,地层因素与有效应力的关系式在乘上了一个低价线性关系后仍然服从3类主要函数关系,虽然曲线会出现轻微的波动,但并不影响其趋势。
当岩石孔隙空间中大量存在ε为10-3数量级的孔隙时,随着有效应力增大,孔隙将在某个压力点发生闭合,导致配位数发生改变,孔喉横截面纵横比函数也会随着有效应力改变,假设配位数与有效应力服从线性关系。此时,地层因素与有效应力间应具有如下关系
| $ \dfrac{{{F_0}}}{{{F_{\rm{p}}}}} = \dfrac{{{f_{\rm{F}}}({\varepsilon _{\rm{p}}})}}{{{f_{\rm{F}}}({\varepsilon _0})}}{\left({\dfrac{{{r_{\rm{Hp}}}}}{{{r_{\rm{H0}}}}}} \right)^2}{\left({\dfrac{{{z_{\rm{p}}}-{z_{\rm{c}}}}}{{{z_0}-{z_{\rm{c}}}}}} \right)^{{\gamma _0}}} $ | (31) |
| $ \sqrt {{F_0}/{F_{\rm{p}}}} = \sqrt {{a_{70}}{e^{{a_{71}}{\sigma _{{\rm{eff}}}}}}} {\left({{a_{30}}{\sigma _{{\rm{eff}}}} + {a_{31}}} \right)^2}{{f^{\frac{\gamma }{2}}{{\sigma _{{\rm{eff}}}}}} } $ | (32a) |
| $ \sqrt {{F_0}/{F_{\rm{p}}}} = \sqrt {{a_{70}}{e^{{a_{71}}{\sigma _{{\rm{eff}}}}}}} \left({{a_{40}}{\sigma _{{\rm{eff}}}}^{{a_{41}}}} \right){{f^{\frac{\gamma }{2}}{{\sigma _{{\rm{eff}}}}} } } $ | (32b) |
| $ \sqrt {{F_0}/{F_{\rm{p}}}} = \sqrt {{a_{70}}{e^{{a_{71}}{\sigma _{{\rm{eff}}}}}}} \left({{a_{50}}\ln {\sigma _{{\rm{eff}}}} + {a_{51}}} \right){{f^{\frac{\gamma }{2}}{{\sigma _{{\rm{eff}}}}} } } $ | (32c) |
式中:a70、a71-拟合系数。
从式(32a)~式(32c)可以看出,当同时存在孔隙形变与微裂缝闭合时,地层因素与有效应力间的函数关系变得十分复杂。当细长裂缝状孔隙完全闭合后,配位数不会在发生改变,此后地层因素与有效应力之间将服从式(29) 所描述的函数关系。
1.3 渗透率与有效应力的关系假设有效应力为零时,渗透率的表达式为
| $ {k_0} = {C_{{{\rm{k}}_0}}}{\left({{r_{{{\rm{H}}_{\rm{0}}}}}/{l_0}} \right)^2}{\left({{z_0}-{z_{\rm{c}}}} \right)^{{\beta _0}}}r_{{{\rm{H}}_{\rm{0}}}}^2 $ | (33) |
式中:
k0-零应力作用下的渗透率,mD。
当有效应力为σeff时
| $ {k_{\rm{p}}} = {C_{{\rm{kp}}}}{\left({\frac{{{r_{{\rm{Hp}}}}}}{{{l_{\rm{p}}}}}} \right)^2}{\left({{z_{\rm{p}}}-{z_{\rm{c}}}} \right)^{{\beta _{\rm{p}}}}}r_{{\rm{Hp}}}^2 $ | (34) |
式中:kp-零应力作用下的渗透率,mD。
结合式(6)、式(13)、式(20)、式(33) 和式(34),则归一化渗透率(kp/k0)可表示为
| $ \dfrac{{{k_{\rm{p}}}}}{{{k_0}}} = \dfrac{{{f_{\rm{k}}}({\varepsilon _{\rm{p}}}){w_{\rm{k}}}({\sigma _{{\rm{rp}}}})}}{{{f_{\rm{k}}}({\varepsilon _0}){w_{\rm{k}}}({\sigma _{r0}})}}{\left({\dfrac{{{r_{{\rm{Hp}}}}}}{{{r_{{{\rm{H}}_{\rm{0}}}}}}}} \right)^4}{\left({\dfrac{{{l_0}}}{{{l_{\rm{p}}}}}} \right)^2}\dfrac{{{{({z_{\rm{p}}}-{z_{\rm{c}}})}^{{\beta _p}}}}}{{{{({z_0}-{z_{\rm{c}}})}^{{\beta _0}}}}} $ | (35) |
根据上节结论,式(35) 可简化为
| $ \dfrac{{{k_{\rm{p}}}}}{{{k_0}}} = \dfrac{{{f_{\rm{k}}}\left({{\varepsilon _{\rm{p}}}} \right)}}{{{f_{\rm{k}}}\left({{\varepsilon _0}} \right)}}{\left({\dfrac{{{r_{{\rm{Hp}}}}}}{{{r_{{{\rm{H}}_{\rm{0}}}}}}}} \right)^4}\dfrac{{{{\left({{z_{\rm{p}}}-{z_{\rm{c}}}} \right)}^{{\beta _{\rm{p}}}}}}}{{{{\left({{z_0}-{z_{\rm{c}}}} \right)}^{{\beta _0}}}}} $ | (36) |
当岩石孔喉横截面纵横比ε≥0.1时(例如中高孔隙度枫丹白露砂岩、无黏土中高孔隙度砂岩),在有效应力作用下无裂缝或微裂缝闭合现象。根据式(14) 和式(19),式(37) 可简化为
| $ \dfrac{{{k_{\rm{p}}}}}{{{k_0}}} = {\left({\dfrac{{{r_{{\rm{Hp}}}}}}{{{r_{{{\rm{H}}_{\rm{0}}}}}}}} \right)^4} $ | (37) |
因此,根据式(18a)~式(18c),可得到渗透率与有效应力具有如下3种关系
| $ {\left({\dfrac{{{k_{\rm{p}}}}}{{{k_0}}}} \right)^{\frac{1}{4}}} = {{{r_{{\rm{Hp}}}}}}/{{{r_{{{\rm{H}}_{\rm{0}}}}}}} = {a_{30}^{'}}{{\sigma _{{\rm{eff}}}}} + {a_{31}^{'}} $ | (38a) |
| $ {\left({\dfrac{{{k_{\rm{p}}}}}{{{k_0}}}} \right)^{\frac{1}{4}}} = {{{r_{{\rm{Hp}}}}}}/{{{r_{{{\rm{H}}_{\rm{0}}}}}}} = {a_{40}^{'}}{{{\sigma _{{\rm{eff}}}}} ^{{a_{41}^{'}}}} $ | (38b) |
| $ {\left({\dfrac{{{k_{\rm{p}}}}}{{{k_0}}}} \right)^{\frac{1}{4}}} = {{{r_{{\rm{Hp}}}}}}/{{{r_{{{\rm{H}}_{\rm{0}}}}}}} = {a_{50}^{'}}\ln {{\sigma _{{\rm{eff}}}}} + {a_{51}^{'}} $ | (38c) |
式中:a′30、a′40、a′50、a′31、a′41、a′51-拟合系数。
在低孔隙度岩石中,当岩石孔隙空间中不存在ε为10-3数量级的孔隙时,其孔隙连通性不会随有效应力发生改变,但孔喉横截面纵横比函数随有效应力改变,此时渗透率与有效应力应具有如下关系
| $ \dfrac{{{k_{\rm{p}}}}}{{{k_0}}} = \dfrac{{{f_{\rm{k}}}({\varepsilon _{\rm{p}}})}}{{{f_{\rm{k}}}({\varepsilon _0})}}{\left({\dfrac{{{r_{{\rm{Hp}}}}}}{{{r_{{{\rm{H}}_{\rm{0}}}}}}}} \right)^4} $ | (39) |
| $ \sqrt[4]{{{k_p}/{k_0}}} = \sqrt[4]{{{a_{60}^{'}}{\sigma _{{\rm{eff}}}} + {a_{61}^{'}}}}\left({{a_{30}^{'}}{\sigma _{{\rm{eff}}}} + {a_{31}^{'}}} \right) $ | (40a) |
| $ \sqrt[4]{{{k_{\rm{p}}}/{k_0}}} = \sqrt[4]{{{a_{60}^{'}}{\sigma _{{\rm{eff}}}} + {a_{61}^{'}}}}\left({{a_{40}^{'}}{\sigma _{{\rm{eff}}}}^{{a_{41}^{'}}}} \right) $ | (40b) |
| $ \sqrt[4]{{{k_{\rm{p}}}/{k_0}}} = \sqrt[4]{{{a_{60}^{'}}{\sigma _{{\rm{eff}}}} + {a_{61}^{'}}}}\left({{a_{50}^{'}}\ln {\sigma _{{\rm{eff}}}} + {a_{51}^{'}}} \right) $ | (40c) |
式中:a′60、a′61-拟合系数。
对于低孔隙度岩石,渗透率与有效应力在乘上了一个线性关系后仍然服从3类主要函数关系。
当岩石孔隙空间中大量存在ε为10-3数量级的孔隙时,如上一节分析所得,该类孔隙将在某个压力点发生闭合,导致配位数z发生改变,假设配位数z与有效应力之间服从直线关系。此时渗透率与有效应力应具有如下关系
| $ \dfrac{{{k_{\rm{p}}}}}{{{k_0}}} = \dfrac{{{f_{\rm{k}}}({\varepsilon _{\rm{p}}})}}{{{f_{\rm{k}}}({\varepsilon _0})}}{\left({\dfrac{{{r_{{\rm{Hp}}}}}}{{{r_{{{\rm{H}}_{\rm{0}}}}}}}} \right)^4}{\left({\dfrac{{{z_{\rm{p}}}-{z_{\rm{c}}}}}{{{z_0}-{z_{\rm{c}}}}}} \right)^{{\beta _0}}} $ | (41) |
| $ \sqrt[4]{{{k_{\rm{p}}}/{k_0}}} = \sqrt[4]{{{a_{70}^{'}}{e^{{a_{71}^{'}}{\sigma _{{\rm{eff}}}}}}}}\left({{a_{30}^{'}}{\sigma _{{\rm{eff}}}} + {a_{31}^{'}}} \right){{f^{\frac{\beta }{4}}{{\sigma _{{\rm{eff}}}}} } } $ | (42a) |
| $ \sqrt[4]{{{k_{\rm{p}}}/{k_0}}} = \sqrt[4]{{{a_{70}^{'}}{e^{{a_{71}^{'}}{\sigma _{{\rm{eff}}}}}}}}\left({{a_{40}^{'}}{\sigma _{{\rm{eff}}}}^{{a_{41}^{'}}}} \right){{f^{\frac{\beta }{4}}{{\sigma _{{\rm{eff}}}}} } } $ | (42b) |
| $ \sqrt[4]{{{k_{\rm{p}}}/{k_0}}} = \sqrt[4]{{{a_{70}^{'}}{e^{{a_{71}^{'}}{\sigma _{{\rm{eff}}}}}}}}\left({{a_{50}^{'}}\ln {\sigma _{{\rm{eff}}}} + {a_{51}^{'}}} \right){{f^{\frac{\beta }{4}}{{\sigma _{{\rm{eff}}}}} } } $ | (42c) |
式中:a′70、a′71-拟合系数。
但要注意的是,当细长裂缝状孔隙完全闭合后,配位数不会在发生改变,此后渗透率与有效应力将服从式(39) 所描述的函数关系。
2 实验数据分析为验证本文推导模型的合理性,选取了部分已发表的地层因素和渗透率实验数据及大牛地气田岩芯数据。地层因素实验数据包括Hausenblas[30]测量的Castlegate地区高孔高渗砂岩和低孔低渗枫丹白露砂岩实验数据,Fredrich等[23]测量的枫丹白露砂岩实验数据及大牛地气田岩芯实测数据;渗透率实验数据包括Fredrich等[23]测量的枫丹白露砂岩实验数据及Nur等[31]测量的高孔隙度多孔介质的实验数据。国内外学者对枫丹白露砂岩的孔隙结构特性进行了大量研究,对于高孔隙度枫丹白露砂岩(孔隙度大于20%),其平均配位数接近6,孔隙形状具有圆形、椭圆形、三角形和GBN形等形状;对于低孔隙度枫丹白露砂岩(孔隙度小于10%的枫丹白露砂岩),平均配位数小于4,孔隙空间中会发育细长呈裂缝形态的孔隙。
所选取的大牛地气田岩芯属于低孔低渗砂岩,其孔隙度为7.3%~14.8%,平均值为8.4%;气测渗透率为0.148 0~0.641 0 mD,平均值是0.359 0 mD;克氏渗透率为0.090 0~0.569 0 mD,平均值是0.295 8 mD。并将岩芯饱和浓度为30 000 ppm的NaCl溶液,测量围压分别为5、10、20、30、45、60、70 MPa下的电阻率,并计算地层因素F的值。
Hausenblas[30]选取Castlegate地区枫丹白露砂岩,测量了不同有效应力下的地层因素,与大牛地气田岩芯实测数据一同绘制地层因素与有效应力的变化关系图(图 6,图 7)。采用乘幂和对数线性关系拟合Castlegate高孔高渗砂岩、低孔低渗枫丹白露砂岩及低孔低渗大牛地气田砂岩地层因素和有效应力的变化关系,拟合程度均较好。
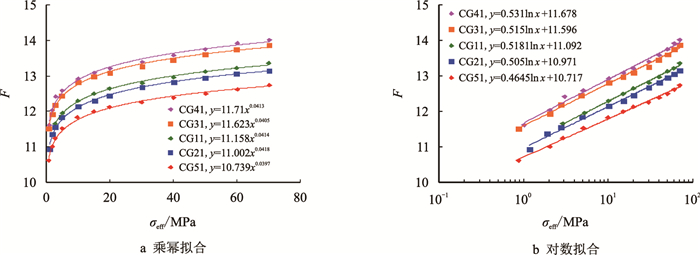 |
| 图6 Caslegate砂岩地层因素(F)与有效应力(σeff)拟合图 Fig. 6 The relationships between F and σeff for Caslegate sandstones |
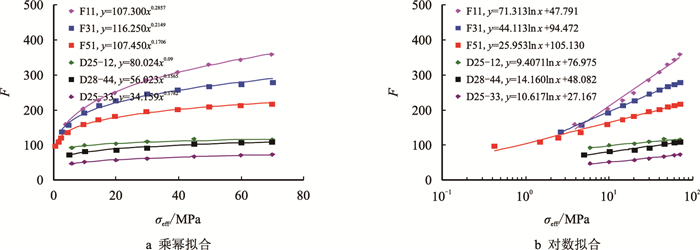 |
| 图7 低孔低渗Fontainebleau砂岩及大牛地砂岩地层因素(F)与有效应力(σeff)拟合图 Fig. 7 The relationships between F and σeff for low porosity-permeability Fontainebleau sandstones |
对Fredrich等[23]测量的不同孔隙度枫丹白露砂岩数据,重新绘制地层因素、渗透率和有效应力的关系曲线并进行曲线拟合(图 8,图 9),对孔隙度为10.3%、15.5%和20.3%的枫丹白露砂岩(F4、F7、F8) 渗透率和地层因素实验数据进行拟合。
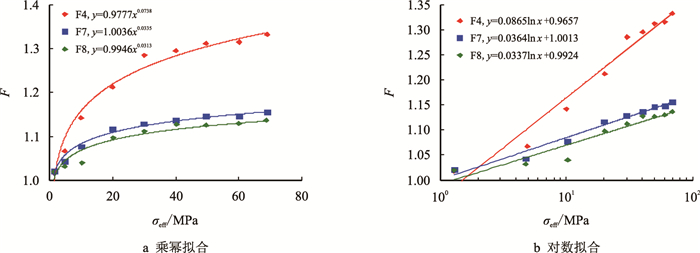 |
| 图8 高孔高渗Fontainebleau砂岩地层因素(F)与有效应力(σeff)拟合图 Fig. 8 The relationships between F and(σeff)for high porosity-permeability Fontainebleau sandstones |
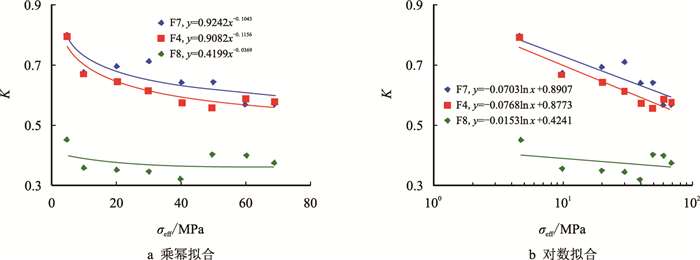 |
| 图9 高孔高渗Fontainebleau砂岩渗透率(k)与有效应力(σeff)拟合图 Fig. 9 The relationships betweenk and σeff for high porosity-permeability Fontainebleau sandstones |
3块岩芯的孔隙度均大于10.0%,采用乘幂和对数线性关系进行拟合,均取得较好的拟合效果(F8的实验数据发散,其原因是Fredrich等[23]在实验结束后取出岩芯时发现其已破损),证实了前文推导模型的正确性。
同时,Fredrich等[23]还测试分析了孔隙度为4.1%的样品(F1) 的地层因素和渗透率随有效应力的变化,实验结果显示,随着有效应力的增加,渗透率呈现两种趋势不同的变化特征(图 10),即渗透率的下降趋势在有效应力大于10 MPa时明显低于有效应力小于10 MPa时;相对而言,地层因素的变化差异相对较小。
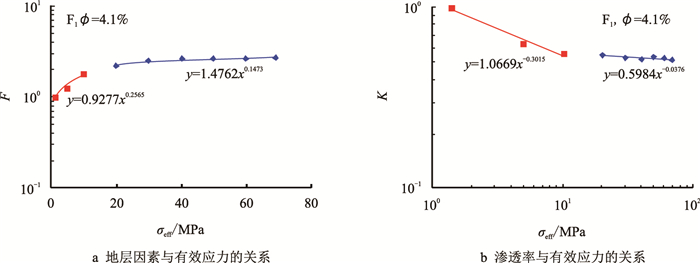 |
| 图10 低孔低渗Fontainebleau砂岩地层因素(F)和渗透率(k)与有效应力(σeff)的乘幂关系 Fig. 10 Power relationship between F, k and σeff for low porosity-permeability Fontainebleau sandstones |
Nur等[31]测量的高孔隙度多孔介质实验数据中,对渗透率进行归一化处理后得到的渗透率和有效应力的关系见图 11。
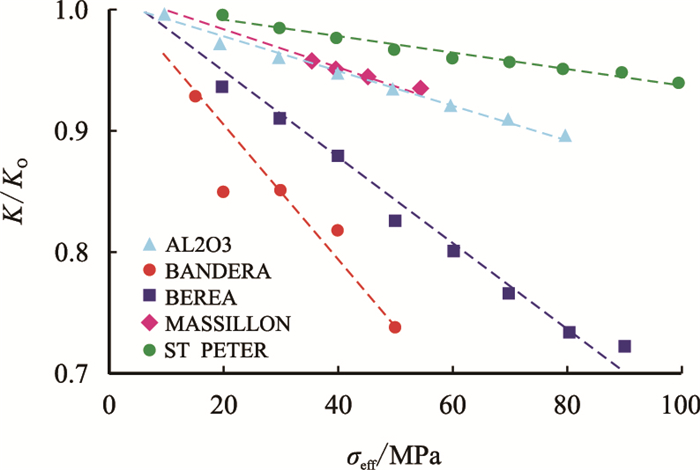 |
| 图11 归一化渗透率k/k0与有效应力σeff线性关系 Fig. 11 Relationships between k/k0 and σeff |
归一化处理后的渗透率和有效应力呈现出明显的直线关系,虽然Nur等[31]在实验过程中施加了2 MPa的内压,但实验围压远大于内压,因此可近似认为,此时的围压等于有效应力。此结果证实了本文推导模型中直线关系是存在的。
3 讨论通过研究和分析不同形状的孔隙在有效应力作用下的变形情况,分析推导出了有效应力对孔隙配位数(z)、孔喉大小分布变异系数(Vr)、孔隙水力半径(rH)、孔喉长度(l)和孔喉横截面纵横比(ε)等5个孔隙结构参数的影响。在此基础上,得出有效应力和地层因素、渗透率之间分别存在乘幂、线性以及对数线性等3种函数关系。
为验证推导模型的合理性,选取了部分已发表的地层因素和渗透率实验数据及大牛地气田岩芯地层因素实测数据。Castlegate高孔高渗砂岩、Hausenblas[30]测量的低孔低渗枫丹白露砂岩及大牛地低孔低渗砂岩地层因素和有效应力间乘幂和对数线性拟合程度均较好。
对比Caslegate砂岩、枫丹白露砂岩及大牛地气田砂岩乘幂拟合中的幂指数可以看到:Caslegate砂岩乘幂拟合中幂指数的数量级为10-2,低孔低渗枫丹白露砂岩及大牛地气田岩芯实验数据乘幂拟合中的幂指数的数量级主要为10-1。出现上述差异的原因在于,不同孔隙形状下其水力半径随压力的变化程度不同,且这一差异与前文所推导的水力半径与有效应力间关系得到的数值吻合。
对于Fredrich等[23]测量的不同孔隙度的枫丹白露砂岩的实验数据,通过对其在不同有效应力下的渗透率和地层因素的关系进行拟合,从拟合关系图中可以看到,在双对数坐标下,除孔隙度为4.1%的岩样外,渗透率、地层因素和有效应力之间均近似呈一条直线。通过对孔隙度为4.1%的枫丹白露砂岩F1的地层因素和渗透率与围压的变化关系进行拟合,得到的拟合结果图 10、图 11。从图 10、11中可以看到在双对数坐标图上出现较为明显的分段情况:当围压较低时,随着压力的增加渗透率和地层因素的变化幅度较大;当围压较高时,随压力的增加,地层因素和渗透率的变化幅度较小。通过观察该岩芯的二维薄片图像[11]可以发现,该岩芯中存在孔隙形状ε为10-3数量级的孔隙。可以推断F1实验数据出现分段的原因在于初始段微裂缝形孔隙闭合导致地层因素和渗透率发生大幅度改变,当微裂缝形的孔隙闭合完成以后,地层因素和渗透率的变化幅度减小。
Nur等[31]测量的高孔隙度多孔介质的实验数据中,其归一化渗透率和有效应力之间服从直线关系,证实了本文推导模型中直线关系是存在的。
以往的实验研究表明围压和地层因素及围压和渗透率的变化关系主要存在二项式、乘幂和指数三种经验关系。本文研究表明,不论是孔隙变形控制的岩石还是微裂缝变形控制的岩石,有效应力和地层因素、渗透率之间主要存在乘幂、线性和对数线性的三种函数关系。对于二项式关系,本文推导过程中发现,地层因素与水力半径之间存在平方关系,进而我们可以认为地层因素与有效应力之间具有二项式关系,而渗透率与水力半径之间存在四次方关系,这里无法证明渗透率与有效应力之间是否具有二项式关系。
4 结论(1) 对于高孔高渗岩芯,地层因素和渗透率产生变化的主要原因是孔隙的水力半径发生变化,即孔隙变形;而对于低孔低渗岩芯,地层因素和渗透率产生变化主要由孔隙的水力半径和配位数两种因素控制。
(2) 地层因素、渗透率与有效应力之间存在乘幂、线性和对数线性等3种主要函数关系。孔隙形状及其分布将决定地层因素、渗透率与有效应力之间的函数关系。在双对数坐标下,低孔低渗岩芯的实验数据曲线出现明显的分段响应特征,原因在于,存在地层因素及渗透率转折点的岩石分别受孔隙和微裂缝变形两种变形机制控制。
| [1] | DOBRYNIN V M. Effect of overburden pressure on some properties of sandstones[J]. Society of Petroleum Engineers Journal, 1962, 2(4): 360–366. doi: 10.2118/461-PA |
| [2] | SOEDER D J, RANDOLPH P L. Porosity, permeability and pore structure of the tight mesaverde sandstone, Piceance Basin, Colorado[J]. SPE Formation Evaluation, 1984, 2(2): 129–136. doi: 10.2118/13134-PA |
| [3] | JELMERT T A, SELSENG H. Permeability function describes core permeability in stress-sensitive rocks[J]. Oil & Gas Journal, 1998, 96(49): 60–63. |
| [4] | LI M, XIAO W, BERNABÉ Y, et al. Nonlinear effective pressure law for permeability[J]. Journal of Geophysical Research, 2014, 119(1): 302–318. doi: 10.1002/2013JB-010485 |
| [5] |
李闽, 肖文联, 赵春兰, 等. 不能用净应力评价低渗砂岩岩石应力敏感性[J].
西南石油大学学报(自然科学版), 2009, 31(5): 183–186.
LI Min, XIAO Wenlian, ZHAO Chunlan, et al. Net stress cann't be used to evaluate the stress sensitivity in the low-permeability sandstone[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2009, 31(5): 183–186. doi: 10.3863/j.issn.1674-5086.2009.05.-041 |
| [6] |
李闽, 肖文联, 郭肖, 等. 塔巴庙低渗致密砂岩渗透率有效应力定律实验研究[J].
地球物理学报, 2009, 51(12): 3166–3174.
LI Min, XIAO Wenlian, GUO Xiao, et al. Laboratory study of the effective pressure law for permeability in Ta-Ba-Miao low-permeability sandstones[J]. Chinese Journal of Geophysics, 2009, 51(12): 3166–3174. doi: 10.3969/j.-issn.0001-5733.2009.12.027 |
| [7] | LI M, BERNABÉ Y, XIAO W, et al. Effective pressure law for permeability of E-bei sandstones[J]. Journal of Geophysical Research, 2009, 114(B7): 223–223. doi: 10.-1029/2009JB006373 |
| [8] |
贺承祖, 华明琪. 低渗砂岩气藏的孔隙结构与物性特征[J].
新疆石油地质, 2005, 26(3): 280–284.
HE Chengzu, HUA Mingqi. Characteristics of pore structure and physical property of low permeability sandstone reservoir[J]. Xinjiang Petroleum Geology, 2005, 26(3): 280–284. doi: 10.3969/j.issn.1001-3873.2005.03.016 |
| [9] |
宋延杰, 周玉婷, 唐晓敏, 等. 基于有效流动孔隙的低孔渗泥质砂岩储层渗透率确定方法[J].
地球物理学进展, 2016, 31(1): 327–333.
SONG Yanjie, ZHOU Yuting, TANG Xiaomin, et al. Method for determination of permeability of shaly sand formation with low porosity and permeability based on efficient flow pore[J]. Progress in Geophysics (in Chinese), 2016, 31(1): 327–333. doi: 10.6038/pg20160138 |
| [10] |
何文祥, 杨乐, 马超亚, 等. 特低渗透储层微观孔隙结构参数对渗流行为的影响——以鄂尔多斯盆地长6储层为例[J].
天然气地球科学, 2011, 33(3): 477–481.
HE Wenxiang, YANG Le, MA Chaoya, et al. Effect of micro-pore structure parameter on seepage characteristics in ultra-low permeability reservoir: A case from Chang6 Reservoir of Ordos Basin[J]. Natural Gas Geoscience, 2011, 33(3): 477–481. doi: 10.11764/j.issn.1672-1926.-2011.03.477 |
| [11] |
张明绿, 石玉江. 复杂孔隙结构砂岩储层岩电参数研究[J].
测井技术, 2005, 44(1): 21–23.
ZHANG Minglu, SHI Yujiang. Archie's electrical parameters of complex pore texture in sandstone reservoir[J]. Well Logging Technology, 2005, 44(1): 21–23. doi: 10.16489/-j.issn.1004-1338.2005.05.016 |
| [12] |
李潮流, 李长喜. 特低渗透率砂岩储集层电学性质研究[J].
测井技术, 2010, 34(3): 233–237.
LI Chaoliu, LI Changxi. Electrical property analysis on especially low-permeability clastic reservoir[J]. Well Logging Technology, 2010, 34(3): 233–237. doi: 10.3969/-j.issn.1004-1338.2010.03.007 |
| [13] |
赵良孝, 陈明江. 论储层评价中的五性关系[J].
天然气工业, 2015, 35(1): 53–60.
ZHAO Liangxiao, CHEN Mingjiang. A discussion on the relationships between five properties in reservoir evaluation[J]. Natural Gas Industry, 2015, 35(1): 53–60. doi: 10.3787/j.issn.1000-0976.2015.01.006 |
| [14] |
王勇, 章成广, 李进福, 等. 岩电参数影响因素研究[J].
石油天然气学报(江汉石油学院学报), 2006, 28(4): 75–77.
WANG Yong, ZHANG Chengguang, LI Jinfu, et al. Study on influence factors of rock-electro parameters[J]. Journal of Oil and Gas Technology (J. JPI), 2006, 28(4): 75–77. doi: 10.3969/j.issn.1004-1338.2007.06.002 |
| [15] |
闫建平, 温丹妮, 李尊芝, 等. 低渗透砂岩孔隙结构对岩电参数的影响及应用[J].
天然气地球科学, 2015, 26(12): 2227–2233.
YAN Jianping, WEN Danni, LI Zunzhi, et al. The influence of low permeable sandstone pore structure on rock electrical parameters and its applications[J]. Natural Gas Geoscience, 2015, 26(12): 2227–2233. doi: 10.11764/-j.issn.1672-1926.2015.12.2227 |
| [16] |
韩学辉, 匡立春, 何亿成, 等. 岩石电学性质实验研究方向展望[J].
地球物理学进展, 2005, 20(2): 384–356.
HAN Xuehui, KUANG Lichun, HENG Yicheng, et al. A view of experiment study on rock electric property[J]. Progress in Geophysics, 2005, 20(2): 384–356. doi: 10.-3969/j.issn.1004-2903.2005.02.016 |
| [17] |
李宁. 电阻率-孔隙度、电阻率-含油(气)饱和度关系一般形式及其最佳逼近函数类型的确定(Ⅰ)[J].
地球物理学报, 1989, 32(5): 580–591.
LI Ning. General forms of the resistivity-porosity and resistivity-oil/gas saturation relations as well as the determination of their optimum approximating function types (Ⅰ)[J]. Acta Geophysica Sinica, 1989, 32(5): 580–591. |
| [18] |
王克文, 孙建孟, 关继腾, 等. 储层岩石电性特征的逾渗网络模型研究[J].
石油学报, 2007, 28(1): 101–106.
WANG Kewen, SUN Jianmeng, GUAN Jiteng, et al. Percolation network modeling of electrical properties of reservoir rock[J]. Acta Petrolei Sinica, 2007, 28(1): 101–106. doi: 10.7623/syxb200701020 |
| [19] |
司马立强, 王超, 王亮, 等. 致密砂岩储层孔隙结构对渗流特征的影响以——四川盆地川西地区上侏罗统蓬莱镇组储层为例[J].
天然气工业, 2016, 36(12): 18–25.
SIMA Liqiang, WANG Chao, WANG Liang, et al. Effect of pore structure on the seepage characteristics of tight sandstone reservoirs: A case study of upper Jurassic Penglaizhen Fm reservoirs in the western Sichuan Basin[J]. Natural Gas Industry, 2016, 36(12): 18–25. doi: 10.3787/j.issn.1000-0976.2016.12.003 |
| [20] |
毛志强, 高楚桥. 孔隙结构与含油岩石电阻率性质理论模拟研究[J].
石油勘探与开发, 2000, 27(2): 87–90.
MAO Zhiqiang, GAO Chuqiao. Theoretical simulation of the resistivity and pore structure of hydrocarbon bearing rocks[J]. Petroleum Exploration and Development, 2000, 27(2): 87–90. |
| [21] | BERNABÉ Y, LI M, MAINEULT A. Permeability and pore connectivity: A new model based on network simulations[J]. Journal of Geophysical Research, 2010, 115(B10): 172–186. doi: 10.1029/2010JB007444 |
| [22] | BERNABÉ Y, ZAMORA M, LI M, et al. Pore connectivity, permeability, and electrical formation factor: A new model and comparison to experimental data[J]. Journal of Geophysical Research, 2011, 116(B11): 112–04. doi: 10.1029/2011JB008543 |
| [23] | FREDRICH J T, GREAVES K H, MARTIN J W. Pore geometry and transport properties of Fontainebleau sandstone[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1993, 30(7): 691–697. doi: 10.1016/0148-9062(93)90007-Z |
| [24] | BOURBIE T, ZINSZNER B. Hydraulic and acoustic properties as a function of porosity in Fontainebleau Sandstone[J]. Journal of Geophysical Research, 1985, 90(B13): 11524–11532. doi: 10.1029/JB090iB13p11524 |
| [25] | SEEBURGER D A, AMOS N. A pore space model for rock permeability and bulk modulus[J]. Journal of Geophysical Research, 1984, 89(B1): 527–536. doi: 10.1029/-JB089iB01p00527 |
| [26] | DONG H, Blunt M J. Pore-network extraction from microcomputerized-tomography images[J]. Physical Review E, 2009, 80(3): 036307. doi: 10.1103/PhysRevE.80.036307 |
| [27] | YALE D P, NUR A. Network modelling of flow, storage and deformation in porous rocks[C]. SEG Technical Program Expanded Abstracts, 1985, 4(1): 437-437. |
| [28] |
康毅力, 张浩, 游利军, 等. 致密砂岩微观孔隙结构参数对有效应力变化的响应[J].
天然气工业, 2007, 27(3): 46–48.
KANG Yili, ZHANG Hao, YOU Lijun, et al. The response of micro-pore structure parameters of tight sandstone to effective stress changes[J]. Natural Gas Industry, 2007, 27(3): 46–48. doi: 10.3321/j.issn:1000-0976.2007.03.014 |
| [29] | CHIERICI G L, CIUCCI G M, EVA F, et al. Effect of the overburden pressure on some petrophysical parameter of reservoir rocks[J]. Society of Petroleum Engineers Journal, 1967: 360–366. |
| [30] | HAUSENBLAS M. Stress dependence of the cementation exponent[C]. SCA Conference Paper Number 9518, 1995. |
| [31] | NUR A M, WALLS J D, WINKLER K, et al. Effect of fluid saturation on waves in porous rock and relations to hydraulic permeability[J]. Society of Petroleum Engineers Journal, 1980, 20(6): 450–458. doi: 10.2118/8235-PA |
 2017, Vol. 39
2017, Vol. 39


