2. 西南石油大学地球科学与技术学院, 四川 成都 610500;
3. 中国石油新疆油田公司开发处, 新疆 克拉玛依 834000;
4. 中国石油吐哈油田公司勘探开发研究院, 新疆 哈密 839009
2. School of Geosciences and Technology, Southwest Petroleum University, Chengdu, Sichuan 610500, China;
3. Development Department, Xinjiang Oilfield Company, PetroChina, Karamay, Xinjiang 834000, China;
4. Expolratin and Development Research Institute, Tuha Oilfield Company, PetroChina, Hami, Xinjiang 839009, China
趋势面分析法是用数学方法通过趋势值掌握区域特征,分析剩余值,突出局部异常,从而研究地质变量的空间分布及变化规律的一种多元统计分析方法[1]。传统的整体趋势面分析基于回归分析原理,运用最小二乘法拟合一个二维非线性函数,得到地理要素的空间变化趋势。Lancaster和Salkzuskas提出的移动曲面拟合方法,以每一个待定点为中心,设定半径系数$R$确定进入拟合范围的源数据点,再根据源数据点定义一个局部趋势面函数进行拟合,从而求取待定点的值,最终获得一个移动趋势面[2]。葛永慧等在移动趋势面分析的基础上,利用“距离越远对插值点的影响越小”的思想,引入加权计算,提出了加权移动趋势面,解决距离对插值点的贡献分配[3]。段滔等将移动趋势面分析法引入工程应用及曲面拟合[4-5],Mullineux针对最小二乘法的非线性拟合系数进行了详细的分析研究[6]。王秋玲在土地勘测中引入移动趋势面法进行城市区域勘测的模拟及成图[7],李广春等利用三维动态趋势面分析地面沉降[8],李随民等将趋势面分析引入地质工程及地球物理勘探的地下形态分析[9-10]。趋势面分析方法应用于地质及地球物理分析的主要目标是“保凸”,即在复杂区域实现对局部或微小异常的有效识别,对地质构造中的微幅构造的识别与刻画具有重要的应用价值[10]。
微幅度构造又为小幅度构造、低幅度构造等,是构造相对平缓、闭合度一般仅有5~ 20 m的构造地质体[11-15],而地震资料在构造形态方面的分辨率与地质体分辨率一致,微幅度构造已经超越了地震资料关于地质体的分辨率极限,且采用精细的地震资料构造解释技术对微幅度构造解释和识别仍较困难[16-17]。通过在相对复杂构造区采用移动趋势面分析法进行微幅度构造的识别实验,获得了一定的成效,基于此,本文采用移动趋势面分析法,在目的层地震资料构造精细解释的基础上,对吐哈盆地葡北地区七克台组微幅度构造进行识别分析,研究和探讨移动趋势面法在微幅度构造识别中的优势,重点分析移动趋势面法计算中关于局域性构造背景信息、局部构造异常、随机干扰的参数分析及优选的原则和方法,从而为采用移动趋势面分析法识别微幅度构造奠定理论基础。
1 构造特征葡北地区位于吐哈盆地北部山前带火焰山逆冲推覆构造带以北的背斜北翼缓坡区域,构造活动强烈,多期构造运动造成其断裂发育,构造形态错综复杂,油气的运移和成藏与构造走向及局部微幅度构造关系密切[18-19]。通过地震资料精细构造解释,其侏罗系七克台组底界面构造形态为以中部微幅度构造为轴线的大型鼻状构造,受构造运动影响,发育的断裂将鼻状构造切分和改造成局部凸起或凹陷,地层高低起伏较小。PB10井东西两侧,受断层影响,发育不同的构造形态,西侧是断层分割的低幅度的微凹,而东侧则为典型的断鼻构造特征。构造解释结果显示,该区七克台组油气藏分布与微幅度构造对应关系良好,但在等值线间距较小的构造图中,除PB101井处的微幅度构造较清晰外,构造图中其他区域的微幅度构造多仅为一条封闭等值线区域,需要根据地震剖面的反射形态进一步确认,或无法获得定论(图 1)。
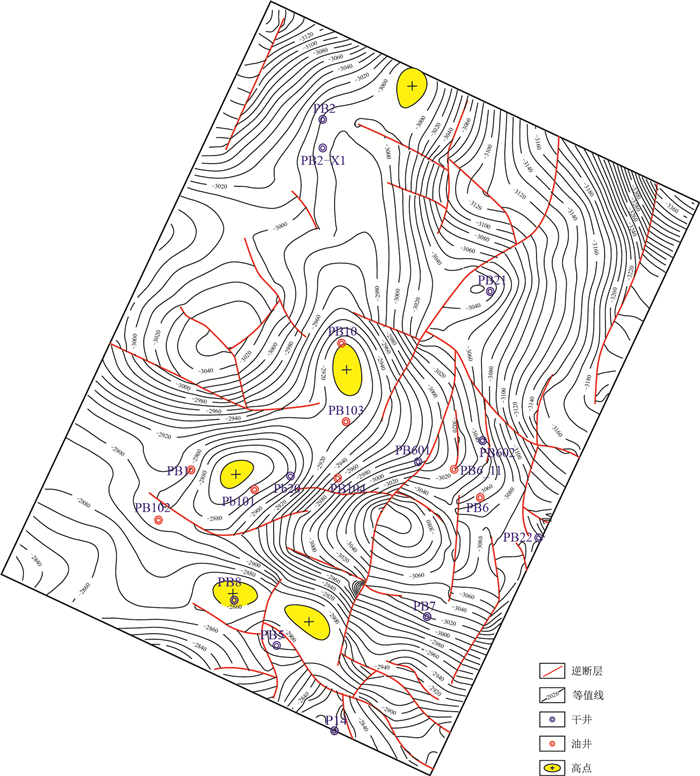 |
| 图1 葡北地区七克台组底界面构造图 Fig. 1 Structure of the bottom of Qiketai Formation in Pubei area |
趋势面分析的一般模型为
| $ z(x, y)=a_0+a_1f_1+a_2f_2+\cdots +a_nf_n $ | (1) |
式中:
$z$-趋势面的拟合值;
$a_n$-需要求取的待定系数;
$f_n$-关于观测点位置$z(x, y)$的函数;
$n$-最大曲面拟合次数。
移动趋势面是在传统趋势面基本模型的基础上设定影响半径$R$,把整个区域划分为若干个小区域,对每一个小区域分别使用不同的趋势面函数来进行拟合,以每一个待定点$O$为中心,定义一个局部趋势面函数来拟合周围的数据点,最终以数据插值的方式获得完整的趋势面[2]。为了达到分区域进行趋势面函数拟合,需要先行将原始数据按一定的采样方式进行离散化(图 2),一般采用等间距$d$的网格进行离散采样,以每个采样点的观测位置和观测值作为趋势面的基本数据(源数据),建立二维多项式趋势面数学模型,然后根据模型计算所得值进行插值计算,最终获得完整的趋势面。
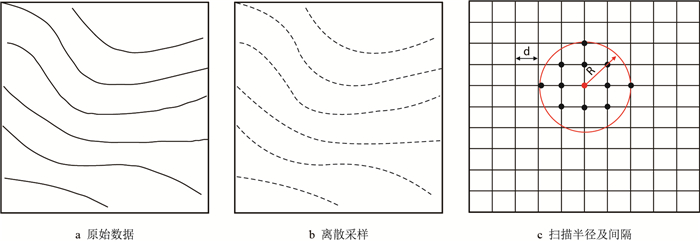 |
| 图2 移动趋势面离散采样过程示意图 Fig. 2 Schematic diagram of the discrete sampling process of moving trend surface |
根据移动趋势面建模及插值过程,其离散采样及趋势面函数拟合的效果主要受控于:拟合次数、影响半径、采样间距及插值方式,针对微幅度构造的识别与刻画,移动趋势面拟合中控制质量的关键参数影响着应用效果。
3.1 断层影响吐哈盆地葡北地区七克台组断裂发育,断裂在平面的分布对移动趋势面的拟合和插值都会产生一定的影响,但由于移动趋势面拟合自身存在分区域进行趋势面函数拟合,因此针对目的层断裂特征,可将断裂在平面的延伸线作为移动趋势面每个分区处理的边界,在断裂附近,可通过调整采样间距,以保证影响半径内的取值点不跨越断裂,从而消除断裂对趋势面拟合的影响。
3.2 拟合次数分析采用葡北地区经钻井资料校正过的七克台组底界面的深度为基础,选用观测点的地震主测线($L$)和联络测线($T$)测线号作为自变量,海拔高程$H$作为因变量,每个观测点的3个数据$L$、$T$、$H$构成了趋势面分析的基本数据,以此构建二维多项式趋势面数学模型。在移动趋势面分析中,分区域进行移动趋势面函数建模的拟合次数分析是所有关键参数分析的基础,根据研究区地震资料的主测线、联络测线间距(50 m)及工区大小选取采样间隔$d$=500 m,影响半径$R$=1 000 m,并采用克里格插值方法分别计算七克台组底界不同拟合次数的趋势面及其残差图(构造海拔高$H$与趋势面差额),从而分析并选择合适的拟合次数。
不同拟合次数下七克台组底界趋势面及其残差图(图 3,图 4,图 5)对比表明,趋势面的整体形态表征该地区主体背景构造为SW-NE-W的大型鼻状构造,二次多项式和三次多项式拟合的趋势面相同,且比(线性)一次拟合的趋势面更加反映构造细节。同时对比其残差值,一次拟合的残差值为-80~50 m,而二次多项式和三次多项式的残差值均为-30~35 m,残差值的负值对应凹陷,正值对应凸起。葡北地区七克台组钻井显示,其已经探明的微幅度构造闭合高度在20 m以内(图 1),因此,二次多项式和三次多项式结果均有利于识别和刻画微幅度构造。
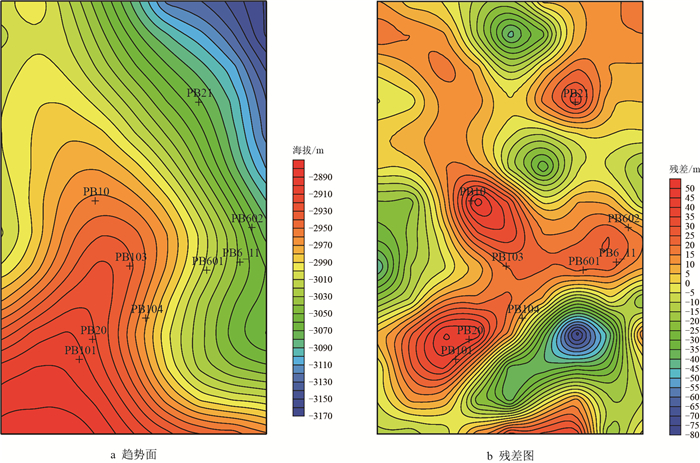 |
| 图3 (线性)一次拟合趋势面及残差图 Fig. 3 Trend surface and its residual graphs of the linear fitting |
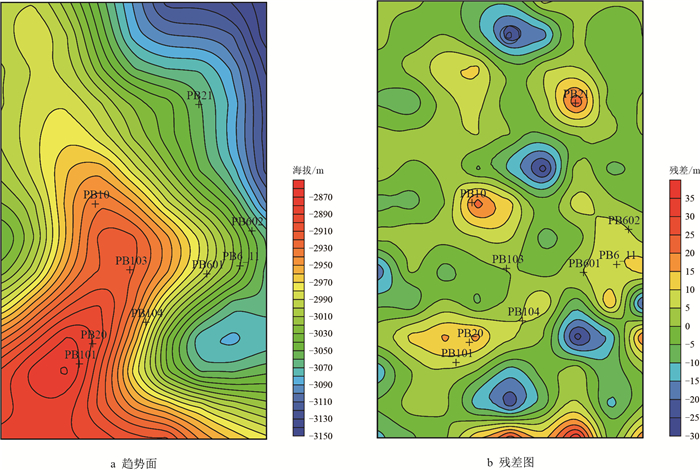 |
| 图4 二次多项式拟合趋势面及残差图 Fig. 4 Trend surface and its residual graphs of the quadratic polynomial fitting |
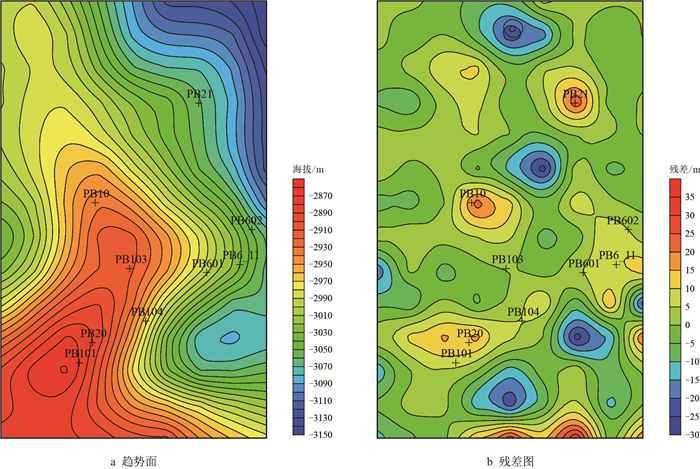 |
| 图5 三次多项式拟合趋势面及残差图 Fig. 5 Trend surface and its residual graphs of the cubic polynomial fitting |
在趋势面及其残差图对比分析的基础上,采用函数拟合的方差参数对不同拟合参数的结果进行定量分析[20],经反复实验对比,3种方法的检验结果$F$均远大于置信水平$\alpha=0.01$下的临界值$F_{0.01}$,证实3种回归拟合模型都极为显著,且拟合度均高于90%。随着拟合次数的增加,算法的不断优化,判定系数随之增加,且残差不断减小,获得的趋势面越逼近于实际情况。二次多项式拟合的趋势面方差评价参数明显优于(线性)一次拟合,说明在其他参数固定不变的情况下,对于复杂构造区,曲面拟合比平面线性拟合更利于识别微幅度构造。在一定范围内,随着拟合次数的增加,越逼近真实构造,对微幅度构造的识别更为准确,但当达到一个最佳拟合次数时,再增加拟合次数意义不大,二次多项式拟合与三次多项式拟合结果基本相同(表 1)。基于此,利用移动拟合趋势面识别微幅度构造,选择二次多项式拟合或三次多项式拟合都能取得理想的对比结果,但拟合次数越大,不仅增加了计算的难度,还有可能在局部形成数值畸变。因此,针对微幅度构造的识别,采用二次多项式拟合即能满足其参数配置的要求,并一定程度减少计算的复杂性。
| 表1 不同拟合次数判定系数及显著性检验表 Table 1 The inspection of determination coefficient and significance of different fitting times |
采样间隔的大小直接决定采样点的数量,对趋势面的分析及后续的微幅度构造的识别具有重要的影响。采用二次多项式拟合函数,影响半径$R$=1 000 m,对比分析不同采样间隔对趋势面及其残差的影响。当采样间隔较大时,采样点较少,局部范围内没有控制点,趋势面主要反映区域构造的基本特征,在残差图上,正值(凸起)以条带状分布为主,主要体现较大或整体的起伏形态,微幅度构造难以识别(图 6)。随着采样间隔逐渐减小,局部控制点增多,在识别微幅度构造时,在残差图上出现一些异常的微凸或微凹,与真实情况不符。同时,随采样间隔的变化,微幅凸起的位置存在一定差异,以PB21井位置为例,当采样间距为700 m,微幅凸起位置在PB21井左侧,当采样间距为400 m,微幅凸起在PB21井位置,结合实际资料分析,当采样间距为400 m和500 m时,PB21井处微幅度凸起位置与实际吻合(图 3,图 4,图 6,图 7,图 8a)。
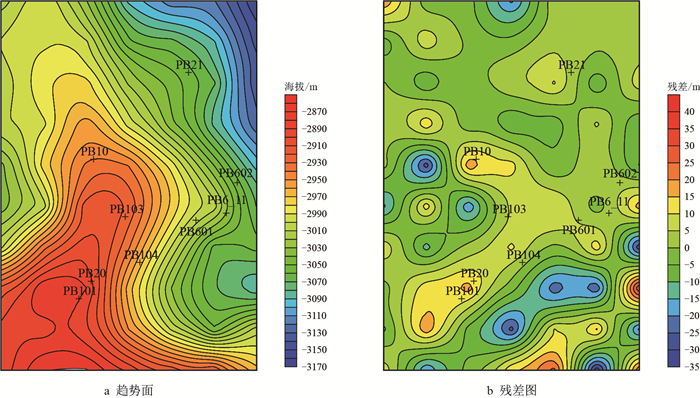 |
| 图6 采样间隔为700 m的趋势面及残差图(二次多项式拟合) Fig. 6 Trend surface and its residual graphs of 700 m sampling interval(the quadratic polynomial fitting) |
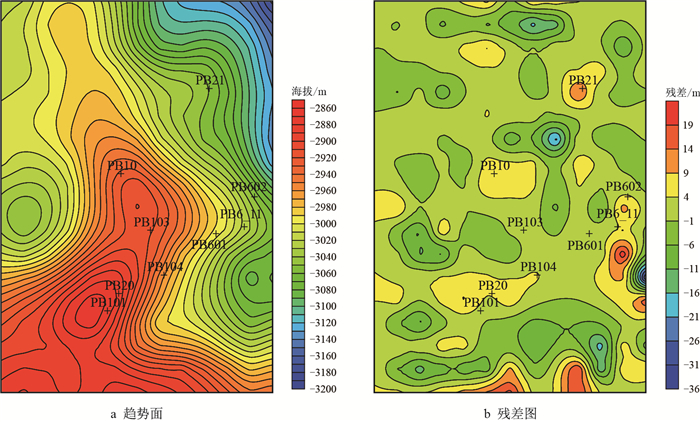 |
| 图7 采样间隔为400 m的趋势面及残差图(二次多项式拟合) Fig. 7 Trend surface and its residual graphs of 400 m sampling interval(the quadratic polynomial fitting) |
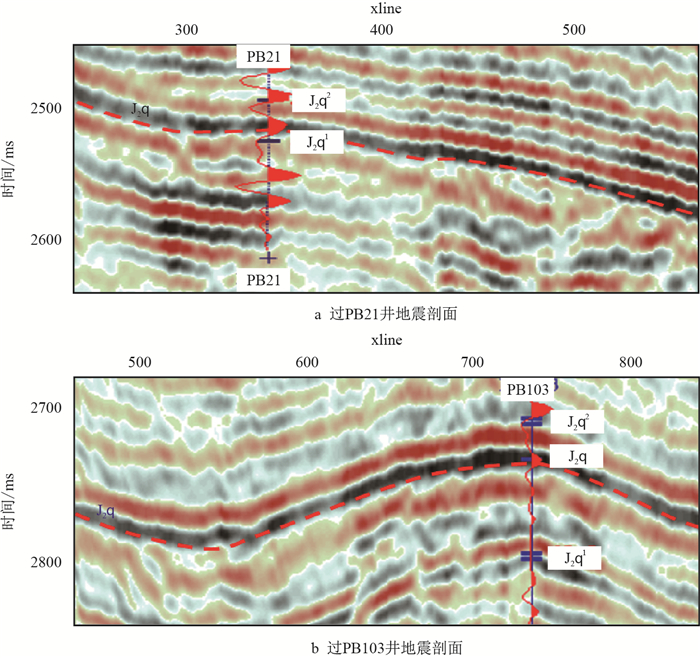 |
| 图8 局部构造地震剖面图 Fig. 8 Seismic profiles of local structure |
同时对比采样间距为500 m和400 m的残差图,在采样间距为400 m的残差图上出现一些异常假值和失真的地方,如在实际地震剖面上PB103井左侧为局部凹陷,然后为斜坡,并没有出现微幅度凸起,因此,在采样间隔为700 m和400 m的残差图上出现的微幅度形态的失真表现(图 6,图 7,图 8b),而当采样间距为500 m时更符合实际情况(图 4)。
经反复成图对比分析和显著性定量参数检验:采样间距过大,采样节点较稀疏,容易忽略或漏掉小型微幅度构造,而采样间距过小,采样节点过于密集,会造成具体细节过于丰富,趋势面拟合度降低,则容易出现假构造或假高点(表 2)。因此,采样间隔应在拟合次数优选的基础上,根据显著性定量参数分析,并结合研究区微幅度构造的平面延伸轴的长度进行综合选择,确保在微幅度构造的延伸长度范围内至少有6个采样点。
| 表2 不同采样间距判定系数及显著性检验表 Table 2 The inspection of determination coefficient and significance of different sampling intervals |
影响半径与采样间隔为相互影响和制约的两个关键参数,影响半径过大,则较远的非微幅度构造的数值点也参与计算,影响构造上真实数据点参与计算的权重,且在采样间隔一定的情况下,增加了采样点数,综合影响趋势面的最终形态;而影响半径过小,则微幅度构造的真实数据点未全部参与计算,所计算的值虽与实际值接近但不能反映趋势形态,进而导致残差部分区域为空值,最终会影响微幅度构造的识别。
采用二次多项式拟合函数,采样间距$d$=500 m,分析不同影响半径下趋势面特征及其残差。当影响半径$R$=750 m时,其趋势面区域构造的整体形态不变,但是局部构造有一定的畸变,其原因是影响半径过小,在分区块拟合时,未考虑相邻区块的影响,导致趋势面成图是局部扭曲严重,并在其残差图上出现大量的零值区,主要是由于计算的趋势值与实际值相等造成,局部细节过于丰富,产生假的微幅度构造,与采样间隔较大的情况类似(图 9)。
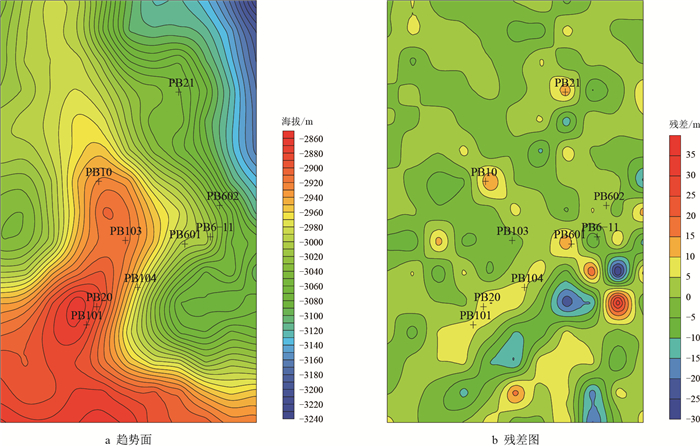 |
| 图9 影响半径为750 m的趋势面及残差图(二次多项式拟合,500 m采样间隔) Fig. 9 Trend surface and its residual graphs of 750 m influence radius(the quadratic polynomial fitting and 500 m sampling interval) |
随着影响半径的增加,趋势面等值线逐渐平滑,局部细节弱化;残差范围增大,较大的微幅度构造可以识别,但小型微幅度构造在大残差背景下容易被忽略,且微幅度构造在局部连成一片(图 10)。
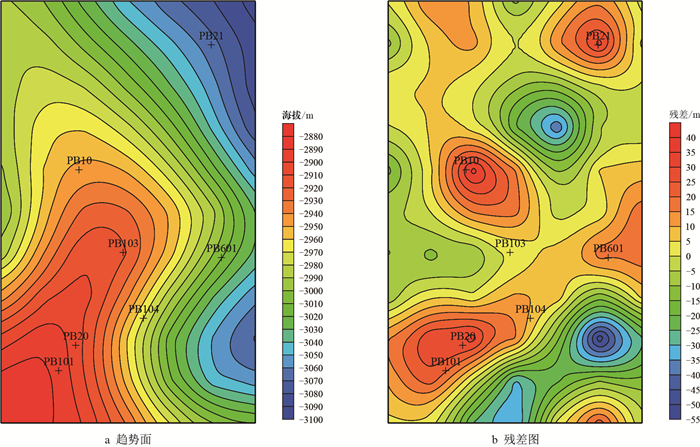 |
| 图10 影响半径为1 500 m的趋势面和残差图(二次多项式拟合,500 m采样间隔) Fig. 10 Trend surface and its residual graphs of 1 500 m influence radius(the quadratic polynomial fitting and 500 m sampling interval) |
根据不同影响半径下的方差显著性定量评价,影响半径越小,趋势面拟合度越高,且误差越小(表 3),但经过反复实验分析,影响半径的选取首先取决于拟合次数,(线性)一次拟合函数包括3个系数,要求影响范围内的采样点不低于2,二次多项式拟合要求影响半径内的采样点不低于6,三次多项式拟合要求影响半径内的采样点不低于10,不同的拟合次数对影响半径的最小值有不同的要求。以二次多项式拟合为例,影响半径起码不小于采样间距1.5倍(图 9), 当影响半径刚好满足采样点要求时,这样的影响半径处于临界点,仍然会导致残差出现假构造。经过成图对比,以二次多项式拟合移动趋势面为例,影响半径选取应为采样间距的2.0倍。
| 表3 不同影响半径判定系数及显著性检验表 Table 3 The inspection of determination coefficient and significance of different influence radius |
移动趋势面计算首先要对源数据进行离散采样,因此需要对计算后的离散数据进行插值计算并最终成图。地质分析中常用的插值方法有:反距离加权法、克里格法、最小曲率法等[21],在固定关键参数基础上,采用不同插值方法对趋势面进行插值计算,对比分析插值结果,反距离加权法的主要特征之一是要在网格区域内产生围绕观测点位置的“牛眼”现象,尽管可以通过调整圆滑参数来降低“牛眼”影响,但并不能全完消除,通过反距离加权方法获得的插值结果和实际构造形态相差巨大,同时也不符合地质规律。克里格和最小曲率法插值结果大体相似,但最小曲率法在数据体边界处的插值效果并不理想,且在相对平滑的大背景下,等值线也存在细小的突变和不平滑现象,而克里格法在移动趋势面识别微幅度构造的插值结果优势明显(图 11)。
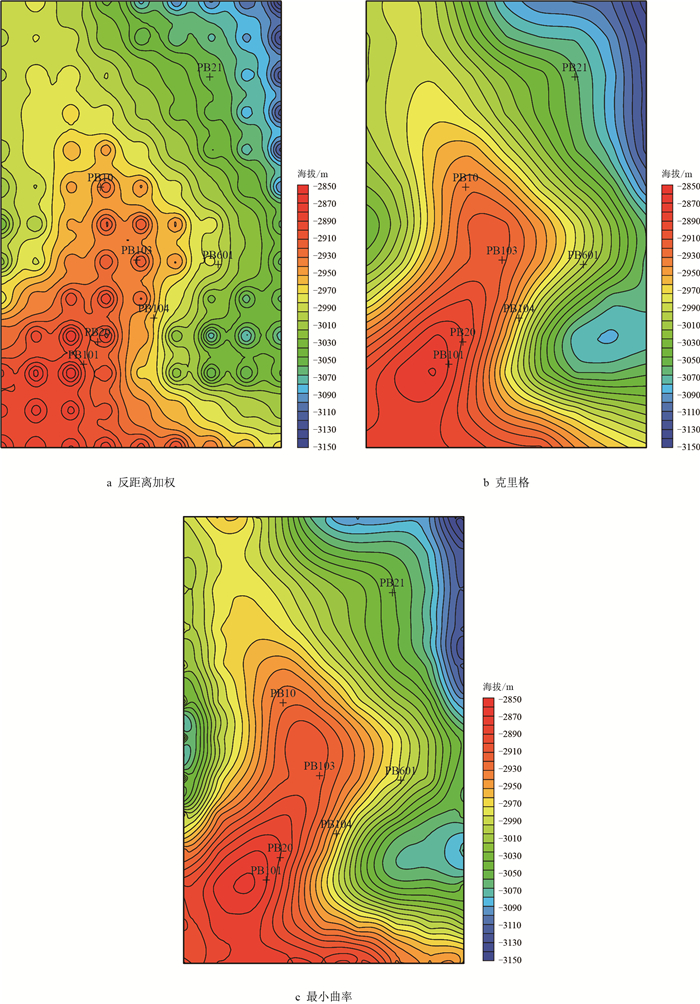 |
| 图11 不同插值方法的移动趋势面对比图 Fig. 11 Comparison of moving trend surface with different interpolation methods |
采用移动趋势面法对微幅度构造进行识别的准确性受控于它的3个关键参数的选取及评价,针对葡北地区七克台组微幅度构造,在井下实钻数据的基础上,参数选取依据方差判定系数与显著性参数,并根据参数间的相互制约关系确定关键参数。最终选取二次多项式多项式拟合、最大拟合度的采样间隔和采样间隔两倍的影响半径的参数组合,应用克里格插值方法,实现了对葡北地区微幅度构造的准确识别和定位。
葡北地区微幅度构造主要分布在构造背景的鼻状构造轴线及其东北部的斜坡上,闭合度及平面范围较小,特别是PB21井处及其西部地区的微幅度构造在移动趋势面法的残差图上具有明显的异常显示,是地震构造解释结果无法准确呈现的微幅度构造区(图 1,图 4,图 8)。
4 结论(1) 移动趋势面分析法对复杂构造区微幅度构造的识别优于地震资料精细构造解释结果,并可根据不同的构造情况构建不同的模型进行趋势面及其残差分析,为微幅度构造识别提供有利依据。
(2) 采用移动趋势面识别微幅度构造的3个关键参数(拟合次数、采样间隔和影响半径)相互影响和制约,通过定量的显著性参数评价,并结合实际地质资料,采用二次多项式拟合,最大拟合度的采样间隔及两倍于采样间隔的影响半径是移动趋势面识别微幅度构造的最佳参数搭配。
(3) 葡北地区七克台组微幅度构造主要分布在鼻状构造背景的轴线及东北部斜坡区,微幅度构造的分布区与钻井及油气吻合度高。
| [1] |
张艳伟, 屠世浩, 王沉, 等. 基于趋势面分析的煤层厚度变化规律研究[J].
西安科技大学学报, 2015, 35(1): 21–27.
ZHANG Yanwei, TU Shihao, WANG Chen, et al. Research on coal seam thickness changing law based on trend surface analysis[J]. Journal of Xi'an University of Science and Technology, 2015, 35(1): 21–27. doi: 10.13800/j.-cnki.xakjdxxb.2015.0104 |
| [2] | LANCASTER P, SALKAUSKAS K. Surfaces generated by moving least squares methods[J]. Mathematics of Computation, 1981, 37(155): 141–158. doi: 10.13800/j.cnki.-xakjdxxb.2015.0104 |
| [3] |
葛永慧, 康志军. 加权移动趋势面拟合[J].
工程图学学报, 2008(2): 110–114.
GE Yonghui, KANG Zhijun. Weighted technology of moving trend surface fitting[J]. Journal of Engineering Graphics, 2008(2): 110–114. doi: 10.3969/j.issn.1003-0158.2008.02.019 |
| [4] |
段滔, 刘耀林. 基于移动趋势面分析法的城市基准地价评价研究[J].
武汉大学学报, 2004, 29(6): 529–532.
DUAN Tao, LIU Yaolin. Urban base land value evaluation based on mobile trend sufacec analysis[J]. Geomatics and Information Science of Wuhan University, 2004, 29(6): 529–532. doi: 10.3321/j.issn:1671-8860.2004.06.-015 |
| [5] |
曾清红, 卢德唐. 基于移动最小二乘法的曲线曲面拟合[J].
工程图学学报, 2004(1): 84–88.
ZENG Qinghong, LU Detang. Curve and surface fitting based on moving least squares[J]. Journal of Engineering Graphics, 2004(1): 84–88. doi: 10.3969/j.issn.1003-0158.-2004.01.017 |
| [6] | MULLINEUX G. Non-linear least squares fitting of coefficients[J]. Applied Mathematical Modelling, 2008, 32(12): 2538–2551. doi: 10.1016/j.apm.2007.09.010 |
| [7] |
王秋玲. 趋势面拟合法在土地勘测中的应用[J].
城市勘测, 2014(5): 146–148.
WANG Qiuling. Application of trend face simulation method to and survey[J]. Urban Geotechnical Investigation & Surveying, 2014(5): 146–148. doi: 10.3969/j.issn.1672-8262.2014.05.047 |
| [8] |
李广春, 戴吾蛟, 曾凡河, 等. 三维动态趋势面模型在地面沉降分析中的应用[J].
大地测量与地球动力学, 2016, 36(6): 508–511.
LI Guangchun, DAI Wujiao, ZENG Fanhe, et al. Application of Three-dimensional dynamic trend surface fitting model on land subsidence[J]. Journal of Geodesy and Geodynamics, 2016, 36(6): 508–511. doi: 10.14075/j.jgg.-2016.06.009 |
| [9] |
李随民, 姚书振, 韩玉丑. Surfer软件中利用趋势面方法圈定化探异常[J].
地质与勘探, 2007, 43(2): 72–75.
LI Suimin, YAO Shuzhen, HAN Yuchou. Using tendency analysis method to deal with geochemical data based on the surfer software[J]. Geology and Prospecting, 2007, 43(2): 72–75. doi: 10.3969/j.issn.0495-5331.2007.02.014 |
| [10] |
管仁荣. 趋势面分析在地球物理勘探中的应用研究[J].
中国矿业, 2012, 21(S1): 474–478.
GUAN Renrong. The study of trend surface analysis[J]. China Mining Magazine, 2012, 21(S1): 474–478. |
| [11] |
王建民, 王佳媛. 鄂尔多斯盆地伊陕斜坡上的低幅度构造与油气富集[J].
石油勘探与开发, 2013, 40(1): 49–57.
WANG Jianmin, WANG Jiayuan. Low-amplitude structures and oil-gas enrichment on Yishaan slope, Ordos Basin[J]. Perroleum Exploration and Development, 2013, 40(1): 49–57. |
| [12] |
白晓寅, 黄玉, 陈永波, 等. 低幅度构造岩性油气藏识别技术[J].
石油地球物理勘探, 2012, 47(2): 291–297.
BAI Xiaoyan, HUANG Yu, CHEN Yongbo, et al. Recognition of low relief structure-lithologic reservoir[J]. OGP, 2012, 47(2): 291–297. doi: 10.13810/j.cnki.issn.1000-7210.2012.02.004 |
| [13] |
姜秀清, 夏斌, 王千军, 等. 微构造的地震识别与应用效果[J].
天然气工业, 2006, 26(2): 57–59.
JIANG Xiuqing, XIA Bin, WANG Qianjun. Seismic identification technology of microstructure and application effect[J]. Natural Gas Industry, 2006, 26(2): 57–59. doi: 10.-3321/j.issn:1000-0976.2006.02.017 |
| [14] |
邓兴梁, 张庆玉, 梁彬, 等. 塔中Ⅱ区奥陶系鹰山组岩溶古地貌恢复方法研究[J].
中国岩溶, 2015, 34(2): 60–64.
DENG Xingliang, ZHANG Qingyu, LIANG Bin, et al. Reconstruction of karst palaeogeomorphology for the Ordovician Yingshan Formation in the central Tarim Basin[J]. Carsologica Sinica, 2015, 34(2): 60–64. doi: 10.-11932/karst20150208 |
| [15] |
李啸, 刘海磊, 王学勇, 等. 坡折带砂体成因及分布规律以准噶尔盆地车排子地区下白垩统清水河组为例[J].
岩性油气藏, 2017, 29(1): 35–42.
LI Xiao, LIU Hailei, WANG Xueyong, et al. Origin and distribution of sand body in slope break zone: A case study of the Lower Cretaceous Qingshuihe Formation in Chepaizi Area, Junggar Basin[J]. Lithologic Reservoirs, 2017, 29(1): 35–42. doi: 10.3969/j.issn.1673-8926.2017.01.005 |
| [16] |
李伟波, 李培明, 睢永平. 地震资料空间分辨率计算及理论分析[J].
石油物探, 2016, 55(2): 173–177.
LI Weibo, LI Peiming, SUI Yongping. Calculation and theoretical analysis of the spatial resolution of seismic data[J]. Geophysical Prospecting for Petroleum, 2016, 55(2): 173–177. doi: 10.3969/j.issn.1000-1441.2016.02.002 |
| [17] |
王元君, 周怀来. 时频域动态反褶积方法研究[J].
西南石油大学学报(自然科学版), 2015, 37(1): 1–10.
WANG Yuanjun, ZHOU Huailai. Research of dynamic deconvolution method in time-frequency domain[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2015, 37(1): 1–10. doi: 10.11885/j.issn.-1674-5086.2014.12.29.01 |
| [18] |
刘玉虎, 赵丹丹, 刘兴旺, 等. 吐哈侏罗系原型盆地演化对烃源岩分布的控制[J].
西南石油大学学报(自然科学版), 2012, 34(4): 29–39.
LIU Yuhu, ZHAO Dandan, LIU Xingwang, et al. The evolution of Turpan-Hami Jurassic prototype Basin and its control on the distribution of source rocks[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2012, 34(4): 29–39. doi: 10.3863/j.issn.1674-5086.2012.04.004 |
| [19] |
杨占龙, 吴青鹏, 黄云峰, 等. 吐哈盆地北部逆冲构造带油气成藏模式与勘探方向[J].
天然气地球科学, 2016, 27(6): 974–981.
YANG Zhanlong, WU Qingpeng, HUANG Yunfeng, et al. Hydrocarbon accumulation and exploration domain of northern thrust belts in Turpan-Kumul Basin[J]. Natural Gas Geoscience, 2016, 27(6): 974–981. doi: 10.11764/j.-issn.1672-1926.2016.06.0974 |
| [20] |
周志军, 薛江龙, 赵立斌. 数值模拟拟合精度方法研究以龙虎泡油田为例[J].
岩性油气藏, 2016, 28(1): 101–105.
ZHOU Zhijun, XUE Jianglong, ZHAO Libin. Numerical simulation fitting technology: A case study from Longhupao Oilfield[J]. Lithologic Reservoirs, 2016, 28(1): 101–105. doi: 10.3969/j.issn.1673-8926.2016.01.013 |
| [21] |
于运治, 田茂军, 姜璐. 空间插值算法在构建海洋地磁图中的应用[J].
舰船科学技术, 2013, 35(7): 37–41.
YU Yunzhi, TIAN Maojun, JIANG Lu. The application of spatial interpolation algorithm in marine geomagnetic mapping[J]. Ship Science and Technology, 2013, 35(7): 37–41. doi: 10.3404/j.issn.1672-7649.2013.07.007 |
 2017, Vol. 39
2017, Vol. 39


