2. 中国石化石油工程机械有限公司, 湖北 荆州 434024;
3. 宝石机械成都装备制造分公司, 四川 成都 610500
2. Petroleum Machinery Co. Ltd., SINOPEC, Jingzhou, Hubei 434024, China;
3. Chengdu Equipment Manufacturing Branch Company, Baoji Oilfield Machinery Co. Ltd., Chengdu, Sichuan 610500, China
涡轮钻具是一种重要的井下动力钻具,广泛应用于深井,定向井、水平井等的钻进,属于轴流式水力透平机械。在涡轮钻具设计中,特别是小直径或高速涡轮钻具的设计中,采用常规方法[1-5]难以得到性能优良的叶片,甚至在某些给定条件下没有相应的解。本文借鉴轴流式水力透平机械中常采用的奇点分布法[6-10]来设计涡轮钻具叶栅叶型,其基本思路如下所述。假定涡轮钻具叶栅中叶片无限薄,叶型与其骨线重合,选用沿骨线分布的点涡层代替骨线,求出骨线上点涡层诱导速度,将诱导速度与无穷远处平面均匀来流速度场叠加,即得到来流绕叶栅速度场。因骨线本身为流场中的一条流线,则骨线上各点的速度向量必与骨线相切。若求得各点速度向量,再求出这些速度向量的包络线,则该包络线就是所求翼型骨线。在求由骨线上某点因点涡引起的诱导速度时,需知道翼型骨线的形状,以便确定点到点涡的距离,而骨线形状又正是要求的,故需假设骨线的初始形状。首次计算时,可假定简单的骨线形状,以方便曲线积分的计算,得到各点的合成速度后,合成速度并不和骨线上该点的切线重合。根据绕流条件,修改首次假定骨线,即得到第二次近似骨线。重复以上计算,直到满足给定的精度为止。设计出叶型骨线后,选择叶型厚度分布规律,沿骨线加厚叶型即得到实际叶型。
1 叶型设计的初始条件叶型的设计属于流体机械的反问题范畴。反问题的奇点分布法设计叶型所要求给定的初始条件为:
(1) 叶栅叶片数Z1;
(2) 叶栅绕叶型环量ΓB;
(3) 无穷远处均匀来流速度
涡轮钻具的叶栅叶片数
| $ {Z_1} = \dfrac{{\pi D}}{t} $ | (1) |
式(1) 中,栅距t和叶栅稠度相关,在涡轮钻具叶栅中用相对截距
| $ \overline t = \dfrac{t}{l} $ | (2) |
相对截距取值在0.65~0.95[11]。
1.2 叶栅中的绕叶型环量由欧拉涡轮机方程,有
| $ M = \dfrac{1}{2}\rho QD({C_{\rm 1u}}-{C_{\rm 2u}}) $ | (3) |
而叶栅中的环量为
| $ \varGamma = \pi D({C_{\rm 1u}}-{C_{\rm 2u}}) $ | (4) |
则叶栅中的绕叶型环量为
| $ {\varGamma _{\rm B}} = \dfrac{{2\pi M}}{{\rho Q{Z_1}}} $ | (5) |
在叶栅绕流中,无穷远处均匀来流的速度为进口处液流质点相对叶栅的滑动速度与出口处液流质点相对叶栅滑动速度的矢量和的一半。由涡轮钻具叶栅进出口速度多边形可得无穷远处均匀来流的速度,为
| $ {W_\infty } = \sqrt {{W_{\rm z}}^2 + {{\left(\dfrac{{{W_{\rm 1u}} + {W_{\rm 2u}}}}{2}\right)}^2}} $ | (6) |
而
| $ \sin {\beta _\infty } = \dfrac{{{W_{\rm z}}}}{{{W_\infty }}} $ | (7) |
根据奇点分布法设计叶型的流程,首先由初始条件得到叶型骨线,然后,选择合适的翼型数据沿骨线加厚,即可得到设计叶型。
2.1 叶型骨线的设计 2.1.1 叶型骨线的第一次设计由奇点分布法的设计思路知,在作第一次骨线设计时,需先假定初始骨线,通常把首次假定的骨线选取为一条直线,而该直线选取为叶型的弦线,长度为弦长l,倾斜角度为叶片安装角βe。选取栅距为t的若干条直线骨线来构成平板直线叶栅,用该平板叶栅近似代替涡轮叶栅,如图 1所示。
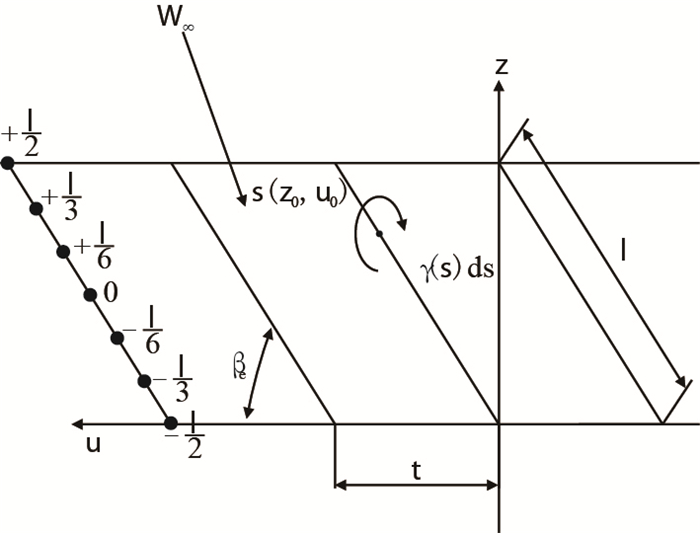 |
| 图1 由直线骨线组成的平板直线叶栅 Fig. 1 The flat linear cascade composed by linear bone line |
在平板直线叶栅中,安装角βe与所选取的环量密度γ(s)有关[12-13]。根据文献[13]选取环量密度为
| $ \gamma(s)= {A_0}\sqrt {\dfrac{{1 +\dfrac{{2s}}{l}}}{{1-\dfrac{{2s}}{l}}}} + {A_1}\sqrt {1-{{\left (\dfrac{{2s}}{l}\right )}^2}} $ | (8) |
则
| $ {\beta _{\rm e}} = {\beta _\infty }-\alpha $ | (9) |
| $ \varGamma = {\rm{\pi }}\alpha l{W_\infty } $ | (10) |
在绕流叶栅时,由于叶栅对来流的影响比单片叶片影响大,相邻两片叶片会同时对栅中流体产生作用。绕叶栅中叶型的环量为
| $ \varGamma = \varGamma {L_{\rm n}} = \pi l{\alpha}{W_\infty }{L_{\rm n}} $ | (11) |
式(11) 中,叶栅修正系数Ln,可按文献[13]查得,它是关于叶栅稠度和安装角的函数。
此外,根据式(8) 知,在当s趋近于
| $ \varGamma '{\rm{ = }}\dfrac{{\pi l}}{2}{A_0} $ | (12) |
根据式(11) 和式(12),有
| $ \alpha = \dfrac{{{A_0}}}{{2{L_{\rm n}}{W_\infty }}} $ | (13) |
叶栅安装角为
| $ {\beta _{\rm e}} = {\beta _\infty }-\dfrac{{{A_0}}}{{2{L_{\rm n}}{W_\infty }}} $ | (14) |
结合第一次设计骨线时所选取的环量密度分布规律γ(s),计算出初始骨线上各点的合成速度,根据叶栅绕流条件,叶型上各点的切向速度应在该点与叶型相切,则可得第二次设计的叶型骨线。
所选定的点涡分布规律γ(s)中有A0和A1两个未知系数,在翼型的第一次设计中,根据冲角计算A0,有
| $ {A_0} = 2{L_{\rm n}}{W_\infty }\alpha $ | (15) |
绕叶型环量ΓB可由式(5)得出,也可将环量密度分布函数沿骨线的积分,得[14]
| $ {\varGamma _{\rm{B}}} = \int_{-\frac{l}{2}}^{\frac{l}{2}} {\gamma(s){\rm d}s = } \dfrac{{\pi l}}{2}\left({A_0} + \dfrac{1}{2}{A_1}\right) $ | (16) |
则A1计算公式为
| $ {A_1} = 2\left(\dfrac{{2{\varGamma _{\rm B}}}}{{\pi l}}-{A_0}\right) $ | (17) |
在图 1所示的平板直线叶栅中,所求叶型上任意一点s0的合成速度为
| $ \mathit{\boldsymbol{W}} = {\mathit{\boldsymbol{W}}_\infty } + {\mathit{\boldsymbol{V}}_1} + {\mathit{\boldsymbol{V}}_2} $ | (18) |
叶栅中无穷远处均匀来流的速度W∞的大小已由(6) 式求得,将合成速度向周向和轴向投影,有
| $ {W_{\rm{u}}} = {W_{\infty {\rm{u}}}} + {V_{1{\rm{u}}}} + {V_{2{\rm{u}}}} $ | (19) |
| $ {W_{\rm{z}}} = {W_{\infty {\rm{z}}}} + {V_{1{\rm{z}}}} + {V_{2{\rm{z}}}} $ | (20) |
根据薄翼绕流的奇点分布法理论知,分布在直线上点涡对直线上s0点的诱导速度V1u、V1z[14]
| $ {V_{1{\rm{u}}}}{\rm{ = }}-\left(\dfrac{1}{2}{A_0}-{A_1}\dfrac{{{s_0}}}{l}\right)\sin {\beta _{\rm e}} $ | (21) |
| $ {V_{\rm 1z}}{\rm{ = }}\left(\dfrac{1}{2}{A_0}-{A_1}\dfrac{{{s_0}}}{l}\right)\cos {\beta _{\rm e }} $ | (22) |
叶栅中,除基本翼型外的其他翼型上的点涡层对s0点的诱导速度V2u、V2z[14]
| $ \begin{array}{l} {V_{{\rm{2u}}}} = \frac{1}{t}\int_{- \frac{l}{2}}^{\frac{l}{2}} a ({s_0}- s) \cdot \\ \left[{{A_0}\sqrt {\frac{{1 + \frac{{2s}}{l}}}{{1-\frac{{2s}}{l}}}} + {A_1}\sqrt {1-{{\left( {\frac{{2s}}{l}} \right)}^2}} } \right]{\rm{d}}s \end{array} $ | (23) |
| $ \begin{array}{l} {V_{{\rm{2z}}}} = \frac{1}{t}\int_{- \frac{l}{2}}^{\frac{l}{2}} b ({s_0}- s) \cdot \\ \left[{{A_0}\sqrt {\frac{{1 + \frac{{2s}}{l}}}{{1-\frac{{2s}}{l}}}} + {A_1}\sqrt {1-{{\left( {\frac{{2s}}{l}} \right)}^2}} } \right]{\rm{d}}s \end{array} $ | (24) |
在计算式(23)、(24) 的积分时,注意到s≠s0,以上两式被积函数在
| $ \begin{array}{l} {V_{{\rm{2u}}}} = \frac{{{\rm{\pi }}l{A_0}}}{{2560t}}\left[{126a\left( {{s_0}, -\frac{l}{3}} \right)-90a\left( {{s_0}, -\frac{l}{6}} \right)} \right] + \\ \;\;\;\;\;\frac{{{\rm{\pi }}l{A_0}}}{{2560t}}\left[{460a\left( {{s_0}, 0} \right)-180a\left( {{s_0}, + \frac{l}{6}} \right)} \right] + \\ \;\;\;\;\;\frac{{{\rm{\pi }}l{A_0}}}{{2560t}}\left[{630a\left( {{s_0}, + \frac{l}{3}} \right) + 334a\left( {{s_0}, + \frac{l}{2}} \right)} \right] + \\ \;\;\;\;\;\frac{{{\rm{\pi }}l{A_1}}}{{2560t}}\left[{210a\left( {{s_0}, -\frac{l}{3}} \right)-120a\left( {{s_0}, -\frac{l}{6}} \right)} \right] + \\ \;\;\;\;\;\frac{{{\rm{\pi }}l{A_1}}}{{2560t}}\left[{460a\left( {{s_0}, 0} \right)-120a\left( {{s_0}, + \frac{l}{6}} \right)} \right] + \\ \;\;\;\;\;\frac{{{\rm{\pi }}l{A_1}}}{{2560t}}\left[{210a\left( {{s_0}, + \frac{l}{3}} \right)} \right] \end{array} $ | (25) |
| $ \begin{array}{l} {V_{{\rm{2z}}}} = \frac{{{\rm{\pi }}l{A_0}}}{{2560t}}\left[{126b\left( {{s_0}, -\frac{l}{3}} \right)-90b\left( {{s_0}, -\frac{l}{6}} \right)} \right] + \\ \;\;\;\;\;\frac{{{\rm{\pi }}l{A_0}}}{{2560t}}\left[{460b\left( {{s_0}, 0} \right)-180b\left( {{s_0}, + \frac{l}{6}} \right)} \right] + \\ \;\;\;\;\;\frac{{{\rm{\pi }}l{A_0}}}{{2560t}}\left[{630b\left( {{s_0}, + \frac{l}{3}} \right){\rm{ + }}334b\left( {{s_0}, + \frac{l}{2}} \right)} \right] + \\ \;\;\;\;\;\frac{{{\rm{\pi }}l{A_1}}}{{2560t}}\left[{210b\left( {{s_0}, -\frac{l}{3}} \right)-120b\left( {{s_0}, -\frac{l}{6}} \right)} \right] + \\ \;\;\;\;\;\frac{{{\rm{\pi }}l{A_1}}}{{2560t}}\left[{460b\left( {{s_0}, 0} \right)-120b\left( {{s_0}, + \frac{l}{6}} \right) + } \right] + \\ \;\;\;\;\;\frac{{{\rm{\pi }}l{A_1}}}{{2560t}}\left[{210b\left( {{s_0}, + \frac{l}{3}} \right)} \right] \end{array} $ | (26) |
在式(25)、式(26) 中
| $ a\left({s_0}, s\right)= \dfrac{1}{2}\dfrac{{{\rm sh}\dfrac{{2\pi }}{t}\left({z_0}-z\right)}}{{{\rm ch}\dfrac{{2\pi }}{t}\left({z_0}-z\right)-\cos \dfrac{{2\pi }}{t}\left({u_0}-u\right)}}-\\{\kern 40pt}\dfrac{t}{{2\pi }}\dfrac{{{z_0}-z}}{{{{\left({u_0}-u\right)}^2} + {{\left({z_0}-z\right)}^2}}} $ | (27) |
| $ b\left({s_0}, s\right)=-\dfrac{1}{2}\dfrac{{\sin \dfrac{{2\pi }}{t}\left({u_0}-u\right)}}{{{\rm ch}\dfrac{{2\pi }}{t}\left({z_0}-z\right)-\cos \dfrac{{2\pi }}{t}\left({u_0}-u\right)}} + \\{\kern 40pt} \dfrac{t}{{2\pi }}\dfrac{{{u_0}-u}}{{{{\left({u_0}-u\right)}^2} + {{\left({z_0}-z\right)}^2}}} $ | (28) |
至此,将式(19)、式(20) 中的各速度分量计算完毕。沿着骨线计算一次即可得到第一次设计骨线上相关点的诱导速度。在作涅泊米宁氏积分时,将骨线分为了6段,7点(图 2),故计算出这7个点的诱导速度后,则可得到第二次设计的叶型骨线。
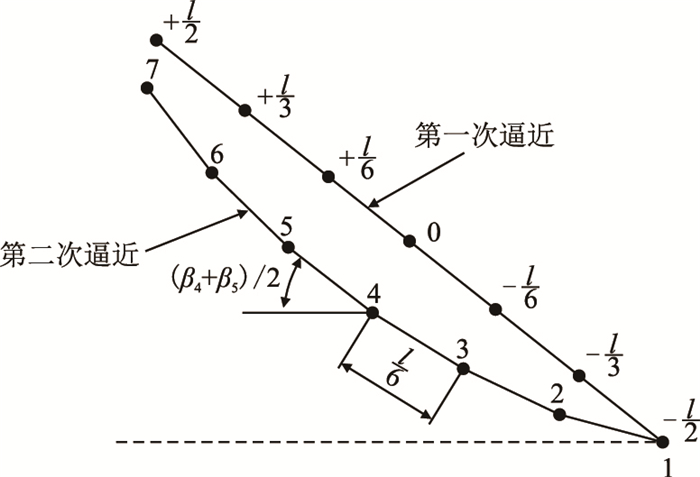 |
| 图2 第二次设计的骨线 Fig. 2 The second designing bone line |
由绕流条件知,第一次设计骨线上各点的合速度向量和第二次设计的骨线应相切。设点i的速度向量与叶栅列线的夹角为βi,则有
| $ \tan\beta_i = \dfrac{{{W_{\infty {\rm{z}}}} + {V_{1{\rm{z}}}} + {V_{2{\rm{z}}}}}}{{{W_{\infty {\rm{u}}}} + {V_{1{\rm{u}}}} + {V_{2{\rm{u}}}}}} $ | (29) |
根据式(29) 可求得第一次逼近的骨线上各点速度向量与列线的夹角
| $ \left\{ {\begin{array}{*{20}{l}} \begin{array}{l} {u_i} = {u_{i - 1}} + \frac{l}{6}\cos {\beta _{i - 1}}\\ {z_i} = {z_{i - 1}} + \frac{l}{6}\sin {\beta _{i - 1}} \end{array} \end{array}} \right. $ | (30) |
在得到各点的坐标后,用线段将各点连接起来,即得到第二次设计的骨线,如图 2所示。
在完成骨线的第二次设计后,还可根据点涡分布规律,求得各点诱导速度,作骨线的第三次设计。在轴流水轮机的奇点分布法反问题设计中表明,第二次设计的骨线与第三次设计的骨线已经相当接近,各点的角度β差已不超过30',第二次设计的骨线已能满足工程需要[15]。
2.2 骨线的光滑前面的计算设计出了折线形式的叶型骨线,但该骨线不连续,不满足骨线为流线的条件,即流线要求其具有连续的三阶导数,因此,需要对其进行光滑。根据常用的叶型参数化设计方法[16-17]及第二次设计的骨线的特点,可采用高次曲线来光滑骨线,但需使得光滑后的骨线能满足骨线为流线的条件,故需采用三次以上高次曲线来光滑骨线。
在第二次设计的骨线上共有7个已知坐标的点,故最多可建七个独立的方程,因此选择6次多项式,其一般表达式为
| $ \begin{array}{l} y = {a_0} + {a_{\rm{1}}}x + {a_2}{x^2} + {a_3}{x^3} + \\ \;\;\;\;{a_4}{x^4} + {a_5}{x^5} + {a_6}{x^6} \end{array} $ | (31) |
将第二次设计骨线上的七个点代入式(31),有
| $ \left[ {\begin{array}{*{20}{l}} {1\;{u_1}\;{u_1}^2\;{u_1}^3\;{u_1}^4\;{u_1}^5\;{u_1}^6}\\ {1\;{u_2}\;{u_2}^2\;{u_2}^3\;{u_2}^4\;{u_2}^5\;{u_2}^6}\\ {1\;{u_3}\;{u_3}^2\;{u_3}^3\;{u_3}^4\;{u_3}^5\;{u_3}^6}\\ {1\;{u_4}\;{u_4}^2\;{u_4}^3\;{u_4}^4\;{u_4}^5\;{u_4}^6}\\ {1\;{u_5}\;{u_5}^2\;{u_5}^3\;{u_5}^4\;{u_5}^5\;{u_5}^6}\\ {1\;{u_6}\;{u_6}^2\;{u_6}^3\;{u_6}^4\;{u_6}^5\;{u_6}^6}\\ {1\;{u_7}\;{u_7}^2\;{u_7}^3\;{u_7}^4\;{u_7}^5\;{u_7}^6} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{a_0}}\\ {{a_{\rm{1}}}}\\ {{a_2}}\\ {{a_3}}\\ {{a_4}}\\ {{a_5}}\\ {{a_6}} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {{z_1}}\\ {{z_2}}\\ {{z_3}}\\ {{z_4}}\\ {{z_5}}\\ {{z_6}}\\ {{z_7}} \end{array}} \right] $ | (32) |
以上7个方程组成了关于系数a的线性方程组,联立求解7个线性方程就可以得到式(31)的具体表达形式。
2.3 叶型的加厚及厚度圆与型线切点的求取光滑后的叶型骨线是一无厚度的叶型,在工程中不可能加工出无厚叶型,实际叶型均有厚度。因此,需对无厚叶型沿骨线进行加厚。在叶型加厚时,通常选用现有的翼型库中一定特性的翼型来加厚。国际上许多研究机构或公司都建立有自己的翼型库,如:NACA翼型库、GOT翼型库、ВИГМ翼型库等,这些翼型均是通过风洞或水洞实验选出的性能优异的翼型。在翼型数据库中,翼型厚度是以对弦长的相对值给出的,其位置坐标是以骨线的曲线坐标形式给出的。
在直角坐标系(u,z)中,设翼型骨线的起点为(u1,z1),而厚度的位置坐标为厚度位置点到骨线起点的距离。因此,可采用两点之间的距离公式,计算得到厚度点在坐标系(u,z)的坐标值。得到该点坐标值后,以厚度为直径作圆,即可表现出该点叶型的厚度,将所有厚度按此方法画圆,即可得到叶型。
骨线方程的表达式为
| $ \begin{array}{l} z = {a_0} + {a_{\rm{1}}}u + {a_2}{u^2} + {a_3}{u^3} + \\ \;\;\;{a_4}{u^4} + {a_5}{u^5} + {a_6}{u^6} \end{array} $ | (33) |
由两点之间的距离公式有
| $ {x_{\rm{i}}} = \sqrt {{{({u_i}-{u_1})}^2} + {{({z_i}-{z_1})}^2}} $ | (34) |
至此,厚度点的位置坐标在坐标系(u,z)中被求出,在该点以厚度为直径作圆即完成对叶型的加厚。
在叶型的性能分析及制造时,需给出叶片型线上若干点的坐标,或型线方程。根据叶型的厚度表达方式知,型线即为厚度圆的包络线。换言之,沿骨线分布的厚度圆必定同时与叶型的压力面型线和吸力面型线相切,若求得所有厚度圆与型线相切的这两个切点,则可根据这些切点制造叶片或计算型线方程。
如图 3所示,厚度圆圆心在O1,沿骨线
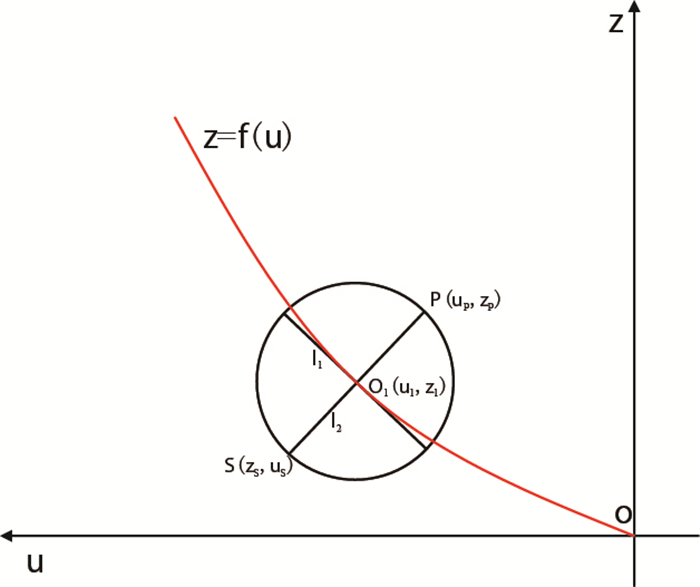 |
| 图3 厚度圆与型线切点的求取示意图 Fig. 3 The schematic diagram of calculating tangent points between thick circle and profile curve |
已知骨线的方程为式(33) 所示,对其求一阶导数,并将O1点的坐标值代入其导数中,则切线l1的斜率k1为
| $ \begin{array}{l} {k_1} = {a_{\rm{1}}} + 2{a_2}{u_1} + 3{a_3}{u_1}^2 + 4{a_4}{u_1}^3 + \\ \;\;\;\;\;5{a_5}{u_1}^4 + 6{a_6}{u_1}^5 \end{array} $ | (35) |
根据切线与法线垂直,知法线l2的斜率k2为
| $ {k_2} =-\dfrac{1}{{{k_1}}} $ | (36) |
则法线方程为
| $ z-{z_1} = {k_2}(u-{u_1}) $ | (37) |
而厚度圆的方程为
| $ {(u-{u_1})^2} + {(z-{z_1})^2} = {r^2} $ | (38) |
将式(37) 代入式(38) 中,得一元二次方程
| $ (1\!+\!{k_2}^2){u^2}\!-\!2(1\! +\! {k_2}^2){u_1}u \!+\!(1 \!+\!{k_2}^2){u_1}^2\!-\!{r^2} \!=\! 0 $ | (39) |
式(39) 有两个实根。如图 3所示,在这两个根中,值较大的那个是压力面上切点的u坐标,较小的是吸力面上切点的u坐标,再分别将这两个u值代入法线l2方程中,即可分别得到这两个切点的z坐标值。
3 算例根据某ϕ127 mm涡轮钻具工况参数为实例作计算,其具体参数见表 1。
| 表1 ϕ127涡轮钻具设计参数 Table 1 The design parameters of ϕ127 mm turbodrill |
根据表 1中参数进行基本水力计算后,采用奇点分布法设计其叶型,第一次与第二次设计的叶型骨线如图 4所示。图 4中,红色直线骨线为第一次设计的叶型骨线;蓝色弯曲折线为第二次设计的叶型骨线,从该图可以看出,第二次逼近的骨线和第一次逼近的骨线很接近。
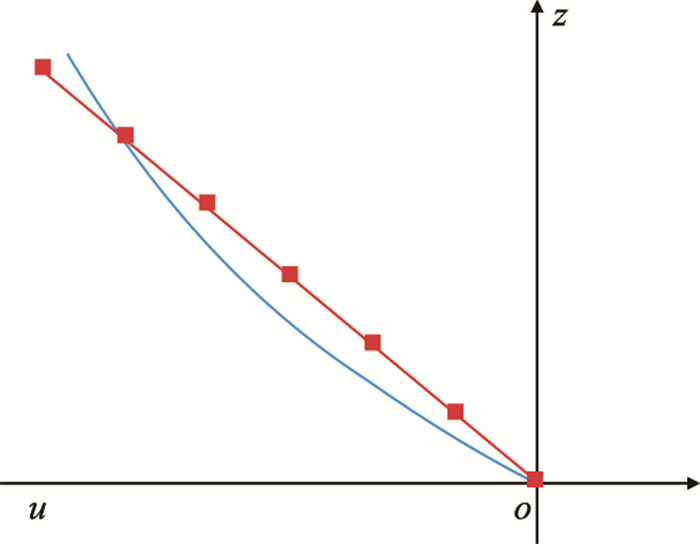 |
| 图4 ϕ127 mm涡轮钻具的叶型骨线 Fig. 4 The bone line of ϕ127 mm turbodrill |
根据第二次设计的叶型骨线,对其进行了光滑,求得六次多项式骨线的系数值如表 2所示。
| 表2 骨线方程系数值 Table 2 The coefficients value of bone line equation |
在对光滑后的叶型骨线加厚时,采用NACA0012翼型,图 5为通过加厚得到的叶型。
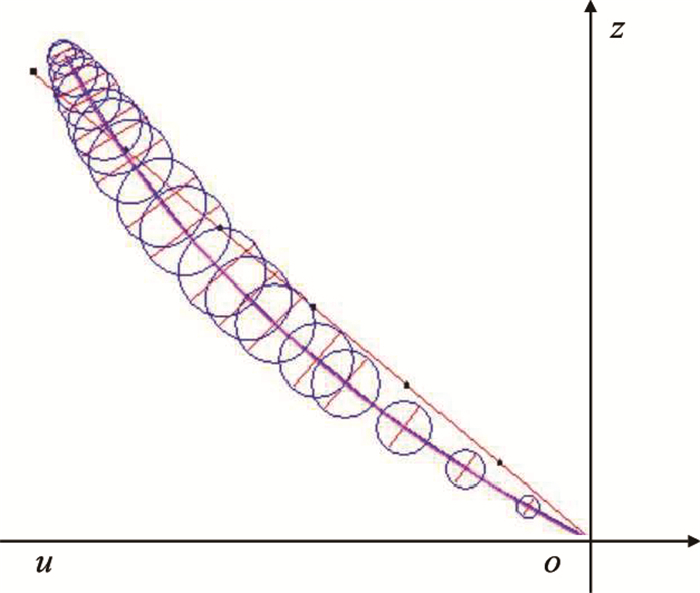 |
| 图5 NACA0012翼型加厚结果 Fig. 5 The thickened effect of NACA0012 |
在求出厚度圆与型线的切点后,将切点输入到AUTOCAD中,以样条曲线来拟合叶型。采用FLUENT软件对设计的叶型进行流场计算。在仿真计算时,采用压力基耦合求解器中的SIMPLEC算法,压力采用标准格式,动量、湍动能、湍动能耗散率均采用二阶迎风格式计算。
图 6为通过FLUENT计算得到的绕叶型流场的速度分布图,由6图可知,从进口到出口,沿流道流体的速度逐渐增加,未发生突变,满足涡轮钻具叶栅中流动的要求。
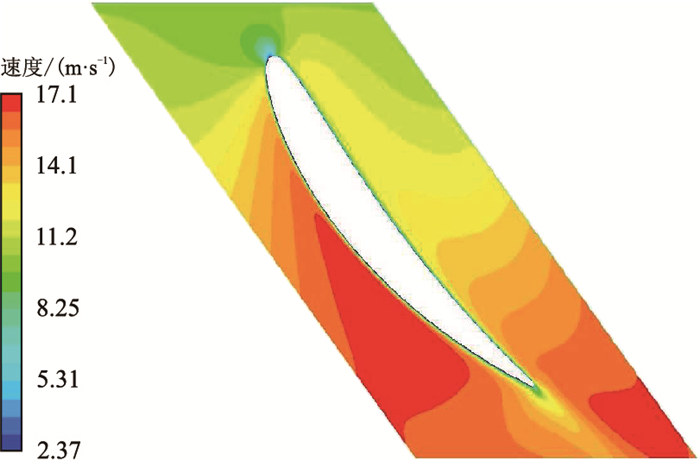 |
| 图6 流场速度分布图 Fig. 6 The image of flow field speed |
图 7为绕叶型流场静压图。图 8为叶型压力面和吸力面型线压力分布情况,图中1#曲线为压力面型线上的压力分布曲线,2#曲线为吸力面型线上的压力分布曲线。
 |
| 图7 流场静压分布图 Fig. 7 The image of flow field static pressure |
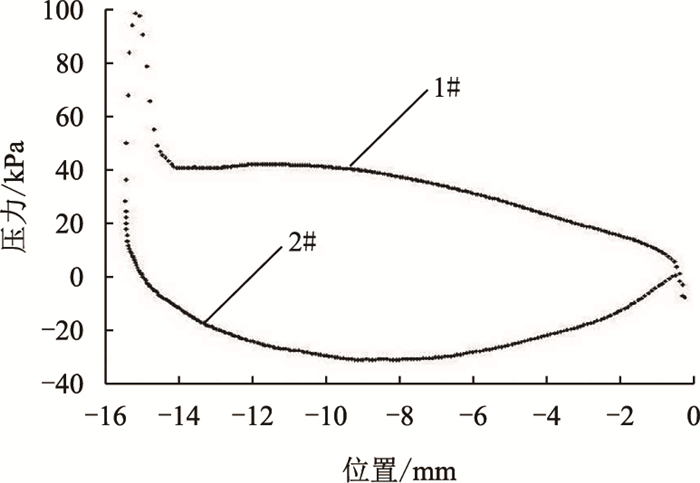 |
| 图8 叶型型线的静压分布 Fig. 8 The static pressure distribution on blade profile |
分析图 7、8可知,叶型的两条型线上压力分布均匀变化,相邻两点间的压力过渡十分平滑,压力线只是在进出口处发生了突变。在图 8中,压力面型线上压力分布曲线1#为上凸,而吸力面型线上的压力分布曲线2#为下凹,使得两条压力分布线围成的区域尽可能大,有利于增大作用于叶型上的合力,表明奇点分布法可以设计出性能良好的叶型。
4 结论(1)采用奇点分布法设计叶型骨线,再选择性能优良的翼型数据沿骨线加厚生成叶型的设计方法对设计涡轮钻具叶型是一种有效的方法,且能设计出性能优良的涡轮钻具叶型。
(2)计算实例表明,奇点分布法是一种有效的设计高速涡轮钻具叶型的方法。
(3)提出了采用六次多项式对叶型骨线光滑的方法,以及基于此沿骨线加厚叶型的方法,实现了对奇点分布法设计的叶型的参数化,方便了叶型的程序化设计,从而提高设计效率。
符号说明
Z1─叶片数;
ΓB─绕叶型环量,m2/s;
D─涡轮叶栅平均水力直径,m;
t─栅距,m;
l─弦长,m;
M─扭矩,N·m;
Q─流量,m
r─两个点涡之间距离的一半,m;
Γ─叶栅中的环量,m2/s;
s─骨线上任意点的曲线坐标;
βe─叶片安装角,(°);
Γ′─s无限逼近
W─液流相对叶片的速度,m/s;
V1─所求薄翼叶型上点涡引起的诱导速度,m/s;
V2─其他薄翼叶型上点涡引起的诱导速度,m/s;
b─其他薄翼叶型上点涡对
a─其他薄翼叶型上点涡对
u─坐标轴u,m;
z─坐标轴z,m;
下标i─第i点。
| [1] |
冯进, 符达良. 涡轮钻具涡轮叶片造型设计新方法[J].
石油机械, 2000, 28(11): 9–12.
FENG Jin, FU Daliang. New design method of turbine blade shape of turbodrill[J]. China Petroleum Machinery, 2000, 28(11): 9–12. doi: 10.3969/j.issn.1001-4578.2000.-11.003 |
| [2] |
董小虎. 适用于连续管的小尺寸涡轮钻具叶型研究[D]. 荆州: 长江大学, 2014.
DONG Xiaohu. Turbine blade research of small size Turbodrill apply to coiled tubing[D]. Jingzhou: Yangtze University, 2014. |
| [3] |
姚坚毅, 刘宝林, 王瑜. 涡轮钻具水力设计与分析方法应用现状研究[J].
石油矿场机械, 2012, 41(3): 4–7.
YAO Jianyi, LIU Baolin, WANG Yu. Application and development of the hydrodynamic performance for turbine drill[J]. Oil Field Equipment, 2012, 41(3): 4–7. doi: 10.-3969/j.issn.1001-3482.2012.03.002 |
| [4] |
张晓东, 余世敏, 龚彦, 等. 基于Bezier曲线的涡轮叶片参数化造型及优化设计[J].
机械强度, 2015, 37(2): 266–271.
ZHANG Xiaodong, YU Shimin, GONG Yan, et al. Modeling and optimization for turbine blades based on Bezier curve[J]. Journal of Mechanical Strength, 2015, 37(2): 266–271. doi: 10.16579/j.issn.1001.9669.2015.02.009 |
| [5] | 万邦烈, 李继志. 石油矿场水力机械[M]. 北京: 石油工业出版社, 1987. |
| [6] | 刘树红, 吴玉林. 水力机械流体力学基础[M]. 北京: 中国水利水电出版社, 2007. |
| [7] |
朱国俊. 基于NSGA-Ⅱ算法的轴流式叶片优化设计[D]. 西安: 西安理工大学, 2009.
ZHU Guojun. The optimal design of Kaplan turbine blade base on NSGA-Ⅱ algorithm[D]. Xi'an: Xi'an University of Technology, 2009. |
| [8] |
严敬, 阚能琪, 周绪成, 等. 轴流叶片翼型骨线漩涡密度函数研究[J].
农业机械学报, 2014, 45(7): 93–97, 143.
YAN Jing, KAN Nengqi, ZHOU Xucheng, et al. Investigation on vortex strength function along midline of axial impeller airfoils[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(7): 93–97, 143. doi: 10.6041/j.issn.1000-1298.2014.07.015 |
| [9] |
张梅, 严敬. 轴流叶轮设计的翼型计算新方法[J].
四川工业学院学报, 2003, 22(1): 55–58, 72.
ZHANG Mei, YAN Jing. An improved program for airfoil calculation in axial flow impeller design[J]. Journal of Sichuan University of Science and Technology, 2003, 22(1): 55–58, 72. |
| [10] |
严敬, 王桃, 肖国华, 等. 基于儒可夫斯基变换的轴流叶片翼型设计[J].
排灌机械工程学报, 2012, 30(3): 265–269.
YAN Jing, WANG Tao, XIAO Guohua, et al. Design program for axial flow impeller blade based on Joukowski transform[J]. Journal of Drainage and Irrigation Machinery Engineering, 2012, 30(3): 265–269. doi: 10.3969/j.-issn.1674-8530.2012.03.004 |
| [11] | 许福东, 张晓东. 带同步减速器涡轮钻具工作力学与性能仿真[M]. 武汉: 中国地质大学出版社, 2004. |
| [12] | 曹鹍, 姚志民. 水轮机原理及水力设计[M]. 北京: 清华大学出版社, 1991. |
| [13] | 高建铭, 姚志民. 水轮机的水力计算[M]. 北京: 电子工业出版社, 1982. |
| [14] |
冯建军. 基于遗传算法的平面叶栅优化设计[D]. 西安: 西安理工大学, 2002.
FENG Jianjun. Waterpower engineering[D]. Xi'an: Xi'an University of Technology, 2002. |
| [15] | 齐学义. 流体机械设计理论与方法[M]. 北京: 中国水利水电出版社, 2008. |
| [16] | TRIGG M A, TUBBY G R, SHEARD A G. Automatic genetic optimization approach to two-dimensional blade profile design for steam turbines[J]. Journal of Turbomachinery, 1999, 121(1): 11–17. doi: 10.1115/1.2841220 |
| [17] |
姜海波, 赵云鹏. 基于中弧线厚度函数的翼型形状解析构造法[J].
图学学报, 2013, 34(1): 50–54.
JIANG Haibo, ZHAO Yunpeng. Analytic expression method of airfoil profile shape based on a mean camber and thickness function[J]. Journal of Graphics, 2013, 34(1): 50–54. doi: 10.3969/j.issn.2095-302X.2013.01.008 |
 2017, Vol. 39
2017, Vol. 39


