2. 中国石油宝鸡石油机械有限责任公司, 陕西 宝鸡 721002
2. Baoji Oilfield Machinery Co. Ltd., CNPC, Baoji, Shaanxi 721002, China
近年来,随着陆地油气资源的衰竭,石油勘探开发正朝着深水海域进军,半潜式平台在深海钻井中起着重要作用。半潜式平台钻机井架结构高耸,除了受到自身重力和工作载荷外,还受到平台运动引起的惯性力、钻具随平台升沉运动引起的附加动载荷以及海洋风载等,因此半潜式钻井平台通常采用稳定性较好的塔形井架。
相比于塔形井架,K型井架在相同载荷条件下可以有效减轻自重,同时增大平台的使用面积和操作空间,目前已被用于南海某深水半潜式钻井平台[1]。但由于K型井架的两条前大腿间没有缀条连接,使得其稳定性能大幅降低。目前国内外尚无浮式平台钻机的设计标准,制造企业通常是选择比陆地钻机井架高一级别的构件配套浮式平台钻机,K型井架的稳定性能否满足海洋工况的要求尚缺乏系统研究。
K型井架属于高耸格构式缀条柱,国内外对于规则形状格构梁柱承载能力的研究有很多[2-10],Aghoury等[11]对角钢组成的四肢缀板柱进行了压缩实验,考虑了残余应力和初缺陷,评价了角钢的宽厚比、长细比及整体结构的长细比对结构极限承载能力的影响,发现中等长细比的缀板柱其失效模式是扭转和弯曲屈曲,从而降低了梁柱的强度,AISI-LRFD和AISC-LRFD标准给出的结果偏于危险。蒋丽忠等[12]测试了K形布设缀条的四肢钢管混凝土格构柱在偏压及轴压下的极限承载力,发现偏心率和长细比对承载力均有较大的影响,缀条布置形式对极限承力影响不大,除个别短柱以外,试件破坏均为整体失稳破坏。Guo[13]研究了棱形多管格构钢柱的稳定性行为,发现多管格构钢柱的极限承载能力强烈地受到剪切变形的影响,建立了考虑剪切变形的修正长细比公式。K型井架的结构比较复杂,对其稳定性的研究主要针对陆地或海洋固定式平台钻机井架,通过特征屈曲载荷的数值计算给出井架失稳的临界载荷[14-18]。
本文以某浮式平台钻机配套的K型井架为对象,从局部稳定性、前大腿稳定性和井架整体稳定性3个方面进行研究,并与陆地钻机井架作对比,评价海洋动边界对K型井架稳定性的影响程度,为深水浮式平台钻机井架的设计提供参考。
1 数值模型K型平台钻机井架的基本几何参数和技术参数如表 1所示,井架结构主要采用H型钢,少部分受力较小的缀条采用双角钢或槽钢,所有型钢材料均为Q345。安装完成后,人字架成为井架的一部分,井架下端与平台之间通过采用销轴连接。
| 表1 K型井架基本参数 Table 1 Basic parameters of K-type derrick |
海洋浮式平台在风、浪、流的作用下会产生六自由度运动(横荡﹑纵荡﹑垂荡﹑横摇﹑纵摇及艏摇),动边界以及承受海洋环境载荷是海洋钻机井架与陆地钻机井架的一个重要区别。以某深水浮式平台在作业工况下、风浪流沿135°入射的运动响应和海洋环境载荷为背景研究井架的稳定性,该工况下的风速为23.1 m/s,平台各个自由度方向的响应幅值如表 2所示。
| 表2 作业工况风浪流135°入射条件下平台的运动响应 Table 2 Responses of platform in the working condition with incidence angle of wave, current and wind being 135° |
将坐标系固定在平台上,则平台运动和海洋环境载荷对井架的作用从以下4个方面模拟:(1) 平台六自由度运动的加速度对井架的作用等效为惯性力施加在井架上;(2) 平台的横摇、纵摇角位移使井架及其附件的重力产生了横向分量,也通过惯性力施加在井架上;(3) 风载沿井架高度的分布如图 1所示[19],等效为分段集中力作用在井架的相应结点上;(4) 平台升沉运动使得钻具随之受迫振动,钻具内产生的轴向应力波通过顶驱作用于井架,这里以集中力的形式施加在井架顶部。升沉运动产生的附加动载荷通过钻具内的弹性波理论近似给出。
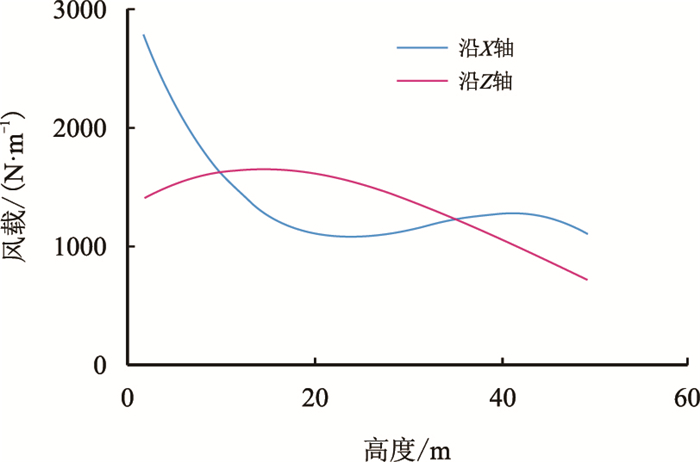 |
| 图1 风载沿井架高度分布图 Fig. 1 Wind load varying along the derrick's height |
依据平台垂荡运动的基频将顶驱处的竖向位移边界条件设为
| $ \left. {u\left( {Y, t} \right)} \right|_{Y = 0} = u_0 \sin \omega t $ | (1) |
式中:
u─平台升沉运动(垂荡)的位移,m;
Y─井架高度坐标,m;
t─时间,s。
忽略钻柱的各种阻力和损失,将钻柱视为半无限长均质直杆,求解波动方程可以得到附加动载荷的幅值[20]
| $ F_{\max } = \dfrac{{E\omega u_0 }}{{c_0 }} \cdot \dfrac{π}{4}(D^2 - d^2 ) $ | (2) |
式中:
D─钻柱的外径,m;
d─钻柱的内径,m;
E─弹性模量,Pa;
这里考虑5ʺ(1ʺ=2.54 cm)钻杆,则平台升沉引起的附加动载荷的幅值近似为158 kN。
1.2 有限元模型将井架与平台的连接简化为铰支座,约束其3个方向的线位移;采用三维空间梁单元,各杆件之间的连接点简化为刚性节点;钩载以集中力的形式平均施加在顶部的4个节点上;顶驱和游车位于最高位置,其重力、惯性力和钻井扭矩通过集中力和集中扭矩施加在井架相应节点上。考虑最大钻具重量的情况,且以该工况下平台沿各个自由度方向位移、速度及加速度绝对值的最大值计算平台运动引起的附加载荷,作为该工况下的载荷上限施加在井架上。为了评价平台运动对井架稳定性的影响,同时还建立了该井架用于陆地钻井条件下的数值模型,较之于浮式平台钻机井架,陆地钻机井架将不考虑惯性力、井架倾斜、升沉附加载荷及其风载。下面先对井架进行强度计算,得到的内力分布将作为稳定性分析的载荷条件。
2 强度分析考虑作业工况风浪流135°入射情况的上限载荷作用,对平台钻机井架进行静力等效分析,得到井架各个杆件的应力、轴力和弯矩,整个井架的Mises应力云图和轴力云图如图 2所示,最大Mises应力(314 MPa)由于应力集中而产生,出现在人字架和后大腿衔接处,范围很小;除此之外,井架前大腿应力较大,最大Mises应力在150 MPa左右,远小于井架材料的屈服极限。从轴力图可以看到两条前大腿受到的轴向压力由上到下逐渐增大,最大压力2 886 kN发生在下部Y=13.9 m附近。最大弯矩发生在人字架上方附近,为427 kN·m。
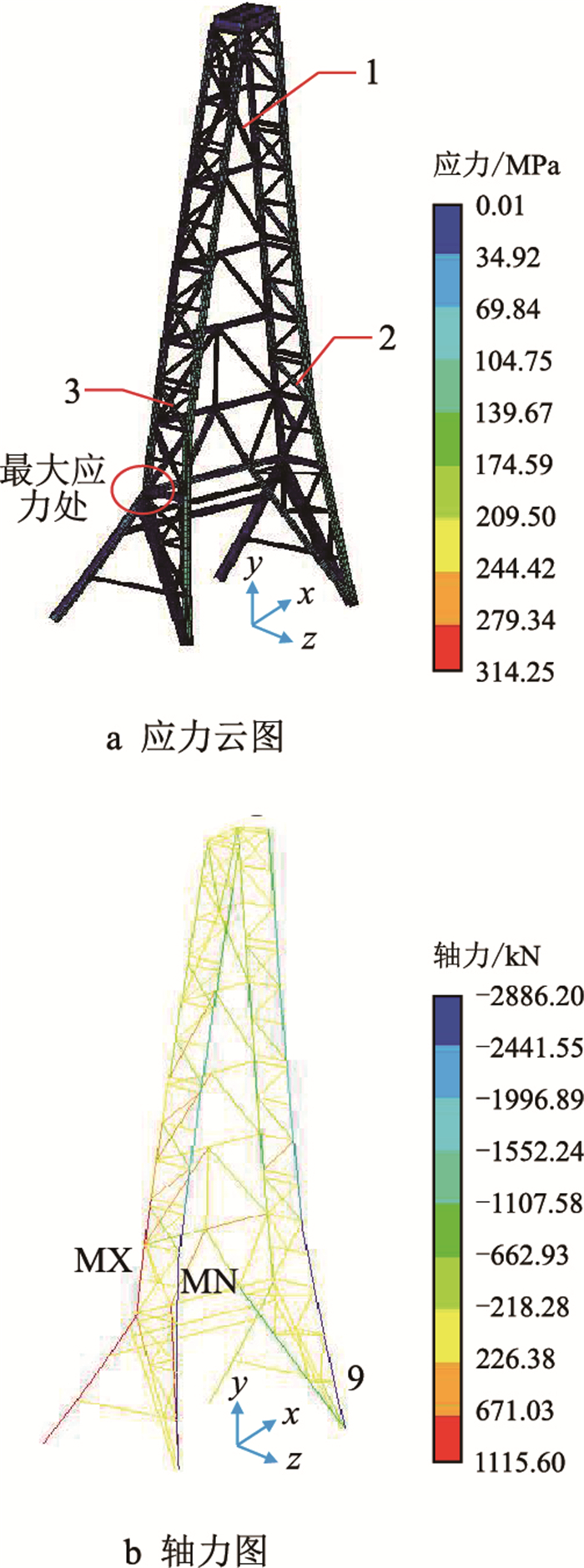 |
| 图2 平台钻机井架 Fig. 2 The derrick used on platform drilling rig |
考虑作业工况下最大钻具重量和最大钻井扭矩,对陆地钻机井架进行强度分析,得到的应力云图及轴力图如图 3所示,最大Mises应力(105 MPa)也属于应力集中,除此之外其他位置的最大Mises应力仅为50 MPa左右。最大轴向压力仍然发生在前大腿上,为857 kN。最大弯矩同样发生在人字架上方附近,为73 kN·m。
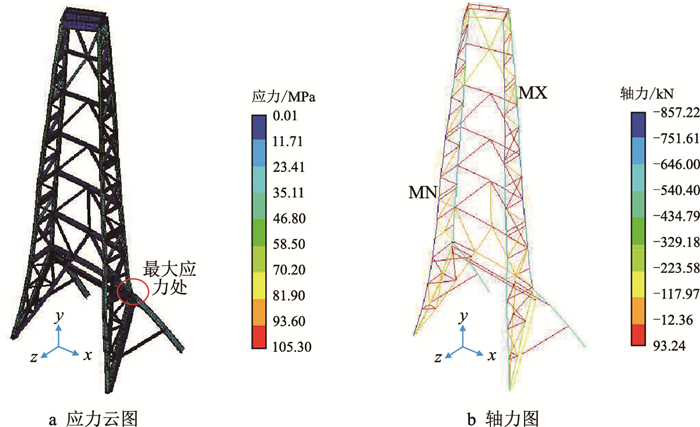 |
| 图3 陆地钻机井架 Fig. 3 The derrick used on land based drilling rig |
从井架在海上和陆地作业的计算结果看,陆地钻机井架的应力和轴力水平仅为海洋浮式平台钻机井架的1/3左右,最大弯矩仅为浮式平台钻机井架的近1/6,可见海洋浮式钻井作业条件下井架的受力状况较之于陆地作业要恶劣得多,但均满足井架材料的强度要求。
3 稳定性分析基于强度分析得到的轴力和弯矩结果,分析各单根杆件的局部稳定性、前大腿的整体稳定性,并在该工况下对井架进行整体稳定性分析。
3.1 局部稳定性将各单根杆件简化为简支梁,一端约束三个方向的位移,另一端只约束两个横向位移,在两个杆端施加大小相等、方向相反的集中压力(
| 表3 危险杆件的稳定安全系数 Table 3 Stability coefficients of the dangerous bars |
陆地钻机井架受到的轴向压力和弯矩均远远小于浮式平台井架,对所有杆件进行局部稳定性计算发现,安全系数最小的杆件仍为图 2a中位置1的杆件,其稳定安全系数n=6.13。平台动边界及海洋环境载荷对浮式平台钻机井架的局部稳定性能虽有较大幅度的降低,但仍能满足局部稳定性要求。
3.2 前大腿的整体稳定性K型井架的两个前大腿间没有腹杆连接,横向约束较弱,在轴向压力作用下前大腿可能会发生平面内失稳。
井架的前大腿均为H型钢,分为上、下两段,高度分别为19.201 m和29.713 m,分别采用H400×300×12×20型钢和H400×350×16×24型钢。井架沿高度方向有6道“横箍”,这些横箍由两个侧片上的横腹杆和后片横腹杆连接而成,阻碍前大腿发生横向位移,可以等效为横向弹簧支撑,该弹簧的刚度系数K通过这三条横腹杆组成的刚架在端部一对反向单位横向力作用下的相对位移$\delta$得到[21]:
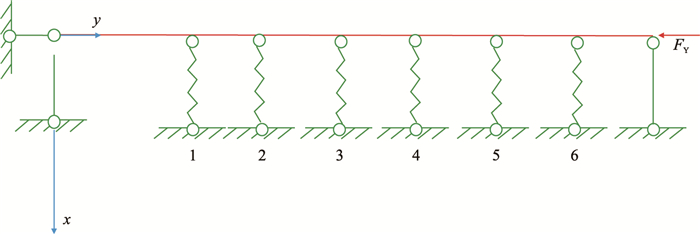 |
| 图4 前大腿稳定计算模型 Fig. 4 Stability model of a front limb |
前大腿在顶部受到的轴向压力
陆地钻井条件下井架前大腿轴向压力的积分平均值为
在作业工况风浪流135°入射条件下,考虑最大钻具重量、顶驱位于最高位置处的最大钻井扭矩、平台6个自由度方向的最大加速度、最大倾角、升沉运动引起的最大钻具附加载荷以及风载,对平台钻机井架进行整体屈曲分析。为保证钩载增大的同时其他载荷保持不变,计算过程中通过调整钩载大小使得屈曲载荷系数达到1.0,这样得到该工况下井架整体失稳的临界载荷为11 761 kN。此工况下井架顶端的最大轴向载荷为3 186 kN(来自于最大钻具重量、平台升沉运动引起的最大钻具附加载荷以及顶驱和游车对井架作用力的轴向分力),因此井架整体稳定安全系数n=3.69,大于结构体稳定性的许用安全系数2.2[22],平台井架满足整体稳定性的要求。
对于陆地钻机井架的整体稳定性计算,同样考虑其作业工况下提升最大钻具重量以及顶驱位于最高位置并施加最大钻井扭矩的情况,钩载为3 014 kN(来自于最大钻具重量及顶驱和游车的重力),得到其整体失稳的临界载荷为14 482 kN,则陆地钻机井架整体稳定安全系数n=4.80,可见平台动边界对浮式平台钻机井架整体稳定性虽有一定程度的降低,但整体稳定性能够满足要求。
4 结论(1)海洋浮式平台钻机井架的最大应力和最大轴力均是陆地作业条件下的3倍左右,最大弯矩约为陆地作业的5.8倍,受力状况恶劣得多。
(2)浮式平台钻机井架所有单根杆件中最小局部稳定性安全系数为3.25,约为陆地作业情况的一半。
(3)将浮式平台钻机井架的前大腿简化为弹性支撑梁,通过屈曲分析得到其稳定安全系数为5.77,不到陆地作业条件下前大腿稳定安全系数的一半,应该引起关注。
(4)浮式平台钻机井架的整体稳定性安全系数为3.69,陆地作业情况下为4.80,海洋环境条件对井架的整体稳定性也有所降低,但降低的幅度不大。
(5)该井架的各种稳定安全系数均大于3,满足该工况的稳定性要求。
| [1] | 陈青, 李晓斌. 海洋半潜式平台将首次采用K型井架[J]. 石油机械, 2012, 40(4): 99. |
| [2] | BONAB A P, HASHEMI B H, HOSSEINI M. Experimental evaluation of the elastic buckling and compressive capacity of laced columns[J]. Journal of Constructional Steel Research, 2013, 86(86): 66–73. doi: 10.1016/j.jcsr.2013.-03.014 |
| [3] | HASHEMI B H, JAFARI M A. Experimental evaluation of elastic critical load in batten columns[J]. Journal of Constructional Steel Research, 2009, 65(1): 125–131. doi: 10.-1016/j.jcsr.2008.02.016 |
| [4] |
张耀烨. 杆系结构稳定分析[D]. 大连: 大连理工大学, 2013.
ZHANG Yaoye. Stability analysis of truss structure[D]. Dalian: Dalian University of Technology, 2013. |
| [5] |
夏志斌, 姚谏.
钢结构原理与设计[M]. 北京: 中国建筑工业出版社, 2004.
XIA Zhibin, YAO Jian. Steel structures behavior and design[M]. Beijing: China Architecture & Building Press, 2004. |
| [6] | 全国起重机械标准化技术委员会. GB/T38112008起重机设计规范[S]. 北京: 中国标准出版社, 2008. |
| [7] | 北京钢铁设计研究总院. GB500172003钢结构设计规范[S]. 北京: 中国计划出版社, 2003. |
| [8] |
王佳. 具有主副臂结构的起重机格构式臂架整体稳定性研究[D]. 哈尔滨: 哈尔滨工业大学, 2006.
WANG Jia. Research on the overall stability of crane's lattice jib with main and vice-jib structure[D]. Harbin: Harbin Institute of Technology, 2006. |
| [9] |
孟丽霞. 具有变截面臂架的格构式起重机结构计算分析方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2008.
MENG Lixia. The study on structural calculation and analysis method of lattice-type crane with variable crosssection boom[D]. Harbin: Harbin Institute of Technology, 2008. |
| [10] |
邓科. 梭形变截面轴心受压柱的稳定性能与设计方法研究[D]. 北京: 清华大学, 2005.
DENG Ke. Studies on stability behaviour and design method of shuttle-shaped axially loaded column[D]. Beijing: Tsinghua University, 2005. |
| [11] | AGHOURY M A E, SALEM A H, HANNA M T, et al. Experimental investigation for the behaviour of battened beam-columns composed of four equal slender angles[J]. Thin-Walled Structures, 2010, 48(9): 669–683. doi: 10.-1016/j.tws.2010.03.007 |
| [12] |
蒋丽忠, 周旺保, 伍震宇, 等. 四肢钢管混凝土格构柱极限承载力的试验研究与理论分析[J].
土木工程学报, 2010, 43(9): 55–62.
JIANG Lizhong, ZHOU Wangbao, WU Zhenyu, et al. Experimental study and theoretical analysis on the ultimate load carrying capacity of four-tube concrete filled steel tubular lattice columns[J]. China Civil Engineering Journal, 2010, 43(9): 55–62. doi: 10.15951/j.tmgcxb.2010.09.-012 |
| [13] | GUO Yanlin, WANG Jie. Instability behavior and application of prismatic multi-tube latticed steel column[J]. Journal of Constructional Steel Research, 2009, 65(1): 12–22. doi: 10.1016/j.jcsr.2008.03.011 |
| [14] |
邹龙庆, 付海龙, 任国友. JJ160/41-K型井架有限元分析与承载能力研究[J].
石油矿场机械, 2004, 33(6): 33–35.
ZOU Longqing, FU Hailong, REN Guoyou. Analysis of finite element and research of load capacity of JJ160/ 41-K type derrick[J]. Oil Field Equipment, 2004, 33(6): 33–35. doi: 10.3969/j.issn.1001-3482.2004.06.008 |
| [15] |
祝娟, 邹龙庆, 冷建成. JJ160/41-K型钻井井架非线性稳定性分析[J].
石油矿场机械, 2008, 37(3): 45–48.
ZHU Juan, ZOU Longqing, LENG Jiancheng. Nonlinear stability analysis of JJ160/ 41-K type oil derrick[J]. Oil Field Equipment, 2008, 37(3): 45–48. doi: 10.3969/j.issn.-1001-3482.2008.03.012 |
| [16] |
潘娜娜. JJ170型钻机井架的整体结构稳定性分析方法[D]. 兰州: 兰州理工大学, 2013.
PAN Nana. The stability analysis method of overall structure of JJ170 type derrick[D]. Lanzhou: Lanzhou University of Technology, 2013. |
| [17] |
王纪海. 石油钻机井架弹性及弹塑性的稳定性分析研究[D]. 西安: 西安建筑科技大学, 2005.
WANG Jihai. Research on elastic and elastic-plastic stability of the oil derrick[D]. Xi'an: Xi'an University of Architecture and Technology, 2005. |
| [18] | 汪尚兵, 王斌. 基于ANSYS分析的海洋K型修井机井架稳定性的分析[J]. 科技传播, 2011, 16: 94–95. |
| [19] | 陈如恒, 沈家俊. 钻井机械的设计计算[M]. 北京: 石油工业出版社, 1995. |
| [20] | 马宏伟, 吴斌. 弹性动力学及其数值方法[M]. 北京: 中国建材工业出版社, 2000. |
| [21] |
郑伯芳, 陈立民, 韩秀清, 等. Ⅱ型井架前大腿的稳定性分析[J].
石油矿场机械, 1985, 14(5): 36–41.
ZHENG Bofang, CHEN Limin, HAN Xiuqing, et al. Analysis of stability for the front legs of the Π-type Mast[J]. Oil Field Equipment, 1985, 14(5): 36–41. |
| [22] |
张学鸿, 刘巨保, 王惠德. 3200 m钻机前开口井架整体稳定性分析[J].
石油机械, 1990, 18(5): 1–3, 28.
ZHANG Xuehong, LIU Jubao, WANG Huide. Integral stability analysis of open-front derricks[J]. China Petroleum Machinery, 1990, 18(5): 1–3, 28. doi: 10.16082/j.-cnki.issn.1001-4578.1990.05.001 |
 2017, Vol. 39
2017, Vol. 39


