相对渗透率曲线是研究油层多相渗流的基础数据之一,其应用十分广泛[1-7]。相渗关系表征主要研究油层各相流体相对渗透率与流体饱和度之间的关系[1-3]。相渗关系表征是油田油水渗流规律研究工作中的一个重要内容,尤其是在油藏工程、水驱油理论以及油藏数值模拟计算等领域,应用十分广泛[1-10]。目前,对于油水两相储层而言,其相渗关系表征主要是通过岩芯样品的室内油水相对渗透率实验数据拟合得到,认为油水相对渗透率之比与含水饱和度指数式呈线性关系[1-11]。但是,由于拟合模型的精度所限,以往的拟合方法在特低含水饱和度和特高含水饱和度时相渗关系表征误差较大,因而造成在这两个阶段油藏工程计算分析、数值模拟历史拟合等方面出现较大误差等问题[11-16]。本文通过重新分析实验数据,以水湿岩石油水两相渗流为例,基于Weibull模型提出了一种新的油水相渗与含水饱和度之间的函数表征关系,以期解决上述问题,提高油藏工程计算和数值模拟的预测精度。
1 传统油水相渗与含水饱和度关系根据传统油层物理学认为,在半对数坐标系中,油水相对渗透率比值
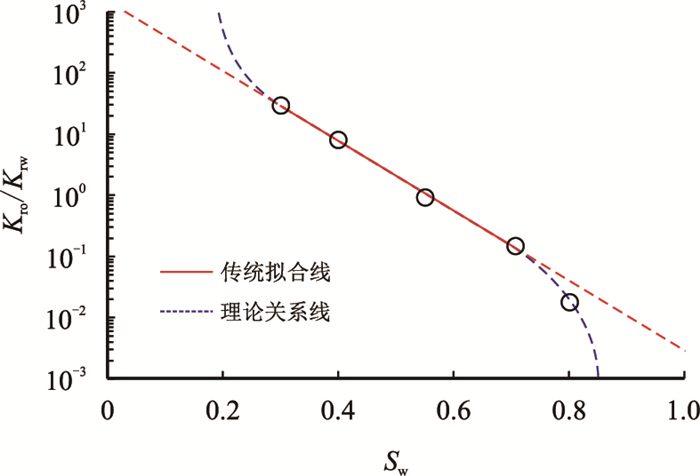 |
| 图1 传统相对渗透率之比与含水饱和度关系图 Fig. 1 Traditional relationship between the ratio of relative permeability and water saturation diagram |
| $ \dfrac{{\mathop K\nolimits_{{\rm{ro}}} }}{{\mathop K\nolimits_{{\rm{rw}}} }} = m{\rm{e}}^{ - nS_{\rm{w}}} $ | (1) |
式中:
m,n─系数,由直线段的截距、斜率求出。
这一直线关系在油田中─高含水阶段具有很好的适应性,但是特低含水期和特高含水期,实际的油水相渗比与含水饱和度的半对数函数关系已明显偏离直线,呈现出非线性关系特征(图 1),传统的拟合计算公式已不再适用。
为了准确描述这种非线性关系,需要建立油水相渗与含水饱和度新的函数表征关系式,使其更符合特低含水饱和度和特高含水饱和度时油藏实际生产状况[7]。
2 基于Weibull模型的相渗关系表征 2.1 Weibull模型Weibull分布是瑞典科学家Weibull于1951年在研究链强度时提出的一种概率分布函数。它适用性广、覆盖性强,在疲劳可靠性分析、工程模拟评估等方面应用广泛[17-18]。其两参数Weibull函数为
| $ y = 1 - {\rm{e}}^{ - ax^b } $ | (2) |
式中:
y─两参数Weibull函数;
x─自变量;
a,b─大于零的待定常数。
该函数具有以下特征:当x趋向于0时,y亦趋向于0,当x趋向于正无穷时,y则趋向于1,即
| $ \left. y \right|_{x \to 0} = 0 $ | (3) |
| $ \left. y \right|_{x \to + \infty } = 1 $ | (4) |
同时,由式(2) 可得
| $ \dfrac{1}{{1 - y}} = {\rm{e}}^{ax^b } $ | (5) |
对式(5) 两边取自然对数,可得
| $ \ln \dfrac{1}{{1 - y}} = ax^b $ | (6) |
对式(6) 两边再取自然对数,可得
| $ \ln \left( {\ln \dfrac{1}{{1 - y}}} \right) = \ln a + b\ln x $ | (7) |
由式(7) 可以看出,两参数Weibull函数y的双对数形式
对岩芯样品相渗实验数进行分析时,为了避免不同区块束缚水饱和度和残余油饱和度数值不同的影响,需对实验数据中的含水饱和度
| $ \mathop S\nolimits_{{\rm{wn}}} = \dfrac{{S_{\rm{w}} - S_{{\rm{wc}}} }}{{1 - S_{{\rm{wc}}} - S_{{\rm{or}}} }} $ | (8) |
| $ S_{{\rm{on}} } = \dfrac{{1 - S_{\rm{w}} - S_{{\rm{or}}} }}{{1 - S_{{\rm{wc}}} - S_{{\rm{or}}} }} $ | (9) |
式中:
通过大量的岩芯样品相渗实验数据的分析,发现将两参数Weibull函数中x换为地层水相对渗透率与原油相对渗透率的比值
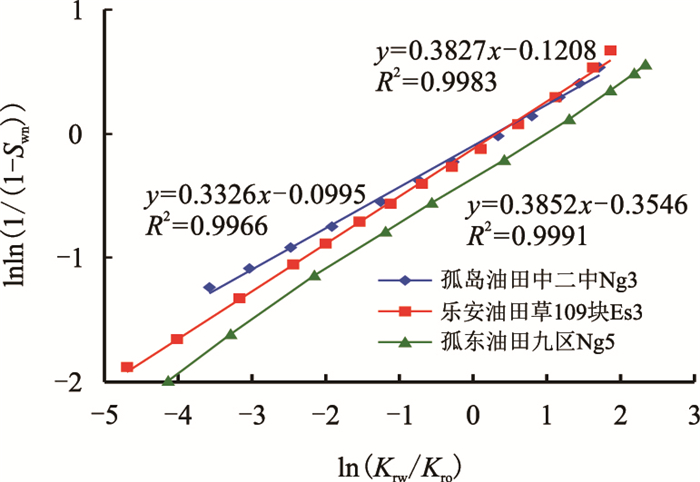 |
| 图2 基于Weibull模型的含水饱和度与相对渗透率之比关系图 Fig. 2 The water saturation and ratio of relative permeability diagram based on Weibull model |
| $ {S_{{\rm{wn}}}} = 1-{{\rm{e}}^{-a{{\left( {{K_{{\rm{rw}}}}/{K_{{\rm{ro}}}}} \right)}^b}}} $ | (10) |
该相渗关系表征函数具有以下特点:当
| $ {S_{{\rm{wn}}}}\left| {_{{K_{{\rm{rw}}}}/{K_{{\rm{ro}}}} \to 0}} \right. = 0 $ | (11) |
| $ {S_{{\rm{wn}}}}\left| {_{{K_{{\rm{rw}}}}/{K_{{\rm{ro}}}} \to + \infty }} \right. = 1 $ | (12) |
式(11) 和式(12) 符合相渗关系表征函数的极限条件,可通过该模型对相渗关系进行表征。
由图 2可见,不同区块的水、油相对渗透率比值的自然对数ln(
孤岛油田中二中Ng3油层
| $ \ln \left( {\ln \dfrac{1}{{1 - S_{{\rm{wn}}} }}} \right) = 0.3326\ln \bigg(\dfrac{{K_{{\rm{rw}}} }}{{K_{{\rm{ro}}} }}\bigg) - 0.0995 $ | (13) |
即
| $ {S_{{\rm{wn}}}} = 1-{{\rm{e}}^{-0.9053{{({K_{{\rm{rw}}}}/{K_{{\rm{ro}}}})}^{0.3326}}}} $ | (14) |
乐安油田草109块Es3油层
| $ \ln \left( {\ln \dfrac{1}{{1 - S_{{\rm{wn}}} }}} \right) = 0.3827\ln \left( {\dfrac{{K_{{\rm{rw}}} }}{{K_{{\rm{ro}}} }}} \right) - 0.1208 $ | (15) |
即
| $ {S_{{\rm{wn}}}} = 1-{{\rm{e}}^{-0.8862{{({K_{{\rm{rw}}}}/{K_{{\rm{ro}}}})}^{0.3827}}}} $ | (16) |
孤东油田九区Ng5油层
| $ \ln \left( {\ln \dfrac{1}{{1 - S_{{\rm{wn}}} }}} \right) = 0.3852\ln \left( {\dfrac{{K_{{\rm{rw}}} }}{{K_{{\rm{ro}}} }}} \right) - 0.3546 $ | (17) |
即
| $ {S_{{\rm{wn}}}} = 1-{{\rm{e}}^{-0.7015{{({K_{{\rm{rw}}}}/{K_{{\rm{ro}}}})}^{0.3852}}}} $ | (18) |
其相关系数
由前文可知,基于Weibull模型的油、水相对渗透率比值
| $ \dfrac{{K_{{\rm{ro}}} }}{{K_{{\rm{rw}}} }} = A\left( {\ln \dfrac{1}{{1 - S_{{\rm{wn}}} }}} \right)^{ - B} $ | (19) |
式中:
在一维条件下,忽略毛管压力和重力的作用,根据达西定律可以得到水相分流量曲线表达式
| $ f_{\rm{w}} = \dfrac{1}{{1 + \dfrac{{\mu _{\rm{w}} }}{{\mu _{\rm{o}} }}\dfrac{{K_{{\rm{ro}}} }}{{K_{{\rm{rw}}} }}}} $ | (20) |
式中:
将式(19) 代入式(20),可以得出基于Weibull模型的分流量方程含水率
| $ f_{\rm{w}} = \dfrac{1}{{1 + \dfrac{{\mu _{\rm{w}} }}{{\mu _{\rm{o}} }}\dfrac{{K_{{\rm{ro}}} }}{{K_{{\rm{rw}}} }}}} = \dfrac{1}{{1 + A\dfrac{{\mu _{\rm{w}} }}{{\mu _{\rm{o}} }}\left( {\ln \dfrac{1}{{1 - S_{{\rm{wn}}} }}} \right)^{ - B} }} $ | (21) |
已知
以上文提到的孤岛油田中二中Ng3油层中3-检18井的岩芯相对渗透率实验数据为例,应用基于Weibull模型推导的相渗分流量方程计算含水率
中3-检18井取芯目的层位为上第三系馆陶组油层,其相渗实验用原油黏度
| 表1 中30-检18井Ng3相对渗透率实验数据表 Table 1 Z30-J18 well Ng3 relative permeability experimental data sheet |
根据上述实验数据,利用Weibull函数模型,通过线性拟合回归,可得到式(13) 待定系数a=0.905 3,b=0.332 6,可计算A=0.741 4,B=3.007,最终得到基于Weibull模型的相渗关系新的表征方法推导的相渗分流量方程为
| $ f_{\rm{w}} = \dfrac{1}{{1 + 0.7414 \times \dfrac{{\mu _{\rm{w}} }}{{\mu _{\rm{o}} }}\left( {\ln \dfrac{1}{{1 - S_{{\rm{wn}}} }}} \right)^{ - 3.007} }} $ | (22) |
其中
| $S_{{\rm{wn}}} = \dfrac{{S_{\rm{w}} - S_{{\rm{wc}}} }}{{1 - S_{{\rm{wc}}} - S_{\rm{or}} }} = 1.845S_{\rm{w}} - 0.3192$ |
而依据传统油层物理方法,可得出的相渗分流量方程为
| $ f_{\rm{w}} = \dfrac{1}{{1 + 4239.9214 \times \dfrac{{\mu _{\rm{w}} }}{{\mu _{\rm{o}} }}{\rm{e}}^{ - 16.7143 \times S_{\rm{w}} } }} $ | (23) |
将两种方法计算的分流率曲线与实际实验结果(图 3)比较可以看出,基于Weibull模型的相渗关系新的表征方法推导的相渗分流量方程较传统油层物理学计算的分流量方程在特低─中含水饱和度范围内能大幅度提高产水率拟合精度,能为油藏开发动态分析,油藏数值模拟精度的提高提供基础。
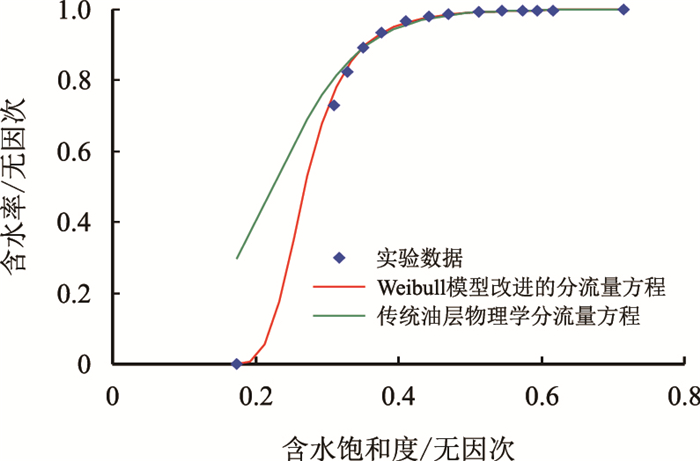 |
| 图3 中3-检18井Ng3相渗含水率拟合结果对比图 Fig. 3 Z3-J18 well relative permeability water cutfitting results comparison chart |
(1)在特低含水期和特高含水期,实际的油、水相对渗透率之比与含水饱和度指数式函数关系已明显偏离直线,呈现出非线性关系,传统的拟合计算公式已不再适用。
(2)大量的岩芯样品相渗实验数据的分析表明,水油相对渗透率比值的自然对数ln(
(3)基于Weibull模型的相渗关系新的表征方法推导的相渗分流量方程,与传统油层物理学计算的分流量方程相比,能在特低-中含水期内能大幅度提高产水率拟合精度,进而提高油藏开发动态分析和油藏数值模拟准确性,具有极大的推广应用价值。
| [1] | 秦积舜, 李爱芬. 油层物理学[M]. 东营: 石油大学出版社, 2001. |
| [2] | 李传亮. 油藏工程原理[M]. 北京: 石油工业出版社, 2005. |
| [3] |
邴绍献. 特高含水期相渗关系表征研究[J].
石油天然气学报, 2012, 34(10): 118–120.
BING Shaoxian. Study on relative permeability equation adapted at ultra-high water-cut stage[J]. Journal of Oil and Gas Technology, 2012, 34(10): 118–120. doi: 10.3969/j.-issn.1000-9752.2012.10.028 |
| [4] |
张金庆, 孙福街. 相渗曲线和水驱曲线与水驱储量的关系[J].
新疆石油地质, 2010, 31(6): 629–631.
ZHANG Jinqing, SUN Fujie. Quantitative relationship between relative permeability curve, water drive curveand waterflood reserve[J]. Xinjiang Petroleum Geology, 2010, 31(6): 629–631. |
| [5] |
薛颖, 石立华, 席天德. 童氏水驱曲线的改进及应用[J].
西南石油大学学报(自然科学版), 2015, 37(1): 141–145.
XUE Ying, SHI Lihua, XI Tiande. Tong's water drive curve improvement and its application[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2015, 37(1): 141–145. doi: 10.11885/j.issn.1674-5086.2012.12.20.02 |
| [6] |
蒋炳金, 唐海, 吕栋梁, 等. 用相对渗透率曲线研究薄层底水油藏产水规律[J].
新疆石油地质, 2006, 27(5): 588–590.
JIANG Bingjin, TANG Hai, LÜ Dongliang, et al. Research on water production law of reservoir with thin thickness and bottom water using relative permeability curve[J]. Xinjiang Petroleum Geology, 2006, 27(5): 588–590. doi: 10.3969/j.issn.1001-3873.2006.05.022 |
| [7] |
耿站立, 孙福街, 田冀. 多层砂岩油藏层内纵向非均质性表征方法探索[J].
西南石油大学学报(自然科学版), 2011, 33(4): 96–100.
GENG Zhanli, SUN Fujie, TIAN Ji. Exploration on reservoir heterogeneity characterization in reservoir numerical modeling of multi-substratum sandstone reservoir[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2011, 33(4): 96–100. doi: 10.3863/j.-issn.1674-5086.2011.04.017 |
| [8] |
吕成远. 油藏条件下油水相对渗透率实验研究[J].
石油勘探与开发, 2003, 30(4): 102–104.
LÜ Chengyuan. Experimenal study on oil-water relative permeability under natural reservoir conditions[J]. Petroleum Exploration and Development, 2003, 30(4): 102–104. doi: 10.3321/j.issn:1000-0747.2003.04.033 |
| [9] |
董大鹏. 非稳态相渗实验数据的处理方法[J].
西南石油大学学报(自然科学版), 2014, 36(6): 110–116.
DONG Dapeng. Processing method to the data of relative permeability in unsteady state displacement[J]. Journal of Southwest Petroleum University(Science & Technology Edition), 2014, 36(6): 110–116. doi: 10.11885/j.issn.1674-5086.2012.08.30.07 |
| [10] |
戴胜群, 付波, 洪秀娥, 等. 油藏综合相渗曲线拟合方法[J].
油气藏评价与开发, 2011, 1(3): 1–4.
DAI Shengqun, FU Bo, HONG Xiu'e, et al. The methods to fit the curve of integrated relative permeability in reservoir[J]. Reservoir Evaluation and Development, 2011, 1(3): 1–4. doi: 10.3969/j.issn.2095-1426.2011.03.-001 |
| [11] |
孙雷, 闫成海, 潘毅, 等. 长岩芯驱替中不同位置的相渗曲线计算[J].
西南石油大学学报(自然科学版), 2014, 36(2): 139–144.
SUN Lei, YAN Chenghai, PAN Yi, et al. Calculation of relative permeability curve at different position in long core displacement experiment[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2014, 36(2): 139–144. doi: 10.11885/j.issn.1674-5086.2013.03.-20.01 |
| [12] |
刘西雷. 基于分形理论计算相渗分流量曲线[J].
大庆石油地质与开发, 2015, 34(1): 59–62.
LIU Xilei. Relative permeability fractional flow curve calculation based on fractal theory[J]. Petroleum Geology and Oilfield Development in Daqing, 2015, 34(1): 59–62. doi: 10.3969/J.ISSN.1000-3754.2015.01.012 |
| [13] |
陈田勇, 毛鑫, 刘仕银, 等. 利用分形理论计算相对渗透率曲线以南襄盆地双河油田核桃园组六油组为例[J].
石油与天然气地质, 2012, 33(4): 578–581, 590.
CHEN Tianyong, MAO Xin, LIU Shiyin, et al. Fractal theory-based calculation method of relative permeability curves: A case study from the Hetaoyuan Formation in Shuanghe Oilfield, Nanxiang Basin[J]. Oil & Gas Geology, 2012, 33(4): 578–581, 590. doi: 10.11743/-ogg20120412 |
| [14] |
黄祥峰, 张光明, 郭俊磊, 等. 计算油藏相渗曲线的新方法及应用[J].
石油地质与工程, 2013, 27(1): 53–55.
HUANG Xiangfeng, ZHANG Guangming, GUO Junlei, et al. New measurement methods for relative permeability curve and its application[J]. Petroleum Geology and Engineering, 2013, 27(1): 53–55. doi: 10.3969/j.issn.1673-8217.2013.01.014 |
| [15] |
凡哲元, 袁向春, 廖荣凤, 等. 制作含水率与采出程度关系理论曲线常犯错误及解决办法[J].
石油与天然气地质, 2005, 26(3): 387–387.
FAN Zheyuan, YUAN Xiangchun, LIAO Rongfeng, et al. Conunon problerns and solutions in plotting thcoretical curves of water-cut vs. recovery percent of reserves[J]. Oil and Gas Geolog, 2005, 26(3): 387–387. doi: 10.3321/j.-issn:0253-9985.2005.03.021 |
| [16] |
王华, 邴绍献, 张海燕, 等. 特高含水期水驱油效率计算新方法[J].
断块油气田, 2013, 20(2): 201–203.
WANG Hua, BING Shaoxian, ZHANG Haiyan, et al. A new method suitable for water-oil displacement efficiency calculation in extra-high water cut period[J]. Fault-block Oil & Gas Field, 2013, 20(2): 201–203. doi: 10.6056/-dkyqt201302016 |
| [17] |
丁剑霆, 程凯, 杨晓丰. Weibull分布及其在混凝土断裂能试验数据分析中的应用[J].
黑龙江工程学院学报(自然科学版), 2009, 23(1): 14–16.
DING Jianting, CHENG Kai, YANG Xiaofeng. Weibull distribution and its application in trial data analysis of fracture energy[J]. Journal of Heilongjiang Institute of Technology, 2009, 23(1): 14–16. doi: 10.3969/j.issn.1671-4679.2009.01.005 |
| [18] |
王亮, 谭洪卫, 季亮. 基于Weibull统计特性的风速条件下的自然通风[J].
太阳能学报, 2014, 35(2): 345–350.
WANG Liang, TAN Hongwei, JI Liang. Natural ventilation under wind speed condition based on Weibull statistic characteristics[J]. Acta Energiae Solaris Sinica, 2014, 35(2): 345–350. doi: 10.3969/j.issn.0254-0096.2014.02.-026 |
| [19] |
宫平志, 刘斌, 郑彬, 等. 相渗曲线处理新方法-半归一化法[J].
石油化工应用, 2015, 34(9): 32–35.
GONG Pingzhi, LIU Bin, ZHENG Bin, et al. A new method for processing relative permeability curves-Seminormalization method[J]. Petrochemical Industry Application, 2015, 34(9): 32–35. doi: 10.3969/j.issn.1673-5285.-2015.09.007 |
| [20] |
李宁, 孙雷, 潘毅, 等. 油水相渗曲线归一化新方法研究[J].
复杂油气藏, 2015, 8(1): 38–40, 51.
LI Ning, SUN Lei, PAN Yi, et al. A new method for normalizing oil-water relative permeability curves[J]. Complex Hydrocarbon Reservoirs, 2015, 8(1): 38–40, 51. doi: 10.16181/j.cnki.fzyqc.2015.01.009 |
 2017, Vol. 39
2017, Vol. 39


