介质的侧压系数为介质水平应力与垂向应力的比值,其主要作用是在已知介质垂向应力的情况下,预测介质的水平应力[1-2]。油气藏储层水平应力的预测研究通常是钻井工程设计和压裂施工的重要依据之一。在地下工程的研究过程中,对土介质水平应力的计算与侧压系数的预测方法研究比较成熟[3-5]。岩石的水平应力与侧压系数的预测方法,通常在土介质水平应力与侧压系数的计算方法中加入构造应力修正项得到。然而,土介质与岩石是两种不同的固体介质,水平应力产生的机理也不相同。
土介质是松散体,地层岩石属于固体,而一般情况下流体的压力都是各向同性的[6],固体和松散体的应力则都是各向异性的[7-8],但是,土和岩石的各向异性又不相同。土介质不同方向的应力之间存在一定的关系,这是由于土的垂向应力是自重产生的,水平侧向应力也是自重产生的,是垂向应力的函数。由于土介质处于地表,受构造作用影响较小。而且土介质具有一定的流动性,因此,土介质的水平应力基本不受构造应力影响,土介质的侧压系数是一个特定值,可以用来预测任意深度的水平侧向应力[9-10]。
但是,岩石不同方向的应力之间没有关系,垂向应力是自重产生的,水平应力则主要是构造作用产生的。由于构造作用的强弱,水平应力可大可小,可正可负,即侧压系数不是一个确定的量,也不是垂向应力的函数。流体的侧压系数为1,土的侧压系数为定值,而岩石的侧压系数并不是垂向应力的函数,岩石的侧压系数本身没有工程意义。
然而,许多关于石油地质和石油工程的文献都还在使用岩石侧压系数这一概念,把土介质的侧压系数直接引用到岩石力学之中。本文通过研究不同介质水平应力的产生机理,分析了不同介质侧压系数的计算方法,希望藉此说明对岩石侧压系数使用的误区。
1 流体的侧压系数流体、土与岩石是3种结构不同的典型介质,以水为例介绍一般流体的侧压系数。水可以流动,静止时没有抗剪切能力,也没有固定的形状。若盆地装满了水(图 1),任意深度D处的垂向压力(上覆压力)就是上覆水柱的重量产生的压力[6],即
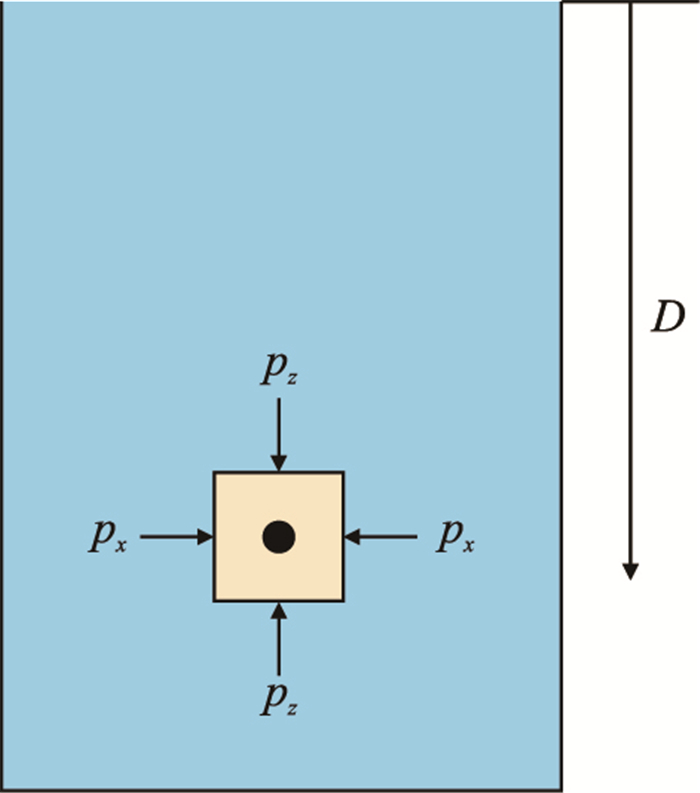 |
| 图1 水不同方向的压力 Fig. 1 Pressure of water at different attitudes |
| $ p_{z} = p_{{\rm{air}}} + \rho _{\rm{w}} {\rm{g}}D $ | (1) |
式中:
g─重力加速度,g=9.8 m/s2;
由于流体的压力是各向同性的,因此,深度D处水的侧向压力(水平压力)与垂向压力相等[6]。水的侧向压力是水的自重(垂向应力)产生的。因此,对水而言,侧压系数为
| $ \lambda = \dfrac{{p_x }}{{p_z }} = \dfrac{{p_y }}{{p_z }} = 1 $ | (2) |
式中:
水的侧压系数恒等于1,也就没必要使用侧压系数来预测水的水平应力了。事实上,流体力学也从不使用这一概念。
2 土介质的侧压系数土是由没有胶结的固体颗粒组成的松散体,其流动性比水差,但有一定的抗剪切能力。若盆地装满了土(图 2),任意深度
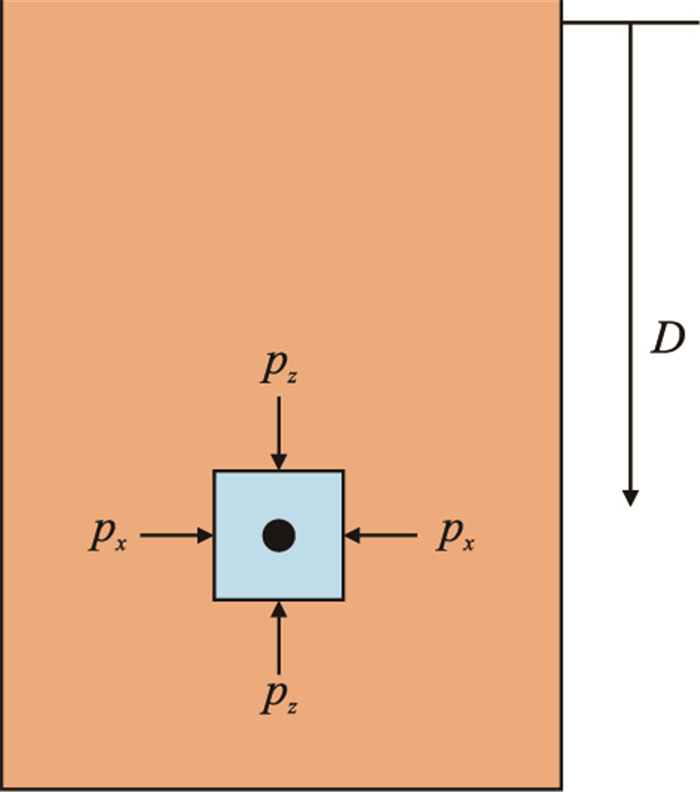 |
| 图2 土不同方向的压力 Fig. 2 Pressure of soil at different attitudes |
| $ \sigma _z = p_{{\rm{air}}} + \rho _{\rm{s}} {\rm{g}}D $ | (3) |
式中:
由于盆地中的土受到一定的侧向限制,土的侧向应变为0,只有垂向上才产生应变。而土介质具有一定的流动性,所以土的水平应力不受构造作用的影响。根据土力学的相关理论,可以推导出深度D处的侧向应力为[9-10]
| $ \sigma _x = \sigma _y = \dfrac{\nu }{{1 - \nu }}\sigma _z $ | (4) |
式中:
由式(4)可以看出,土的侧向应力实际上也是土的自重即垂向应力产生的。土的侧压系数为[6-7]
| $ \lambda = \dfrac{{\sigma _x }}{{\sigma _z }} = \dfrac{{\sigma _y }}{{\sigma _z }} = \dfrac{\nu }{{1 - \nu }} $ | (5) |
流体的泊松比为0.5,土的泊松比随土的性质而变化,但比水低,一般在0.2~0.5,因此,土的侧压系数在0.2~1.0,硬质土的侧压系数比较低,软质土的侧压系数比较高[9-10]。对于特定的土介质,土的侧压系数是一个特定的值。
因此,工程应用中就不能将其忽略了。有了侧压系数的计算方法,在已知土介质的垂向应力的条件下,就可以通过式(5) 预测土的水平应力了。
3 岩石的侧压系数岩石与土的主要区别在于岩石为固体,而土为松散体。组成岩石的固体颗粒是胶结在一起的,因此,岩石具有一定的形状,而且能够抗剪切,构造作用对水平应力具有较大的影响。石油工程和石油地质研究的对象都是岩石,而且是处于一定构造应力下的岩石,不是土介质。若盆地全部沉积了岩石(图 3),任意深度D处的垂向应力就是上覆岩石层的重量产生的压力,大小与岩石的上覆岩石压力
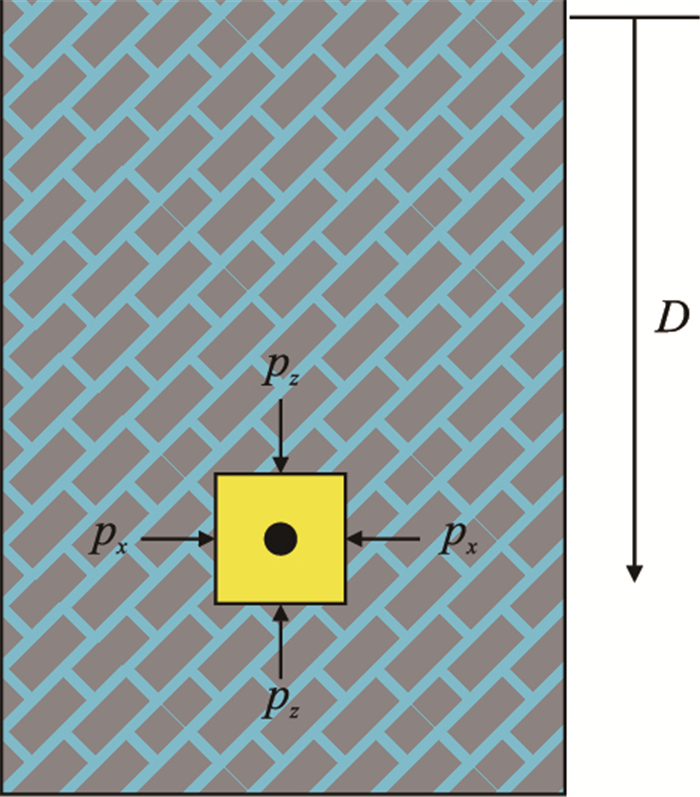 |
| 图3 岩石不同方向的压力 Fig. 3 Pressure of rock at different attitudes |
| $ \sigma _z = p_{{\rm{air}}} + \rho _{\rm{r}} {\rm{g}}D $ | (6) |
式中:
但是,岩石的侧向应力与垂向应力没有关系,侧向应力也不是由岩石的重量即垂向应力引起的,而主要是与构造作用有关。挤压构造的侧向应力很高,拉伸构造的侧向应力很低,甚至为负值。不同方向的侧向应力也不相同。位于地面的岩石柱,水平应力与大气压力平衡,不管石柱的高度如何,岩石柱的侧向应力始终为大气压。可见,岩石的侧向应力与垂向应力无关。而位于地下的岩石,由于构造作用的不同,侧压系数变化范围较大,与垂向深度和垂向应力关系不大。因此,岩石侧压系数的预测工作也就没有意义了。
但是,有些文献依然按照土力学的方法计算岩石的侧向应力或水平地应力[12],只是计算时采用了Biot有效应力,即
| $ \sigma _x = \sigma _y = \dfrac{\nu }{{1 - \nu }}(\sigma _z - \alpha p) + \alpha p $ | (7) |
式中:
p─孔隙中的流体压力,MPa;
用式(7) 预测的水平地应力数值都很小,且是各向同性的,并且都小于垂向应力或上覆压力,当然是没有实际意义的。
| $ \sigma _x = \left( {\dfrac{\nu }{{1 - \nu }} + A} \right)(\sigma _z - \alpha p) + \alpha p $ | (8) |
| $ \sigma _y = \left( {\dfrac{\nu }{{1 - \nu }} + B} \right)(\sigma _z - \alpha p) + \alpha p $ | (9) |
式中:
A,B─构造应力系数,无因次。
由式(8) 和式(9) 可以看出,地层岩石有两个侧压系数
| $ \lambda _x = \dfrac{\nu }{{1 - \nu }} + A $ | (10) |
| $ \lambda _y = \dfrac{\nu }{{1 - \nu }} + B $ | (11) |
式中:
若知道了侧压系数
在油气藏地质条件下,水平地应力在一定区域内变化较小,水平地应力已经通过实测得到之后,基本上可以代表本地区的水平应力情况,也不需要再通过侧压系数进行预测了。因此,通过侧压系数再次进行不同井水平应力的预测就失去了工程意义。若沿用土力学侧压系数的计算方法,根据式(5) 计算,由于岩石的泊松比在0.2~0.3,侧压系数只有0.2~0.4,这与测得的岩石侧压系数相距甚远。文献[15]统计的特定地区的岩浆岩侧压系数在0~6,沉积岩的侧压系数在0~4,变化范围都很宽,无法用来预测水平地应力。
其实,储层水平地应力的确定并不困难,通过一次小型压裂即可确定,通过测井方法也能确定。因此,没必要花精力去研究岩石的侧压系数的理论计算公式和具体数值,也根本研究不出来。
石油工程界的经常做法是,在确定了一口井的地应力剖面之后,用式(8) 和式(9) 反算出不同深度的侧压系数,然后再代回到式(8) 和式(9) 预测邻井的地应力剖面。这个做法其实没有必要。一般情况下地应力在一个小的区域内变化不大,知道了一口井的地应力分布,也就知道了临近区域的地应力分布,直接使用即可,没必要再经过侧压系数回算一次。
式(8) 和式(9) 的另外一个问题是,用侧压系数预测的水平地应力总是随深度增大或随深度分段增大的,实际上一个地层的水平地应力完全有可能比上覆地层的水平地应力小,更多情况下是一个地层的水平地应力基本为常数,并不随深度而变化。
4 致裂法确定岩石水平地应力压裂是常用的油气增产技术[16-19]。通过小型压裂可以方便地确定地层岩石的水平地应力[20],图 4为压裂施工曲线。岩石的破裂压力与裂缝的重张压力的差值为岩石的拉伸应力强度,即
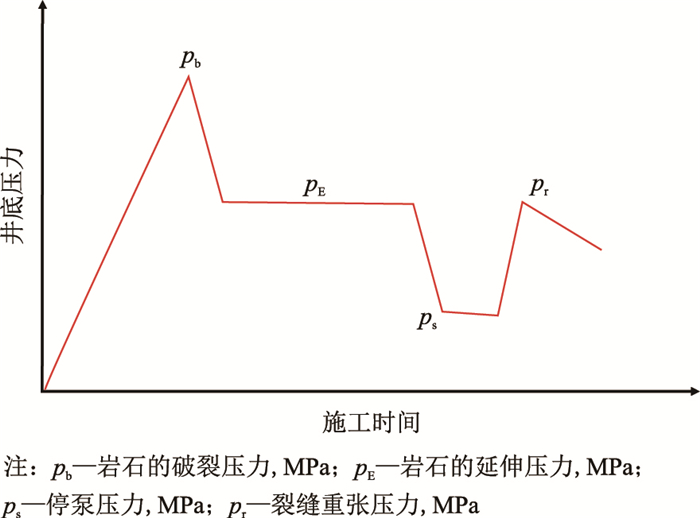 |
| 图4 地层压裂施工曲线 Fig. 4 Pressure performance during hydraulic fracturing |
| $ \sigma _{\rm{f}} = p_{\rm{b}} - p_{\rm{r}} $ | (12) |
式中:
岩石的最小水平地应力等于停泵时的井底压力(裂缝闭合压力),即
| $ \sigma _{\rm{h}} = p_{\rm{s}} $ | (13) |
式中:
岩石的最大水平地应力可以用下式计算
| $ \sigma _{\rm{H}} = 3p_{\rm{s}} - p_{\rm{r}} - p $ | (14) |
式中:
南海某井在井深4 340 m处对地层实施压裂,孔隙流体压力为52.08 MPa,由压裂获得的施工参数为
代入式(13) 和式(14),计算得到的最小水平地应力为
有了这两个侧向应力,就可以用于该地层在附近地区的地应力研究了。若再借助于侧压系数,必须进行下面的计算。
地层岩石的平均密度为2.35 g/cm3,由式(6) 计算的上覆地层压力为
若岩石的泊松比为0.2,Biot系数为0.6,代入式(8) 和式(9),得地层的构造应力系数为A=0.53,B=1.46或侧压系数
若把反求的构造应力系数或侧压系数代入式(8) 和式(9),计算出的水平地应力与前面的实测值完全相同,也就是所谓的“自己验证自己”。
如果用构造应力系数或侧压系数预测临近区域的地应力,若预测结果与新井的实测地应力有偏差时,一般会修正构造应力系数或侧压系数重新进行计算。但是岩石的水平应力与垂向应力并不相关,用修正后的侧压系数对地应力计算也是基于实测的基础上,侧压系数预测本身的意义并不大,修正后的还不如直接采用新井的实测水平地应力,修正后的侧压系数也难以应用于其他井的预测。若事前无法做到准确预测,事后的修正计算毫无意义。
5 结论(1)大多数流体压力是各向同性的,因此流体的侧压系数恒等于1,没必要采用侧向系数预测流体的水平压力。
(2)土介质是松散体,具有一定的抗剪切能力,受到构造应力的影响较小,因此土介质的侧压系数为特定数值,可以用来预测不同深度土介质的水平地应力。
(3)岩石是固体,可以抗剪切,岩石的水平应力与垂向应力没有直接的关系;岩石的水平应力主要受构造应力的影响,与垂向应力关系不大,因此岩石的侧压系数并不能用来预测地层岩石的水平地应力。
(4)岩石的水平地应力大小可以通过实测得到,因此修正的侧压系数对水平应力预测意义不大,修正后的侧压系数也难以应用于其他井的预测。
| [1] | ZHENG H P, JIANG Y M. A nonlinear elastic analysis of static stress and lateral pressure coefficient for granular couette systems[J]. Acta Physica Sinica, 2008, 57(12): 7919–7927. |
| [2] | XU Z Y. A new apparatus for the determination of the coefficient of lateral earth pressure at rest[J]. Science in China, Ser. A, 1958(6): 86–98. |
| [3] | LEE J, LEE D, PARK D. Experimental investigation on the coefficient of lateral earth pressure at rest of silty sands: Effect of fines[J]. Geotechnical Testing Journal, 2014, 37(6): 20130204. doi: 10.1520/GTJ20130204 |
| [4] | SONG P, CHEN K, DONG Z. A theoretical analysis of the lateral pressure coefficients in a soft-packed stuffing-box seal[J]. Tribology International, 1997, 30(10): 759–765. doi: 10.1016/S0301-679X(97)00069-8 |
| [5] | MASLOV N N. Coefficient of lateral pressure of soils: 2R soil mech[J]. International Journal of Rock Mechanics & Mining Sciences & Geomechanics Abstracts, 1974, 11(10): 200–200. doi: 10.1016/0148-9062(74)91155-3 |
| [6] | 贺礼清. 工程流体力学[M]. 北京: 石油工业出版社, 2004. |
| [7] | 刘鸿文. 材料力学(上册)[M]. 第2版. 北京: 高等教育出版社, 1982. |
| [8] |
李传亮, 杜文博. 油气藏岩石的应力和应变状态研究[J].
新疆石油地质, 2003, 24(4): 351–352.
LI Chuanliang, DU Wenbo. Study of stress and strain state in reservoir rocks[J]. Xinjiang Petroleum Geology, 2003, 24(4): 351–352. doi: 10.3969/j.issn.1001-3873.2003.04.-027 |
| [9] | 杨进良. 土力学[M]. 第3版. 北京: 中国水利水电出版社, 2006. |
| [10] | 张怀静. 土力学[M]. 北京: 机械工业出版社, 2011. |
| [11] | 李传亮. 油藏工程原理[M]. 第2版. 北京: 石油工业出版社, 2011. |
| [12] | 李颖川. 采油工程[M]. 第2版. 北京: 石油工业出版社, 2009. |
| [13] | 陈平. 钻井与完井工程[M]. 北京: 石油工业出版社, 2005. |
| [14] | 陈勉, 金衍, 张广清. 石油工程岩石力学基础[M]. 北京: 石油工业出版社, 2011. |
| [15] |
景锋, 边智华, 陈昊, 等. 不同岩性侧压系数分布规律的统计分析[J].
长江科学院院报, 2008, 25(4): 48–52.
JING Feng, BIAN Zhihua, CHEN Hao, et al. Statistical analysis of lateral pressure coefficient distribution law for different lithologys[J]. Journal of Yangtze River Scientific Research Institute, 2008, 25(4): 48–52. doi: 10.3969/-j.issn.1001-5485.2008.04.013 |
| [16] |
胡永全, 贾锁刚, 赵金洲, 等. 缝网压裂控制条件研究[J].
西南石油大学学报(自然科学版), 2013, 35(4): 126–132.
HU Yongquan, JIA Suogang, ZHAO Jinzhou, et al. Study on controlling conditions in network hydraulic fracturing[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2013, 35(4): 126–132. doi: 10.-3863/j.issn.1674-5086.2013.04.018 |
| [17] |
段伟刚, 卢聪, 张立会, 等. 基于精细三维地质模型的压裂裂缝参数优化[J].
西南石油大学学报(自然科学版), 2013, 35(5): 109–117.
DUAN Weigang, LU Cong, ZHANG Lihui, et al. Optimization design of integral fracturing parameters based on fine 3-D geology model[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2013, 35(5): 109–117. doi: 10.3863/j.issn.1674-5086.2013.05.-015 |
| [18] |
罗志锋, 赵立强, 刘平礼, 等. 裂缝性油藏压裂水平井生产动态模拟研究[J].
西南石油大学学报(自然科学版), 2011, 33(1): 88–94.
LUO Zhifeng, ZHAO Liqiang, LIU Pingli, et al. Simulation of horizontal wells production performance in fractured reservoir[J]. Journal of Southwest Petroleum University(Science & Technology Edition), 2011, 33(1): 88–94. doi: 10.3863/j.issn.1674-5086.2011.01.015 |
| [19] |
米强波, 伊向艺, 罗攀登, 等. 塔中超深致密砂岩油藏水平井分段压裂技术[J].
西南石油大学学报(自然科学版), 2015, 37(2): 114–118.
MI Qiangbo, YIN Xiangyi, LUO Pandeng, et al. Horizontal well staged fracturing technology of tight sandstone reservoirs with super depth in Tazhong Area[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2015, 37(2): 114–118. doi: 10.11885/j.issn.1674-5086.2013.01.05.02 |
| [20] | 楼一珊. 岩石力学与石油工程[M]. 北京: 石油工业出版社, 2006. |
 2017, Vol. 39
2017, Vol. 39


