研究资料表明,裂缝性储层的地质储量已经达到探明储量的50%[1],然而对裂缝性储层的建模和数值模拟一直是油气田开发领域的难点和热点。在裂缝性储层研究中,离散裂缝网络模型由于能更好地描述裂缝的复杂性和强烈的非均质性而被广泛运用[2-4]。该模型包括裂缝网络地质建模和渗流数值模拟两部分。目前,对于裂缝网络地质建模,基于对象的Monte-Carlo模拟方法常常被用来生成随机裂缝网络[5-10],但这种方法难以考虑裂缝之间的空间相关性,并且难以匹配条件数据[11];对于裂缝性储层离散裂缝网络模型的数值模拟,有限元法和有限体积法应用得比较广泛[12-14],但是无论采用何种方法,前人多在假想的裂缝网络的基础上研究渗流场,这使得研究的成果与真实的地质裂缝网络模型有较大的差异。
本文将广泛运用于沉积相建模的多点地质统计学方法引入到裂缝网络的建模中[15-19],由于该方法引入了训练图像,因此内在地考虑了模拟对象的空间关联性,使建立出的裂缝网络更加符合真实情况。然后在建立的裂缝模型基础之上,建立基于有限元的油水两相流动的数值模拟计算格式,研究了一注一采井的水驱油动态过程,有机地耦合了裂缝网络建模与渗流数值模拟。
1 FILTERSIM基本原理 1.1 FILTERSIM方法原理FILTERSIM方法主要包含3个部分:模板降维,模板分类和序贯模拟。但在这之前,需要用搜索模板扫描训练图像以构建数据模板数据库。
假设用一个像素为NDT×NDT的搜索模板去扫描一个像素为NTI×NTI的训练图像,那么将获得一个包含(NTI-NDT + 1)2个数据模板的模板数据库。在这个数据库中,每个数据模板t(u)可以由其中心点u和邻近点u +hj(j=1,2,...,N)来表示,它可以被视为一个N维向量,表示为
| $ \boldsymbol{t}(u) = \left[t(u + {h_1}), t(u + {h_2}), \cdots, t(u + {h_N})\right] $ | (1) |
一般来说,在模拟过程中,如果直接用上述的N维数据模板与数据事件作比较,将会产生巨大的计算量。因此,对数据模板降维处理显得很有必要。
FILTERSIM算法给出一组滤波器fk,(k = 1, 2, ..., F),将每一个滤波器作用在一个数据模板t(u)上,就会得到一个滤波分。这样,一组滤波器作用在一个数据模板上将会产生F个滤波分,表示为S(u),F = Sk(u),(k = 1, 2, ..., F),Sk(u)的计算公式为
| $ {S_k}(u) = \sum\limits_{j = 1}^N {{f_k}({h_j})} t(u + {h_j}), {\kern 20pt}k = 1, 2, ...F $ | (2) |
一般要求F个滤波分要能比较全面地描述这个数据模板的特征。此时,原来N维向量所表示的数据模板被现在的F维向量所表示
当每个数据模板被一个F维向量所表示的时候,它同时也可以被看做是F维空间的一个点,因此,对数据模板的分类其实就是对F维空间点的分类。交叉分类和聚类分析可以实现对数据模板分类,它们把具有相似特征的数据模板划分成一类。待分类完成之后,用式(3)求出该类的数据原型prot(hj),以便于在序贯模拟时和数据事件对比。
| $ {p_{{\rm{rot}}}}({h_j}) = \dfrac{1}{{{c}}}\sum\limits_{i = 1}^{{c}} {t(u_i + {h_j})}, {\kern 10pt}j = 1, 2, \cdots, N $ | (3) |
序贯模拟的实质是逐点模拟。将当前模拟点所在的数据事件dat(u)与每一类的数据原型prot(hj)对比,求出它们的距离D(u),将距离最近的那一类中的数据模板值赋给当前数据事件,作为该点的模拟值。距离公式为[20-21]
| $ D(u) = \sum\limits_{d = 1}^3 {\omega (d){\rm{Ave}}\left| {{d_{{\rm{at}}}}(u + {h_j}) - {p_{{\rm{rot}}}}({h_j})} \right|} $ | (4) |
条件数据包括原始硬数据,确定模拟值和不确定模拟值,它们的权重依次降低。由式(4)逐点模拟,直到所有的点都被访问,就完成了一次模拟。
1.2 FILTERSIM方法建立离散裂缝模型运用多点地质统计学建立裂缝网络模型不需要事先知道裂缝的诸如密度,产状等统计信息,因为裂缝的信息都包含在所选取的训练图像中。本文将文献[17]中伊朗西南部某区块的裂缝网络作为训练图像(图 1),它的像素为240×240,然后采用13×13像素的搜素模板扫描训练图像获得模板数据库,以存储裂缝特征和分布信息。对训练图像扫描结束后,采用文献[11]中给出的6个滤波分作为滤波器F,对数据模板降维,然后在训练图像上随机抽取1.5%的数据作为硬条件数据,设定权值ω(1) = 0.5,ω(2) = 0.3,ω(3) = 0.2,进行随机模拟。图 2给出了25次模拟结果的平均值。由它得到的裂缝网络作为后续的渗流数值模拟的研究载体。与训练图像中的裂缝网络相比,模拟结果较好地再现了裂缝网络的分布信息。
 |
| 图1 裂缝网络训练图像 Fig. 1 The training image of the fracture networks |
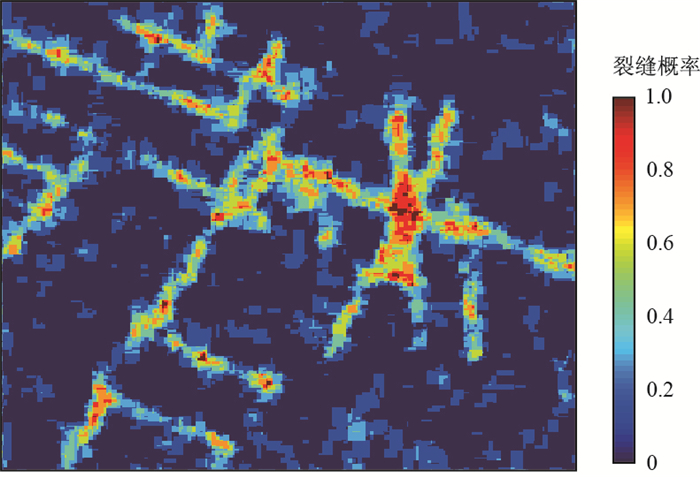 |
| 图2 25次模拟结果的平均值 Fig. 2 The E-types of 25 simulations |
为了便于模型的建立和求解,本文将裂缝视为一维实体,基岩区域视为二维平面。其他假设条件如下:
(1) 油藏中仅仅存在油水两相,且它们的流动均符合达西定律;
(2) 流体在基岩中为二维流动,考虑毛细管压力;裂缝中为一维流动,不考虑毛管力作用;
(3) 基岩与基岩中的流体皆为压缩系数为常数的微可压缩介质,裂缝与裂缝中的流体不可压缩;
(4)不考虑重力作用。
2.2 数学模型根据渗流力学中运动方程,状态方程和连续性方程,可以推导出基岩系统中的油水两相压力方程和水相饱和度方程
| $ -{\phi _{{\rm{m0}}}}{C_{{\rm{tm}}}}\dfrac{{\partial {p_{{\rm{wm}}}}}}{{\partial t}} + \nabla \cdot ({\lambda _{{\rm{om}}}}{p_{{\rm{cm}}}}) + \\ \nabla \cdot ({\lambda _{{\rm{tm}}}}\nabla {p_{{\rm{wm}}}}) + {Q_{{\rm{ovm}}}} +{Q_{{\rm{wvm}}}} - \delta q_{{\rm{mfT}}}^{\rm{*}} = 0 $ | (5) |
| $ - \nabla \cdot {\rm{(}}{{\rm{\lambda }}_{{\rm{wm}}}}\nabla {{{p}}_{{\rm{wm}}}}{\rm{)}} + {{\rm{\phi }}_{{\rm{m0}}}}\dfrac{{\partial {{{S}}_{{\rm{wm}}}}}}{{\partial {{t}}}} = {{{Q}}_{{\rm{wvm}}}} - \delta q_{{\rm{mfw}}}^{\rm{*}} $ | (6) |
裂缝系统中的压力控制方程和水相饱和度方程分别为
| $ \dfrac{\partial }{{\partial l}}\left({\lambda _{{\rm{tf}}}}\dfrac{{\partial {p_{{\rm{wf}}}}}}{{\partial l}}\right) + \delta q_{{\rm{mfT}}}^{\rm{*}} = 0 $ | (7) |
| $ - \dfrac{\partial }{{\partial l}}\left({\lambda _{{\rm{wf}}}}\dfrac{{\partial {p_{{\rm{wf}}}}}}{{\partial l}}\right) + {\phi _{{\rm{f0}}}}\dfrac{{\partial {S_{{\rm{wf}}}}}}{{\partial t}} = - \delta q_{{\rm{mfw}}}^{\rm{*}} $ | (8) |
补充方程为
| $ \begin{array}{*{20}{c}} {{\lambda _{ij}} = \dfrac{{{K_{{\rm{r}}ij}}{K_j}}}{{{\mu _i}}}}, {\kern 10pt}{(i = {\rm{o, w;}}j = {\rm{m, f}})} \end{array} $ | (9) |
| $ \begin{array}{*{20}{c}} {{\lambda _{{\rm{t}}j}} = {\lambda _{{\rm{o}}j}} + {\lambda _{{\rm{w}}j}}}, {\kern 10pt}{(j = {\rm{m, f}})} \end{array} $ | (10) |
| $ {C_{\rm{t}}} = {C_{{\rm{to}}}}{S_{\rm{o}}} + {C_{{\rm{tw}}}} + {S_{\rm{w}}} $ | (11) |
| $ {{C}_{\text{t}i}}={{C}_{\mathtt{ϕ}}}+{{C}_{i}}\left( i=\text{o},\text{w} \right) $ | (12) |
| $ q_{{\rm{mfT}}}^{\rm{*}} = q_{{\rm{mfo}}}^{\rm{*}} + q_{{\rm{mfw}}}^{\rm{*}} $ | (13) |
| $ \delta = \left\{ \begin{array}{l} \begin{array}{*{20}{c}} 1&{(\mbox{汇源处})} \end{array}\\ \begin{array}{*{20}{c}} 0&{(\mbox{非汇源处})} \end{array} \end{array} \right. $ | (14) |
将水相压力作为基本变量,对基岩采用三角形单元、对裂缝采用一维杆单元剖分。由于在裂缝和基岩的交界面处,水相压力相等,因此本文将裂缝系统的整体刚度矩阵和基岩系统的整体刚度矩阵叠加在一起,得到系统的总体刚度矩阵。这样处理的一个好处是使裂缝与基岩系统的窜流量互相抵消,不代入系统总体刚度矩阵中。基岩裂缝系统的整体刚度矩阵为
| $ \left({{\boldsymbol{K}}_{\rm{m}}} + {{\boldsymbol{K}}_{\rm{f}}}\right){{\boldsymbol{p}}_{\rm{w}}} + {\boldsymbol{C}}\dfrac{{\partial {{\boldsymbol{p}}_{\rm{w}}}}}{{\partial t}} = {\boldsymbol{F}} $ | (15) |
式(15)中,各项具体表达式为
| $ {{\boldsymbol{K}}_{\rm m}} = \sum {{{\boldsymbol{K}}_{{\rm{m, e}}}}} $ |
| $ {{\boldsymbol{K}}_{\rm{f}}} = \sum {{{\boldsymbol{K}}_{{\rm{f, e}}}}} $ |
| $ {\boldsymbol{C}} = \sum {{{\boldsymbol{C}}_{\rm{e}}}} $ |
| $ {\boldsymbol{F}} = \sum {{{\boldsymbol{F}}_{\rm{e}}}} $ |
| $ {{\boldsymbol{K}}_{{\text{m, e}}}} = \iint\limits_{{{\varOmega} _{\text{m}}}} {\left( {{\lambda _{{\text{tm}}x}}\dfrac{{\partial {\boldsymbol{N}}_{\text{m}}^{\text{T}}}}{{\partial x}}\dfrac{{\partial {{\boldsymbol{N}}_{\text{m}}}}}{{\partial x}} + {\lambda _{{\text{tm}}y}}\dfrac{{\partial {\boldsymbol{N}}_{\text{m}}^{\text{T}}}}{{\partial y}}\dfrac{{\partial {{\boldsymbol{N}}_{\text{m}}}}}{{\partial y}}} \right)}{\text{d}}{{\varOmega} _{\text{m}}} $ |
| $ {{\boldsymbol{K}}_{{\text{f, e}}}} = \int\limits_{{{\varOmega} _l}} {{\lambda _{{\text{tf}}}}\dfrac{{\partial {\boldsymbol{N}}_l^{\text{T}}}}{{\partial l}}\dfrac{{\partial {{\boldsymbol{N}}_l}}}{{\partial l}}} {\text{d}}l $ |
| $ {{\boldsymbol{C}}_{\text{e}}}=\iint\limits_{{{\mathit{\Omega} }_{\text{m}}}}{{{\phi }_{\text{m}0}}}{{\boldsymbol{C}}_{\text{tm}}}\boldsymbol{N}_{\text{m}}^{\text{T}}{{\boldsymbol{N}}_{\text{m}}}\text{d}{{\mathit{\Omega }}_{\text{m}}}; $ |
| $ {{\boldsymbol{F}}_{\text{e}}} = - \iint\limits_{{{\varOmega} _{\text{m}}}} {\left( {{\lambda _{{\text{t m}}x}}\dfrac{{\partial {\boldsymbol{N}}_{\text{m}}^{\text{T}}}}{{\partial x}}\dfrac{{\partial {p_{\text{c}}}}}{{\partial x}} + {\lambda _{{\text{tm}}y}}\dfrac{{\partial {\boldsymbol{N}}_{\text{m}}^{\text{T}}}}{{\partial y}}\dfrac{{\partial {p_{\text{c}}}}}{{\partial y}}} \right)}{\text{d}}{{\varOmega} _{\text{m}}} - \\{\kern 40pt}\iint\limits_{{{\varOmega} _{\text{m}}}} {\left( {{Q_{{\text{ovm}}}} + {Q_{{\text{wvm}}}}} \right){\boldsymbol{N}}_{\text{m}}^{\text{T}}{\text{d}}{{\varOmega} _{\text{m}}}} $ |
由于该渗流问题是非稳态渗流问题,即包含水相压力的时间导数项,故采用向后差分对时间离散。离散后的控制方程表达为
| $ \left( {{{\boldsymbol{K}}_{\text{m}}} + {{\boldsymbol{K}}_{\text{f}}}} \right){\boldsymbol{p}}_{\text{w}}^{(n + 1)} + {\boldsymbol{C}}\dfrac{{{\boldsymbol{p}}_{\text{w}}^{(n + 1)} - {\boldsymbol{p}}_{\text{w}}^{(n)}}}{{\Delta t}} = {\boldsymbol{F}} $ | (16) |
当求出基岩和裂缝中的水相压力分布后,分别根据式(6)和式(8)采用向后差分的格式可求出基岩和裂缝中的水相饱和度。差分格式为
| $ S_{{\text{wm}}}^{(n + 1)} = S_{{\text{wm}}}^{(n)} + \frac{{\Delta t}}{{{\phi _{{\text{m0}}}}}}\left[ {{Q_{{\text{wvm}}}} - \delta q_{{\text{mfw}}}^{\text{*}} + \nabla \cdot \left( {{\lambda _{{\text{wm}}}}\nabla {p_{{\text{wm}}}}} \right)} \right] $ | (17) |
| $ S_{{\text{wf}}}^{(n + 1)} = S_{{\text{wf}}}^{(n)} + \dfrac{{\Delta t}}{{{\phi _{{\text{f0}}}}}}(\dfrac{\partial }{{\partial l}}({\lambda _{{\text{wf}}}}\dfrac{{\partial {p_{{\text{wf}}}}}}{{\partial l}}) - \delta q_{{\text{mfw}}}^{\text{*}}) $ | (18) |
采用前文建立的离散裂缝网络模型作为研究对象,研究在该区域的油水两相流的饱和度变化规律以及采油井处的含水率变化规律。
基于裂缝网络模拟平均值图(图 2)描绘出裂缝网络得到离散裂缝网络模型(图 3)。对离散裂缝网络模型进行网格剖分后(图 4),采用有限元数值求解格式,研究油水两相饱和度的变化规律和采油井处的含水率上升规律。
 |
| 图3 图像处理后的离散裂缝网络模型 Fig. 3 Discrete fracture networks model after image processing |
 |
| 图4 网格剖分 Fig. 4 Mesh generation |
在油水两相流动数值模拟中,模拟模型的基本参数如下:研究区域尺寸96 m×90 m;在图 3左下角处为一口注水井,在右上角处为一口采油井;孔隙度为2%; x和y方向的基岩渗透率均为50 mD;裂缝渗透率为833 D;岩石,油相和水相的压缩系数分别为0.6×10-4,10×10-4和5×10-4 MPa-1;油相和水相的黏度分别为5和1 mPa·s;注水井和采油井的流体流速均为1.5×10-6 m/s。
对于采油井,给出了离散裂缝模型和均质模型情况下的含水率上升曲线(图 5)。从含水率上升曲线可以看出,由于裂缝网络的存在,注入水沿着裂缝网络窜进,过早地导致采油井见水。当采油井见水以后,两种模型的含水率上升表现较一致的变化趋势。
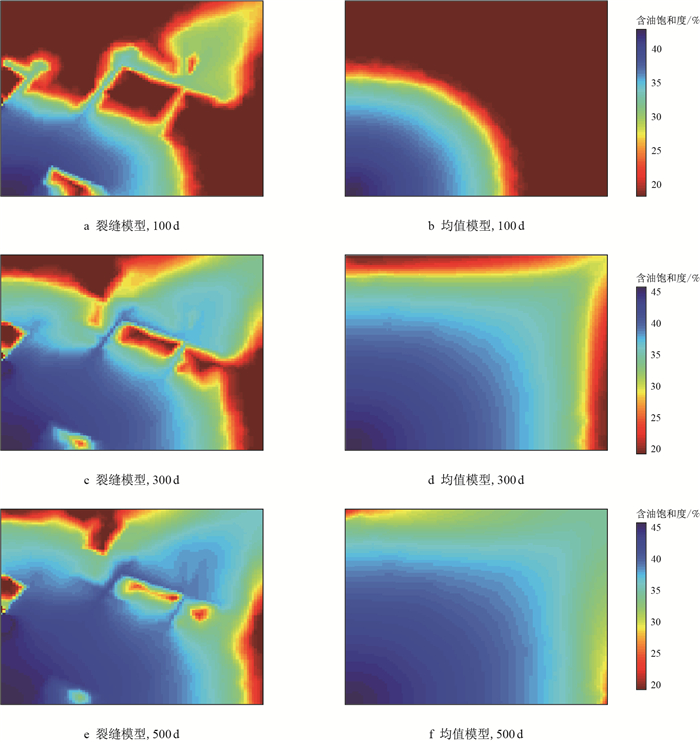 |
| 图5 采油井含水率曲线图 Fig. 5 The water cut of production well |
为了更好地观察注入水在裂缝网络中的窜流,给出了均质地层的模拟结果以作对比。图 6给出了在100,300和500 d时,离散裂缝模型和均质模型中油水两相的饱和度分布图。由图 6以看出,离散裂缝作为流体流动的控制通道,大量的注入水沿着裂缝流过,从而使其他非裂缝区域的波及时间大大延迟。在500 d的时候,均质模型中的所有区域几乎都已经被波及,而离散裂缝模型中还有少量的区域并没有被注入水扫过。
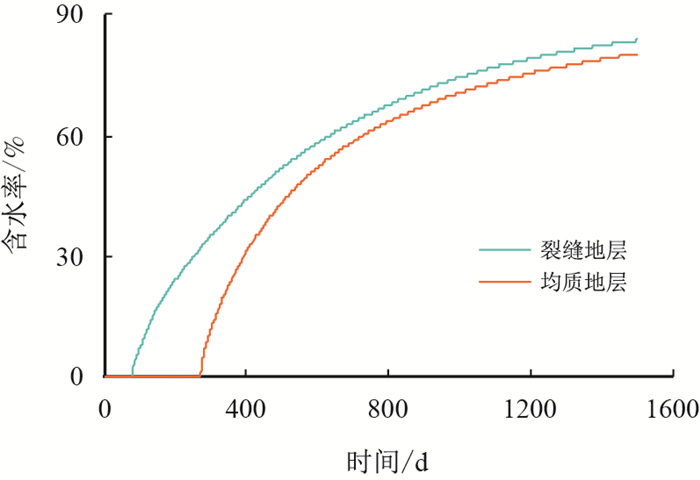 |
| 图6 离散裂缝模型和均质模型中的油相饱和度分布图 Fig. 6 Oil phase saturation distribution in discrete fracture model and homogeneity model |
(1) 将广泛运用于沉积相建模的多点地质统计学方法引入到离散裂缝网络建模中,能够较好地再现训练图像中裂缝分布信息,为油藏模拟提供了较可靠的裂缝网络模型。
(2) 耦合离散裂缝网络建模与有限元数值模拟,能够较好地模拟复杂裂缝网络非均质储层水驱动态。
符号说明
NDT-搜索模板像素;
NTI-训练模板像素;
t(u)-中心点为u的数据模板;
u + hj-中心点为u的邻近点;
N-数据模板维数;
fk-第k个滤波器;
F-滤波器数目;
Sk(u)-第k个滤波分;
prot(hj)-数据原型;
c-某一类中的数据模板个数;
dat(u)-中心点为u的数据事件;
D(u)-数据事件与数据原型的距离;
ω(d)-第d类条件数据的权值;
Ave-求平均值函数;
φm0-初始基质孔隙度,%;
Ctm-基质总压缩系数,MPa-1;
pwm-基质水相压力,MPa;
t-时间,s;
λom-基质油相流度,D/(mPa·s);
pcm-基质毛细管压力,MPa;
λtm-基质总流度,D/(mPa·s);
Qovm-基质油相汇源,s-1;
Qwvm-基质水相汇源,s-1;
δ-δ函数;
qmfT*-裂缝和基质之间总的窜流量,s-1;
λwm-基质水相流度,D/(mPa·s);
Swm-基质水相饱和度,无因次;
qmfw*-裂缝和基质之间水相窜流量,s-1;
λtf-裂缝总流度,D/(mPa·s);
pwf-裂缝水相压力,MPa;
l-沿裂缝走向的局部坐标,m;
λwf-裂缝水相流度,D/(mPa·s);
φf0-初始裂缝孔隙度,%;
Swf-裂缝水相饱和度,无因次;
Kr-相对渗透率,%;
K-渗透率,D;
Ct-油水两相总压缩系数,MPa-1;
Cto-油相总压缩系数,MPa-1;
So-油相饱和度,%;
Ctw-水相总压缩系数,MPa-1;
Sw-水相饱和度,%;
Cφ-孔隙度压缩系数,MPa-1;
Co-油相压缩系数,MPa-1;
Cw-水相压缩系数,MPa-1;
qmfo*-裂缝和基质之间油相窜流量,s-1;
Km-基质渗透率总体矩阵;
Kf-裂缝渗透率总体矩阵;
pw-压力总体矩阵;
C-压缩系数总体矩阵;
F-外力总体矩阵;
Km, e-基质渗透率单位矩阵;
Kf, e-裂缝渗透率单位矩阵;
Ce-压缩系数单位矩阵;
Fe-外力单位矩阵;
Ωm-基质内求解单位渗透率矩阵积分区域;
x, y-积分区域坐标系;
λtmx-x方向基质总流度,D/(mPa·s);
λtmy-y方向基质总流度,D/(mPa·s);
Nm-基质中形状函数矩阵;
Nl-裂缝中形状函数矩阵;
Ctm-基质中油水两相总压缩系数,MPa-1;
pc-毛细管压力,MPa;
pw(n+1)-n + 1时间步时的压力矩阵;
Δt-时间步长,s;
Swm(n+1)-n + 1时间步时的基质水相饱和度,%;
Swm(n)-n时间步时的基质水相饱和度,%;
Swf(n+1)-n + 1时间步时的裂缝水相饱和度,%;
Swf(n)-n时间步时的裂缝水相饱和度,%。
| [1] | BEYDOUN ZIAD R. Arabian plate oil and gas: Why so rich and so prolific?[J]. Episodes-Newsmagazine of the International Union of Geological Sciences, 1998, 21(2): 74–81. |
| [2] | DERSHOWITZ W S, LA POINTE P R, EIBEN T, et al. Integration of discrete fracture network methods with conventional simulator approaches[C]. SPE 62498, 2000. doi: 10.2118/62498-PA |
| [3] | KIM J G, DEO M D. Comparison of the performance of a discrete fracture multiphase model with those using conventional methods[C]. SPE 51928, 1999. doi: 10.2118/-51928-MS |
| [4] | OUENES A, HARTLEY L J. Integrated fractured reservoir modeling using both discrete and continuum approaches[C]. SPE 62939, 2000. doi: 10.2118/62939-MS |
| [5] | BEACHER G B, LANNEY N A, EINSTEIN H H. Statistical description of rock properties and sampling[C]. SPE 77-0400, 1977. |
| [6] | TRAN N H, CHEN Z, RAHMAN S S. Integrated conditional global optimization for discrete fracture network modeling[J]. Computers & Geosciences, 2006, 32: 17–27. doi: 10.1016/j.cageo.2005.03.019 |
| [7] | XU C, DOWD P. A new computer code for discrete fracture network modeling[J]. Computers & Geosciences, 2010, 36: 292–301. doi: 10.1016/j.cageo.2009.05.012 |
| [8] |
宋晓晨, 徐卫亚. 裂隙岩体渗流模拟的三维离散裂隙网络数值模型(Ⅰ):裂隙网络的随机生成[J].
岩石力学与工程学报, 2004, 23(12): 2015–2020.
SONG Xiaochen, XU Weiya. Numerical model of threedimensional discrete fracture network for seepage in fractured rocks(Ⅰ): generation of fracture network[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(12): 2015–2020. doi: 10.3321/j.issn:1000-6915.2004.-12.012 |
| [9] |
郑松青, 张宏方, 刘中春, 等. 裂缝性油藏离散裂缝网络模型[J].
大庆石油学院学报, 2011, 35(6): 49–54.
ZHENG Songqing, ZHANG Hongfang, LIU Zhongchun, et al. Discrete fracture network model for fractured reservoirs[J]. Journal of Daqing Petroleum Institute, 2011, 35(6): 49–54. doi: 10.3969/j.issn.2095-4107.2011.06.009 |
| [10] |
杨坚, 呂心瑞, 李江龙, 等. 裂缝性油藏离散裂缝网络随机生成及数值模拟[J].
油气地质与采收率, 2011, 18(6): 74–77.
YANG Jian, LÜ Xinrui, LI Jianglong, et al. Study on discrete fracture network random generation and numerical simulation of fractured reservoir[J]. Petroleum Geology and Recovery Efficiency, 2011, 18(6): 74–77. doi: 10.-3969/j.issn.1009-9603.2011.06.019 |
| [11] | ZHANG T F. Filter-based training pattern classification for spatial pattern simulation[D]. Stanford: Stanford University, 2006. |
| [12] |
姚军, 王子胜, 张允, 等. 天然裂缝性油藏的离散裂缝网络数值模拟方法[J].
石油学报, 2010, 31(2): 284–288.
YAO Jun, WANG Zisheng, ZHANG Yun, et al. Numerical simulation method of discrete fracture network for naturally fractured reservoirs[J]. Acta Petrolei Sinica, 2010, 31(2): 284–288. doi: 10.7623/syxb201002018 |
| [13] |
张芮菡. 基于有限元有限体积法的裂缝性油藏数值模拟研究[D]. 成都: 西南石油大学, 2014.
ZHANG Ruihan. Study on fractured reservoir numerical simulation based on infinite element-infinite volume method[D]. Chengdu: Southwest Petroleum University, 2014. |
| [14] |
吕心瑞, 姚军, 黄朝琴, 等. 基于有限体积法的离散裂缝模型两相流动模拟[J].
西南石油大学学报(自然科学版), 2012, 34(6): 123–130.
LÜ Xinrui, YAO Jun, HUANG Zhaoqin, et al. Study on discrete fracture model two-phase flow simulation based on finite volume method[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2012, 34(6): 123–130. doi: 10.3863/j.issn.1674-5086.2012.06.-018 |
| [15] |
孟欣然, 梁堰波, 孟宪海, 等. 基于FILTERSIM算法的油藏沉积微相模拟研究[J].
计算机工程设计, 2013, 34(2): 545–549.
MENG Xinran, LIANG Yanbo, MENG Xianhai, et al. Using FILTERSIM for reservoir faces simulation[J]. Computer Engineering and Design, 2013, 34(2): 545–549. doi: 10.16208/j.issn1000-7024.2013.02.041 |
| [16] |
尹艳树, 张昌民, 李玖勇, 等. 多点地质统计学研究进展与展望[J].
古地理学报, 2011, 13(2): 245–252.
YIN Yanshu, ZHANG Changmin, LI Jiuyong, et al. Progress and prospect of multiple-point geostatistics[J]. Journal of Palaeogrography, 2011, 13(2): 245–252. doi: 10.7605/gdlxb.2011.02.013 |
| [17] | Ahmadi R, Masihi M, Rasaei M R, et al. A sensitivity study of FILTERSIM algorithm when applied to DFN modeling[J]. J Petrol Explor Prod Technol, 2014, 4(2): 153–174. doi: 10.1007/s13202-014-0107-0 |
| [18] |
周金应, 桂碧雯, 林闻. 多点地质统计学在滨海相储层建模中的应用[J].
西南石油大学学报(自然科学版), 2010, 32(6): 70–73.
ZHOU Jinying, GUI Biwen, LIN Wen. Application of multi-point geostatistics in offshore reservoir modeling[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2010, 32(6): 70–73. doi: 10.3863/j.issn.1674-5086.2010.06.014 |
| [19] |
吴小军, 李晓梅, 谢丹, 等. 多点地质统计学方法在冲积扇构型建模中的应用[J].
岩性油气藏, 2015, 27(5): 87–91.
WU Xiaojun, LI Xiaomei, XIE Dan, et al. Application of multi-point geostatistics method to structure modeling of alluvial fan[J]. Lithologic Reservoirs, 2015, 27(5): 87–91. doi: 10.3969/j.issn.1673-8926.2015.05.015 |
| [20] | ZHANG T, DU Y, HUANG T, et al. Stochastic simulation of patterns using ISOMAP for dimensionality reduction of training images[J]. Computers & Geosciences, 2015, 79: 82–93. doi: 10.1016/j.cageo.2015.03.010 |
| [21] | WU J B, BOUCHER A, ZHANG T F. A SGeMS code for pattern simulation of continuous and categorical variables: FILTERSIM[J]. Computers & Geosciences, 2008, 34(12): 1863–1876. doi: 10.1016/j.cageo.2007.08.008 |
 2017, Vol. 39
2017, Vol. 39


