2. "煤燃烧"国家重点实验室·华中科技大学, 湖北 武汉 430074;
3. 中国石油勘探开发研究院廊坊分院, 河北 廊坊 065007;
4. 中国石化石油勘探开发研究院, 北京 海淀 100083
2. State Key Laboratory of Coal Combustion, Huazhong University of Science and Technology, Wuhan, Hubei 430074, China;
3. Langfang Branch of Research Institute of Petroleum Exploration & Development, Langfang, Hebei 065007, China;
4. Petroleum Exploration and Production Research Institute, Sinopec, Haidian, Beijing 100083, China
油藏的润湿性是描述油水相对渗透率和孔喉结构内部毛管力的一个重要特征参数,在低渗透率油藏注水开发过程中,毛管力由阻力变成动力以及注入流体自发渗析进入细小孔喉是降低驱替阻力和提高采收率的一个重要机理[1-3]。表面活性剂驱通过降低界面张力和改变润湿性机理成为低渗、特低渗油田解决注水井高压欠注问题的有效方法[4-6]。为了评价表面活性剂降压效果,一般进行不同浓度的表面活性剂驱降压实验,由于表面活性剂浓度不仅改变油水界面张力,而且也改变了流体/固体壁面的润湿性能,因此实验得到的降压率是界面张力和润湿性综合作用的结果。为了考虑润湿性对驱替压力的影响,部分学者通过化学药剂对玻璃毛细管进行预处理,通过改变化学剂浓度来达到玻璃毛细管的不同亲油性的要求,但是这种方法很难控制接触角连续变化。格子Boltzmann方法通过流体间作用参数控制流体间的界面张力,流体固体间作用参数控制流体的润湿性,能够有效避免实际实验中界面张力和润湿性相互耦合的现象,并能够量化模拟接触角变化,因此应用格子Boltzmann模型研究润湿性对水驱压力的影响是一种非常有效的方法。
目前研究多组分多相流体系统的格子Boltzmann方法主要包括颜色模型、伪势模型(Shan-Chen模型)、自由能模型、相场模型[7-8]。由于伪势模型具有自动追踪相界面、计算效果高、易编程和能够处理壁面润湿性等特点,在多相流领域得到了广泛关注和充分发展,如多孔介质渗流[9-10]、黏性指进[11-12]、润湿滞后[13-14]等,本文采用伪势模型。
1 多组分伪势模型Shan等[15-16]于1993年提出一种能直接描述粒子之间相互作用的LBM模型,该模型通过建立一种伪势来反映流体之间的相互作用,称为伪势模型。设流体包含S个不同组分,每个组分均有各自的分布函数,所有组分均采用单松弛碰撞,该模型第α(上下标α=w,i;分别代表水和油,以下均同)类组分演化方程为
| $ f_j^\alpha \left( {x + {e_j}\Delta t, t + \Delta t} \right) - f_j^\alpha \left( {x, t} \right) = \\{\kern 40pt} - \dfrac{{f_j^\alpha \left( {x, t} \right) - f_j^{{\rm{eq}}, \alpha }\left( {x, t} \right)}}{{{\tau _\alpha }}} $ | (1) |
式中:fjα (x, t)-第α类组分在位置x和时间t时刻对应的密度分布函数;
feq, a-第α类组分的平衡态分布函数;
ej-离散速度;
Δt-时间步长,这里取1.0;
τα-第α类组分的碰撞松弛时间,无因次;
下标j-离散速度方向,和选择的模型有关。
值得注意的是,在格子Boltzmann模拟计算中,变量均为格子单位,为了得到对应物理量纲,需要根据物理系统和格子系统无因次数相等进行转化,详细转换方法见参考文献[12],若无特殊说明,文中符号说明均默认为格子单位。
文中采用D2Q9模型,模型中
| $ {e_j} \!=\! \left\{ \begin{array}{l} c\left( {0, 0} \right), {\kern 10pt}j = 0\\ c\left[{\cos \left( {\dfrac{{j-1}}{2}\pi } \right), \sin \left( {\dfrac{{j-1}}{2}\pi } \right)} \right], \\{\kern 40pt}j = 1, ..., 4\\[5pt] \sqrt 2 c\left[{\cos \left( {\dfrac{{2j-1}}{4}\pi } \right), \sin \left( {\dfrac{{2j-1}}{4}\pi } \right)} \right], \\{\kern 40pt}j = 5, ..., 8 \end{array} \right. $ | (2) |
式中:c-速度,c = Δx=Δt;
Δx空间步长,这里取1.0。
每个流体组分的运动黏度和其松弛时间有关
| $ {v_{\alpha }} = c_{\rm{s}}^2\left( {{\tau _a} - \dfrac{1}{2}} \right)\Delta t $ | (3) |
式中:vα第α类组分的运动黏度;
cs2-流体声速,D2Q9模型中
第α类组分平衡态分布函数定义为
| $ f_j^{{\rm{eq}}, \alpha } = {\rho _\alpha }{w_j}\left[{1 + \dfrac{{{e_j}{\cdot}u_\alpha ^{{\rm{eq}}}}}{{c_{\rm{s}}^2}} + \dfrac{{{{\left( {{e_j}{\cdot}u_\alpha ^{{\rm{eq}}}} \right)}^2}}}{{2c_{\rm{s}}^4}}-\dfrac{{{{\left| {u_\alpha ^{{\rm{eq}}}} \right|}^2}}}{{2c_{\rm{s}}^2}}} \right] $ | (4) |
式中:ρα-第α类组分的密度;
wj-权重系数,无因次;
uαeq-第α类组分的平衡态速度。
伪势模型中假设流体粒子之间存在非局部的相互作用势函数,根据相互作用势,可得到第α类组分粒子受到周围粒子的作用力为
| $ {F^\alpha }\left( {x, t} \right) = - {\psi ^\alpha }\left( {x, t} \right)\mathop \Sigma \limits_{\overline \alpha \ne \alpha } {G_{\alpha \overline \alpha }}\mathop \Sigma \limits_j {w_j}{\cdot}\\{\kern 40pt}{\psi ^{\overline \alpha }}\left( {x + {e_j}\Delta t, t} \right){e_j}\Delta t $ | (5) |
式中:Fα-第α类组分粒子受到周围粒子的作用力;
Gαα-流体间相互作用强度;
ψα (x, t)-第α类组分的有效密度;
ψα (x, t)-非α类组分的有效密度。
Shan和Chen[16]推荐,ψ(ρ) = ρα0(1-e-ρα/ρα0) (ρα0-第α类组分的参考密度,本文计算过程中取为1)。
考虑流体-固体相互作用时
| $ F_{\rm s}^\alpha \left( {x, t} \right) = - {\psi ^\alpha }\left( {x, t} \right){G_{\alpha {\rm s}}}\Sigma {w_j}s\left( {x + {e_j}\Delta t} \right){e_j}\Delta t $ | (6) |
式中:Fsα-考虑流体-固体相互作用时,第α类组分粒子受到周围粒子的作用力;
s(x + ejΔt)-布尔函数,取值为0(流体节点)或1(固体节点);
Gαs-控制流体固体相互作用强度,一般在大于0时表示流体不润湿固体表面,小于0时表示流体润湿固体表面。
伪势模型通过平衡态速度uαeq来实现流体-流体、流体-固体及外力的影响
| $ u_\alpha ^{\rm eq} = u' + \dfrac{{{\tau _\alpha }\left( {{F^\alpha } + F_s^\alpha + G} \right)}}{{{\rho _\alpha }}} $ | (7) |
式中:u′-所有组分的平均速度;
G-体积力。
组分的平均速度u′定义为
| $ u' = \dfrac{{\sum\limits_\alpha {{\rho _\alpha }{u_\alpha }/{\tau _\alpha }} }}{{\sum\limits_\alpha {{\rho _\alpha }/{\tau _\alpha }} }} $ | (8) |
式中:uα-第α类组分粒子的速度。
每个组分的密度和速度,通过其密度分布函数的零阶矩和一阶矩得到
| $ \left\{ \begin{array}{l} {\rho _\alpha } = \sum\limits_j {f_j^\alpha } {\rm{ }}\\ {\rho _\alpha }{u_\alpha } = \sum\limits_j {f_j^\alpha {e_j}} \end{array} \right. $ | (9) |
混合流体速度为碰撞前后的速度的平均
| $ v = \dfrac{{\sum\nolimits_\alpha {{\rho _\alpha }{u_\alpha }} }}{{\sum\nolimits_\alpha {{\rho _\alpha }} }} + \dfrac{{\sum\nolimits_\alpha {\left( {{F^\alpha } + F_{\rm s}^\alpha + G} \right)} }}{{2\sum\nolimits_\alpha {{\rho _\alpha }} }} $ | (10) |
混合流体压力为
| $ p\left( x \right) \!=\! c_{\rm{s}}^2\sum\limits_\alpha {{\rho _{\alpha }}\left( x \right)} \! + \! \dfrac{{c_{\rm{s}}^2\Delta t}}{2}\sum\limits_{\alpha, \overline \alpha } {{G_{\alpha \overline \alpha }}{\psi _\alpha }\left( x \right){\psi _{\overline \alpha }}\left( x \right)} $ | (11) |
Laplace定律通常作为验证多相流计算模型算法准确性的标准。在界面张力作用下,液滴内部压强会高于液滴外部压强,在平衡状态下,液滴内外压强差与液滴半径的倒数呈线性关系
| $ {p_{{\rm{in}}}} - {p_{{\rm{out}}}} = \dfrac{\sigma }{R} $ | (12) |
式中:pin,pout-液滴内部和外部的压力;
σ-界面张力;
R-液滴的平衡半径。
取计算区域大小为80×80,这里均默认使用格子单位。内部流体记为相1,外部流体记为相2,计算参数为:相1流体密度0.86, 相2流体密度1.0;相间互作用强度= 3.0,碰撞松弛时间相1为1.1,相2为1.0;分别计算4种不同平衡半径(10,14,16,18) 条件下压强差与半径关系,计算结果如图 1所示。由图 1可见,压差和1/R具有很好的线性关系,直线斜率即为界面张力。
 |
| 图1 Laplace定律验证 Fig. 1 Simulation of Laplace law |
为了模拟不同数量级界面张力,改变相间相互作用强度大小,分别取3、4、5、6、7,其他参数保持不变,重复计算,结果如图 2所示。图 2表明,界面面张力和相间相互作用强度具有较好的线性关系。
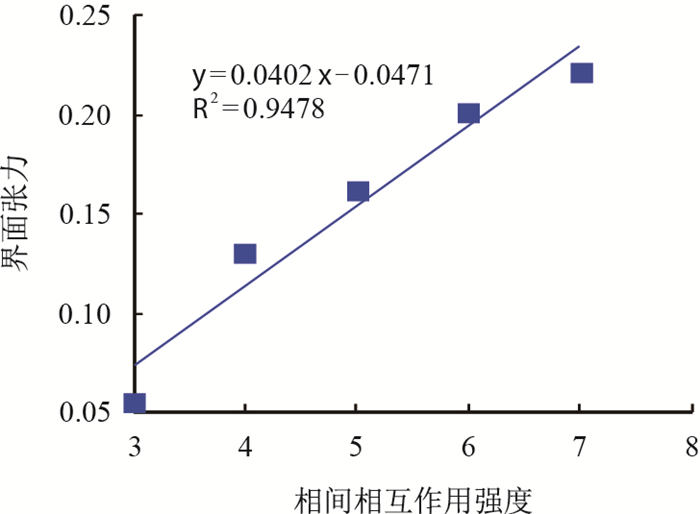 |
| 图2 界面张力和相间相互作用强度关系 Fig. 2 The curve of interfacial tension with Interphase interaction strength |
润湿性的强弱一般由接触角大小表征,接触角大于90°表明流体不润湿固体表面,接触角小于90°表明流体润湿固体表面。
在Shan-Chen模型中,通过控制固体流体之间作用参数Gαs来改变接触角。接触角计算主要有公式法和几何法[17-18],公式法是根据杨氏方程计算接触角,黄海波[17]应用流体流体间作用系数和密度参数代替杨氏方程,得出直接计算接触角的方法
| $ \cos {\theta _1} = \dfrac{{{\sigma _{{\rm{s}}2}} - {\sigma _{{\rm{s}}1}}}}{{{\sigma _{12}}}} = \dfrac{{{G_{{\rm{s}}, 2}} - {G_{{\rm{s}}, 1}}}}{{{G_{12}}\dfrac{{{\rho _1} - {\rho _2}}}{2}}} $ | (13) |
式中:θ1-相1的接触角,(°);
σs2-相2和固体的界面张力;
σs1-相1和固体的界面张力;
σ12-相1和相2的界面张力;
Gs, 2-相2和固体的相互作用强度;
Gs, 1-相1和固体的相互作用强度;
G12-相1和相2相互作用强度;
ρ1-平衡态时主要组分(如水)的密度;
ρ2-平衡态时溶解组分(如油)密度。
几何法接触角示意图如图 3所示(θ2-相2的接触角,(°);a-液滴的高度;b-液滴在壁面上铺展长度),由图 3,有
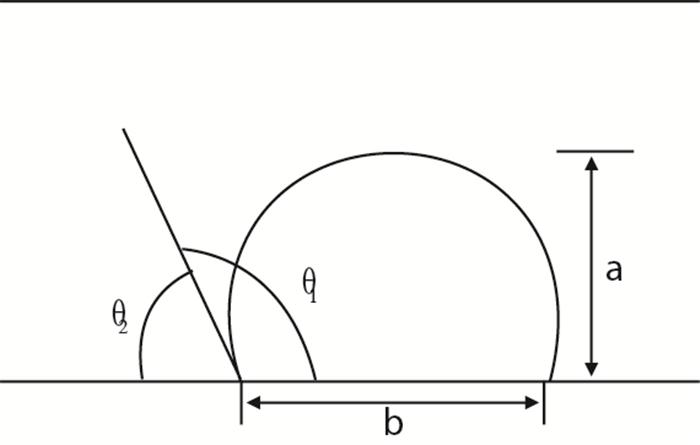 |
| 图3 接触角示意图 Fig. 3 Contact angle diagram |
| $ \tan \theta_1 = \dfrac{b}{{2\left( {R - a} \right)}} $ | (14) |
| $ R = \dfrac{{4{a^2} + {b^2}}}{{8a}} $ | (15) |
模拟过程中,计算区域为50×100,紧贴固体壁面为半径18的半圆液滴,保持其他参数不变,改变流体和固体壁面作用强度,可以得到不同的接触角,测量接触角结果如图 4所示。
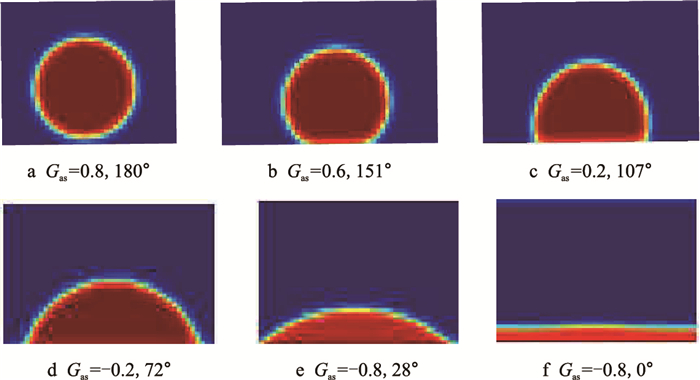 |
| 图4 不同流体-固体相互作用强度下的接触角 Fig. 4 Contact angle at different fluid-solid interaction intensity |
随着流体和固体相互作用强度减小,接触角减小,接触角和固体-流体间作用参数具有较好的线性关系,结果如图 5所示。
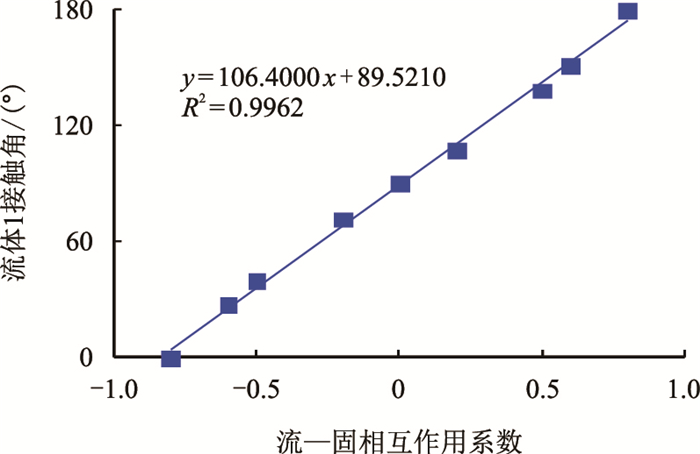 |
| 图5 接触角和流-固相互作用强度的关系 Fig. 5 The curve of contact angle and fluid/solid interaction intensity |
在油气藏开发过程中,非润湿流体驱替润湿性流体是一种常见现象,一般润湿流体在孔隙表面流动,记为相1,而非润湿性流体在孔隙中间流动,记为相2,如图 6所示。
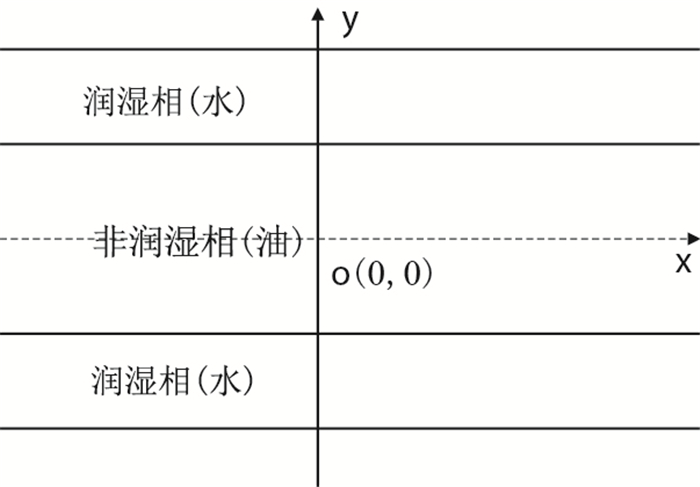 |
| 图6 平板并流示意图 Fig. 6 Co-flowing diagram |
假设润湿性流体在a < |y| < b,非润湿性流体在0 < |y| < a,则润湿性流体饱和度为
| $ {K_{11}} = S_{{\rm{nw}}}^3 + 3MS_{{\rm{nw}}}^3 - 3MS_{{\rm{nw}}}^3 $ | (16) |
| $ {K_{22}} = {\left( {1 - {S_{{\rm{nw}}}}} \right)^3} $ | (17) |
式中:K11-非润湿相的相对渗透率,%;
Snw-非润湿性流体饱和度,%;
M-润湿流体和非润湿流体黏度比;
K22-润湿相的相对渗透率,%。
渗透率不仅是饱和度的函数,也是黏度比函数。为了确定相对渗透率,执行两次独立实验,第一次实验是润湿流体受沿流动方向的体积力不等于0,非润湿流体受沿流动方向的体积力等于0,通过计算得到K22;第二实验是润湿流体受沿流动方向的体积力等于0,非润湿流体受沿流动方向的体积力不等于0,通过计算得到K11。
模拟中,计算区域为4×200,上下边界执行标准反弹,左右周期边界,流体通过体积力驱动,计算参数:体积力大小为5 × 10-5;油水密度为1.0(对模型进行验证时的取值),油水相碰撞松弛时间均为1:0,黏度比1.0,油水两相的相间间互作用强度为3.0,润湿相和固体间相互作用强度为0.2。模拟结果见图 7,LBM模拟结果与解析解吻合较好。
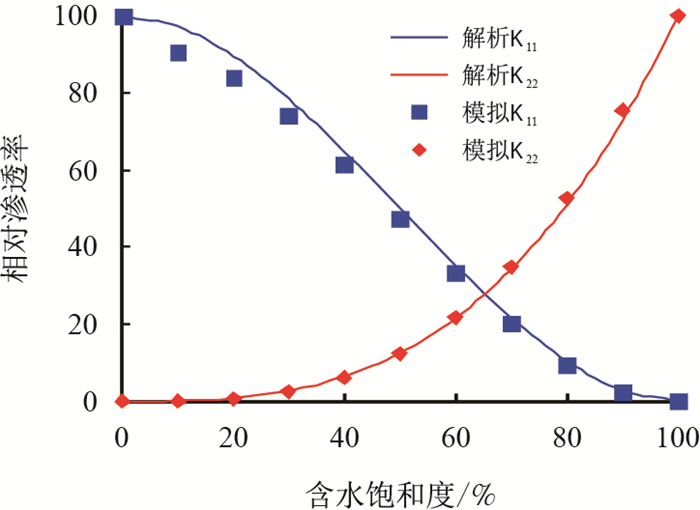 |
| 图7 相对渗透随润湿相饱和度变化曲线 Fig. 7 The curve of Relative permeability and wetting phase saturation |
水驱油过程主要涉及雷诺数,毛管数及邦德数等无因次量,在模拟计算过程中,一般不需要所有无量纲数和物理模型无量纲数相等,保证主要的无量纲数相等,就能够得到相似的规律,在毛细管水驱油过程中,毛管数,邦德数起到重要作用,因此重点考察了毛管数,邦德数和黏度比条件下润湿性对驱替压力的影响。模拟计算网格大小为40×80,左边界为驱替流体(注入水),设置为恒速边界,入口速度为0.05,右边界为定压边界,上下边界为固体,采用标准反弹边界,速度和压力边界参考Zou-He提出的边界格式[21]。模型中ρw = 1.0,ρi = 0.86,松弛时间τw = 1.0,τi = 1.1。忽略同组分流体间的相互作用,改变不同组分流体间作用系数和流固体间作用系数,分别模拟界面张力和润湿性对压力的影响,计算模型对应的物理模型参数为:水密度1.00 g/cm3;油密度0.86 g/cm3;水黏度1.0 mPa·s;油黏度1.0 mPa·s;油水界面张力0.12 mN/m;毛细管直径0.665 mm;毛细管长度1.33 mm;驱替流速0.018 m/s;出口压力1.0×102 kPa。
模拟中平板表面为理想光滑表面,而实际油藏岩石表面都存在一定的粗糙度,为了更接近真实情况,通过设置梯度微结构代替光滑表面,梯度微结构[22-23]如图 8所示(a梯度结构的宽度;d梯度结构的间距,h梯度结构的高度),模拟中设置h = 2,a = 1,d = 3,最终模拟示意图如图 9所示(Uo-入口速度)。
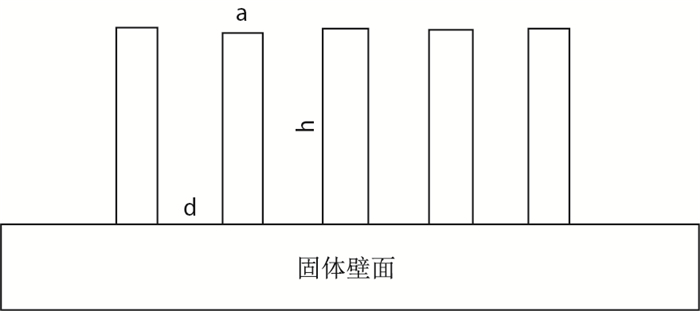 |
| 图8 梯度微结构壁面 Fig. 8 The gradient microstructure wall |
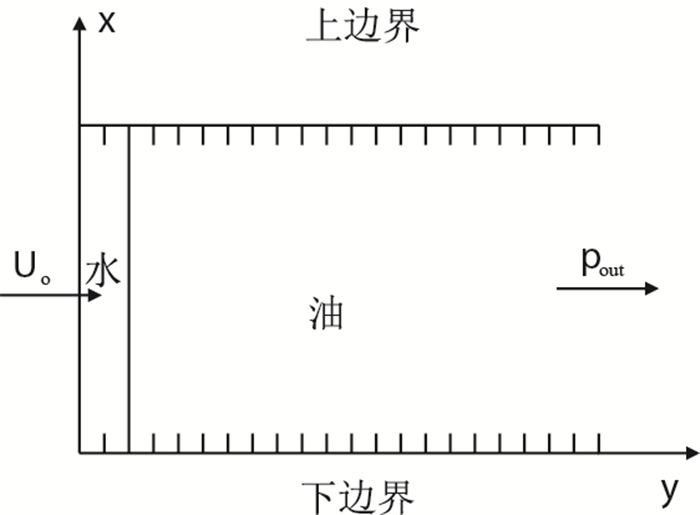 |
| 图9 模拟体系示意图 Fig. 9 Simulation system schematic diagram |
为了对比不同条件下改变润湿性的降压效果,定义降压率为
| $ R_{\rm p} = \dfrac{\Delta p_{\rm max}-\Delta p_{\rm w} }{\Delta p_{\rm max}}\times 100\% $ | (18) |
式中:Rp-压降率,%;
Δpmax-最大压差;
Δpw-某润湿条件下的压差。
当计算区域内速度误差小于10-5时,结束计算。
3.1 不同毛管数下润湿性对压力的影响毛管数表征黏滞力与界面张力的相对大小,计算公式为
| $ {N_{\rm{c}}} = \dfrac{{{\mu _{\rm{w}}}{u_{\rm{w}}}}}{\sigma } $ | (19) |
式中:Nc-毛管数;
μw-黏度;
uw-速度。
通过改变驱替流体的注入速度可以改变毛管数的大小,在给定的毛管数的条件下,改变接触角,统计出入口压差变化。驱替流体注入速度为0.005,0.050,0.010,0.100,分别对应的毛管数为0.015,0.030,0.150,0.300,计算结果如图 10所示。结果表明,毛管数越小,亲水性越强,降压效果越好。
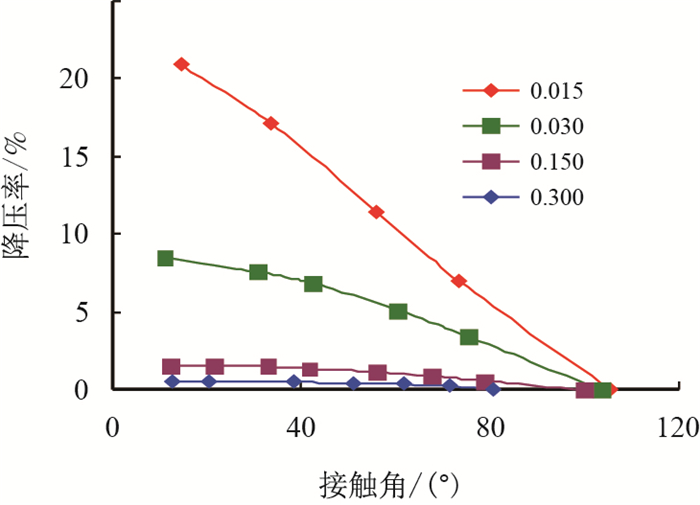 |
| 图10 不同毛管数条件下降压率随接触角变化 Fig. 10 The curve of pressure drop rates and contact angles at different capillary numbers |
邦德数是表征界面张力的影响确定的一个无因次量,计算公式为
| $ B{\rm{o}} = \dfrac{{\left( {{\rho _{\rm{w}}} - {\rho _{\rm{i}}}} \right){\rm{g}}{m^2}}}{\sigma } $ | (20) |
式中:Bo-邦德数,无因次;
g-重力加速度;
m-二维平板的宽度。
通过改变二维平板宽度,可以模拟不同的邦德数,在给定的邦德数条件下,改变接触角,统计出入口压差变化。模拟过程中,加速度固定为10-6, 二维平板宽度分别为10,20,30,40,对应的邦德数分别为2.53 × 10-5,1.01 × 10-4,2.27 × 10-4,4.04 × 10-4。模拟结果见图 11。
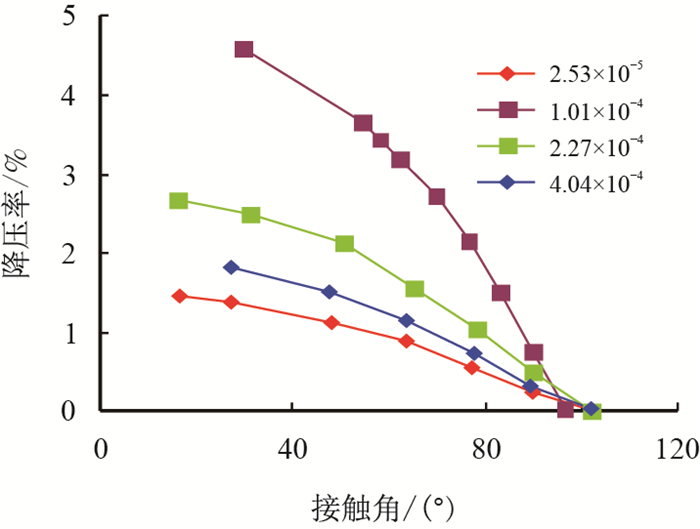 |
| 图11 不同邦德数条件下降压率随接触角变化 Fig. 11 The curve of pressure drop rates and contact angles at different bond numbers |
图 11表明,邦德数越小,亲水性越强,降压效果越好,当接触角小于40°时,继续降低接触角,降压效果明显减弱。
3.3 不同黏度比条件下润湿性对压力的影响由黏度比
 |
| 图12 不同黏度条件下降压率随接触角的变化 Fig. 12 The curve of pressure drop rates and contact angles at different viscosity ratios |
为了对比界面张力和润湿性分别对降压效果的影响,模拟过程中分别令,对应的界面张力为0.0554,0.1308,0.162。在同一种界面张力条件下,分别改变接触角,模拟结果见13、图 14。
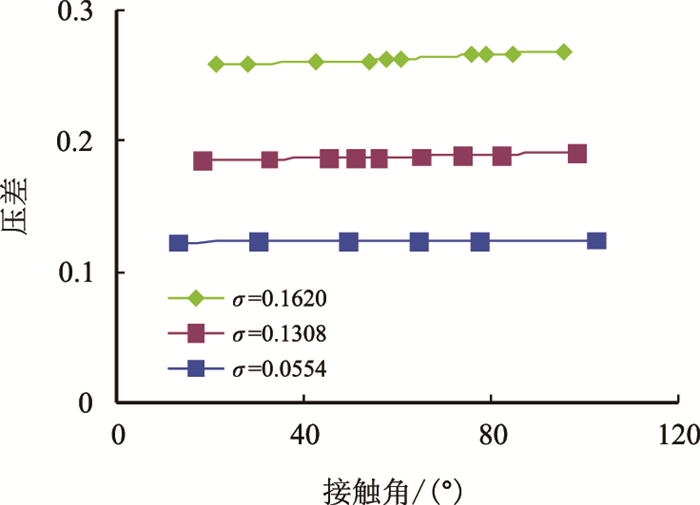 |
| 图13 不同界面张力条件下压差随接触角变化 Fig. 13 The curve of pressure and contact angles at different interfacial tensions |
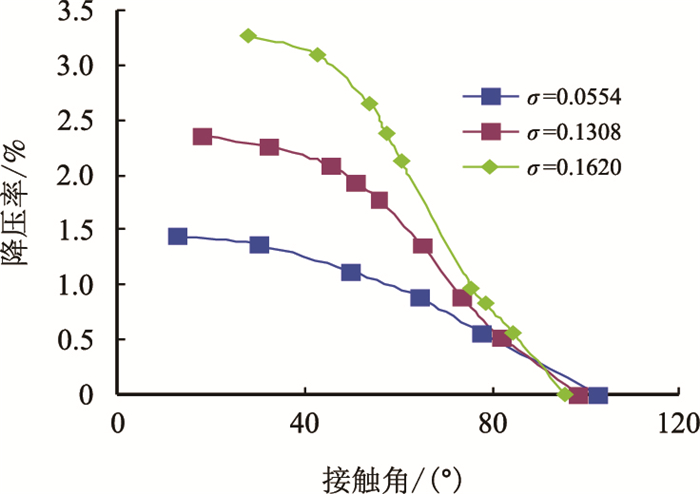 |
| 图14 不同界面张力条件下降压率随接触角变化 Fig. 14 The curve of pressure drop rates and contact angles at different interfacial tensions |
从图 13可以看出,降低界面张力能够明显降低注水压力,当界面张力由0.162 0降低到0.055 4时,降压率达到53.5%,而改变润湿性后,降压率均在5%内。
图 14表明,界面张力越大(毛管数越小),亲水性越强,降压效果越好,与前文所得的结论一致;当接触角小于40 °时,继续降低接触角,降压效果明显减弱。
4 油水界面特征 4.1 单通道内流体驱替润湿性决定孔道中毛管力的方向,亲水毛管中,油水界面为凹面,毛管力与注水压力方向一致,毛管力为动力;亲油毛管中,油水界面为凸面,毛管力为阻力。为了研究界面形状变化,改变接触角,计算至1 000步时,截取界面形状,结果如图 15所示。
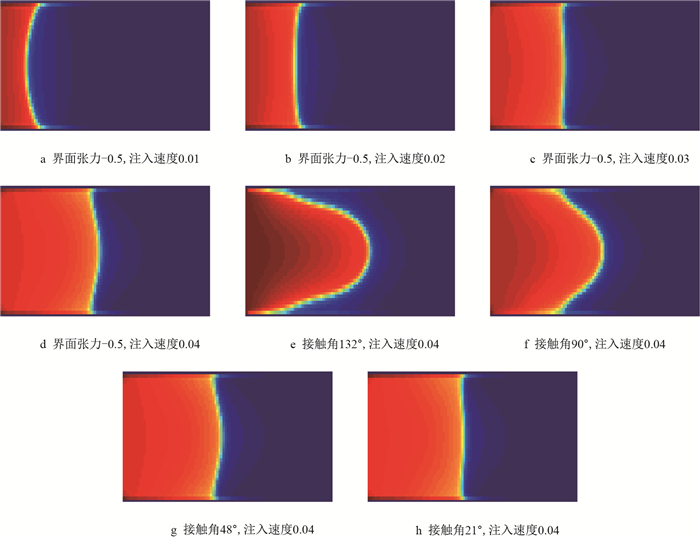 |
| 图15 界面形状 Fig. 15 Cross-section shape |
图 15a~图 15d是保持界面张力和接触角不变条件下(流体间作用强度为3.0,流固间作用强度为0.5),不同注入速度(或毛管数)对应的界面形状。随着驱替速度的增加,毛管数增加,凹界面逐渐变成凸界面,毛管力由动力变成阻力。保持注入速度和界面张力不变(流体间作用强度为3.0,入口速度为0.04),改变润湿性,降低接触角,结果如图 15e~图 15h所示。图 15e~图 15h表明,接触角越大,油水界面越凸起,黏性指进现象被强化,接触角越小,油水界面越平坦,黏性指进现象被抑制。尽管固体壁面由亲油变成亲水,但是毛管力并没有由阻力变成动力,界面形状仍为凸界面,这是由于水驱速度过大的造成的。为了能够使毛管力由阻力变成动力,驱替速度不宜过大,但是驱替速度过小,油藏开发经济效益不佳,因此对于低渗、特低透油藏孔隙喉道细小,应注重改变润湿性,保持适当的速度驱替,有利于毛细管阻力转变成驱动动力,进入更细小喉道,提高采收率;对于中高渗透油藏,改变润湿性的同时可以适当提高注入速度,提高经济效益。
4.2 多孔介质内流体驱替流体润湿性不仅影响单通道驱替界面变化,而且对固体界面更加复杂的多孔介质的流体流动过程及分布也具有重要影响,图 16为一多孔介质,计算区域大小为160×150,油水间作用强度为3.0,τw = 1,τi = 1.1。分别设置亲水表面流固作用强度为–0.5,疏水表面流固作用强度为0.5,得到不同时刻对应的驱替状态如图 17所示。
 |
| 图16 多孔介质 Fig. 16 Porous medium |
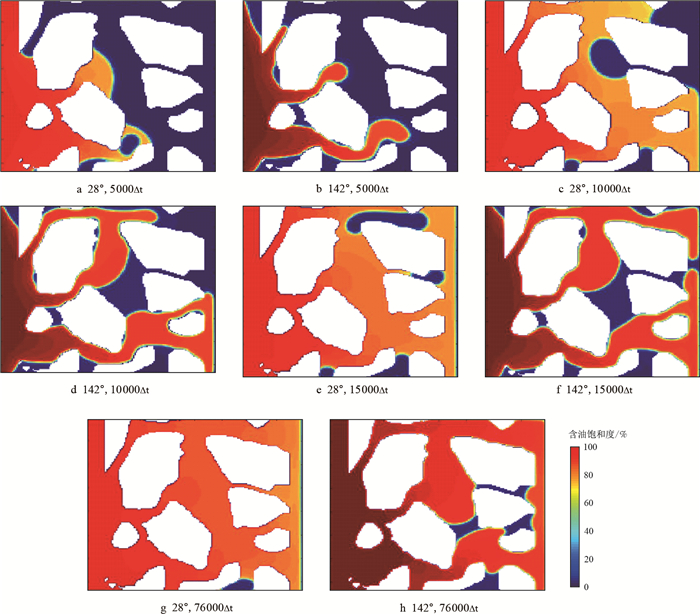 |
| 图17 不同时刻多孔介质内驱替状态 Fig. 17 The glance of motion morphology at different 08:52:47 |
从图 17可以看出,亲水表面情况下,黏性指进现象减弱,同时流体能够进入更细的喉道,驱替面积更大,疏水表面情况下,流体指进现象明显,并且流体不容易进入更细喉道,导致被驱替流体滞留在孔隙中,这从微观机理上说明了改变润湿性能够提高驱油效率。通过统计出入口压差发现,当多孔介质润湿性由亲油条件转变亲水条件时,降压率达到20.31%,与第3部分单通道驱替对比发现,在多孔介质中将多孔介质壁面由亲油改变成亲水,降压效果比单通道降压效果更加明显。
5 结论(1) Shan-Chen伪势模型能够模拟水驱油过程,通过调整流流/固之间作用参数,能够模拟油水两相分离、黏性指进现象及润湿性转变现象。
(2) 毛管数越小,邦德数越小,界面张力越大,油水黏度比越大,接触角越小,降压率越大,降压效果越明显。接触角存在一个最佳范围,超过此范围继续降低接触角,降压率不明显增加。
(3) 降低界面张力能够显著降低压力,界面张力越大,改变润湿性对降压效果影响越明显;对于储层多孔介质,驱替压差受润湿性影响比单通道更加显著。
(4) 从界面形状可以看出,接触角大于90°时,黏性指进现象被强化,接触角小于90°时,黏性指进现象被抑制。当多孔介质由弱亲油转变为亲水时,驱替流体能够进入更细小的孔隙喉道,增加驱油面积,提高采收率。
| [1] |
王所良, 汪小宇, 黄超, 等. 改变低渗透油藏润湿性提高采收率技术研究进展[J].
断块油气田, 2012, 19(4): 472–475.
WANG Suoliang, WANG Xiaoyu, HUANG Chao, et al. Research progress of EOR with alteration of rock wettability in low-permeability reservoir[J]. Faulti-Block Oil & Gas Field, 2012, 19(4): 472–475. doi: 10.6056/-dkyqt201204016 |
| [2] |
彭钰, 康毅力. 润湿性及其演变对油藏采收率的影响[J].
油气地质与采收率, 2008, 15(1): 72–76.
PENG Jue, KANG Yili. Effects of wettability and its evolution on oil reservoir recovery[J]. PGRE, 2008, 15(1): 72–76. doi: 10.3969/j.issn.1009-9603.2008.01.022 |
| [3] |
王斐, 岳湘安, 王雯舰, 等. 润湿性对模拟原油微尺度流动和渗流的影响[J].
石油学报, 2010, 31(2): 302–305.
WANG Fei, YUE Xiang'an, WANG Wenjiang, et al. Influence of wettability on micro-scale flow and seepage characteristics of simulated crude oil[J]. Acta Petrolei Sinica, 2010, 31(2): 302–305. doi: 10.7623/syxb201002022 |
| [4] |
张朔, 蒋官澄, 郭海涛, 等. 表面活性剂降压增注机理及其镇北油田应用[J].
特种油气藏, 2013, 20(2): 111–114.
ZHANG Shuo, JIANG Guancheng, GUO Haitao, et al. Mechanism of reducing injection pressure and increasing injection by surfactant and its application in zhenbei oilfield[J]. Special Oil & Gas Reservoirs, 2013, 20(2): 111–114. doi: 10.3969/j.issn.1006-6535.2013.02.028 |
| [5] |
李瑞冬, 王冬梅, 张子玉, 等. 复合表面活性剂提高低渗透油田采收率研究[J].
油田化学, 2013, 30(2): 221–225.
LI Ruidong, WANG Dongmei, ZHANG Ziyu, et al. Studies on surfactant enhanced oil recovery for low permeability oilfield[J]. Oilfield Chemistry, 2013, 30(2): 221–225. |
| [6] |
李瑞东, 葛际江, 李光辉, 等. 低渗透油田超低界面张力表面活性剂降压增注研究[J].
石油与天然气化工, 2012, 41(4): 415–418.
LI Ruidong, GE Jijiang, LI Guanghui, et al. Research on depressurization and augmented injection for ultra low interfacial tension surfactants in low permeability reservoirs[J]. Chemical Engineering of Oil & Gas, 2012, 41(4): 415–418. doi: 10.3969/j.issn.1007-3426.2012.04.015 |
| [7] |
付宇航, 赵述芳, 王文坦. 多相/多组分LBM模型及其在微流体领域的应用[J].
化工学报, 2014, 65(7): 2535–2541.
FU Yuhang, ZHAO Shufang, WANG Wentan. Application of lattice Boltzmann method for simulation of multiphase/multicomponent flow in microfluidics[J]. CIESC Journal, 2014, 65(7): 2535–2541. doi: 10.3969/j.issn.0438-1157.2014.07.015 |
| [8] |
郭照立, 郑楚光.
格子Boltzmann方法的原理及应用[M]. 北京: 科学出版社, 2008.
GUO Zhaoli, ZHENG Chuguang. Theory and applications of lattice Boltzmann method[M]. Beijing: Science Press, 2008. |
| [9] |
柴振华, 郭照立, 施保昌. 利用多松弛格子Boltzmann方法预测多孔介质的渗透率[J].
工程热物理学报, 2010, 31(1): 107–109.
CHAI Zhenhua, GUO Zhaoli, SHI Baochang. Prediction of permeability in porous media with multi-relaxationtime lattice Boltzmann method[J]. Journal of Engineering Thermophysics, 2010, 31(1): 107–109. |
| [10] | HUANG Haibo, LI Zhitao, LIU Shuaishuai, et al. Shanand-chen-type multiphase lattice boltzmann study of viscous coupling effects for two-phase flow in porous media[J]. International Journal for Numeircal Methods in Fluids, 2008, 61(3): 341–354. doi: 10.1002/fld.1972 |
| [11] |
李维仲, 董波, 宋永臣. 水平通道内黏性指进现象LBM模拟[J].
大连理工大学学报, 2012, 52(3): 343–348.
LI Weizhong, DONG Bo, SONG Yongchen. LBM simulation of viscous fingering phenomenon in a horizontal channel[J]. Journal of Dalian University of Technology, 2012, 52(3): 343–348. doi: 10.7511/dllgxb201203006 |
| [12] |
董波. 非混相驱替过程的格子Boltzmann模拟[D]. 大连: 大连理工大学, 2011.
DONG Bo. Lattice Boltzmann simulation of immiscible displacement[D]. Dalian: Dalian University of Technology, 2011. |
| [13] | WANG L, HUANG H B, LU X Y. Scheme for contact angle and its hysteresis in a multiphase lattice Boltzmann method[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2013, 87(1): 013301. doi: 10.1103/-PhysRevE.87.013301 |
| [14] | AHRENHOLZ B, TÖLKE J, LEHMANN P, et al. Prediction of capillary hysteresis in a porous material using lattice-Boltzmann methods and comparison to experimental data and a morphological pore network model[J]. Advances in Water Resources, 2008, 31(9): 1151–1173. doi: 10.1016/j.advwatres.2008.03.009 |
| [15] | SHAN X, CHEN H. Lattice Boltzmann model for simulating flows with multiple phases and components[J]. Physical Review E, 1993, 47(3): 1815–1819. doi: 10.1103/Phys-RevE.47.1815 |
| [16] | SHAN X, DOOLEN G. Multicomponent lattice-Boltzmann model with interparticle interaction[J]. Journal of Statistical Physics, 1995, 81(1): 379–393. doi: 10.1007/BF-02179985 |
| [17] | HUANG H, THORNE JR D T, SCHAAP M G, et al. Proposed approximation for contact angles in Shan-and-Chen-type multicomponent multiphase lattice Boltzmann models[J]. Physical Review E, 2007, 76(6): 066701. doi: 10.1103/PhysRevE.76.066701 |
| [18] | SCHMIESCHEK S, HARTING J. Contact angle determination in multicomponent lattice Boltzmann simulations[J]. Communications in Computational Physics, 2011, 9(5): 1165–1178. doi: 10.4208/cicp.201009.271010s |
| [19] | HUANG H, LU X. Relative permeabilities and coupling effects in steady-state gas-liquid flow in porous media: A lattice Boltzmann study[J]. Physics of Fluids, 2009, 21(9): 092104. doi: 10.1063/1.3225144 |
| [20] | LANGAAS K Å, PAPATZACOS P. Numerical investigations of the steady state relative permeability of a simplified porous medium[J]. Transport in Porous Media, 2001, 45(2): 241–266. doi: 10.1023/A:1012002002804 |
| [21] | ZOU Q, HE X. On pressure and velocity boundary conditions for the lattice Boltzmann BGK model[J]. Physics of Fluids, 1997, 9(6): 1591–1598. doi: 10.1063/1.869307 |
| [22] |
林林, 袁儒强, 张欣欣, 等. 液滴在梯度微结构表面上铺展动力学分析[J].
物理学报, 2015, 64(15): 1–7.
LIN Lin, YUAN Ruqiang, ZHANG Xinxin, et al. Spreading dynamics of liquid droplet on gradient microstructured surfaces[J]. Acta Physica Sinica, 2015, 64(15): 1–7. doi: 10.7498/aps.64.154705 |
| [23] | ZHANG R L, DI Q F, WANG X L, et al. Numerical study of wall wettabilities and topography on drag reduction effect in micro-channel flow by lattice Boltzmann Method[J]. Journal of Hydrodynamics, Ser. B, 2010, 22(3): 366–372. doi: 10.1016/S1001-6058(09)60066-4 |
 2017, Vol. 39
2017, Vol. 39


