2. 中国石油川庆钻探工程公司地质勘探开发研究院, 四川 成都 610056;
3. 中海石油湛江分公司, 广东 湛江, 524057
2. Geological Exploration and Development Research Institute of CNPC Chuanqing Drilling Engineering Ltd., Chengdu, Sichuan 610056, China;
3. CNOOC Zhanjiang Co. Ltd., Zhanjiang, Guangdong 524057, China
低渗气藏由于储层物性差、产量下降快、递减期长等地质与开发特征,开发难度高于常规气藏[1]。针对低渗储层启动压力梯度的研究,1999年,Prada等[2]提出达西公式应进行启动压力梯度的校正。Zeng等[3]于2011年测出超低渗储层的最小启动压力梯度值并提出利用拟启动压力梯度和非线性系数确定该值的方法。其他国内外学者在实验方法、新算法等方面也做了大量工作[4-11],为低渗储层渗流规律研究提供了理论基础。
水平井具有增大泄气面积、降低渗流阻力等优势,正在大规模应用于低渗气藏开发。高海红和杨学云等[12-13]分别建立了受启动压力梯度影响的水平井产能方程。在低渗气藏水平井的非稳态渗流规律方面,多数研究成果主要集中在瞬态压力动态分析[14-21],如Jalali等[16]分析了天然裂缝储层水平井的压力动态,Guo等[19]建立了考虑启动压力梯度的水平井试井分析模型,而对于不稳定产量递减特征的关注较少。在低渗气藏实际生产中,定压投产和定产投产都可能出现,由于不稳定压力动态是在定产生产条件下获得,不稳定产量递减则是在定压生产条件下获得,本文将针对定压生产制度下的不稳定产量递减特征展开研究。
以水平气井非稳态渗流理论为基础,主要考虑低速非达西效应即启动压力梯度的影响,利用拉普拉斯变换与正交变换相结合的方法,详细推导了裂缝性低渗气藏水平井不稳定压力及产量公式。利用Stehfest数值反演算法绘制出双重介质水平井产量递减典型曲线,继而研究了启动压力梯度、弹性储容比和窜流系数对产量递减曲线的影响。本文的研究可用于水平井现代产量递减分析,对于精确有效地预测裂缝性低渗气藏水平井生产动态具有积极的指导意义。
1 渗流数学模型启动压力梯度的概念最早由Florin于1951年提出,20世纪中叶国外学者相继发现流体在低渗致密储层的渗流过程中产生了存在启动压力梯度的非达西渗流[22]。实验结果表明,对于低速渗流,渗流速度与压力梯度关系曲线为一条不通过原点的曲线,图 1为启动压力梯度示意图。此时,低速非达西渗流的运动方程为[23]
| $ v =\left\{ \begin{array}{cl} -3.6\dfrac{K}{\mu}(\nabla p-\lambda_{\text{B}}) &, \quad \nabla p > \lambda_{\text{B}} \\ 0 &, \quad \nabla p \leqslant \lambda_{\text{B}} \end{array} \right. $ | (1) |
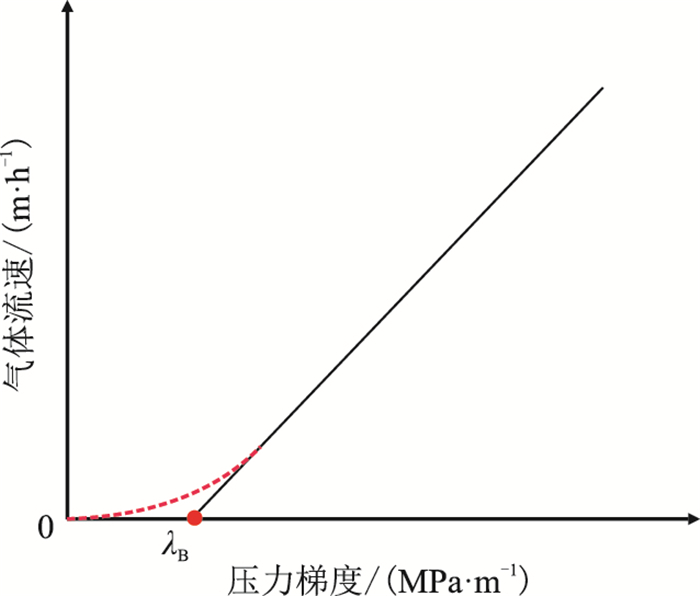 |
| 图1 低渗气藏非达西渗流曲线关系 Fig. 1 Non-Darcy flow relationship with threshold pressure gradient in low permeability gas reservoir |
假设裂缝性低渗气藏厚度为h,水平方向无限大,顶底为封闭边界,初始地层压力为pi。双重介质物理结构为Warren-Root模型,气体从基质流向裂缝再流至井筒,基质系统向裂缝系统为拟稳态窜流。长度为2L的水平井处在气藏的任一位置zw处,平行于顶底边界,其水平和垂直方向的渗透率分别为Kfh和Kfv。单相气体微可压缩并具有恒定黏度和压缩系数,服从低速非达西流动,忽略重力和毛管力的影响。水平井渗流的物理模型见图 2。
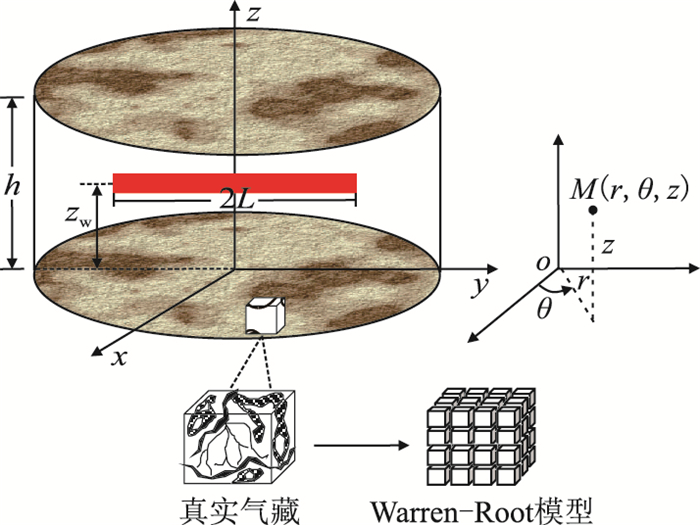 |
| 图2 双孔裂缝性气藏水平井渗流物理模型 Fig. 2 Sketch map of horizontal gas well percolation in dual-porosity media |
考虑启动压力梯度的影响,裂缝系统中拟压力形式的渗流微分方程为
| $ \dfrac{1}{r}\dfrac{\partial }{\partial r}\left[{r\left( {\dfrac{\partial m_\text{f} }{\partial r}-\dfrac{2p}{\mu Z}\lambda _\text{B} } \right)} \right]+\dfrac{K_{\text{fv}} }{K_{\text{fh}} }\dfrac{\partial }{\partial z}\left( {\dfrac{\partial m_\text{f} }{\partial z}-\dfrac{2p}{\mu Z}\lambda _\text{B} } \right)+\\[4pt]{\kern 40pt}\dfrac{\alpha K_\text{m} }{K_{\text{fh}} }\left( {m_\text{m} -m_\text{f} } \right)=\dfrac{\phi _\text{f} \mu C_{\text{ft}} }{3.6K_{\text{fh}} }\dfrac{\partial m_\text{f} }{\partial t} $ | (2) |
基质系统中拟压力形式的渗流微分方程为
| $ \alpha K_\text{m} \left( {m_\text{m} -m_\text{f} } \right)+\dfrac{\phi _\text{m} \mu C_{\text{mt}} }{3.6}\dfrac{\partial m_\text{m} }{\partial t}=0 $ | (3) |
裂缝和基质系统拟压力函数表达式分别为
| $ {m_{\text{f}}} = \int_{{p_0}}^{{p_{\text{f}}}} {\frac{{2p}}{{\mu Z}}{\text{d}}p} $ | (4) |
| $ {m_m} = \int_{{p_0}}^{{p_m}} {\frac{{2p}}{{\mu Z}}{\text{d}}p} $ | (5) |
引入拟启动压力梯度λmB,有
| $ \lambda _{\text{mB}} =\dfrac{2p}{\mu Z}\lambda _\text{B} $ | (6) |
裂缝系统控制方程式(2)可化为
| $ \dfrac{1}{r}\dfrac{\partial }{\partial r}\left( {r\dfrac{\partial m_\text{f} }{\partial r}} \right)-\dfrac{\lambda _{\text{mB}} }{r}+\dfrac{K_{\text{fv}} }{K_{\text{fh}} }\dfrac{\partial ^2m_\text{f} }{\partial z^2}+\\[4pt]{\kern 40pt}\dfrac{\alpha K_\text{m} }{K_{\text{fh}} }\left( {m_\text{m} -m_\text{f} } \right)=\dfrac{\phi _\text{f} \mu C_{\text{ft}} }{3.6K_{\text{fh}} }\dfrac{\partial m_\text{f} }{\partial t} $ | (7) |
将式(3)、式(7)进行无因次化,可得无因次渗流微分方程
| $ \lambda \left( {m_{\text{mD}} -m_{\text{fD}} } \right)+\left( {1-\omega } \right)\dfrac{\partial m_{\text{mD}} }{\partial t_\text{D} }=0 $ | (8) |
| $ \dfrac{1}{r_\text{D} }\dfrac{\partial }{\partial r_\text{D} }\left( {r_\text{D} \dfrac{\partial m_{\text{fD}} }{\partial r_\text{D} }} \right)+\dfrac{\lambda _{\text{mBD}} }{r_\text{D} } +\lambda \left({h_\text{D} L_\text{D} } \right)^2\left( {m_{\text{mD}}-m_{\text{fD}} } \right)\\{\kern 40pt} +L_\text{D}^2 \dfrac{\partial ^2m_{\text{fD}} }{\partial z_\text{D} ^2}=\omega \left( {h_\text{D} L_\text{D} } \right)^2\dfrac{\partial m_{\text{fD}} }{\partial t_\text{D} } $ | (9) |
内边界条件
| $ \begin{align} & \underset{\begin{smallmatrix} {{\varepsilon }_{\text{D}}}\to 0 \\ {{r}_{\text{D}}}\to 0 \end{smallmatrix}}{\mathop{\lim }}\,\int_{{{z}_{\text{wD}}}-\frac{{{\varepsilon }_{\text{D}}}}{2}}^{{{z}_{\text{wD}}}+\frac{{{\varepsilon }_{\text{D}}}}{2}}{{{r}_{\text{D}}}}\left( \frac{\partial {{m}_{\text{fD}}}}{\partial {{r}_{\text{D}}}}+{{\lambda }_{\text{mBD}}} \right)\text{d}{{z}_{\text{wD}}}=-\frac{1}{2}, \\ & \ \ \ \ \ \ \left| {{z}_{\text{D}}}-{{z}_{\text{wD}}} \right|\le \frac{{{\varepsilon }_{\text{D}}}}{2} \\ \end{align} $ | (10) |
水平方向外边界条件
| $ m_{\text{fD}} \left( {r_\text{D} \!\to\! \infty, z_\text{D}, t_\text{D} } \right)\!=\!m_{\text{mD}} (r_\text{D} \!\to\! \infty, z_\text{D}, t_\text{D} )\!=\!0 $ | (11) |
垂直方向外边界条件
| $ \left\{ \begin{array}{l} \dfrac{\partial m_{\text{fD}} }{\partial z_\text{D} }\left| {_{z_\text{D} =0} } \right.=\dfrac{\partial m_{\text{mD}} }{\partial z_\text{D} }\left| {_{z_\text{D} =0} } \right.=0\\[2pt] \dfrac{\partial m_{\text{fD}} }{\partial z_\text{D} }\left| {_{z_\text{D} =1} } \right.=\dfrac{\partial m_{\text{mD}} }{\partial z_\text{D} }\left| {_{z_\text{D} =1} } \right.=0 \end{array} \right. $ | (12) |
初始条件:
| $ m_{\text{fD}} \left( {r_\text{D}, z_\text{D}, 0} \right)=m_{\text{mD}} \left( {r_\text{D}, z_\text{D}, 0} \right)=0 $ | (13) |
联立式(8)~式(13),即为考虑启动压力梯度影响的裂缝性低渗气藏水平气井渗流数学模型。
2 数学模型求解考虑到该数学模型的非线性,先对时间变量进行拉普拉斯变换,再对空间变量进行正交变换,从而获得模型的精确解。对拟压力miD (rD, zD, tD)关于tD进行Laplace变换于s(i = f, m),并记miD为miD的拉氏变换函数
| $ \bar {m}_{\text{iD}} \left( {r_\text{D}, z_\text{D}, s} \right)=L\left[ {m_{i\text{D}} \left( {r_\text{D}, z_\text{D}, t_\text{D} } \right)} \right] =\\{\kern 40pt}\int_0^{+\infty } {m_{i\text{D}} \left( {r_\text{D}, z_\text{D} , t_\text{D} } \right){\rm e}^{-st_\text{D} }} {\rm d}t_\text{D} $ | (14) |
根据拉氏变换的微分性质,并利用初始条件,则拟压力对时间导数的拉氏变换写为
| $ L\left[{\dfrac{\partial m_{i\text{D}} \left( {r_\text{D}, z_\text{D} , t_\text{D} } \right)}{\partial t_\text{D} }} \right]=s\cdot L\left[ {m_{i\text{D}} \left( {r_\text{D}, z_\text{D}, t_\text{D} } \right)} \right]-\\[4pt]{\kern 40pt}m_{i\text{D}} \left( {r_\text{D}, z_\text{D}, t_\text{D} } \right)\left| {_{t_\text{D} =0} =} \right.s\bar {m}_{\text{iD}} $ | (15) |
把方程和边界条件进行Laplace变换,并利用初始条件,得到
| $ \left\{ \begin{align} & \frac{1}{{{r}_{\text{D}}}}\frac{\partial }{\partial {{r}_{\text{D}}}}\left( {{r}_{\text{D}}}\frac{\partial {{{\bar{m}}}_{\text{fD}}}}{\partial {{r}_{\text{D}}}} \right)+\frac{{{\lambda }_{\text{mBD}}}}{s{{r}_{\text{D}}}}+L_{\text{D}}^{2}\frac{{{\partial }^{2}}{{{\bar{m}}}_{\text{fD}}}}{\partial z_{\text{D}}^{2}}= \\ &{{\left( {{h}_{\text{D}}}{{L}_{\text{D}}} \right)}^{2}}\left[ \omega s{{{\bar{m}}}_{\text{fD}}}+\left( 1-\omega \right)s{{{\bar{m}}}_{\text{mD}}} \right] \\ & {{{\bar{m}}}_{\text{mD}}}=\frac{\lambda }{\lambda +\left( 1-\omega \right)s}{{{\bar{m}}}_{\text{fD}}} \\ & \underset{\begin{smallmatrix} {{\varepsilon }_{\text{D}}}\to 0 \\ {{r}_{\text{D}}}\to 0 \end{smallmatrix}}{\mathop{\lim }}\,\int_{{{z}_{\text{wD}}}-\frac{{{\varepsilon }_{\text{D}}}}{2}}^{{{z}_{\text{wD}}}+\frac{{{\varepsilon }_{\text{D}}}}{2}}{{{r}_{\text{D}}}}\left( \frac{\partial {{{\bar{m}}}_{\text{fD}}}}{\partial {{r}_{\text{D}}}}+\frac{{{\lambda }_{\text{mBD}}}}{s} \right)\text{d}{{z}_{\text{wD}}}= \\ &-\frac{1}{2s},\left| {{z}_{\text{D}}}-{{z}_{\text{wD}}} \right|\le \frac{{{\varepsilon }_{\text{D}}}}{2} \\ & {{{\bar{m}}}_{\text{fD}}}\left( {{r}_{\text{D}}}\to \infty ,{{z}_{\text{D}}},s \right)={{{\bar{m}}}_{\text{mD}}}\left( {{r}_{\text{D}}}\to \infty ,{{z}_{\text{D}}},s \right)=0 \\ & \frac{\partial {{{\bar{m}}}_{\text{fD}}}}{\partial {{z}_{\text{D}}}}\left| _{{{z}_{\text{D}}}=0} \right.=\frac{\partial {{{\bar{m}}}_{\text{mD}}}}{\partial {{z}_{\text{D}}}}\left| _{{{z}_{\text{D}}}=0} \right.=0 \\ & \frac{\partial {{{\bar{m}}}_{\text{fD}}}}{\partial {{z}_{\text{D}}}}\left| _{{{z}_{\text{D}}}=1} \right.=\frac{\partial {{{\bar{m}}}_{\text{mD}}}}{\partial {{z}_{\text{D}}}}\left| _{{{z}_{\text{D}}}=1} \right.=0 \\ \end{align} \right. $ | (16) |
为确定正交变换的核函数,需求解关于zD的施图姆刘维尔特征值问题(式(17))
| $ \left\{ \begin{split} & Z''+\theta Z=0, \;\;0 < z_\text{D} < 1 \\ & \dfrac{{\rm d}Z}{{\rm d}z_\text{D} }\left|_ {z_\text{D} =0} \right.=\dfrac{{\rm d}Z}{{\rm d}z_\text{D} }\left|_ {z_\text{D} =1 }=0 \right. \\ \end{split} \right. $ | (17) |
因为边值问题,式(17)并非对于任何θ都有非零解,只有当θ取某些特定值时才能有非零解存在。对特征方程分情况讨论,得到施图姆刘维尔问题式(17)的特征值为θn = (nπ)2,所对应的特征函数系为Zn (zD) = cosnπzD,其中n = 0, 1, 2...。该函数系构成[0,1]上的完备正交系。
以特征函数cosnπzD作为核函数引入正交变换,记
| $ \bar {\bar {m}}_{\text{fD}} \left( {r_\text{D}, n, s} \right)=F\left[{\bar {m}_{\text{fD}} \left( {r_\text{D}, z_\text{D}, s} \right)} \right]\\{\kern 40pt} =\int_0^1 {\bar {m}_{\text{fD}} \left( {r_\text{D}, z_\text{D}, s} \right)\cos n\pi z_\text{D} } {\rm d}z_\text{D} $ | (18) |
关于
| $ \left\{ \begin{array}{l} \left[{\left( {h_\text{D} L_\text{D} } \right)^2\dfrac{\lambda +s\omega (1-\omega )}{\lambda +(1-\omega )s}s+n^2\pi ^2L_\text{D}^2 } \right]\bar {\bar {m}}_{\text{fD}} -\\[5pt]{\kern 40pt} \dfrac{1}{r_\text{D} }\dfrac{\partial }{\partial r_\text{D} }\left[ {r_\text{D} \dfrac{\partial \bar {\bar {m}}_{\text{fD}} }{\partial r_\text{D} }} \right]-\dfrac{\varphi _n }{r_\text{D} }=0 \\[6pt] \mathop {\lim }\limits_{r_\text{D} \to 0} r_\text{D} \dfrac{\partial \bar {\bar {m}}_{\text{fD}} }{\partial r_\text{D} }=\dfrac{-\cos n\pi z_{\text{wD}} }{2s} \\ \bar {\bar {m}}_{\text{fD}} \left( {r_\text{D} \to \infty, n, s} \right)=0 \end{array} \right. $ | (19) |
式(19)中,φn为
| $ \begin{gathered} {\varphi _n} = F\left[{\frac{{{\lambda _{{\text{mBD}}}}}}{s}} \right] = \int_0^1 {\frac{{{\lambda _{{\text{mBD}}}}}}{s}} \cos n\pi {z_{\text{D}}}{\text{d}}{z_{\text{D}}} = \hfill \\ \left\{ \begin{gathered} \frac{{{\lambda _{{\text{mBD}}}}}}{s}, n = 0 \hfill \\ 0, n \ne 0 \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} $ | (20) |
令
| $ \dfrac{1}{r_\text{D} }\dfrac{\partial }{\partial r_\text{D} }\left( {r_\text{D} \dfrac{\partial \bar {\bar {m}}_{\text{fD}} }{\partial r_\text{D} }} \right)+\dfrac{\varphi _n }{r_\text{D} }-u_n \bar {\bar {m}}_{\text{fD}} =0 $ | (21) |
(1) 当n≠0时,φn = 0,则式(21)化为
| $ \dfrac{\partial ^2\bar {\bar {m}}_{\text{fD}} }{\partial r_\text{D}^2 }+\dfrac{1}{r_\text{D} }\dfrac{\partial \bar {\bar {m}}_{\text{fD}} }{\partial r_\text{D} }-u_n \bar {\bar {m}}_{\text{fD}} =0 $ | (22) |
两边同乘以rD2,有
| $ r_\text{D}^2 \dfrac{\partial ^2\bar {\bar {m}}_{\text{fD}} }{\partial r_\text{D}^2 }+r_\text{D} \dfrac{\partial \bar {\bar {m}}_{\text{fD}} }{\partial r_\text{D} }-u_n r_\text{D}^2 \bar {\bar {m}}_{\text{fD}} =0 $ | (23) |
令
| $ r_\text{D}^2 u_n \dfrac{\partial ^2\bar {\bar {m}}_{\text{fD}} }{\partial x^2}+r_\text{D} \sqrt {u_n } \dfrac{\partial \bar {\bar {m}}_{\text{fD}} }{\partial x}-r_\text{D}^2 u_n \bar {\bar {m}}_{\text{fD}} =0 $ | (24) |
式(24)可表示为
| $ x^2\dfrac{\partial ^2\bar {\bar {m}}_{\text{fD}} }{\partial x^2}+x\dfrac{\partial \bar {\bar {m}}_{\text{fD}} }{\partial x}-\left( {x^2+\upsilon ^2} \right)\bar {\bar {m}}_{\text{fD}} =0 $ | (25) |
式(25)中,v= 0,此处v表示虚宗量贝塞尔方程的阶数,故n≠ 0时,方程(21)为零阶虚宗量贝塞尔方程,其通解为
| $ \bar {\bar {m}}_{\text{fD}} =AI_0 \left( {r_\text{D} \sqrt {u_n } } \right)+BK_0 \left( {r_\text{D} \sqrt {u_n } } \right) $ | (26) |
(2)当n = 0时,
| $ \bar {\bar {m}}_{\text{fD}} =AI_0 \left( {r_\text{D} \sqrt {u_n } } \right)+BK_0 \left( {r_\text{D} \sqrt {u_n } } \right)+\\[4pt]{\kern 40pt}\int_0^{+\infty } {G\left( {r_D, \tau } \right)} {\rm d}\tau $ | (27) |
式(27)中,G(rD, τ)为格林函数,表达式为
| $ G\left( {r_D, \tau } \right)=\left\{ {{\begin{array}{*{20}c} {\dfrac{\lambda _{\text{mBD}} }{s}K_0 \left( {r_\text{D} \sqrt {u_0 } } \right)I_0 \left( {\tau \sqrt {u_0 } } \right)}, \\{\kern 40pt} {\left( {0 < \tau < r_\text{D} } \right)} \\ {\dfrac{\lambda _{\text{mBD}} }{s}K_0 \left( {\tau \sqrt {u_0 } } \right)I_0 \left( {r_\text{D} \sqrt {u_0 } } \right)}, \\{\kern 40pt} {(r_\text{D} < \tau < +\infty )} \hfill \\ \end{array} }} \right. $ | (28) |
利用式(19)中内外边界条件并结合贝塞尔函数的性质,确定式(27)中的系数A,B,可得
| $ \bar {\bar {m}}_{\text{fD}} =\dfrac{\cos n\pi z_{\text{wD}} }{2s}K_0 \left( {r_\text{D} \sqrt {u_n } } \right)+\\{\kern 40pt}\int_0^{+\infty } {G\left( {r_D, \tau } \right)} {\rm d}\tau $ | (29) |
根据特征函数系的完备正交性,正交逆变换的表达式为
| $ \begin{array}{*{20}c} \bar {m}_{\text{fD}} \left( {r_\text{D}, z_\text{D}, s} \right)=F^{-1}\left[ {\bar {\bar {m}}_{\text{fD}} \left( {r_\text{D}, n, s} \right)} \right]=\\{\kern 40pt} \sum\limits_{n=0}^\infty {\dfrac{\bar {\bar {m}}_{\text{fD}} \left( {r_\text{D}, n, s} \right)}{\left\| {\cos n\pi z_\text{D} } \right\|^2}} \cos n\pi z_\text{D} \end{array} $ | (30) |
因此,通过正交逆变换可得裂缝系统无因次拟压力的拉氏空间解为
| $ \bar {m}_{\text{fD}} =\dfrac{1}{s}\sum\limits_{n=1}^\infty {K_0 \left( {r_\text{D} \sqrt {u_n } } \right)} \cos n\pi z_{\text{wD}} \cos n\pi z_\text{D}+\\{\kern 40pt}\dfrac{1}{2s}K_0 \left( {r_\text{D} \sqrt {u_0 } }\right)+\int_0^{+\infty } {G\left( {r_D, \tau } \right)} {\rm d}\tau $ | (31) |
根据源的思想,对点源解式(31)沿水平井筒方向积分,可得拉氏空间下考虑启动压力梯度影响的裂缝性低渗气藏水平井井底拟压力表达式
| $ \bar {m}_{\text{fD}} =\dfrac{1}{2s}\int_{-1}^1 K_0 \left( {\left| {x_\text{D} -\alpha } \right|\sqrt {u_0 } } \right){\rm d}\alpha + \int_0^{+\infty } {\int_{-1}^1 {G\left( {\left| {x_\text{D} -\alpha } \right|, \tau } \right)} {\rm d}\alpha {\rm d}\tau } + \\[5pt]{\kern 40pt} \dfrac{1}{s}\sum\limits_{n=1}^\infty {\int_{-1}^1 {K_0 \left( {\left| {x_\text{D} -\alpha } \right|\sqrt {u_n } } \right)\cos n\pi z_{\text{wD}} \cos n\pi z_\text{D} {\rm d}\alpha } } $ | (32) |
根据Duhamel叠加原理,考虑井筒储集效应和表皮效应影响,水平井井底拟压力响应的表达式为
| $ \bar {m}_{\text{wD}} =\dfrac{s\bar {m}_{\text{fD}} +S}{s+C_\text{D} s^2(s\bar {m}_{\text{fD}} +S)} $ | (33) |
根据Van Everdingen和Hurst的研究[24],拉氏空间下定压产量解与定产压力解的关系为
| $ \bar {q}_\text{D} \left( s \right)=\dfrac{1}{s^2\bar {m}_{\text{wD}} \left( s \right)} $ | (34) |
式(34)为获取定压产量解的常用方法,已为诸多学者(Nie、Huang、Xie等[25-27])所用并证实了其正确性。
联合(32)~(34)式,即可获得考虑启动压力梯度影响的裂缝性低渗气藏水平井无因次产量在拉氏空间下的解。
3 产量递减典型曲线不稳定产量递减分析与不稳定试井分析都是基于经典的渗流理论,均采用图版拟合的方法获取参数。但不稳定产量递减分析方法只需采用每日计量的生产数据,可以省去高精度要求的压力不稳定测试流程,有效避免测压工序的繁琐。
根据德国经济统计学家Stehfest提出的数值反演算法[28],绘制出裂缝性低渗气藏水平井无因次产量递减典型曲线,如图 3所示。根据图 3可以将不稳定产量递减曲线划分为7个流动阶段。
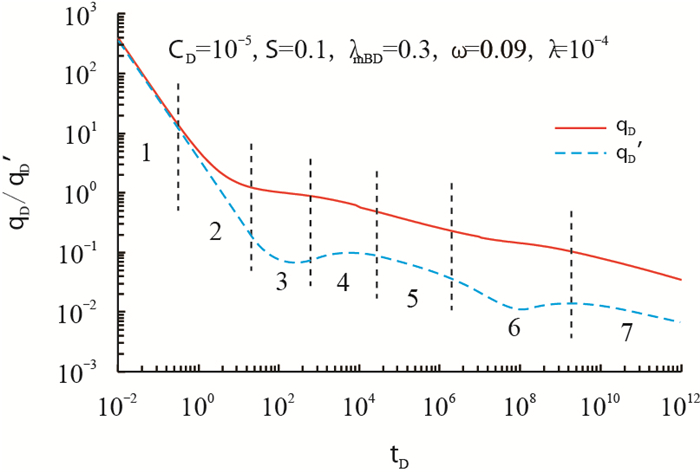 |
| 图3 裂缝性低渗气藏水平井产量递减典型曲线 Fig. 3 Type curves of transient production decline of horizontal well in fractured low permeability gas reservoir |
第1阶段为纯井筒储集效应流,表现为无因次产量及其导数曲线重合为相同斜率的下降直线。第2阶段为表皮效应过渡流,产量曲线的下降程度变缓,产量导数曲线继续下降。第3阶段为早期垂向径向流,产量导数曲线近似成一条水平线,其值与LD有关。当水平井井筒储集系数较大时,表征早期垂向径向流的水平直线段有可能被井筒储集所掩盖。第4阶段为早期裂缝线性流,产量导数曲线呈现轻微上翘的趋势,裂缝系统作为充足的气源涌向井筒,表明该阶段产量的下降不太明显。第5阶段为中期裂缝径向流,无因次产量与其导数近似呈两条平行线,反映了裂缝系统的径向流。第6阶段为基质向裂缝窜流,最明显的特征为产量导数曲线的下凹部分,该阶段裂缝与基质的压差已增大到使气体从基质窜流到裂缝。第7阶段为晚期系统径向流,产量及其导数曲线继续下降,这一阶段描述了整个系统的径向流。
图 4表示启动压力梯度对裂缝性低渗气藏水平井产量递减的影响。从图中可以看出,除了早期井储效应和表皮过渡流,启动压力梯度几乎影响了整个曲线形态。启动压力梯度越大,表明储层物性越差,气体流动越困难,因此气体产量越低。相应地,产量导数曲线的位置也越靠下。
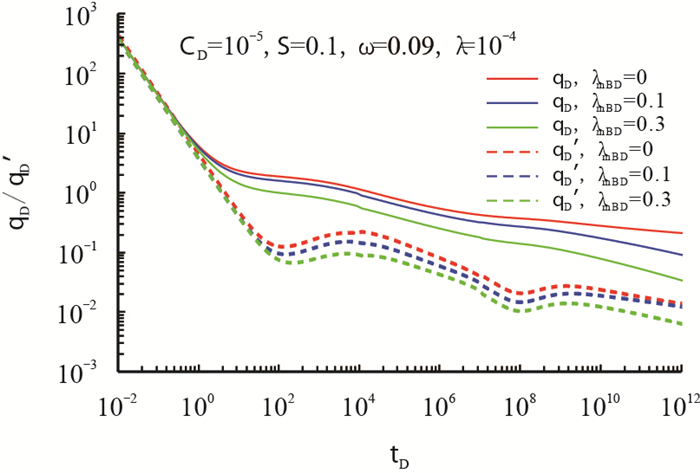 |
| 图4 启动压力梯度对产量递减曲线的影响 Fig. 4 Effect of threshold pressure gradient on transient production decline curves |
图 5表示弹性储容比对裂缝性低渗气藏水平井产量递减的影响。从图中可以看出,弹性储容比对典型曲线的中期影响最为明显,储容比越大,裂缝系统的储集能力越强,储集的流体越多,产量递减的总体速度越慢。在曲线上表现为储容比越小,基质窜流发生越早,产量导数的下凹部分出现时间越早,下凹的程度越深,持续的时间越长。
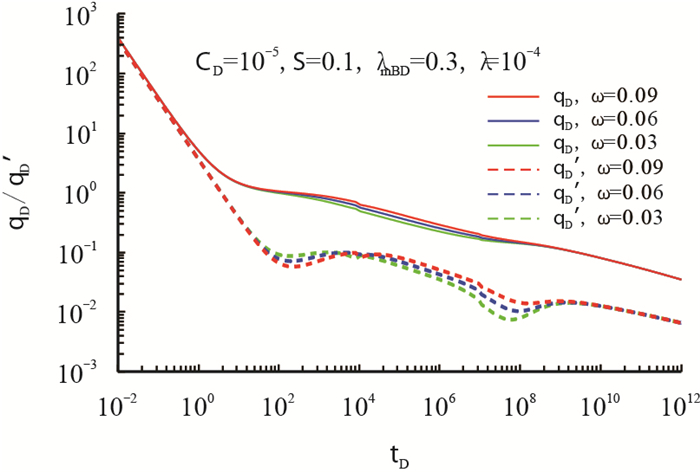 |
| 图5 弹性储容比对产量递减曲线的影响 Fig. 5 Effect of elastic storativity ratio on transient production decline curves |
图 6表示窜流系数对裂缝性低渗气藏水平井产量递减的影响。窜流系数越小,基质的流体越难发生窜流作用流动到裂缝中去,产量较低。从图 6中可以看出,随着窜流系数的减小,产量曲线的位置越低,产量导数的下凹部分出现时间越晚,表明窜流阶段的发生越滞后。
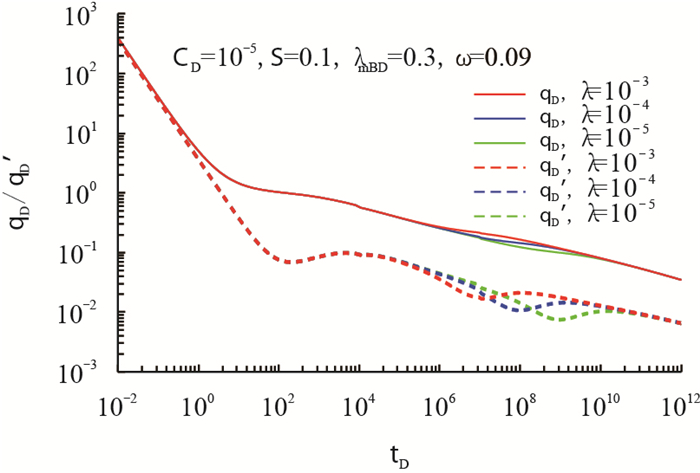 |
| 图6 窜流系数对产量递减曲线的影响 Fig. 6 Effect of cross flow coefficient on transient production decline curves |
(1) 考虑低速渗流时启动压力梯度的影响,建立了双重介质水平井产量不稳定分析模型,其递减曲线主要变现为7个流动阶段。该模型可以用于水平井生产动态的现代产量递减分析。
(2) 启动压力梯度对水平井产量递减曲线的影响显著。启动压力梯度在一定程度上表征了储层低渗程度,其值越大表明储层物性越差,水平井产量越低,产量递减曲线位置越低。
(3) 弹性储容比和窜流系数的影响与常规气藏水平井的渗流规律一致,弹性储容比主要影响下凹部分的宽度和深度,窜流系数主要影响下凹部分出现的位置。
符号说明
v-气体流速,m/h;
K-渗透率,D;
μ-气体黏度,mPa·s;
∇-哈密尔顿算子;
p-压力,MPa;
λB-启动压力梯度,MPa/m;
h-气层厚度,m;
pi-初始地层压力,MPa;
L-水平段半长,m;
zw-水平井垂向距离,m;
Kfh,Kfv-水平和垂直方向的渗透率,D;
M-空间中任意一点;
r,θ,z-柱坐标分量;
m-拟压力,MPa2/(mPa·s);
Z-气体偏差因子,无因次;
z-垂向距离,m;
α-形状因子,m-2;
φ-孔隙度,无因次;
Cft-裂缝系统综合压缩系数,MPa-1;
t-时间,h;
Cmt-基质系统综合压缩系数,MPa-1;
λmB-拟启动压力梯度,MPa2/(mPa·s·m);
λmBD-无因次拟启动压力梯度;
mfD-无因次裂缝系统拟压力;
mmD-无因次基质系统拟压力;
qD-无因次产量;
mfD-mfD拉氏变换后的对应函数;
mwD-井底拟压力拉氏变换后的对应函数;
tD-无因次时间;
ω-弹性储容比,无因次;
λ-窜流系数,无因次;
CD-无因次井筒储集系数;
LD-无因次水平井段长度;
hD-无因次气层厚度;
rD-无因次径向距离;
rwD-无因次井筒半径;
zD-无因次垂向距离;
zwD-无因次水平井位置;
ε-无穷小量;
T-绝对温度,K;
q-产量,×104 m3/d;
C-井筒储集系数,m3/MPa;
s-Laplace变量;
v-虚宗量贝塞尔函数的阶数;
A、B-系数。
I0-第一类零阶虚宗量的贝塞尔函数;
K0-第二类零阶虚宗量的贝塞尔函数;
S-表皮系数,无因次;
qD-qD拉氏变换后的对应函数;
q′ D-无因次产量的导数;
下标f-裂缝系统;
下标m-基质系统。
| [1] | 郭平, 张茂林, 黄全华, 等. 低渗透致密砂岩气藏开发机理研究[M]. 北京: 石油工业出版社, 2009. |
| [2] | PRADA A, CIVAN F. Modification of Darcy's law for the threshold pressure gradient[J]. Journal of Petroleum Science and Engineering, 1999, 22(4): 237–240. doi: 10.1016/S0920-4105(98)00083-7 |
| [3] | ZENG B, CHENG L, LI C. Low velocity non-linear flow in ultra-low permeability reservoir[J]. Journal of Petroleum Science and Engineering, 2011, 80(1): 1–6. doi: 10.1016/j.petrol.2011.10.006 |
| [4] |
冯文光. 非达西低速渗流的研究现状与展望[J].
石油勘探与开发, 1986, 13(4): 76–80.
FENG Wenguang. Research status and prospect of non-Darcy low velocity percolation[J]. Petroleum Exploration and Development, 1986, 13(4): 76–80. |
| [5] |
许建红, 程林松, 钱俪丹, 等. 低渗透油藏启动压力梯度新算法及应用[J].
西南石油大学学报, 2007, 29(4): 64–66.
XU Jianghong, CHENG Linsong, QIAN Lidan, et al. A new method and the application on calculation startup pressure gradient in low permeability reservoirs[J]. Journal of Southwest Petroleum University, 2007, 29(4): 64–66. doi: 10.3863/j.issn.1674-5086.2007.04.015 |
| [6] |
王道成, 李闽, 谭建为, 等. 气体低速非线性渗流研究[J].
大庆石油地质与开发, 2007, 26(6): 74–77.
WANG Daocheng, LI Min, TAN Jianwei, et al. Research on low velocity non-linear fluid flow through porous medium of gas[J]. Daqing Petroleum Geology and Development, 2007, 26(6): 74–77. doi: 10.3969/j.issn.1000-3754.2007.06.019 |
| [7] | HAO F, CHENG L, HASSAN O, et al. Threshold pressure gradient in ultra-low permeability reservoirs[J]. Petroleum Science and Technology, 2008, 26(9): 1024–1035. doi: 10.1080/10916460701675033 |
| [8] |
李中超, 李闽, 蒋雨江. 确定低渗岩芯气体启动压力梯度的一种新方法[J].
西南石油大学学报(自然科学版), 2013, 35(3): 105–110.
LI Zhongchao, LI Min, JIANG Yujiang. A new method for determining gas threshold pressure gradient in lowpermeability rock[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2013, 35(3): 105–110. doi: 10.3863/j.issn.1674-5086.2013.03.014 |
| [9] | DING J, YANG S, NIE X, et al. Dynamic threshold pressure gradient in tight gas reservoir[J]. Journal of Natural Gas Science and Engineering, 2010(20): 155–160. doi: 10.1016/j.jngse.2014.06.019 |
| [10] |
王晓冬, 郝明强, 韩永新. 启动压力梯度的含义与应用[J].
石油学报, 2013, 34(1): 188–191.
WANG Xiaodong, HAO Mingqiang, HAN Yongxin. Implication of the threshold pressure gradient and its application[J]. Acta Petrolei Sinica, 2013, 34(1): 188–191. doi: 10.7623/syxb201301025 |
| [11] |
白瑞婷, 李治平, 南珺祥, 等. 考虑启动压力梯度的致密砂岩储层渗透率分形模型[J].
天然气地球科学, 2016, 27(1): 142–148.
BAI Ruiting, LI Zhiping, NAN Junxiang, et al. The fractal permeability model in tight sand reservoir accounts for start-up gradient[J]. Natural Gas Geoscience, 2016, 27(1): 142–148. doi: 10.11764/j.issn.1672-1926.2016.01.0142 |
| [12] |
高海红, 程林松, 冯儒勇. 考虑启动压力梯度的低渗气藏水平井产能计算[J].
天然气工业, 2008, 28(7): 75–77.
GAO Haihong, CHENG Linsong, FENG Ruyong. Productivity calculation of horizontal wells in low permeability gas reservoirs considering starting pressure gradient[J]. Journal of Natural Gas Industry, 2008, 28(7): 75–77. doi: 10.3787/j.issn.1000-0976.2008.07.023 |
| [13] |
杨学云, 张学婧, 蒋国斌, 等. 启动压力梯度影响下低渗透气藏水平井产能模型的建立[J].
特种油气藏, 2010, 17(1): 85–87.
YANG Xueyun, ZHANG Xuejing, JIANG Guobin, et al. Horizontal well deliverability model of low permeability gas reservoirs considering threshold pressure gradient[J]. Special Oil & Gas Reservoirs, 2010, 17(1): 85–87. doi: 10.3969/j.issn.1006-6535.2010.01.023 |
| [14] |
苏海波. 反映动态启动压力梯度的低渗透油藏渗流模型[J].
西南石油大学学报(自然科学版), 2015, 37(6): 105–111.
SU Haibo. A flow model reflecting dynamic kick-off pressure gradient for low permeability reservoirs[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2015, 37(6): 105–111. doi: 10.11885/j.issn.1674-5086.2015.05.06.05 |
| [15] |
程时清, 徐论勋, 张德超. 低速非达西渗流试井典型曲线拟合法[J].
石油勘探与开发, 1996, 23(4): 50–53.
CHENG Shiqing, XU Lunxun, ZHANG Dechao. Type curves matching of well test data for non-Darcy flow at low velocity[J]. Petroleum Exploration and Development, 1996, 23(4): 50–53. |
| [16] | JALALI Y, ERSHAGI I. Pressure transient analysis of heterogeneous naturally fractured reservoirs[C]. SPE 16341, 1987. doi: 10.2118/16341-MS |
| [17] |
王建忠, 姚军. 裂缝性低渗油藏试井模型与非稳态压力特征[J].
特种油气藏, 2013, 20(2): 69–71.
WANG Jianzhong, YAO Jun. Well test model and transient pressure characteristic of low permeability reservoirs with natural fractures[J]. Special Oil & Gas Reservoirs, 2013, 20(2): 69–71. doi: 10.3969/j.issn.1006-6535.2013.02.016 |
| [18] | NIE R, MENG Y, JIA Y, et al. Dual porosity and dual permeability modeling of horizontal well in naturally fractured reservoir[J]. Transport in Porous Media, 2012, 92(1): 213–235. doi: 10.1007/s11242-011-9898-3 |
| [19] | GUO J, ZHANG S, ZHANG L, et al. Well testing analysis for horizontal well with consideration of threshold pressure gradient in tight gas reservoirs[J]. Journal of Hydrodynamics, 2012, 24(4): 561–568. doi: 10.1016/S1001-6058(11)60278-3 |
| [20] | CAO Lina, LI Xiaoping, LUO Cheng, et al. Horizontal well transient rate decline analysis in low permeability gas reservoirs employing an orthogonal transformation method[J]. Journal of Natural Gas Science and Engineering, 2016(33): 703–716. doi: 10.1016/j.jngse.2016.06.001 |
| [21] |
谢维扬, 李晓平, 张烈辉, 等. 页岩气多级压裂水平井不稳定产量递减探讨[J].
天然气地球科学, 2015, 26(2): 384–390.
XIE Weiyang, LI Xiaoping, ZHANG Liehui, et al. Transient production decline analysis for multi-fractured horizontal well in shale gas reservoirs[J]. Natural Gas Geoscience, 2015, 26(2): 384–390. doi: 10.11764/j.issn.1672-1926.2015.02.0384 |
| [22] |
李奇, 高树生, 杨朝蓬, 等. 致密砂岩气藏阈压梯度对采收率的影响[J].
天然气地球科学, 2014, 25(9): 1444–1450.
LI Qi, GAO Shusheng, YANG Chaopeng, et al. Influence of the threshold pressure gradient on tight sandstone gas reservoir recovery[J]. Natural Gas Geoscience, 2014, 25(9): 1444–1450. doi: 10.11764/j.issn.1672-1926-.2014.09.1444 |
| [23] | 李晓平. 地下油气渗流力学[M]. 北京: 石油工业出版社, 2007: 27-28. |
| [24] | VAN E A, HURST W. The application of the Laplace transformation to flow problems in reservoirs[J]. Trans. AIME, 1949, 186(305): 97–104. doi: 10.2118/949305-G |
| [25] | NIE R S, GUO J C, JIA Y L, et al. New modeling of transient well test and rate decline analysis for a horizontal well in a multiple-zone reservoir[J]. Journal of Geophysics and Engineering, 2011, 8(3): 464–476. doi: 10.1088/1742-2132/8/3/007 |
| [26] | HUANG T, GUO X, CHEN F. Modeling transient pressure behavior of a fractured well for shale gas reservoirs based on the properties of nanopores[J]. Journal of Natural Gas Science and Engineering, 2015, 23: 33–46. doi: 10.1016/j.jngse.2015.02.020 |
| [27] | XIE W Y, LI X P, ZHANG L H, et al. Production decline analysis for two-phase flow in multifractured horizontal well in shale gas reservoirs[J]. Journal of Chemistry, 2015(2): 1–10. doi: 10.1155/2015/212103 |
| [28] | STEHFEST H. Algorithm 368: Numerical inversion of Laplace transforms[J]. Communications of the ACM, 1970, 13(1): 47–49. doi: 10.1145/361953.361969 |
 2017, Vol. 39
2017, Vol. 39


