2. 西南石油大学石油与天然气工程学院, 四川 成都 610500;
3. 中海油田服务股份有限公司, 河北 三河 101149
2. School of Petroleum and Natural Gas Engineering, Southwest Petroleum University, Chengdu, Sichuan 610500, China;
3. China Oilfield Services Limited, Sanhe, Hebei 101149, China
井壁稳定(井壁坍塌、井眼缩径和地层破裂)问题一直是石油钻井过程中一个十分复杂的问题,自从Westergaard[1]发表第一篇关于井壁稳定的论文以来,国内外已存在相当多的井壁失稳分析研究成果。为了评价钻井过程中井眼的稳定性,首先需要确定两个基本要素:第一是井筒周围岩石的应力状态,第二是岩石的屈服准则和本构关系。因此研究者们往往立足于井壁所受的原地应力(最大水平主地应力、最小水平主地应力以及上覆地层压力),结合井眼轨迹状态(不同井斜角、方位角、井眼曲率等)进行井壁岩石的应力状态分析,随后采用相应的岩石力学准则即可进行井壁失稳分析,图 1则给出了斜井眼在原地应力状态下的坐标转换以及应力分析情况[2]。然而,随着石油钻井的发展和井壁失稳分析理论的进步,地层流体、钻井液性能、地层温度等因素所产生的作用场同样对井壁稳定有着巨大的影响。因此,多场耦合对于井壁稳定分析具有重要实际意义。
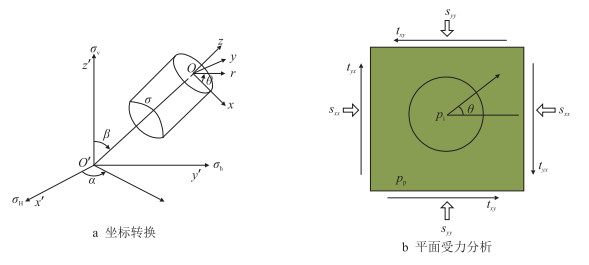 |
| 图1 斜井眼应力分析情况 Fig. 1 The schematic for coordinate transformation and stress state of wellbore rocks |
在钻井过程中,井壁岩石在原地应力、井内有效液柱压力和地层孔隙压力的作用下,并结合温度、钻井液化学作用以及流体渗流作用等的影响,其应力状态相应地发生改变。此外,岩石类型和岩石结构对于井壁失稳分析以及钻井液优选同样具有重要的影响。因此根据钻井工程实际,可以将钻井过程中井壁失稳的各类影响因素分为5类作用场[3]:岩石结构场、应力场、渗流场、化学场和温度场。
1.1 岩石结构场不同类型岩石(砂岩、泥岩、碳酸盐岩等)在钻井过程中有着不同的力学和化学表现形式,岩石结构场根据岩石类型和性质不同可以分为3个方面的内容[3]:一是岩石的物质组成,包括岩石所含黏土矿物、原生矿物、次生矿物以及气液固含量等;二是岩石的结构参数,包括岩石的粒度组成、结构类型(孔隙、裂缝、弱面、层理面等)以及结构连接特征等;三是岩石的物性参数,包括岩石的变形方式以及压缩系数、渗透率、孔隙度等。
1.2 应力场应力场主要是指地应力的作用以及其他工程活动所产生的附加应力场 (不包括温度和化学作用产生的附加应力场),而地应力包括上覆地层压力 (
在钻井过程中,井筒内存在液柱压力,地层中存在地层孔隙压力,渗流场正是由这两者的相互作用产生的。不同钻井方式下井筒内有效液柱压力和地层孔隙压力的大小关系不一样,相应的渗流方式也不一样。如图 2所示,在过平衡钻井过程中,有效液柱压力大于地层孔隙压力,井内流体渗入地层;在平衡钻井过程中,有效液柱压力等于地层孔隙压力,井内流体与地层流体实现压力平衡;在欠平衡钻井过程中,有效液柱压力小于地层孔隙压力,地层流体流入井筒,由此3种不同钻井方式下就会存在相应的渗流场。
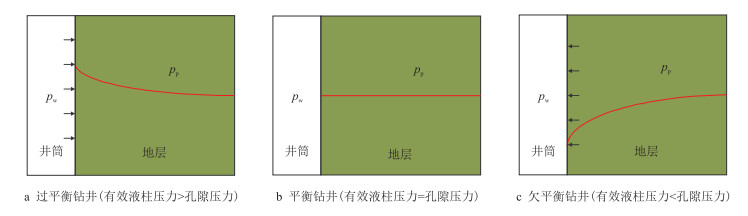 |
| 图2 3种不同钻井方式下的流体渗流形式 Fig. 2 The schematic for ways of fluid seepage under three drilling conditions |
化学场主要来自井筒内流体和井壁岩石的化学作用,主要表现为岩石性质以及应力状态的改变。钻井过程中钻井液和钻遇岩石的类型决定了化学场的作用,特别是对于泥页岩而言,泥页岩层段钻井过程中的化学场作用主要包括离子交换、化学势差产生的渗透作用[5]和水化应力、岩石力学参数变化等内容。
1.5 温度场当钻井液通过钻柱和环空不断循环,由于钻井液和地层之间存在温度差,二者不断发生热交换(热传导和热对流),造成钻井液和井壁岩石温度的改变,从而使得井眼温度场发生变化。当地层温度变化为T-T0时,井壁由于温度变化引起的附加应力为[6]
| $ {\sigma _{\rm{a}}} = - E{\varepsilon _{\rm{a}}} = E{\alpha _{\rm{T}}}\left( {T - {T_0}} \right) $ | (1) |
在进行井壁稳定多场耦合分析时,应力场和岩石结构场是分析的基础。在目前的井壁失稳分析过程中,应力场以前文论述的5种地应力机制为主,岩石结构场中岩石的物质组成大致包括:正长石、斜长石、石英、黑云母、白云母、角闪石等;岩石按照其地质成因可以分为岩浆岩、沉积岩以及变质岩4大类[7];而按照结构参数的不同,岩石大致可以分为以下几种类型,如表 1所示[6, 8-14]。
| 表1 井壁稳定分析岩石结构类型 Table 1 The types of rock structures for wellbore stability analysis |
不同物性参数下井壁岩石的变形机制也不一样,表 2列出了目前井壁失稳分析过程中采用较多的岩石变形机制[15-24]。基于此,在进行井壁失稳的多场耦合分析时,即以应力场和岩石结构场为基础,结合渗流场、化学场、温度场的影响进行三场、四场和五场耦合分析。
| 表2 井壁稳定分析岩石变形机制 Table 2 Different schemes of rock deformation for wellbore stability analysis |
井壁稳定三场耦合分析主要包括:岩石结构场-应力场-化学场、岩石结构场-应力场-温度场、岩石结构场-应力场-渗流场3种耦合情况。
2.1.1 岩石结构场-应力场-化学场耦合岩石结构场-应力场-化学场耦合主要考虑钻井液化学作用对井壁岩石的影响。在以往的井壁稳定研究过程中,通过结合钻井液浸泡实验、分散实验以及封堵抑制实验等,已经有大量关于钻井液化学力学耦合作用的研究成果。而关于钻井液化学作用的研究主要针对于泥页岩层段的井壁失稳[25],对于纯砂岩和碳酸盐岩等水化能力较弱的岩层,钻井液化学作用通常可以忽略。
泥页岩通常结构松散且复杂,其强度跟黏土矿物的含量和类型有着密切联系。而泥页岩浸水后会发生水化膨胀,使得岩石力学参数发生变化,从而对井壁稳定造成巨大影响。基于此,根据泥页岩的性质,Yew等[26]定量化分析了井壁稳定的力化耦合作用,并结合质量守恒方程给出了吸附水量的表达式(式2);Hale等[25]则根据半透膜理论给出了化学势差作用下孔隙压力的计算公式(式3),从而进行力化耦合时井壁应力的重分布分析。
| $ \dfrac{C}{r}\cdot\dfrac{\partial }{{\partial r}}\left (\dfrac{r{\partial w}}{{\partial r}} \right ) = \dfrac{{\partial w}}{{\partial t}} $ | (2) |
| $ \dfrac{{\rm R}T}{{V_{{\rm{mw}}}}}\ln ({a_{{\rm{wdf}}}}/{a_{{\rm{wsh}}}}) = {p_{{\rm{nw}}}} - {p_{{\rm{pf}}}} $ | (3) |
针对泥页岩的各向异性,弱面理论[27-29]和横观各向同性理论[30]在其井壁失稳分析时应用较为广泛。在进行各向异性条件下泥页岩井壁失稳分析时,化学作用主要体现在岩石力学参数与泥页岩吸水量的关系上,黄荣樽等[31]通过研究发现,泥页岩层理面弱化可以采用岩石内聚力和内摩擦角与含水量的关系进行描述;基于此,通过分析可以发现考虑化学作用时含弱面泥页岩层更容易失稳[32],如图 3所示。
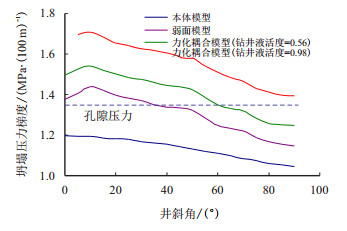 |
| 图3 力化耦合时弱面和本体条件下的坍塌压力分析 Fig. 3 Analysis of collapse pressure under the condition of mechanic-chemical coupling when bedding planes are considered |
以目前的实验和理论研究为基础,根据钻井液化学作用对井壁岩石的作用,可以将井壁失稳的化学动力学因素分为[33]:范德华力、静电引力、平板电势能、毛细管张力、基质吸力、渗透压及浓差极化边界阻力;而由此泥页岩力化耦合研究的理论和方法总体可以分为[34]:泥页岩内水的传输机理、等效孔隙压力法、总吸附水相关法、总水势的增量弹性理论4种类型。
2.1.2 岩石结构场-应力场-温度场耦合岩石结构场-应力场-温度场的耦合主要针对高温高压深井超深井的情况,对于浅井或温度变化不大的地层,温度场对井壁稳定的影响可以忽略。目前国内外关于此方面的主要研究内容大致可以分为以下几类。
(1)井内流体和地层岩石温度的变化规律。
(2)不同温度场下岩石和所含流体性质的变化。
(3)温度场变化所产生的附加应力。
在井内流体和地层岩石温度变化规律的研究过程中,通常根据热力学及传热学的相关理论,取管柱内流体、管柱壁、环空内流体和地层岩石为控制体(图 4),结合能量守恒方程,确定井内的循环温度场[35]。而对于不同地层岩石而言,往往根据其渗透率状况采用不同的分析方式:低渗透地层岩石(低渗透泥页岩)往往只考虑热传导,高渗透地层岩石(高渗透砂岩、碳酸盐岩等)则以考虑热对流为主[24]。此外,不同温度场下地层温度变化往往导致岩石热力学性质以及岩石强度的变化:弹性模量随温度的升高而减小、泊松比随温度的升高而增大、热膨胀系数随温度的升高而逐渐增大[36]。
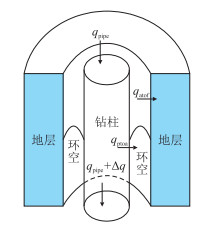 |
| 图4 管柱-环空-地层温度场控制体 Fig. 4 The control volume of string-tubular-formation |
在分析温度变化所产生的井壁附加应力时,可以由热弹性理论给出,其中典型的温度扩散方程如式(4)和式(5)所示[37-38]。
| $ \dfrac{{\partial T}}{{\partial t}} = {c_{\rm o}}\left (\dfrac{{{\partial ^2}T}}{{\partial {r^2}}} + \dfrac{1}{r}\dfrac{{\partial T}}{{\partial r}}\right ) $ | (4) |
| $ T(r, t) = {T_{\rm{o}}} + ({T_{\rm{w}}} - {T_{\rm{o}}}){L^{ - 1}}\left( {\dfrac{1}{s}\cdot\dfrac{r}{{r_{\rm{w}} }}} \right) $ | (5) |
研究发现,泥页岩层段钻井液和井壁岩石接触时温度降低所产生的附加应力与原有应力场进行叠加,会导致岩石径向应力的减小,最终使坍塌压力和破裂压力均降低(图 5),从而在一定程度上降低安全钻井液密度窗口[38-39]。
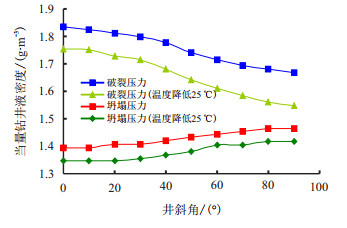 |
| 图5 考虑温度影响下井壁坍塌压力和破裂压力的变化 Fig. 5 The variation of collapse pressure and fracture pressure when temperature is considered |
当钻井液流体和地层流体二者之间压力不均衡时,渗流场就会相应的产生(图 2);不同钻井方式下存在着不同的渗流场,而渗流场和岩石结构场的相互作用通常被称作“流固耦合”作用。
在过平衡钻井过程中,钻井液向地层渗流时往往伴随着化学作用,这种条件下的渗流场通常和泥饼性质、岩石性质(岩石类型、渗透率、孔隙度等)以及与地层孔隙压力之间的大小关系等存在密切联系[40],同时不同岩石类型(泥页岩、砂岩、碳酸盐岩和煤岩等)下流体的浸入深度也不一致[41]。
在欠平衡钻井过程中,由于负压差的存在(钻井液的化学作用常被忽略),地层流体不断流入井筒,从而造成地层孔隙压力的变化以及井壁附加应力[42]。泥页岩由于其本身的低渗特性,欠平衡钻井时压力的变化往往会造成泥页岩的压实效应以及井壁失稳的时间延迟效应,如图 6所示。对于砂岩、碳酸盐岩而言,渗透作用所产生的渗透力[43]可由式(6)求出,将其代入平衡方程(式(7)),结合边界条件,即可求得欠平衡钻井时渗流产生的附加应力。分析发现,考虑渗流时的径向应力和周向应力值大于不考虑渗流时的值,且考虑渗流时的坍塌压力通常大于不考虑渗流时的坍塌压力(图 7)[44-46]。
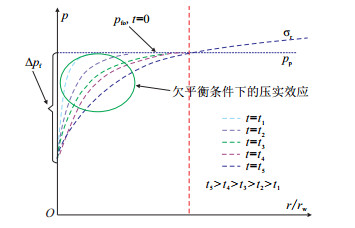 |
| 图6 泥页岩欠平衡钻井过程中的时间延迟效应和压实效应 Fig. 6 The schematic for time delayed effect and compaction effect when underbalanced drilling in shale |
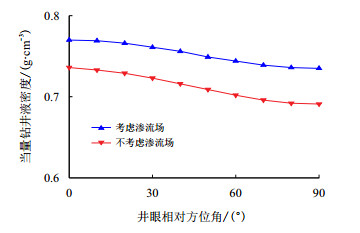 |
| 图7 考虑渗流场与不考虑渗流场时的坍塌压力对比分析 Fig. 7 Comparison of collapse pressures when fluid seepage is considered and fluid seepage is not considered |
| $ {F_{\rm{s}}} = \dfrac{{{\rm{d}}{p_{\rm{p}}}}}{{{\rm{d}}r}} $ | (6) |
| $ \dfrac{{{\rm{d}}{\sigma _{\rm r}}}}{{{\rm{d}}r}} + \dfrac{{{\sigma _{\rm r}} - {\sigma _\theta }}}{r} + {F_{\rm{s}}} = 0 $ | (7) |
可以看出,上述井壁稳定的三场耦合分析在一定程度上可以简化分析和计算流程,且具体体现了化学场、温度场以及渗流场分别对井壁稳定的影响;但三场耦合分析结果与实际情况存在一定偏差,不能完全反映井壁失稳的实际情况,因此需要进行更为准确的四场和五场耦合下的井壁失稳分析。
2.2 井壁稳定四场耦合分析以岩石结构场与应力场为基础,井壁稳定四场耦合分析目前主要集中在温度场渗流场和渗流场化学场两种耦合情况上。对于化学场和温度场的耦合,温度场的变化会影响化学反应速率,而化学反应在一定程度上会产生附加温度,但是目前针对这类耦合的研究成果较少。
2.2.1 岩石结构场-应力场-温度场渗流场耦合岩石结构场-应力场-温度场渗流场耦合的研究主要集中在孔隙介质-热弹性理论上,即研究不同孔隙介质条件下温度场对地层孔隙压力以及地层流体渗流的影响,并结合渗流场的作用(附加应力、对温度传导速率的影响等)对井壁稳定进行分析[47]。
在不同孔隙结构条件下,对于孔隙-裂缝的双重孔隙介质而言,由于温度的影响以及双重介质中的压差作用,地层流体会在两种介质中不断传递流动;与单一孔隙介质相比,双重孔隙介质条件下的井壁更容易失稳[48]。
因此,基于温度和渗流对井壁稳定的影响,王炳印等[49]分析了单一孔隙介质条件下疏松砂岩储层井壁失稳的情况,并发现在考虑温度升高及井壁渗流影响时,地层破裂压力和坍塌压力均升高,但安全钻井液密度窗口缩小;Tao等[50]则在分析了温度和渗流对花岗岩层井壁稳定影响的基础上,确定了考虑孔隙介质-热弹性时地应力和岩石力学参数的变化规律。对于泥页岩而言,结合钻遇地层的孔隙度、流度比、热扩散系数等参数,单一孔隙介质-热弹性条件下(只考虑孔隙)的井壁失稳分析模型主要包括[51]:平衡方程、孔隙介质-热弹性应力应变和应力位移关系、流体温度渗流耦合方程、热扩散方程以及相应的岩石破坏准则,Zhai等[51]给出了模型的各部分表达式。
(1)用位移表示的平衡方程(改进的Navier方程)
| $ G{u_{i, jj}} + \dfrac{G{u_{j, ji}}}{1 - 2\nu } = \alpha_{\rm b} {p_{, i}} + \dfrac{2{\alpha _{\rm m}}{T_{, i}}G(1 + \nu )}{3\left (1 - 2\nu \right) } $ | (8) |
(2)应力应变方程
| $ {\sigma _{ij}} = 2G\left ({\varepsilon _{ij}} + \dfrac{\nu }{{1 - 2\nu }}{\varepsilon _{\rm kk}}{\delta _{ij}}\right ) - \alpha_{\rm b} p{\delta _{ij}} - \\[5pt]{\kern 40pt}\dfrac{{2G{\alpha _{\rm m}}\left (1 + \nu\right )}}{{3\left (1 - 2\nu \right)}}T{\delta _{ij}} $ | (9) |
(3)流体温度渗流耦合方程
| $ \dfrac{{\partial p}}{{\partial t}} = {c^{\rm f}}\dfrac{1}{r}\dfrac{\partial }{{\partial r}}\left(r\dfrac{{\partial p}}{{\partial t}}\right) + {c^{\rm fT}}\dfrac{{\partial T}}{{\partial t}} $ | (10) |
(4)热扩散方程,见式(4)。
在上述公式的基础上,选用合适的岩石力学准则,即可进行泥页岩孔隙介质-热弹性条件下的井壁失稳分析,其简易分析流程如图 8所示。
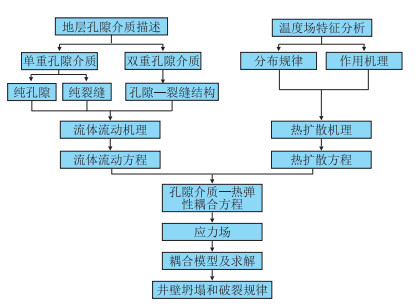 |
| 图8 结构场-应力场-温度场-渗流场耦合简易分析流程 Fig. 8 Simple analysis procedure for the coupling of rock structure-stress-temperature-seepage |
在整个岩石结构场-应力场-温度场渗流场耦合分析过程中,孔隙结构的描述和定义对于孔隙介质-热弹性理论的分析结果存在较大影响,而目前的研究成果大都集中在单重孔隙机制上(通常只考虑孔隙的影响),对于裂缝-孔隙结构的分析也只在定性层面,因此具体分析其他双重结构和多重结构对于促进孔隙介质-热弹性理论的应用具有重要意义。
2.2.2 岩石结构场-应力场-渗流场-化学场耦合在考虑岩石结构场-应力场-渗流场-化学场耦合时,目前主要针对泥页岩层段过平衡钻井过程中的井壁失稳问题。其中水基钻井液和泥页岩接触时会产生渗透水化作用,主要包括3方面的内容[52]:(1)水力压差作用下流体在地层中的流动;(2)化学势差下流体穿过泥页岩半透膜的运移;(3)溶质、离子等运移。渗透水化会导致井壁产生附加应力,同时造成岩石强度和孔隙压力的变化。因此,需要耦合渗流场和化学场来进行分析。图 9给出了过平衡状态时水力压差和化学势差作用下流体的流动情况。
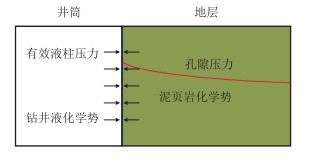 |
| 图9 水力压差和化学势差作用下井壁岩石内流体流动情况 Fig. 9 The schematic for fluid flow in wellbore rocks when hydraulic pressure and chemical potential difference are considered |
对于这种条件下的井壁失稳情况,Ghassemi等[53-54]首先分析了岩石结构场-应力场-渗流场-化学场耦合下地层孔隙压力和井周应力分布的变化规律,且发现溶质和离子扩散以及水力压差下流体流动主要受泥页岩渗透率的影响;而结合实验和数值分析,Wang等[55]根据泥页岩-钻井液体系电化势渗透产生的非线性流体流动、溶质扩散和离子运移,基于四场耦合建立了泥页岩的流-固-化耦合模型并进行了井壁失稳分析。
总体来说,岩石结构场-应力场-渗流场-化学场的四场耦合在等温条件下分析了渗流作用和化学作用的影响,能较好地体现过平衡钻井时井壁岩石的应力状态;但是不考虑温度场的影响会使得分析结果与实际情况存在一定偏差,特别是对于深井、超深井和地热井钻井时的高温情况。同时目前的四场耦合理论尚不能对欠平衡钻井时的井壁失稳问题进行准确分析,对此需要进一步研究。
2.2.3 岩石结构场-应力场-温度场化学场耦合目前岩石结构场-应力场-温度场-化学场耦合的研究整体较少,且主要针对泥页岩层段的井壁失稳情况。针对此种耦合类型,Yu等[56-57]通过结合温度和化学作用对泥页岩的影响,分析了溶质扩散、温度变化、滤液浸入等因素对地层孔隙压力和井壁应力的影响,并发现地层内部的岩石也会发生剪切破坏、岩石热膨胀系数是研究温度对井壁稳定影响的首要因素。由此结合岩石结构场-应力场-温度场-化学场耦合下的井壁失稳分析结果,即可对井眼轨迹、钻井液配方等进行优化设计。
2.3 井壁稳定五场耦合分析关于岩石结构场、应力场、渗流场、化学场以及温度场的五场耦合,通常是指温度-渗流-应力-化学耦合(THMC)理论[58]以及孔隙介质化学热弹性理论的应用,主要包括孔隙介质的热膨胀性质、温度对化学势的影响、化学渗透和热渗透对溶质和溶液流动规律的影响等内容。对于高温高压环境下的泥页岩,五场耦合时的井壁失稳模型主要包括[59]:岩石本构方程(平衡方程、应力应变和应力位移关系等)、流体渗流方程、溶质扩散方程、热传导和热对流方程,如式(11)~式(14)所示。通过将上述方程进行耦合,Zhou等[59]给出了该条件下的井壁失稳分析模型,运用有限元法即可进行求解。
| $ \left(k + \dfrac{G}{3}\right)\nabla (\nabla \cdot \boldsymbol{{u}}) + G{\nabla ^2}\boldsymbol{{u}}) + \\{\kern 40pt}\boldsymbol{{m}}({\alpha ^{'}}\nabla p - \chi \nabla {C^{\rm s}} + {\gamma _1}\nabla T) = 0 $ | (11) |
| $ \alpha \left(\nabla \dot{\boldsymbol{{u}}} \right) + B \dot{p} + {\chi ^{'}}{\dot{C^{\rm s}}} + {\gamma _2}\dot{T} - \\[5pt]{\kern 40pt}\dfrac{K}{\eta }{\nabla ^2}p + \dfrac{K}{\eta }{L_{\rm{D}}}{\nabla ^2}{C^{\rm{s}}} = 0 $ | (12) |
| $ \phi \dot{{C^{\rm s}}} + {D^{\rm s}}{\nabla ^2}{C^{\rm s}} - {C^{\rm s}}{D^{\rm T}}{\nabla ^2}T = 0 $ | (13) |
| $ \dot{T} - {C^{\rm{T}}}{\nabla ^2}T = 0 $ | (14) |
五场耦合分析是目前对井壁失稳时各类因素影响较为全面的考虑,但是井壁稳定五场耦合分析理论还需要不断丰富,特别其在欠平衡钻井中的应用,同时五场耦合之外的作用场对于井壁失稳的影响也需要进一步的研究。
3 井壁稳定多场耦合分析展望通过前文总结分析,可以得出井壁稳定的多场耦合分析示意图,如图 10所示,为简便表示,岩石结构场和应力场统一表示。对于目前的井壁稳定多场耦合分析而言,特别是针对过平衡或者平衡钻井时的井壁失稳分析,其分析方法已经取得了较大的进步,而井壁稳定多场耦合分析未来的发展趋势主要有以下4个方面。
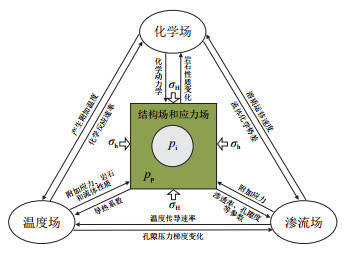 |
| 图10 井壁稳定多场耦合分析示意图 Fig. 10 The schematic for multi filed coupling analysis of wellbore stability |
对于深井和超深井钻井而言,由于深部地层构造运动的影响以及高温高压条件下复杂的水化学环境,地应力条件以及岩石性质会相应地发生变化。因此在深入研究井壁稳定的五场耦合过程中,首先需要建立较为准确的地质力学模型,从而分析研究区域的地应力状态和变化规律;其次岩石结构场的构建和描述以及化学场和温度场扰动的研究对于解决五场耦合(THMC)问题至关重要,这决定了后期模型建立和求解的难易程度;同时借助有限元、有限差分等相关理论进行模型建立、求解和验证也是五场耦合(THMC)中的一个重要方面。特别是对于模型验证,目前少有能够实现井壁稳定多场耦合的模拟装置,因此也需要进一步研究多场耦合实验的设计原理,从而多开展井壁稳定的多场耦合试验。
3.2 欠平衡钻井条件下化学场的作用研究化学场在以往的欠平衡钻井井壁失稳分析过程中往往被忽略,因此在进行欠平衡钻井时,分析负压差条件下化学场对井壁岩石的作用机理至关重要,主要包括确定钻井液滤液侵入地层的条件、方式和侵入量以及地层流体和钻井液对井壁岩石的双向作用等内容。在理论和实验研究方面,钻井过程中井壁岩石毛管自吸、毛管力等相关研究已经取得了一定成果;但针对欠平衡钻井过程中流体侵入方式以及化学场作用机理的实验和理论研究较少且不深入,特别是在实验研究上,如何确定化学场作用的实验表征是极为棘手的问题。
3.3 岩石结构场在多场耦合作用下变形机制的深入研究岩石结构场的表征和监测是井壁稳定多场耦合分析的重要基础条件之一。在多场耦合分析过程中,不同岩石结构场在多场耦合作用下的变形机制各异,并且其变化存在实时性、动态性和长期性等特点,这就增加了多场耦合下岩石结构场模拟和监测的困难。因此需要通过结合实验和理论研究,加强相关模拟和监测技术的应用和研发,对单重介质(纯孔隙结构、纯裂缝结构以及纯溶洞结构)、双重介质(孔隙-裂缝结构、孔隙溶洞结构以及裂缝-溶洞结构)和三重介质(孔隙-裂缝-溶洞结构)在多场耦合下的变形机理进行深入研究,从而探索不同介质变形机理下化学场、温度场和渗流场的变化规律。
3.4 其他作用场对井壁稳定的影响研究其他作用场主要包括井下工具作用、钻井液与井壁岩石之间的流固耦合作用等内容,而在其研究过程中,多学科领域(管柱力学、流体力学等)交叉应用是其成功分析的关键。井下工具的作用主要指钻具的振动,以往的研究已经对钻具振动时井壁稳定所受影响作了一定阐述[60-61],但结合钻具振动和前文所列5类作用场的研究较少。而井筒内钻井液与井壁岩石之间的流固耦合作用主要指钻井液流动对井壁岩石的影响以及井壁岩石对钻井液流动的影响,其中建立相应的流固耦合作用模型(包括作用机制、耦合方式、应力分解等)是分析的关键。
4 结论(1)井壁失稳的各类影响因素可以分为5类作用场,即岩石结构场、应力场、渗流场、温度场和化学场,同时给出了各类作用场的具体内容和产生原因。
(2)在井壁稳定多场耦合分析过程中,应力场和岩石结构场是分析的基础,文章总结了井壁稳定分析的岩石结构类型和岩石变形机制。
(3)在目前的井壁稳定多场耦合研究中,三场耦合分析主要包括:岩石结构场-应力场-化学场、岩石结构场-应力场-温度场、岩石结构场-应力-场-渗流场三种耦合情况;四场耦合分析时,主要以岩石结构场与应力场为基础,进行温度场-渗流场以及渗流场-化学场两种情况的耦合;在四场和五场耦合分析中,孔隙介质-热弹性理论和孔隙介质-化学-热弹性理论应用较为广泛。
(4)对于井壁稳定的多场耦合研究,今后的相关课题包括:THMC耦合作用的深入探究、欠平衡钻井过程中化学场的作用研究、岩石结构场在多场耦合条件下变形机制的深入研究以及其他作用场对井壁稳定的影响等。
符号说明
R——普适气体常数,R=8.314 J/(K
下标
| [1] | WESTERGAARD H M. Plastic state of stress around a deep well[J]. Elasticity, 1940, 27: 1–5. |
| [2] | ZHANG Jincai. Borehole stability analysis accounting for anisotropies in drilling to weak bedding planes[J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 60: 160–170. doi: 10.1016/j.ijrmms.2012.12.025 |
| [3] |
施斌. 论工程地质中的场及其多场耦合[J].
工程地质学报, 2013, 21(5): 673–680.
SHI Bin. On fields and their coupling in engineering geology[J]. Journal of Engineering Geology, 2013, 21(5): 673–680. doi: 10.3969/j.issn.1004-9665.2013.05.001 |
| [4] | REISABADI Z, KAFFASH A, SHADIZADEH S R. Determination of optimal well trajectory during drilling and production based on borehole stability[J]. International Journal of Rock Mechanics & Mining Sciences, 2012, 56: 77–87. doi: 10.1016/j.ijrmms.2012.07.018 |
| [5] |
徐四龙, 余维初, 张颖. 泥页岩井壁稳定的力学与化学耦合 (协同) 作用研究进展[J].
石油天然气学报, 2014, 36(1): 151–153.
XU Silong, YU Weichu, ZHANG Ying. Research progress of mechanic and chemical coupling for shale wellbore stability[J]. Journal of Oil and Gas Technology, 2014, 36(1): 151–153. doi: 10.3969/j.issn.1000-9752.2014.01.032 |
| [6] | FJAR E, HOLT R M, RAAEN A M, et al. Petroleum related rock mechanics[M]. 2nd ed. Elsevier, 2008. |
| [7] |
楼一珊, 金业权.
岩石力学与石油工程[M]. 北京: 石油工业出版社, 2006.
LOU Yishan, JIN Yequan. Rock mechanics and petroleum engineering[M]. Beijing: Petroleum Industry Press, 2006. |
| [8] |
申瑞臣, 屈平, 杨恒林. 煤层井壁稳定技术研究进展与发展趋势[J].
石油钻探技术, 2010, 38(3): 1–7.
SHEN Ruichen, QU Ping, YANG Henglin. Advancement and development of coal bed wellbore stability technology[J]. Petroleum Drilling Techniques, 2010, 38(3): 1–7. doi: 10.3969/j.issn.1001-0890.2010.03.001 |
| [9] | JIN Yan, CHEN Kangping, CHEN Mian. Development of tensile stress near a wellbore in radial porous media flows of a high pressure gas[J]. International Journal of Rock Mechanics & Mining Sciences, 2011, 48: 1313–1319. doi: 10.1016/j.ijrmms.2011.09.013 |
| [10] | HONG Wang, TOWLER B F, SOLIMAN M Y. Fractured wellbore stress analysis:Sealing cracks to strengthen a wellbore[C]. SPE 104947, 2007. doi:10.2118/104947-MS |
| [11] | ZHANG Jincai, BAI Mao, ROEGIERS J C. On drilling directions for optimizing horizontal well stability using a dual-porosity poroelastic approach[J]. Journal of Petroleum Science and Engineering, 2006, 53: 61–76. doi: 10.1016/j.petrol.2006.02.001 |
| [12] | CROOK T, WILLSON S, YU Jianguo, et al. Computational modeling of the localized deformation associated with borehole breakout in quasi-brittle materials[J]. Journal of Petroleum Science and Engineering, 2003, 38: 177–186. doi: 10.1016/S0920-4105(03)00031-7 |
| [13] | SCHOENBALL M, SAHARA D P, KOHL T. Timedependent brittle creep as a mechanism for time-delayed wellbore failure[J]. International Journal of Rock Mechanics & Mining Sciences, 2014, 70: 400–406. doi: 10.1016/j.ijrmms.2014.05.012 |
| [14] |
卢运虎, 陈勉, 袁建波, 等. 各向异性地层中斜井井壁失稳机理[J].
石油学报, 2013, 34(3): 563–568.
LU Yunhu, CHEN Mian, YUAN Jianbo, et al. Borehole instability mechanism of a deviated well in anisotropic formations[J]. Acta Petrolei Sinica, 2013, 34(3): 563–568. doi: 10.7623/syxb201303022 |
| [15] | BRADLEY W B. Mathematical concept-stress cloud can predict borehole failure[J]. Oil & Gas Journal, 1979, 77(8): 92–102. |
| [16] |
张广清. 分支井筒稳定的塑性力学模型及分析[J].
中国石油大学学报 (自然科学版), 2013, 37(5): 81–87.
ZHANG Guangqing. Plastic mechanics model for wellbore stability analysis of branched wells[J]. Journal of China University of Petroleum, 2013, 37(5): 81–87. doi: 10.3969/j.issn.1673-5005.2013.05.012 |
| [17] |
张立松, 闫相祯, 杨秀娟, 等. 基于Hoek-Brown准则的深部煤层钻井坍塌压力弹塑性分析[J].
煤炭学报, 2013, 38(1): 85–90.
ZHANG Lisong, YAN Xiangzhen, YANG Xiujuan, et al. Elasto-plastic analysis of collapse pressure for deep coal seam drilling based on Hoek-Brown criterion[J]. Journal of China Coal Society, 2013, 38(1): 85–90. |
| [18] | LEE Y K. A nonlinear rock failure criterion taking account of the intermediate principal stress[C]. ISRM-ARMS 7-2012-027, 2012. |
| [19] |
张培丰. 地层温度对科学超深井井壁稳定的影响[J].
探矿工程 (岩土钻掘工程), 2011, 38(10): 1–5.
ZHANG Peifeng. Effect of the formation temperature on the hole-wall stability in ultra-deep scientific drilling[J]. Exploration Engineering (Rock & Soil Drilling and Tunneling), 2011, 38(10): 1–5. doi: 10.3969/j.issn.1672-7428.2011.10.001 |
| [20] | HODGE M O, VALENCIA K L, CHEN Zhixi. Analysis of time-dependent wellbore stability of underbalanced wells using a fully coupled poroelastic model[C]. SPE 102873, 2006. doi:10.2118/102873-MS |
| [21] | ABOUSLEIMAN Y, ROEGIERS J C, CUI L, et al. Poroelastic solution of an inclined borehole in a transversely isotropic medium[C]. USRMS 0313, 1995. |
| [22] | XU G, GUO Q, ZHENG Z. A finite element poro-inelastic analysis of borehole problems[J]. International Journal of Rock Mechanics & Mining Sciences, 1997, 34: 342.e1–342.e10. doi: 10.1016/S1365-1609(97)00258-X |
| [23] | MULLER A L, VARGAS E A, VAZ L E, et al. Borehole stability analysis considering spatial variability and poroelastoplasticity[J]. International Journal of Rock Mechanics & Mining Sciences, 2009, 46: 90–96. doi: 10.1016/j.-ijrmms.2008.05.001 |
| [24] | WU Bailin, WU Bisheng, ZHANG Xi, et al. Wellbore stability analyses for HPHT wells using a fully coupled thermo-poroelastic model[C]. SPE 144978, 2011. doi:10.2118/144978-MS |
| [25] | HALE A H, MODY F K. The influence of chemical potential on wellbore stability[J]. spe drilling & completion, 1993, 8(3): 207–216. doi: 10.2118/23885-PA |
| [26] | YEW C H, CHENEVERT M E, WANG C L. Wellbore stress distribution produced by moisture adsorption[J]. SPE Drilling Engineering, 1990, 5(4): 311–316. doi: 10.2118/19536-PA |
| [27] | JAEGER J C, COOK N G W, ZIMMERMAN R. Fundamentals of rock mechanics[M]. John Wiley & Sons, 2009. |
| [28] | LEE H, ONG S H, AZEEMUDDIN M, et al. A wellbore stability model for formations with anisotropic rock strengths[J]. Journal of Petroleum Science and Engineering, 2012, 96: 109–119. doi: 10.1016/j.petrol.2012.08.-010 |
| [29] | ZOBACK M D. Reservoir geomechanics[M]. Cambridge University Press, 2010. |
| [30] | AADNOY B S. Modeling of the stability of highly inclined boreholes in anisotropic rock formations (includes associated papers 19213 and 19886)[J]. SPE Drilling Engineering, 1988, 3(3): 259–268. doi: 10.2118/16526-MS |
| [31] |
黄荣樽, 陈勉, 邓金根, 等. 泥页岩井壁稳定力学与化学的耦合研究[J].
钻井液与完井液, 1995, 12(3): 15–21.
HUANG Rongzun, CHEN Mian, DENG Jingen, et al. Study on shale stability of wellbore by mechanics coupling with chemistry method[J]. Drilling Fluid and Completion Fluid, 1995, 12(3): 15–21. |
| [32] |
温航, 陈勉, 金衍, 等. 硬脆性泥页岩斜井段井壁稳定力化耦合研究[J].
石油勘探与开发, 2014, 41(6): 748–754.
WEN Hang, CHEN Mian, JIN Yan, et al. A chemomechanical coupling model of deviated borehole stability in hard brittle shale[J]. Petroleum Exploration and Development, 2014, 41(6): 748–754. doi: 10.11698/PED.2014.-06.16 |
| [33] |
张艳娜, 孙金声, 王强, 等. 井壁稳定的化学动力学分析[J].
断块油气田, 2011, 18(6): 794–798.
ZHANG Yanna, SUN Jinsheng, WANG Qiang, et al. Analysis on chemical kinetics of wellbore stability[J]. Fault-Block Oil & Gas Field, 2011, 18(6): 794–798. |
| [34] |
邓虎, 孟英峰. 泥页岩稳定性的化学与力学耦合研究综述[J].
石油勘探与开发, 2003, 30(1): 109–111.
DENG Hu, MENG Yingfeng. A discussion on shale stability coupling with mechanics and chemistry[J]. Petroleum Exploration and Development, 2003, 30(1): 109–111. doi: 10.3321/j.issn:1000-0747.2003.01.033 |
| [35] |
何世明, 尹成, 徐壁华. 确定注水泥与钻井过程中井内循环温度的数学模型[J].
天然气工业, 2002, 22(1): 42–45.
HE Shiming, YIN Cheng, XU Bihua, et al. Mathematical model of determining borehole circulating temperatures in cementing and drilling processes[J]. Natural Gas Industry, 2002, 22(1): 42–45. doi: 10.3321/j.issn:1000-0976.2002.-01.012 |
| [36] |
郤保平, 赵阳升. 高温高压下花岗岩中钻孔围岩的热物理及力学特性试验研究[J].
岩石力学与工程学报, 2010, 29(6): 1245–1253.
XI Baoping, ZHAO Yangsheng. Experimental study of thermophysico-mechanical property of drilling surrounding rock in granite under high temperature and high pressure[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(6): 1245–1253. |
| [37] |
赵金洲, 彭瑀, 李勇明, 等. 基于双层非稳态导热过程的井筒温度场半解析模型[J].
天然气工业, 2016, 36(1): 68–75.
ZHAO Jinzhou, PENG Yu, LI Yongming, et al. A semi-analytic model of wellbore temperature field based on double-layer unsteady heat conducting process[J]. Natural Gas Industry, 2016, 36(1): 68–75. doi: 10.3787/j.issn.1000-0976.2016.01.008 |
| [38] | CHEN G, CHENEVERT M E, SHARMA M M, et al. A study of wellbore stability in shales including poroelastic, chemical, and thermal effects[J]. Journal of Petroleum Science and Engineering, 2003, 38(3): 167–176. doi: 10.1016/S0920-4105(03)00030-5 |
| [39] | NGUYEN D A, MISKA S Z, YU M, et al. Modeling thermal effects on wellbore stability[C]. SPE 133428, 2010. doi:10.2118/133428-MS |
| [40] |
魏臣兴, 练章华, 丁亮亮, 等. 分支井渗流-应力耦合场分析[J].
岩性油气藏, 2011, 23(4): 124–128.
WEI Chenxing, LIAN Zhanghua, DING Liangliang, et al. Analysis of seepage-stress coupling field for lateral wells[J]. Lithologic Reservoirs, 2011, 23(4): 124–128. |
| [41] | GENTZIS T, DEISMAN N, CHALATURNYK R J. A method to predict geomechanical properties and model well stability in horizontal boreholes[J]. International Journal of Coal Geology, 2009, 78(2): 149–160. doi: 10.1016/j.-coal.2008.11.001 |
| [42] |
何世明, 安文华, 王书琪, 等. 渗流对欠平衡钻井井壁稳定性的影响[J].
石油钻采工艺, 2008, 30(4): 12–16.
HE Shiming, AN Wenhua, WANG Shuqi, et al. Effect of percolation on wellbore stability of underbalanced drilling[J]. Oil Drilling & Production Technology, 2008, 30(4): 12–16. |
| [43] |
黄阜, 杨小礼. 考虑渗透力和原始Hoek-Brown屈服准则时圆形洞室解析解[J].
岩土力学, 2010, 31(5): 1627–1632.
HUANG Fu, YANG Xiaoli. Analytical solution of circular openings subjected to seepage in Hoek-Brown media[J]. Rock and Soil Mechanics, 2010, 31(5): 1627–1632. doi: 10.3969/j.issn.1000-7598.2010.05.048 |
| [44] | HE S, WANG W, TANG M, et al. Effects of fluid seepage on wellbore stability of horizontal wells drilled underbalanced[J]. Journal of Natural Gas Science and Engineering, 2014, 21: 338–347. doi: 10.1016/j.jngse.2014.08.016 |
| [45] | HE S, WANG W, SHEN H, et al. Factors influencing wellbore stability during underbalanced drilling of horizontal wells-When fluid seepage is considered[J]. Journal of Natural Gas Science and Engineering, 2015, 23: 80–89. doi: 10.1016/j.jngse.2015.01.029 |
| [46] | ISLAM M A, SKALLE P, FARUK A O, et al. Analytical and numerical study of consolidation effect on time delayed borehole stability during underbalanced drilling in shale[C]. SPE 127554, 2009. |
| [47] | LI L C, TANG C A, TANG S B, et al. Coupled thermo-hydro-mechanical analyses of thermal effects on fluid flow with 2D finite element method[C]. ISRM-ARMS5-2008-155, 2008. |
| [48] | GELET R, LORET B, KHALILI N. Borehole stability analysis in a thermoporoelastic dual-porosity medium[J]. International Journal of Rock Mechanics & Mining Sciences, 2012, 50: 65–76. doi: 10.1016/j.ijrmms.2011.12.-003 |
| [49] |
王炳印, 蔚宝华, 邓金根. 温度及渗流对疏松砂岩储层钻井液密度窗口的影响规律研究[J].
钻井液与完井液, 2005, 22(4): 40–42.
WANG Binyin, WEI Baohua, DENG Jin'gen. Temperature and seepage effects on safe mud window of unconsolidated sand reservoir formation[J]. Drilling Fluid & Completion Fluid, 2005, 22(4): 40–42. doi: 10.3969/j.issn.-1001-5620.2005.04.013 |
| [50] | TAO Q, GHASSEMI A. Poro-thermoelastic borehole stress analysis for determination of the in situ stress and rock strength[J]. Geothermics, 2010, 39(3): 250–259. doi: 10.1016/j.geothermics.2010.06.004 |
| [51] | ZHAI Z, ZAKI K, MARINELLO S. Coupled thermo-poro-mechanical effects on borehole stability[C]. SPE 123427, 2009. doi:10.2118/123427-MS |
| [52] |
毕博. 泥页岩渗透水化作用对井壁稳定的影响[J].
钻井液与完井液, 2011, 28(S): 1–3.
BI Bo. Research on borehole stability affected by shale penetration and hydration[J]. Drilling Fluid and Completion Fluid, 2011, 28(S): 1–3. doi: 10.3969/j.issn.1001-5620.2011.z1.001 |
| [53] | GHASSEMI A, DIEK A. Linear chemo-poroelasticity for swelling shales:theory and application[J]. Journal of Petroleum Science and Engineering, 2003, 38(3): 199–212. doi: 10.1016/S0920-4105(03)00033-0 |
| [54] | ROSHAN H, RAHMAN S S. A fully coupled chemo-poroelastic analysis of pore pressure and stress distribution around a wellbore in water active rocks[J]. Rock Mechanics and Rock Engineering, 2011, 44(2): 199–210. doi: 10.1007/s00603-010-0104-7 |
| [55] | WANG Qian, ZHOU Yingcao, WANG Gang, et al. A fluid-solid-chemistry coupling model for shale wellbore stability[J]. Petroleum Exploration and Development, 2012, 39(4): 475–480. doi: 10.1016/S1876-3804(12)60069-X |
| [56] | YU M, CHEN G, CHENEVERT M E, et al. Chemical and thermal effects on wellbore stability of shale formations[C]. SPE 71366, 2001. doi:10.2118/71366-MS |
| [57] | AL-BAZALI T, ZHANG J, CHENEVERT M E, et al. Maintaining the stability of deviated and horizontal wells:Effects of mechanical, chemical and thermal phenomena on well designs[J]. Geomechanics and Geoengineering:An International Journal, 2008, 3(3): 167–178. doi: 10.2118/100202-MS |
| [58] | YIN S, TOWLER B F, DUSSEAULT M B, et al. Fully coupled THMC modeling of wellbore stability with thermal and solute convection considered[J]. Transport in porous media, 2010, 84(3): 773–798. doi: 10.1007/s11242-010-9540-9 |
| [59] | ZHOU X, GHASSEMI A. Finite element analysis of coupled chemo-poro-thermo-mechanical effects around a wellbore in swelling shale[J]. International Journal of Rock Mechanics & Mining Sciences, 2009, 46: 769–778. doi: 10.1016/j.ijrmms.2008.11.009 |
| [60] | HELIO S, PLACIDO J C R, CLAUDIO W. Consequences and relevance of drillstring vibration on wellbore stability[C]. SPE 52820, 1999. doi:10.2118/52820-MS |
| [61] | ZHU Xiaohua, LIU Weiji. The effects of drill string impacts on wellbore stability[J]. Journal of Petroleum Science and Engineering, 2013, 109: 217–229. doi: 10.1016/j.-petrol.2013.08.004 |
 2017, Vol. 39
2017, Vol. 39 图1(Fig. 1)
图1(Fig. 1)



