近年来,管道安全观念不断增强,对管道内检测技术的要求不断提高。管道内检测技术包括管内缺陷的定位和特征确定两方面,指在不影响管道正常运作的条件下,运用智能检测设备对管道内部存在的安全隐患,实施检测定位并确定其类别、范围和损坏程度,以进行及时有效的维护,用检修代替抢修,避免安全事故的发生,保障管道的安全运行。
目前,中国主要运用里程仪进行管道内部定位[1]。由于里程仪属于接触式定位,其定位精度受加工差异、管道内壁状况(石蜡、油污等)、焊缝引起的里程轮转动失常等因素影响,在管道内部长距离运行会产生较大的累积误差。沈跃[2]提出了脉冲总数均分算法和速度补偿算法来提高里程仪定位精度,陈建军等[3]提出在清管器上加装钢刷,清除管内壁的石蜡,降低里程轮打滑的可能性,提高定位精度,虽然提出了大量的新算法及结构改进方案,但里程仪仍然有较大的定位误差,增加维修维护、抢险工作量和工作时间,不能满足实际工程需要。捷联惯性导航系统利用陀螺仪确定检测设备的姿态信息,利用加速度计得到比力信息,根据姿态信息分解比力到参考坐标系,对分解后的比力值进行积分,得到检测设备的速度和位置信息。惯性导航以其自主性强,不依赖于外界条件,可独立完成导航任务和短期内具有较高精度和稳定性等优点,在一定程度上弥补了里程仪等单一管道内部定位方法的不足[4]。国外管道内部定位主要采用以惯性导航为主的组合导航定位技术,实现了管道内部的高精度定位[5-6]。由于国际上的技术封锁,近年来组合导航技术在中国管道内部定位应用中刚刚起步。
基于此,本文探讨运用里程仪和捷联惯性导航系统(Strap-down Inertial Navigation System,SINS)进行管道内部组合导航定位,克服单一定位方法的缺陷,建立了轨迹仿真器、惯导器件和里程仪仿真模型,并结合卡尔曼滤波数据融合技术进行仿真试验,从组合导航的管道内部定位误差结果分析来看,大幅提高了管道内部缺陷定位精度,为管道内部精确定位提供了重要的理论指导。
1 里程仪速度解算及其误差模型由检测设备运动特点可知,管道内的定位具有不完整性约束的特点[7],检测设备沿管道的轴向有速度,而在与之垂直的其他两个方向速度可记为零。图 1为管道内部导航的速度特征简图 ($v$——速度,m/s;$x$,$y$,$z$——机体坐标系的3个方向)。假设检测器行驶的速度是$v$,方向是检测器运行管道的正前方$x$轴方向,则可以将里程仪的速度特征公式描述为${\boldsymbol{{v}}_{\rm b}} = {\left[v_{{x}}, 0, 0\right]^{\rm T}}$。
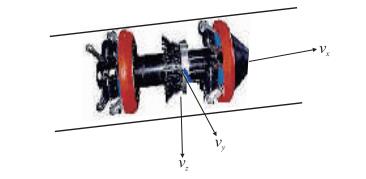 |
| 图1 管道内部导航速度特征简图 Fig. 1 Velocity characteristics diagram of pipeline internal navigation |
根据机体坐标系和导航坐标系(地理系)之间的转换关系,可以将里程仪的速度公式转换到导航坐标系中
| $ {\boldsymbol{ v}_{\rm n}} = \boldsymbol{ C}_{\rm b}^{\rm n}{\boldsymbol{ v}_{\rm b }} $ | (1) |
式中:${\boldsymbol{ v}_{\rm n}}$——导航坐标系中里程仪速度,m/s;
${\boldsymbol{ v}_{\rm b}}$——机体坐标系中里程仪速度,m/s;
$\boldsymbol{ C}_{\rm b}^{\rm n}$——姿态转换矩阵,无因次。
式(1)计算可得到导航坐标系下速度方程,对速度做积分运算得到里程仪的位置方程,同样可以将得到的方程经推导得到位置的经纬度参数。
由里程仪的速度计算方程以及里程仪的误差特点可以推导导航坐标系下速度误差方程,如式(2)所示
| $ \delta {\boldsymbol{ v}_{\rm n}} =-\boldsymbol{ \phi} \times {\boldsymbol{ v}_{\rm n}} + \boldsymbol{ C}_{\rm b}^{\rm n}\delta {\boldsymbol{ v}_{\rm b}} $ | (2) |
式中:$\delta {\boldsymbol{ v}_{\rm n}}$——导航坐标系中速度误差,m/s;
$\delta {\boldsymbol{ v}_{\rm b}}$——机体坐标系中里程仪量测噪声,m/s;
$\boldsymbol{\phi}$——姿态角误差矩阵,无因次。
$\boldsymbol{ \phi}$,$\delta {\boldsymbol{ v}_{\rm b}}$由检测管道的环境以及里程仪的性能参数决定[8],本文将其考虑成一阶马尔科夫过程,其误差满足$E\left ({\delta {\boldsymbol{ v}_{\rm b}}} \right)= 0$,$E\left ({\delta {\boldsymbol{ v}_{\rm b}}, \delta {\boldsymbol{ v}_{\rm b}}{^{\rm T}}} \right)= {{\boldsymbol{R}}}$的条件(${\boldsymbol{R}}$为正定阵)。
2 组合导航数据融合技术数据融合技术是使用多个器件对系统中某一特定问题而展开的数据处理研究。利用多个器件获得的不同数据,得出对研究对象特征全面的、正确的认识,克服了单一器件带来的误报、可信度差和容错能力低的缺点。
2.1 数据融合方法管道内部缺陷定位数据融合包括回路反馈法和最优估计法两种方法,其中回路反馈法是采用经典的控制方法,抑制系统误差,使子系统间性能互补;最优估计法是采用现代控制理论中的最优估计法,从概率统计最优的角度估算出系统误差并消除。由于组合导航系统的各子系统误差具有随机特性,所以最优估计法远优于回路反馈法,本文采用最优估计法作为数据融合的方法。当前基于最优化估计法的数据融合算法较多,主要有最小二乘法、极大验后、贝叶斯估计、维纳滤波以及卡尔曼滤波等方法。其中最小二乘估计适用于对常值向量的估计,估计中不必使用与被估计量有关的动态信息与统计信息,甚至连量测误差的统计信息都可以不必使用,所以估计精度不高。极大验后、贝叶斯估计、极大似然估计都与条件概率密度有关,除一些特殊的分布(如正态分布)外,计算都十分困难,这些估计常用于故障检测和识别的算法中。维纳滤波器是一种线性定常系统,适用于对有用信号和噪声都是零均值的平稳随机过程的处理;设计维纳滤波器时必须已知有用信号和噪音的自功率谱和互功率谱。与卡尔曼滤波相比,维纳滤波在适用范围和设计方法方面存在很多不足。
卡尔曼滤波是对随机信号作估计的主要方法之一,与最小二乘、贝叶斯、维纳滤波等诸多计算方法相比,卡尔曼滤波具有以下显著的特点[9]:首先,采用状态空间法在时域内设计滤波器,用状态方程描述复杂多维信号的动力学特性,避开了在频域内对信号功率谱作分析带来的麻烦。其次,采用递推算法实时量测得到的信息,分析后用于系统状态参数的估计,而不必储存过程中的量测值。第三,具有连续型和离散型两类算法,对于连续型的也可以通过将算法进行离散化处理,得到离散型的卡尔曼方程,可以直接在计算机上实现。采用卡尔曼滤波技术对组合导航系统进行数据融合处理具有以下优势。
(1)充分利用各子系统的定位信息,获得单个子系统不具备的功能和精度。
(2)各子系统能够优势互补,扩大系统的适用范围。
(3)各子系统观测同一信息源,提高测量值的数量,增加冗余度,提高整个系统的可靠性。
2.2 卡尔曼滤波在组合定位系统中的应用 2.2.1 卡尔曼滤波基本原理卡尔曼滤波是一种递推线性最小方差估计,用状态参数来表征各物理量,用状态方程和量测方程来描述系统的动力学特征。对于组合导航系统,卡尔曼滤波就是根据当前检测器运动的量测信息推测下一时刻检测器运行情况。但是因为各种误差的引入使下一刻可能出现两个(预测和实际)坐标位置[10],为了得到下一时刻误差更小的目标位置,通常将二者折中,即以量测的信息校正预测的位置。相对于其他滤波技术,该方法主要从数据处理的角度估算噪声造成的误差大小,并进行修正,从而提高定位精度。
2.2.2 离散型卡尔曼滤波方程如果假设${k}$时刻被估计状态${X_k}$受系统噪声序列${W_{k-1}}$驱动,则驱动机理可以按式(3)描述系统的状态方程
| $ {{{\boldsymbol{X}}}_k} = {\boldsymbol{ \varPhi} _{k, k-1}}{{{\boldsymbol{X}}}_{k-1}} + {\boldsymbol{ \varGamma} _{k, k-1}}{{\boldsymbol{W}}_{k-1}} $ | (3) |
式中:${{\boldsymbol{X}}}_k$——${k}$时刻的状态矩阵,$k=1, 2, \cdots$;
${\boldsymbol{ \varPhi} _{k, k-1}}$——${{k-1}}$时刻至${k}$时刻的转移矩阵;
${\boldsymbol{ \varGamma} _{k, k-1}}$——${{k-1}}$时刻至${k}$时刻的噪声驱动矩阵;%,为系统的激励噪声序列;
${{\boldsymbol{W}}_{k-1}}$——${{k-1}}$时刻的系统激励噪声序列。
对${{\boldsymbol{X}}_k}$的量测满足线性关系,量测方程为
| $ {{\boldsymbol{Z}}_k} = {{\boldsymbol{H}}_k}{{\boldsymbol{X}}_k} + {{\boldsymbol{V}}_k} $ | (4) |
式中:${\boldsymbol{Z}}_k$——${k}$时刻状态${\boldsymbol{X}}_k$的量测值;
${{\boldsymbol{H}}_k}$——${k}$时刻的量测阵;
${{\boldsymbol{V}}_k}$——${k}$时刻的量测噪声。
同时,${{{\boldsymbol{W}}}_{k-1}}$和${{{\boldsymbol{V}}}_k}$两个参数满足式(5)
| $ \left\{ \begin{array}{l} E\left({{{{\boldsymbol{W}}}_{k-1}}} \right)= 0\\ E\left({{{{\boldsymbol{V}}}_k}} \right)= 0 \\ E\left({{{{\boldsymbol{W}}}_k}{{{\boldsymbol{W}}}_i}^{\rm T}} \right)= {{{\boldsymbol{Q}}}_k}{\delta _{ki}}\\ E\left({{{{\boldsymbol{V}}}_k}{{{\boldsymbol{V}}}_i}^{\rm T}} \right)= {{{\boldsymbol{R}}}_k}{\delta _{ki}}\\ E\left({{{{\boldsymbol{W}}}_k}{{{\boldsymbol{V}}}_i}^{\rm T}} \right)= 0 \end{array} \right. $ | (5) |
式中:$E ()$——数学期望运算函数;
${{{\boldsymbol{Q}}}_k}$——系统噪声的方差阵,为零阵或正定阵;
${{{\boldsymbol{R}}}_k}$——量测噪声的方差阵,为正定阵;
${{{\boldsymbol{W}}}_i}$——$i$时刻的系统激励噪声序列;
${{{\boldsymbol{V}}}_i}$——$i$时刻的量测噪声,
${\delta _{ki}}$——Kronecker-$\delta$函数,如果$k=i$,则${\delta _{ki}} = 0$;如果$k\neq i$,则${\delta _{ki}} = 0$。
基于上述状态方程和量测方程,对${{{\boldsymbol{X}}}_k}$的估计可以按以下的步骤求解。
(1)计算状态一步预测值${{{\boldsymbol{X}}}_{k, k-1}}$
| $ {{{\boldsymbol{X}}}_{k, k-1}} = {\boldsymbol{ \varPhi} _{k, k-1}}{{{\boldsymbol{X}}}_{k-1}} $ |
式中:${{{\boldsymbol{X}}}_{k, k-1}}$——状态一步预测值。
(2)计算一步预测均方误差${{{\boldsymbol{X}}}_k}$:
| $ {{{\boldsymbol{P}}}_{k, k - 1}} = {\boldsymbol{ \varPhi} _{k, k - 1}}{{{\boldsymbol{P}}}_{k - 1}}{\boldsymbol{ \varPhi} ^{\rm T}}_{k, k - 1} + {{{\boldsymbol{Q}}}_{k - 1}} $ |
式中:${{{\boldsymbol{P}}}_{k, k-1}}$——一步预测均方误差;
${{{\boldsymbol{Q}}}_{k-1}}$——$k$时刻的系统噪声方差。
(3)计算滤波增益
| $ {{{\boldsymbol{K}}}_k} = {{{\boldsymbol{P}}}_{k, k-1}}{{{\boldsymbol{H}}}_k}^{\rm T}{\left[{{{{\boldsymbol{H}}}_k}{{{\boldsymbol{P}}}_{k, k-1}}{{{\boldsymbol{H}}}_k}^{\rm T} + {{{\boldsymbol{R}}}_k}} \right]^{-1}} $ |
式中:${{\boldsymbol{K}}}_{k}$——滤波增益。
(4)计算状态估计值:
| $ {{{\boldsymbol{X}}}_k} = {\boldsymbol{ \varPhi} _{k, k-1}}{{{\boldsymbol{P}}}_{k-1}}{\boldsymbol{ \varPhi} ^{\rm T}}_{k, k-1} + {{{\boldsymbol{Q}}}_{k-1}} $ |
(5)计算估计均方误差
| $ {{{\boldsymbol{P}}}_k} = \left({{{\boldsymbol{E}}}-{{{\boldsymbol{K}}}_k}{{{\boldsymbol{H}}}_k}} \right){{{\boldsymbol{P}}}_{k, k-1}} $ |
式中:${{\boldsymbol{E}}}$——标准单位矩阵。
上述5个步骤为离散型卡尔曼滤波的基本过程,给定初值($k=0$)时${{{\boldsymbol{X}}}_0}$和${{\boldsymbol{P}}_0}$,就可以递推计算得到$k$时刻的状态估计${{{\boldsymbol{X}}}_k}$。
3 组合定位系统的数学模型 3.1 组合定位系统的设计模式 3.1.1 组合定位滤波状态量的选取组合定位滤波状态量的选取包括直接法和间接法两种方法[11],直接法是以导航参数作为估计对象,系统方程多为非线性的,能直接描述系统导航动态过程的参数,反映真实状态的演变。但是状态参数既有位置和速度等自身状态参数,也有数值较小的误差(姿态误差角),数值相差大,导航精度低。间接法是以各子系统的误差量(位置误差、速度误差等)作为状态,即以导航参数误差作为估计对象,描述的系统方程是误差方程,且多为线性方程,相应状态参数的数量级相近,导航精度高。因此,本文选择间接法卡尔曼滤波方程。基于卡尔曼滤波的组合定位系统数学模型包括滤波状态方程和量测方程[12-13],其中,状态方程表示检测器的动力学特性,描述一个运动系统随着时间而改变其状态特性的一组或多组量;量测方程是对观测运动系统状态手段的数学描述。
3.1.2 滤波估计的输出校正对卡尔曼滤波得到的估计值有两种利用方法,一是开环法,将估计值作为捷联惯导系统输出的校正量;另一种是闭环法,将估计值反馈到捷联惯导系统中,估计的误差参数作为捷联惯导解算模型中相应参数的校正量,将捷联惯导或者其他导航设备中的误差校正掉。间接法中的开环法称为输出校正,闭环法称为反馈校正,本文采用输出校正的处理方式。图 2是输出校正滤波示意图[14-15]。
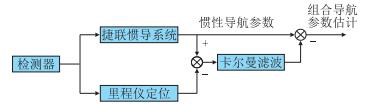 |
| 图2 基于输出校正的间接法滤波示意图 Fig. 2 Indirect Filter Schematic Diagram Based on Output Correction |
为提高卡尔曼滤波器的工作效率,应控制系统状态的数量。结合捷联惯性导航的误差特点,组合定位系统选择的误差状态量为15个,包括北、天、东方向的姿态误差、速度误差和位置误差9个变量和北、天、东方向的陀螺仪漂移、加速度计零偏6个变量,则误差状态量和连续状态方程为
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot X}} = \mathit{\boldsymbol{FX}} + \mathit{\boldsymbol{GW}}\\ \mathit{\boldsymbol{X}} = {\left[ {{\varphi _{\rm{N}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\varphi _{\rm{U}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\varphi _{\rm{E}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \delta {\mathit{\boldsymbol{V}}_{\rm{N}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \delta {\mathit{\boldsymbol{V}}_{\rm{U}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \delta {\mathit{\boldsymbol{V}}_{\rm{E}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \delta \lambda {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \delta L{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \delta h{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\nabla _{\rm{N}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\nabla _{\rm{U}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\nabla _{\rm{E}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\varepsilon _{\rm{N}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\varepsilon _{\rm{U}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\varepsilon _{\rm{E}}}} \right]^{\rm{T}}} \end{array} \right. $ | (6) |
式中:${{\boldsymbol{X}}}$——状态向量;
$\dot {{\boldsymbol{X}}}$——状态向量微分形式;
$\varphi$——姿态误差,rad;
$V$——速度误差,m/s;
$\lambda$——经度;
$L$——纬度;
$h$——高度,m;
$\nabla $——加速度计误差;
$\varepsilon $——和陀螺仪误差;
λ经度;
L纬度;
h高度,m;
$\nabla $加速度计误差;
ε和陀螺仪误差;
| $ \boldsymbol{ F} = \left[{\begin{array}{*{20}{c}} {{\boldsymbol{ F}_{11}}}&{{\boldsymbol{ F}_{12}}}&{{\boldsymbol{ F}_{13}}}&{-\boldsymbol{ C}_b^n}&{{0_{3 \times 3}}}\\ {{\boldsymbol{ F}_{21}}}&{{\boldsymbol{ F}_{22}}}&{{\boldsymbol{ F}_{23}}}&{{0_{3 \times 3}}}&{\boldsymbol{ C}_b^n}\\ {{\boldsymbol{ F}_{31}}}&{{\boldsymbol{ F}_{32}}}&{{\boldsymbol{ F}_{33}}}&{{0_{3 \times 3}}}&{{0_{3 \times 3}}}\\ {{0_{3 \times 3}}}&{{0_{3 \times 3}}}&{{0_{3 \times 3}}}&{{\boldsymbol{ F}_{\rm g}}}&{{0_{3 \times 3}}}\\ {{0_{3 \times 3}}}&{{0_{3 \times 3}}}&{{0_{3 \times 3}}}&{{0_{3 \times 3}}}&{{\boldsymbol{ F}_{\rm a}}} \end{array}} \right]; \boldsymbol{ G} = \left[{\begin{array}{*{20}{c}} {{0_{3 \times 3}}}&{{0_{3 \times 3}}}\\ {{0_{3 \times 3}}}&{{0_{3 \times 3}}}\\ {{0_{3 \times 3}}}&{{0_{3 \times 3}}}\\ {{\boldsymbol{ I}_{3 \times 3}}}&{{0_{3 \times 3}}}\\ {{0_{3 \times 3}}}&{{\boldsymbol{ I}_{3 \times 3}}} \end{array}} \right];\\ {\boldsymbol{ F}_{11}} = \left[{\begin{array}{*{10}{c}} 0&{{w_{\rm E}}}&{ \!-\! {\Omega _{\rm U}} \!-\! {w_{\rm N}}\tan L}\\ { \!-\! {w_{\rm E}}}&0&{{\Omega _{\rm N}} \!+\! {w_{\rm N}}}\\ {{\Omega _{\rm U}} \!+\! {w_{\rm N}}\tan L}&{ \!-\! {\Omega _{\rm N}} \!-\! {w_{\rm N}}}&0 \end{array}} \right]; {\boldsymbol{ F}_{12}} = \left[{\begin{array}{*{20}{c}} 0&0&1\\ 0&0&{\tan L}\\ {-1}&0&0 \end{array}} \right];\\ {\boldsymbol{ F}_{13}} = \left[{\begin{array}{*{20}{c}} 0&{-{\Omega _{\rm{U}}}}&{{w_{\rm{N}}}/{R_{\rm 0}}}\\ 0&{{\Omega _{\rm{U}}} + {w_{\rm{N}}}{{\sec }^2}L}&{{w_{\rm{N}}}\tan L/{R_{\rm 0}}}\\ 0&0&{-{w_{\rm{E}}}/{R_{\rm 0}}} \end{array}} \right]; {\boldsymbol{ F}_{21}} = \left[{\begin{array}{*{20}{c}} 0&{-{f_{\rm{E}}}}&{{f_{\rm{U}}}}\\ {{f_{\rm{E}}}}&0&{-{f_{\rm{N}}}}\\ {-{f_{\rm{U}}}}&{{f_{\rm{N}}}}&0 \end{array}} \right];\\ {\boldsymbol{ F}_{22}} = \left[{\begin{array}{*{20}{c}} {{V_{\rm{U}}}/{R_{\rm 0}}}&{{w_{\rm{E}}}}&{- 2({\Omega _{\rm{U}}} + {w_{\rm{N}}}\tan L)}\\ {- 2{w_{\rm{E}}}}&0&{2({\Omega _{\rm{N}}} \!+\! {w_{\rm{N}}})}\\[4pt] {2{\Omega _{\rm{U}}} \!+\! {w_{\rm{N}}}\tan L}&{ \!-\! 2{\Omega _{\rm{N}}} \!-\! {w_{\rm{N}}}}&{\dfrac{{{V_{\rm{N}}}\tan L \!-\! {V_{\rm{U}}}}}{{{R_{\rm 0}}}}} \end{array}} \right];\\ {\boldsymbol{ F}_{31}} = \left[{\begin{array}{*{20}{c}} 0&0&0\\ 0&0&0\\ 0&0&0 \end{array}} \right]; {\boldsymbol{ F}_{32}} = \left[{\begin{array}{*{20}{c}} 0&0&{\sec L/{R_{\rm 0}}}\\ {1/{R_{\rm 0}}}&0&0\\ 0&1&0 \end{array}} \right];\\ {\boldsymbol{ F}_{23}} = \left[{\begin{array}{*{20}{c}} 0&{-(2{\Omega _{\rm N}} + {w_{\rm N}}{{\sec }^2}L){V_{\rm E}}}&{{w_{\rm N}}^2\tan L-{w_{\rm E}}{V_{\rm U}}/{R_{\rm 0}}}\\ 0&{-2{\Omega _{\rm U}}{V_{\rm E}}}&{ - {w_{\rm N}}^2 - {w_{\rm E}}^2}\\ 0&{2{\Omega _{\rm N}}{V_{\rm N}} + 2{\Omega _{\rm U}}{V_{\rm U}} + {w_{\rm N}}{V_{\rm N}}{{\sec }^2}L}&{{w_{\rm N}}{w_{\rm E}}\tan L + {w_{\rm N}}{V_{\rm U}}/{R_{\rm 0}}} \end{array}} \right];\\ {\boldsymbol{ F}_{33}} = \left[{\begin{array}{*{20}{c}} 0&0&{\sec L/{R_{\rm 0}}}\\ {1/{R_{\rm 0}}}&0&0\\ 0&1&0 \end{array}} \right]; $ |
${\Omega _{\rm N}} = {w_{\rm ie}}\cos L$;
${\Omega _{\rm U}} = {w_{\rm ie}}\sin L$;
${w_{\rm N}} = {V_{\rm E}}/({R_{\rm 0}} + h)$;
${w_{\rm E}} = {V_{\rm N}}/({R_{\rm N}} + h)$;
$R_{\rm 0}$——地球半径,m;
${\boldsymbol{ F}_{\rm g}} = \left ({-1/{T_{\rm g}}} \right){I_{3 \times 3}}$;
${\boldsymbol{ F}_{\rm a}} = \left ({-1/{T_{\rm a}}} \right){I_{3 \times 3}}$;
$w_{\rm ie}$——地理坐标系相对于地球坐标系的转动角速度,rad/s;
$R_{\rm N}$——卯酉圈曲率半径,m;
${T_{\rm g}}$——陀螺仪相关时间系数;
${T_{\rm a}}$——加速度计相关时间系数;
$\boldsymbol{ I}$——单位矩阵;
$f$——检测器加速度分量,
下标N,U,E——北向、天向和东向。
3.3 滤波量测方程滤波量测方程是对运动系统状态的数学描述,反映系统的状态量和量测量之间的关系,鉴于里程计测量的信息不包含绝对的位置信息,组合定位系统采用速度的组合方式,里程仪的速度测量值经过刻度系数误差和姿态误差角修正后分解到导航坐标系上,与SINS的速度值相减${{\boldsymbol{Z}}} = {{{\boldsymbol{V}}}_{\rm SINS}}-{{{\boldsymbol{V}}}_{\rm n}}$,构成卡尔曼滤波的观测量[16],进而得到系统的量测方程
| $ {{\boldsymbol{Z}}} = {{{\boldsymbol{V}}}_{\rm SINS}}-{{{\boldsymbol{V}}}_{\rm n}} = {{\boldsymbol{H}}}{{\boldsymbol{X}}} + \delta {{{\boldsymbol{V}}}_{\rm n}} $ | (7) |
式中:${{\boldsymbol{Z}}}$——状态${{\boldsymbol{X}}}$的量测值;
${{\boldsymbol{H}}}$——观测矩阵;
${{{\boldsymbol{V}}}_{\rm SINS}}$——SINS的速度,m/s。
式(7)中,$H = \left[{\begin{array}{*{20}{c}} {{0_{3{\times}3}}}&{{{\left ({C_{\rm{b}}^{\rm{n}}} \right)}^{\rm T}}}&{{0_{3*9}}} \end{array}} \right]$,表征无噪声时量测值与真实状态矢量间的几何关系;$\delta {{{\boldsymbol{V}}}_{\rm n}}$由检测管道的环境确定,其均值为零,协方差矩阵为正定的随机序列,满足$E\left ({\delta {\boldsymbol{ v}_{\rm b}}} \right)= 0$,$E\left ({\delta {\boldsymbol{ v}_{\rm b}}, \delta {\boldsymbol{ v}_{\rm b}}{^{\rm T}}} \right)= {{\boldsymbol{R}}}$,它表示在量测中始终存在噪声的影响,即量测永远有噪声。机体坐标系向导航坐标系转%换的方向余弦矩阵姿态转换矩阵$\boldsymbol{ C}_{\rm b}^{\rm n}$由组合系统中的捷联惯导子系统姿态信息确定,计算公式为
| $ \begin{array}{l} C_{\rm{b}}^{\rm{n}}\left[ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{cos}}\gamma c{\rm{os}}\psi - {\rm{sin}}\gamma {\rm{sin}}\theta {\rm{sin}}\psi {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - \sin \psi \cos \theta {\kern 1pt} \\ \cos \gamma \sin \psi + \sin \gamma \cos \psi \sin \theta {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \cos \psi \cos \theta \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - \sin \gamma \cos \theta {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sin \theta {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \end{array} \right.\\ \left. \begin{array}{l} \sin \gamma \cos \psi + \cos \gamma \sin \psi \sin \theta \\ \sin \gamma \sin \psi - \cos \gamma \cos \psi \sin \theta \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \cos \gamma \cos \theta \end{array} \right] \end{array} $ | (8) |
式中:$\psi$——导航角,rad;
$\theta$——俯仰角,rad;
$\gamma$——横滚角,rad。
3.4 卡尔曼滤波方程离散化根据滤波的状态方程和量测方程,建立连续状态下的数学模型如式(9)所示。
| $ \left\{ \begin{array}{l} \dot {{\boldsymbol{X}}} = {{\boldsymbol{F}}}{{\boldsymbol{X}}} + {{\boldsymbol{W}}}\\ {{{\boldsymbol{Z}}}} = {{\boldsymbol{V}}}{{\boldsymbol{X}}} + \delta {{{\boldsymbol{V}}}_{\rm n}} \end{array} \right. $ | (9) |
由导航器件的工作原理可知,得到的都是离散数据,所以在应用卡尔曼滤波时需要将数学模型中的系统方程和量测方程进行离散处理[10],得到式(9)的离散化方程
| $ \left\{ \begin{array}{l} {{{\boldsymbol{X}}}_k} = {\boldsymbol{ \varPhi} _{k, k-1}}{{{\boldsymbol{X}}}_{k-1}} + {\boldsymbol{ \varGamma} _{k, k-1}}{{{\boldsymbol{W}}}_{k-1}}\\ {{{\boldsymbol{Z}}}_k} = {{{\boldsymbol{H}}}_k}{{{\boldsymbol{X}}}_k} + \delta {{{\boldsymbol{V}}}_{\rm n}}_k \\ {\boldsymbol{ \varPhi} _{k, k-1}} = E + F\left({{t_k}} \right)\Delta T + \dfrac{1}{2}{\left[{F\left({{t_k}} \right)\cdot \Delta T} \right]^2} +\\{\kern 20pt} \dfrac{1}{{3!}}{\left[{F\left({{t_k}} \right)\cdot \Delta T} \right]^3} +\cdots \\[6pt] \dfrac{\boldsymbol{ \varGamma} _{k, k-1}}{G\left({{t_k}} \right)\cdot \Delta T} = {{\boldsymbol{E}}} + \dfrac{1}{2}\left[{F\left({{t_k}} \right)\cdot \Delta T} \right]+ \\[4pt]{\kern 20pt} \dfrac{1}{{3!}}{{\left[{F\left({{t_k}} \right)\cdot \Delta T} \right]}^2} +... \end{array} \right. $ | (10) |
式中:${{{\boldsymbol{V}}}_{\rm n}}_k$——$k$时刻导航坐标系中里程仪速度,m/s;
$t_k$——$k$时刻对应的时间,s;
$\Delta T$——离散时间步长,s。
因此,组合定位的滤波方程为
| $ \left\{ \begin{array}{l} {{\hat {{\boldsymbol{X}}}}_{k, k-1}} = {\boldsymbol{ \varPhi} _{k, k-1}}{{\hat {{\boldsymbol{X}}}}_{k-1}}\\ {{\hat {{\boldsymbol{X}}}}_k} = {{\hat {{\boldsymbol{X}}}}_{k, k-1}} + {{{\boldsymbol{X}}}_k}\left({{{{\boldsymbol{X}}}_k}-{{{\boldsymbol{X}}}_k}{{\hat {{\boldsymbol{X}}}}_{k, k-1}}} \right)\\[4pt] {{{\boldsymbol{K}}}_k} = {{{\boldsymbol{P}}}_{k, k-1}}{{{\boldsymbol{H}}}_k}^{\rm T}{\left({{{{\boldsymbol{H}}}_k}{{{\boldsymbol{P}}}_{k, k-1}}{{{\boldsymbol{H}}}_k}^{\rm T} + {{{\boldsymbol{R}}}_k}} \right)^{-1}}\\[4pt] {{{\boldsymbol{P}}}_{k, k-1}} = {\boldsymbol{ \varPhi} _{k, k-1}}{{{\boldsymbol{P}}}_{k-1}}{\boldsymbol{ \varPhi} ^{\rm T}}_{k, k-1} + {{{\boldsymbol{Q}}}_{k-1}}\\[4pt] {{{\boldsymbol{P}}}_k} = \left({{{\boldsymbol{E}}}-{{{\boldsymbol{K}}}_k}{{{\boldsymbol{H}}}_k}} \right){{{\boldsymbol{P}}}_{k, k-1}} \end{array} \right. $ | (11) |
式中:${{\hat {{\boldsymbol{X}}}}_{k, k-1}}$——状态一步最优预测值;
${{\hat {{\boldsymbol{X}}}}_{k}}$——状态最优预测值;
${{{\boldsymbol{P}}}_{k, k-1}}$——一步预测均方矩阵;
${{{\boldsymbol{P}}}_k}$——估计均方误差。
4 组合定位系统的仿真设计仿真试验中,由轨迹发生器得到的是理想的位置、速度和姿态信息,根据陀螺仪和加速度计的测量特点对其进行修正(包括误差修正和坐标系转换),然后获得理论上应该由陀螺仪和加速度计测量得到的角速度值和加速度值,将这些值输入到导航解算模型中得到位置和姿态信息,得到的速度值与里程仪仿真速度相减作为组合导航系统的观测量[17-18],进而根据卡尔曼滤波器算法的输出修正,得到组合算法的误差曲线,验证算法是否满足管道检测器在管道内运行要求的误差精度。
4.1 轨迹发生器仿真仿真轨迹数据包括姿态数据和轨迹数据两类,其中姿态数据包含姿态角和姿态角速率;轨迹数据包含位置、速度和加速度。假设姿态数据和轨迹数据相互独立,姿态角速率为姿态角的一阶导数,根据姿态角数据和机体坐标系相对于地理坐标系的转换矩阵,通过相关的计算得到姿态角速率在机体坐标系下的投影如式(12)所示
| $ \left[{\begin{array}{*{20}{c}} {{\omega _{{\rm{b}}x}}}\\ {{\omega _{{\rm{b}}y}}}\\ {{\omega _{{\rm{b}}z}}} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {\cos \gamma }&0&{\sin \gamma \cos \theta }\\ 0&1&{-\sin \theta }\\ {\sin \gamma }&0&{\cos \gamma \cos \theta } \end{array}} \right]\left[{\begin{array}{*{20}{c}} {\dot \theta }\\ {\dot \gamma }\\ {\dot \psi } \end{array}} \right] $ | (12) |
式中:$\omega _{{\rm b}x}$——机体坐标系中$x$轴姿态角速率,rad/s;
$\omega _{{\rm b}y}$——机体坐标系中$y$轴姿态角速率,rad/s;
$\omega _{{\rm b}z}$——机体坐标系中$z$轴姿态角速率,rad/s;
${\dot \theta }$——俯仰角$\theta$的一阶导数,rad/s;
${\dot \gamma }$——俯仰角$\gamma$的一阶导数,rad/s;
${\dot \psi }$——俯仰角$\psi$的一阶导数,rad/s。
导航系统将地理坐标系作为导航坐标系,将地球坐标系的方程转换到地理坐标系,通过地球自转和公转的修正,轨迹数据中加速度在地理系中的投影如式(13)所示
| $ {a^{\rm{n}}} = {a_{\rm{t}}} - {w_{\rm{t}}} \times {v_{\rm{t}}} = {\boldsymbol{{C}}}_{\rm{e}}^{\rm{t}} \times \left[{\begin{array}{*{20}{c}} {{a_x}}\\ {{a_y}}\\ {{a_z}} \end{array}} \right] - {w_{\rm{t}}} \times {v_{\rm{t}}} $ | (13) |
式中:${a^{\rm{n}}}$——地理坐标系中速度投影值,m/s;
${a_{\rm{t}}}$——修正前加速度在地理系中的投影,m/s$^2$;
${v_{\rm{t}}}$——地理坐标系中速度投影值,m/s;
${w_{\rm{t}}}$——地理坐标系相对于地球坐标系的转动角速度,rad/s;
${\boldsymbol{{C}}}_{\rm{e}}^{\rm{t}} $——地球坐标系到地理坐标系的转换矩阵,
| $ {\boldsymbol{{C}}}_{\rm{e}}^{\rm{t}} = \left[{\begin{array}{*{20}{c}} {-\sin \lambda }&{\cos \lambda }&0\\ {-\sin L\cos \lambda }&{-\sin L\sin \lambda }&{\cos L}\\ {\cos L\cos \lambda }&{\cos L\sin \lambda }&{\sin L} \end{array}} \right] $ |
$a_x$——地球坐标系下$x$轴方向的加速度,m/s$^2$;
$a_y$——地球坐标系下$y$轴方向的加速度,m/s$^2$;
$a_z$——地球坐标系下$z$轴方向的加速度,m/s$^2$。
4.2 惯导器件的仿真设计惯导器件的仿真设计包括陀螺仪和加速度计的仿真模型,根据器件测量的特点,其仿真模型可以用轨迹发生器生成的数据作相关的修正后得到。根据陀螺仪的原理和测量特点,陀螺仪仿真模型如式(14)所示
| $ {\omega _{\rm{b}}} = {\bar \omega _{\rm{b}}} + \bar \varepsilon $ | (14) |
式中:${\omega _{\rm{b}}}$——实际陀螺仪输出量,rad/s;
${\bar \omega _{\rm{b}}}$——理想陀螺仪输出量,rad/s;
$\bar \varepsilon $——陀螺仪本身的误差,rad/s。
式(14)中,${\bar \omega _{\rm{b}}}$表示转动角速度在机体坐标系中的投影;$\bar \varepsilon $包括陀螺仪的随机常数误差、随机偏移误差和高斯白噪声。
由建立的陀螺仪仿真数学模型可知,完成仿真器的设计需要的输入量包括检测器的东、北向速度,纬度、高度,航向角、横滚角、俯仰角3个姿态角和3个方向的角度率。
加速度计是用来测量检测器运动的敏感元件,一般加速度计自身存在误差,所以加速度计仿真模型如式(15)所示。
| $ {f_{\rm{b}}} = {\bar f_{\rm{b}}} + {\nabla _{\rm{b}}} $ | (15) |
式中:${f_{\rm{b}}}$——实际检测器加速度值,m/s$^2$;
${\bar f_{\rm{b}}}$——理想检测器加速度值,m/s$^2$;
${\nabla _{\rm{b}}}$——加速度计本身的误差,m/s$^2$。
式(15)中,${\bar f_{\rm{b}}}$是通过检测器的姿态和轨迹输出得到,考虑了3部分有害加速度,包括哥式加速度(由运载体相对地球运动和地球旋转引起的)、对地向心加速度(运载体保持在地球表面运动引起的对地向心加速度)和重力加速度(地球对运载体的引力引起的);将${\nabla _{\rm{b}}}$考虑为一阶马尔科夫过程。
由加速度计仿真模型的设计可知,建立该仿真模型所需的输入量包括以下几方面的数据:东、北、天方向速度,东、北、天方向的加速度、3个姿态角信息以及纬度和高度。
4.3 里程仪仿真模型里程仪仿真是组合定位系统仿真的重要组成部分[19],根据组合定位的特点,选择速度作为组合系统的观测量,推导里程仪的速度仿真模型。里程仪在检测定位中总存在误差,所以假设里程仪仿真模型中速度值是理想的里程仪输出与误差的和,如式(16)所示
| $ {{{v}}_{\rm{b}}} = {\bar {{{v}}_{\rm{b}}}} + {{ \kappa} _{\rm{b}}} $ | (16) |
式中:${v_{\rm{b}}}$——里程仪仿真模型中速度值,m/s;
$\bar {{{v}}_{\rm{b}}}$——理想检测器的速度值,m/s;
$ {{ \kappa} _{\rm{b}}}$——里程仪的速度误差,m/s。
$\bar {{{v}}_{\rm{b}}}$是由惯性器件的仿真模型计算得到检测器加速度计的理想值(${{{\bar f}_{\rm{b}}}}$)后,将加速度计值积分得到检测器的理想速度值,可以通过式(17)得到。把$ {{ \kappa} _{\rm{b}}}$看作是里程仪的刻度系数误差,根据相关研究成果,将其考虑成一阶马尔科夫过程,如式(18)所示。
| $ {\bar v_{\rm{b}}} = \int_0^{{T_{\rm{b}}}} {{{\bar f}_{\rm{b}}}} {\rm d}t $ | (17) |
| $ {\kappa _{\rm{b}}} = - \dfrac{1}{{{T_{\rm{b}}}}}{\kappa _{\rm{b}}} + {w_{\rm{b}}} $ | (18) |
式中:${T_{\rm{b}}}$——里程仪的相关时间系数,无因次;
${w_{\rm b}}$——里程仪的马尔科夫噪声,m/s。
4.4 仿真试验与误差分析 4.4.1 仿真分析条件系统仿真需要SINS和里程仪两个导航设备的数据,包括轨迹发生器、捷联惯导器件仿真模型以及捷联惯导误差初值和相关状态的取值。对于组合导航系统,量测噪声的大小对于系统的误差水平是一个重要的参数指标,由油气管道导航定位特点可知,里程仪只有在纵轴有量测噪声,且与里程仪的分辨率有关[20],本文选择量测噪声方差$R = {{\rm{(0}}{\rm{.005 m/s}})^{\rm{2}}}$,组合系统量测噪声(里程仪的刻度系数误差)为0.5%,马尔科夫相关时间常数取1000 s;里程仪的初始位置误差设置为经度0.002$''$,纬度0.002$''$,高度0.05 m;初始速度误差(北向、天向、东向)均为0.01 m/s。
4.4.2 试验结果分析基于上述仿真模型的%用MATLAB软件编译成可执行程序,然后输入解算参数得到仿真结果。仿真试验内容如下。
(1)设定组合导航系统解算模型初值以及部分模型参数的取值。
(2)设计并编写轨迹仿真器、捷联惯导器件的仿真程序,用于组合定位系统数据生成。
(3)设计并编写里程仪仿真模型可执行程序,用于组合导航系统里程仪仿真数据生成。
(4)设计并编写卡尔曼滤波组合定位系统的数据融合数学模型的可执行程序,用于仿真滤波数据的生成。
(5)采用上述初值、参数、仿真模型和误差模型输出组合导航系统的误差结果。
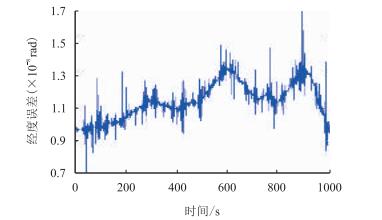 |
| 图3 组合系统经度误差曲线图 Fig. 3 Longitude error curve of integrated system |
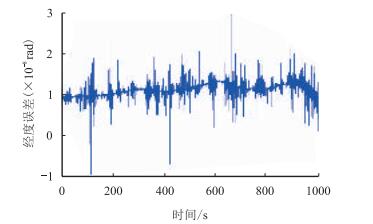 |
| 图4 组合系统纬度误差曲线图 Fig. 4 Latitude error curve of integrated system |
由仿真实验得到的位置误差曲线可知,惯导的位置误差随时间逐渐增大,在仿真时间为1000 s,在经度和纬度方向各航行约2.5 km的情况下,误差值由经、纬度值转换为距离后分别为16和17 m,导航精度约为0.5%和0.6%。即使有地面标记、定点磁标等辅助设备的条件下,目前国内导航精度也仅可以达到0.1%。而在组合导航条件下,误差值由经、纬度值转换为距离后分别为0.79和1.35 m,由于经、纬度方向各航行约2.5 km,所以导航精度分别约为0.03%和0.05%。进行多次试验,由经、纬度误差转换的距离误差值变化较小,取平均值后进行导航精度解算,导航精度仍分别约为0.03%和0.05%。
5 结语在油气管道导航特征的分析基础上,选择里程仪和SINS作为组合定位的两个子系统,推导了轨迹仿真器、捷联惯导器件和里程仪的数学模型,建立基于卡尔曼滤波技术的组合导航系统的解算模型。设计了轨迹仿真器、捷联惯导器件和里程仪的仿真模型,实现组合系统的仿真和解算程序,通过对组合系统误差结果图的分析可知该组合方式精度较高,在没有辅助设备的情况下,完成2.5 km的导航距离时,精度可达到0.03%,所以在其他导航辅助设备的协助下可满足管道检测定位的工程需要。
| [1] |
杨理践, 沈博, 高松巍. 基于组合导航技术的管道地理坐标定位算法[J].
沈阳工业大学学报, 2014, 36(1): 66–71.
YANG Lijian, SHEN Bo, GAO Songwei. Geographical position locating algorithm for pipeline based on integrated navigation technique[J]. Journal of Shenyang University of Technology, 2014, 36(1): 66–71. doi: 10.7688/j.issn.-1000-1646.2014.01.12 |
| [2] |
沈跃. 智能清管器检测管道缺陷的定位算法研究[J].
科学技术与工程, 2008, 8(20): 5603–5607, 5615.
SHEN Yue. Research on flaw location algorithms of the smart PIG for pipeline inspecting[J]. Science Technology and Engineering, 2008, 8(20): 5603–5607, 5615. doi: 10.3969/j.issn.1671-1815.2008.20.017 |
| [3] |
陈建军, 匙胜利. 浅析影响管道漏磁腐蚀检测器定位精度的因素[J].
管道技术与设备, 2002(6): 42–43.
CHEN Jianjun, SHI Shengli. Interfering factors of locating accurary for MFL tool[J]. Pipeline Technique and Equipment, 2002(6): 42–43. doi: 10.3969/j.issn.1004-9614.-2002.06.017 |
| [4] | 秦永元. 惯性导航[M]. 北京: 科学出版社, 2006. |
| [5] | YU J, LEE J G, PARK C G, et al. An off-line navigation of a geometry PIG using a modified nonlinear fixed-interval smoothing filter[J]. Control Engineering Practice, 2005, 13(11): 1403–1411. doi: 10.1016/j.conengprac.2004.12.-016 |
| [6] | SADOVNYCHIY S, LOPEZ J. Improvement of pipeline odometer system accuracy[C]//Canadian International Petroleum Conference. Calgary, Alberta:Petroleum Society of Canada, 2005:1-7. |
| [7] | SLAUGHTER M J, PORTER T. Pipeline mapping:using INS/GPS data as the fundamental tool for integrating historical and current pipeline data[C]. SPE 02084, 2002. |
| [8] | 王耀金. 高精度里程仪测速精度研究[D]. 西安: 西北工业大学, 2007. |
| [9] | 秦永元, 张洪钺, 汪叔华. 卡尔曼滤波与组合导航原理[M]. 西安: 西北工业大学出版社, 1998. |
| [10] | 付梦印, 邓志红, 张继伟. Kalman滤波理论及其在导航系统中的应用[M]. 北京: 宇航出版社, 2003. |
| [11] | 卫育新. GPS/INS组合导航定位定向系统研究[D]. 西安: 西北工业大学, 2004. |
| [12] | 邱醒亚, 谢泼德S J. 海洋开发中的定位与测量技术[M]. 北京: 国防工业出版社, 1986. |
| [13] |
吉翠萍, 雷宏杰, 冯培德. 捷联惯性/里程仪组合定位定向系统方案设计及仿真计算[J].
弹箭与制导学报, 2008, 28(4): 55–58.
JI Cuiping, LEI Hongjie, FENG Peide. Scheme design and simulation of hybrid navigation system composed of a strapdown inertial reference system and an odometer[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2008, 28(4): 55–58. doi: 10.3969/j.issn.1673-9728.2008.-04.017 |
| [14] |
杨坤明. 组合导航系统的卡尔曼滤波器的设计[J].
西华大学学报 (自然科学版), 2005, 24(4): 86–88.
YANG Kunming. The design of Kalman filter on integrated navigation system[J]. Journal of Xihua University (Natural Science), 2005, 24(4): 86–88. doi: 10.3969/j.-issn.1673-159X.2005.04.028 |
| [15] |
赵净净, 王艳东. INS/SMNS组合导航信息融合算法[J].
北京航空航天大学学报, 2009, 35(3): 292–295.
ZHAO Jingjing, WANG Yandong. Information fusion algorithm in INS/SMNS integrated navigation system[J]. Journal of Beijing University of Aeronautics and Astronautics, 2009, 35(3): 292–295. |
| [16] | HANNA P L. Strapdown inertial systems for pipeline navigation[C]//Proceedings of 1990 IEE colloquium on inertial navigation sensor development. Las Vegas, NV:IEEE, 1990. |
| [17] |
刘勇, 赵红庆, 寇烈, 等. 捷联惯导系统/GPS/里程仪组合导航系统的研究[J].
弹箭与制导学报, 2006, 26(2): 47–48, 56.
LIU Yong, ZHAO Hongqing, KOU Lie, et al. A study on SINS/GPS/OD combined navigation system[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2006, 26(2): 47–48, 56. doi: 10.3969/j.issn.1673-9728.2006.02.017 |
| [18] | 易维勇. 惯性导航及组合导航研究及仿真[D]. 郑州: 中国人民解放军信息工程大学, 2002. |
| [19] | SHIN E H, EI-SHEIMY N. Backward smoothing for pipeline surveying applications[C]//Proceedings of the 2005 national technical meeting of the institute of navigation. San Diego, CA:ION, 2005:921-927. |
| [20] |
赵长山, 秦永元, 夏家和. 车载惯导里程仪组合导航系统安装误差标定研究[J].
计算机测量与控制, 2008, 16(10): 1393–1395.
ZHAO Changshan, QIN Yongyuan, XIA Jiahe. On SINS installation error calibration of a multimode vehicular navigation system[J]. Computer Measurement & Control, 2008, 16(10): 1393–1395. |
 2017, Vol. 39
2017, Vol. 39


