近年来,随着深井、超深井以及特殊工艺钻井作业的不断增加,钻头的需求量越来越大,同时对钻头的性能也提出了更高的要求。PDC钻头因具有破岩能耗低、工作可靠性高等优点,在石油天然气钻井中得到了广泛的应用,有逐步取代牙轮钻头的趋势[1]。但在硬质、夹层、高研磨性地层以及复杂定向钻井作业中,该类钻头对地层的适应性较差,还无法取代牙轮钻头。牙轮钻头对地层的适应性较好,适于在硬地层中钻进,但在塑性地层中机械钻速较低。
为了结合牙轮钻头和PDC钻头各自的优点,世界各大钻头公司相继开发了复合钻头,包括3牙轮、3刀翼或2牙轮、2刀翼两种结构形式。前者主要应用于大尺寸钻头,后者用于较小尺寸钻头。贝克休斯公司最早开发出的复合钻头在加拿大、沙特阿拉伯以及北德克萨斯州的现场实践证明其相比单独的PDC钻头和牙轮钻头更具优势[2]。而在中国,由中石油天然气钻井提速提效新技术基础研究项目资助,西南石油大学、川庆钻探钻采工程技术研究院联合研发,宝石机械成都装备制造分公司制造的“ 2+2”型牙轮PDC复合钻头于2013年7月在四川成功下井试验,现场实践证明复合钻头比PDC钻头机械钻速快近20%、同时工作稳定性也较PDC钻头明显提高[3]。
虽然实践证明复合钻头在某些地层钻进中具有很大优势,但是该型钻头的基础技术研究基本还处于摸索阶段,其破岩机理和力学行为还没有研究清楚。为此,利用三维实体建模软件Pro/E设计了一种8${\frac{1}{2}}''$(1$''$=2.54cm) 的“ 2+2”型牙轮PDC复合钻头,如图 1所示。
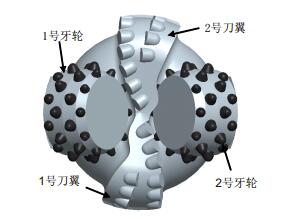 |
| 图1 牙轮-PDC复合钻头 Fig. 1 Hybrid bit with roll-cones & PDC cutters |
设计的钻头通过改变牙轮和刀翼的相对高差,该钻头可以变化成牙轮主导型CL(ConeLeading)和刀翼主导型BL(Blade-Leading)两种型式[2]。所谓牙轮主导型就是同一半径上的牙轮切削齿高于PDC切削齿;而刀翼主导型刚好相反。并采用显式动力学有限元软件LS DYNA模拟了两种钻头分别钻进凝灰岩和花岗岩的物理过程,得到了钻进过程中的机械钻速、钻压的分配以及切削齿轴向载荷分布等信息。通过分析,得出了一些有用的结论,对指导钻头的结构设计和现场选用具有一定意义。
1 岩石H-J-C动态本构模型复合钻头是依靠牙轮齿对井底的冲击、碾压和PDC齿的长距离刮削两种方式联合破岩的,钻头钻进时存在一定的冲击载荷,井底岩石的性质较静态时有较大的差异,属于典型的瞬态动力学问题。
目前,比较常见的岩石本构模型主要有Druker-Prager模型[4]、K & C模型[5],H-J-C模型[6-10]以及CSCM模型[11]等。考虑到H-J-C模型具有参数容易确定、本构方程包含累积损伤和应变率效应对岩石强度的影响等优点以及被很多学者采用,是比较理想的岩石动态本构模型。
H-J-C模型包括状态方程、屈服面方程和损伤演化方程3个方面的内容[6, 10, 12]。
1.1 状态方程状态方程用于描述岩石的静水压力$p$与体积应变$\mu$之间关系 (图 2),包括3个阶段。
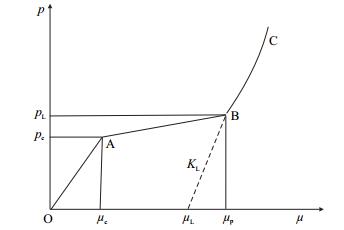 |
| 图2 状态方程 Fig. 2 The equation of state |
(1)线弹性阶段(OA段)。此阶段静水压$p$和体积应变$\mu$之间呈线性关系,加载或卸载时均有
| $ \left\{ \begin{array}{l} p = {K_{\rm{e}}}\mu \\[4pt] {K_{\rm{e}}} = \dfrac{{{p_{\rm{c}}}}}{{{\mu_{\rm{c}}}}} \end{array} \right. $ | (1) |
式中:$p$——压力,MPa;
$K_{\rm e}$——弹性体积模量,MPa;
$\mu$——体积应变,无因次;
$p_{\rm c}$——岩石的压碎体积压力,MPa;
$\mu_{\rm c}$——压碎体积应变,无因次。
(2)过渡阶段(AB)段。此阶段岩石内部的空洞被逐渐压实,从而产生塑性变形,加载和卸载方程分别为
| $ p = {p_{\rm{c}}} + \dfrac{{\mu - {\mu _{\rm{c}}}}}{{{\mu _{\rm{p}}} - {\mu _{\rm{c}}}}}\left( {{p_{\rm{L}}} - {p_{\rm{c}}}} \right) $ | (2) |
| $ p = {p_{\rm{m}}} - \left[{\left( {1-F} \right){K_{\rm{e}}} + F{K_{\rm{L}}}} \right]\left( {{\mu _{\rm{m}}} - \mu } \right) $ | (3) |
式中:${\mu_{\rm{p}}}$——压实体积压力$p_{\rm L}$对应的体积应变,无因次;
$p_{\rm L}$——压实体积压力,MPa;
$p_{\rm m}$——卸载前的体积压力,MPa;
$F$——卸载比例系数,$F = \left ({{\mu _{\rm{m}}}-{\mu _{\rm{c}}}} \right)/\left ({{\mu _{\rm{p}}}-{\mu _{\rm{c}}}} \right)$,无因次;
$K_{\rm L}$——岩石的塑性体积模量,MPa;
${\mu_{\rm{m}}}$——卸载前的体积压力$p_{\rm m}$对应的体积应变,无因次。
(3)完全密实阶段(BC)。在这一阶段的岩石内部气孔已经被完全排除,可以视为完全密实材料。加载和卸载方程分别
| $ p = {K_1}\bar \mu + {K_2}{{\bar \mu }^2} + {K_3}{{\bar \mu }^3} $ | (4) |
| $ p = {K_{\rm{L}}}\bar \mu $ | (5) |
式中:$\bar \mu$——修正后的体积应变,无因次,$\bar \mu = \left ({\mu-{\mu _{\rm{L}}}} \right)/\left ({1 + {\mu _{\rm{L}}}} \right)$;
${\mu_{\rm{L}}}$——压实极限体积应变,无因次。
$K_1$,$K_2$,$K_3$——压力系数,GPa。
1.2 屈服面方程岩石H-J-C模型的屈服面方程为
| $ {\sigma _{{\rm{eq}}}} = {f_{\rm{c}}}\left[{A\left( {1-D} \right) + B{{\left( {\dfrac{p}{{{f_{\rm{c}}}}}} \right)}^N}} \right]\left( {1 + C\ln \dfrac{{ \varepsilon }}{{{{ \varepsilon }_0}}}} \right) $ | (6) |
式中:$\sigma_{\rm eq}$——岩石单元的等效应力,MPa;
$f_{\rm c}$——岩石的准静态单轴抗压强度,MPa;
$A$——标准化的内聚强度,无因次;
$B$——标准化的压力硬化系数,无因次;
$C$——应变率系数,无因次;
$N$——压力硬化指数,无因次;
$D$——损伤度,无因次,$0{\leqslant}D{\leqslant}1$;
$\varepsilon$——真实应变率,无因次;
$\varepsilon _0$——参考应变率,无因次。
1.3 损伤演化方程H-J-C模型的损伤演化方程考虑了由等效塑性应变和塑性体积应变引起的损伤,表达为
| $ D = \sum{\dfrac{{\Delta \varepsilon _{{\rm{eq}}}^p + \Delta \varepsilon _{\rm{V}}^p}}{{{D_1}{{\left( {\dfrac{p}{{{f_{\rm{c}}}}} + \dfrac{T}{{{f_{\rm{c}}}}}} \right)}^{{D_2}}}}}} $ | (7) |
式中:$T$——岩石的最大拉伸静水压,MPa;
$D_1$、$D_2$——岩石的损伤系数,无因次;
$\Delta \varepsilon _{{\rm{eq}}}^p$,$\Delta \varepsilon _{\rm{V}}^p$——一个计算周期内单元的等效塑性应变增量和塑性体积应变增量,无因次。
当$p=-T$时,从式 (7) 可以看出,岩石此时不能承受任何塑性应变,与实际情况不符。为了使岩石在断裂时仍然存在较小的塑性应变,需要定义另一个损伤常数$E_{\rm fmim}$。
2 有限元模型基本假设在实际钻井过程中,影响钻进的因素有钻头结构、钻压、转速、地层岩性和泥浆排量等,在有限元模拟中为便于研究,忽略次要因素是极其必要的。同时作如下假设:(1)不考虑温度、井底流场和围压对破岩过程的影响。
(2)假设岩石为均匀、各向同性材料,不考虑岩石中原生裂纹和初始应力场的存在。
(3)岩石失效后即刻被移除。
(4)钻头旋转中心位置固定,即钻头不发生径向位移。
2.1 有限元模型的建立 2.1.1 材料模型及参数本次研究不考虑切削齿的变形和应力分布,将所有切削齿均视为刚体,采用刚体材料模型[6]描述;凝灰岩和花岗岩均采用H-J-C模型描述,定义岩石的失效方式为剪切应变失效[13-14],切削齿和岩石模型的具体参数分别见表 1、表 2。
| 表1 切削齿刚体材料模型参数 Table 1 Rigid material model parameters of cutters |
| 表2 岩石H-J-C本构模型参数 Table 2 Rock H-J-C constitutive model parameters |
在有限元模拟中,为减少计算时间,有必要对几何模型进行适当简化。考虑到钻头钻进过程实际上就是钻头上的切削齿与岩石的互作用过程,将钻头几何模型简化,只保留切削齿的出刃部分,同时对岩石预设初始井底。采用六面体网格划分后的切削齿—岩石互作用有限元模型如图 3所示。
 |
| 图3 切削齿-岩石互作用有限元模型 Fig. 3 Interactional FE model of cutters & rock |
钻头上的约束及边界条件的施加见图 4。图中的绿点代表附加节点,钻头的质量集中在9#节点上。1#、2#、5#、6#、9#节点以及PDC切削齿之间形成刚体;钻头体牙掌轴颈中心线上的1#、2#节点与1号牙轮中心线上的3#、4#节点间形成摩擦旋转铰,用于代替滑动轴承连接,2#牙轮的连接方式与1#牙轮完全相同;9#节点位于钻头中心线上,约束其除钻头轴向平移和旋转自由度以外的所有自由度,同时施加10 kN的钻压和顺时针100 r/min的钻头转速;切削齿与岩石之间选用侵蚀单面接触算法,保证表面岩石单元失效后,内部岩石单元与切削齿间依然能形成接触,并考虑接触摩擦系数;固定岩石的底面和侧面,并施加无反射边界条件以模拟无限域[15]。
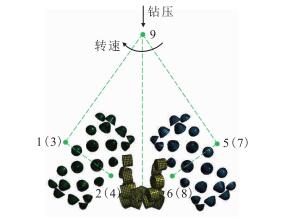 |
| 图4 约束及边界条件 Fig. 4 Constraints and boundary conditions |
为保证统计结果的可靠性和普遍性,模拟时间应足够长,使钻头机械钻速达到稳定,模拟时间设为10 s,采用默认的计算时间步长。由于单元计算采用了单点积分算法,容易激起沙漏模式[16],需要对模型进行沙漏控制,使整体沙漏能不超过内能峰值的10%[17]。
3 结果分析 3.1 钻进过程中的能量模型的能量信息是检验计算结果是否可靠的重要依据。以CL型的复合钻头钻进花岗岩为例,图 5给出了钻进过程中模型的动能、内能、界面滑移能和沙漏能。
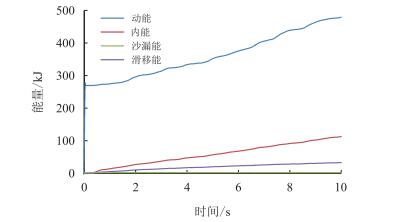 |
| 图5 钻进过程中的能量 Fig. 5 Energies in drilling process |
由图 5可见,单点积分引起的沙漏能相对系统内能很小,经计算,沙漏能不足内能峰值的0:02%远小于10%,说明系统沙漏的影响几乎可以忽略不计。同时牙齿与岩石接触的界面滑移能始终为正值,说明模型的接触定义是可靠的。
3.2 井底模式井底模式是反映钻头破岩方式和效果最直接的体现。以钻进花岗岩为例,两种钻头的井底破碎坑形态和损伤分布如图 6所示。从图 6可以看出,CL型钻头井眼中心部位无明显破碎坑,只有PDC齿形成的刮削环槽,而井眼外围的岩石有明显的破碎坑,也有长距离的刮削环槽,说明该部位岩石的破碎是由牙轮和PDC齿共同完成的;BL型钻头整个井底均有明显的刮削环槽,破碎坑相对较少。
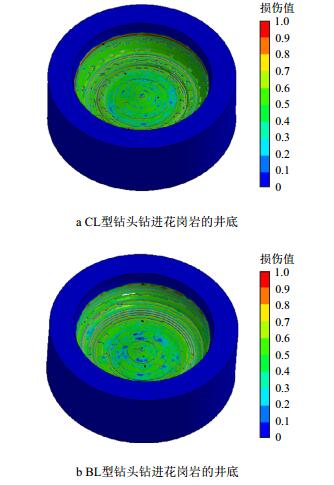 |
| 图6 井底破碎坑形态和损伤分布 Fig. 6 Bottom-hole pattern and damage distribution |
机械钻速是评价钻头性能的最重要指标之一[18],两种钻头分别钻进凝灰岩和花岗岩的机械钻速如图 7所示。由图 7可见,CL型钻头比BL型钻头在钻进花岗岩时的机械钻速快,这是因为花岗岩非常坚硬,牙轮齿的冲击压入比PDC齿的剪切刮削更容易使其破碎;BL型钻头比CL型钻头在钻进质地较软的凝灰岩中的机械钻速快,主要是因为凝灰岩塑性较强,剪切刮削比冲击压入更容易使其破碎;两种结构的钻头在花岗岩中的机械钻速差异明显比在凝灰岩中的机械钻速差异大,这是由于牙轮齿和PDC齿在软岩中接触的差异性比在硬岩中小。
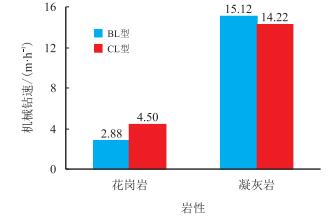 |
| 图7 钻进过程中的机械钻速 Fig. 7 Rate of penetration in drilling process |
钻头各部分承担的钻压是进行钻头结构设计、布齿设计、齿形选择以及强度分析等的基础。对复合钻头而言,钻压由牙轮和刀翼共同承担,钻压是如何分配的,是钻头设计者和使用者关心的问题。图 8给出了两种钻头钻进花岗岩过程中钻压在牙轮和刀翼上的分配情况。可以看出,CL型钻头的牙轮钻压是刀翼钻压的约2倍,而BL型钻头的刀翼钻压是牙轮钻压的约3.4倍,说明了钻压的分配与钻头的结构类型直接相关。
 |
| 图8 钻压在牙轮和刀翼上的分配 Fig. 8 WOB distribution among cones & blades |
切削齿的轴向载荷反映了钻进过程中钻头上各切削齿分担的钻压多少,对优化钻头结构和布齿设计至关重要。按齿的类型以及所在位置的不同,对牙轮切削齿和PDC切削齿的轴向载荷分别进行研究。
(1)牙轮切削齿轴向载荷沿钻头径向的分布
牙轮同一齿圈上的切削齿具有相似的井底轨迹和大致相等的载荷统计峰值[19-21],为此每个齿圈上取一颗齿进行研究。对两种结构的钻头分别钻进花岗岩和凝灰岩过程中牙轮各齿圈上的单颗切削齿轴向载荷峰值进行统计平均,得到其与齿的径向位置之间的关系如图 9所示。经过对比分析发现,无论是CL型还是BL型的钻头,钻进花岗岩比钻进凝灰岩时的牙轮切削齿轴向载荷大得多,这是因为花岗岩比凝灰岩硬度大、强度高,切削齿受到岩石反作用力相对较大;对于同一种岩石而言,无论是花岗岩还是凝灰岩,CL型钻头比BL型钻头牙轮切削齿上的轴向载荷大,这是因为CL型钻头牙轮切削齿位置较高,更容易接触到岩石;牙轮切削齿的轴向载荷峰值在齿圈间的变化无明显规律,可能是由于井底凹凸不平导致切削齿接触井底存在很大的随机性。
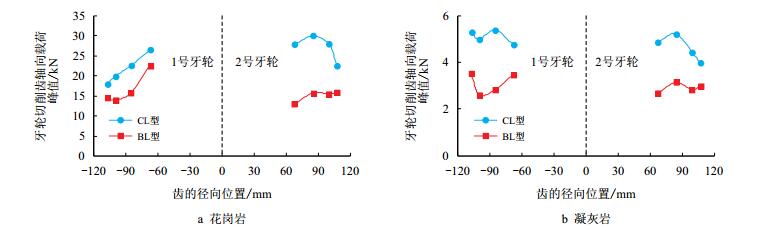 |
| 图9 牙轮切削齿轴向载荷沿钻头径向的分布 Fig. 9 Distribution of axial force on each cone tooth along the radial direction of the bit |
(2)PDC切削齿轴向载荷沿钻头径向的分布
以CL型钻头钻进花岗岩过程为例,图 10给出了各PDC齿轴向载荷均值沿钻头径向的分布。可以看出,主刀翼切削齿的轴向载荷沿钻头径向的分布形态与刀翼的冠部形状相似,从内锥到外锥,轴向载荷先增大后减小,位于锥顶的齿轴向载荷最大;副刀翼切削齿的轴向载荷相对较小,且距钻头中心越远轴向载荷越小。
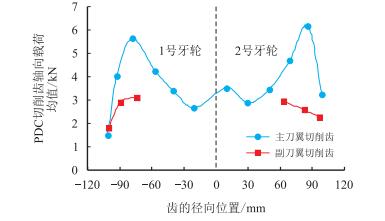 |
| 图10 PDC切削齿轴向载荷沿钻头径向的分布 Fig. 10 Distribution of axial force on each PDC cutter along the radial direction of the bit |
(1)CL型钻头适合于钻进较硬的地层,BL型钻头适合于钻进较软的地层。
(2)CL型钻头的牙轮钻压约为刀翼钻压的2倍,BL型钻头的刀翼钻压是牙轮钻压的约3.4倍,钻压的分配与钻头的结构类型直接相关。
(3)两种钻头钻进硬岩时的牙轮切削齿轴向力均比钻进软岩时的牙轮切削齿轴向力大,在相同岩石中钻进时CL型钻头比BL型钻头的牙轮切削齿轴向力大。
(4)PDC切削齿轴向载荷沿钻头径向的分布形态与刀翼冠部形状相似,位于锥顶的切削齿轴向载荷最大、最容易失效。应该选用强度和耐磨性更好的PDC复合片,同时应在该部位适当增加布齿密度,以降低单个PDC齿的载荷。
| [1] |
江晓乐. 石油天然气钻采用PDC切削齿的最新发展[J].
金刚石与磨料磨具工程, 2010, 30(2): 1–7.
JIANG Xiaole. Progress of polycrystalline diamond compact cutters for oil and gas drilling[J]. Diamond & #38; Abrasives Engineering, 2010, 30(2): 1–7. doi: 10.3969/j.issn.1006-852X.2010.02.001 |
| [2] |
王福修. PDC钻头新技术[J].
石油工程技术, 2011, 9(1): 42–46.
WANG Fuxiu. The latest development of PDC bits[J]. Petroleum Engineering & Technology, 2011, 9(1): 42–46. |
| [3] |
韩烈祥. 国产PDC+牙轮复合钻头问世[J].
钻采工艺, 2013, 36(5): 36.
HAN Liexiang. Homebred PDC & roller-cone hybrid bit comes out[J]. Drilling & Production Technology, 2013, 36(5): 36. |
| [4] |
姜福兴, 刘金海, 王平. 基于Druker-Prager准则的煤层冲击失稳模型[J].
煤炭学报, 2011, 36(5): 727–731.
JIANG Fuxing, LIU Jinhai, WANG Ping. Model of coal burst and instability based on Druker-Prager yield criterion[J]. Journal of China Coal Society, 2011, 36(5): 727–731. |
| [5] |
刘金龙, 栾茂田, 许成顺, 等. Drucker-Prager准则参数特性分析[J].
岩石力学与工程学报, 2006, 25(S2): 4009–4015.
Jinlong, LUAN Maotian, XU Chengshun, et al. Study on parametric characters of Drucker-Prager criterion[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(S2): 4009–4015. doi: 10.3321/j.issn:1000-6915.2006.z2.106 |
| [6] |
彭先泽, 杨军, 李顺波, 等. 爆炸冲击载荷作用下双层钢板混凝土板与钢筋混凝土板动态响应对比研究[J].
防灾科技学院学报, 2012, 14(3): 18–23.
PENG Xianze, YANG Jun, LI Shunbo, et al. Comparative study on dynamic response of bi-steel slab and reinforced concrete slab under blast loading[J]. Journal of Institute of Disaster Prevention, 2012, 14(3): 18–23. doi: 10.3969/j.issn.1673-8047.2012.03.004 |
| [7] | HALLQUIST J O. LS-DYNA keyword user's manual[R]. Livermore Software Technology Corporation, 2006. |
| [8] |
王政, 楼建锋, 勇珩, 等. 岩石、混凝土和土抗侵彻能力数值计算与分析[J].
高压物理学报, 2010, 24(3): 175–180.
WANG Zheng, LOU Jianfeng, YONG Heng, et al. Numerical computation and analysis on anti-penetration capability of rock, concrete and soil[J]. Chinese Journal of High Pressure Physics, 2010, 24(3): 175–180. doi: 10.3969/j.issn.1000-5773.2010.03.003 |
| [9] | FANG Qin, ZHANG Jinhua. 3D numerical modeling of projectile penetration into rock-rubble overlays accounting for random distribution of rock-rubble[J]. International Journal of Impact Engineering, 2014, 63: 118–128. doi: 10.1016/j.ijimpeng.2013.08.010 |
| [10] |
赵健, 韩烈祥, 徐依吉, 等. 粒子冲击钻井理论与现场试验[J].
天然气工业, 2014, 4(8): 1–6.
ZHAO Jian, HAN Liexiang, XU Yiji, et al. A theoretical study and field test of the particle impact drilling technology[J]. Natural Gas Industry, 2014, 4(8): 1–6. doi: 10.3787/j.issn.1000-0976.2014.08.01 |
| [11] |
方秦, 孔祥振, 吴昊, 等. 岩石Holmquist-Johnson-Cook模型参数的确定方法[J].
工程力学, 2014, 1(3): 197–204.
FANG Qin, KONG Xiangzhen, WU Hao, et al. Determination of Holmquist-Johnson-Cook constitutive model parameters of rock[J]. Engineering Mechanics, 2014, 1(3): 197–204. doi: 10.6052/j.issn.1000-4750.2012.10.0780 |
| [12] | TAO Ming, LI Xibing, LI Diyuan. Rock failure induced by dynamic unloading under 3D stress state[J]. Theoretical and Applied Fracture Mechanics, 2013, 65: 47–54. doi: 10.1016/j.tafmec.2013.05.007 |
| [13] |
常永奎, 常凯, 许超. 对LS-DYNA中混泥土HJC模型的探讨[J].
吉林建筑工程学院学报, 2013, 30(2): 27–29.
CHANG Yongkui, CHANG Kai, XU Chao. The discuss of concrete HJC model in LS-DYNA[J]. Journal of Jilin Institute of Architecture and Civil Engineering, 2013, 30(2): 27–29. doi: 10.3969/j.issn.1009-0185.2013.02.008 |
| [14] |
朱梅, 王镇全, 张德龙. 岩石三维模型及破坏的有限元方法[J].
西部探矿工程, 2010, 11: 35–38.
ZHU Mei, WANG Zhenquan, ZHANG Delong. Rock 3D model and FEM method for destroy[J]. Westchina Exploration Engineering, 2010, 11: 35–38. doi: 10.3969/j.issn.1004-5716.2010.11.01 |
| [15] |
樊赟赟, 王思敬, 王恩志, 等. 岩土材料剪切破坏点安全系数的研究[J].
岩土力学, 2009, 30(S2): 200–203.
FAN Yunyun, WANG Sijing, WANG Enzhi, et al. Research on point safety factor of shear failure geomaterials[J]. Rock and Soil Mechanics, 2009, 30(S2): 200–203. doi: 10.16285/j.rsm.2009.s2.059 |
| [16] |
王生武, 石秀华, 王永虎, 等. 基于ANSYS/LS-DYNA加筋板入水冲击仿真[J].
计算机测量与控制, 2010, 18(6): 1401–1406.
WANG Shengwu, SHI Xiuhua, WANG Yonghu, et al. Simulation of stiffened-plate water-entry impact based on ANSYS/LS-DYNA[J]. Computer Measurement & Control, 2010, 18(6): 1401–1406. |
| [17] |
白金泽.
LS-DYNA3D理论基础与实例分析[M]. 北京: 科学出版社, 2005.
BAI Jinze. LS-DYNA3D theory foundation and examples analysis[M]. Beijing: Science Press, 2005. |
| [18] |
黄志强, 范永涛, 魏振强, 等. 冲旋钻头破岩机理仿真研究[J].
西南石油大学学报 (自然科学版), 2010, 32(1): 148–150.
HUANG Zhiqiang, FAN Yongtao, WEI Zhenqiang, et al. Emulation study on rock-breaking mechanism of percussion-rotary bit[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2010, 32(1): 148–150. doi: 10.3863/j.issn.1674-5086.2010.01.030 |
| [19] |
黄春申, 练章华. 软地层牙轮钻头台架试验研究[J].
西南石油学院学报, 1996, 18(2): 78–81.
HUANG Chunsheng, LIAN Zhanghua. Study on staging testing of soft formation roller bit[J]. Journal of Southwestern Petroleum Institute, 1996, 18(2): 78–81. |
| [20] |
杨迎新, 张先普, 钟功祥. 牙轮钻头破岩机理的探讨和各齿圈载荷的预测[J].
石油机械, 1991, 19(12): 19–25.
YANG Yingxin, ZHANG Xianpu, ZHONG Gongxiang. Investigation into the penetrating mechanism of roller bits and the load on each tooth row[J]. CPM, 1991, 19(12): 19–25. doi: 10.16082/j.cnki.issn.1001-4578.1991.12.005 |
| [21] |
许京国, 陶瑞东, 郑智冬, 等. 牙轮PDC混合钻头在迪北103井的应用试验[J].
天然气工业, 2014, 34(10): 71–74.
XU Jingguo, TAO Ruidong, ZHENG Zhidong, et al. Pilot tests of a roller-PDC hybrid bit in Well Dibei 103, Tarim Basin[J]. Natural Gas Industry, 2014, 34(10): 71–74. doi: 10.3787/j.issn.1000-0976.2014.10.010 |
 2017, Vol. 39
2017, Vol. 39


