2. 长江大学石油工程学院, 湖北 武汉 430000;
3. 中国石化西南油气分公司工程技术研究院, 四川 德阳 618000;
4. 中国石油西南油气田公司, 四川 成都 610000;
5. "油气藏地质及开发工程"国家重点实验室西南石油大学, 四川 成都 610500
2. School of Petroleum Engineering, Yangtze University, Wuhan, Hubei 430000, China;
3. Engineering and Technology Research Institute Company Southwest Oil and Gas Field, SINOPEC, Deyang, Sichuan 618000, China;
4. Southwest Oil and Gas Field Company, PetroChina, Chengdu, Sichuan 610000, China;
5. State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation, Southwest Petroleum University, Chengdu, Sichuan 610500, China
油气上窜速度计算方法是井控作业关键技术,直接决定钻井液/完井液密度及性能参数设计、压井工艺及其参数确定,准确计算油气上窜速度可为钻井安全作业提供保障[1-3]。当停泵后,钻井液处于静止状态,地层中油气不断侵入井筒并逐渐累积起来,轻则为游离天然气存在,严重时将形成气柱。开泵后,被油气侵入过的钻井液循环至地面时,会出现类似油气层的特征,这种停泵一段时间并在此开泵循环而出现的气测异常现象,均可以归纳为油气上窜现象。
目前,钻井行业通常利用相对时间法[4]、泵冲法[5]、迟到时间法(修改迟到时间法)[6]、修改系数法[7]、钻具排代法[8]、全烃曲线法[9]等计算油气上窜速度,这些方法在很大程度上为计算油气上窜速度提供便捷。然而,常规方法不考虑油相与气相滑脱,而以相同的上窜速度运移。由于气液密度差异较大,造成气体运移过程中滑脱现象较严重。基于此,笔者提出了离散滑脱滞后时间法计算油气上窜速度。
在钻井井控行业标准及诸多文献中[10-13],均统一用油气上窜速度的概念。当未考虑油气滑脱时,可以将油相及气相的上窜速度认为是相等,统一用油气上窜速度是合理的。当考虑油气滑脱后,油相及气相以不同的滑脱速度向井口运移,油相上窜速度与气相上窜速度应分开研究,文中着重研究气窜速度。由于不同井深,静止钻井液中气体上窜速度不相等,严格来说气体上窜速度应为平均气体上窜速度,为叙述方便,文中将静止钻井液中气体上窜平均速度统称为气窜速度。
1 模型建立模型建立在以下假设条件下:(1)钻遇单一储层;(2)不考虑气液相间相互作用力;(3)假设开泵后,气相停止侵入井底。
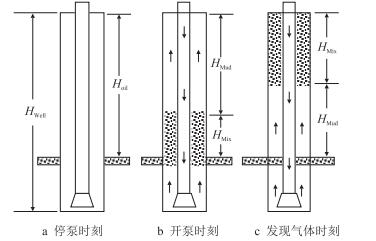
图 1为气窜发展过程的3个时刻。图中$H_{\rm{Well}}$——井深,m;$H_{\rm{Oil}}$——油气储层深度,m;$H_{\rm{Mud}}$——单相钻井液段,m;$H_{\rm{Mix}}$——气—钻井液混合段,m。
 |
| 图1 气窜发展过程示意图 Fig. 1 Process diagram of gas upward velocity |
图 1a为停泵时刻,此时气体开始侵入井筒中的静止钻井液。图 1b为开泵时刻,此时气体停止侵入井筒,部分井筒中混入气体。图 1c为井口监测到气体时刻,此时气—钻井液混合段沿井筒向井口运移,由于所受压力逐渐降低,气—钻井液混合段长度逐渐增大。
1.1 离散滑脱滞后时间模型滑脱滞后时间定义为,当油气层中同井深气钻井液两相共同向井口运移过程中,由于气体滑脱现象,引发的钻井液相较气相滞后到达井口时间。模型建立在气体流动的两阶段中,第一阶段为停泵阶段,气体在静止钻井液中以浮游状态向井口运移。第二阶段为开泵阶段,气体以气钻井液两相流动形态向井口运移。
在第一阶段停泵中,气窜速度模型为
| $ v = \frac{{{H_{{\rm{Oil}}}}-{H_{{\rm{Mud}}}}}}{{{T_{{\rm{Sta}}}}}} $ | (1) |
式中:$v$——气窜速度,m/s;
$T_{{\rm{Sta}}}$——停泵钻井液静止时间,s。
在第二阶段开泵中,假设钻井液相段长度为$H_{\rm{Mud}}$,将$H_{\rm{Mud}}$井段离散为$n$等份,每份井段长度为$H_{{\rm{Mud}, }i}$ ($i$=1,2…$n$),则$H_{\rm{Mix}}$井段顶界气体从开泵时刻运移至井口的计算时间为
| $ {T_{\rm{c}}} = \sum\limits_{i = 1}^n {\frac{{{H_{{\rm{Mud}}, i}}}}{{({H_{{\rm{Bit}}}}/{T_{{\rm{Lat}}}}) + {v_{{\rm{s}}, i}}}}} $ | (2) |
式中:${T_{\rm{c}}}$——油气层顶界气体从开泵时刻运移至井口计算时间,s;
$ v_{{\rm{s}, }i}$——$i$井段气体滑脱速度,m/s;
$H_{{\rm{Bit}}}$——钻井液循环时钻头深度,m;
$T_{{\rm{Lat}}}$——钻头位置的钻井液迟到时间,s;
$H_{{\rm{Mud}, }i}$——$i$井段长度,m。
借助气体的显示时间,得到时间判断条件为
| $ \left| {{T_{\rm{c}}}-{T_{\rm{s}}}} \right|<\Delta {T_{\rm{r}}} $ | (3) |
式中:$T_{\rm{s}}$——从开泵到监测到气体时间,s;
$\Delta {T_{\rm{r}}}$——计算精度,s。
当不考虑气体滑脱时,$v_{\rm{s}}$=0,则式 (1) 及式 (2) 变为常规的迟到时间模型[6]
| $ v = \dfrac{{{H_{{\rm{Oil}}}}-({H_{{\rm{Bit}}}}/{T_{{\rm{Lat}}}}) {T_{\rm{s}}}}}{{{T_{{\rm{Sta}}}}}} $ | (4) |
欲求解式(2)中气体滑脱速度,需建立气/钻井液连续方程、气/钻井液运动方程。
气/钻井液相连续方程为
| $ \dfrac{\partial }{{\partial t}}\iiint\limits_{{\Omega _{\rm{m}}}} {{\rho _{\rm{m}}}{\rm{d}}\Omega } + \iint\limits_{{A_{\rm{m}}}} {{\rho _{\rm{m}}}{v_{\rm{m}}}{n_{\rm{m}}}{\rm{d}}A} = 0 $ | (5) |
式中:$\Omega_{\rm{m}}$——气/钻井液相控制体;
$\rho_{\rm{m}}$——气/钻井液相密度,kg/m$^3$;
$v_{\rm{m}}$——气/钻井液相速度,m/s;
${\boldsymbol{n}_m}$——钻井液相法向;
$A_{\rm{m}}$——气/钻井液相占控制体有效横截面积,m$^2$。
气/钻井液相运动方程为
| $ \dfrac{\partial }{{\partial t}}\iiint\limits_{{\Omega _{\rm{m}}}} {{\rho _{\rm{m}}}{v_{\rm{m}}}{\rm{d}}\Omega } + \iint\limits_{{A_{\rm{m}}}} {\rho _{\rm{m}}}v_{\rm{m}}^2{\boldsymbol{n}_{\rm{m}}}{\rm{d}}A =\\ \iint\limits_{{A_{\rm{m}}}} p{\boldsymbol{n}_{\rm{g}}}{\rm{d}}A-\iiint\limits_{{\Omega _{\rm{m}}}} {{\rho _{\rm{m}}}{\rm{g}}{\rm{d}}\Omega }-{\tau _{{\rm{m}}0}}{S_{{\rm{m}}0}}-{\tau _{{\rm{m}}1}}{S_{{\rm{m}}1}} $ | (6) |
式中:$\tau_{\rm{m0}}$——气/钻井液相与裸眼井壁的摩擦力,N/m$^2$;
${\boldsymbol{n}_{\rm{g}}}$——气相法向量,无因次;
$S_{\rm{m0}}$——气/钻井液相与裸眼井壁的接触面积,m$^2$;
$\tau_{\rm{m1}}$——气/钻井液相与套管的摩擦应力,Pa;
$S_{\rm{m1}}$——气/钻井液相与套管壁的接触面积,m$^2$;
$p$——压力,N/m$^2$;
g——重力加速度,g=9.8 m/s$^2$。
1.3 辅助模型气体状态方程符合Redlich-Kwong[14]方程为
| $ p = \dfrac{{{\rm{R}}{T_{\rm{e}}}}}{{V-b}}-\dfrac{a}{{{T^{0.5}}V(V + b)}} $ | (7) |
混相气体组分参数
| $ a = {(\sum {{y_i}a_i^{0.5}})^2}, b = \sum {{y_i}{b_i}} $ | (8) |
其中
| $ {a_i} = {\Omega _{\rm{a}}}{{\rm{R}}^2}T_{\rm{c}}^{2.5}/{p_{\rm{c}}}, {b_i} = {\Omega _{\rm{b}}}{\rm{R}}{T_{\rm{ct}}}/{p_{\rm{c}}} $ | (9) |
式中:$\Omega_{\rm{a}}$=0.42748;
$\Omega_{\rm{b}}$=0.08664;
$a_i$——组分$i$的$a$值;
$b_i$——组分$i$的$b$值;
R——气体常数,R=8.314 J/(kg$ \cdot $K);
$V$——酸性气体体积,m$^3$;
$T_{\rm{e}}$——温度,K;
$T_{\rm{ct}}$——临界温度,K;
$p_{\rm{c}}$——临界压力,MPa;
$y_i$——组分的摩尔分数。
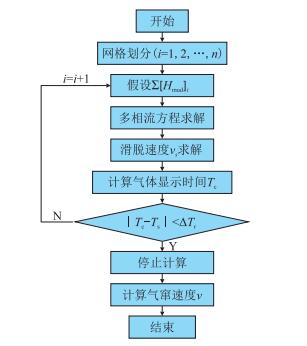
2 模型求解需用试算法求解气窜速度模型,分别将$ i$=1,2,…,$ n$代入式(2),如果满足式(3),则跳出试算循环,气窜速度具体求解流程见图 2,具体求解过程为:
 |
| 图2 气窜速度计算流程图 Fig. 2 The calculation flow chart of gas upward velocity |
(1)将环空划分为$ n$个网格,每个网格长度为$ {L_i}$;
(2)气体从网格i移动至网格$i$+1,所需用的时间为${T_{i}}= ({H}_{\rm{Oil}}/{n}) /{V_{{\rm{g}}_i}}$。
(3)利用漂移模型可求出空隙率,利用动量守恒可求出压力。
(4)假设上网格的压力与空隙率,利用式(3)中计算结果与漂移模型中的假设参数验证,可求出压力与空隙率,如收敛跳出循环,不收敛继续迭代。
这里,$T_i$——气体通过第$i$个滑移网格时间,s;$V_{{\rm{g}}_i}$——第$i$网格处气体运移速度,m/s。
求解式(5)及式(6)需用差分方法。将式(5)气 相连续方程差分为
| $ \begin{array}{l} \frac{{(A{\rho _{\rm{g}}}{v_{{\rm{sg}}}})_{i + 1}^{n + 1} - (A{\rho _{\rm{g}}}{v_{{\rm{sg}}}})_i^{n + 1}}}{{\Delta s}} = \\ \frac{{(A{\rho _{\rm{g}}}{\phi _{\rm{g}}})_i^n}}{{2\Delta t}} + \frac{{(A{\rho _{\rm{g}}}{\phi _{\rm{g}}})_{i + 1}^n}}{{2\Delta t}} - \\ \frac{{(A{\rho _{\rm{g}}}{\phi _{\rm{g}}})_i^{n + 1} - (A{\rho _{\rm{g}}}{\phi _{\rm{g}}})_{i + 1}^{n + 1}}}{{2\Delta t}} \end{array} $ | (10) |
式(5)钻井液相连续方程差分为
| $ \dfrac{{(Av_{{\rm{sl}}} )_{i + 1}^{n + 1} - (Av_{{\rm{sl}}} )_i^{n + 1} }}{{\Delta s}} =\dfrac{{(A\phi _{\rm{l}} )_i^n + (A\phi _{\rm{l}} )_{i + 1}^n - (A\phi _{\rm{l}} )_i^{n + 1} - (A\phi _{\rm{l}} )_{i + 1}^{n + 1} }}{{2\Delta t}} $ | (11) |
式(6)气/钻井液相运动方程差分为
| $ (Ap)_{i + 1}^{n + 1}-(Ap)_i^{n + 1} = {K_1} + {K_2} + {K_3} + {K_4} $ | (12) |
其中
| $ \begin{array}{l} {K_1} = \frac{{\Delta s}}{{2\Delta t}}\left\{ {\left[ {A({\rho _{\rm{l}}}{v_{{\rm{sl}}}} + {\rho _{\rm{g}}}{v_{{\rm{sg}}}})} \right]_i^n + \left[ {A({\rho _{\rm{l}}}{v_{{\rm{sl}}}} + {\rho _{\rm{g}}}{v_{{\rm{sg}}}})} \right]_{i + 1}^n} \right.\\ \left. { - \left[ {A({\rho _{\rm{l}}}{v_{{\rm{sl}}}} + {\rho _{\rm{g}}}{v_{{\rm{sg}}}})} \right]_i^{n + 1} - \left[ {A({\rho _{\rm{l}}}{v_{{\rm{sl}}}} + {\rho _{\rm{g}}}{v_{{\rm{sg}}}})} \right]_{i + 1}^{n + 1}} \right\} \end{array} $ | (13) |
| $ K_2 = \left[{A\left( {\dfrac{{\rho _{\rm{l}} v_{{\rm{sl}}}^2 }}{{\phi _{\rm{l}} }} + \dfrac{{\rho _{\rm{g}} v_{{\rm{sg}}}^2 }}{{\phi _{\rm{g}} }}} \right)} \right]_i^{n + 1} - \left[{A\left( {\dfrac{{\rho _{\rm{l}} v_{{\rm{sl}}}^2 }}{{\phi _{\rm{l}} }} + \dfrac{{\rho _{\rm{g}} v_{{\rm{sg}}}^2 }}{{\phi _{\rm{g}} }}} \right)} \right]_{i + 1}^{n + 1} $ | (14) |
| $ K_3 = - \dfrac{{{\rm{g}}\Delta s}}{2}[(A\rho _{\rm{l}} )_i^{n + 1} + (A\rho _{\rm{l}} )_{i + 1}^{n + 1}] $ | (15) |
| $ K_4 = - \dfrac{{\Delta s}}{2}\left\{ {\left[{A\left( {\dfrac{{\partial p}}{{\partial s}}} \right)} \right]_{{\rm{fr}}i}^{n + 1} + \left[{A\left( {\dfrac{{\partial p}}{{\partial s}}} \right)} \right]_{{\rm{fr}}i + 1}^{n + 1} } \right\} $ | (16) |
式中:$v_{\rm{sl}}$——钻井液相的表观速度,m/s;
$v_{\rm{sg}}$——地层气相的表观速度,m/s;
${\phi _{\rm{l}}}$——持液率;
${\phi _{\rm{g}}}$——空隙率;
$\Delta s$——控制体长度,m;
$\Delta t$——微元时间,s;
${\rho _{\rm{g}}}$——气相密度,kg/m$^3$
${\rho _{\rm{l}}}$——液相密度,kg/m$^3$。
3 现场后效测试及应用以四川元坝某井为例,2014-11-21T07:16该井停泵,此时钻至5 008 m,钻头下至4 999 m。2014 11 21T22:24该井开泵,排量为39.15 L/s,钻井液密度为2.19 g/cm$^3$,测得钻头下深迟到时间为128 min,油气层位置为4 559 m,全烃、${{\rm{C}}_1}$及${{\rm{C}}_2}$的监测数据如图 3所示。
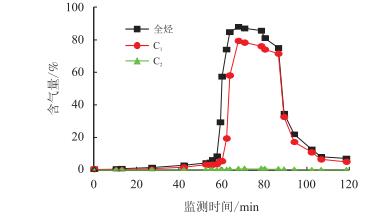 |
| 图3 全烃、${{\rm{C}}_1}$及${{\rm{C}}_2}$监测数据变化趋势 Fig. 3 The monitoring data of total hydrocarbon, ${{\rm{C}}_1}$and ${{\rm{C}}_2}$ |
不考虑气相滑脱,利用迟到时间法计算的气窜速度为56.21 m/h,考虑气相滑脱,利用本文模型计算的气窜速度为13.29 m/h。本模型计算的气窜速度应用于元坝205–2深井,在停泵过程中无钻井复杂事故出现。
4 模型分析下文模型分析均以四川元坝某井为依托,分析各参数对气窜速度影响。
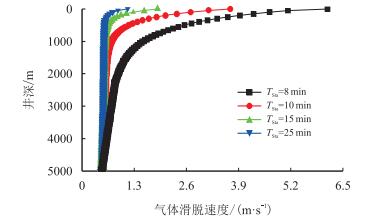
4.1 井深对气体滑脱速度影响图 4给出了井深对气体滑脱速度影响。随静止时间增大,气体滑脱速度减小。在井口监测到气体总量是一定的,随静止时间增长,气体侵入速度减小,滑脱速度随之减小。在井底处,由于气体处于高压状态,气体处于超临界状态,气体滑脱现象不明显。当气体运移至井口时,气体体积急剧膨胀,气相与液相密度差异增大,气体所受合外力增大,气体加速度增大,因此气体滑脱速度明显增大,在4 999 m井底处气体滑脱速度为0.21 m/s,井口处高达6.13 m/s,气体滑脱速度迅猛增大29.1倍。
 |
| 图4 环空气体滑脱速度 Fig. 4 Gas slippage velocity along annulus |
图 5给出了油气层顶界位置对气窜速度影响。随油气层顶界位置上移,根据式(1)计算可得到,气体上窜速度减小。当气体显示时间、停泵时间等参数一定时,油气层顶界位置上移,使静止钻井液中有效气体上窜高度减小,从而气体上窜速度减小。当${T_{{\rm{Lat}}}}$为128 min时,油气层顶界位置${H_{{\rm{Oil}}}}$从4 350 m下移至4 950 m,气窜速度从0.046 m/h增至42.810 m/h。
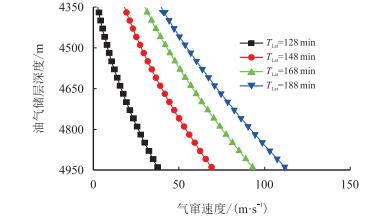 |
| 图5 油气层顶界位置对气窜速度影响 Fig. 5 The influence of the reservoir top boundary on gas slippingupward velocity |
图 6给出了停泵钻井液静止时间对气窜速度影响。随静止时间延长,气体上窜速度减小。当静止时间延长,单位时间内气窜高度减小,从而使气窜速度减小。当${T_{{\rm{Lat}}}}$为128 min时,停泵钻井液静止时间从7.5 h延长至15.0 h,气窜速度从32.49 m/h减至13.29 m/h。
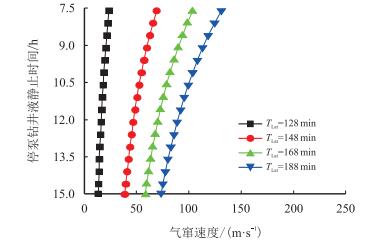 |
| 图6 停泵钻井液静止时间对气窜速度影响 Fig. 6 The influence of static time on gas upward velocity in closing pump operations |
图 7给出了迟到时间对气窜速度影响。随迟到时间延长,钻井液速度减小,从而使气体在两相流动中滑脱速度减小,由于监测到气体时间一定,钻井液相段为${H_{{\rm{Mud}}}}$相应减小,从而气体上窜速度增大。当${T_{{\rm{Sta}}}}$为900 min时,迟到时间从128 min延长至288 min,气窜速度从13.29 m/h增至119.65 m/h。
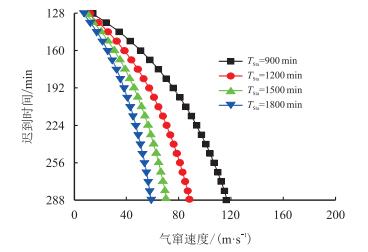 |
| 图7 迟到时间对气窜速度影响 Fig. 7 The influence of the lag time on gas upward velocity |
(1)由于油相、气相密度差异较大,油相上窜速度与气相上窜速度应分开研究。
(2)气体滑脱速度较大,对计算气窜速度影响较大,不可忽略。不考虑气体滑脱的影响,计算的气窜速度较考虑气体滑脱计算的气窜速度偏大。
(3)无论采用任何模型预测气窜速度,在钻井停泵作业中应预留一定的安全作业时间。以确保停泵过程中气体不能上窜至井口,避免钻井事故发生。
| [1] | SANTOSH K D.Ultra deep water drilling riser[C]//SPE Asia Pacific Oil and Gas Conference and Exhibition, Jakarta, 2011. doi:10.2118/145704-MS |
| [2] | GANEVA M, KASHTANOV P V, SMIRNOV B M, et al. Angular and velocity distribution of nano-size cluster beams in a gas flow[J]. Vacuum, 2014, 110(110): 140–145. doi: 10.1016/j.vacuum.2014.08.019 |
| [3] | FATTAH K A, EL-KATATNEY S M, DAHAB A A. Potential implementation of underbalanced drilling technique in egyptian oil fields[J]. Journal of King Saud University, 2011, 23(1): 49–66. doi: 10.1016/j.jksues.2010.-02.001 |
| [4] |
张桂林. 油气上窜速度实用计算方法[J].
石油钻探技术, 2006, 34(6): 23–26.
ZHANG Guilin. The practical method calculating oil and gas upward velocity[J]. Petroleum Drilling Techniques, 2006, 34(6): 23–26. doi: 10.3969/j.issn.1001-0890.2006.-06.008 |
| [5] |
应维民, 胡耀德. 油气上窜速度的现场计算[J].
海洋石油, 2002(2): 63–64, 19.
YING Weimin, HU Yaode. Calculation of the oil and gas rising speed at the scene of drilling[J]. Offshore Oil, 2002(2): 63–64, 19. doi: 10.3969/j.issn.1008-2336.2002.-02.013 |
| [6] |
李振海, 覃保锏, 金庭科, 等. 油气上窜速度计算方法的修改[J].
录井工程, 2011, 22(2): 12–13, 26.
LI Zhenhai, QIN Baojian, JIN Tingke, et al. Amendment of the calculation method of oil and gas ascending velocity[J]. Mud Logging Engineering, 2011, 22(2): 12–13, 26. doi: 10.3969/j.issn.1672-9803.2011.02.004 |
| [7] |
王文忠, 赵军, 张秀红. 油气上窜速度计算公式的修正[J].
断块油气田, 2003, 10(1): 64–65.
WANG Wenzhong, ZHAO Jun, ZHANG Xiuhong. The modified formula of calculating oil & gas upward flow velocity[J]. Fault Block Oil & Gas Field, 2003, 10(1): 64–65. doi: 10.3969/j.issn.1005-8907.2003.01.021 |
| [8] |
成萍, 周文君, 胥仁强, 等. 气测后效油气上窜高度计算方法完善[J].
录井工程, 2010, 21(1): 26–28.
CHENG Ping, ZHOU Wenjun, XU Renqiang, et al. Perfecting method for calculating oil and gas fleeting height of gas logging aftereffect[J]. Mud Logging Engineering, 2010, 21(1): 26–28. doi: 10.3969/j.issn.1672-9803.2010.-01.007 |
| [9] | 潘前林. 油气上窜速度计算方法的探讨[J]. 录井技术, 1999, 10(4): 37–38. |
| [10] |
孔祥伟, 林元华, 邱伊婕, 等. 气侵钻井过程中井底衡压的节流阀开度控制研究[J].
应用数学和力学, 2014, 35(5): 572–580.
KONG Xiangwei, LIN Yuanhua, QIU Yijie, et al. Research on the throttle valve opening degree control to keep bottomhole pressure in balance when gas influx occurs during drilling operations[J]. Applied Mathematics and Mechanics, 2014, 35(5): 572–580. doi: 10.3879/j.issn.1000-0887.2014.05.011 |
| [11] | FILIPPOV A I, AKHMETOVA O V, ZELENOVA M A, et al. Investigation of the temperature fields of a gas flow in a well[J]. Journal of Engineering Physics and Thermophysics, 2011, 84(5): 1132–1147. doi: 10.1007/s10891-011-0577-6 |
| [12] | BYMASTER A S, OLSON M D, GRAVE E J, et al. High pressure gas-liquid separation:an experimental study on separator performance of natural gas streams at elevated pressures[J]. Growth in the EU", 2011, 55(2): 92–97. doi: 10.4043/21781-MS |
| [13] | ETTEHADI O R, OZBAYOGLU M E, OZBAYOGLU M A. A mechanistic model to characterize the two phase drilling fluid flow through inclined eccentric annular geometry[C]. SPE 155147, 2012. doi:10.2118/155147-MS |
| [14] | 陈家琅, 陈涛平. 石油气液两相管流[M]. 北京: 石油工业出版社, 2010. |
 2017, Vol. 39
2017, Vol. 39


