2. 中国石油玉门油田勘探开发研究院, 甘肃 酒泉 735000;
3. 兰石能源装备工程研究院, 山东 青岛 266000
2. Research Institute of Exploration and Development, Yumen Oilfield, PetroChina, Jiuquan, Gansu 735000, China;
3. Lanshi Energy Equipment Engineering Institute, Qingdao, Shandong 266000, China
作为一种油气藏动态分析和预测的常用工具,物质平衡模型已经较为成熟,在气藏工程快速发展的同时,针对气藏的物质平衡研究也获得了许多重要研究成果,比如分区物质平衡方程[1-3]、用于计算产能的物质平衡方程[4-6]等,由此,使物质平衡模型的应用分析更符合生产实际,也为生产动态分析增加了重要分析方法和手段。随着页岩气藏的规模开发,页岩气藏的渗流机理及开发对策方面的研究较多[7-10],但针对页岩气储层的物质平衡模型的研究还较少[11-12],尤其是基于动态渗流区域的物质平衡模型研究处于空白。
页岩气渗流机理受到扩散、解吸吸附、滑脱、应力敏感等多因素影响,通过建立数学模型进行解析推导产能公式或者数值模拟都很复杂[13-14],物质平衡方程的应用简化了渗流机理的分析过程,也能较为全面地分析渗流规律[15-16]。因此,本文通过建立包括基岩、天然裂缝、人工裂缝、气水产量4个部分的分区物质平衡模型,以实际压裂水平井为研究实例,预测并分析气井产能及供气来源变化规律,为水平井生产动态预测提供不同层面的分析方法。
1 页岩气藏渗流规律页岩气藏水平井通过体积压裂形成复杂的体积缝网(图 1),把缝网区域分为3个渗流区域:基岩渗流区、天然裂缝渗流区和人工裂缝渗流区。基岩渗流区由纳米孔隙构成,气源有孔隙中的游离气和固体颗粒中的吸附气,随着基岩压力的下降,气体通过纳米孔隙的扩散渗流到天然裂缝或者人工裂缝中;天然裂缝渗流区是指压裂时未被人工裂缝开启的剩余天然裂缝部分,除了自身所含的游离气和原始水外,其渗流功能主要是接收与之接触的基岩系统流入的页岩气,并借助于较高的(相对于基岩渗流区)渗透率把气体输送到人工裂缝渗流区;人工裂缝渗流区具有很高的渗透率,一方面提供气源的运输通道,另一方面,通过大面积的与基岩、天然裂缝的接触面接收气源,由于人工裂缝中留有大部分的压裂液返排后的剩余水,因此,人工裂缝中渗流体现为气水两相渗流,并成为水平井产水量的主要来源。
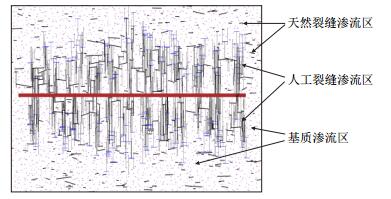 |
| 图1 页岩气藏压裂水平井渗流区域示意图 Fig. 1 Dynamic seepage area of the fractured horizontal well |
根据页岩气藏压裂水平井的渗流规律,由于渗流介质的差别,3个渗流区域的渗透率相差很大,基岩的纳米孔隙渗透率极低,一般为微达西级(甚至纳达西级),其中的压力降传播很慢,天然裂缝的渗透率比基岩可高达10~100倍,但相对于人工裂缝的几百毫达西渗透率仍然较低。因此,生产过程中的压力降在各渗流区域有明显的快慢不同,亦即真正的渗流区域是随着生产时间的推进而不断扩大的,当设计物质平衡模型时,直接应用压裂缝网体积参与弹性计算明显是错误的。因此,物质平衡模型不能把气藏看成封闭的定容储层,而应该根据渗流规律计算不同时间的渗流动态区域,并进一步设计不同区域的平均地层压力计算方法。
根据导压系数的物理意义,设计动态渗流区域及平均地层压力计算方法。
定义各渗流区的导压系数[17-18],其物理意义是单位时间内压力降传播的面积
| $ {\eta _i} = \frac{{{K_i}}}{{{\phi _i}{\mu _{g, i}}{C_{t, i}}}} \times {10^{-4}} $ | (1) |
式中:η-导压系数,m2/s;
K-渗透率,mD;
ϕ-孔隙度,%;
µg-黏度,mPa·s;
Ct-综合压缩系数,MPa−1;
下标i-可取值为m、f、F,分别表示基岩、天然裂缝和人工裂缝。
则实际渗流区域长度与生产时间的关系式为
| $ {r_i} = \sqrt {\frac{{{\eta _i}t}}{{\rm{\pi }}}} $ | (2) |
式中:r-渗流区域半长,m;
t-生产时间,s。
动态渗流区域体积可表示为
| $ {V_i} = 2Lh{r_i} $ | (3) |
式中:L-水平井长度,m;
h-储层厚度,m。
人工裂缝和天然裂缝系统假设为以水平井为中心的长方形剖面[19],按拟稳定流处理,其平均地层压力近似公式为
| $ {p_{\rm{F}}} = {p_{\rm{o}}}-\frac{{{p_{\rm{o}}}-{p_{\rm{w}}}\left( t \right)}}{{\ln \frac{{2.066{A_{\rm{F}}}^{\frac{1}{2}}}}{{{r_{\rm{w}}}}}}} $ | (4) |
| $ {p_{\rm{f}}} = {p_{\rm{m}}}-\frac{{{p_{\rm{m}}}-{p_{\rm{F}}}}}{{\ln \frac{{2.066{A_{\rm{f}}}^{\frac{1}{2}}}}{{{r_{\rm{w}}}}}}} $ | (5) |
式中:pF-人工裂缝系统地层压力,MPa;
po-原始地层压力,MPa;
pw(t)-井底压力,MPa;
AF-人工裂缝剖面面积,m2;
rw-井眼半径,m;
pf-天然裂缝系统地层压力,MPa;
pm-基岩系统地层压力,MPa;
Af-天然裂缝剖面面积,m2。
基岩渗流可以近似看作基岩向裂缝方向的平面单向流,其基岩系统地层压力公式表示为
| $ {p_{\rm{m}}} = \frac{{{p_{\rm{o}}} + {p_{\rm{F}}}}}{2} $ | (6) |
动态渗流分区的边界与压裂体积缝网的参数有关,人工裂缝、天然裂缝的最大边界为压裂体积缝网的边界,基岩是通过裂缝面向内部的传播,渗流区域与裂缝条数有关。设人工裂缝都垂直于井筒均匀分布,总渗流区域半长为B,则基岩压降最大渗流区域半径rmax可表示为
| $ {r_{\max }} = \frac{{BL}}{{{L_{{\rm{tF}}}}}} $ | (7) |
| $ {L_{{\rm{tF}}}} = \frac{{LB{\phi _{\rm{F}}}}}{{{w_{\rm{F}}}}} $ | (8) |
式中:rmax-基岩压降最大渗流区域半径,m;
B-总渗流区域半长,m;
LtF-人工裂缝总长度,m;
ϕF-人工裂缝孔隙度,%;
wF-人工裂缝宽度,m。
联立式(7)和式(8),有
| $ {r_{\max }} = \frac{{{w_{\rm{F}}}}}{{{\phi _{\rm{F}}}}} $ | (9) |
当rm > rmax时,整个系统的压降遇到边界,储层压力整体下降,此时人工裂缝的平均压力为
| $ {p_{\rm{F}}} = \left( {{p_{\rm{o}}}-\frac{{{p_{\rm{o}}}-{p_{\rm{w}}}\left( t \right)}}{{\ln \frac{{2.066{A_{\rm{F}}}^{\frac{1}{2}}}}{{{r_{\rm{w}}}}}}}} \right)\left( {1-\frac{1}{{\ln \frac{{{r_{\max }}}}{{{r_{\rm{w}}}}}}} + \frac{1}{{\ln \frac{{{r_{\rm{m}}}}}{{{r_{\rm{w}}}}}}}} \right) $ | (10) |
式中:rm-基岩系统渗流区域半长,m。
在基岩压降范围达到最大值之前,若基岩渗流区域半长rF > B,则rF = B;若天然裂缝渗流区域半长rf > B,则rf = B。
3 含水计算假设储层中有基岩原始含水饱和度Smwo和天然裂缝原始含水饱和度Sfwo,压裂时由于渗吸作用,使与人工裂缝接触的基岩面较小深度范围d内的含水达到基岩的束缚水饱和度Smwc,当井生产时此饱和度不会降低(一般页岩基岩的Smwo < Smwc);人工裂缝有时会沿着天然缝压裂,部分天然缝转变为人工裂缝,因此,天然裂缝的含水仍为Sfwo。人工裂缝的含水与压裂有关,其含水饱和度SFw的计算式为
| $ {S_{{\rm{Fw}}}} = \frac{{{V_{{\rm{in}}}}\left( {1-{R_{\rm{r}}}} \right)-{V_{{\rm{ms}}}}}}{{LBh{\phi _{\rm{F}}}}} $ | (11) |
| $ {\phi _{\rm{F}}} = \frac{{{V_{{\rm{in}}}}\left( {1-{R_{\rm{r}}}} \right)}}{{LBh}} $ | (12) |
| $ {V_{{\rm{ms}}}} = 2{L_{{\rm{tF}}}}hd\left( {{S_{{\rm{mwc}}}}-{S_{{\rm{mwo}}}}} \right) $ | (13) |
式中:SFw-人工裂缝的含水饱和度,%;
Vin-压裂液注入体积,m3;
Rr-压裂液返排率,%;
Vms-渗吸体积,m3;
Smwc-基岩的束缚水饱和度,%;
Smwo-基岩的原始含水饱和度,%;
d-渗吸深度,m。
联立式(11)式(12)和式(13),整理,可得
| $ {S_{{\rm{Fw}}}} = 1-\frac{{2d}}{{{w_{\rm{F}}}}}\left( {{S_{{\rm{mwc}}}}-{S_{{\rm{mwo}}}}} \right) $ | (14) |
由式(14)可以看出,人工裂缝的含水主要取决于人工裂缝缝宽、渗吸深度、孔隙的原始含水饱和度和束缚水饱和度。
4 物质平衡模型的建立由动态渗流分区和含水计算,可以确定不同时间的孔隙体积、岩石体积、水体积、游离气体积及吸附气体积,结合产出的气和水体积,可以建立物质平衡模型,按照物质平衡关系,假设产出水全部来自压裂液返排后的滞留液,储层中原始水不参与渗流;产出部分由基岩、天然裂缝和人工裂缝的岩石弹性、水弹性、游离气弹性及解吸气弹性等组成。随着各系统的压力降低,物质平衡模型见式(15)。
| $ {N_{\rm{w}}} + {N_{\rm{g}}} = {B_1} + {B_2} + {B_3} + {B_4} + {B_5} + {B_6} + {B_7} + {B_8} + {B_9} + {B_{10}} $ | (15) |
其中:$N_{\rm{w}} = {W_{\rm{p}}}{B_{\rm{w}}}$,累产水项;
$N_{\rm{g}} = {G_{\rm{p}}}{B_{{\rm{go}}}}$,累产气项;
$B_1 = {V_{\rm{m}}}{\phi _{\rm{m}}}{C_{\rm{r}}}\left ({{p_{\rm{o}}}-{p_{\rm{m}}}} \right)$,基岩岩石项;
$B_2 = {V_{\rm{m}}}{\phi _{\rm{m}}}{S_{{\rm{mwc}}}}{C_{\rm{w}}}\left ({{p_{\rm{o}}}-{p_{\rm{m}}}} \right)$,基岩水项;
$B_3 = {V_{\rm{m}}}{\phi _{\rm{m}}}\left ({1-{S_{{\rm{mwc}}}}} \right)\frac{{{B_{{\rm{gm}}}}-{B_{{\rm{go}}}}}}{{{B_{{\rm{go}}}}}}$,基岩游离气项;
$B_4 = {V_{\rm{m}}}{\rho _{\rm{s}}}{V_{\rm{L}}}\left ({\frac{{{p_{\rm{o}}}}}{{{p_{\rm{L}}} + {p_{\rm{o}}}}}-\frac{{{p_{\rm{m}}}}}{{{p_{\rm{L}}} + {p_{\rm{m}}}}}} \right){B_{{\rm{gm}}}}$,基岩解吸气项;
$B_5 = {V_{\rm{f}}}{\phi _{\rm{f}}}{C_{\rm{r}}}\left ({{p_{\rm{o}}}-{p_{\rm{f}}}} \right)$,天然裂缝岩石项;
$B_6 = {V_{\rm{f}}}{\phi _{\rm{f}}}{S_{{\rm{fwo}}}}{C_{\rm{w}}}\left ({{p_{\rm{o}}}-{p_{\rm{f}}}} \right)$,天然裂缝水项;
$B_7 = {V_{\rm{f}}}{\phi _{\rm{f}}}\left ({1-{S_{{\rm{fwo}}}}} \right)\frac{{{B_{{\rm{gf}}}}-{B_{{\rm{go}}}}}}{{{B_{{\rm{go}}}}}}$,天然裂缝气项;
$B_8 = {V_{\rm{F}}}{\phi _{\rm{F}}}{C_{\rm{r}}}\left ({{p_{\rm{o}}}-{p_{\rm{F}}}} \right)$,人工裂缝岩石项;
$B_9 = {V_{\rm{F}}}{\phi _{\rm{F}}}{S_{{\rm{Fw}}}}{C_{\rm{w}}}\left ({{p_{\rm{o}}}-{p_{\rm{F}}}} \right)$,人工裂缝水项;
$B_{10} = {V_{\rm{F}}}{\phi _{\rm{F}}}\left ({1-{S_{{\rm{Fw}}}}} \right)\frac{{{B_{{\rm{gF}}}}-{B_{{\rm{go}}}}}}{{{B_{{\rm{go}}}}}}$,人工裂缝气项;
Wp-累产水量,m3;
Gp-累产气量,m3;
Bgm,Bgf,BgF-基岩、天然裂缝、人工裂缝中天然气体积系数,无因次;
Bw水的体积系数,无因次;
Vm-基岩体积,m3;
ϕm-基岩孔隙度,%;
Cr-岩石压缩系数,MPa−1;
Cw-水的压缩系数,MPa−1;
ρs-岩石密度,g/cm3;
VL-朗缪尔体积,m3/t;
pL-朗缪尔压力,MPa;
Vf-天然裂缝体积,m3;
ϕf-天然裂缝孔隙度,%;
Sfwo-天然裂缝原始含水饱和度,%;
Bgo-原始地层压力状态下,天然气体积系数,无因次;
VF-人工裂缝体积,m3。
物质平衡模型由基岩渗流项、天然裂缝渗流项、人工裂缝渗流项、累产项4大部分组成,各部分依据岩石、水、游离气和解吸气进行划分,由此构成了由12项组成的综合物质平衡方程。
5 实例分析以W201-H1井为例进行模型的应用分析,计算参数如表 1所示。
| 表1 W201-H1井物质平衡方程计算参数 Table 1 Parameters of the W201–H1 well for the model |
该井初期气产量13 239 m3/d,随着井底压力的较快降低,生产到1 a时气产量为10 800 m3/d,下降了18.42%,然后基本保持稳定产量;从产水量上看,初期生产时为关键排水期,100 d内的排水量由开始的70 m3/d降到约10 m3/d,累计排水可达50%。
由物质平衡模型得出产气量拟合如图 2所示。把理论产气量趋势分成4个阶段。
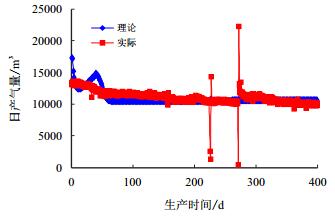 |
| 图2 理论与实际日产气量对比 Fig. 2 Comparison of the production by theory and practice |
第1阶段:人工裂缝排水阶段(第1天~第12天)。初期生产,能量充足,主要功能为人工裂缝排水(累排水量占预测总排水量的10.31%),由于人工裂缝渗透率高,气水混排,初始产气量较大,压力下降较快,存在于人工裂缝的较小储量的自由气衰竭较快,致使产量迅速下降,到第12天降幅达到27.84%。
第2阶段:人工裂缝供气阶段(第13天~第40天)。人工裂缝渗流区域增大,压力降低变缓,产水量降低,与基岩和天然裂缝接触面气源快速补充,产气量处于增加趋势,增幅可达18.74%,持续时间较短。
第3阶段:天然裂缝渗流区过渡阶段(第41天~第122天)。人工裂缝动态渗流区域在第42天到达边界,天然裂缝及基质渗流区域供气逐渐明显,但由于较慢的压力降和较低的渗透率,产气量处于下降趋势,相对于初期产量下降幅度为40.35%。
第4阶段:天然裂缝导流阶段(第122天~第400天)。随着压力降在天然裂缝渗流储层的传播,与缝网接触的基质中,越来越多的游离气慢慢渗流到裂缝中参与渗流,同时基质储层中的吸附气分解,用以补充游离气源,产量得以稳定并略有增长。
预测该水平井未来40余年产量变化如图 3所示。
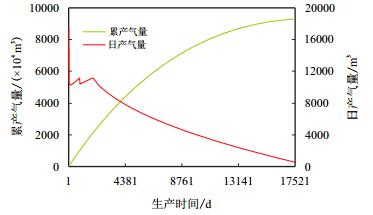 |
| 图3 物质平衡方程预测生产参数变化 Fig. 3 Forecasting the production by the modal |
由图 3可知,生产400 d后产气量仍然沿着第4阶段继续稳中有升,天然裂缝渗流区继续扩大与基质的接触面积,同时基质也继续缓慢补充游离态的气源。
第5阶段:基质主渗流过渡阶段(第860天~第872天)。到第860天,由于天然裂缝渗流动态区域到达边界,产量出现短期小幅下降,但这一过渡阶段很短,储层整体压力的降低引起的基质压力降也相应增大,渗流和解吸的动力增强,气量的补充比较迅速,到第872天产量不降反升。
第6阶段:基质主渗流区供气阶段(第872天~第1 897天)。这一阶段,基质实际渗流区域逐渐扩大,来自于基质的游离气与解吸气成为主要供气源,尤其是缓慢解吸的气源成为产气量增加的主要动力,但产量增加幅度并不高,约3 a的时间产量增加7.33%。
第7阶段:产量主体递减阶段(第1 898天~第14 600天),当压力降传播到基质渗流区的边界时,储层能量呈现衰竭状态,产气量缓慢下降,到第2 530天(6.9年)产量降到1×104 m3/d,到第8 391天(约23年)产量降到5 000 m3/d,到第14 236天(约39年)产量降到2 000 m3/d,该阶段也是页岩气压裂水平井最长、最具有区别于常规储层生产特点的阶段,即生产约5 a后产量缓慢递减并持续很长时间。
以上压裂水平井生产的7个阶段是根据物质平衡模型理论分析得出的,与该气井Ecllipse数值模拟结果进行对比,年产量的变化趋势基本一致,但7个阶段没有办法验证。
从供给气源能量贡献角度分析,井底的产气量构成主要有基质游离气、基质解吸气、天然缝游离气和人工缝游离气4大类,对这4大类的累产气量及日产气量供气比例分析如图 4和图 5所示。
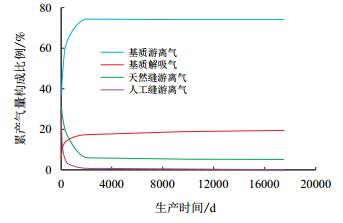 |
| 图4 累产气量供气构成比例图 Fig. 4 The proportion of the total production by the different source |
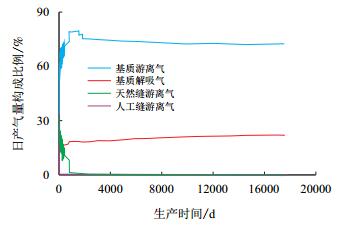 |
| 图5 日产气量供气构成比例图 Fig. 5 The proportion of the daily production by the different source |
由图 4和图 5可知,从物质平衡模型分析结果看,该井初期很短时间内(约60 d内)人工裂缝和天然裂缝游离气占50%以上,之后基质游离气开始发挥主体作用,并在第1 574天(约4.3年)其日产气量供气比例达到79.59%的最大值,此时累产量构成占72.97%(累产量构成比例最高为第3 528天的74.36%)。随着储层压降的传播及增大,基质中的解吸气供给能力增强,其日产气量供气比例开始缓慢增大,基质中的游离气供气比例随之小幅下降,一直到气井生产废弃。但是,从整体供气结构来看,基质储层中的游离气供气比例仍处于主体作用,其累产气量构成比例和日产气量构成比例都维持在70%以上。在日产气量构成中,裂缝系统在后期生产中主要起流动通道作用,供气作用已经不存在,基质解吸气的供气比例最高达到22%。
基于该井的生产规律认识到,页岩气藏压裂水平井生产具有与渗流特征相吻合的7个生产阶段,产气量主要依靠的是基质中游离气的扩散与渗流,解吸气的作用小于25%。把该模型中的含气量35%分别调整为50%和70%,解吸气在日产气量构成比例中可分别达到40%和50%,游离气的主体作用仍然较为明显。
6 结论(1) 基于页岩储层压裂水平井的动态分区物质平衡方程的原理建立了与时间相关的动态渗流分区域的物质平衡模型。随着生产的进行,不同渗流区域的大小及压降会随着时间变化而变化的,动态渗流区域计算清晰地模拟了复杂渗流过程,提供了一种全新的页岩气井产量预测和综合分析方法。
(2) 模型考虑了返排后滞留地层中的水对物质平衡的影响,设计了产出液和产出气的综合物质平衡方程,更加客观全面地反映了生产的实际情况。
(3) 物质平衡模型预测与页岩气藏压裂水平井渗流规律相结合,归纳出了水平井生命周期的7个生产阶段,并由此深入地分析了供气来源结构比例,指出基岩游离气才是气井长期生产的主要气源,填补了许多方法不能定量分析供气来源的计算方法。
(4) 物质平衡方程应用过程中涉及的参数较多,在拟合时要考虑参数之间的相互约束,比如基岩孔隙度、岩石密度、吸附气含量与实测含气量、储量等相互制约,人工裂缝含水饱和度与压裂参数、压裂液量、渗吸等相互约束,产水量与压裂液用量、返排率、渗吸等相互约束。
| [1] |
程时清, 杨秀祥, 谢林峰, 等. 物质平衡法分区计算定容气藏动储量和压力[J].
石油钻探技术, 2007, 35(3): 66–68.
CHENG Shiqing, YANG Xiuxiang, XIE Linfeng, et al. Multi-region calculation of dynamic reserve and pressure of constant volume reservoirs using material balance[J]. Petroleum Drilling Techniques, 2007, 35(3): 66–68. doi: 10.3969/j.issn.1001-0890.2007.03.020 |
| [2] |
周涌沂, 车雄伟. 低渗透油藏分区物质平衡方法研究[J].
西安石油大学学报, 2010, 25(6): 42–47.
ZHOU Yongyi, CHE Xiongwei. Regional material balance method for low permeability reservoir[J]. Journal of Xi'an Shiyou University, 2010, 25(6): 42–47. doi: 10.3969/j.issn.1673-064X.2010.06.010 |
| [3] |
鲜俊, 黄炳光, 王焰东, 等. 结合物质平衡的气井产能计算方法[J].
内蒙古石油化工, 2011, 18: 42–44.
XIAN Jun, HUANG Bingguang, WANG Yandong, et al. New combined with the material balance of gas well deliverability calculation method[J]. Inner Mongolia Petrochemical Industry, 2011, 18: 42–44. doi: 10.3969/j.issn.1006-7981.2011.18.017 |
| [4] | SHI Juntai, ZHANG Lei. Diffusion and flow mechanisms of shale gas through matrix pores and gas production forecasting[J]. Society of Petroleum Engineers, 2013: 2–19. |
| [5] |
陈小刚, 王宏图, 刘宏, 等. 气藏动态储量预测方法综述[J].
特种油气藏, 2009, 16(2): 9–12.
CHEN Xiaogang, WANG Hongtu, LIU Hong, et al. An overview of prediction methods for dynamic reserves of gas reservoirs[J]. Special Oil and Gas Reservoir, 2009, 16(2): 9–12. doi: 10.3969/j.issn.1006-6535.2009.02.002 |
| [6] |
尚颖雪, 李晓平, 宋力. 考虑水溶气的页岩气藏物质平衡方程及储量计算方法[J].
天然气地球科学, 2015, 26(6): 1183–1189.
SHANG Yingxue, LI Xiaoping, SONG Li. Material Balance equation and reserves calculation method considering water soluble gas for shale gas reservoirs[J]. Natural Gas Geoscience, 2015, 26(6): 1183–1189. doi: 10.11764/j.issn.1672-1926.2015.06.1183 |
| [7] |
赵金洲, 李志强, 胡永全, 等. 考虑页岩储层微观渗流的压裂产能数值模拟[J].
天然气工业, 2015, 35(6): 53–58.
ZHAO Jinzhou, LI Zhiqiang, HU Yongquan, et al. Numerical simulation of productivity after fracturing with consideration to micro-seepage in shale reservoirs[J]. Natural Gas Industry, 2015, 35(6): 53–58. doi: 10.3787/j.issn.-1000-0976.2015.06.007 |
| [8] |
杨兆中, 黄馨, 覃兆勇, 等. 致密油藏层内爆燃压裂缝网渗流及产能特征[J].
天然气地球科学, 2016, 27(6): 1092–1100.
YANG Zhaozhong, HUANG Xin, QIN Zhaoyong, et al. The flow and deliverability in tight oil reservoir after explosive fracturing[J]. Natural Gas Geoscience, 2016, 27(6): 1092–1100. doi: 10.11764/j.issn.1672-1926.2016.-06.1092 |
| [9] |
田冷, 肖聪, 刘明进, 等. 考虑页岩气扩散的多级压裂水平井产能模型[J].
东北石油大学学报, 2014, 38(5): 93–101.
TIAN Leng, XIAO Cong, LIU Mingjin, et al. Productivity model for multi-stage fractured horizontal well for shale gas reservoir taking diffusion into consideration[J]. Journal of Northeast Petroleum University, 2014, 38(5): 93–101. doi: 10.3969/j.issn.1006-6535.2009.02.002 |
| [10] |
朱苏阳, 杜志敏, 李传亮, 等. 基于复合解吸理论的煤层气物质平衡方法[J].
天然气地球科学, 2016, 27(6): 1128–1133.
ZHU Suyang, DU Zhimin, LI Chuanliang, et al. The coalbed methane material balanced equation based on the compound desorption[J]. Natural Gas Geoscience, 2016, 27(6): 1128–1133. |
| [11] |
张烈辉, 陈果, 赵玉龙, 等. 改进的页岩气藏物质平衡方程及储量计算方法[J].
天然气工业, 2013, 33(12): 66–70.
ZHANG Liehui, CHEN Guo, ZHAO Yulong, et al. A modified material balance equation for shale gas reservoir and a calculation method of shale gas reserve[J]. Natural Gas Industry, 2013, 33(12): 66–70. doi: 10.3787/j.issn.1000-0976.2013.12.009 |
| [12] |
边瑞康, 张金川. 页岩气成藏动力特点及其平衡方程[J].
地学前缘, 2013, 20(3): 255–259.
BIAN Ruikang, ZHANG Jinchuan. Accumulation dynamic characteristics and the dynamic equations of shale gas[J]. Earth Science Frontiers, 2013, 20(3): 255–259. |
| [13] |
程远方, 董丙响, 时贤, 等. 页岩气藏三孔双渗模型的渗流机理[J].
天然气工业, 2012, 32(9): 44–47.
CHENG Yuanfang, DONG Bingxiang, SHI Xian, et al. Seepage mechanism of a triple-porosity/dual-permeability model for shale gas reservoir[J]. Natural Gas Industry, 2012, 32(9): 44–47. doi: 10.3787/j.issn.1000-0976.2012.09.010 |
| [14] |
张小涛, 吴建发, 冯曦, 等. 页岩气藏水平井分段压裂渗流特征数值模拟[J].
天然气工业, 2013, 33(3): 47–52.
ZHANG Xiaotao, WU Jianfa, FENG Xi, et al. Numerical simulation of seepage flow characteristics of multi-stage fracturing (MSF) in horizontal shale gas wells[J]. Natural Gas Industry, 2013, 33(3): 47–52. doi: 10.3787/j.issn.1000-0976.2013.03.011 |
| [15] | XIE Weiyang, LI Xiaoping. Research on fractured horizontal wells productivity and productivity influence in shale gas reservoir[C]. SPE 167674, 2014. |
| [16] | GUO Chaohua, BAI Baojun. Study on gas permeability in nano pores of shale gas reservoirs[C]. SPE 167179, 2013. |
| [17] | AUSTIN U K, ONYEKONWU M O. Advancement in material balance analysis[C]. SPE 172415, 2014. |
| [18] | 程林松. 渗流力学[M]. 北京: 石油工业出版社, 2011. |
| [19] | 张琪. 采油工程原理与设计[M]. 东营: 中国石油大学出版社, 2000. |
 2017, Vol. 39
2017, Vol. 39


