2. 保利协鑫石油天然气集团控股有限公司, 北京 东城 100010
2. POLY-GCL Petroleum Group Holdings Limited, Dongcheng, Beijing 100010, China
渗吸是两相或者多相体系中与驱替有关的重要流体流动现象。在大量有关油气藏渗吸机理的研究成果中,关于致密气藏渗吸机理的研究成果却很少,特别是对页岩气这类超低渗气藏。其主要原因可归结为在获得准确合理的页岩岩石物理特性描述方面存在很大困难,如毛管压力曲线、相渗曲线及基质渗透率。与渗吸作用在油藏提高采收率方面所起到的积极作用不同,通常认为渗吸作用在通过水驱或水力压裂进行开采的低渗透气藏中是一种不利因素[1-3]。Roychaudhuri等[4]使用来自Appalachian盆地的页岩样品来研究自然渗吸作用对产气的影响。Makhanov等[5-6]研究了Horn River页岩气藏中的自然吸附现象。Li和Horne[7-8]研究了水自然渗吸至由气体饱和的岩石中的过程,发现了由自然渗吸作用所产生的初始含水饱和度严重影响了残余气饱和度。Egermann等[9]推断致密和多孔的碳酸盐岩吸入水的过程很缓慢,这是由于水相相对渗透率很低。由毛管力所造成的自发水相渗吸作用能够解释滞留水进入页岩基质的现象[10]。
研究表明,低渗透气藏中的渗吸作用相对于常规油藏表现出了不同的特征。其主要原因为:(1)较高毛管力(高达约103 psi(1 psi = 6.895 kPa));(2)流体压缩性相比油相更强;(3)气-水界面张力相比油-水界面张力更高;(4)由于基质渗透率较低(低至10-4 mD)采用水力压裂增产措施以提高单井产能。
本文通过气藏数值模拟方法来探究水力压裂增产的页岩气藏中的渗吸机理。所有的模拟都是基于Barnett页岩气藏的生产数据。此外,提供了渗吸作用对气井生产所造成的储层伤害的评估。本文对于合理分析页岩气藏生产动态至关重要,尤其是在早期生产阶段以及降低由渗吸作用可能造成的储层伤害来优化生产。
1 渗吸机理和数学模型 1.1 渗吸机理渗吸包括自发渗吸和强制渗吸。相比之下自发渗吸是最经常发生的,并完全依赖于储层岩石储存的天然能量。自发渗吸的开采原理如图 1所示。
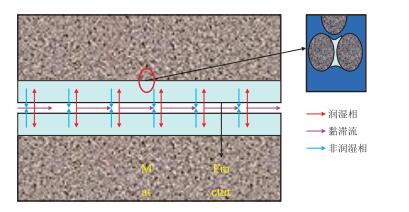 |
| 图1 自发渗吸原理图 Fig. 1 Schematic of spontaneous imbibition. |
自发渗吸现象通常存在于具有低初始含水饱和度的低渗透性储层中[11]。在低渗透性储层中往往存在非毛细管平衡以及非常低的初始含水饱和度或束缚水饱和度。在这种储层中一旦岩块暴露到水基液中,潜在的毛细管力能够作为附加驱动力驱使润湿相(水)进入非常小的孔隙空间。自发渗吸主要取决于毛管力,这与岩石的表面性质有关,比如润湿性和孔隙结构[12-16]。润湿性是自发渗吸的本质。孔隙结构特征包括孔隙喉道半径,孔隙尺寸分布,孔隙网络,其中孔隙喉道半径是决定渗吸力的关键参数。
1.2 机理模型 1.2.1 控制方程对于基质孔隙中的流体流动,气体解吸作为流动系统的汇项,而从孔隙流动到裂缝的流量作为源项。所以该质量守恒方程可以写成如下形式
| $ \frac{{\partial \left( {{\rho _{\rm{m}}}{\phi _{\rm{m}}}} \right)}}{{\partial t}} + \nabla \left( {{\rho _{\rm{m}}}{v_{\rm{m}}}} \right) + \frac{{\partial \left[ {\left( {1 - {\phi _{\rm{m}}}} \right)q} \right]}}{{\partial t}} - {\rho _{\rm{m}}}\frac{{{K_{\rm{m}}}}}{{{\mu _{\rm{m}}}}}\left( {{p_{\rm{m}}} - {p_{\rm{f}}}} \right) = 0 $ | (1) |
式中:
${\rho _{\rm{m}}}$-气体密度,lb/ft3(1 lb/ft = 0.016 03 g/cm3);
${\phi _{\rm{m}}}$-基质孔隙度,%;
t-时间,s;
${v_{\rm{m}}}$-气体表观速度,ft/s(1 ft = 30.48 cm);
${K_{\rm{m}}}$-气体渗透率,mD;
${\mu _{\rm{m}}}$-气体黏度,lbf·s/ft2(1 lbf·s/ft=147.88 Pa·s);
q-每单位体积有机物气体解吸量,Mscfd(1 Mscfd = 28.317 m3/d);
${p_{\rm{m}}}$-孔隙流动压力,psi;
${p_{\rm{f}}}$-裂缝流动压力,psi。
裂缝系统是井筒质量交换的主要通道。从孔隙流入到裂缝的量作为源项,从井筒流出的量作为汇项。因此,该质量守恒方程可以写为
| $ \frac{{\partial \left( {{\rho _{\rm{f}}}{\phi _{\rm{f}}}} \right)}}{{\partial t}} + \nabla \left( {{\rho _{\rm{f}}}{v_{\rm{f}}}} \right){\rm{ + }}{\rho _{\rm{m}}}\frac{{{K_{\rm{m}}}}}{{{\mu _{\rm{m}}}}}\left( {{p_{\rm{m}}}-{p_{\rm{f}}}} \right)-{\rho _0}{Q_{\rm{b}}} = 0 $ | (2) |
式中:$\rho _{\rm{f}}$-裂缝内气体的密度,lb/ft3;
$\phi _{\rm{f}}$-裂缝孔隙度,%;
$v_{\rm{f}}$-裂缝内气体速度,ft/s;
$\rho _0$-在标准条件下的页岩气密度,lb/ft3;
$Q_{\rm{b}}$-井筒流出量,ft3。
1.2.2 辅助方程(1)基质的毛细管压力曲线
式(3)经常用来将空气水银毛管压力转化为油气藏情况下的气水毛管压力
| $ {p_{{\rm{gw}}}} = {p_{{\rm{ma}}}} \cdot \frac{{{\gamma _{{\rm{gw}}}} \cdot \cos {\theta _{{\rm{gw}}}}}}{{{\gamma _{{\rm{ma}}}} \cdot \cos {\theta _{{\rm{ma}}}}}} = 40{p_{{\rm{ma}}}} \cdot {\gamma _{{\rm{gw}}}} $ | (3) |
式中:$p_{{\rm{gw}}}$-气-水系统毛管压力,psi;
$p_{{\rm{ma}}}$-空气-汞系统毛管压力,psi;
${\theta _{{\rm{gw}}}}$-气和水的接触角,(°);
${\theta _{{\rm{ma}}}}$-汞和空气的接触角,(°);
$\gamma _{{\rm{gw}}}$-气-水界面张力,lbf/ft;
${\gamma _{{\rm{ma}}}}$-汞-空气界面张力,lbf/ft。
(2)相对渗透率曲线
相对渗透率曲线见式(4)~式(6)。
| $ {K_{{\rm{rw|dr}}}} = S{{_{{\rm{wt}}}^*}^{\frac{{2 + 3\lambda }}{\lambda }}} $ | (4) |
| $ {K_{{\rm{rnw|dr}}}} = {\left( {1-S_{{\rm{wt}}}^*} \right)^2}\left( {1-S{{_{{\rm{wt}}}^*}^{\frac{{2 + \lambda }}{\lambda }}}} \right) $ | (5) |
| $ {K_{{\rm{rg}}{{\rm{|}}_{{\rm{imb}}}}}} = {\left( {\frac{{{S_{\rm{m}}}- 1}}{{{S_{\rm{m}}}- {S_{{\rm{wi}}}}}} + S_{{\rm{gf}}}^*\frac{{1- {S_{{\rm{wi}}}}}}{{{S_{\rm{m}}} - {S_{{\rm{wi}}}}}}} \right)^2} \cdot \left[{1-{{\left( {1-S_{{\rm{gf}}}^*} \right)}^{\frac{{2 + \lambda }}{\lambda }}}} \right] $ | (6) |
式中:$K_{{\rm{rw|dr}}}$-驱替过程水相相对渗透率,%;
Swt*-有效水相饱和度,%;
λ-孔隙分布指数,无因次;
$K_{{\rm{rnw|dr}}}$-驱替过程气相相对渗透率,%;
Krg|imb-渗吸过程气相相对渗透率,%;
Sm-非润湿相初始水相饱和度,%,取Sm = 90%;
Swi-束缚水饱和度,取Swi = 20%;
Sgf*-有效自由气饱和度,%。
式(4)和式(5)用来建立基质和裂缝的驱替相渗曲线,式(4)和式(6)用来建立基质的渗吸相渗曲线。孔隙分布指数Iϕ的计算见式 (7)
| $ {I_\Phi } = \lg {p_{\rm{c}}} = \lg {p_{\rm{e}}}-\frac{{\rm{l}}}{\lambda }\lg S_{{\rm{wt}}}^* $ | (7) |
式中:pc-毛管压力,psi;
pe-端点毛管压力,psi。
基质的孔隙分布指数计算结果为4.3,裂缝的孔隙分布指数为4.0,裂缝的相对渗透率曲线与未胶结沉积下的Brooks-Corey的气驱替水的驱替曲线接近。在一些润湿相饱和度下基质的渗吸相对渗透率的值总是低于基质的驱替相对渗透率。
有效自由气饱和度计算公式为
| $ S_{{\rm{gt}}}^* = \frac{1}{2}\left( {S_{\rm{g}}^{\rm{*}}-S_{{\rm{gr}}}^*} \right) + \frac{1}{2}\sqrt {{{\left( {S_{\rm{g}}^*-S_{{\rm{gr}}}^*} \right)}^2} + \frac{4}{c}\left( {S_{\rm{g}}^*-S_{{\rm{gr}}}^*} \right)} $ | (8) |
式中:Sg*-有效含气饱和度,%;
Sgr*-有效残余气饱和度,%;
c-系数,无因次。
(3)裂缝渗透率
在增产措施过程中,在开始压裂时用100目的支撑剂,后来转为40/70,最后为20/40。为了建立一个简单的理想模型,假设裂缝用40/70目的支撑剂来充填。
N目支撑剂下的裂缝渗透率计算公式为
| $ {K_N} = {K_M} \cdot \frac{{r_N^2}}{{r_M^2}} $ | (9) |
式中:KN-N目支撑剂下的裂缝渗透率,mD;
KM-M目支撑剂下的裂缝渗透率,mD;
rN-N目支撑剂下的支撑剂直径,ft;
rM-M目支撑剂下的支撑剂直径,ft。
40/70目的支撑剂下的裂缝渗透率计算公式为
| $ {K_{40/70}} = {K_{20/40}} \cdot \frac{{r_{40/70}^2}}{{r_{20/40}^2}} $ | (10) |
式中:K40/70-40/70目支撑剂下的裂缝渗透率,mD;
K20/40-20/40目支撑剂下的裂缝渗透率,mD;
r20/40-20/40目支撑剂下的支撑剂直径,ft;
r40/70-40/70目支撑剂下的支撑剂直径,ft。
(4)裂缝的毛管压力
在未胶结砂岩的典型曲线的基础上,式(3)中所得的孔喉尺寸用来建立裂缝中气水两相系统的毛管压力曲线。
(5)地层伤害评估
通过量化裂缝压裂表皮因子来评估在裂缝洗井以及随后的生产过程中由渗吸机理所引起的地层伤害。计算公式为[15]
| $ {S_{\rm{t}}} = \frac{{\rm{\pi }}}{{{\rm{2}}{{\rm{X}}_{\rm{f}}}}}\sum\limits_{j = 2}^n {{w_j}} \left[{\frac{{{{\left( {\frac{{{K_{{\rm{rg}}}}}}{{{\mu _{\rm{g}}}}}} \right)}_{\rm{o}}}{X_{\rm{f}}}}}{{\sum\limits_{i = 1}^m {{{\left( {\frac{{{K_{{\rm{rg}}}}}}{{{\mu _{\rm{g}}}}}} \right)}_{ij}}{X_i}} }}-1} \right] $ | (11) |
式中:St-裂缝表皮因子,无因次;
Xf-裂缝半长,ft;
wj-距离裂缝面j处的网格的宽度,ft;
Krg-气相对渗透率,%;
µg-气体黏度,mPa·s;
n-裂缝表面网格j方向的最大值;
m-裂缝表面网格i方向的最大值;
${{\left ({\frac{{{K_{{\rm{rg}}}}}}{{{\mu _{\rm{g}}}}}} \right)}_{\rm{o}}}$-在参考点处无伤害时气体的流度,mD/(mPa·s);
${{\left ({\frac{{{K_{{\rm{rg}}}}}}{{{\mu _{\rm{g}}}}}} \right)}_{ij}}$-网格(i,j)处地层伤害下的气体流度,mD/(mPa·s);
Xi-沿裂缝面i处的网格的长度,ft。
1.2.3 求解方法选择基质驱替,孔隙中的流动压力和裂缝中的流动压力作为基础变量,运用有限元方法离散求解。首先,运用Galerkin方法把方程转变为空间离散化形式;然后,用全隐式方法对时间进行一级差分,最终得到全隐式的联合求解方程。
2 数值模型及方案设计图 2a为研究地层伤害的数值模型示意图,图 2b为相应的网格模型,表 1为数值模型基本参数。模拟研究方案中,气体流量取500 Mscf/d,表示代表沿裂缝的相邻网格区域的原始含水饱和度取30%,油藏温度180 °F(1 °F= 1.8×℃+32),考虑了相同曲率基质的3类毛管压力曲线(图 3)。
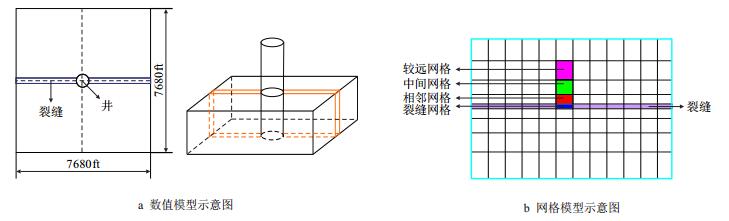 |
| 图2 模型示意图 Fig. 2 Schematic of model |
| 表1 模型基本参数 Table 1 Basic parameters of model |
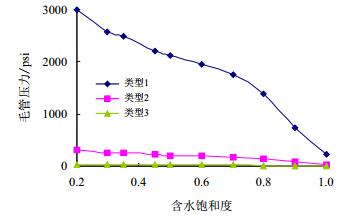 |
| 图3 基质毛管压力曲线 Fig. 3 CPCs for matrix |
图 4a和4b为相邻网格的气体相对渗透率分别在驱替和渗吸相对渗透率曲线下随时间的变化曲线。两种情况下的气体相对渗透率表现出了相似的动态特征。图 4b中,由于渗吸作用引起的高含水饱和度导致了相邻网格中气体相对渗透率从第10 d到第75 d降到了接近于0。因此自由气在这个阶段几乎不能流动,这严重影响气体的生产能力。如果这个阶段持续时间较长,这将导致没有气体产出,且会发生水封。此外,模拟结果表明,渗吸相对渗透率曲线下气体相对渗透率比驱替相对渗透率曲线下的要低。
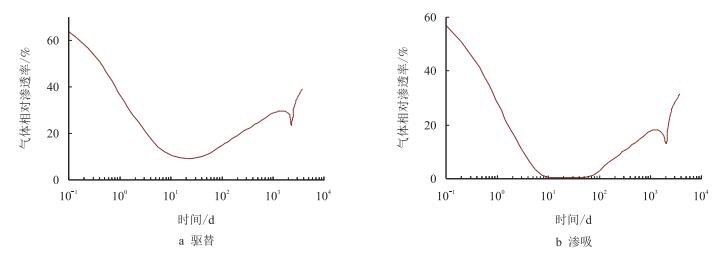 |
| 图4 驱替和渗吸情况下相邻网格的气体相对渗透率随时间的变化曲线 Fig. 4 Plot of Krg vs. time for adjacent block |
图 5为裂缝面表皮因子在驱替相对渗透率曲线和渗吸相对渗透率曲线两种情况下随时间的变化。显然渗吸作用会比驱替相对渗透率曲线造成更大的裂缝面表皮因子。在第10 d渗吸相对渗透率曲线下的裂缝面表皮因子是驱替相对渗透率曲线下的132倍。在图 5上可看到渗吸相对渗透率曲线下有紫色表示的水平段。但是,在驱替相对渗透率曲线下的曲线中看不到这个水平段。通过对比这两种情况下的裂缝面表皮曲线可以得出以下两个重要结论:(1)渗吸作用能够引起理论的水封,从而极大地影响井的生产能力,因此有水存在的页岩气藏开采时,为了保持高采收率和长期生产,很有必要降低这个负面影响,(2)由于强水湿和低渗透率气藏,在应用驱替相对渗透率曲线时很可能高估井的生产能力。
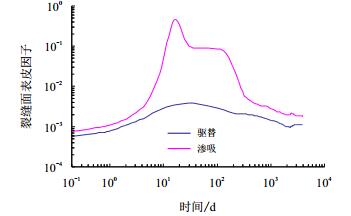 |
| 图5 驱替相对渗透率曲线和渗吸相对渗透率曲线下的裂缝面表皮因子的对比 Fig. 5 Comparison of fracture face skin between drainage and imbibition RPC |
另外,由图 5可知,两种情况下计算的裂缝面表皮因子都小于1,这与实际生产中的正常表皮值比起来仍然小。实际上所研究的较低的裂缝面表皮因子主要是由于在计算时仅仅考虑了渗吸作用的贡献。通常裂缝面表皮因子要远远低于由于钻完井而引起的机械表皮因子。机械伤害本质上是不可逆的,而从工程角度看由水封引起的地层伤害是可消除的。
3.2 毛管压力曲线的影响在参数研究中,比较了3种毛管压力曲线类型下相邻网格中的气体相对渗透率的动态(图 6~图 8)。中间网格和较远网格中的气体相对渗透率动态和相对渗透率曲线影响下的研究结果表现相似,气体相对渗透率随着时间增加。
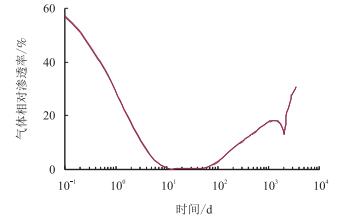 |
| 图6 第1类毛管压力曲线下相邻网格的气体相对渗透率随时间的变化 Fig. 6 Plot of type 1 CPC Krg vs. time for adjacent block |
图 6中的水平段的持续时间比图 7中的短,在图 8中没有出现水平段,而且水平段开始出现的时间也随着毛管压力的降低而逐渐的推迟。图 9为3种毛管压力曲线下的裂缝面表皮因子的对比图。毛管压力曲线类型1和2表现为两个阶段,也就是在第1 100 d之前的增加阶段和降低阶段,但是毛管压力曲线类型3在第1 100 d之前仅仅表现出降低阶段,原因主要是类型3的毛管压力比较小,低于压降,这引起在裂缝周围区域内的含水饱和度降低。此外在图 9中可以看到毛管压力曲线类型1和3下的裂缝面表皮因子的显著差别。因此裂缝面表皮因子对毛管压力很敏感。
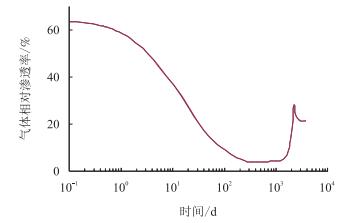 |
| 图7 第2类毛管压力曲线下相邻网格的气体相对渗透率随时间的变化 Fig. 7 Plot of type 2 CPC Krg vs. time for adjacent block |
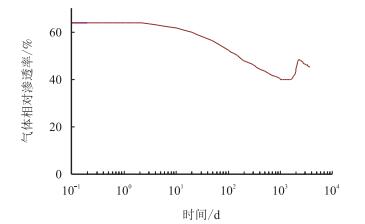 |
| 图8 第3类毛管压力曲线曲线下相邻网格的气体相对渗透率随时间的变化 Fig. 8 Plot of type 3 CPC Krg vs. time for adjacent block |
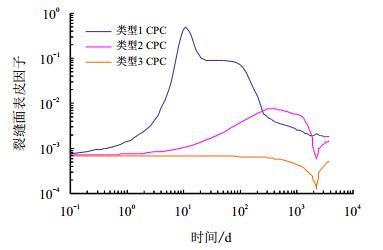 |
| 图9 3类毛管压力曲线下裂缝面表皮因子对比 Fig. 9 Comparison of fracture face skin of three types of CPCs |
此外,图 4和(图 6~图 8)中1 100 d后的曲线下凹或凸起是由于相邻网格中的含水饱和度取决于相邻的裂缝和中间网格毛管力和相渗共同作用的结果。
4 结论(1) 建立了考虑不同影响因素的页岩水力压裂渗吸数值模型,应用实际气水毛管压力曲线建立了渗吸相对渗透率曲线,讨论了在水力压裂和后续生产期间如何通过量化裂缝面表皮演变来评估由于渗吸机制导致的储层伤害现象,也阐述了由于相对渗透率滞后导致的相阻塞所引起的地层伤害评估。
(2) 在有水共存的页岩气藏中,应该更多地注意由于基质渗透率伤害而引起的渗吸。就水力压裂气井而言,渗吸机理主要控制早期生产动态。在致密岩石中所储存的潜在的大毛管力会在水力压裂缝周围区域引起由渗吸机理所控制的两相流动。通常要花几个星期甚至几个月才能在地层中达到毛管力平衡。同时,这个现象也启示我们对于实施了水力压裂增产措施的新井通过探测裂缝压力可以获得原始气体压力。在非毛管压力平衡过程中最好不要测试油藏压力,因为这个阶段内测试的油藏压力不代表真实的原始油藏压力。
(3) 地层伤害分析证明,与相对渗透率滞后有关的润湿相阻塞是在洗井过程中发生地层伤害的主要原因。在致密地层中润湿相阻塞导致水封,这会降低气井的生产能力。尽管由于相对渗透率降低引起的裂缝面表皮因子与机械伤害引起的裂缝面表皮因子相比较小,但是在一些情况下由于高毛管压力和低压力降,这个副作用很难消除。
| [1] | POW M, ALLAN V, MALLMES R, et al. Production of gas from tight naturally-fractured reservoirs with active water[C]. The 48th Annual Technical Meeting of the Petroleum Society of CIM held in Calgary, Canada, 1997. doi:10.2118/97-03 |
| [2] | BEATTIE D R, ROBERTS B E. Water coning in naturally fractured reservoirs[C]. SPE 35643, 1996. doi:10.2118/35643-MS |
| [3] | ZHOU Z, HOFFMAN B, BEARINGER D, et al. Experimental and numerical study on spontaneous imbibition of fracturing fields in shale gas formation[C]. SPE 171600, 2014. doi:10.2118/171600-MS |
| [4] | ROYCHAUDHURI B. TSOTSIS T, JESSEN K. An experimental investigation of spontaneous imbibition in gas shale[C]. SPE 147652, 2011. doi:10.2118/147652-MS |
| [5] | MAKHANOV K, DEHGANPOUR H, KURU E. An experimental study of spontaneous imbibition in Horn River Shale[C]. SPE 162650, 2011. doi:10.2118/162650-MS |
| [6] | MAKHANOV K, DEHGANPOUR H, KURU E. Measuring liquid uptake of organic shale:A workflow to estimate water loss during shut-in periods[C]. SPE 167157, 2013. doi:10.2118/167157-MS |
| [7] | LI K W, HORNE R N. Characterization of spontaneous water imbibition into gas-saturated rocks[C]. SPE 62552, 2000. doi:10.2118/62552-MS |
| [8] | LI K W, CHOW K, HORNE R N. Effect of initial water saturation on spontaneous water imbibition[C]. SPE 76727, 2002. doi:10.2118/76727-MS |
| [9] | EGERMANN P, LAROCHE C, DELAMAIDE E, et al. Experimental and numerical study of water/gas imbibition phenomena in vuggy carbonates[C]. SPE 89421, 2004. doi:10.2118/89421-MS |
| [10] | CHENG Y. Impact of water dynamics in fractures on the performance of hydraulically fractured wells in gas-shale reservoirs[J]. Journal of Canadian Petroleum Technology, 2012, 51(2): 143–151. doi: 10.2118/127863-PA |
| [11] | BENNION D B, THOMAS F B, MA T. Formation damage processes reducing productivity of low permeability gas reservoirs[C]. SPE 60325, 2000. doi:10.2118/60325-MS |
| [12] | HATIBOGLU C U, BABADAGLI T. Dynamics of spontaneous counter-current imbibition for different matrix shape factors, interfacial tensions, wettabilities and oil types[C]. The Petroleum Society 5th Canadian International Petroleum Conference (55th Annual Technical Meeting), Calgary, Alberta, Canada, 2004. doi:10.2118/2004-091 |
| [13] | SCHOWALTER T T. Mechanics of secondary hydrocarbon migration and entrapment[J]. The American Association of Petroleum Geology Bulletin, 1979, 63(5): 723–760. |
| [14] | CINO-LEY H, SAMANIEGO V. Effect of wellbore storage and damage on the transient pressure behavior of vertically fractured wells[C]. SPE 6752, 1977. doi:10.2118/6752-MS |
| [15] | GDANSKI R, FULTOND, SHEN C. Fracture face skin evolution during cleanup[C]. SPE 101083, 2006. doi:10.2118/101083-PA |
| [16] |
侯磊, DEREKElsworth, 孙宝江, 等. 页岩支撑裂缝中渗透率变化规律实验研究[J].
西南石油大学学报 (自然科学版), 2015, 37(3): 31–37.
HOU Lei, DEREK Elsworth, SUN Baojiang, et al. Expermental study on permeability evolution in propped shale fracture[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2015, 37(3): 31–37. doi: 10.11885/j.issn.16745086.2015.03.10.03 |
 2017, Vol. 39
2017, Vol. 39 图1(Fig. 1)
图1(Fig. 1)



