随着互联网市场的兴起,网络直销渠道成为众多企业打开市场的重要方式之一。如在手机制造业,不同于OPPO和VIVO等手机制造商采用传统的分销渠道销售手机,小米早期利用互联网直销的优势,把渠道、营销等流程全部重构,降低了产品的整体成本,获取了低成本优势,提高了产品的市场竞争力;在彩电制造业,创维、海信等传统电视品牌主要采用分销渠道销售彩电,而乐视、小米、酷开等电视品牌则采用网络渠道进行直销。互联网和电子商务的高速发展加剧了手机、家电等市场的渠道竞争,在日益激烈的渠道竞争环境下,制造型企业,特别是采用传统分销渠道的制造型企业,如何通过创新优化流程,降低生产成本,以提高企业乃至整条供应渠道的竞争优势?当竞争对手通过流程创新降低了生产成本,获取了低成本优势,本渠道中的制造商是否也需要进行流程创新以降低生产成本?渠道间的竞争强度、创新投入水平等对制造商进行流程创新的选择有何影响?笔者将基于一个制造商采用直销渠道、另一个竞争对手制造商采用分销渠道进行销售的竞争模型,识别制造商选择流程创新的博弈均衡和动态演化过程,为竞争环境下采用不同渠道结构的企业进行流程创新实践提供借鉴。
关于流程创新的研究,Brander & Spencer[1]基于古诺竞争模型,识别了进行流程创新降低边际成本的条件;Qiu[2]基于差异化的双寡头模型,比较了进行成本改进时的Cournot均衡与Bertrand均衡;Petrakis & Roy[3]基于竞争性的企业进行降低成本的投资和行业无成本进入的假设,研究了同质品行业的动态性重组问题等;Piccion & Tan [4]基于多个供应商与一个买方的供应链模型,研究了多个供应商进行投资研发创新以降低产品的供应成本,从而获取买方采购订单的问题;Gilbert & Cvsa[5]基于需求不确定环境下的双边垄断竞争模型,研究了使用最高限价合约鼓励下游企业进行流程改进以降低成本的策略;Kim[6]针对一个供应商和一个制造商的供应链模型,研究了当制造商分担其供应商的创新投入成本时实现上下游双赢的条件;Cho & Gerchak[7]基于一对一的零售商成本降低型创新投入模型,分别研究了零售商的可变成本为线性与非线性函数条件下的渠道协调问题;Bernstein & Kök [8]研究了供应商在整个产品生命周期内进行成本削减的动态性投资问题,并分析了供应商的成本削减策略及带来的企业利润与制造商采购策略的关系。这些研究主要基于竞争性企业或供应链内的流程创新进行探索,均未基于两条渠道进行竞争的模型研究生产成本改进的流程创新策略选择问题。
Gupta & Loulou [9]基于两个制造商与两个零售商组成的渠道竞争模型,分析了两个制造商均进行流程创新时渠道结构的选择问题,并指出授权合同可以激励制造商降低生产成本;Gilbert & Xia等[10]假设制造商和上游供应商都有成本降低的机会,分析了两个竞争性制造商的外包策略,并研究了以下游制造商为主导的纵向渠道结构选择策略;Gupta & Loulou[11]通过考虑过程创新行为的知识溢出效应,进一步拓展了Gupta & Loulou[9]的结论。这类研究主要考察进行流程创新时的渠道结构选择、外包策略和知识溢出效应,但并未以不创新为基准探讨不同渠道结构下制造商绩效改进的流程创新选择动态博弈演化过程,且未识别制造商绩效改进的占优均衡。
笔者将基于直销渠道与分销渠道竞争的模型,分别考察直销渠道与分销渠道中的制造商均不进行流程创新、均进行流程创新、仅直销渠道的制造商进行创新、仅分销渠道中的制造商进行流程创新四种情形时的渠道成员绩效,并以不进行流程创新的情形为基准,研究制造商如何选择流程创新策略以实现低成本优势,同时识别企业进行流程创新选择的博弈均衡特征和动态演化过程,分析横向竞争强度和创新投资系数对流程创新选择的影响。所做研究充分拓展了Gupta & Loulou[9]等现有理论的研究成果,为渠道竞争环境下企业的流程创新实践提供参考和借鉴。
1 基本模型与假定本文基于一个制造商进行直销,另一个竞争对手制造商采用零售商进行分销的渠道竞争模型,研究制造商是否对自身生产流程进行改进的创新投资选择问题。根据Ha & Tong的研究[12],零售商的逆需求函数为:
| ${p_i} = a - {q_i} - b{q_j}$ | (1) |
其中:a为最高可行零售价格,j = 3 -i,i∈{1, 2},qi为渠道i中产品的需求量;pi为渠道i中产品的价格;b为两种产品的数量竞争强度,且0<b<1,b越大表明渠道间的横向竞争越激烈。
同时,设定流程创新的投资额为rxi2,其中xi为单位成本的改进量,r为创新投资系数,为保证模型计算的运行,令r>1/4。制造商未进行流程改进时的单位生产成本为c,且c<a,改进后的单位生产成本为c -xi。博弈顺序为:首先,两条渠道中的制造商选择是否进行流程创新,如果进行流程创新,则直销渠道中的制造商选择单位成本改进量,分销渠道中的制造商决定单位成本改进量和批发价格;然后,直销渠道中的制造商选择生产量;同时分销渠道中的零售商选择订货量;最后,两条渠道均满足市场需求,形成横向数量竞争市场。
另外,假定:(1)分销渠道中批发价格不可被竞争对手所观测;(2)渠道中的生产量正好满足市场需求,且供应链中的其他成本如销售成本、库存成本等均为零;(3)绩效主要指产出绩效,即收益减去成本之后的净利润;(4)竞争对手无法获取流程创新的相关知识,即没有横向溢出效应。
据此,笔者将分别针对直销渠道与分销渠道均不进行流程创新、均进行流程创新、仅直销渠道创新、仅分销渠道创新4种情形分别进行计算,并识别两渠道制造商进行流程创新选择的博弈均衡条件。
2 基本模型的表达式 2.1 均不进行流程创新首先,记M1、R2和M2分别为制造商1、零售商2和制造商2的利润函数,他们的决策函数表达式分别为:
| $\mathop {Max{M_1}}\limits_{{q_1}} = {\rm{ }}\left( {{p_1}{\rm{ }} - {\rm{ }}c} \right){\rm{ }}{q_1}$ | (2) |
| $\mathop {Max{R_2}}\limits_{{q_2}} = {\rm{ }}\left( {{p_2}{\rm{ }} - {\rm{ }}{w_2}} \right){\rm{ }}{q_2}$ | (3) |
| $\mathop {Max{M_2}}\limits_{{w_2}} = {\rm{ }}\left( {{w_2}{\rm{ }} - {\rm{ }}c} \right){\rm{ }}{q_2}$ | (4) |
记此结构为NN结构,根据不可观测性,采用倒推法(具体可参考McGuire & Staelin[13]),得到各渠道成员利润、零售价格和批发价格等均衡表达式分别如下:
q1NN/(a -c) (4 -b) = (8 -b2);
q2NN/(a -c) (2 -b) = (8 -b2);
w2NN = (4a -2ab + 2bc + 4c -b2c)/(8 -b2);
M1NN = (a -c)2(4 -b)2/(8 -b2)2;
M2NN = 2(a -c)2(2 -b)2/(8 -b2)2;
R2NN = (a -c)2(2 -b)2/(8 -b2)2。
2.2 均进行流程创新考虑两条渠道中的制造商均进行流程创新,此时各方决策函数表达式如下:
| $\mathop {Max{M_1}}\limits_{{q_1},{x_1}} = {\rm{ }}{p_1}{q_1}{\rm{ }} - {\rm{ }}\left( {c{\rm{ }} - {\rm{ }}{x_1}} \right){\rm{ }}{q_1} - {\rm{ }}rx_1^2$ | (5) |
| $\mathop {Max{R_2}}\limits_{{q_2}} = \left( {{p_2} - {w_2}} \right){q_2}$ | (6) |
| $\mathop {Max{M_2}}\limits_{{w_2},{x_2}} = {\rm{ }}{w_2}{q_2}{\rm{ }} - {\rm{ }}\left( {c{\rm{ }} - {\rm{ }}{x_2}} \right){\rm{ }}{q_2}{\rm{ }} - {\rm{ }}rx_2^2$ | (7) |
令A = 4b2r2 -32r2 + 12r -1,且记此结构为PP结构,根据不可观测性和倒推法,可得到如下各种均衡表达式:
q1PP = 2r (a -c) (2br -8r + 1) /A;
q2PP = 2r (a -c) (2br -4r + 1) /A;
x1PP = (a -c) (2br -8r + 1) /A;
x2PP = (a -c) (2br -4r + 1) /A;
w2PP = [(4r-1) (2br-4r + 1) a+2cr(b-8r-4br+2b2r + 2)]/A;
M1PP = r(a -c)2 (4r -1) (2br -8r + 1)2/A2;
M2PP = r(a -c)2 (8r -1) (2br -4r + 1)2/A2;
R2PP = 4r2(a -c)2(2br -4r + 1)2/A2。
2.3 仅直销渠道的制造商进行流程创新假设直销渠道中的制造商进行流程创新,而分销渠道中的制造商不进行创新,则此时两条渠道中各成员的决策函数分别为:
| ${\mathop {Max{M_1}}\limits_{{q_1},{x_1}} = {\rm{ }}{p_1}{q_1}{\rm{ }} - {\rm{ }}\left( {c{\rm{ }} - {\rm{ }}{x_1}} \right){\rm{ }}{q_1}{\rm{ }} - {\rm{ }}rx_1^2}$ | (8) |
| ${\mathop {Max{R_2}}\limits_{{q_2}} = {\rm{ }}\left( {{p_2}{\rm{ }} - {\rm{ }}{w_2}} \right){\rm{ }}{q_2}}$ | (9) |
| ${\mathop {Max{M_2}}\limits_{{w_2}} = {\rm{ }}\left( {{w_2}{\rm{ }} - {\rm{ }}c} \right){\rm{ }}{q_2}}$ | (10) |
令B = rb2 + 2 -8r,且记此结构为PN结构,根据不可观测性和倒推法,可得如下各种均衡表达式:
q1PN = r (a -c) (b -4)/B;
q2PN = (a -c) (2br -4r + 1)/(2B);
x1PN = (a -c) (b -4)/(2B);
w2PN = c + (a -c) (2br -4r + 1) /B;
M1PN = r (4r -1) (a -c)2(b -4)2/(2B)2;
R2PN = (a -c)2(2br -4r + 1)2/(4B2);
M2PN = (a -c)2(2br -4r + 1)2/(2B2)。
2.4 仅分销渠道中的制造商进行流程创新考虑仅分销渠道中的制造商进行流程创新,则此时各方决策函数分别为:
| ${\mathop {Max{M_1}}\limits_{{q_1}} = {\rm{ }}\left( {{p_1}{\rm{ }} - {\rm{ }}c} \right){\rm{ }}{q_1}}$ | (11) |
| ${\mathop {Max{R_2}}\limits_{{q_2}} = {\rm{ }}\left( {{p_2}{\rm{ }} - {\rm{ }}{w_2}} \right){\rm{ }}{q_2}}$ | (12) |
| ${\mathop {Max{M_2}}\limits_{{w_2},{x_2}} = {\rm{ }}{w_2}{q_2}{\rm{ }} - {\rm{ }}\left( {c{\rm{ }} - {\rm{ }}{x_2}} \right){\rm{ }}{q_2}{\rm{ }} - {\rm{ }}rx_2^2}$ | (13) |
令D = rb2 + 1 -8r,并记此结构为NP结构,根据合同的不可观测性,采用倒推法,可得到如下各种均衡:
q1NP=(a -c) (2br -8r + 1)/(2D);
q2NP = r (a -c) (b -2) /D;
w2NP = [(4ab-8c-8a-4bc + 2b2c)r + 2a + cb -ab]/(2D);
x2NP = (a -c) (b -2) /(2D);
M1NP = (a -c)2(2br -8r + 1)2/(4D2);
R2NP = r2(a -c)2(b -2)2/D2;
M2NP = r (8r -1) (a -c)2(b -2)2/(4D2)。
3 竞争因子和创新投资系数对成本改进量的影响为考察竞争强度和创新投资系数对成本改进量的影响,记B = rb2 + 2 -8r,关于竞争强度b的有效解为b1 =
引理1:
(1)当1/4<r<2/7时,b1<1。(2)当1/4<r<(
命题1:
(1)当1/4<r<2/7且0<b<b1<1;或者当r>2/7时,x1PN > 0,M1PN > M2PN。
(2)当1/4<r<(
(3)当1/4<r<2/7且1>b > b1时,x1PN<0,M1PN<M2PN。
(4)当1/4<r<(
命题1中(1)和(2)表明,不管制造商2是否进行流程创新,当创新投资系数较大且不管渠道竞争强度如何,或者创新投资系数相对较小,且渠道竞争相对较弱时,制造商1进行流程创新可以降低生产成本,且获得比竞争对手更高的利润。(3)和(4)表明,若创新投资系数相对较小且渠道竞争加剧,则改进量为负,无法通过流程创新实现生产成本的降低,且自身利润小于竞争对手制造商的利润(不管竞争对手制造商是否进行流程创新)。
命题2:
(1)当r>1/4时,x2NP>0。
(2)当1/4<r<(
(3)当1/4<r<(
命题2中(1)表明,当直销渠道不进行创新,则分销渠道中的制造商进行创新的投资系数大于1/4时,其改进量为正。(2)表明,若直销渠道进行创新,则当创新投资系数位于(1/4, (
为直观观测横向竞争对成本改进量的影响,令a = 2, c = 1, r = 0.4,则有图 1所示。由图 1可知,采用直销渠道进行创新的改进量均高于分销渠道的改进量,且直销渠道中的成本改进量随横向竞争的加剧而逐渐增大,而分销渠道中的成本改进量随横向竞争加剧而逐渐减小,由此表明横向竞争加剧时直销渠道更适宜进行流程创新。
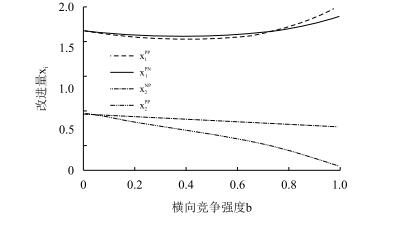 |
| 图1 a = 2, c = 1, r = 0.4时改进量与横向竞争的关系 |
另外,对于直销渠道而言,分销渠道是否进行创新影响其改进量的大小,当横向竞争相对较弱,则分销渠道不创新时的直销渠道改进量大于分销渠道创新时的改进量;若横向竞争加剧,则分销渠道创新会带动直销渠道加大改进量。对于分销渠道而言,直销渠道不创新较创新带给分销渠道的改进量更大;直销渠道创新时分销渠道也创新的改进量随横向竞争加剧而逐渐减小,当横向竞争超过一定程度时,改进量为负。
为直观观测创新投资系数对成本改进量的影响,令a = 2, b = 0.5, c = 1,具体图示如图 2。图 2表明,横向竞争强度适中时,直销渠道时的成本改进量依然高于分销渠道时的成本改进量,但直销渠道的改进量随创新投资系数的增大而逐渐减小,而分销渠道时的改进量则不一定。即当直销渠道不创新、分销渠道创新时,其改进量随创新投资系数的增大而逐渐减少;但直销渠道创新时,分销渠道创新的改进量先增大后减小,且当创新投资系数非常小时,分销渠道并不能实现成本改进,仅当创新投资系数相对较大时才能实现生产成本的降低。
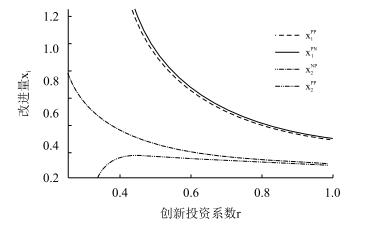 |
| 图2 a = 2, b = 0.5, c = 1时改进量与创新投资系数的关系 |
为考察成本改进后分销渠道的批发价格情况,记f2 = rb2 + 1 -4r关于b的有效解为b4 =
引理2:
(1)当1/4<r<1/3时,b4<1;(2)0<b3<b4<b2<b1。
命题3:
(1)当r>1/4时,w2NP<w2NN。
(2)存在以下任意一种情形时,w2PP>w2PN:
(a)当1/4<r<2/7且b2<b<b1<1;(b)当2/7<r<(
命题3(1)表明,若直销渠道不进行流程创新,则分销渠道由不创新转为创新,能实现批发价格的降低。命题(2)表明,若直销渠道进行流程创新,则分销渠道由不创新转为创新,其并不一定能实现批发价格的降低,而是依赖于外部的横向竞争环境和创新投资系数。当流程创新投资系数在(1/4, 2/7) 内且横向竞争强度在(b2, b1)范围内时;或者当创新投资系数在(2/7, (
为直观观测横向竞争强度对制造商2进行流程创新后批发价格的影响,令a = 2, c = 1, r = 0.5,可得批发价格函数随横向竞争强度的变化图(图 3)。由图 3可知,制造商2进行流程创新后降低了批发价格,但批发价格随横向竞争的加剧而逐渐减小,且批发价格降低量逐渐减小。
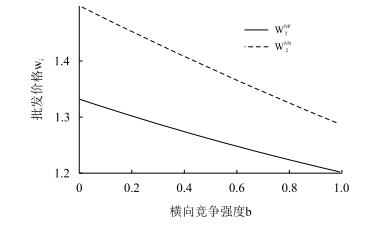 |
| 图3 a = 2, c = 1, r = 0.5时的w2NP与w2NN |
为直观观测创新投资系数对制造商2进行流程创新后批发价格的影响,令a = 2, b = 0.5, c = 1,得到批发价格函数随创新投资系数的变化图(图 4)。由图 4可知,随着创新投资系数的增大,创新投资成本的加大,制造商的批发价格逐渐增大,但小于不进行创新时的批发价格,即通过流程创新可以使批发价格得以降低,但随着创新投资成本的加大,批发价格降低的空间会逐渐缩小。
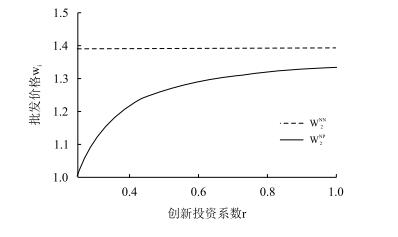 |
| 图4 a = 2, b = 0.5, c = 1时的w2NP与w2NN |
若竞争对手进行流程创新,令a=2,c=1,r=0.4,可直观观测横向竞争对制造商2进行流程创新后批发价格的影响,如图 5所示。由图 5可知,当横向竞争逐渐增强时,批发价格均下降,且当竞争强度小于3/4时,制造商2进行流程创新以后批发成本得以降低,但超过3/4时,则批发价格无法降低。
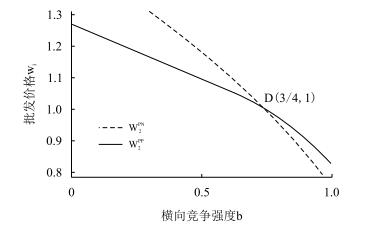 |
| 图5 a = 2, c = 1, r = 0.4时的w2PN与w2PP |
另外,为直观观测制造商1创新时制造商2由不创新转为创新后创新投资系数对批发价格的影响,令a=2,b=0.5,c=1,可得图 6。由图 6可知,若竞争对手进行流程创新,则仅当创新投资系数大于1/3时,分销渠道中的制造商进行流程创新降低生产成本能实现批发价格的降低。
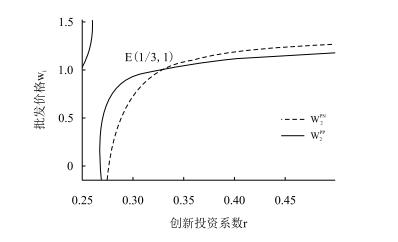 |
| 图6 a = 2, b = 0.5, c = 1时的w2PN与w2PP |
命题4:
(1)M1NN>M2NN;(2)当r>1/4时,M1NP>M2NP。
命题4中(1)表明,若两渠道均不进行创新,则直销渠道的制造商绩效高于分销渠道的绩效;(2)表明,若直销渠道制造商不创新,而分销渠道制造商进行流程创新,且进行创新的投资系数大于1/4时,则其利润依然低于直销渠道的制造商利润。
4 直销渠道中制造商的流程创新选择 4.1 竞争对手制造商不进行流程创新时的选择记M1PN = M1NN,关于竞争强度r的边界函数值为r1 = 16/(64 -b4)。
命题5:
当r>r1>1/4时,M1PN>M1NN。
命题5表明,若竞争对手制造商(即分销渠道中的制造商)不进行流程创新,则当直销渠道中制造商进行流程创新的投资系数大于r1(该值依赖于竞争强度)时,制造商可降低生产成本,并实现绩效改进。
4.2 竞争对手制造商进行流程创新时的选择记M1PP = M1NP,关于横向竞争强度r的有效边界函数为:
| $\begin{array}{l} {r_2}{\rm{ }} = {\rm{ }}{\left[ {\sqrt {{G^2} - {H^3}} - G} \right]^{1{\rm{/}}3}}{\rm{ }} - {\rm{ }}32{\rm{/}}\left( {3F} \right) + \\ H{\rm{/}}{\left[ {\sqrt {{G^2} - {H^3}} - G} \right]^{1{\rm{/}}3}} \end{array}$ |
其中,F = b4 -64;
| $H = 5{\rm{/}}\left( {3F} \right) + 1024{\rm{/}}\left( {9{F^2}} \right);$ |
| $G = 80/\left( {3{F^2}} \right) + 32768/\left( {27{F^3}} \right) + 1/\left( {8F} \right)。$ |
命题6:
当r>r2时,M1PP>M1NP。
命题6表明,若竞争对手制造商进行流程创新,则当直销渠道中制造商进行流程创新的投资系数大于r2(该边界值依赖于横向竞争强度)时,制造商进行流程创新不仅可降低生产成本,还能增加利润。
4.3 均进行或不进行流程创新时的选择记M1PP = M1NN,关于竞争强度r的有效边界函数为:
| ${r_3} = {\left[ {\sqrt {f_3^2 - f_4^3} {\rm{ }} - {f_3}} \right]^{1/3}}{\rm{ }} - {\rm{ }}J/\left( {3I} \right)$ |
其中,J = 2048 + 4b5 -28b4 + 400b2 -1408b;
| ${I = 4{b^6} - 4096 - 48{b^5} + 160{b^4} - 1024{b^2} + 3072b;}$ |
| ${{f_3} = \frac{{{J_3}}}{{27{I^3}}} + \frac{{KJ}}{{6{I^2}}} + \frac{{\left( {16 - 8b + {b^2}} \right)}}{{2I}};}$ |
| ${K = 320 - {b^4} + 40{b^2} - 192b;}$ |
| ${{f_4} = \frac{{{J^2}}}{{9{I^2}}} + \frac{K}{{3I}}}$ |
命题7:
当r>r3时,M1PP>M1NN。
命题7表明,若两个竞争渠道均采用相同的策略,即均进行创新或均不进行创新,则当直销渠道中制造商的创新系数大于r3时,直销渠道均创新时的制造商绩效高于均不创新时的绩效。
4.4 创新投资选择的博弈均衡演化过程由命题5、命题6和命题7可得命题8:
当r>max (r1, r2, r3)时,直销渠道制造商进行流程创新选择的博弈均衡过程为:NN→NP/PN→PP,且进行生产流程创新对于直销渠道制造商来说是占优决策。
命题8表明,若流程创新投资系数大于r1, r2, r3中的最大值(该最大值的大小依赖于渠道竞争强度),如图 7中区域Ⅰ所示,则直销渠道的制造商进行流程创新投资选择的博弈过程由不进行生产流程的创新演化为进行生产流程改进的创新,且进行流程创新是直销渠道制造商的占优均衡决策。该结论充分拓展了Gupta & Loulou[9]等人的研究结果,识别了渠道竞争环境下制造商进行流程创新的占优均衡,为企业实践提供了参考价值,也丰富了现有理论研究。
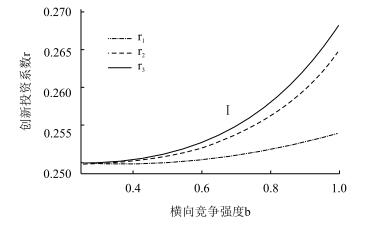 |
| 图7 r1, r2, r3与b的关系图 |
通过比较M2NP与M2NN的大小,可得命题9:
当r>1/4时,M2NP>M2NN。
命题9表明,若竞争对手不进行流程创新,则只要分销渠道中制造商愿意进行流程创新,其创新所带来的制造商绩效优于不创新时的绩效。
5.2 竞争对手制造商进行创新时的选择记M2PP = M2PN,关于竞争强度b的有效解为
引理3:
当0.25<r<0.299时,b5<1。
命题10:
当0.25<r<0.299,且0<b5<1时;或者当r>0.299时,M2PP>M2PN。
命题10表明,若直销渠道进行流程创新,分销渠道中的制造商想通过流程创新既降低生产成本又提高利润,则需考虑渠道竞争和创新投资系数双重因素的影响,即在外部渠道竞争较弱时投入相对较少的流程创新投资额(此时对流程创新的投资系数相对较小);或者投入较高的创新投入成本(即创新投资系数较大)且不管外部渠道竞争强度如何,可实现创新后制造商绩效的改进。
6 结语不同于Gupta & Loulou [9]等现有研究仅考虑流程创新时的渠道绩效比较,笔者以不进行流程创新的情形为基准,研究直销渠道与分销渠道在进行竞争的环境下两制造商如何选择流程创新策略以实现低成本优势,并从制造商绩效改进角度分析了制造商进行流程创新选择的博弈均衡特征,识别了占优均衡和均衡动态演化过程,揭示了横向竞争和流程创新投资系数对创新策略选择的影响,所得主要结论如下:
(1)不管分销渠道制造商是否进行流程创新,当直销渠道制造商的创新投资系数较大且不管横向竞争强度如何,或者创新投资系数相对较小,且横向竞争相对较弱时,则其制造商进行流程创新可以降低生产成本,且可获得比竞争对手更高的利润。但若其创新投资系数相对较小且横向竞争加剧,则无法通过流程创新实现生产成本的降低,其利润也小于分销渠道制造商的利润。
(2)对直销渠道制造商而言,若流程创新投资系数较大(该值大小依赖于渠道竞争强度),则进行流程创新选择的博弈过程由不进行生产流程的创新最终演化为进行生产流程的创新,且进行流程创新是直销渠道的占优均衡决策。
(3)对分销渠道而言,若直销渠道不进行流程创新,则只要本渠道中制造商愿意进行流程创新,则其所带来的绩效优于不创新时的绩效;若直销渠道进行流程创新,则本渠道中制造商想通过流程创新一方面降低生产成本,另一方面又提高利润,则需在渠道竞争较弱时投入相对较少的流程创新投资额(此时流程创新的投资系数相对较小);或者投入较高的创新投入成本(此时要求较高的创新投资系数),且不管外部渠道竞争强度如何。
总之,本研究的结论充分拓展了现有的研究成果,识别了渠道竞争环境下制造商进行流程创新的博弈均衡特征和占优均衡,为企业进行流程创新实践提供了参考价值。但本研究也存在不足,如没有考虑市场需求的不确定性、差异化的创新投资水平等因素,这将在后续研究中进行拓展。
| [1] | Brander J A, Spencer B J. Strategic commitment with R&D:the symmetric case[J]. Bell Journal of Economics, 1982, 14(1): 225–235. |
| [2] | Qiu L D. On the dynamic efficiency of Bertrand and Cournot equilibria[J]. Journal of Economic Theory, 1997, 75(1): 213–229. DOI:10.1006/jeth.1997.2270 |
| [3] | Petrakis E, Roy S. Cost-reducing investment, competition, and industry dynamics[J]. International Economic Review, 1999, 40(2): 381–401. DOI:10.1111/iere.1999.40.issue-2 |
| [4] | Piccione M, Tan G. Cost-reducing investment, optimal procurement and implementation by auctions[J]. International Economic Review, 1996, 37(3): 663–685. DOI:10.2307/2527446 |
| [5] | Gilbert S M, Cvsa V. Strategic commitment to price to stimulate downstream innovation in a supply chain[J]. European Journal of Operational Research, 2003, 150(3): 617–639. DOI:10.1016/S0377-2217(02)00590-8 |
| [6] | Kim B. Coordinating an innovation in supply chain management[J]. European Journal of Operational Research, 2005, 123(3): 568–584. |
| [7] | Cho K R, Gerchak Y. Supply chain coordination with downstream operating costs:coordination and investment to improve downstream operating efficiency[J]. European Journal of Operational Research, 2005, 162(3): 762–772. DOI:10.1016/j.ejor.2003.08.064 |
| [8] | Bernstein F, Kök A. Dynamic cost reduction through process improvement in assembly networks[J]. Management Science, 2009, 55(4): 552–567. DOI:10.1287/mnsc.1080.0961 |
| [9] | Gupta S, Loulou R. Process innovation, production differentiation, and channel structure:strategic incentives in a duopoly[J]. Marketing Science, 1998, 17(4): 301–316. DOI:10.1287/mksc.17.4.301 |
| [10] | Gilbert S M, Xia Y, Yu G. Strategic outsourcing for competing OEMs that face cost reduction opportunities[J]. ⅡE Transactions, 2006, 38(11): 903–915. |
| [11] | Gupta S, Loulou R. Channel structure with knowledge spillovers[J]. Marketing Science, 2008, 27(2): 247–261. DOI:10.1287/mksc.1070.0285 |
| [12] | Ha A Y, Tong S, Zhang H T. Sharing imperfect demand information in competing supply chains with production diseconomies[J]. Management Science, 2011, 57(3): 566–581. DOI:10.1287/mnsc.1100.1295 |
| [13] | McGuire W, Staelin R. An industry equilibrium analysis of downstream vertical integration[J]. Marketing Science, 1983, 2(2): 161–191. DOI:10.1287/mksc.2.2.161 |
 2017, Vol. 19
2017, Vol. 19
