2. 波现象与智能反演成像研究组(WPI), 同济大学海洋与地球科学学院, 上海 200092
2. Wave Phenomena and Intelligent Inversion Imaging Group (WPI), School of Ocean and Earth Science, Tongji University, Shanghai 200092, China
地震波反演成像是勘探地球物理学的核心环节[1], 其终极目标为获得地下全波数带的参数场。全波形反演(FWI)是理论完备的地震波反演成像方法, 理想情况下能得到地下全频带参数场的估计。经典的FWI是强非线性反演问题, 易受到各种客观实际因素制约而出现收敛到局部极值或不收敛的情况。因此, 在实际地震数据处理中, 通常将FWI分解为一系列更为线性化的子问题求解[2-3]。估计背景参数场的层析成像和估计高波数参数场的保真成像是最为常见的分解方法。本文主要关注估计高波数参数扰动的保真成像方法。
最小二乘偏移是一种具有代表性的保真成像技术, 其试图通过匹配模拟数据和观测数据的振幅值来估计参数的高波数扰动。然而, 最小二乘偏移的理想实现需将Hessian逆算子作用到常规成像结果上。在三维实际资料处理过程中, 由于Hessian矩阵规模巨大, 通常采用迭代方式求取Hessian的逆算子, 因而使得最小二乘偏移成像成为一种计算昂贵的保真成像方法。另外, Hessian逆算子的估计精度很容易受到叠前数据观测不完备、正算子对物理波现象的描述不够准确以及地震子波未知等多种因素影响, 从而出现迭代收敛慢甚至不收敛情况, 这进一步增加了最小二乘偏移成像在大规模实际资料保真成像中应用的难度。RICKETT[4]和GUITTON[5]提出的利用偏移、反偏移和再偏移的方式估计近似Hessian逆矩阵的做法, 提高了估计近似Hessian逆的计算效率。利用此种方式能估计出近似对角Hessian逆矩阵中对应的低秩的部分[6], 其代价是增加了两次偏移的计算量。
真振幅成像是另一种较为常见的保真成像方法。真振幅成像是一种线性化的反演成像方法, 其通过在高频近似下校正波传播过程中的几何扩散期望得到参数扰动的带限估计。根据不同模型参数化方式, 真振幅成像可以依赖于ray+Born或是ray+Kirchhoff两种近似下的线性化正问题加以实现[7]。其中Born和Kirchhoff近似分别对应于体散射和面散射的情况。从线性化后的正问题出发, 可以从积分算子理论或是优化理论构造对应反问题的解, 得到所谓真振幅成像公式[8-10]。真振幅成像公式可以基于射线实现[11]、Gaussian-Beam实现[12]、单程波实现[13]以及双程波实现[14]。在真振幅成像的原始推导中, 由于无需考虑中低波数参数成分估计问题, 隐含假设源检两端波场是单向传播的, 即只存在源端的下行波场和检端的上行波场, 因此, 在基于双向波传播算子实现真振幅成像方法过程中, 会出现源检两端波场相关能量中对应大散射角部分的低波数噪声。高通滤波或是角度域衰减是消除这些低波数噪声的常规方法[14-18], 然而这些方法需要在成像过程外增加额外计算步骤, 另外这些方法没有考虑低波数噪声去除过程中对目标反射层波形的畸变效应。STOLK等[19]在ray+Born近似下给出了能自动消除低波数噪声的基于逆时偏移(RTM)实现的真振幅成像公式。该方法的优点在于隐式考虑波场角度域滤波, 无需显式进行波场角度域分解, 在成像过程中能自动去除低波数噪声, 另外, 由于该方法基于严格的反问题框架导出, 自动考虑了角度域滤波算子非单位化的问题, 输出结果具有明确物理意义。WHITMORE等[20]进一步从波传播角度解释了STOLK等[19]的研究成果中角度滤波因子的物理意义。
在常密度声学介质中和高频近似意义下, 如果忽略透射损失, 影响成像保真度主要有两大因素。第一个因素为波场传播过程中的几何扩散, 这是高频近似下波场传播所要满足的物理规律之一, 它会影响射线路径及其领域内振幅分布, 从而影响成像结果的振幅值。第二个因素为观测系统对地下成像点照明炮检射线对空间分布的均匀程度。对地面观测系统来说, 影响成像点处照明射线分布的主要因素为地震观测系统的排布以及地下介质参数场的分布。传统真振幅成像方法仅仅校正波传播过程的几何扩散效应, 对于观测系统, 总假设为连续的无限孔径观测, 即对于地下任意成像点, 对其有照明的炮检射线对分布总是一致的, 这显然与实际情况不符。传统真振幅成像对观测系统过于理想化的假设会在较大程度上影响成像结果的保真度[21]。
本文首先回顾了Bayes反演框架下的ray+Born和ray+Kirchhoff两种近似情况下的反演成像公式及其基于波动方程的实现, 然后针对传统基于波动方程实现的高频渐进反演成像公式中存在的不足, 给出了基于波场隐式角度分解的低波数噪声消除方法以及高效稳健的角度域照明补偿方法。同时, 本文还简单讨论了直接输出角度域反射系数和阻抗扰动的方法。本文还简单讨论了直接输出角度域反射系数和阻抗扰动的方法。本文给出的是二维情况下的具体计算公式, 但本文方法可以很方便地推广到三维情况。
1 高频近似下的反演成像及其波动方程实现 1.1 散射场的表达在勘探地震中, 介质参数的高波数扰动量((方位角度)反射系数、速度扰动和波阻抗扰动)的估计, 理论上都归结为最小二乘线性反演理论。更确切地, 都归结为利用线性化散射场正演模型预测扰动波场与实测扰动波场之间的预测误差满足Gauss分布时的Bayes估计理论框架下的线性反演问题。
正问题是求解反问题的基础, 地震波线性化反演成像对应的正问题为地震波线性化散射场的计算。散射场计算问题可以由表示定理导出。考虑由边界∂D围成的计算区域D中的散射场计算问题, 且假设波场在计算区域二次连续可微, 假设子波的频谱F(ω)为常数。对于常密度声学介质, 在点源情况下表示定理形式可以写为[22]:
| $ \begin{array}{l} {u_{\rm{S}}}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}, \omega } \right) = \int_{\partial D} {\left[ {g\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, \mathit{\boldsymbol{x}}, \omega } \right)\frac{{\partial {u_{\rm{s}}}\left( {\mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}, \omega } \right)}}{{\partial \mathit{\boldsymbol{n}}}} - } \right.} \\ \;\;\;{u_{\rm{S}}}\left( {\mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}, \omega } \right)\frac{{\partial g\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, \mathit{\boldsymbol{x}}, \omega } \right)}}{{\partial \mathit{\boldsymbol{n}}}}]{\rm{d}}S + \\ \;\;\;\int_D {\left\{ {g\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, \mathit{\boldsymbol{x}}, \omega } \right)\frac{{{\omega ^2}}}{{c_0^2(\mathit{\boldsymbol{x}})}}\alpha (\mathit{\boldsymbol{x}})\left[ {{u_I}\left( {\mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}, \omega } \right) + } \right.} \right.} \\ \;\;\;{u_{\rm{S}}}\left( {\mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}, \omega } \right)]\} {\rm{d}}V \end{array} $ | (1) |
式中:uS(xr, xS, ω)为炮点xS激发, 检波点xr接收到的频率域散射场; g(xr, x, ω)为地下任意点x到检波点xr的格林函数; uI(x, xS, ω)为炮点xS激发, 传播经过x处的入射波场; n代表边界∂D的外法线方向; c0(x)为x处背景速度; α(x)为慢度平方扰动; dS为∂D上的面积微元; dV为D中的体积微元。公式(1)即为常密度声学情况下的表示定理。从(1)式可以看出, 在最广义的情况下, 散射场可以由一个面积分加一个体积分来表达。在不同的散射模式假设下, (1)式的体积分或面积分会起到不同的主导作用, 从而可以导出不同的散射模式下散射波的计算公式。下面分别讨论公式(1)中面积分和体积分起主导作用时散射波场的计算。
在体散射假设下, 边界∂D不产生散射场, 散射场全部由∂D内部的非均匀体产生, 则(1)式退化为:
| $ \begin{array}{l} {u_{\rm{S}}}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}, \omega } \right) = \int_D {\left\{ {g\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, \mathit{\boldsymbol{x}}, \omega } \right)\frac{{{\omega ^2}}}{{c_0^2(\mathit{\boldsymbol{x}})}}\alpha (\mathit{\boldsymbol{x}})} \right.} \bullet \\ \;\;\;\;\;\;\left[ {{u_I}\left( {\mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}, \omega } \right) + {u_{\rm{s}}}\left( {\mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_s}, \omega } \right)} \right]\} {\rm{d}}V \end{array} $ | (2) |
类似的, 假设在∂D围成的计算区域D中, ∂D内部没有散射源, 所有散射源仅来自于边界∂D上, 则(1)式退化为:
| $ \begin{array}{l} {u_{\rm{S}}}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}, \omega } \right) = \int_{\partial D} {\left[ {g\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, \mathit{\boldsymbol{x}}, \omega } \right)\frac{{\partial {u_{\rm{s}}}\left( {\mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}, \omega } \right)}}{{\partial \mathit{\boldsymbol{n}}}} - } \right.} \\ \left. {\;\;\;{u_{\rm{S}}}\left( {\mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}, \omega } \right)\frac{{\partial g\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, \mathit{\boldsymbol{x}}, \omega } \right)}}{{\partial \mathit{\boldsymbol{n}}}}} \right]{\rm{d}}S \end{array} $ | (3) |
注意到(2)式和(3)式均是非线性积分方程, 在(2)式中, 等式右端uS(x, xS, ω)既是散射势α(x)/c02(x)的函数, 又是非均匀体体积微元dV的函数。而在(3)式右端uS(x, xS, ω)是面积微元dS的函数。
为了导出线性化反演成像中使用的线性化的散射场计算公式, 需要进一步做线性化近似。对于体散射积分公式(2), 引入Born近似[23], 即假设散射场较弱, 入射场与散射场的和约等于入射场有:
| $ {u_I} + {u_{\rm{s}}} \approx {u_I} $ | (4) |
将公式(4)代入公式(2), 有:
| $ \begin{array}{l} {u_{\rm{S}}}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}, \omega } \right) = \int_D g \left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, \mathit{\boldsymbol{x}}, \omega } \right)\frac{{{\omega ^2}}}{{c_0^2(\mathit{\boldsymbol{x}})}}\alpha (\mathit{\boldsymbol{x}}) \bullet \\ \;\;\;{u_I}\left( {\mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}, \omega } \right)dV \end{array} $ | (5) |
公式(5)描述了散射场和速度扰动强度之间的线性化关系, 我们将其简称为Born近似下散射场计算公式。对于面散射公式(3), 引入Kirchhoff近似[23], 即在∂S1处有如下关系式成立:
| $ \begin{array}{*{20}{l}} {{u_{\rm{s}}} = R{u_I}}\\ {\frac{{\partial {u_{\rm{S}}}}}{{\partial \mathit{\boldsymbol{n}}}} = - R\frac{{\partial {u_I}}}{{\partial \mathit{\boldsymbol{n}}}}} \end{array} $ | (6) |
式中:R为反射系数。(6)式的负号表示相对于∂S1的外法线方向入射波与反射波的传播方向相反。将公式(6)代入公式(3), 有:
| $ {u_{\rm{S}}}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}, \omega } \right) = \int_{{S_1}} R \frac{{\partial \left[ {{u_I}\left( {\mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}, \omega } \right)g\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, \mathit{\boldsymbol{x}}, \omega } \right)} \right]}}{{\partial \mathit{\boldsymbol{n}}}}{\rm{d}}S $ | (7) |
公式(7)即为线性化的Kirchhoff积分法散射波计算公式[21]。对比(5)式和(7)式可以看出, Born近似下散射场(体散射假设)计算公式和Kirchhoff近似下散射场(面散射假设)计算公式的模型空间假设是不同的。在Born近似下, 体状的散射势产生散射场, 数学上接近于Heaviside阶跃函数。在Kirchhoff近似下, 层状分布的角度反射系数产生散射场, 数学上接近单位脉冲函数。对于实际的带限数据反演, Born近似下和Kirchhoff近似下反演的模型参数可以认为是带限的阶跃函数和带限的脉冲函数[24]。
基于线性化的散射场计算公式(5)或者公式(7), 可以构造相应的反演成像公式。然而, 由前面讨论可知, 直接估计完整Hessian的逆在实际情况下较为困难。Hessian矩阵是一个主对角占优的带状矩阵, 其特征值主要由对角元素贡献, 利用线性Hessian矩阵的主对角元素代替整个矩阵是一种较为可行的反演策略[25]。本文在高频近似框架下实现Hessian矩阵的对角化, 因此, 需要对线性化的体散射和面散射公式(5)以及公式(7)做进一步的高频近似展开。
对线性化体散射积分公式(5), 在二维情况下其高频近似的形式(2D ray+Born近似)[26]:
| $ \begin{array}{l} {u_S}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}, \omega } \right) = \int {\rm{d}} \mathit{\boldsymbol{x}}\delta m(\mathit{\boldsymbol{x}}) \bullet \\ \;\;\sum\limits_{n = 1}^{N\left( {{x_{\rm{r}}}, x} \right)} {\sum\limits_{l = 1}^{\left( {x, {x_{\rm{s}}}} \right)} {G_{nl}^{RB}} } \left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, \mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}, \omega } \right) \end{array} $ | (8) |
式中:δm(x)=α(x)/c02(x); l, n分别为震源端和检波点端的射线标记, 核函数GnlRB(xr, x, xS, ω)的表达式为:
| $ G_{nl}^{RB}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, \mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}, \omega } \right) = {\rm{i}}\omega {A_{nl}}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, \mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}} \right){{\rm{e}}^{{\rm{i}}\omega {T_{nl}}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, \mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)}} $ | (9) |
在(9)式中, Anl(xr, x, xS)表示从炮点xS出发到地下任一点x然后被xr处接收到射线振幅的变化。相位项Tnl(xr, x, xS)的表达式为:
| $ \begin{array}{l} {T_{nl}}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, \mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}} \right) = \tau \left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, \mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}} \right) - \frac{\pi }{2}\frac{{{\mathop{\rm sign}\nolimits} (\omega )}}{\omega } \bullet \\ \;\;K\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, \mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}} \right) \end{array} $ | (10) |
式中:τ(xr, x, xS)为从炮点xS出发到地下任一点x然后被xr处接收到射线的总旅行时。K(xr, x, xS)为KMAH标号, 其描述射线从炮点xS出射, 被检波点xr接收到所经历的一阶焦散点的总个数, 在每一个一阶焦散点处, 高频近似下的波场发生π/2的相移[27]。
对线性化面散射积分公式, 在二维情况下其高频近似的形式为(2D ray+Kirchhoff近似)[7]:
| $ \begin{array}{l} {u_S}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}, \omega } \right) = \int {\rm{d}} \mathit{\boldsymbol{x}}R\left( {\mathit{\boldsymbol{x}}, {\theta _{\rm{r}}}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, \mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)} \right) \bullet \\ \;\;\sum\limits_{n = 1}^{N\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, \mathit{\boldsymbol{x}}} \right)} {\sum\limits_{l = 1}^{\left( {\mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)} {G_{nl}^{RK}} } \left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, \mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}, \omega } \right) \end{array} $ | (11) |
式中:R(x, θr)为反射系数; θr(xr, x, xS)为反射角; 核函数GnlRK(xr, x, xS, ω)的形式为:
| $ \begin{array}{l} G_{nl}^{RK}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, \mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}, \omega } \right) = - \left| {{\mathit{\boldsymbol{q}}_{nl}}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, \mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)} \right| \bullet \\ {A_{nl}}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, \mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}} \right){{\rm{e}}^{{\rm{i}}\omega {T_{nl}}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, \mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)}} \end{array} $ | (12) |
这里|qnl(xr, x, xS)|为偏移倾角矢量的模[26], 其定义为:
| $ \left| {{\mathit{\boldsymbol{q}}_{nl}}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, \mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)} \right| = \frac{{2\cos \left( {{\theta _{\rm{r}}}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, \mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)} \right)}}{{{c_0}(\mathit{\boldsymbol{x}})}} $ | (13) |
考虑如下Bayes框架下的反问题:
① 线性问题d=Gm或可在初始模型mprior处线性展开的非线性问题g(mprior);
② 不考虑正算子的不确定性, 通常也不考虑模型的先验信息;
③ 考虑数据的先验信息, 即考虑数据的协方差算子的逆CD-1;
④ 选择合适的CD-1使得Hessian对角化。
据TARANTOLA[28], 基于以上四点考虑, 可以得到最小二乘意义下法方程的解形式为:
| $ \delta \mathit{\boldsymbol{m}} = {\left( {{{\mathit{\boldsymbol{\hat H}}}_0}} \right)^{ - 1}}{\mathit{\boldsymbol{\hat \gamma }}_0} $ | (14) |
其中梯度项为:
| $ {\mathit{\boldsymbol{\hat \gamma }}_0} = - \mathit{\boldsymbol{G}}_0^{\rm{T}}\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{D}}^{ - 1}{\mathit{\boldsymbol{d}}_{{\rm{obs}}}} $ | (15) |
式中:G0为线性化正算子; G0T为其共轭转置; dobs为观测数据。
| $ {\mathit{\boldsymbol{\hat H}}_0} \approx \mathit{\boldsymbol{G}}_0^{\rm{T}}\mathit{\boldsymbol{C}}_D^{ - 1}{\mathit{\boldsymbol{G}}_0} $ | (16) |
注意:梯度和拟Hessian记号中的上标代表其为对偶空间的元素[27]。进一步地, 可以构建法方程解的迭代格式(拟Newton算法):
| $ {\mathit{\boldsymbol{m}}_{n + 1}} = {\mathit{\boldsymbol{m}}_n} - {\mu _n}{\left( {\mathit{\boldsymbol{G}}_n^{\rm{T}}\mathit{\boldsymbol{C}}_D^{ - 1}{\mathit{\boldsymbol{G}}_n}} \right)^{ - 1}}\left[ {\mathit{\boldsymbol{G}}_n^{\rm{T}}\mathit{\boldsymbol{C}}_D^{ - 1}\left( {{\mathit{\boldsymbol{d}}_n} - {\mathit{\boldsymbol{d}}_{{\rm{obs}}}}} \right)} \right] $ | (17) |
式中:mn, mn+1分别为当前模型和下一次更新模型; μn为步长。本文仅考虑非迭代格式的求解。
1.3 高频近似下的反演成像公式将ray+Born近似下散射场的计算公式(8)代入公式(14)~公式(16), 得到ray+Born近似在最小二乘意义下法方程解的具体形式为[26]:
| $ \begin{array}{l} \delta m(\mathit{\boldsymbol{x}}) = \frac{1}{{\left[ {{\theta _s}} \right]_{{\theta _{{\rm{smin}}}}}^{{\theta _{{\mathop{\rm smax}\nolimits} }}}}}\int {\int {\int {{\rm{d}}{\mathit{\boldsymbol{x}}_{\rm{s}}}{\rm{d}}{\mathit{\boldsymbol{x}}_{\rm{r}}}{\rm{d}}\omega \sum\limits_{n = 1}^{N\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, \mathit{\boldsymbol{x}}} \right)} {\mathop \sum \limits_{l = 1}^{N\left( {\mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)} } \bullet } } } \\ \;\;\;\;{{\rm{e}}^{ - {\rm{i}}\omega {T_{nl}}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, \mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)}}\varepsilon _{nl}^{BK}{\mathit{\boldsymbol{d}}_{{\rm{obs}}}}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}, \omega } \right) \end{array} $ | (18) |
式中:θsmin, θsmax分别为当前观测系统对地下成像点能达到的最小和最大散射角度值。振幅权重εnlBK的形式为:
| $ \varepsilon _{nl}^{BK} = \frac{{{J_{\left( {{\mathit{\boldsymbol{x}}_{\rm{s}}}, {\mathit{\boldsymbol{x}}_{\rm{r}}}, \omega } \right) \to \left( {{k_\mathit{\boldsymbol{x}}}, {k_z}, {\theta _{\rm{s}}}} \right)}}}}{{{\rm{i}}\omega {A_{nl}}\left( {{\mathit{\boldsymbol{x}}_r}, \mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_s}} \right)}} $ | (19) |
式中:
| $ \begin{array}{l} {J_{\left( {{\mathit{\boldsymbol{x}}_{\rm{s}}}, {\mathit{\boldsymbol{x}}_{\rm{r}}}, \omega } \right) \to \left( {{k_\mathit{\boldsymbol{x}}}, {k_z}, {\theta _s}} \right)}} = |\omega |{\left| {{\mathit{\boldsymbol{q}}_{nl}}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, \mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)} \right|^2} \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\left| {\frac{{\partial {\beta _{{\mathit{\boldsymbol{x}}_{\rm{s}}}}}}}{{\partial {\mathit{\boldsymbol{x}}_{\rm{s}}}}}} \right|{\left| {\frac{{\partial {\beta _{{\mathit{\boldsymbol{x}}_{\rm{r}}}}}}}{{\partial {\mathit{\boldsymbol{x}}_{\rm{r}}}}}} \right|_n} \end{array} $ | (20) |
式中:βxS, βxr分别为源检两端的起飞角。公式(18)~公式(20)即为ray+Born近似下的反演成像公式。类似地, 基于公式(11)和公式(14)~公式(16)可以得到ray+Kirchhoff近似最小二乘意义下法方程解的具体形式为[7]:
| $ \begin{array}{*{20}{l}} {R\left( {\mathit{\boldsymbol{x}},{\theta _{\rm{r}}}} \right) = - \frac{1}{{[\theta ]_{{\theta _{\min }}}^{{\theta _{\max }}}}}\int {\int {\int {\int {{\rm{d}}{\mathit{\boldsymbol{x}}_{\rm{s}}}{\rm{d}}{\mathit{\boldsymbol{x}}_{\rm{r}}}{\rm{d}}\omega {\rm{d}}{\theta ^\prime }_{\rm{r}}} } } } \sum\limits_{n = 1}^{N\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}},\mathit{\boldsymbol{x}}} \right)} {\mathop \sum \limits_{l = 1}^{N\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)} } }\\ {{{\rm{e}}^{ - {\rm{i}}\omega {T_{nl}}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}},\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)}}\varepsilon _{nl}^{RK}{\mathit{\boldsymbol{d}}_{{\rm{obs}}}}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}},\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)\delta \left( {\theta _{\rm{r}}^\prime - {\theta _{\rm{r}}}} \right)} \end{array} $ | (21) |
其中振幅权重εnlRK的形式为:
| $ \varepsilon _{nl}^{RK} = \frac{{{J_{\left( {{\mathit{\boldsymbol{x}}_{\rm{s}}}, {\mathit{\boldsymbol{x}}_{\rm{r}}}, \omega } \right) \to \left( {{k_\mathit{\boldsymbol{x}}}, {k_z}, {\theta _s}} \right)}}}}{{{{(2{\rm{ \mathit{ π} }})}^2}\left| {{\mathit{\boldsymbol{q}}_{nl}}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, \mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)} \right|{A_{nl}}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, \mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)}} $ | (22) |
公式(21)中的δ(θ′r-θr)为角度采样函数, 使得积分仅对在成像点x处入射角为θr的炮数据进行[7]。公式(21)~公式(22)即为ray+Kirchhoff近似下的反演成像公式。
1.4 高频近似反演的RTM实现-保真的RTM偏移成像方法本文主要讨论基于反射波的保真成像, 因此本小节仅讨论ray+Kirchhoff真振幅成像公式的波动方程实现方法, ray+Born真振幅成像公式的波动方程实现方法可以利用类似的方式得出。据BLEISTEIN等[31], 公式(21)可以利用如下波场相关运算实现:
| $ \begin{array}{l} R\left( {\mathit{\boldsymbol{x}}, {\theta _{\rm{r}}}} \right) = 8{\rm{ \mathit{ π} }}\int {\int {\int {\rm{d}} } } {\mathit{\boldsymbol{x}}_{\rm{s}}}{\rm{d}}\omega {\rm{d}}\theta _{\rm{r}}^\prime |\mathit{\boldsymbol{q}}|[ - {\rm{i}}{\mathop{\rm sign}\nolimits} (\omega )] \bullet \\ \;\;\;\left[ {P_{\rm{F}}^*\left( {\mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_s}, \omega } \right){P_{\rm{B}}}\left( {\mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_s}, \omega } \right)} \right]{\rm{ \mathit{ δ} }}\left( {\theta _{\rm{r}}^\prime - {\theta _{\rm{r}}}} \right) \end{array} $ | (23) |
式中:PF(x, xS, ω), PB(x, xS, ω)分别为频率域的正传播及反传播波场。我们将(23)式反变换回时间域有:
| $ \begin{array}{l} R\left( {\mathit{\boldsymbol{x}}, {\theta _{\rm{r}}}} \right) = 4{\mathit{\boldsymbol{x}}_{\rm{s}}}{\rm{d}}t{\rm{d}}\theta _{\rm{r}}^\prime |\mathit{\boldsymbol{q}}|H\left( {{P_{\rm{F}}}\left( {\mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}, t} \right)} \right. \bullet \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{P_{\rm{B}}}\left( {\mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}, t} \right)){\rm{ \mathit{ δ} }}\left( {\theta _{\rm{r}}^\prime - {\theta _{\rm{r}}}} \right) \end{array} $ | (24) |
这里H代表Hilbert变换。注意到ZHANG等[13]给出的输出为R′(x, θr)=R(x, θr)/|q|, 即有:
| $ \begin{array}{l} {R^\prime }\left( {\mathit{\boldsymbol{x}}, {\theta _{\rm{r}}}} \right) = 4\int {\int {\int {\rm{d}} } } {\mathit{\boldsymbol{x}}_{\rm{s}}}{\rm{d}}t{\rm{d}}\theta _{\rm{r}}^\prime H\left[ {{P_{\rm{F}}}\left( {\mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}, t} \right)} \right. \bullet \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{P_{\rm{B}}}\left( {\mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}, t} \right)} \right]\mathit{\delta }\left( {\theta _{\rm{r}}^\prime - {\theta _{\rm{r}}}} \right) \end{array} $ | (25) |
公式(25)即为ZHANG等[13]给出的二维情况下利用波动方程实现的ray+Kirchhoff真振幅成像公式。注意到|q|的作用是为了校正在水平层状介质假设下子波峰值振幅随角度的变化[32], 对保真角度反射系数的获取是有必要的[33]。因此在下文中, 采用公式(24)作为二维ray+Kirchhoff近似下RTM真振幅成像条件。
2 基于波场隐式分解的RTM真振幅成像条件高频近似下成像点处波矢量的表达式可以表示为[34]:
| $ \mathit{\boldsymbol{k}} = \omega \mathit{\boldsymbol{q}}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, \mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}} \right) $ | (26) |
其中:
| $ \mathit{\boldsymbol{q}}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}}, \mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_{\rm{s}}}} \right) = \frac{{2\cos \left( {\frac{{{\theta _{\rm{s}}}}}{2}} \right)}}{{c(\mathit{\boldsymbol{x}})}}\mathit{\boldsymbol{n}} $ | (27) |
(27) 式中的n为单位化的偏移倾角。从公式(26)和公式(27)可以看出, 当震源端和检波点端波场对应的射线慢度矢量之间散射角较大时, 利用成像公式(24)进行基于波场相关成像会产生低波数能量。对于估计参数场中的高波数部分, 这些低波数成分是成像噪声应当去除[18]。
为了消除这些低波数噪声, STOLK等[19]在ray+Born近似意义下给出了能自动消除低波数噪声的基于逆时偏移(RTM)实现的真振幅成像公式, 在其它文献中也被称之为逆散射成像条件[20]。该成像条件能够在不显式的进行波场角度分解情况下完成角度域滤波, 是一种高效稳健的低波数噪声消除方法。对于ray+Kirchhoff近似下的RTM, 我们可以构造类似能自动消除低波数噪声的反演成像条件。
3 高效稳健的角度域照明补偿经典的高频近似下基于hit-count方式进行角度域照明补偿成像可以表示如下[33]:
| $ {R^c}\left( {\mathit{\boldsymbol{x}}, {\theta _{\rm{r}}}} \right) = \int {\rm{d}} \psi \frac{{R\left( {\mathit{\boldsymbol{x}}, {\theta _{\rm{r}}}, \psi } \right)}}{{C\left( {\mathit{\boldsymbol{x}}, {\theta _{\rm{r}}}, \psi } \right)}} $ | (28) |
式中:ψ为对应于照明倾角的积分变量; C(x, θr, ψ)为照明圆单位面积上落入的单位偏移倾角矢量的数量; R(x, θr, ψ)为未校正前成像点x对应于反射角θr的共照明倾角道集; Rc(x, θr)为成像点x处对应于反射角θr校正后的成像结果。在三维情况下, 有类似公式:
| $ {R^c}\left( {\mathit{\boldsymbol{x}}, {\theta _{\rm{r}}}, {\varphi _{\rm{r}}}} \right) = \int {\int {\rm{d}} } \psi {\rm{d}}\lambda \frac{{R\left( {\mathit{\boldsymbol{x}}, {\theta _{\rm{r}}}, {\varphi _{\rm{r}}}, \psi , \lambda } \right)}}{{C\left( {\mathit{\boldsymbol{x}}, {\theta _{\rm{r}}}, {\varphi _{\rm{r}}}, \psi , \lambda } \right)}} $ | (29) |
式中:φr为反射方位角; λ为照明方位角。关于公式(28)及公式(29)中角度的定义可以参见文献[35]。由公式(28)和公式(29)可知, 传统基于照明倾角道集的照明校正方法物理上直观清晰, 并且由于校正过程仅需显式计算偏移倾角矢量的空间分布密度, 因此计算较为稳健。然而, 基于照明倾角道集的校正方法需要在高维空间进行, 计算量和存储量相较于传统真振幅成像方法大大增加。即使将照明校正投影到地表坐标上完成, 也仅能减少1维的数据处理量, 对于3维观测仍然需要处理6维数据, 同时, 将照明校正投影到地表坐标上完成也会引入新的计算量[36], 计算和存储量依然较大。另外, 如果考虑用波动方程算子去实现传统照明校正方法, 在目前的计算机硬件条件下对3维实际问题几乎不可行。基于与公式(28)和公式(29)相同的物理意义, 可以在波动方程类成像过程中高效稳健实施角度域照明补偿方法, 这些方法将在另文单独讨论。
4 角度反射系数的输出及阻抗成像从公式(24)可以看出, 直接利用基于ray+Kirchhoff反演类的波动方程成像条件得到结果是角度域的反射系数, 因此可以直接输出该角度域反射系数, 即所谓的角度道集。同时, 为了在不输出角度反射系数的情况下得到有物理意义的叠加结果, 也可以利用常密度声学近似下的AVA近似关系式[37]将利用公式(24)得到的不同角度反射系数结果校正到零角度进行叠加成像[38], 最终输出零角度反射系数成像剖面。
对于勘探地震学中的储层参数建模, 波阻抗是比反射系数更加贴近储层描述的参数。在已知零角度反射系数的情况下, 可以通过道积分来得到波阻抗分布[39]。但在零角度反射系数存在一定的误差时, 直接利用道积分计算波阻抗容易产生数值噪声。为了更加稳健地利用零角度反射系数估计波阻抗, 可以利用稀疏反演方法由零角度反射系数计算波阻抗[40-41]。
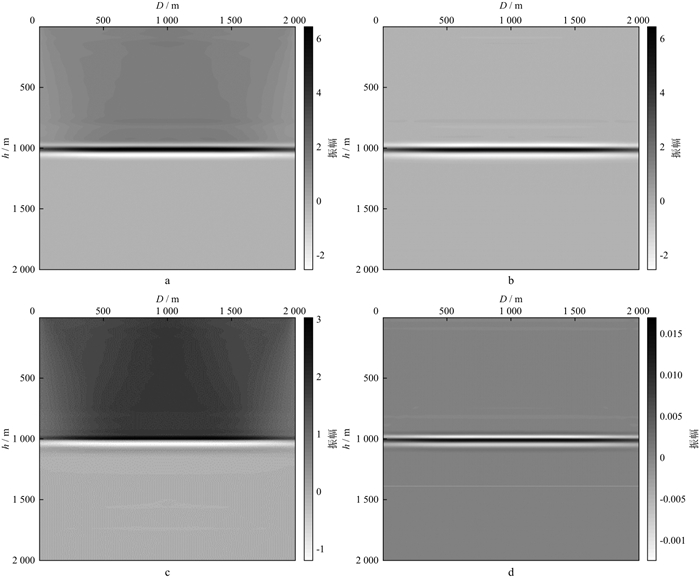
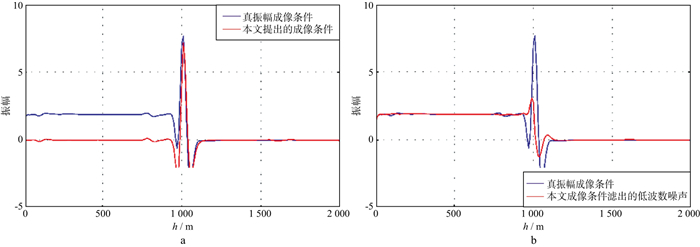
5 数值实验首先利用层状模型验证本文提出的成像条件的有效性。模型第一层速度为3000m/s, 第二层速度为4000m/s。模型的x和z方向范围均为0~4 000m, 两个方向上网格大小均为10m。利用真实模型正演得到的数据作为输入炮记录, 利用半径为10的Gussian函数平滑真实速度后的模型作为成像算法采用的背景速度。图 1a为利用不带角度滤波的ray+Kirchhoff近似下真振幅成像条件(公式(24))得到的成像结果, 从成像结果上可以看出, 目标反射层的成像为带限的脉冲函数, 这与ray+Kirchhoff真振幅成像的期望输出一致[24]。同时, 在目标反射层上方存在可以预期的低波数噪声。图 1b为利用本文提出的成像条件得到的成像结果, 可以看出, 低波数噪声被消除, 同时成像结果的振幅量级与图 1a保持一致。图 1c为利用本文提出的成像条件滤出的低波数噪声。图 1d为利用带角度滤波不带振幅校正成像条件得到的成像结果, 在这种情况下, 虽然低波数噪声被消除了, 但是由于角度域滤波算子的非单位化效应未被消除, 成像结果的振幅量级相较于原始成像结果(图 1a)发生了明显变化。图 2为单层模型不同成像条件成像结果抽道的对比。图 2a为本文提出成像条件成像结果与不带角度滤波的ray+Kirchhoff近似下真振幅成像条件得到成像结果抽道结果对比, 图 2b为本文提出成像条件滤出的低波数噪声结果与不带角度滤波的ray+Kirchhoff近似下真振幅成像条件得到成像结果抽道结果对比。我们可以更加清晰地看出利用不带角度滤波的ray+Kirchhoff近似下真振幅成像条件得到成像结果浅部存在的低波数噪声, 利用本文提出的成像条件得到的反射层成像结果以及滤出的低波数噪声在振幅和相位上与不带角度滤波成像结果中对应成分具有很好的对应关系。这说明了本文提出的成像条件在自动消除低波数成像噪声的同时较好保持了目标反射层的振幅和相位信息。
|
图 1 单层模型不同成像条件成像结果的对比 a利用不带角度滤波的ray+Kirchhoff近似下真振幅成像条件((24)式)成像结果; b利用本文提出的成像条件成像结果; c 图 1a被滤出的低波数噪声; d利用带角度滤波不带振幅校正的成像条件的成像结果 |
|
图 2 单层模型不同成像条件成像结果抽道的对比 a利用不带角度滤波的真振幅成像条件((24)式)成像结果(蓝色实线)与利用本文提出的成像条件成像结果(红色实线)对比; b利用不带角度滤波的真振幅成像条件((24)式)成像结果与利用本文提出成像条件滤出的低波数噪声(红色实线)对比 |
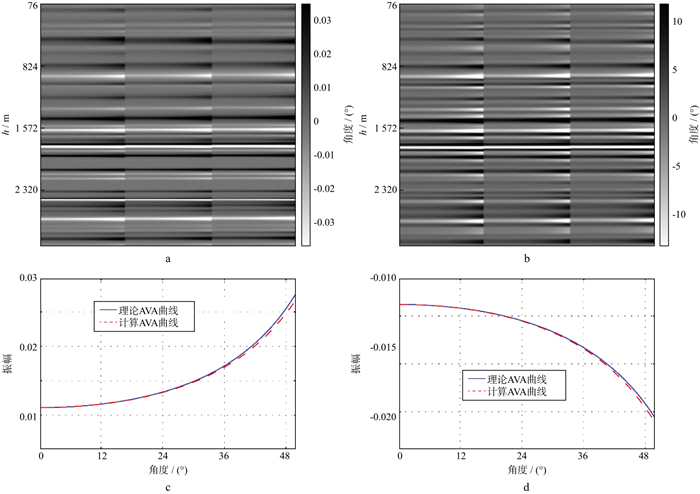
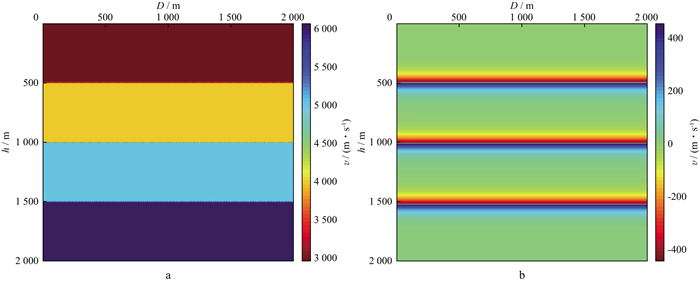
对于角度反射系数输出, 我们利用Marmousi模型进行数值实验, 并对输出角度反射系数结果进行对比。图 3和图 4展示了数值实验结果。从中可以看出利用本文方法输出角度反射系数与理论值具有较好的匹配关系。Marmousi模型数值实验结果表明了本文提出成像条件输出角度反射系数对复杂模型的适应性。对于角度域照明补偿及阻抗成像, 首先利用层状模型进行测试。层状模型参数见图 5和图 6。图 7展示了在真振幅RTM基础上不进行和进行角度域照明补偿的带限反射系数估计结果。可以看出, 在正确校正几何扩散的基础上进一步校正成像点处照明补偿不均匀效应, 能够大大提高带限反射系数的估计精度。在得到的带限反射基础上, 进一步得到了阻抗扰动的估计, 结果见图 8和图 9。很明显, 在考虑了照明补偿后, 阻抗扰动估计结果的精度也有较大程度的提高。为了验证本文讨论的角度域照明补偿及阻抗成像在复杂模型上的测试结果, 我们进一步利用部分Sigsbee模型进行测试。图 10为部分Sigsbee模型参数。带限反射系数以及阻抗扰动成像结果分别见图 11、图 12以及图 13。由图可见, 与前面层状模型测试结果类似, 在真振幅成像基础上进一步考虑角度域照明补偿能够大大提高反射系数以及阻抗扰动反演成像精度。

|
图 3 Marmousi模型所有CDP的理论角度道集(a)和计算得到的角度道集(b) |
|
图 4 Marmousi模型角度反射系数输出对比 a CDP119~CDP121理论角度道集; b CDP119~CDP121计算得到的角度道集; c CDP120、深度824m处理论AVA曲线(蓝色实线)与计算AVA曲线(红色曲线)对比; d CDP120、深度1572m处理论AVA曲线与计算AVA曲线对比 |
|
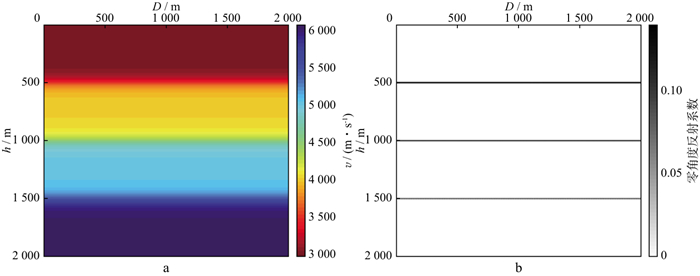
图 5 层状模型模型参数场 a真实速度模型; b真实速度扰动 |
|
图 6 成像采用的平滑模型(a)及真实零角度反射系数(b) |
|
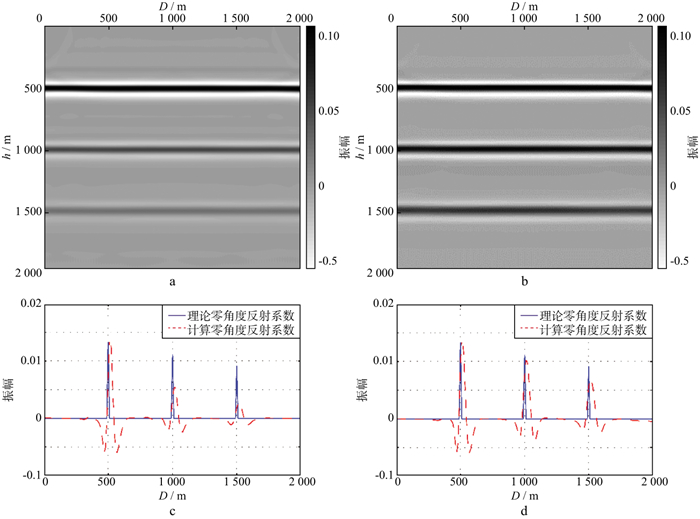
图 7 层状模型带限反射系数成像对比 a不考虑照明校正的零角度反射系数成像结果; b利用本文提出的照明补偿算子进行照明校正的零角度反射系数成像结果; c, d分别为图 7a、图 7b抽取中间一道零角度反射系数和理论零角度系数的对比 |
|
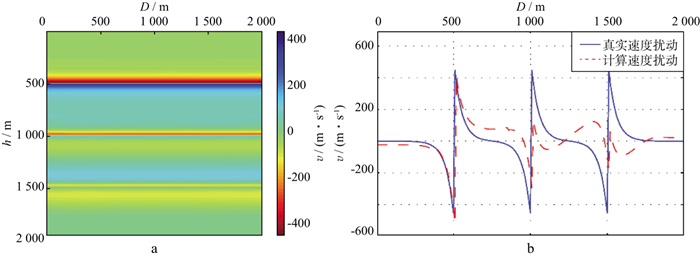
图 8 层状模型利用零角度反射系数反演速度扰动结果(Ⅰ) a基于不考虑照明校正的零角度反射系数估计结果反演得到的速度扰动场; b抽取中间道和理论速度扰动的对比 |
|
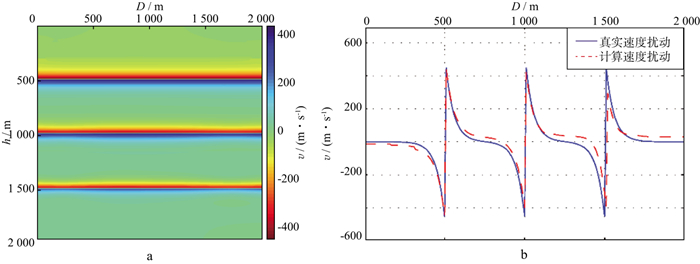
图 9 层状模型利用零角度反射系数反演速度扰动结果(Ⅱ) a基于本文提出照明补偿算子进行照明校正的零角度反射系数估计结果反演得到的速度扰动场; b抽取中间道和理论速度扰动的对比 |
|
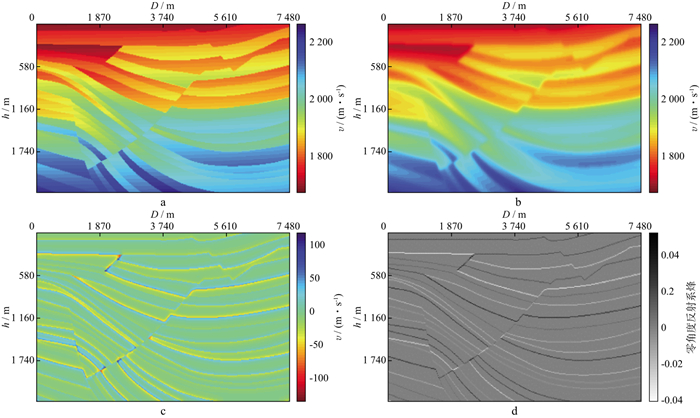
图 10 部分Sigsbee模型参数场 a真实速度模型; b成像采用的平滑模型; c真实速度扰动; d真实零角度反射系数 |
|
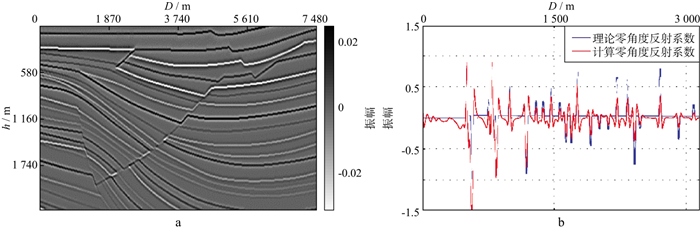
图 11 部分Sigsbee模型带限反射系数成像对比(Ⅰ) a不考虑照明校正的零角度反射系数成像结果; b抽取中间一道的零角度反射系数和理论零角度反射系数的对比结果 |
|
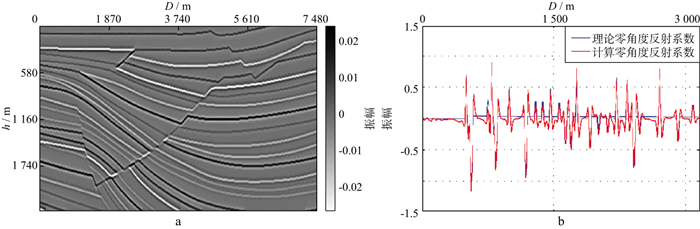
图 12 部分Sigsbee模型带限反射系数成像对比(Ⅱ) a利用本文提出的照明补偿算子进行照明校正的零角度反射系数成像结果; b抽取中间一道的零角度反射和理论零角度反射系数的对比结果 |
|
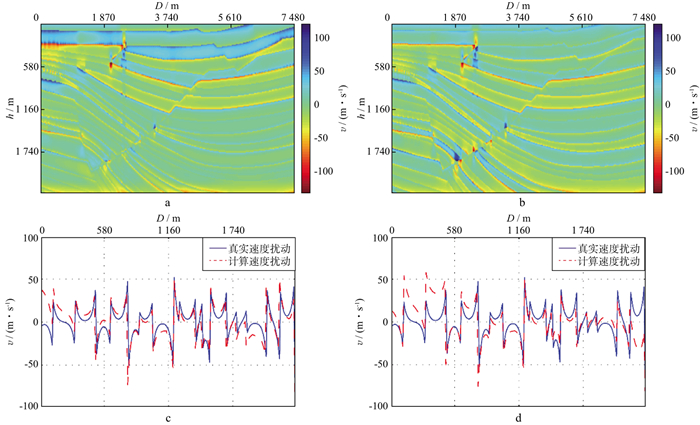
图 13 部分Sigsbee模型利用零角度反射系数反演速度扰动结果 a基于不考虑照明校正的零角度反射系数估计结果反演得到的速度扰动场; b基于本文提出照明补偿算子进行照明校正的零角度反射系数估计结果反演得到的速度扰动场; c, d分别为图a、图b抽取中间道速度扰动和真实速度扰动的对比 |
本文系统地讨论了体散射以及面散射模式下的散射场计算。在高频近似框架下, 本文进一步讨论了不同散射模式下的反演成像公式及其波动方程实现。在反射模式下, 我们给出了改进的真振幅RTM成像条件, 用以在成像过程中自动且保真地消除低波数噪声。在此基础上, 我们还讨论了角度反射系数的输出、角度域的照明补偿以及阻抗成像方法。模型数据的数值试验结果证明了本文方法相较于传统基于反射模式真振幅成像条件的优势。本文结果可以推广到三维情况, 相应的分析测试工作是本文下一步的工作重点之一。
致谢: 感谢中石油勘探开发研究院及西北分院、中海油研究院和湛江分公司、中国石油化工股份有限公司石油物探技术研究院和胜利油田分公司对波现象与智能反演成像研究组(WPI)研究工作的资助与支持。| [1] |
王华忠, 冯波, 刘少勇, 等. 叠前地震数据特征波场分解、偏移成像与层析反演[J]. 地球物理学报, 2015, 58(6): 2024-2034. WANG H Z, FENG B, LIU S Y, et al. Characteristic wavefield decomposition, imaging and inversion with prestack seismic data[J]. Chinese Journal of Geophysics, 2015, 58(6): 2024-2034. |
| [2] |
王华忠, 冯波, 王雄文, 等. 特征波反演成像理论框架[J]. 石油物探, 2017, 56(1): 38-49. WANG H Z, FENG B, WANG X W, et al. The theoretical framework of characteristic wave inversion imaging[J]. Geophysical Prospecting for Petroleum, 2017, 56(1): 38-49. DOI:10.3969/j.issn.1000-1441.2017.01.005 |
| [3] |
王华忠, 胡江涛, 郭颂. 最小二乘叠前深度偏移成像理论与方法[J]. 石油物探, 2017, 56(2): 159-170. WANG H Z, HU J T, GUO S. Theory and method of least square prestack depth migration and imaging[J]. Geophysical Prospecting for Petroleum, 2017, 56(2): 159-170. DOI:10.3969/j.issn.1000-1441.2017.02.001 |
| [4] |
RICKETT J E. Illumination-based normalization for wave-equation depth migration[J]. Geophysics, 2003, 68(4): 1371-1379. DOI:10.1190/1.1598130 |
| [5] |
GUITTON A. Amplitude and kinematic corrections of migrated images for nonunitary imaging operators[J]. Geophysics, 2004, 69(4): 1017-1024. DOI:10.1190/1.1778244 |
| [6] |
GUITTON A. Fast 3D least-squares RTM by preconditioning with nonstationary matching filters[J]. Expanded Abstracts of 87thAnnual Internat SEG Mtg, 2017, 4395-4399. |
| [7] |
XU S, CHAURIS H, LAMBARE' G, et al. Common-angle migration:A strategy for imaging complex media[J]. Geophysics, 2001, 66(6): 1877-1894. DOI:10.1190/1.1487131 |
| [8] |
BEYLKIN G. Imaging of discontinuities in the inverse scattering problem by inversion of a causal generalized Radon transform[J]. Journal of Mathematical Physics, 1985, 26(1): 99-108. DOI:10.1063/1.526755 |
| [9] |
BLEISTEIN N. On the imaging of reflectors in the earth[J]. Geophysics, 1987, 52(7): 931-942. DOI:10.1190/1.1442363 |
| [10] |
JIN S, MADARIAGA R, VIRIEUX J, et al. Two-dimensional asymptotic iterative elastic inversion[J]. Geophysical Journal International, 1992, 108(2): 575-588. DOI:10.1111/gji.1992.108.issue-2 |
| [11] |
DONG W J, BLEISTEIN N. Common-shot inversion in c(x, z) media[J]. Expanded Abstracts of 59th Annual Internat SEG Mtg, 1989, 928-931. |
| [12] |
GRAY S H, BLEISTEIN N. True-amplitude Gaussian-beam migration[J]. Geophysics, 2009, 74(2): S11-S23. DOI:10.1190/1.3052116 |
| [13] |
ZHANG Y, XU S, BLEISTEIN N, et al. True amplitude angle domain common image gathers from one-way wave equation migrations[J]. Geophysics, 2007, 72(1): S49-S58. DOI:10.1190/1.2399371 |
| [14] |
ZHANG Y, SUN J. Practical issues of reverse time migration:True amplitude gathers, noise removal and harmonic-source encoding[J]. First Break, 2009, 26(1): 19-25. |
| [15] |
FLETCHER R F, FOWLER P, KITCHENSIDE P, et al. Suppressing artifacts in prestack reverse time migration[J]. Expanded Abstracts of 75th Annual Internat SEG Mtg, 2005, 2049-2051. |
| [16] |
GUITTON A, KAELIN B, BIONDI B. Least-squares attenuation of reverse-time-migration artifacts[J]. Geophysics, 2006, 71(1): S19-S23. DOI:10.1190/1.2168011 |
| [17] |
XIE X B, WU R S. Extracting angle domain information from migrated wavefield[J]. Expanded Abstracts of 72nd Annual Internat SEG Mtg, 2002, 1360-1363. |
| [18] |
LIU F, ZHANG G, MORTON S A, et al. An effective imaging condition for reverse-time migration using wavefield decomposition[J]. Geophysics, 2011, 76(1): S29-S39. DOI:10.1190/1.3533914 |
| [19] |
STOLK C C, DE HOOP M, OP'T ROOT T. Inverse scattering of seismic data in the reverse time migration (RTM) approach[J]. Proceedings of the Project Review, Geo-Mathematical Imaging Group, Purdue University, 2009, 91-108. |
| [20] |
WHITMORE N D, CRAWLEY S. Applications of RTM inverse scattering imaging conditions[J]. Expanded Abstracts of 82nd Annual Internat SEG Mtg, 2012, 1-6. |
| [21] |
ALBERTIN U, JARAMILLO H, YINGST D, et al. Aspects of true amplitude migration[J]. Expanded Abstracts of 69th Annual Internat SEG Mtg, 1999, 1358-1361. |
| [22] |
WAPENAAR C P A, BERKHOUT A J. Elastic wave field extrapolation[M]. Amsterdam: Elsevier Science Publishers B V, 1989: 1-465.
|
| [23] |
BLEISTEIN N. Mathematical methods for wave phenomena[M]. New York: Academic Press Inc(Harcourt Brace Jovanovich Publishers), 1984: 1-341.
|
| [24] |
BLEISTEIN N, COHEN J K, STOCKWELL J W. Mathematics of multidimensional seismic inversion[M]. NewYork: Springer-Verlag Inc, 2001: 1-23.
|
| [25] |
SHIN C, JANG S, MIN D J. Improved amplitude preservation for prestack depth migration by inverse scattering theory[J]. Geophysical Prospecting, 2001, 49(5): 592-606. DOI:10.1046/j.1365-2478.2001.00279.x |
| [26] |
OPERTO M S, XU S, LAMBARÉ G. Can we quantitatively image complex structures with rays?[J]. Geophysics, 2000, 65(4): 1223-1238. DOI:10.1190/1.1444814 |
| [27] |
ČERY'VENY V. Seismic ray theory[M]. Cambridge: Cambridge University Press, 2001: 1-722.
|
| [28] |
TARANTOLA A. Inverse problem theory and methods for model parameter estimation[M]. Philadelphia: Society for Industrial and Applied Mathematics (SIAM), 2005: 1-342.
|
| [29] |
THIERRY P, OPERTO M S, LAMBARÉ G. Fast 2-D ray+ Born migration/inversion in complex media[J]. Geophysics, 1998, 64(1): 162-181. |
| [30] |
XU S, ZHANG Y, TANG B. 3D angle gathers from reverse time migration[J]. Geophysics, 2011, 76(2): S77-S92. DOI:10.1190/1.3536527 |
| [31] |
BLEISTEIN N, ZHANG Y, XU S, et al. Migration/inversion:think image point coordinates, process in acquisition surface coordinates[J]. Inverse Problems, 2005, 21(5): 1715-1744. DOI:10.1088/0266-5611/21/5/013 |
| [32] |
TYGEL M, SCHLEICHER J, HUBRAL P. Pulse distortion in depth migration[J]. Geophysics, 1994, 59(10): 1561-1569. DOI:10.1190/1.1443545 |
| [33] |
KVHL H, SACCHI M D. Least-squares wave-equation migration for AVP/AVA inversion[J]. Geophysics, 2003, 68(1): 262-273. DOI:10.1190/1.1543212 |
| [34] |
FORGUES E, LAMBARÉ G. Parameterization study for acoustic and elastic ray+Born inversion[J]. Journal of Seismic Exploration, 1997, 6(2/3): 253-277. |
| [35] |
KOREN Z, RAVVE I. Full-azimuth subsurface angle domain wavefield decomposition and imaging Part I:Directional and reflection image gathers[J]. Geophysics, 2011, 76(1): S1-S13. |
| [36] |
AUDEBERT F, NICOLETIS L, FROIDEVAUX P. Regularization of illumination in angle domains-A key to true amplitude migration[J]. The Leading Edge, 2005, 24(6): 643-654. DOI:10.1190/1.1946222 |
| [37] |
SHUEY R T. A simplification of the Zoeppritz equations[J]. Geophysics, 1985, 50(4): 609-614. DOI:10.1190/1.1441936 |
| [38] |
ROUSSEAU V, NICOLETIS L, SVAY-LUCAS J, et al. 3D true amplitude migration by regularisation in angle domain[J]. Expanded Abstracts of 62nd EAGE Conference & Exhibition, 2000. DOI:10.4049/jimmunol.181.9.6672 |
| [39] |
BERTEUSSEN K A, URSIN B. Approximate computation of the acoustic impedance from seismic data[J]. Geophysics, 1983, 48(10): 1351-1358. DOI:10.1190/1.1441415 |
| [40] |
KIYASHCHENKO D, PLESSIX R E, KASHTAN B, et al. A modified imaging principle for true-amplitude wave-equation migration[J]. Geophysical Journal International, 2007, 168(3): 1093-1104. DOI:10.1111/gji.2007.168.issue-3 |
| [41] |
SACCHI M D. Reweighting strategies in seismic deconvolution[J]. Geophysical Journal International, 1997, 129(3): 651-656. DOI:10.1111/gji.1997.129.issue-3 |



