精细的油藏描述首先需要信噪比较高的地震数据, 然后是基于此数据的地震波反演成像。“两宽一高”地震数据采集代表了当前地震数据采集技术的发展方向, 基于“两宽一高”地震数据进行地震波反演成像实现目标油藏精细描述严重受限于地震数据的信噪比。
“两宽一高”地震数据采集为去噪提供了更好的数据基础, 把去噪方法推进到高维空间中能更好地把握数据中蕴含的信号特征, 从而去除噪声更为彻底。地震信号分析理论中, 实际观测的地震数据被视为确定性信号与各种随机噪声叠加形成的所谓随机信号。随机信号分析是基于随机信号的概率分布特征。针对离散实测数据的信号分析, 基于其统计特征, 在常见的一维随机信号的统计分析中, 通常假设随机信号是平稳的, 并满足高斯分布。考虑到地震信号是蕴含结构特征的高维信号, 结构特征的存在破坏了统计去噪方法的平稳性假设, 因此基于随机信号统计特征的去噪方法或滤波器设计要充分体现地震信号的结构特征。各向异性高斯滤波器和中值滤波器设计, 包括各向异性扩散方程滤波方法都是上述思想的具体体现。另外在贝叶斯框架下用信号模型对实测信号进行预测, 预测误差假定是高斯的(尤其假定是高斯白噪声), 信号模型是线性的, 优化求解得到最佳滤波器, 从而实现观测数据中噪声的压制, 是另一种经典的地震数据去噪思路。在“两宽一高”地震数据采集已成常规的情况下, 贝叶斯框架下的去噪方法同样亟需推进到高维空间中。针对高维数据去噪, 上述两种去噪方法具有逐渐融合的发展趋势, 本文重点分析基于随机信号理论的统计去噪思想与方法。
实际观测的地震数据可视为带限子波形成的确定性信号与随机噪声叠加形成的随机信号, 当对地震数据进行统计滤波时, 滤除的随机噪声主要有服从高斯分布的高斯白噪声和服从拉普拉斯分布的脉冲噪声。针对高斯白噪声, 主要采用统计均值类滤波器。在地震数据去噪方法研究中, 关于统计均值类滤波器的研究目前主要集中在如何构建沿着信号结构方向的均值类滤波器和如何依据地震数据变化自适应地选择合适的滤波参数。LUO等[1]提出了保边平滑滤波方法, 在包含当前滤波点且方差最小的数据窗内进行均值滤波。在保边滤波的基础上, AN等[2]设计了最大一致性倾角扫描算法, 准确地拾取地层倾角信息, 沿着同相轴进行滤波。范桃园等[3]通过相干技术和图像分割技术考察了滤波点周围地震数据的结构信息, 自适应确定均值滤波器的形状。HALE[4]设计了沿着构造方向的双边滤波器, 对地震图像进行增强处理。华岗等[5]在双边滤波的基础上提出一种基于地震数据局部结构属性的三边滤波算法。BONAR等[6]将非局部均值滤波引入到时空域地震资料处理中。SHANG等[7]提出了自适应地震数据分块非局部均值算法(ABNLM), 通过估算图像噪声方差, 选择合适的滤波参数。针对脉冲噪声, 主要采用统计排序类滤波器。目前在地震数据处理中, 关于统计排序类滤波器的研究主要集中在构建沿着构造方向的中值滤波器及加权中值滤波器。LIU等[8]在多个方向上应用一维中值滤波器, 构建了自适应二维多级中值滤波器, 有效降低了地震数据中的高频随机噪声。LIU等[9]提出一维自适应非平稳时变中值滤波器, 依据地震数据改变滤波器的范围。刘洋等[10]提出了局部相关加权中值滤波技术, 通过平面波分解滤波器求出局部地层倾角, 在数据点倾角方向上应用加权中值滤波器。王伟等[11]假设地震反射同相轴具有局部线性结构, 通过结构张量构造了依据地层倾向和地层结构自适应变化滤波范围的中值滤波器。LIU[12]将三维中值滤波引入到地震数据的处理中。AL-DOSSARY等[13]基于局部噪声水平设计了自适应滤波范围的中值滤波器来压制三维地震数据中的随机噪声。寻超等[14]采用矢量中值滤波器, 通过相关分析自适应地选择最佳矢量中值滤波窗对三分量地震数据进行滤波。
“两宽一高”地震数据是一个典型的五维数据体, 我们认为该地震数据是线性和/或非线性的连续同相轴处在满足不同统计特征的随机噪声中, 形成所谓的高维随机信号, 二维以上的地震数据都可以认为是高维数据。这就是基于统计特征进行去噪时所要建立的概念信号模型。基于这样的概念信号模型构建统计滤波器时, 首先需要对数据进行加窗处理, 接着判别窗内数据中确定性信号的几何特征(主要是方向特征), 然后基于噪声的统计特征设计滤波器(原则上也应该在贝叶斯框架下设计最佳统计滤波器!), 最后采用该滤波器进行去噪处理。
本文主要讨论统计滤波器的设计与应用。统计滤波的核心思想是根据观测数据的统计特征设计合适的统计滤波器。首先讨论了地震数据中常见随机噪声的概率密度函数, 重点分析了图像处理中压制高斯白噪声的各向同性高斯滤波器及压制脉冲噪声的统计排序类滤波器。各向同性高斯滤波器主要包括均值滤波器和高斯(加权)滤波器, 统计排序类滤波器主要有中值滤波器、最大值滤波器、最小值滤波器。指出统计滤波方法是基于信号预测模型滤波方法的重要补充, 在地震数据去噪中有着不可替代的作用。由于高维地震数据中同相轴的存在破坏了统计滤波的平稳性假设, 因此, 在统计滤波的过程中为了不破坏同相轴(即地震信号)的保真性, 必须引入同相轴结构的预测算子, 把各向同性统计滤波器修改成基于同相轴结构信息的各向异性统计滤波器。然后, 具体分析了邻域滤波器、双边滤波器、非局部均值滤波器三类各向异性高斯(加权)滤波器的设计思想, 并在非局部均值滤波算法的基础上, 设计了自适应变化搜索窗的非局部均值滤波算法, 该方法通过局部数据窗的相关来考察地震数据中的结构特征, 依据地震数据变化自适应地改变非局部均值滤波算法中的搜索窗。最后, 用合成地震数据验证了所提方法的有效性。
1 地震数据统计滤波器的基本思想 1.1 实测地震数据中常见的随机噪声地震信号处理主要包括两方面的核心内容:信号建模和在贝叶斯估计理论下对信号模型中所含参数的最佳估计。具体的信号分析或处理工作就是对上述两种内容的具体应用, 譬如去噪、插值、信号恢复等。比较而言, 信号建模更为基础, 在希尔伯特空间中构建一组(或多组)基函数形成子空间, 在子空间中对信号进行基函数线性组合的表达是信号建模的最基本方法或最常用方法。但是实测数据通常都是随机的, 针对随机数据(或称随机信号)用概率统计的方法进行统计建模, 并基于此进行信号分析也是非常普遍的做法。
首先建立如下的概念模型, 认为实际测量的地震数据是确定性信号与满足各种概率分布的随机噪声的叠加, 即:
| $\mathit{\boldsymbol{u}}(x, y, t) = \mathit{\boldsymbol{s}}(x, y, t) + \mathit{\boldsymbol{\eta }}(x, y, t) $ | (1) |
式中:(x, y, t)表示地震数据的空间时间坐标; u(x, y, t)表示实际测量的地震数据; s(x, y, t)表示对应的确定性信号(在贝叶斯反演框架下, 要预测的信号也是随机的!); η(x, y, t)是满足某种概率分布的加性随机噪声, 并假定各坐标点处的噪声分量为独立同分布的随机变量且与该点处的信号s(x, y, t)无关。在实际地震信号的统计处理中, (1)式的信号模型还可以表达在常见的五维空间(譬如u(mx, my, hx, hy, t), 其中mx, my为中心点坐标, hx, hy为偏移距坐标)中, 在更高维的空间中进行统计信号分析, 统计特征会更符合既定的假设, 滤波效果会更好。(1)式定义的信号模型的应用非常普遍, 当前绝大部分地震信号处理方法的构建都从此概念模型出发, 其核心工作就是实现对信号s(x, y, t)的最佳预测或最佳(特征)表达, 从而达到最佳去噪、插值、压缩等目的。
从统计意义下建立一个模型实现对信号的预测, 就是建立(1)式中噪声满足的概率分布模型, 而联合概率密度函数是刻画随机信号特征的最基本形式。在地震勘探中, 最基本的随机噪声类型主要有:满足高斯分布的高斯白噪声、满足拉普拉斯分布的脉冲噪声以及满足均匀分布的随机噪声。满足均匀分布的随机噪声具有重要的数学意义, 但物理世界中应该很少有如此类型的噪声, 尤其在勘探地震的实际数据中。
高斯白噪声满足的概率密度函数为:
| $p[\mathit{\boldsymbol{\eta }}(x, y, t)] = \frac{1}{{\sqrt {2\pi } \sigma }}{{\rm{e}}^{ - \frac{{{{[{\boldsymbol{u}}(x, y, t) - {\boldsymbol{s}}(x, y, y, t)]}^2}}}{{2{\sigma ^2}}}}} $ | (2) |
式中:σ2为η(x, y, t)的方差。实际地震数据包含的噪声往往并非高斯白噪声, 更多的是一般高斯噪声, 甚至是高斯有色噪声, 设计统计滤波器时这是非常重要的考虑因素。
脉冲噪声(或称椒盐噪声)的概率密度函数为:
| $p[\mathit{\boldsymbol{\eta }}(x, y, t)] = \left\{ {\begin{array}{*{20}{l}} {{P_a}}&{\mathit{\boldsymbol{\eta }}(x, y, t) = a}\\ {{P_b}}&{\mathit{\boldsymbol{\eta }}(x, y, t) = b}\\ {1 - {P_a} - {P_b}}&{{\rm{其他}}} \end{array}} \right. $ | (3) |
若Pa或Pb为零, 则脉冲噪声称为单极脉冲噪声; 若Pa和Pb都不为零, 且近似相等时, 则脉冲噪声类似于在图像上随机分布的胡椒和盐粉微粒, 称为双极脉冲噪声, 也称为椒盐噪声[15]。此类噪声在实际地震数据中经常出现:譬如未知源的野值, 同时源激发数据按主炮伪解码后副炮信号表现为脉冲噪声等。
均匀分布的随机噪声满足的概率密度函数为:
| $p[\mathit{\boldsymbol{\eta }}(x, y, t)] = \left\{ {\begin{array}{*{20}{l}} c&{\mathit{\boldsymbol{\eta }}(x, y, t) \in \Omega }\\ 0&{{\rm{其他}}} \end{array}} \right. $ | (4) |
式中:Ω代表随机噪声η(x, y, t)的取值范围。服从均匀分布的随机噪声在进行理论(数值)分析时非常有用。
另外, 基于随机噪声的概率分布特征进行噪声η(x, y, t)的压制时, 对信号s(x, y, t)是有假定条件的。即假设信号是局部缓变的, 最好是不变的, 设计任何统计滤波器时必须充分注意这个假设条件。
1.2 基于高斯分布的随机噪声压制的滤波器设计思想 1.2.1 均值滤波器的设计思想在局部信号缓变、高斯白噪声的假设下, 设ũ(x, y, t)是以(x, y, t)为中心点的局部邻域Sxyt内实测(随机)数据{u(xi, yj, tk)|(xi, yj, tk)∈Sxyt}的统计期望值(E), 在某种程度上, ũ(x, y, t)是对其中蕴含的确定性信号s(x, y, t)的估计结果。一般地, 可将上述估计问题定义为均方误差最小意义下的最优化问题:
| $\begin{array}{l} \mathit{\boldsymbol{\tilde u}}(x, y, t) = {\min\limits_{\left( {{x_i}, {y_j}, {t_k}} \right) \in {S_{xyt}}}}E\left\{ {\left[ {\mathit{\boldsymbol{u}}\left( {{x_i}, {y_j}, {t_k}} \right)} \right.} \right. - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{\widetilde u}}(x, y, t){]^2}\} \end{array} $ | (5) |
很显然, 该问题的解为:
| $\mathit{\boldsymbol{\widetilde u}}(x, y, t) = \mathop E\limits_{\left( {{x_i}, {y_j}, {t_k}} \right) \in {S_{xyt}}} \left[ {\mathit{\boldsymbol{u}}\left( {{x_i}, {y_j}, {t_k}} \right)} \right] $ | (6) |
由于实际地表观测的地震信号都是离散的, 在离散情形下, 最简单的估计方程为:
| $\mathit{\boldsymbol{\tilde u}}(x, y, t) = \frac{1}{{{N_x}{N_y}{N_t}}}\sum\limits_{\left( {{x_i}, {y_j}, {t_k}} \right) \in {S_{xyt}}} \mathit{\boldsymbol{u}} \left( {{x_i}, {y_j}, {t_k}} \right) $ | (7) |
式中:Nx, Ny, Nt分别为定义的邻域Sxyt内x, y, t各方向离散点数。这意味着在均方误差最小意义下确定性信号s(x, y, t)的估计值ũ(x, y, t)是NxNyNt个观测数据的算术平均值。(7)式定义了统计均值滤波器, 对于高斯白噪声, 平均值即为极大似然估计。此外(7)式还可以进一步扩展到五维数据空间中。针对加性噪声的数学模型, LEE[16]和YAROSLAVSKY[17]给出了统计均值滤波器的解释:假设加性噪声η(x, y, t)服从零均值和方差为σ2的高斯分布, 概率论中的方差定律保证, 通过(7)式取NxNyNt个数据的算术平均值时, 加性噪声η(x, y, t)的方差缩小到原方差的1/(NxNyNt), 这是在高斯白噪声情况下利用(7)式去噪的统计学理论基础。在共反射面元(CRS)叠加、超道集叠加中同样应用了(7)式的思想; 高密度地震采集及成像叠加也隐含地应用了(7)式表达的观点。需要指出的是, 应用(7)式的前提条件是假定噪声为零均值的高斯白噪声, 否则噪声压制效果会不理想。
1.2.2 线性高斯加权滤波器的设计思想理论上, 实测(随机)数据u(x, y, t)的统计期望值的计算式为:
| $\mathit{\boldsymbol{\widetilde u}}(x, y, t) = \int_{{S_{xyt}}} \mathit{\boldsymbol{u}} (x, y, t)p[\mathit{\boldsymbol{\eta }}(x, y, t)]{\rm{d}}(x, y, t) $ | (8) |
很显然, (7)式是假定(8)式中的概率密度函数为均匀分布的概率密度函数, 然而实际物理数据不可能满足此条件。大数定律指出, 当随机试验次数足够多时任意随机变量的概率分布都可以用高斯分布很好地逼近, (7)式定义的均值滤波器是为了计算简单而引入的一种对噪声分布的简化处理。很明显, 均值滤波器的问题是估计值ũ(x, y, t)的方差过大, 即对信号的平滑过于严重, 在图像处理中, 均值滤波在平滑噪声的同时, 降低了图像的尖锐变化, 造成了图像边缘的模糊。
当概率密度函数为高斯函数时, (8)式称为(各向同性)高斯(平滑)加权滤波器。针对实测的离散随机数据, (8)式可改写为:
| $\begin{array}{l} \mathit{\boldsymbol{\widetilde u}}(x, y, t) = \\ \frac{{\sum\limits_{i = - a}^a {\sum\limits_{j = - b}^b {\sum\limits_{k = - c}^c {\boldsymbol{w}} } } (i, j, k)\mathit{\boldsymbol{u}}(x + i, y + j, t + k)}}{{\sum\limits_{i = - a}^a {\sum\limits_{j = - b}^b {\sum\limits_{k = - c}^c {\boldsymbol{w}} } } (i, j, k)}} \end{array} $ | (9) |
(9) 式含义为:在给定的空间加权模板上, 信号(或图像)中的每一个离散点(x, y, t)的滤波结果为空间加权模板与以该离散点为中心的模板所覆盖区域内的观测值的加权平均。式中:w(i, j, k)为定义的空间加权模板, 其大小为(2a+1)×(2b+1)×(2c+1), 当w(i, j, k)中所有系数都相等时, (9)式就退化成(7)式。
一般地, 设计线性高斯加权滤波器时, 理论上应该用高斯概率密度函数来定义加权函数w(i, j, k), 即:
| ${p_{{\rm{Ga}}}}(\mathit{\boldsymbol{\eta }}(x, y, t), \mathit{\boldsymbol{\mu }}, \sigma ) = C \cdot {{\rm{e}}^{ - \frac{{{{[\mathit{\boldsymbol{\eta }}(x, y, y, t) - \mathit{\boldsymbol{\mu }}]}^2}}}{{2{\sigma ^2}}}}} $ | (10) |
式中:μ为期望, 被认为等于0;σ2为方差, 其大小由噪声水平决定; C为常数。由于(10)式定义的概率密度函数是钟形函数, 其积分总和等于1, 在离散情形下, (9)式中的加权系数w(i, j, k)可以定义为:
| $\mathit{\boldsymbol{w}}(i, j, k) = {{\rm{e}}^{ - \frac{{{{(i - a - 1)}^2} + {{(j - b - 1)}^2} + {{(k - c - 1)}^2}}}{{2{h^2}}}}} $ | (11) |
很显然, 加权系数w(i, j, k)是“钟形”的, h控制它的“紧度”。当h趋于0时, w(i, j, k)接近于脉冲函数, 高斯加权模板w(i, j, k)的中心点系数趋于1, 其它点趋于0, 对当前点无滤波作用; h越大, 线性高斯加权滤波器对信号(图像)的平滑作用越明显。相比于(7)式定义的均值滤波器, (9)式定义的线性高斯加权滤波器考虑了滤波模板内不同数据点的加权作用。一般地, 应按照偏离滤波模板中心点的距离在方差的控制下决定加权系数, 更本质地, 还应该按照信号s(x, y, t)的变化特征来构造更复杂的加权函数, 高维数据空间中各向异性高斯加权滤波器据此产生。这是当前统计去噪领域中重要的研究内容, 也是本文的核心关注点。
在高斯白噪声的假设下, 线性高斯加权滤波器较均值滤波器效果更好, 这是统计滤波的理论要求, (8)式清楚地说明了这一点。实际计算中的问题是很难得到噪声的实际概率密度函数, (10)式实际上是人为给出的, (11)式定义的加权函数是在(10)式的启发下给出的。针对实测随机数据的统计去噪, 本质上需要确定噪声所满足的概率密度函数, 然后通过(5)式定义的均方误差最小的逼近问题来估计概率密度函数中的系数, 最后利用估计的最佳滤波器进行加权滤波处理, 这才是理论上完善的统计滤波方法, 但是数值计算不易实现。
1.3 基于拉普拉斯分布的随机噪声压制的滤波器设计思想在统计滤波器中, 除了压制高斯白噪声的均值滤波器和线性高斯加权滤波器, 针对服从拉普拉斯分布的脉冲噪声, 主要采用统计排序类滤波器, 譬如中值滤波器以及它的变种(最大值滤波器及最小值滤波器)。
拉普拉斯分布的基本形式为:
| ${p_{{\rm{La}}}}[\mathit{\boldsymbol{\eta }}(x, y, t), \alpha , \beta ] = \frac{1}{{2\beta }}{{\rm{e}}^{ - \frac{{|\mathit{\boldsymbol{\eta }}(x, y, t) - \alpha |}}{\beta }}} $ | (12) |
式中:α和β分别为拉普拉斯分布的位置参数和尺度参数。根据拉普拉斯分布可以从估计理论的角度来说明统计中值滤波器的设计思想。
假设局部信号缓变, 设um(x, y, t)是以(x, y, t)为中心点的局部邻域Sxyt内实测(随机)数据{u(xi, yj, tk)|(xi, yj, tk)∈Sxyt}的中位数, 同样地, 在某种程度上, 它是对其中蕴含的确定性信号s(x, y, t)的估计结果。在离散数据情形下, 根据噪声满足拉普拉斯分布的假设, 可将上述估计问题表示为绝对值误差最小意义下的最优化问题:
| $\begin{array}{l} {\mathit{\boldsymbol{u}}_{\rm{m}}}(x, y, t) = {\min\limits_{\left( {{x_i}, {y_j}, {t_k}} \right) \in {S_{xyt}}}}J\left( {{\mathit{\boldsymbol{u}}_{\rm{m}}}} \right) = \\ \min \sum\limits_{_{\left( {{x_i}, {y_j}, {t_k}} \right) \in {S_{xyt}}}} {\left| {{\mathit{\boldsymbol{u}}_{\rm{m}}}(x, y, t) - \mathit{\boldsymbol{u}}\left( {{x_i}, {y_j}, {t_k}} \right)} \right|} \end{array} $ | (13) |
求解上式, 有:
| $\frac{{\partial J}}{{\partial {\mathit{\boldsymbol{u}}_{\rm{m}}}(x, y, t)}} = 0 $ | (14) |
即:
| $\begin{array}{l} \frac{{\partial J}}{{\partial {\mathit{\boldsymbol{u}}_{\rm{m}}}(x, y, t)}} = \frac{\partial }{{\partial {\mathit{\boldsymbol{u}}_{\rm{m}}}(x, y, t)}} \cdot \\ \sum\limits_{\left( {{x_i}, {y_j}, {t_k}} \right) \in {S_{xyt}}} {\sqrt {{{\left[ {{\mathit{\boldsymbol{u}}_{\rm{m}}}(x, y, t) - \mathit{\boldsymbol{u}}\left( {{x_i}, {y_j}, {t_k}} \right)} \right]}^2}} } = \\ \sum\limits_{\left( {{x_i}, {y_j}, {t_k}} \right) \in {S_{xyt}}} {\frac{{{\mathit{\boldsymbol{u}}_{\rm{m}}}(x, y, t) - \mathit{\boldsymbol{u}}\left( {{x_i}, {y_j}, {t_k}} \right)}}{{\left| {{\mathit{\boldsymbol{u}}_{\rm{m}}}(x, y, t) - \mathit{\boldsymbol{u}}\left( {{x_i}, {y_j}, {t_k}} \right)} \right|}}} = \\ \sum\limits_{\left( {{x_i}, {y_j}, {t_k}} \right) \in {S_{xyt}}} {{\mathop{\rm sign}\nolimits} } \left[ {{\mathit{\boldsymbol{u}}_{\rm{m}}}(x, y, t) - \mathit{\boldsymbol{u}}\left( {{x_i}, {y_j}, {t_k}} \right)} \right] = 0 \end{array} $ | (15) |
式中:sign为符号函数。当um(x, y, t)>u(xi, yj, tk)时, sign为正; 当um(x, y, t) < u(xi, yj, tk)时, sign为负; 当um(x, y, t)=u(xi, yj, tk)时, sign为零。很显然, 从统计意义上讲, 在选择um(x, y, t)时, 应在N=NxNyNt个数据中选择数值居中的值, 即中值滤波器可表示如下:
| ${{\mathit{\boldsymbol{u}}}_{\rm{m}}}(x,y,t) = \mathop {{\rm{median}}}\limits_{_{\left( {{x_i},{y_j},{t_k}} \right) \in {S_{xyt}}}} \left[ {{\mathit{\boldsymbol{u}}}\left( {{x_i},{y_j},{t_k}} \right)} \right] $ | (16) |
其含义为在一个以(x, y, t)为中心的邻域Sxyt中取N=NxNyNt个数据的中位数来替代点(x, y, t)的值, 作为该点的滤波结果。很明显, 窗口Sxyt中N=NxNyNt个数据的中位数作为滤波结果并不代表这是最佳的滤波结果, 是否最佳取决于噪声真实的概率密度函数。然而实际上很难知道此概率密度函数, 根据经验, 可以取中值的百分数作为滤波结果, 可能会得到更好的滤波结果, 不同的百分比选择可以构建不同的变种中值滤波器, 譬如最大值滤波器、最小值滤波器等。
很明显, 中值滤波是一种非线性滤波, 在平稳信号及加性高斯白噪声的情况下, 此时观测值的分布为正态分布, 观测值的中位数与平均值一致, 可以代表对一组观测值中信号的最佳估计。在这种理论假设下, 中值滤波可以压制高斯白噪声, 但是, 这种假设太苛刻, 实际上还是尽量不要寄希望于用这样的方法压制高斯白噪声。当噪声的概率分布符合脉冲分布时, 观测数据中存在少数特别大和/或特别小的观测值, 中位数可以不受它们的影响, 能得到更好的估计结果um(x, y, t), 因此滤除椒盐噪声用中值滤波器及其相应的变种滤波器是比较好的选择。
相对于线性高斯加权滤波器, 中值滤波器及其相应的变种滤波器对信号突变的保持效果更好, 对信号的光滑作用小。但是, 即便如此, 此类统计排序滤波器还是假定实测数据中蕴含的信号尽可能平稳, 否则对信号幅值的改变也是不可接受的。地震数据的特征是反映各种波现象的同相轴分布在满足不同概率分布假设的随机噪声中, 因此不能认为实测数据中的信号是满足平稳性假设的, 尤其在小窗口内更是如此。在高维数据空间中, 首先预测高维地震数据蕴含的结构信息, 然后沿着信号的结构方向设计合理的中值滤波器进行滤波是合理的逻辑选择。
2 高维数据空间中高斯加权滤波器设计思想前已述及, 无论是统计均值滤波器、线性高斯加权滤波器还是中值滤波器的理论设计中, 都假设实测随机数据中蕴含的信号是平稳的、变化缓慢的, 最好是不变的。实际上信号的变化可能相当剧烈, 这就会导致滤波后的信号受到伤害, 统计均值滤波器、线性高斯加权滤波器会对信号进行光滑化处理, 中值滤波器会改变信号的幅值。
地震数据一定是高维的, 尤其在“两宽一高”地震勘探中, 地震去噪一定要在高维空间中进行。高维空间中的地震信号有显著的结构特征, 沿着信号的结构方向设计统计滤波器, 更容易满足统计滤波器要求信号必须是平稳变化的假设, 各向异性高斯加权滤波器和自适应信号结构特征的中值滤波器就是基于这样的想法提出的。
在前述统计滤波器设计思想的基础上, 高维数据空间中自适应数据结构特征的滤波器设计的重点是如何检测出随机数据中蕴含的信号结构特征, 目前在地震数据中常用的测量结构特征的方法主要包括:①基于空间数据相关的倾角扫描方法[2-3, 10, 14, 18]; ②结构张量方法[5, 11, 19-21]; ③局部平面波分解[10, 22-25]。第一种方法的抗噪性强, 测量结果比较稳健, 相关方法选择不好时精度较低; 第二种方法精度高、局部性好, 但不稳健; 第三种方法最好, 采用局部平面波匹配的方法, 稳健性和计算效率都有保证。
2.1 保持信号结构的非线性高斯加权滤波器通过对数据的加权平均来压制随机噪声是一种重要的去噪方法, 但其假设是数据中蕴含的信号(幅值)是缓变的, 否则一般的线性高斯加权类滤波器就会对信号进行较为严重的平滑处理。因此, 在高维数据空间中, 设计保持信号结构的高斯加权滤波器变得非常必要, 其基本思想是自适应信号幅值的变化来调整高斯加权滤波器, 而不是仅仅按前述的“距离”关系定义高斯加权滤波系数, 更进一步地, 应该根据高维信号(图像)中蕴含的结构模式来设计加权滤波器, 当然, 中值滤波器也应该根据高维信号(图像)中蕴含的结构模式合理设计。
2.1.1 邻域滤波器邻域滤波器[16-17]的设计思想是通过计算邻域内各点数据幅值(或图像灰度值)与滤波中心点数据幅值的相似程度确定滤波模板系数。
针对高维数据空间中的滤波中心点x(x=(x, y, t)), 其空间邻域定义为:
| $\mathit{\Omega} = \{ \mathit{\boldsymbol{y}} \in \mathit{\Omega} ||\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{y}}||< d\} $ | (17) |
式中:y为邻域内任意一点; d为邻域半径。在(17)式定义的邻域内考虑离散信号在幅值上的相似性, 设计出如下邻域滤波器:
| $\begin{array}{l} {u_{{\rm{NF}}}}(\mathit{\boldsymbol{x}}) = \frac{1}{{C(\mathit{\boldsymbol{x}})}}\sum\limits_{y \in \mathit{\Omega} } {{w_{\rm{r}}}} (\mathit{\boldsymbol{y}})u(\mathit{\boldsymbol{y}})\\ {w_{\rm{r}}}(\mathit{\boldsymbol{y}}) = {{\rm{e}}^{ - \frac{{|u(x) - u(y){|^2}}}{{{h^2}}}}}\\ C(\mathit{\boldsymbol{x}}) = \sum\limits_{y \in \mathit{\Omega} } {{w_{\rm{r}}}} (\mathit{\boldsymbol{y}}) \end{array} $ | (18) |
式中:uNF(x)为点x处的邻域滤波结果; wr(y)为依据幅值相似性定义的高斯加权系数; C(x)为归一化参数; h为滤波参数; u(y)为邻域内任一点y的含噪声数据。显然, 邻域滤波器不仅考虑了空间上的相邻关系‖x-y‖ < d, 也依据像素点的幅值相似性定义了高斯加权系数wr(y)。在线性高斯加权滤波器的设计中仅仅考虑了离散信号在空间距离上的相邻关系, 却没有考虑幅值上的相似性, 所设计的滤波器是不合理的。
参数h依据幅值相似性决定高斯加权的权重大小, 在当前滤波点的邻域内, 邻域滤波器的加权系数根据像素点幅值的相似性来决定, 对于幅值差异较小的点给予较大的权重, 对于幅值差异较大的点给予较小的权重, 从而自适应数据幅值的变化来调整加权系数, 降低了对信号的光滑化程度, 能更好地保持信号的结构特征。
2.1.2 双边滤波器事实上, 任何空间相邻的物理信号大多都有更紧密的关系, 即幅值上具有相似性, 在邻域滤波器的基础上, TOMASI等[26]于1998年提出了双边滤波算法, 同时考虑了邻域内任一点与滤波中心点之间幅值的相似程度和二者的距离关系来定义高斯加权系数。双边滤波器的定义如下:
| $\begin{array}{l} {u_{{\rm{BF}}}}(\mathit{\boldsymbol{x}}) = \frac{1}{{C(\mathit{\boldsymbol{x}})}}\sum\limits_{y \in \Omega } {{w_{\rm{d}}}} (\mathit{\boldsymbol{y}}){w_{\rm{r}}}(\mathit{\boldsymbol{y}})u(\mathit{\boldsymbol{y}})\\ {w_{\rm{d}}}(\mathit{\boldsymbol{y}}) = {{\rm{e}}^{ - \frac{{|x - y{|^2}}}{{{\rho ^2}}}}}\\ {w_{\rm{r}}}(\mathit{\boldsymbol{y}}) = {{\rm{e}}^{ - \frac{{|u(x) - u(y){|^2}}}{{{h^2}}}}}\\ C(\mathit{\boldsymbol{x}}) = \sum\limits_{y \in \Omega } {{w_{\rm{d}}}} (\mathit{\boldsymbol{y}}){w_{\rm{r}}}(\mathit{\boldsymbol{y}}) \end{array} $ | (19) |
式中:uBF(x)为点x处的双边滤波结果; wd(y)为依据邻域Ω内点y与滤波中心点x之间的距离定义的高斯加权系数; wr(y)为依据幅值相似性定义的高斯加权系数; ρ为空间域滤波参数; h为与幅值有关的滤波参数; C(x)为归一化参数。
从(19)式可以看出, 双边滤波的加权系数同时取决于空间域滤波参数ρ和幅值相似参数h。邻域滤波器和双边滤波器在灰度域内都进行高斯滤波, 不同的是, 对于邻域滤波器, 在邻域内的所有像素点空间加权系数都为1, 即空间域进行均值滤波, 对于双边滤波器, 靠近滤波中心点的像素点空间加权系数wd(y)大, 即在空间域进行高斯滤波, 因此相较邻域滤波, 双边滤波器具有更好的保持边缘特征(或结构特征)的能力。
2.1.3 非局部均值滤波器无论是邻域滤波器或是双边滤波器的设计都仅仅是在一个邻域内基于单个像素点距离和/或幅值相似性进行的。当前信号分析的原则性思想是利用更高维空间的数据中蕴含的信号的结构信息对信号进行更彻底的分析, 即使在基于高维数据定义的局部邻域内, 基于单个像素点相似性的滤波器也难以准确地感知到高维信号的结构(或纹理)特征, 有必要基于单个像素点的局部邻域的相似性设计加权滤波器。
依据上述思想, BUADES等[27]设计了一种非局部均值滤波器, 核心思想是在一个较大搜索窗I(甚至整幅图像中)对上述单个像素点x的局部邻域Ω搜索相似的局部邻域, 可认为在进行“升维”处理(我们认为这是一种升维处理), 即将I内任一点y都视为一个新的中心点, 据此定义一个新的邻域Ω′, 通过考察邻域Ω和邻域Ω′的模式相似性(用图像处理的语言, 是两个邻域的模式相似性), 定义非局部均值滤波器。
非局部均值滤波器定义为:
| $\begin{array}{l} {u_{{\rm{NLM}}}}(\mathit{\boldsymbol{x}}) = \frac{1}{{C(\mathit{\boldsymbol{x}})}}\sum\limits_I {{w_{\rm{p}}}} (\mathit{\boldsymbol{y}})u(\mathit{\boldsymbol{y}})\\ {w_{\rm{p}}}\left( \mathit{\boldsymbol{y}} \right) = {{\rm{e}}^{ - \frac{{Z\left( {{{\left| {{u_\mathit{\Omega} }\left( \mathit{\boldsymbol{x}} \right) - {u_{\mathit{\Omega} '}}\left( \mathit{\boldsymbol{y}} \right)} \right|}^2}} \right)}}{{{h^2}}}}}\\ C(\mathit{\boldsymbol{x}}) = \sum\limits_I {{w_p}} (\mathit{\boldsymbol{y}}) \end{array} $ | (20) |
式中:uNLM(x)为点x处的非局部均值滤波结果; wp(y)为依据邻域Ω和邻域Ω′的模式相似性定义的加权系数; Z(|uΩ(x)-uΩ′(y)|2)是模式相似性度量函数; h为滤波参数; C(x)为归一化参数。
度量两个邻域内信号(图像)结构模式相似性的方法有很多, 直接对信号结构模式进行检测就是合乎逻辑的方法, 譬如前述的局部倾角扫描法、结构张量方法和平面波分解方法。当然也可以根据邻域Ω和邻域Ω′内信号(图像)幅值差的某种范数来判断其中包含的信号(图像)模式是否一致, 并根据一致性的定量评判结果来设计非局部均值滤波器。
| $\begin{array}{l} Z\left( {{{\left| {{u_\mathit{\Omega} }(\mathit{\boldsymbol{x}}) - {u_{{\mathit{\Omega} ^\prime }}}(\mathit{\boldsymbol{y}})} \right|}^2}} \right) = \\ \sum\limits_{x + s \in \mathit{\Omega} :y + s \in {\mathit{\Omega} ^\prime }} {{G_\sigma }} {\left| {{u_\mathit{\Omega} }(\mathit{\boldsymbol{x}} + \mathit{\boldsymbol{s}}) - {u_{{\mathit{\Omega} ^\prime }}}(\mathit{\boldsymbol{y}} + \mathit{\boldsymbol{s}})} \right|^2} \end{array} $ | (21) |
(21) 式再次引入方差为σ2的高斯函数Gσ加权来考察两个邻域中模式的相似度, 这样要优于不考虑高斯加权。
相比于邻域滤波器和双边滤波器, 非局部均值滤波器以邻域Ω和邻域Ω′中的模式相似性替代用孤立的像素点来考虑像素点之间的相似性, 具有较强的抗噪能力, 可以更加准确地检测出信号的结构信息, 能够更好地实现保持信号结构特征的去噪。
2.2 高维数据中信号结构导引滤波器设计的进一步评述针对高维数据空间中的概念信号模型, u(x, y, t)=s(x, y, t)+η(x, y, t), 滤除噪声的基本思想是设计最佳的信号预测器压制噪声或者设计最佳的噪声统计预测模型从而压制噪声。前者是选择合适的基函数族(或基函数字典)进行线性组合并在贝叶斯估计理论下得到最佳的信号预测器。后者是前面讨论的在信号的结构导引下设计高斯加权滤波器。实际上, 在线性(此处线性的含义是:信号可线性预测或信号线性变化或信号平缓变化)最小二乘(隐含地指噪声是高斯分布的)意义下, 二者的差异非常小。由于二者的实现方式和控制参数不同, 有必要沿着这两种方式发展高维数据空间中的滤波器, 处理“两宽一高”数据中不同类型的噪声, 尤其是针对偏离高斯分布的噪声两种方法都有各自广阔的发展空间。
基于扩散方程进行图像(信号)的滤波也是一类压制随机噪声的方法, 扩散方程本质上也是一种滤波器, 通过局部邻域加权平均的思想, 即可实现基于扩散方程的去噪。BUADES等[28]和SCHERZER[29]论证了邻域滤波器与Perona-Malik扩散方程是渐近一致的。利用各向异性扩散方程滤波更容易实现保持结构特征的随机噪声压制, 尤其是对于存在结构连续性的图像(信号)。各向异性高斯加权滤波器与各向异性扩散方程滤波本质上相同, 因为实现方式和参数控制上的不同使得两类方法并存。
最后, 基于拉普拉斯分布下的L1范数最小导出的中值滤波及变种方法同样需要拓展到高维数据, 也同样有必要在信号结构特征的导引下设计出更好的滤波器。
3 自适应搜索窗的非局部均值滤波器 3.1 自适应搜索窗的非局部均值滤波器原理在地震勘探中, 由于地震图像与常规图像存在明显不同, HALE[4]给出了地震图像中边缘产生的两种原因:①地震数据对应于波阻抗变化引起的反射波, 由于子波带限, 地震数据表现为波峰和波谷交替出现的正弦特征, 这与常规图像边缘存在明显差异; ②地震反射横向不连续性对应的边缘(如断层等)。对地震数据中的高斯白噪声进行滤波处理时, 直接进行均值滤波或线性高斯加权滤波在平滑噪声的同时会伤害有效地震信号。
考虑到地震数据中蕴含的结构特征, 在将上述非局部均值滤波器用于压制地震记录中的高斯白噪声时, 存在两个关键的问题:首先是如何精确地检测出地震数据中蕴含的信号的结构特征, 使得滤波器沿着同相轴方向进行滤波; 其次是滤波参数的选取, 小滤波参数不能较好地滤除噪声, 大滤波参数在滤除噪声的同时会伤害有效信号, 需要考虑如何设计合适的滤波参数, 在滤除随机噪声的同时尽可能地保护有效地震信号。
对于如何精确地检测出地震数据中蕴含的信号的结构特征这一问题, 主要有基于空间数据相关的倾角扫描方法、结构张量方法和局部平面波分解等方法。考虑到相关类方法抗噪性强, 测量结果比较稳健, 本文选择采用局部数据窗的相关算法来考察数据点之间的结构特征, 设计了自适应地震数据变化搜索窗的非局部均值滤波器, 将(20)式中的固定搜索窗I改成对于数据点u(x)自适应搜索窗Ix, 即:
| $\begin{array}{l} {u_{{\rm{AWNLM}}}}(\mathit{\boldsymbol{x}}) = \frac{1}{{C(\mathit{\boldsymbol{x}})}}\sum\limits_{{I_x}} {{w_{\rm{p}}}} (\mathit{\boldsymbol{y}})u(\mathit{\boldsymbol{y}})\\ {w_{\rm{p}}}(\mathit{\boldsymbol{y}}) = {{\rm{e}}^{ - \frac{{Z\left( {{{\left| {{u_\Omega }(\mathit{\boldsymbol{x}}) - {u_{{\Omega ^\prime }}}(\mathit{\boldsymbol{y}})} \right|}^2}} \right)}}{{{h^2}}}}}\\ C(\mathit{\boldsymbol{x}}) = \sum\limits_{{I_x}} {{w_p}} (\mathit{\boldsymbol{y}}) \end{array} $ | (22) |
式中:uAWNLM为自适应搜索窗的非局部均值滤波结果。图 1为局部窗滑动相关示意图, 在滤波点处开窗(图 1中蓝色窗), 与相邻地震道的滑动数据窗(图 1中绿色窗)进行相关计算。
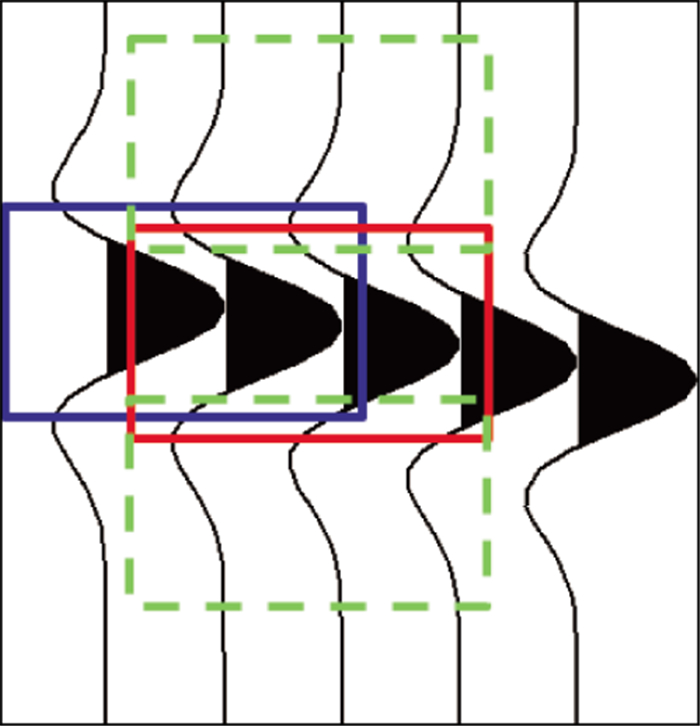
|
图 1 局部开窗滑动相关示意 |
相关系数计算公式为:
| $\begin{array}{l} r = \\ \frac{{\sum\limits_{a = - m}^m {\sum\limits_{b = - n}^n u } (x - a, t - b)u\left( {{x^\prime } - a, {t^\prime } - b} \right)}}{{\sqrt {\sum\limits_{a = - m}^m {\sum\limits_{b = - n}^n u } {{(x - a, t - b)}^2}\sum\limits_{a = - m}^m {\sum\limits_{b = - n}^n u } {{\left( {{x^\prime } - a, {t^\prime } - b} \right)}^2}} }} \end{array} $ | (23) |
式中:(x, t)表示当前滤波点位于第x道第t个采样时间; (x′, t′)表示滑动窗口的中心位于第x′道第t′个采样时间; r表示两个数据窗之间的相关系数。进行相关计算的数据窗大小为(2m+1)×(2n+1)。当相关系数最大时, 将此窗(图 1中红色窗)的中心点以及同地震道的上、下两点加到自适应搜索窗, 继续进行下一道搜索, 当最大相关系数小于阈值时, 停止修改自适应搜索窗。
在滤波点(x, t)处开窗对下一道地震数据进行相关计算, 寻找结构相似点的具体流程如表 1所示, 完成该点右边地震道相关搜索以后还需进行左边地震道的计算。
| 表 1 自适应搜索窗口算法 |
对于当前滤波点(x, t), 完成自适应搜索窗的计算后, 当搜索窗内的点数大于一定阈值时, 可以认为该滤波点周围包含较多相关信息, 计算得到的自适应搜索窗是沿着地震数据同相轴截取的数据窗, 在自适应搜索窗内对该点进行非局部均值滤波, 反之, 则认为该点无结构信息, 在该点处取大小固定的搜索窗进行非局部均值滤波。
3.2 数值算例为了测试自适应搜索窗的非局部均值滤波算法, 本文采用合成地震数据进行去噪试验(图 2)。合成地震记录的子波主频为40Hz, 时间采样间隔为2ms, 共41道, 如图 2a所示。图 2b为加入-1dB高斯白噪声的数据。图 2c为采用21×21的固定搜索窗, 7×7的邻域窗, 滤波参数h=2.5, σ为1的非局部均值滤波结果, 可以看到, 非局部均值滤波虽然可以剔除一定噪声, 但也损失了部分有效信号。图 2d为采用自适应搜索窗的非局部均值滤波结果, 在该算法(表 1)中, 局部相关的数据窗大小为11×3, 相关系数阈值设为0.35, 搜索窗内的点数阈值设为9, 固定搜索窗的大小为21×21, 邻域窗的大小为7×7, 滤波参数h=2.5, σ为1。从图 2d中可以看到采用自适应搜索窗的非局部均值滤波算法在滤除一定噪声的同时也能保护有效地震信号。取滤波参数h=5.0, 其余参数与图 2d的滤波参数相同, 可得到图 2e所示的自适应搜索窗的非局部均值滤波结果。图 2f为图 2c所示的滤波结果与合成地震数据之间的差剖面, 从中可以明显看到残留的同相轴信息。图 2g为图 2d所示的滤波结果与合成地震数据之间的差剖面, 与图 2f相比, 其中残留的同相轴信息极少。图 2h为图 2e所示的滤波结果与合成地震数据之间的差剖面。对比图 2d和图 2e可知, 随着滤波参数的增大, 自适应搜索窗的非局部均值滤波算法能在压制更多随机噪声的同时较好地保护有效地震信号。
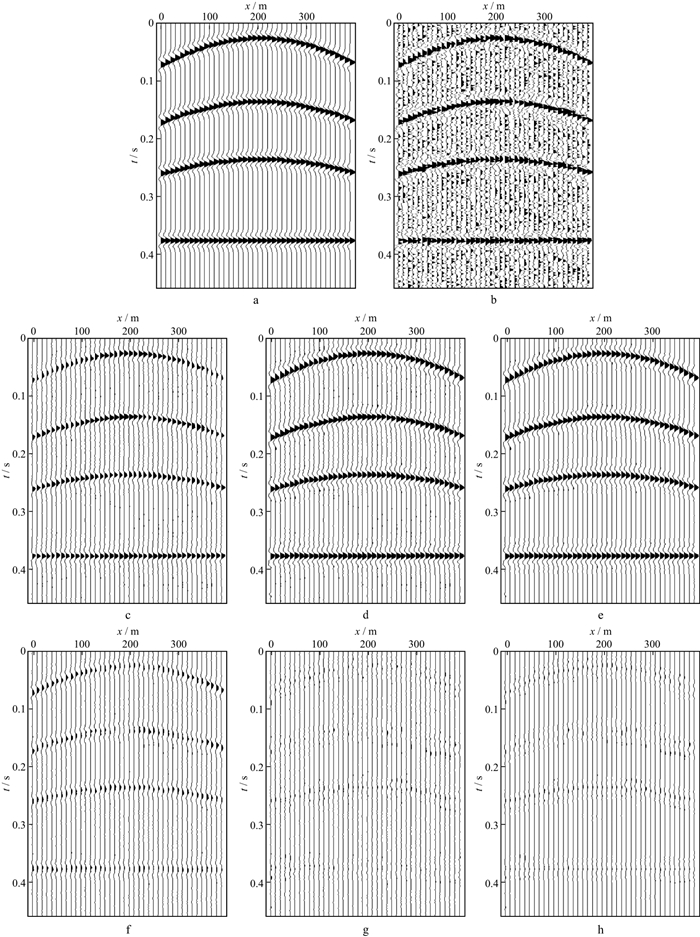
|
图 2 合成地震数据去噪效果 a原始记录; b含-1dB高斯白噪地震数据; c滤波参数h=2.5的非局部均值滤波结果; d滤波参数h=2.5的自适应搜索窗非局部均值滤波结果; e滤波参数h=5.0的自适应搜索窗非局部均值滤波结果; f, g, h分别为与c, d, e对应的滤波结果与合成地震数据之间的差剖面 |
上述数值试验结果表明, 自适应搜索窗的非局部均值滤波算法在压制随机噪声和保护有效地震信号上的表现优于固定搜索窗的非局部均值滤波算法。
4 结论与讨论“两宽一高”地震数据采集越来越普及, 但地震数据预处理和地震波反演成像的方法技术滞后于数据采集技术的发展。海量数据中蕴含的与地下地质结构和岩性参数相关的信息不能被充分提取出来, 信噪比低是关键的制约因素。与“两宽一高”地震数据采集技术一同进步的首先应该是在高维空间中在新的理论框架下提出的各种噪声压制技术, 尽可能满足后续反演成像方法对噪声的假设及对信噪比的要求。
高维地震数据去噪的核心在于对表达在不同域中的地震数据所蕴含的信号特征有透彻的理解, 并建立合适的表达、预测及描述方法。对随机信号而言, 随机信号的统计特征是设计合适的滤波器的基础。在高维地震数据的去噪过程中, 由于都需要在已知信号结构特征的基础上进行最佳滤波器的设计, 因此基于线性信号预测器与贝叶斯反演理论的最佳滤波(包括插值)方法与基于高维随机信号统计特征的滤波方法正在走向融合。
本文系统地分析了在随机噪声服从高斯分布和拉普拉斯分布下统计滤波器设计的基本思想, 并重点讨论了高维数据情形下, 保持信号结构特征的各种各向异性高斯加权滤波器的设计思想。考虑到高维地震数据的特点, 设计了自适应搜索窗的非局部均值滤波器, 并通过数值试验验证了该方法在滤除高维地震数据中高斯白噪声的有效性。针对高维地震数据中复杂的信号变化和多变的噪声类型, 该类方法还有较大的发展空间。
目前, 统计滤波器已广泛用于压制地震数据中的随机噪声, 与各种地震信号结构提取方法结合实现了沿着信号结构方向的滤波。但是, 在高维数据空间中进行各向异性统计滤波器的最佳设计目前并没有有效的方法, 也缺乏真正保持边界特征的最佳滤波方法, 缺乏自动适应随机信号统计特征变化的滤波器设计方法。笔者认为基于随机信号统计特征的高维滤波方法在压制随机噪声(包括不相干噪声)方面有明显的优点, 在“两宽一高”地震勘探中需要深入研究此类方法, 进一步提高地震数据的信噪比。
致谢: 感谢中国石油天然气股份有限公司勘探开发研究院、西北分院, 中海石油(中国)有限公司北京研究中心、湛江分公司以及中国石油化工股份有限公司石油物探技术研究院、胜利油田分公司对波现象与智能反演成像研究组(WPI)研究工作的资助与支持。| [1] |
LUO Y, MARHOON M I, DOSSARY S M, et al. Edge-preserving smoothing and its applications in seismic edge detection[J]. The Leading Edge, 2010, 21(2): 136-141. |
| [2] |
AN Y, WEI L C, YANG C C. The most homogeneous dip-scanning method using edgepreserving smoothing for seismic noise attenuation[J]. Applied Geophysics, 2006, 3(4): 210-217. DOI:10.1007/s11770-006-4003-3 |
| [3] |
范桃园, 杨长春. 自适应三维地震保边界去噪方法及应用[J]. 石油地球物理勘探, 2009, 44(5): 558-563. FAN T Y, YANG C C. 3D adaptive seismic edge-preserving smoothing and its application[J]. Oil Geophysical Prospecting, 2009, 44(5): 558-563. DOI:10.3321/j.issn:1000-7210.2009.05.007 |
| [4] |
HALE D. Structure-oriented bilateral filtering[J]. Expanded Abstracts of 81st Annual Internat SEG Mtg, 2011, 3596-3600. |
| [5] |
华岗, 刘芳, 林海, 等. 地震数据的多属性三边滤波算法[J]. 计算机辅助设计与图形学学报, 2011, 23(6): 1034-1040. HUA G, LIU F, LIN H, et al. Multi-attribute trilateral filtering algorithm for seismic data[J]. Journal of Computer-Aided Design&Computer Graphics, 2011, 23(6): 1034-1040. |
| [6] |
BONAR D, SACCHI M. Denoising seismic data using the nonlocal means algorithm[J]. Geophysics, 2012, 77(1): A5-A8. DOI:10.1190/geo2011-0235.1 |
| [7] |
SHANG S, HAN L G, LV Q T, et al. Seismic random noise suppression using an adaptive nonlocal means algorithm[J]. Applied Geophysics, 2013, 10(1): 33-40. DOI:10.1007/s11770-013-0362-8 |
| [8] |
LIU C, LIU Y, YANG B, et al. A 2D multistage median filter to reduce random seismic noise[J]. Geophysics, 2006, 71(5): V105-V110. DOI:10.1190/1.2236003 |
| [9] |
LIU Y, LIU C, WANG D. A 1D time-varying median filter for seismic random spike-like noise elimination[J]. Geophysics, 2009, 74(1): V17-V24. DOI:10.1190/1.3043446 |
| [10] |
刘洋, 王典, 刘财, 等. 局部相关加权中值滤波技术及其在叠后随机噪声衰减中的应用[J]. 地球物理学报, 2011, 54(2): 358-367. LIU Y, WANG D, LIU C, et al. Weighted median filter based on local correlation and its application to poststack random noise attenuation[J]. Chinese Journal of Geophysics, 2011, 54(2): 358-367. DOI:10.3969/j.issn.0001-5733.2011.02.012 |
| [11] |
王伟, 高静怀, 陈文超, 等. 基于结构自适应中值滤波器的随机噪声衰减方法[J]. 地球物理学报, 2012, 55(5): 1732-1741. WANG W, GAO J H, CHEN W C, et al. Random seismic noise suppression via structure-adaptive median filter[J]. Chinese Journal of Geophysics, 2012, 55(5): 1732-1741. |
| [12] |
LIU Y. Noise reduction by vector median filtering[J]. Geophysics, 2013, 78(3): V79-V86. DOI:10.1190/geo2012-0232.1 |
| [13] |
AL-DOSSARY S, ARAMCO S. Random noise cancellation in seismic data using a 3D adaptive median filter[J]. Expanded Abstracts of 84th Annual Internat SEG Mtg, 2014, 2512-2516. |
| [14] |
寻超, 汪超, 王赟. 多方向矢量中值滤波在多分量地震数据中的应用[J]. 石油物探, 2016, 55(5): 703-710. XUN C, WANG C, WANG Y. The application of multi-directional vector median filtering in multi-component seismic data[J]. Geophysical Prospecting for Petroleum, 2016, 55(5): 703-710. DOI:10.3969/j.issn.1000-1441.2016.05.009 |
| [15] |
GONZALEZ R C, WOODS R E.Digital image processing[M].4th ed.UK: Pearson, 2018: 317-398
|
| [16] |
LEE J S. Digital image smoothing and the sigma filter[J]. Computer Vision, Graphics, and Image Processing, 1983, 24(2): 255-269. DOI:10.1016/0734-189X(83)90047-6 |
| [17] |
YAROSLAVSKY L P. Digital picture processing[M]. Berlin: Springer, 1985: 166-183.
|
| [18] |
WU C L, WANG H Z. Nonlinear optimal stacking for enhancing Pre-Stack seismic data[J]. Expanded Abstracts of 80th EAGE Annual Conference, 2018, TH-C-04. |
| [19] |
WEICKERT J. Anisotropic diffusion in image processing[M]. Stuttgart, Germany: Teubner-Verlag, 1998: 55-74.
|
| [20] |
FEHMERS G C, HÖCKER C F W. Fast structural interpretation with structure-oriented filtering[J]. Geophysics, 2003, 68(4): 1286-1293. DOI:10.1190/1.1598121 |
| [21] |
BROX T, WEICKERT J, BURGETH B, et al. Nonlinear structure tensors[J]. Image and Vision Computing, 2006, 24(1): 41-55. DOI:10.1016/j.imavis.2005.09.010 |
| [22] |
CLAERBOUT J F. Earth soundings analysis:Processing versus inversion[M]. London: Blackwell Scientific Publications, 1992: 94-99.
|
| [23] |
FOMEL S. Appliations of plane-wave destruction filters[J]. Geophysics, 2002, 67(6): 1946-1960. DOI:10.1190/1.1527095 |
| [24] |
FOMEL S, Guitton A. Regularizing seismic inverse problems by model reparameterization using plane-wave construction[J]. Geophysics, 2006, 71(5): A43-A47. DOI:10.1190/1.2335609 |
| [25] |
LIU Y, FOMEL S, LIU G C. Nonlinear structure-enhancing filtering using plane-wave prediction[J]. Geophysical Prospecting, 2010, 58(3): 415-427. DOI:10.1111/(ISSN)1365-2478 |
| [26] |
TOMASI C, MANDUCHI R.Bilateral filtering for gray and color images[C]//Proceedings of the 6th International Conference on Computer Vision (ICCV 98).Bombay: Narosa Publishing House, 1998: 839-846
|
| [27] |
BUADES A, COLL B, MOREL J M.A non-local algorithm for image denoising[C]//IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2005(CVPR 05).San Diego: IEEE Comput.Soc, 2005: 60-65
|
| [28] |
BUADES A, COLL B, MOREL J M. Neighborhood filters and PDE's[J]. Numerische Mathematik, 2006, 105(1): 1-34. |
| [29] |
SCHERZER O. Handbook of mathematical methods in imaging[M]. Berlin: Springer Science&Business Media, 2010: 1159-1201.
|





