随着我国油气勘探程度的加深, 勘探区域的范围与地质构造的复杂程度愈发加大, 采集到的地震数据的规模与复杂度不断增加。复杂、大范围的勘探区域与地形、障碍物等环境因素以及仪器等经济因素一起, 加剧了地震数据的不规则性或稀疏分布, 这将不同程度地影响地震数据的后续处理效果, 因此需要对不完整采样下的缺失地震道进行插值处理, 即地震数据重建。目前地震数据重建的方法主要分为3类:基于滤波器的策略、基于波动方程算子的方法以及基于某种变换的重建技术。基于滤波器的重建技术利用褶积插值滤波器将不规则数据当做规则数据处理, 常用的方法是预测误差滤波法[1-2], 此类方法会造成较大误差, 其结果也具有不确定性。基于波动方程的插值方法主要通过正演与反演算子来迭代求解一个反问题, 如NMO、反DMO、方位角时差校正AMO等[3-4], 此类方法需要地下结构的先验信息, 计算量大, 对采样率要求较高。基于某种变换的方法通常是对地震数据进行某种变换, 然后在变换域对地震数据进行重建。主要有傅里叶变换、小波变换[5]、Randon变换[6]、curvelet变换[7]、Seislet变换、contourlet变换[8]等方法。
压缩感知理论[9-10]是一种以低于Nyquist采样率采样的理论, 其本质是当信号具有稀疏性或者在某个变换域可以稀疏表示时, 利用一个与稀疏变换基不相关的观测矩阵, 将该信号从高维映射到低维, 然后利用稀疏促进算法求解最优化问题, 实现数据的高概率重构。地震信号可以通过某种变换进行稀疏表示满足了压缩感知理论应用的条件。基于压缩感知的地震数据重建常用的变换方法主要有离散余弦变换(DCT)、傅里叶变换、小波变换、curvelet变换和学习型超完备字典等。DCT与傅里叶变换是全局变换, 无法有效识别地震信号局部时频特征; 短时傅里叶变换时频局部化能力有限, 无法满足不同频率与时间的信号分辨要求; 小波变换虽然弥补了短时傅里叶变换的缺点, 但是无法很好地描述二维信号中的线性特征; curvelet变换具有方向识别能力, 可近似最优地表示二维信号中的曲线特征, 然而其冗余度较高, 计算效率低; 学习型超完备冗余字典的变换能够很好地稀疏表示信号, 但迭代次数多, 训练时间长。相较于傅里叶变换与小波变换, contourlet变换以其方向性、局部性与各向异性, 可较好地处理信号的线性、曲线特征, 善于处理信号的奇异性, 捕捉地震记录中由直达波、反射波、绕射波等波场构成的轮廓信息, 从而能够较清晰地描述信号中因复杂构造产生的各种波场。与学习型超完备字典相比, contourlet变换运算时间短, 算法简单, 更加符合实际应用中的计算效率要求。
在基于压缩感知的地震数据重建方法中, 重建算法是重要的一环。近年来基于压缩感知的重建算法主要有3种, 分别是贪婪算法、组合算法和凸优化算法。其中贪婪算法通过迭代寻找一组与观测值匹配的最稀疏原子, 实现信号重建, 包括匹配追踪(MP)[11]和正交匹配追踪(OMP)[12-13]等。组合算法要求原始信号能够支持快速分组测试重建, 包括组测试和数据流草图[14-15], 该算法需要对观测矩阵进行进一步设计。凸优化算法是将非凸问题转化为凸问题求解, 寻找信号的逼近, 该算法的一个极为突出的优点是, 在目标函数为严格凸函数时, 用此算法求解得到的局部极大值(极小值)就是全局最大值(最小值), 并且所求结果只有一个。凸优化算法包括基追踪[16]、迭代阈值[17]、内点法和梯度投影法[18-19]。其中基追踪算法为凸优化算法中的基本算法, 由于计算量大, 基本上用于一维信号处理; 迭代阈值法运算简单, 但收敛速度慢; 内点法一般用于中小规模问题; 投影梯度算法[20-22]应用简单并且适合大规模与复数域问题, 其中SPGL1收敛速度较普通的梯度投影法快[19]。
综合以上3种重建方法, 考虑各稀疏变换与重建算法的精度及计算效率, 本文提出了一种基于压缩感知的地震数据重建方法, 该方法以contourlet变换为稀疏变换基, 以L1范数谱投影梯度法为重建算法。该方法应用于模型数据和实际地震数据的处理结果验证了其在大规模、复杂地震数据情况下的有效性。
1 方法理论基于压缩感知的L1范数谱投影梯度算法地震数据重建方法由三部分组成:压缩感知理论、contourlet变换与SPGL1算法, 其中压缩感知理论为主体, contourlet变换为压缩感知的稀疏变换阶段, SPGL1为压缩感知的重建阶段。
1.1 压缩感知理论压缩感知理论为地震数据的压缩采样提供了可能。在该理论框架下, 地震数据的采样表达式为:
| $ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{\varphi f}} $ | (1) |
式中:f∈Rn为原始地震数据; y∈Rm(
| $ \mathit{\boldsymbol{x}} = \phi \mathit{\boldsymbol{f}} $ | (2) |
式中:ϕ为稀疏变换算子; x为f的稀疏表示系数。将(1)式和(2)式结合, 那么压缩感知理论框架下的数据重建可以表述成:
| $ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{\varphi }}{\phi ^{\rm{H}}}\mathit{\boldsymbol{x}} $ | (3) |
式中:ϕH为稀疏逆变换算子。以感知矩阵A代替φϕH, 则(3)式可写为:
| $ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{Ax}} $ | (4) |
该问题的求解方法为:
| $ \mathop {\min }\limits_\mathit{\boldsymbol{x}} {\left\| \mathit{\boldsymbol{x}} \right\|_0}\;\;\;{\rm{s}}.\;{\rm{t}}.\;\;\;\mathit{\boldsymbol{y}} = \mathit{\boldsymbol{Ax}} $ | (5) |
此方法也称之为L0优化问题, 但是由于离散性与L0范数的非凸性, 它是一个NP难题。为了解决此问题, 人们用L1替代L0[23]:
| $ \mathop {\min }\limits_\mathit{\boldsymbol{x}} {\left\| \mathit{\boldsymbol{x}} \right\|_1}\;\;\;{\rm{s}}.\;{\rm{t}}.\;\;\;\mathit{\boldsymbol{y}} = \mathit{\boldsymbol{Ax}} $ | (6) |
在压缩感知中, 为了保证(4)式的可解性, 对矩阵A进行了限定, 即矩阵A应满足有限等距性(restricted lsometry property, RIP)[23]。矩阵A是否满足RIP, 由φ与ϕH是否相干决定, 两者不相干时, A大概率满足RIP。在地震勘探中, 常常把缺失的地震道看做0, 未缺失的地道看做1[24], 由此组成的对角矩阵被作为采样矩阵φ时, φ与ϕH不相干, 满足了矩阵A的限定条件。因此, 本文将此对角矩阵作为采样矩阵。
1.2 contourlet变换随着地震勘探的深入, 采集到的信号中包括越来越多的反射波、绕射波等轮廓信息, 但是傅里叶变换与小波变换无法稀疏表示轮廓线, 难以适应包含较多轮廓信息的复杂地震信号, 因此, DO[25]提出了contourlet变换, 这是一种二维可采集信号内在几何结构的变换, 具有灵活的方向性和各向异性。它用类似于轮廓段的基结构来逼近几何结构, 基的支撑区间是长宽比随尺度变化的“长条形”结构, 可以对分段函数实现最优近似。
在压缩感知理论下, 稀疏表示地震信号的contourlet变换步骤如下:
1) 使用拉普拉斯金字塔滤波器(LP)对地震信号进行多尺度分解, 捕获不同尺度上的边缘奇异点。每一级LP分解首先对上一级低频信息进行下采样产生本级低频信息, 然后对此低频信息进行上采样并与上一级低频信息相减得到高频信息, 最后对低频信息进行LP分解迭代即实现了多尺度分解。
2) 对由LP分解产生的高频信息使用方向滤波器组(DFB)进行方向分解, 并连接同方向的奇异点, 得到contourlet变换系数。如DO[25]提出的contourlet变换中的DFB, 将双通道梅花滤波器组与剪切算子结合, 采用简化的二叉树分解方法, 可获得较好的方向信息。
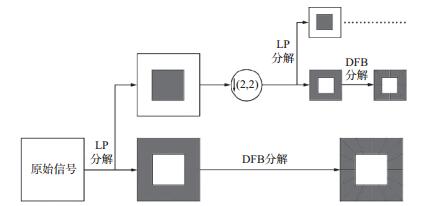
|
图 1 contourlet变换流程 |
针对凸优化问题一般具有规模大、目标函数非光滑的特点, 本文采用L1范数谱投影梯度算法(SPGL1)来解决凸问题, 得到重建的信号。
(6) 式又被称为基追踪问题(basis pursuit, BP), 其中A为m×n的矩阵, y为m列的列向量。当数据含有噪声或数据不完整时, 基追踪问题变为基追踪去噪(basis pursuit denoise, BPDN):
| $ \mathop {\min }\limits_\mathit{\boldsymbol{x}} {\left\| \mathit{\boldsymbol{x}} \right\|_1}\;\;\;{\rm{s}}.\;{\rm{t}}.\;\;\;{\left\| {\mathit{\boldsymbol{Ax}} - \mathit{\boldsymbol{y}}} \right\|_2} \le \sigma \left( {{\rm{B}}{{\rm{P}}_\sigma }} \right) $ | (7) |
式中:正参数σ为对噪声水平的估计, σ=0时为BP问题的解。
BPDN仅为L1范数正则化最小二乘问题中的一种, 它还包括Lasso问题, 其表达式如下:
| $ \mathop {\min }\limits_\mathit{\boldsymbol{x}} {\left\| {\mathit{\boldsymbol{Ax}} - \mathit{\boldsymbol{y}}} \right\|_2}\;\;{\rm{s}}.\;{\rm{t}}.\;\;\;{\left\| \mathit{\boldsymbol{x}} \right\|_1} \le \tau \left( {{\rm{L}}{{\rm{S}}_\tau }} \right) $ | (8) |
式中:τ为阈值。
BPDN常用在惩罚最小二乘问题上, 其形式是:
| $ \mathop {\min }\limits_\mathit{\boldsymbol{x}} \left\| {\mathit{\boldsymbol{Ax}} - \mathit{\boldsymbol{y}}} \right\|_2^2 + \lambda {\left\| \mathit{\boldsymbol{x}} \right\|_1}\left( {{\rm{O}}{{\rm{P}}_\lambda }} \right) $ | (9) |
其中, λ是一个与Lasso问题中的约束拉格朗日乘数和BPDN问题中的约束乘数的倒数有关的参数。参数σ, λ, τ的适当选择, 使得BPσ问题、LSτ问题、QPλ问题的解在某些情况下一致。在σ已知的情况下, λ可用同伦算法求取[19]。
因此, SPGL1算法的思想是将BPDN问题转化为一系列的Lasso子问题, 通过谱投影梯度法(SPG)求解Lasso问题, 以得到BPDN问题的解。
令xτ为LSτ问题的最优解, 对于任意τ≥0, Lasso问题的最优值为:
| $ \psi \left( \tau \right) = {\left\| {{\mathit{\boldsymbol{r}}_\tau }} \right\|_2}\;\;\;且\;\;\;{\mathit{\boldsymbol{r}}_\tau }: = \mathit{\boldsymbol{y}} - \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{x}}_\tau } $ | (10) |
Pareto曲线定义了残差r的L2范数与解x的L1范数之间的平衡, BPDN与Lasso是同一条曲线的两个不同特征, 可以用参数τ参数化Pareto曲线。对于定义域内所有的点, ψ都是连续可微的, 这样可以使用牛顿法求解(11)式:
| $ \psi \left( \tau \right) = \sigma $ | (11) |
(11) 式定义了一系列正则化参数τk→τσ, 可表示为:
| $ {\tau _{k + 1}} = {\tau _k}\;\;且\;\;\;\Delta {\tau _k}: = \left[ {\sigma - \psi \left( {{\tau _k}} \right)} \right]/\psi '\left( {{\tau _k}} \right) $ | (12) |
式中:ψ′(τk)为ψ(τk)的导数。这样Lasso问题的相关解xτσ收敛到xσ, 参数τσ使得BPDN与Lasso得到相同解。
SPGL1算法流程如下:
1) 初始化参数, 步长α0∈[αmin, αmax], 充分下降常数γ∈(0, 1), 初始迭代x0←Pτ[x], 初始残差r0←y-Ax0, 初始梯度方向g0←-ATr0, l←0, 整数线性搜索步长M≥1。
2) 计算对偶间隙δl←‖rl‖2-(yTrl-τ‖gl‖∞)/‖rl‖2, 收敛则退出, 转步骤6)。
3) 起始步长α←αl, 预备搜索迭代
4) 更新迭代
5) 返回步骤2)。
6) 输出xτ←xl, rτ←rl。
其中, 右上角标T表示矩阵的转置;
本文采用信噪比来衡量地震数据的重建效果:
| $ {R_{{\rm{SN}}}} = 10\lg \frac{{\left\| \mathit{\boldsymbol{f}} \right\|_2^2}}{{\left\| {\mathit{\boldsymbol{\hat f}} - \mathit{\boldsymbol{f}}} \right\|_2^2}} $ | (13) |
式中:f为原始地震数据;
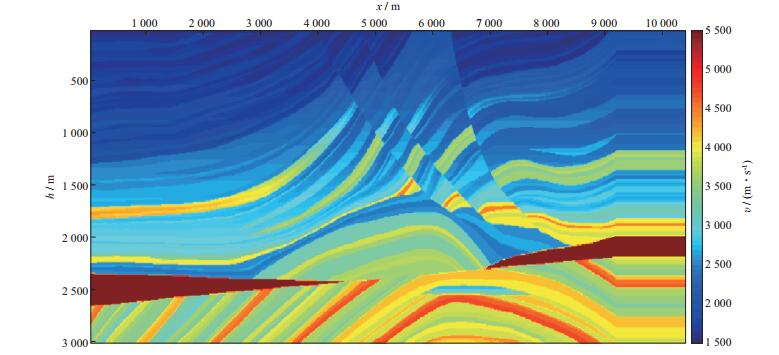
选择大规模复杂合成地震记录测试本文方法的重建效果, 速度模型(Marmousi模型)如图 2所示。
|
图 2 大规模复杂合成数据的速度模型(Marmousi模型) |
该模型包括1043×302个网格点, 空间网格间距为10m, 模型上部与2500m深度处共有4个断层, 断层的存在使得地震记录有多处绕射波, 增大了地震数据重建的难度。
在地表激发地表接收观测系统下, 以主频为20Hz的Ricker子波为震源, 在该模型地表 4000m处激发, 放置1043个检波器, 时间采样间隔为1ms, 得到原始地震记录如图 3a所示。
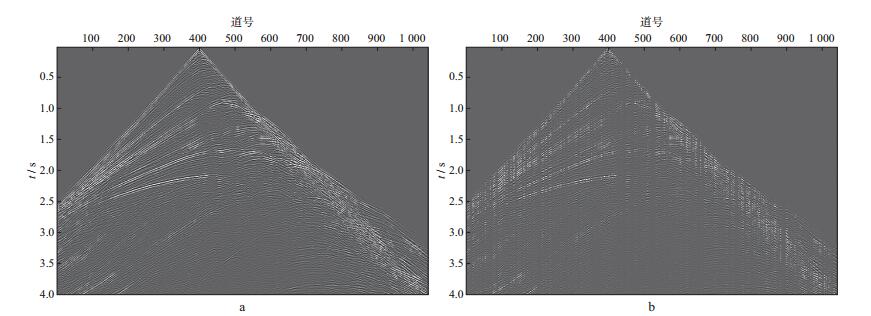
|
图 3 原始地震记录(a)与随机缺失50%的地震记录(b) |
在压缩感知理论下采用同一种重建算法, 不同的稀疏变换基对随机缺失50%的地震记录(图 3b)进行重建。图 4a至图 4c分别为以傅里叶变换、小波变换、contourlet变换为稀疏变换基, 应用SPGL1算法进行数据重建的结果, 参数σ=0.05, 最大迭代次数为30[27]。表 1对比了3种稀疏变换基采用相同重建算法的信噪比(RSN)。由图 3可以看到, 合成地震数据中含有较多直达波、反射波、绕射波等波场轮廓信息。由图 4可见, 由于傅里叶变换识别局部时频特征的能力有限, 无法有效处理地震记录中的轮廓信息, 在稀疏变换时只能勉强识别能量较强的同相轴, 无法较好识别震源处地震记录特征, 重建结果存在噪声, 能量较弱的反射波、绕射波等难以识别(图 4a中红色箭头处); 小波变换相较于傅里叶变换可以较为清晰地识别同相轴, 然而依旧无法较好地刻画各种轮廓信息, 因此重建结果仍然有噪声存在, 能量较弱的反射波、绕射波无法清晰刻画(图 4b); 而采用contourlet变换得到的重建地震记录质量好, 同相轴连贯, 反射波、绕射波均清晰可见(图 4c)。

|
图 4 不同稀疏变换基下应用SPGL1算法的重建效果 a傅里叶变换; b小波变换; c contourlet变换 |
| 表 1 3种稀疏变换基重构合成地震记录的信噪比 |
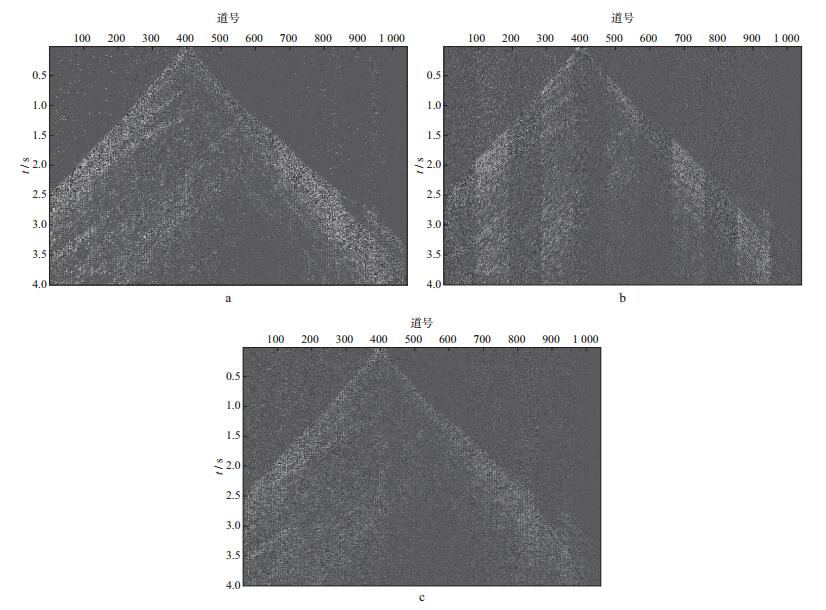
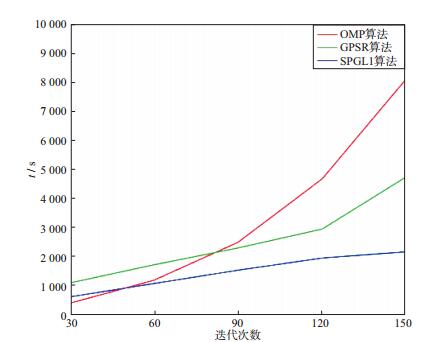
采用基于压缩感知和L1范数谱投影梯度算法重建地震数据的方法对图 3b地震数据进行重建。其中SPGL1算法参数选择为σ=0.01, 迭代次数为50次[27]。图 5对比了contourlet稀疏变换基下OMP、GPSR、SPGL1算法重建的合成地震记录。图 6为相应的残差, 表 2给出了3种重建算法重构合成地震记录的信噪比。由图 5、图 6和表 2可以看到, 3种算法均可较好地完成合成地震记录的重建, 而且差别不大。但是在相同稀疏变换基下, 采用OMP算法进行重建的50次平均CPU时间为8164s, GPSR算法为14532s, 而SPGL1算法为991s, 远远小于前两种算法重建所用的时间。图 7为CPU时间随迭代次数变化的曲线, 可见, 随着迭代次数的增加, SPGL1算法不仅用时较少, 而且整体变化不大; GPSR算法用时渐长; OMP算法随着迭代次数的增加, CPU时间大幅增加。
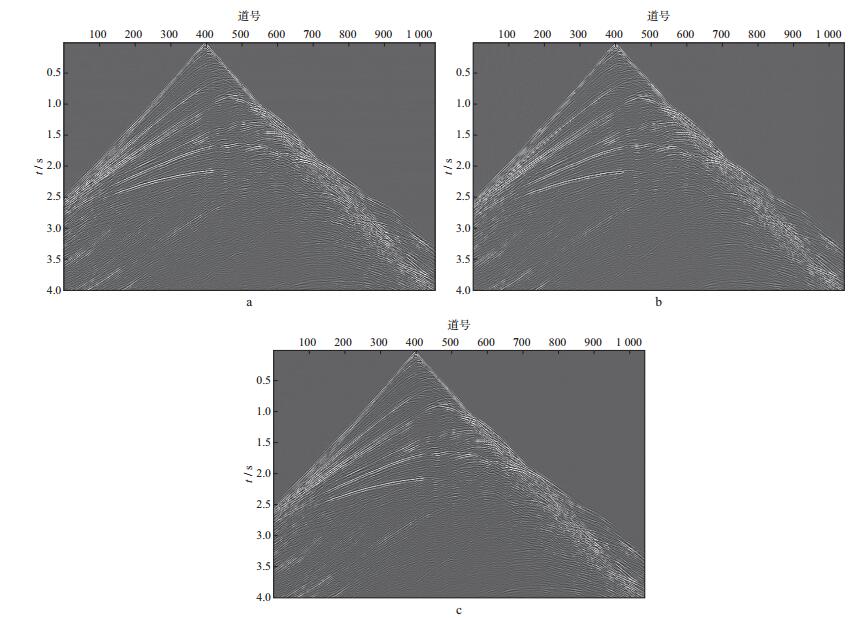
|
图 5 3种算法重建的合成地震记录对比 a OMP算法; b GPSR算法; c SPGL1算法 |
|
图 6 3种重建算法重建结果的残差 a OMP算法; b GPSR算法; c SPGL1算法 |
| 表 2 3种重建算法重构合成地震记录的信噪比 |
|
图 7 计算时间随迭代次数变化的曲线 |
注意到在相同稀疏变换基下对合成数据进行重建时, 虽然3种算法重建结果差别不大, 但是OMP算法信噪比低于其它两种算法, 这是由于OMP算法通过迭代得到的局部最优解并不一定是全局最优解, 凸优化算法的特点是利用L1范数求解优化问题时得到的局部最优解为全局最优解。GPSR与SPGL1算法重建信噪比相同。
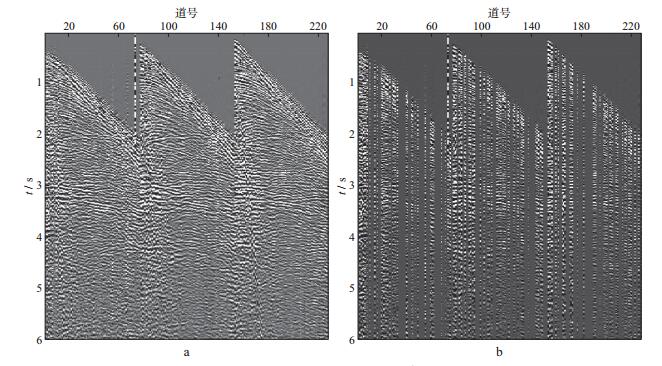
3 实际地震数据处理及分析选择复杂地区实际地震数据进行处理和分析。图 8a为原始记录, 共228道, 每道3001个检波器, 道间距为25m, 时间采样间隔为2ms。SPGL1算法参数与2.2节中SPGL1算法参数的选择相同。
|
图 8 实际地震记录(a)与随机缺失50%的地震记录(b) |
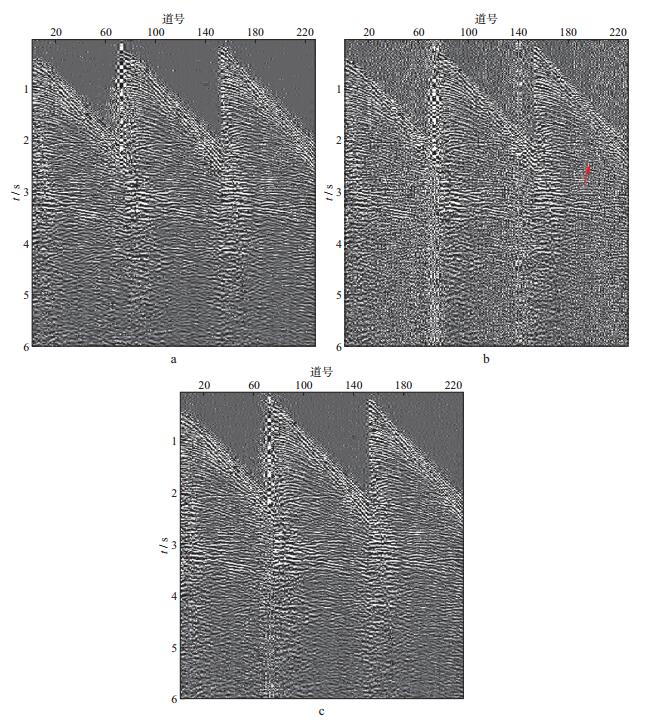
针对原始记录随机缺失50%的记录(图 8b), 使用基于压缩感知和L1范数谱投影梯度算法重建地震数据的方法进行地震数据重建。图 9为在contourlet稀疏变换基下, 采用OMP、GPSR、SPGL1算法的重建结果, 图 10为相应的残差, 表 3为3种算法重建实际地震数据的信噪比。可以看出, 波场中直达波、绕射波发育, 3种算法均可实现地震记录的重建, 其中OMP算法重建效果与SPGL1算法类似。但对比相应的残差(图 10a和图 10c)可知, OMP算法重建信噪比较低, 留有较多残差, 其运行50次的平均CUP时间为39365s, 而同样情况下SPGL1算法运行50次的平均CPU时间为476s。GPSR算法的重建结果信噪比低, 只能较好地识别能量较强的同相轴, 能量较弱的反射波基本为噪声所覆盖(图 9b红色箭头处), 其重建用时达10506s, 远不能满足实际工作中对于精度与效率的要求。
|
图 9 在contourlet稀疏变换基下3种算法对实际地震数据重建的结果对比 a OMP算法; b GPSR算法; c SPGL1算法 |

|
图 10 3种重建算法的残差对比 a OMP算法; b GPSR算法; c SPGL1算法 |
| 表 3 三种重建算法重构实际地震记录的信噪比 |
对表 3进行分析并与表 2比较发现, OMP的重建精度低于SPGL1算法, 但却高于GPSR算法。这是由于实际数据中含有大量噪声, 在对此数据进行重建时, GPSR算法相对于SPGL1算法的鲁棒性较差, 受噪声影响大。在对实际数据进行滤波后, 再采用3种算法进行重建后发现, OMP算法重建精度依然较低, 信噪比为23.8, GPSR与SPGL1算法的信噪比相差不大, 分别为26.2与26.8, 与合成数据重建结果较为一致。
4 结束语本文基于压缩感知理论, 以contourlet变换做为稀疏变换基, 结合SPGL1重建算法, 提出了一种基于压缩感知的L1范数谱投影梯度算法地震数据重建方法。
合成地震数据和实际地震数据测试结果验证了该方法的可行性和有效性。在相同重建算法下, 相比傅里叶变换与小波变换, 在高精度重建能量较强的同相轴之余, contourlet变换清晰刻画了由复杂地质构造产生的能量较弱的反射波、绕射波信息; 在相同稀疏变换基下, SPGL1算法实现了较高精度的重建, 且计算效率最高。在实际地震数据测试中, 相比OMP算法与GPSR算法, SPGL1算法重建精度高、速度快、残差小, 同时兼顾了对能量较弱的反射波、绕射波的重建。
对于大规模复杂数据的重建, 精度与效率是两个需要考量的重要因素。近年来学者们在压缩感知理论框架下提出了许多卓有成效的地震数据重建方法, 然而面对地质情况复杂、勘探面积大、地震数据量剧增的情况, 今后仍需要在进一步提高重建精度的同时兼顾计算效率方面展开相关研究。
| [1] |
SPITZ S. Seismic trace interpolation in the F-X domain[J]. Geophysics, 1991, 56(6): 785-794. DOI:10.1190/1.1443096 |
| [2] |
NAGHIZADEH M, SACCHI M D. Multistep autoregressive reconstruction of seismic records[J]. Geophysics, 2007, 72(6): 111-118. DOI:10.1190/1.2771685 |
| [3] |
CHEMINGUI N, BIONDI B. Handling the irregular geometry in wide-azimuth surveys[J]. Expanded Abstracts of 69th Annual Internat SEG Mtg, 1999, 32-35. |
| [4] |
RONEN J. Wave-equation trace interpolation[J]. Geophysics, 1987, 52(7): 973-984. DOI:10.1190/1.1442366 |
| [5] |
陈祖斌, 王丽芝, 宋杨, 等. 基于压缩感知的小波域地震数据实时压缩与高精度重构[J]. 石油地球物理勘探, 2018, 53(4): 674-681, 693. CHEN Z B, WANG L Z, SONG Y, et al. Seismic data real-time compression and high-precision reconstruction in the wavelet domain based on the compressed sensing[J]. Oil Geophysical Prospecting, 2018, 53(4): 674-681, 693. |
| [6] |
王升超, 韩立国, 巩向博. 基于各向异性Radon变换的叠前地震数据重建[J]. 石油物探, 2016, 55(6): 808-815. WANG S H, HAN L G, GONG X B. Prestack seismic data reconstruction by anisotropic Radon transform[J]. Geophysical Prospecting for Petroleum, 2016, 55(6): 808-815. DOI:10.3969/j.issn.1000-1441.2016.06.005 |
| [7] |
白兰淑, 刘伊克, 卢回忆, 等. 基于压缩感知的Curvelet域联合迭代地震数据重建[J]. 地球物理学报, 2014, 57(9): 2937-2945. BAI L S, LIU Y K, LU H Y, et al. Curvelet-domain joint iterative seismic data reconstruction based on compressed sensing[J]. Chinese Journal of Geophysics, 2014, 57(9): 2937-2945. |
| [8] |
张良, 韩立国, 刘争光, 等. 基于压缩感知和Contourlet变换的地震数据重建方法[J]. 石油物探, 2017, 56(6): 804-811. ZHANG L, HAN L G, LIU Z G, et al. Seismic data reconstruction based on compressed sensing and contourlet transform[J]. Geophysical Prospecting for Petroleum, 2017, 56(6): 804-811. DOI:10.3969/j.issn.1000-1441.2017.06.005 |
| [9] |
王华忠, 冯波, 王雄文, 等. 压缩感知及其在地震勘探中的应用[J]. 石油物探, 2016, 55(4): 467-474. WANG H Z, FENG B, WANG X W, et al. Compressed sensing and its application in seismic exploration[J]. Geophysical Prospecting for Petroleum, 2016, 55(4): 467-474. DOI:10.3969/j.issn.1000-1441.2016.04.001 |
| [10] |
张岩, 任伟建, 唐国维. 基于波原子域的地震数据压缩感知重建[J]. 地球物理学进展, 2017, 32(5): 2152-2161. ZHANG Y, REN W J, TANG G W. Compressed sensing reconstruction of seismic data based on wave atoms domain[J]. Progress in Geophysics, 2017, 32(5): 2152-2161. |
| [11] |
MALLAT S G, ZHANG Z F. Matching pursuit with time-frequency dictionary[J]. IEEE Transactions on Signal Processing, 1993, 41(12): 3397-3415. DOI:10.1109/78.258082 |
| [12] |
TROPP J A, GILBERT A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2007, 53(12): 4655-4666. DOI:10.1109/TIT.2007.909108 |
| [13] |
宋维琪, 李艳清, 刘磊. 独立分量分析与压缩感知微地震弱信号提取方法[J]. 石油地球物理勘探, 2017, 52(5): 984-989, 1041. SONG W Q, LI Y Q, LIU L. Microseismic weak signal extraction based on the independent component analysis and compressive sensing[J]. Oil Geophysical Prospecting, 2017, 52(5): 984-989, 1041. |
| [14] |
GILBERT A C, STRAUSS M J, TROPP J A, et al.One sketch for all: fast algorithms for compressed sensing[C]//Proceedings of the 39th Annual ACM Symposium on Theory of Computing.New York: Association for Computing Machiner, 2007: 237-246
|
| [15] |
MISHALI M, ELDAR Y C, DOUNAEVSKY O, et al. Xampling:analog to digital at sub-Nyquist rates[J]. IET Circuits, Devices & Systems, 2011, 5(1): 8-20. |
| [16] |
CHEN S S, SAUNDERS M A, DONOHO D L. Atomic decomposition by basis pursuit[J]. SIAM Journal on Scientific Computing, 1998, 20(1): 33-61. DOI:10.1137/S1064827596304010 |
| [17] |
DAUBECHIES I, DEFRISE M, MOL C D. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint[J]. Communications on Pure and Applied Mathematics, 2004, 57(12): 1412-1457. |
| [18] |
CAND E J, ROMBERG J, TAO T. Robust uncertainty principles:exact signal reconstruction from highly incomplete Fourier information[J]. IEEE Transation on Information Theory, 2006, 52(2): 489-509. DOI:10.1109/TIT.2005.862083 |
| [19] |
MARIO A T F, ROBERT D N, STEPHEN J W. Gradient projection for sparse reconstruction:application to compressed sensing and other inverse problems[J]. IEEE Journal of Selected Topics in Signal Processing, 2007, 1(4): 586-597. DOI:10.1109/JSTSP.2007.910281 |
| [20] |
BIRGIN G E, MARTINEZ J M, RAYDAN M. Nonmonotone spectral projected gradient methods on convex sets[J]. SIAM Journal on Optimization, 2000, 10(4): 1196-1211. DOI:10.1137/S1052623497330963 |
| [21] |
BERG E V D, FRIEDLANDER M. Sparse optimization with least-squares constraints[J]. SIAM Journal on Optimization, 2011, 21(4): 1201-1229. DOI:10.1137/100785028 |
| [22] |
BERG E V D, FRIEDLANDER M. Probing the pareto frontier for basis pursuit solutions[J]. SIAM Journal on Scientific Computing, 2008, 30(2): 890-912. |
| [23] |
BARANIUK R G. Compressive sensing[J]. IEEE Signal Processing Magazine, 2007, 24(4): 118-121. DOI:10.1109/MSP.2007.4286571 |
| [24] |
周亚同, 刘志峰, 张志伟. 形态分量分析框架下基于DCT与曲波字典组合的地震信号重建[J]. 石油物探, 2015, 54(5): 560-568. ZHOU Y T, LIU Z F, ZHANG Z W. Seismic signal reconstruction under the morphological component analysis framework combined with discrete cosine transform (DCT) and curvelet dictionary[J]. Geophysical Prospecting for Petroleum, 2015, 54(5): 560-568. DOI:10.3969/j.issn.1000-1441.2015.05.009 |
| [25] |
DO M N. The contourlet transform:an efficient directional multiresolution image representation[J]. IEEE Fransactions on Image Processing, 2005, 14(12): 2091-2106. DOI:10.1109/TIP.2005.859376 |
| [26] |
刘燕峰, 邹少峰, 居兴国. 基于contourlet变换的K-L变换地震随机噪声自适应衰减方法[J]. 石油物探, 2017, 56(5): 676-683. LIU Y F, ZOU S F, JV X G. Seismic random noise self-adaptive attenuation method based on K-L transform in the contourlet-domain[J]. Geophysical Prospecting for Petroleum, 2017, 56(5): 676-683. DOI:10.3969/j.issn.1000-1441.2017.05.008 |
| [27] |
郑雪辰, 包乾宗, 孔啸, 等. 地震数据重建的谱投影梯度算法中的参数选取[J]. 石油物探, 2018, 57(1): 58-64. ZHENG X C, BAO Q Z, KONG X, et al. Parameter selection of spectral projection gradient algorithm for seismic data reconstruction[J]. Geophysical Prospecting for Petroleum, 2018, 57(1): 58-64. DOI:10.3969/j.issn.1000-1441.2018.01.008 |




