2. 海洋国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266071
2. Laboratory for Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao 266071, China
地震波的传播速度是地震勘探中重要参数之一。研究表明, 地下介质具有广泛的各向异性特征[1], 而各向异性介质中地震波的传播速度受很多因素的影响。随着地震勘探的不断发展以及勘探目标越来越复杂, 各向同性的假设条件已经不能满足勘探精度的需求[2]。由于地震波在各向同性介质和各向异性介质中传播时存在差异, 所以地震数据的处理、解释和反演等方面需要考虑地下介质的各向异性, 否则可能会导致错误的处理和解释结果[3-4]。因此, 进行各向异性介质中地震波传播速度的研究具有重要的实际意义[5]。很多国内外学者对各向异性介质中地震波传播特征、速度分析、数值模拟、参数提取和属性分析等方面进行了研究[6-18]。
目前油气勘探的主要勘探目标仍然以沉积岩为主。沉积岩石中各向异性是指在横向各向同性而在纵向上为非均质性, 一般称之为横向各向同性(TI)介质, 其对称轴垂直于水平面时称为VTI介质, 对称轴平行于水平面时称为HTI介质。而在页岩油气勘探中, 页岩的各向异性特征也可以用TI介质来刻画[19-24], 但是页岩一般具有中强各向异性。在褶皱和逆冲作用下, 部分地层发生倾斜时, TI介质的对称轴不再水平或者垂直。当VTI/HTI介质的本构坐标系和观测坐标系不重合时, VTI/HTI介质在观测系统下转变为TTI介质[25]。关于TTI介质的波场传播、偏移成像、速度分析、AVO等方面的研究成果较多[26-35]。但利用Christoffel方程得到的TTI介质的相速度理论精确公式比较复杂, 在实际应用中推广比较困难。根据Thomsen理论, 地球介质中绝大部分的地层可以近似为弱各向异性介质[36]。梁锴等[25]、吴国忱等[37-39]基于弱各向异性假设提出了精确相速度的近似公式。基于弱各向异性假设的近似公式在各向异性参数值比较小的情况下, 可以得到较好的结果。然而, 随着勘探目标的不断复杂化, 加上页岩油气勘探中页岩的各向异性程度较大, 因而弱各向异性近似公式的精度不能满足勘探需要, 甚至不再适用。
本文以TTI介质弹性波相速度的精确表达式为出发点, 经过Thomsen参数表征后, 利用近似的配方法将精确公式内的D项近似表示为两项的平方和, 从而实现多项式的开方运算, 进一步推导了TTI介质弹性波相速度的一般性近似表达式, 并与精确值、弱各向异性近似值进行了对比。一般性近似表达式比精确公式简洁, 在一定范围内与精确解吻合较好。
1 TTI介质弹性波相速度 1.1 精确解TTI介质的刚度矩阵(CTTI)可以由VTI介质刚度矩阵(CVTI)经Bond变换[40]得到, 即:
| $ {\mathit{\boldsymbol{C}}_{{\rm{TTI}}}} = {\mathit{\boldsymbol{M}}_{{\theta _R}}}{\mathit{\boldsymbol{C}}_{{\rm{VTI}}}}\mathit{\boldsymbol{M}}_{{\theta _R}}^{\rm{T}} $ | (1) |
式中: MθR表示Bond变换矩阵[37]; θR表示TTI介质对称轴的极化角。
根据弹性力学的本构方程、几何方程、运动微分方程和TTI介质的刚度矩阵(CTTI), 并且忽略体力项, 建立TTI介质弹性波波动方程:
| $ \rho \frac{{{\partial ^2}}}{{\partial {t^2}}}\mathit{\boldsymbol{U}} = \mathit{\boldsymbol{L}}\left( {{\mathit{\boldsymbol{C}}_{{\rm{TTI}}}}{\mathit{\boldsymbol{L}}^{\rm{T}}}\mathit{\boldsymbol{U}}} \right) $ | (2) |
式中: U=(ux, uy, uz)T为位移矢量; ρ为介质密度; t为时间变量; L为偏导数矩阵[37]。
假设平面波解为:
| $ \mathit{\boldsymbol{U}} = \mathit{\boldsymbol{P}}\exp \left[ {{\rm{i}}k\left( {\mathit{\boldsymbol{n}} \cdot \mathit{\boldsymbol{x}} - vt} \right)} \right] $ | (3) |
式中: x=(x, y, z)T为位移矢量; n=(nx, ny, nz)T= (sinθcosφ, sinθsinφ, cosθ)为平面波传播方向, 其中θ为传播方向的极化角, φ为传播方向的方位角; v为平面波传播速度(相速度); k=ω/v为波数, 其中ω为角频率; P=(px, py, pz)T为平面波偏振方向(在波前满足n·x-vt为常数)。
将平面波解((3)式)代入TTI介质弹性波波动方程((2)式), 得到TTI介质Kelvin-Christoffel方程[37-39]。Kelvin-Christoffel方程存在非零解的条件是其系数矩阵行列式为零, 求解得到行列式方程的3个根, 即为TTI介质的P波, SV波, SH波相速度的精确表达式:
| $ \left\{ \begin{array}{l} {v_{\rm{P}}} = \sqrt {\frac{1}{{2\rho }}\left[ {\left( {{C_{11}} + {C_{44}}} \right)A + \left( {{C_{33}} + {C_{44}}} \right)B + \sqrt D } \right]} \\ {v_{{\rm{SV}}}} = \sqrt {\frac{1}{{2\rho }}\left[ {\left( {{C_{11}} + {C_{44}}} \right)A + \left( {{C_{33}} + {C_{44}}} \right)B - \sqrt D } \right]} \\ {v_{{\rm{SH}}}} = \sqrt {\frac{1}{\rho }\left[ {{C_{66}}A + {C_{44}}B} \right]} \end{array} \right. $ | (4) |
式中:A=sin2θsin2φ+(sinθcosφcosθR+cosθsinθR)2; B=(cosθcosθR-sinθcosφsinθR)2; D=[(C11-C44)A-(C33-C44)B]2+4(C13+C44)2AB; Cij表示VTI介质的刚度矩阵元素。
1.2 弱各向异性近似由刚度矩阵元素表示的相速度公式较为复杂, 各向异性的度量不直观。THOMSEN提出了一套表征TI介质弹性性质的参数, 称为Thomsen参数[36]。因此, VTI介质刚度矩阵的Thomsen参数表征为:
| $ {C_{11}} = {C_{22}} = \left( {1 + 2\varepsilon } \right)\rho v_{{{\rm{P0}}}}^2 $ | (5a) |
| $ {C_{12}} = \rho v_{{{\rm{P0}}}}^2\left[ {1 + 2\varepsilon - 2\left( {1 - f} \right)\left( {1 + 2\gamma } \right)} \right] $ | (5b) |
| $ {C_{13}} = {C_{23}} = \rho v_{{{\rm{P0}}}}^2\sqrt {f\left( {f + 2\delta } \right)} - \rho v_{{{\rm{S0}}}}^2 $ | (5c) |
| $ {C_{33}} = \rho v_{{{\rm{P0}}}}^2 $ | (5d) |
| $ {C_{44}} = {C_{55}} = \rho v_{{{\rm{S0}}}}^2 $ | (5e) |
| $ {C_{66}} = \left( {1 + 2\gamma } \right)\rho v_{{{\rm{S0}}}}^2 $ | (5f) |
| $ f = 1 - \frac{{v_{{{\rm{S0}}}}^2}}{{v_{{{\rm{P0}}}}^2}} = 1 - \frac{{{C_{55}}}}{{{C_{33}}}} $ | (5g) |
式中:vP0为沿TI介质对称轴方向的纵波速度; vS0为沿TI介质对称轴方向的横波速度; ε为度量准纵波各向异性强度的参数; γ为度量准横波各向异性强度的参数; δ为连接vP和vS的一种过渡性参数; f为用于简化表示的过渡性参数。
将公式(5)代入TTI介质弹性波相速度表达式((4)式)中, 并令φ=0, 则可以得到XOZ平面内TTI介质弹性波相速度的Thomsen表征, 即:
| $ \left\{ \begin{array}{l} {v_{\rm{P}}} = {v_{{{\rm{P0}}}}}\sqrt {1 - \frac{f}{2} + \varepsilon {{\sin }^2}\left( {\theta + {\theta _R}} \right) + \frac{1}{{2v_{{{\rm{P0}}}}^2}}\sqrt D } \\ {v_{{\rm{SV}}}} = {v_{{{\rm{P0}}}}}\sqrt {1 - \frac{f}{2} + \varepsilon {{\sin }^2}\left( {\theta + {\theta _R}} \right) - \frac{1}{{2v_{{{\rm{P0}}}}^2}}\sqrt D } \\ {v_{{\rm{SH}}}} = {v_{{{\rm{S0}}}}}\sqrt {1 + 2\gamma {{\sin }^2}\left( {\theta + {\theta _R}} \right)} \end{array} \right. $ | (6) |
式中:D=vP04f2{1+4(ε2/f2)sin4(θ+θR)+(4/f)· sin2(θ+θR){2δcos2(θ+θR)+ε[sin2(θ+θR)-cos2(θ+θR)]}}。
在(6)式中, 根据弱各向异性近似方法(即假设ε和δ充分小)可以忽略其高阶项(2次及以上), 且因ε和δ充分小,
| $ \begin{array}{*{20}{c}} {\sqrt D \approx v_{{{\rm{P0}}}}^2f\left\{ {1 + \frac{2}{f}{{\sin }^2}\left( {\theta + {\theta _R}} \right)\left\{ {2\delta {{\cos }^2}\left( {\theta + {\theta _R}} \right) + } \right.} \right.}\\ {\left. {\left. {\varepsilon \left[ {{{\sin }^2}\left( {\theta + {\theta _R}} \right) - {{\cos }^2}\left( {\theta + {\theta _R}} \right)} \right]} \right\}} \right\}} \end{array} $ | (7) |
将(7)式代入(6)式, 得到TTI介质Thomsen弱各向异性近似弹性波相速度:
| $ \left\{ \begin{array}{l} {v_{\rm{P}}} \approx {v_{{{\rm{P0}}}}} \cdot \\ \sqrt {1 + 2\delta {{\sin }^2}\left( {\theta + {\theta _R}} \right){{\cos }^2}\left( {\theta + {\theta _R}} \right) + 2\varepsilon {{\sin }^4}\left( {\theta + {\theta _R}} \right)} \\ {v_{{\rm{SV}}}} \approx {v_{{{\rm{S0}}}}} \cdot \\ \sqrt {1 + 2\frac{{v_{{{\rm{P0}}}}^2}}{{v_{{{\rm{S0}}}}^2}}\left( {\varepsilon - \delta } \right){{\sin }^2}\left( {\theta + {\theta _R}} \right){{\cos }^2}\left( {\theta + {\theta _R}} \right)} \\ {v_{{\rm{SH}}}} = {v_{{\rm{S0}}}}\sqrt {1 + 2\gamma {{\sin }^2}\left( {\theta + {\theta _R}} \right)} \end{array} \right. $ | (8) |
对(8)式再次应用
| $ \begin{array}{l} {v_{\rm{P}}} \approx {v_{{{\rm{P0}}}}}\left[ {1 + \delta {{\sin }^2}\left( {\theta + {\theta _R}} \right){{\cos }^2}\left( {\theta + {\theta _R}} \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\left. {\varepsilon {{\sin }^4}\left( {\theta + {\theta _R}} \right)} \right] \end{array} $ | (9a) |
| $ \begin{array}{l} {v_{{\rm{SV}}}} \approx {v_{{{\rm{S0}}}}}\left[ {1 + \frac{{v_{{{\rm{P0}}}}^2}}{{v_{{{\rm{S0}}}}^2}}\left( {\varepsilon - \delta } \right){{\sin }^2}\left( {\theta + {\theta _R}} \right) \cdot } \right.\\ \;\;\;\;\;\;\;\;\left. {{{\cos }^2}\left( {\theta + {\theta _R}} \right)} \right] \end{array} $ | (9b) |
| $ {v_{{\rm{SH}}}} \approx {v_{{{\rm{S0}}}}}\left[ {1 + \gamma {{\sin }^2}\left( {\theta + {\theta _R}} \right)} \right] $ | (9c) |
(9) 式是TTI介质相速度的弱各向异性近似公式的另一种表征[37-39], 该形式下弹性波相速度是各向异性参数的线性函数。
1.3 一般性近似弱各向异性近似的条件是假设各向异性参数数值较小, 各向异性程度较弱, 因此对于页岩等中强各向异性介质, 采用弱各向异性近似计算其相速度, 其精度可能无法满足勘探需要。为了得到更为一般性的近似表达式, 在不限制各向异性参数大小的前提下, 采取近似的配方法对(4)式中的
将公式(5)代入TTI介质弹性波相速度表达式((4)式)的D中, 并令φ=0, 则有:
| $ \begin{array}{l} D = {\left[ {\left( {1 + 2\varepsilon } \right)\rho v_{{{\rm{P0}}}}^2 - \rho v_{{{\rm{S0}}}}^2} \right]^2}{\sin ^4}\left( {\theta + {\theta _R}} \right) + \left( {\rho v_{{{\rm{P0}}}}^2 - } \right.\\ \;\;\;\;\;\;{\left. {\rho v_{{{\rm{S0}}}}^2} \right)^2}{\cos ^4}\left( {\theta + {\theta _R}} \right) - 2\left[ {\left( {1 + 2\varepsilon } \right)\rho v_{{{\rm{P0}}}}^2 - \rho v_{{{\rm{S0}}}}^2} \right] \cdot \\ \;\;\;\;\;\;\left( {\rho v_{{{\rm{P0}}}}^2 - \rho v_{{{\rm{S0}}}}^2} \right){\sin ^2}\left( {\theta + {\theta _R}} \right){\cos ^2}\left( {\theta + {\theta _R}} \right) + \\ \;\;\;\;\;\;4\left[ {\left( {1 + 2\delta } \right)\rho v_{{{\rm{P0}}}}^2 - \rho v_{{{\rm{S0}}}}^2} \right]\left( {\rho v_{{{\rm{P0}}}}^2 - \rho v_{{{\rm{S0}}}}^2} \right){\sin ^2}\left( {\theta + } \right.\\ \;\;\;\;\;\;\left. {{\theta _R}} \right){\cos ^2}\left( {\theta + {\theta _R}} \right) = \left\{ {\left[ {\left( {1 + 2\varepsilon } \right)\rho v_{{{\rm{P0}}}}^2 - \rho v_{{{\rm{S0}}}}^2} \right] \cdot } \right.\\ \;\;\;\;\;\;{\left. {{{\sin }^2}\left( {\theta + {\theta _R}} \right) + \left( {\rho v_{{{\rm{P0}}}}^2 - \rho v_{{{\rm{S0}}}}^2} \right){{\cos }^2}\left( {\theta + {\theta _R}} \right)} \right\}^2} + \\ \;\;\;\;\;\;4{\rho ^2}v_{{{\rm{P0}}}}^2\left( {\delta - \varepsilon } \right) \cdot 2\left( {1 - \frac{{v_{{{\rm{P0}}}}^2}}{{v_{{{\rm{S0}}}}^2}}} \right){\sin ^2}\left( {\theta + {\theta _R}} \right) \cdot \\ \;\;\;\;\;\;{\cos ^2}\left( {\theta + {\theta _R}} \right) \end{array} $ | (10) |
在(10)式中, 对4ρ2vP04(δ-ε)·2(1-vS02/vP02)sin2(θ+θR)cos2(θ+θR)进行以下近似(具体近似过程见附录A), 即:
| $ \begin{array}{l} 4{\rho ^2}v_{{{\rm{P0}}}}^2\left( {\delta - \varepsilon } \right) \cdot 2\left( {1 - \frac{{v_{{{\rm{S0}}}}^2}}{{v_{{{\rm{P0}}}}^2}}} \right){\sin ^2}\left( {\theta + {\theta _R}} \right){\cos ^2}\left( {\theta + } \right.\\ \left. {{\theta _R}} \right) \approx 4{\rho ^2}v_{{{\rm{P0}}}}^2\left( {\delta - \varepsilon } \right){\sin ^2}\left( {\theta + {\theta _R}} \right){\cos ^2}\left( {\theta + {\theta _R}} \right) \cdot \\ \left( {1 - \frac{{v_{{{\rm{P0}}}}^2}}{{v_{{{\rm{S0}}}}^2}}} \right) + 4{\rho ^2}v_{{{\rm{P0}}}}^2\left( {\delta - \varepsilon } \right){\sin ^2}\left( {\theta + {\theta _R}} \right){\cos ^2}\left( {\theta + } \right.\\ \left. {{\theta _R}} \right)\left[ {2\varepsilon {{\sin }^2}\left( {\theta + {\theta _R}} \right) + \left( {\delta - \varepsilon } \right){{\sin }^2}\left( {\theta + {\theta _R}} \right) \cdot } \right.\\ \left. {{{\cos }^2}\left( {\theta + {\theta _R}} \right)} \right] \end{array} $ | (11) |
将(11)式代入(10)式, 得到:
| $ \begin{array}{l} D \approx \left\{ {\left[ {\left( {1 + 2\varepsilon } \right)\rho v_{{{\rm{P0}}}}^2 - \rho v_{{{\rm{S0}}}}^2} \right]{{\sin }^2}\left( {\theta + {\theta _R}} \right) + } \right.\\ \;\;\;\;{\left. {\left( {\rho v_{{{\rm{P0}}}}^2 - \rho v_{{{\rm{S0}}}}^2} \right){{\cos }^2}\left( {\theta + {\theta _R}} \right)} \right\}^2} + 4{\rho ^2}v_{{{\rm{P0}}}}^4\left( {\delta - } \right.\\ \;\;\;\;\left. \varepsilon \right){\sin ^2}\left( {\theta + {\theta _R}} \right){\cos ^2}\left( {\theta + {\theta _R}} \right) \cdot \left[ {1 - \frac{{v_{{{\rm{S0}}}}^2}}{{v_{{{\rm{P0}}}}^2}} + 2\varepsilon {{\sin }^2} \cdot } \right.\\ \;\;\;\;\left. {\left( {\theta + {\theta _R}} \right) + \left( {\delta - \varepsilon } \right){{\sin }^2}\left( {\theta + {\theta _R}} \right){{\cos }^2}\left( {\theta + {\theta _R}} \right)} \right]\\ \;\;\;\; = {a^2} + b\left( {2a + b} \right)\\ \;\;\;\; = {\left( {a + b} \right)^2} \end{array} $ | (12) |
式中:a=(ρvP02-ρvS02)cos2(θ+θR)+[(1+2ε)ρvP02-ρvS02]sin2(θ+θR); b=2ρvP02(δ-ε)sin2(θ+θR)cos2(θ+θR)。
将(12)式代入(6)式, 整理后得:
| $ \left\{ \begin{array}{l} {v_{\rm{P}}} = {v_{{{\rm{P0}}}}}\left[ {1 + 2\varepsilon {{\sin }^2}\left( {\theta + {\theta _R}} \right) + \left( {\delta - \varepsilon } \right) \cdot } \right.\\ \;\;\;\;\;\;\;{\left. {{{\sin }^2}\left( {\theta + {\theta _R}} \right){{\cos }^2}\left( {\theta + {\theta _R}} \right)} \right]^{\frac{1}{2}}}\\ {v_{{\rm{SV}}}} \approx {v_{{{\rm{S0}}}}}\left[ {1 + \frac{{v_{{{\rm{P0}}}}^2}}{{v_{{{\rm{S0}}}}^2}}\left( {\varepsilon - \delta } \right){{\sin }^2}\left( {\theta + {\theta _R}} \right) \cdot } \right.\\ \;\;\;\;\;\;\;\;{\left. {{{\cos }^2}\left( {\theta + {\theta _R}} \right)} \right]^{\frac{1}{2}}} \end{array} \right. $ | (13) |
(13) 式即为基于近似的配方法推导的TTI介质弹性波相速度的一般性近似表达式。
2 数值算例 2.1 近似项数值测试为了考察一般性近似((11)式)中关键近似项的近似程度, 对精确项:
| $ 4{\rho ^2}v_{{{\rm{P0}}}}^2\left( {\delta - \varepsilon } \right){\sin ^2}\left( {\theta + {\theta _R}} \right){\cos ^2}\left( {\theta + {\theta _R}} \right) \cdot \left( {1 - \frac{{v_{{{\rm{S0}}}}^2}}{{v_{{{\rm{P0}}}}^2}}} \right) $ | (14) |
和其近似项:
| $ \begin{array}{*{20}{c}} {4{\rho ^2}v_{{{\rm{P0}}}}^2\left( {\delta - \varepsilon } \right){{\sin }^2}\left( {\theta + {\theta _R}} \right){{\cos }^2}\left( {\theta + {\theta _R}} \right)\left[ {2\varepsilon {{\sin }^2}\left( {\theta + } \right.} \right.}\\ {\left. {\left. {{\theta _R}} \right) + \left( {\delta - \varepsilon } \right){{\sin }^2}\left( {\theta + {\theta _R}} \right){{\cos }^2}\left( {\theta + {\theta _R}} \right)} \right]} \end{array} $ | (15) |
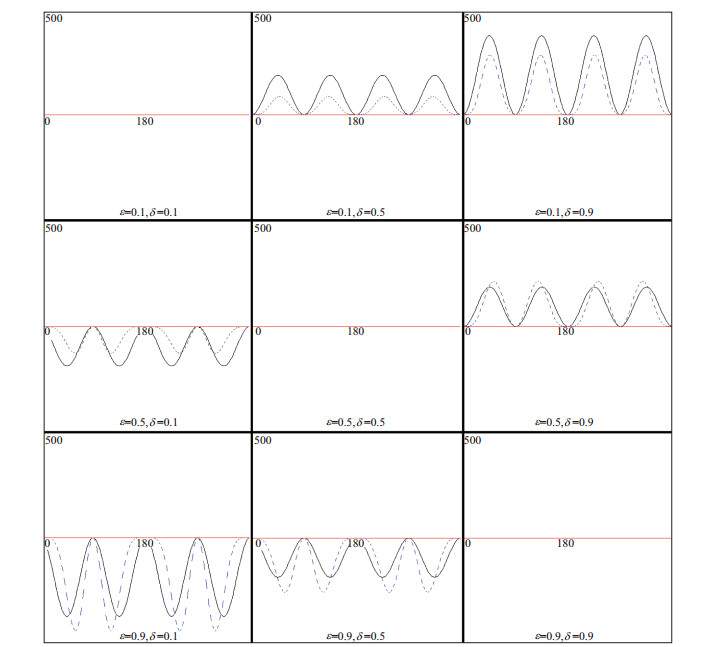
进行了数值测试。所用模型为一组均匀TTI介质模型, 模型中相同参数为vP0=3 300 m/s, vS0=1 905 m/s, ρ=2.440×103 kg/m3, θR=45°, φ=0, 不同的各向异性参数ε和δ如图 1所示。
|
图 1 近似项的近似效果(实线表示精确值, 虚线表示一般性近似值) |
由图 1可以看到, 近似项在一定精度范围内与精确值吻合较好。当ε=δ, 即椭圆各向异性介质时, 近似值与精确值相等。如果θR发生变化, 则精确值与近似值曲线相应地往右(或左)整体移动, 对近似程度不产生影响。
2.2 相速度数值测试为了比较两种近似的效果, 针对上述均匀TTI介质模型, 利用TTI介质弹性波相速度的精确表达式((4)式)、弱各向异性近似表达式((8)式)和一般性近似表达式((13)式)计算qP波和qSV波的相速度, 结果如图 2和图 3所示。
|
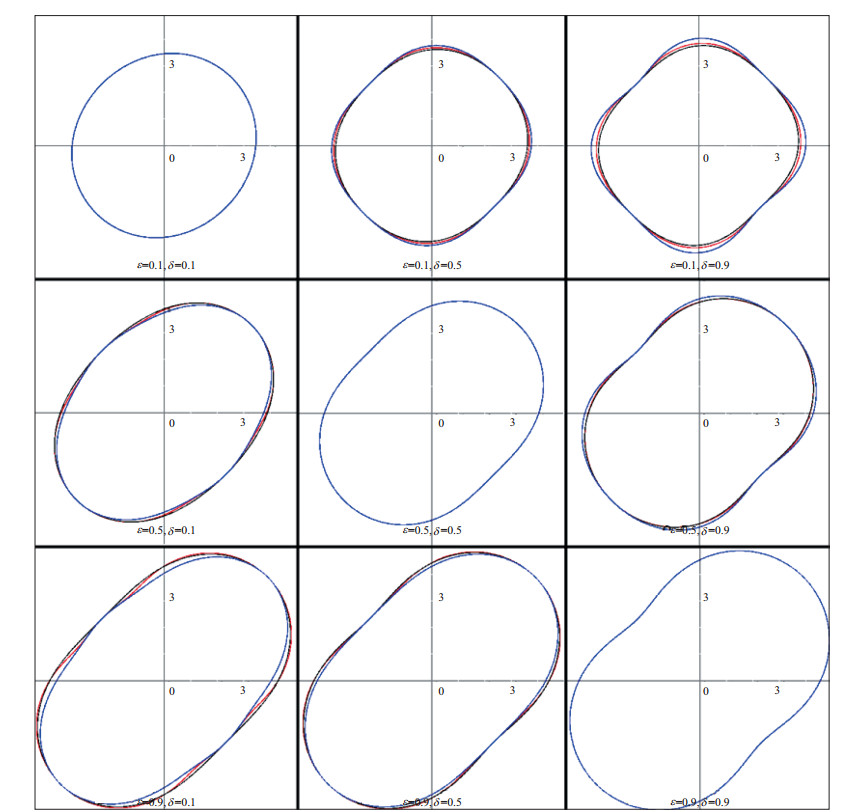
图 2 qP波相速度近似效果对比 (红线表示精确值, 蓝线表示弱各向异性近似, 黑线表示一般性各向异性近似; 速度单位为km/s) |
|
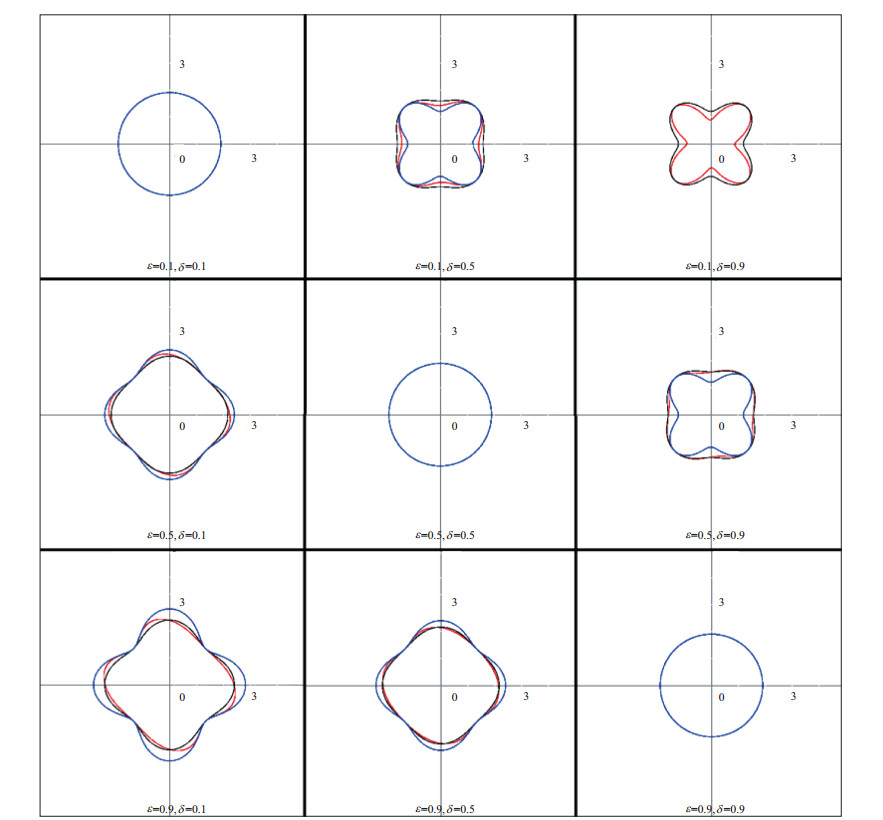
图 3 qSV波相速度近似效果对比 (红线表示精确值, 蓝线表示弱各向异性近似, 黑线表示一般性各向异性近似; 速度单位为km/s) |
图 2对比了不同TTI介质模型qP波的精确值、弱各向异性近似值和一般性各向异性近似值。由图 2可以看出, 在大多数角度范围内, 无论是弱各向异性情况还是中强各向异性情况, 一般性各向异性近似值比弱各向异性近似值更接近精确值。弱各向异性近似和一般性各向异性近似均受各向异性参数ε和δ的影响。当ε和δ相等时, 公式(4)、公式(8)和公式(13)相等, 所以3条速度曲线均重叠。近似效果还受|ε-δ|大小的影响, 当ε和δ的差值较小时, 一般性近似的近似程度比ε和δ的差值较大时好。
一般性近似的近似效果还受传播方向(θ)的影响, 并且沿对称轴方向的近似程度等于垂直对称轴方向的近似程度。
图 3对比了qSV波的精确值、弱各向异性近似值和一般性各向异性近似值。由图 3可以看出, 与qP波类似, 对于TTI介质, qSV波相速度的一般性各向异性近似效果较好, 大部分情况下, 一般性各向异性近似值要比弱各向异性近似值更接近精确值, 并且对中强各向异性参数也能有较好的近似效果。对比图 2和图 3可以发现, qP波速度的近似效果更优于qSV波速度。另外, 在图 3中, 当ε=0.1, δ=0.9时, 因弱各向异性近似表达式的根号中出现负值, 不存在弱各向异性近似值, 而一般性各向异性近似值是存在的, 这也从另一个角度说明了一般性各向异性近似表达式的适用范围更广。
3 结论本文从TTI介质弹性波相速度精确表达式出发, 根据近似的配方法将表达式中的D近似地表示成两项的平方和, 从而消去一重根号, 推导出TTI介质qP波和qSV波相速度的一般性近似。通过相速度精确表达式、弱各向异性近似和一般性近似的对比, 得到如下认识和结论:
1) 一般性近似由于在推导过程中没有直接利用弱各向异性的假设, 因此不仅适用于弱各向异性, 也适用于中强各向异性的情况, 即在较大范围内, 一般性近似的精度高于弱各向异性近似的精度;
2) 对于同一种TTI介质, 由于qSV波相速度中各向异性参数有vP02/vS02的系数起放大作用, 所以qP波的一般性近似精度高于qSV波的精度。对于弱各向异性近似也有类似结论;
3) 与弱各向异性近似类似, TTI介质弹性波相速度一般性近似表达式仍然是vP0, vS, ε, δ, θ, θR的函数, 并受这些参数控制。
本文推导的TTI介质弹性波相速度一般性近似表达式, 虽然比精确公式简单, 但是仍然含有开方项, 具有一定的复杂性, 下一步研究可以考虑如何进一步消除开方项从而得到更为简洁的表征形式。
附录A 一般性近似公式的推导过程Thomsen参数表征的TTI介质弹性波相速度的精确表达式为:
| $ {v_{\rm{P}}} = \sqrt {\frac{1}{{2\rho }}\left\{ {\left[ {\left( {1 + 2\varepsilon } \right)\rho v_{{\rm{P0}}}^2 + \rho v_{{\rm{S0}}}^2} \right]{{\sin }^2}\left( {\theta + {\theta _R}} \right) + \left( {\rho v_{{\rm{P0}}}^2 + \rho v_{{\rm{S0}}}^2} \right){{\cos }^2}\left( {\theta + {\theta _R}} \right) + \sqrt D } \right\}} $ | (A1) |
| $ {v_{{\rm{SV}}}} = \sqrt {\frac{1}{{2\rho }}\left\{ {\left[ {\left( {1 + 2\varepsilon } \right)\rho v_{{\rm{P0}}}^2 + \rho v_{{\rm{S0}}}^2} \right]{{\sin }^2}\left( {\theta + {\theta _R}} \right) + \left( {\rho v_{{\rm{P0}}}^2 + \rho v_{{\rm{S0}}}^2} \right){{\cos }^2}\left( {\theta + {\theta _R}} \right) - \sqrt D } \right\}} $ | (A2) |
其中:
| $ \begin{array}{l} D =\\ {\left\{ {\left[ {\left( {1 + 2\varepsilon } \right)\rho v_{{\rm{P0}}}^2 + \rho v_{{\rm{S0}}}^2} \right]{{\sin }^2}\left( {\theta + {\theta _R}} \right) + \left( {\rho v_{{\rm{P0}}}^2 + \rho v_{{\rm{S0}}}^2} \right){{\cos }^2}\left( {\theta + {\theta _R}} \right)} \right\}^2} + 4{\rho ^2}v_{{\rm{P0}}}^2\left( {\delta - \varepsilon } \right) \cdot \\ \;\;\;\;\;\;2\left( {1 - \frac{{v_{{\rm{S0}}}^2}}{{v_{{\rm{P0}}}^2}}} \right){\sin ^2}\left( {\theta + {\theta _R}} \right){\cos ^2}\left( {\theta + {\theta _R}} \right) \end{array} $ | (A3) |
对比qP波和qSV波相速度精确表达式, 发现二者有一个共同项, 即:
| $ \left[ {\left( {1 + 2\varepsilon } \right)\rho v_{{\rm{P0}}}^2 + \rho v_{{\rm{S0}}}^2} \right]{\sin ^2}\left( {\theta + {\theta _R}} \right) + \left( {\rho v_{{\rm{P0}}}^2 + \rho v_{{\rm{S0}}}^2} \right){\cos ^2}\left( {\theta + {\theta _R}} \right) $ | (A4) |
如果从(A3)式中可以直接提出以下项, 即:
| $ \left[ {\left( {1 + 2\varepsilon } \right)\rho v_{{\rm{P0}}}^2 - \rho v_{{\rm{S0}}}^2} \right]{\sin ^2}\left( {\theta + {\theta _R}} \right) + \left( {\rho v_{{\rm{P0}}}^2 - \rho v_{{\rm{S0}}}^2} \right){\cos ^2}\left( {\theta + {\theta _R}} \right) $ | (A5) |
就能抵消(A4)中的部分项从而简化qP波和qSV波的相速度表达式。
为了使用近似的配方法将(A5)从D中整体提出, 令(A5)式为a, 即:
| $ \begin{array}{l} a = \left[ {\left( {1 + 2\varepsilon } \right)\rho v_{{\rm{P0}}}^2 - \rho v_{{\rm{S0}}}^2} \right]{\sin ^2}\left( {\theta + {\theta _R}} \right) + \left( {\rho v_{{\rm{P0}}}^2 - \rho v_{{\rm{S0}}}^2} \right){\cos ^2}\left( {\theta + {\theta _R}} \right)\\ {\rm{ = }}\left( {\rho v_{{\rm{P0}}}^2 - \rho v_{{\rm{S0}}}^2} \right){\sin ^2}\left( {\theta + {\theta _R}} \right) + 2\varepsilon \rho v_{{\rm{P0}}}^2{\sin ^2}\left( {\theta + {\theta _R}} \right) + \left( {\rho v_{{\rm{P0}}}^2 - \rho v_{{\rm{S0}}}^2} \right){\cos ^2}\left( {\theta + {\theta _R}} \right)\\ {\rm{ = }}\rho v_{{\rm{P0}}}^2\left[ {\left( {1 - \frac{{v_{{\rm{P0}}}^2}}{{v_{{\rm{S0}}}^2}}} \right) + 2\varepsilon {{\sin }^2}\left( {\theta + {\theta _R}} \right)} \right] \end{array} $ | (A6) |
将(A6)式代入(A3)式进行整理可得:
| $ \begin{array}{l} D = {a^2} + 4{\rho ^2}v_{{\rm{P0}}}^4\left( {\delta - \varepsilon } \right) \cdot 2\left( {1 - \frac{{v_{{\rm{S0}}}^2}}{{v_{{\rm{P0}}}^2}}} \right) \cdot {\sin ^2}\left( {\theta + {\theta _R}} \right){\cos ^2}\left( {\theta + {\theta _R}} \right)\\ = {a^2} + 2 \cdot \rho v_{{\rm{P0}}}^2\left( {1 - \frac{{v_{{\rm{S0}}}^2}}{{v_{{\rm{P0}}}^2}}} \right) \cdot 2\rho v_{{\rm{P0}}}^2\left( {\delta - \varepsilon } \right){\sin ^2}\left( {\theta + {\theta _R}} \right){\cos ^2}\left( {\theta + {\theta _R}} \right) + \\ 4{\rho ^2}v_{{\rm{P0}}}^4\left( {\delta - \varepsilon } \right){\sin ^2}\left( {\theta + {\theta _R}} \right){\cos ^2}\left( {\theta + {\theta _R}} \right) \cdot \left( {1 - \frac{{v_{{\rm{S0}}}^2}}{{v_{{\rm{P0}}}^2}}} \right) \end{array} $ | (A7) |
如果令:
| $ b = 2\rho v_{{\rm{P0}}}^2\left( {\delta - \varepsilon } \right){\sin ^2}\left( {\theta + {\theta _R}} \right){\cos ^2}\left( {\theta + {\theta _R}} \right) $ | (A8) |
并试算(a+b)2, 有:
| $ \begin{array}{l} {\left( {a + b} \right)^2} = {a^2} + 2ab + {b^2}\\ = {a^2} + 2\rho v_{{\rm{P0}}}^2\left[ {\left( {1 - \frac{{v_{{\rm{S0}}}^2}}{{v_{{\rm{P0}}}^2}}} \right) + 2\varepsilon {{\sin }^2}\left( {\theta + {\theta _R}} \right)} \right] \cdot 2\rho v_{{\rm{P0}}}^2\left( {\delta - \varepsilon } \right){\sin ^2}\left( {\theta + {\theta _R}} \right){\cos ^2}\left( {\theta + {\theta _R}} \right) + \\ 4{\rho ^2}v_{{\rm{P0}}}^4{\left( {\delta - \varepsilon } \right)^2}{\sin ^4}\left( {\theta + {\theta _R}} \right){\cos ^4}\left( {\theta + {\theta _R}} \right)\\ = {a^2} + 4{\rho ^2}v_{{\rm{P0}}}^4\left( {\delta - \varepsilon } \right){\sin ^2}\left( {\theta + {\theta _R}} \right){\cos ^2}\left( {\theta + {\theta _R}} \right) \cdot \left( {1 - \frac{{v_{{\rm{S0}}}^2}}{{v_{{\rm{P0}}}^2}}} \right) + \\ 4{\rho ^2}v_{{\rm{P0}}}^4\left( {\delta - \varepsilon } \right){\sin ^2}\left( {\theta + {\theta _R}} \right){\cos ^2}\left( {\theta + {\theta _R}} \right)\\ \left[ {2\varepsilon {{\sin }^2}\left( {\theta + {\theta _R}} \right) + \left( {\delta - \varepsilon } \right){{\sin }^2}\left( {\theta + {\theta _R}} \right){{\cos }^2}\left( {\theta + {\theta _R}} \right)} \right] \end{array} $ | (A9) |
对比(A7)式与(A9)式, 不难发现, 两个表达式之间存在差异的项为:
| $ 4{\rho ^2}v_{{\rm{P0}}}^4\left( {\delta - \varepsilon } \right){\sin ^2}\left( {\theta + {\theta _R}} \right){\cos ^2}\left( {\theta + {\theta _R}} \right) \cdot \left( {1 - \frac{{v_{{\rm{S0}}}^2}}{{v_{{\rm{P0}}}^2}}} \right) $ | (A10) |
和
| $ 4{\rho ^2}v_{{\rm{P0}}}^4\left( {\delta - \varepsilon } \right){\sin ^2}\left( {\theta + {\theta _R}} \right){\cos ^2}\left( {\theta + {\theta _R}} \right)\\ \left[ {2\varepsilon {{\sin }^2}\left( {\theta + {\theta _R}} \right) + \left( {\delta - \varepsilon } \right){{\sin }^2}\left( {\theta + {\theta _R}} \right){{\cos }^2}\left( {\theta + {\theta _R}} \right)} \right] $ | (A11) |
如果令(A10)式和(A11)近似相等, 即:
| $ \begin{array}{l} 4{\rho ^2}v_{{\rm{P0}}}^4\left( {\delta - \varepsilon } \right){\sin ^2}\left( {\theta + {\theta _R}} \right){\cos ^2}\left( {\theta + {\theta _R}} \right)\left( {1 - \frac{{v_{{\rm{S0}}}^2}}{{v_{{\rm{P0}}}^2}}} \right)\\ \approx 4{\rho ^2}v_{p{\rm{0}}}^4\left( {\delta - \varepsilon } \right){\sin ^2}\left( {\theta + {\theta _R}} \right){\cos ^2}\left( {\theta + {\theta _R}} \right)\\ \left[ {2\varepsilon {{\sin }^2}\left( {\theta + {\theta _R}} \right) + \left( {\delta - \varepsilon } \right){{\sin }^2}\left( {\theta + {\theta _R}} \right){{\cos }^2}\left( {\theta + {\theta _R}} \right)} \right] \end{array} $ | (A12) |
就能使用配方法消除
| $ \begin{array}{l} \sqrt D \approx \sqrt {{{\left( {a + b} \right)}^2}} = a + b\\ \;\;\;\;\;\;\;\;\; = \left[ {\left( {1 + 2\varepsilon } \right)\rho v_{{\rm{P0}}}^2 - \rho v_{{\rm{S0}}}^2} \right]{\sin ^2}\left( {\theta + {\theta _R}} \right) + \left( {\rho v_{{\rm{P0}}}^2 - \rho v_{{\rm{S0}}}^2} \right){\cos ^2}\left( {\theta + {\theta _R}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;2\rho v_{{\rm{P0}}}^2\left( {\delta - \varepsilon } \right){\sin ^2}\left( {\theta + {\theta _R}} \right){\cos ^2}\left( {\theta + {\theta _R}} \right) \end{array} $ | (A13) |
由于该方法在进行配方时采用了近似, 所以称该方法为近似的配方法。
将(A13)式代入(A1)式, 可以得到TTI介质qP波一般性近似相速度, 即:
| $ {v_{\rm{P}}} \approx \\ {\left\{ {\frac{1}{{2\rho }}\left\{ {\left[ {\left( {1 + 2\varepsilon } \right)\rho v_{{\rm{P0}}}^2 - \rho v_{{\rm{S0}}}^2} \right]{{\sin }^2}\left( {\theta + {\theta _R}} \right) + \left( {\rho v_{{\rm{P0}}}^2 - \rho v_{{\rm{S0}}}^2} \right){{\cos }^2}\\ \left( {\theta + {\theta _R}} \right) + \sqrt {{{\left( {a + b} \right)}^2}} } \right\}} \right\}^{\frac{1}{2}}}\\ \;\;\;\; = \left\{ {\frac{1}{{2\rho }}\left\{ {\left[ {\left( {1 + 2\varepsilon } \right)\rho v_{{\rm{P0}}}^2 - \rho v_{{\rm{S0}}}^2} \right]{{\sin }^2}\left( {\theta + {\theta _R}} \right) + \left( {\rho v_{{\rm{P0}}}^2 - \rho v_{{\rm{S0}}}^2} \right){{\cos }^2}\\ \left( {\theta + {\theta _R}} \right) + \left[ {\left( {1 + 2\varepsilon } \right)\rho v_{{\rm{P0}}}^2 - \rho v_{{\rm{S0}}}^2} \right] \cdot } \right.} \right.\\ \;\;\;\;{\left. {\left. {{{\sin }^2}\left( {\theta + {\theta _R}} \right) + \left( {\rho v_{{\rm{P0}}}^2 - \rho v_{{\rm{S0}}}^2} \right){{\cos }^2}\left( {\theta + {\theta _R}} \right) + 2\rho v_{{\rm{P0}}}^2\left( {\delta - \varepsilon } \right){{\sin }^2}\left( {\theta + {\theta _R}} \right){{\cos }^2}\\ \left( {\theta + {\theta _R}} \right)} \right\}} \right\}^{\frac{1}{2}}}\\ \;\;\;\; = {\left\{ {\frac{1}{{2\rho }}\left[ {2\left( {1 + 2\varepsilon } \right)\rho v_{{\rm{P0}}}^2{{\sin }^2}\left( {\theta + {\theta _R}} \right) + 2\rho v_{{\rm{P0}}}^2{{\cos }^2}\left( {\theta + {\theta _R}} \right) + 2\rho v_{{\rm{P0}}}^2\\ \left( {\delta - \varepsilon } \right){{\sin }^2}\left( {\theta + {\theta _R}} \right){{\cos }^2} \left( {\theta + {\theta _R}} \right)} \right]} \right\}^{\frac{1}{2}}}\\ \;\;\;\; = v_{{\rm{P0}}}{\left[ {\left( {1 + 2\varepsilon } \right){{\sin }^2}\left( {\theta + {\theta _R}} \right) + {{\cos }^2}\left( {\theta + {\theta _R}} \right) + \left( {\delta - \varepsilon } \right){{\sin }^2}\left( {\theta + {\theta _R}} \right){{\cos }^2}\left( {\theta + {\theta _R}} \right)} \right]^{\frac{1}{2}}}\\ \;\;\;\; = {v_{{\rm{P0}}}}{\left[ {1 + 2\varepsilon {{\sin }^2}\left( {\theta + {\theta _R}} \right) + \left( {\delta - \varepsilon } \right){{\sin }^2}\left( {\theta + {\theta _R}} \right){{\cos }^2}\left( {\theta + {\theta _R}} \right)} \right]^{\frac{1}{2}}} $ | (A14) |
同理, 可以得到TTI介质qSV波一般性近似相速度, 即:
| $ {v_{{\rm{SV}}}} \approx {v_{{\rm{S0}}}}\sqrt {1 + \frac{{v_{{\rm{P0}}}^2}}{{v_{{\rm{S0}}}^2}}\left( {\varepsilon - \delta } \right){{\sin }^2}\left( {\theta + {\theta _R}} \right){{\cos }^2}\left( {\theta + {\theta _R}} \right)} $ | (A15) |
| [1] |
王咸彬. TTI各向异性逆时偏移技术及应用[J]. 石油物探, 2017, 56(4): 534-542. WANG X B. Anisotropic reverse time migration technique in TTI media and its application[J]. Geophysical Prospecting for Petroleum, 2017, 56(4): 534-542. DOI:10.3969/j.issn.1000-1441.2017.04.009 |
| [2] |
居兴国, 郭恺, 刘定进. 基于相速度的TTI介质射线追踪方法研究[J]. 石油物探, 2017, 56(2): 171-178. JU X G, GUO K, LIU D J. Research on a ray tracing method for TTI medium based on phase velocity[J]. Geophysical Prospecting for Petroleum, 2017, 56(2): 171-178. DOI:10.3969/j.issn.1000-1441.2017.02.002 |
| [3] |
黄光南, 刘洋, 李红星, 等. TTI介质相速度对弹性模量参数的敏感性研究[J]. 石油物探, 2014, 53(3): 262-271. HUANG G N, LIU Y, LI H X, et al. Research on sensitivity of phase velocity with respect to elastic moduli parameters in TTI media[J]. Geophysical Prospecting for Petroleum, 2014, 53(3): 262-271. DOI:10.3969/j.issn.1000-1441.2014.03.003 |
| [4] |
万志超, 滕吉文, 张秉明. 各向异性介质中地震波速度分析的研究现状[J]. 地球物理学进展, 1997, 12(3): 35-44. WAN Z C, TENG J W, ZHANG B M. Velocity analysis in anisotropic media[J]. Progress in Geophysics, 1997, 12(3): 35-44. |
| [5] |
张衡, 刘洪, 丁仁伟, 等. TTI介质伪解析解耦波动方程[J]. 地球物理学进展, 2016, 31(4): 1752-1761. ZHANG H, LIU H, DING R W, et al. Pseudo-analytical decoupling wave equation for TTI media[J]. Progress in Geophysics, 2016, 31(4): 1752-1761. |
| [6] |
CRAMPIN S. A review of wave motion in anisotropic and cracked elastic-media[J]. Wave Motion, 1981, 3: 343-391. DOI:10.1016/0165-2125(81)90026-3 |
| [7] |
TSVANKIN I. P-wave signatures and notation for transversely isotropic media:an overview[J]. Geophysics, 1996, 61(2): 467-483. DOI:10.1190/1.1443974 |
| [8] |
PŠEŇCÍK I, GAJEWSKI D. Polarization, phase velocity, and NMO velocity of qP-waves in arbitrary weakly anisotropic media[J]. Geophysics, 1998, 63(5): 1754-1766. DOI:10.1190/1.1444470 |
| [9] |
ALKHALIFAH T. Acoustic approximation for processing in transversely isotropic media[J]. Geophysics, 1998, 63(2): 623-631. DOI:10.1190/1.1444361 |
| [10] |
ALKHALIFAH T. An acoustic wave equation for anisotropic media[J]. Geophysics, 2000, 65(4): 1239-1250. DOI:10.1190/1.1444815 |
| [11] |
SCHOENBERG A M, De HOOP V M. Approximate dispersion relations for qP-qSV-waves in transversely isotropic media[J]. Geophysics, 2000, 65(3): 919-933. DOI:10.1190/1.1444788 |
| [12] |
魏周拓, 范宜仁, 陈雪莲, 等. 横波各向异性分析方法及其在复杂储层中的应用[J]. 石油物探, 2011, 50(3): 275-280. WEI Z T, FAN Y R, CHEN X L, et al. S-wave anisotropy analysis method and its application on complex reservoir[J]. Geophysical Prospecting for Petroleum, 2011, 50(3): 275-280. DOI:10.3969/j.issn.1000-1441.2011.03.011 |
| [13] |
贾福宗, 李道善, 曹孟起, 等. 宽方位纵波地震资料HTI各向异性校正方法研究与应用[J]. 石油物探, 2013, 52(6): 650-654. JIA F Z, LI D S, CAO M Q, et al. Study and application of HTI anisotropy moveout correction to wide azimuth P-wave seismic data[J]. Geophysical Prospecting for Petroleum, 2013, 52(6): 650-654. |
| [14] |
胡起, 陈小宏, 李景叶. 基于各向异性岩石物理模型的页岩气储层横波速度预测[J]. 石油物探, 2014, 53(3): 254-261. HU Q, CHEN X H, LI J Y. Shear wave velocity prediction for shale gas reservoirs based on anisotropic rock physics model[J]. Geophysical Prospecting for Petroleum, 2014, 53(3): 254-261. DOI:10.3969/j.issn.1000-1441.2014.03.002 |
| [15] |
孙炜, 何治亮, 李玉凤, 等. 基于HTI介质各向异性正演的裂缝预测属性优选[J]. 石油物探, 2014, 53(2): 223-231. SUN W, HE Z L, LI Y F, et al. Seismic attributes optimization for fractures prediction based on the anisotropy forwarding of the HTI media[J]. Geophysical Prospecting for Petroleum, 2014, 53(2): 223-231. DOI:10.3969/j.issn.1000-1441.2014.02.013 |
| [16] |
裴云龙, 王立歆, 邬达理, 等. 井控各向异性速度建模技术在YKL地区的应用[J]. 石油物探, 2017, 56(3): 390-399. PEI Y L, WANG L X, WU D L, et al. The application of well-controlled anisotropy velocity modeling in YKL region[J]. Geophysical Prospecting for Petroleum, 2017, 56(3): 390-399. DOI:10.3969/j.issn.1000-1441.2017.03.009 |
| [17] |
徐亦鸣, 黄中玉, 刘路佳. 各向异性介质纵波速度分析[J]. 石油物探, 2004, 43(5): 438-440. XU Y M, HUANG Z Y, LIU L J. P-wave velocity analysis in anisotropy medium[J]. Geophysical Prospecting for Petroleum, 2004, 43(5): 438-440. DOI:10.3969/j.issn.1000-1441.2004.05.005 |
| [18] |
李源, 刘伟, 刘微, 等. 各向异性全速度建模技术在山地地震成像中的应用[J]. 石油物探, 2015, 54(2): 157-164. LI Y, LIU W, LIU W, et al. Application of anisotropic full velocity modeling in the mountainous seismic imaging[J]. Geophysical Prospecting for Petroleum, 2015, 54(2): 157-164. DOI:10.3969/j.issn.1000-1441.2015.02.006 |
| [19] |
周进举, 王德利, 靳松, 等. 含倾斜裂隙页岩介质地震波场传播特征研究[J]. 石油物探, 2014, 53(5): 501-508. ZHOU J J, WANG D L, JIN S, et al. Research on seismic wavefield propagation characteristics in shale medium containing tilt fracture[J]. Geophysical Prospecting for Petroleum, 2014, 53(5): 501-508. DOI:10.3969/j.issn.1000-1441.2014.05.001 |
| [20] |
李金磊, 尹正武. 四川盆地焦石坝地区页岩气储层地震定量预测方法[J]. 石油物探, 2015, 54(3): 324-330. LI J L, YIN Z W. Seismic quantitative prediction method of shale gas reservoirs in the Jiaoshiba Area, Sichuan Basin[J]. Geophysical Prospecting for Petroleum, 2015, 54(3): 324-330. DOI:10.3969/j.issn.1000-1441.2015.03.011 |
| [21] |
刘喜武, 刘宇巍, 霍志周, 等. 页岩油气层地震岩石物理计算方法研究[J]. 石油物探, 2016, 55(1): 10-17. LIU X W, LIU Y W, HUO Z Z, et al. Study on seismic rock physics computational method for shale reservoir[J]. Geophysical Prospecting for Petroleum, 2016, 55(1): 10-17. DOI:10.3969/j.issn.1000-1441.2016.01.002 |
| [22] |
印兴耀, 刘欣欣. 储层地震岩石物理建模研究现状与进展[J]. 石油物探, 2016, 55(3): 309-325. YIN X Y, LIU X X. Research status and progress of the seismic rock-physics modeling methods[J]. Geophysical Prospecting for Petroleum, 2016, 55(3): 309-325. DOI:10.3969/j.issn.1000-1441.2016.03.001 |
| [23] |
李金磊. 涪陵焦石坝页岩气层压力预测技术研究[J]. 石油物探, 2017, 56(4): 567-574. LI J L. Pressure prediction of Jiaoshiba shale gas reservoir in the Fuling Shale Gasfield[J]. Geophysical Prospecting for Petroleum, 2017, 56(4): 567-574. DOI:10.3969/j.issn.1000-1441.2017.04.013 |
| [24] |
张水山, 熊晓军, 刘阳, 等. 基于综合信息的三维层速度场建立及其在涪陵页岩气田应用研究[J]. 石油物探, 2018, 57(1): 122-128. ZHANG S S, XIONG X J, LIU Y, et al. Three-dimensional interval velocity building based on comprehensive data analysis and its application in Fuling shale gas field exploration[J]. Geophysical Prospecting for Petroleum, 2018, 57(1): 122-128. DOI:10.3969/j.issn.1000-1441.2018.01.016 |
| [25] |
梁锴, 吴国忱, 印兴耀, 等. 三维TTI介质波动方程分解[J]. 石油地球物理勘探, 2009, 44(1): 19-27. LIANG K, WU G C, YIN X Y, et al. Wave equation decomposition in 3-D TTI Medium[J]. Oil Geophysical Prospecting, 2009, 44(1): 19-27. DOI:10.3321/j.issn:1000-7210.2009.01.005 |
| [26] |
TSVANKIN I. Moveout analysis for transversely isotropic media with a tilted symmetry axis[J]. Geophysical Prospecting, 1997, 45(3): 479-512. DOI:10.1046/j.1365-2478.1997.380278.x |
| [27] |
OPERTO S, VIRIEUX J, RIBODETTI A, et al. Finite-difference frequency-domain modeling of visco-acoustic wave propagation in 2D tilted transversely isotropic (TTI) media[J]. Geophysics, 2009, 74(5): T75-T95. DOI:10.1190/1.3157243 |
| [28] |
OROPEZA E, MCMECHAN G. Common-reflection-point migration velocity analysis of 2D P-wave data from TTI media[J]. Geophysics, 2014, 79(3): C65-C79. DOI:10.1190/geo2013-0295.1 |
| [29] |
SHRAGGE J. Acoustic wave propagation in tilted transversely isotropic media:Incorporating topography[J]. Geophysics, 2016, 81(5): C265-C278. DOI:10.1190/geo2015-0311.1 |
| [30] |
WANG H W, PENG S P, DU W F. Azimuthal AVO for tilted TI medium[J]. Geophysics, 2017, 82(1): C21-C33. DOI:10.1190/geo2015-0430.1 |
| [31] |
WAHEED B U, ALKHALIFAH T. A fast sweeping algorithm for accurate solution of the tilted transversely isotropic eikonal equation using factorization[J]. Geophysics, 2017, 82(6): WB1-WB8. DOI:10.1190/geo2016-0712.1 |
| [32] |
XU S G, LIU Y. Pseudoacoustic tilted transversely isotropic modeling with optimal k-space operator-based implicit finite-difference schemes[J]. Geophysics, 2018, 83(3): T139-T157. DOI:10.1190/geo2017-0472.1 |
| [33] |
ZHANG L J, ZHOU B. Calculation of slowness vectors from ray directions for qP-, qSV-, and qSH-waves in tilted transversely isotropic media[J]. Geophysics, 2018, 83(4): C153-C160. DOI:10.1190/geo2017-0751.1 |
| [34] |
姚振岸, 孙成禹, 谢俊法, 等. 黏弹TTI介质旋转交错网格微地震波场模拟[J]. 石油地球物理勘探, 2017, 52(2): 253-263. YAO Z A, SUN C Y, XIE J F, et al. Micro-seismic forward modeling in visco-elastic TTI media based on rotated staggered grid finite-difference method[J]. Oil Geophysical Prospecting, 2017, 52(2): 253-263. |
| [35] |
黄金强, 李振春, 黄建平, 等. TTI介质Lebedev网格高阶有限差分正演模拟及波型分离[J]. 石油地球物理勘探, 2017, 52(5): 915-927. HUANG J Q, LI Z C, HUANG J P, et al. Lebedev grid high-order finite-difference modeling and elastic wave-mode separation for TTI media[J]. Oil Geophysical Prospecting, 2017, 52(5): 915-927. |
| [36] |
THOMSEN L. Weak elastic anisotropy[J]. Geophysics, 1986, 51(10): 1954-1966. DOI:10.1190/1.1442051 |
| [37] |
吴国忱. 各向异性介质地震波传播与成像[M]. 东营: 中国石油大学出版社, 2006: 1-25. WU G C. Seismic wave propagation and imaging in anisotropic media[M]. Dongying: China University of Petroleum Press, 2006: 1-25. |
| [38] |
吴国忱, 梁锴, 戚艳平. 三维TTI介质相速度和群速度[J]. 地球物理学进展, 2009, 24(6): 2097-2105. WU G C, LIANG K, QI Y P. Phase velocity and group velocity in 3D TTI media[J]. Progress in Geophysics, 2009, 24(6): 2097-2105. DOI:10.3969/j.issn.1004-2903.2009.06.023 |
| [39] |
吴国忱, 梁锴, 印兴耀. TTI介质弹性波相速度与偏振特征分析[J]. 地球物理学报, 2010, 53(8): 1914-1923. WU G C, LIANG K, YIN X Y. The analysis of phase velocity and polarization feature for elastic wave in TTI media[J]. Chinese Journal of Geophysics, 2010, 53(8): 1914-1923. DOI:10.3969/j.issn.0001-5733.2010.08.017 |
| [40] |
WINTERSTEIN D F. Velocity anisotropy terminology for geophysicists[J]. Geophysics, 1990, 55(8): 1070-1088. DOI:10.1190/1.1442919 |



