2. 成都理工大学地球勘探与信息技术教育部重点实验室, 四川成都 610059
2. Key Laboratory of Earth Exploration and Information Techniques of Ministry of Education, Chengdu University of Technology, Chengdu 610059, China
传统的AVO分析技术基于Zoeppritz方程描述反射系数与界面上下地层纵横波速度及密度之间的关系, 利用岩层弹性参数变化对地震振幅的影响, 实现有利油气储层预测[1]。CHAPMAN等[2]基于喷射流理论提出了动态等效介质模型, 描述了岩石中流体流动所引起的速度频散与衰减效应, 研究发现对流体敏感的频散衰减效应会导致地震波产生依赖频率的AVO响应[3-4], 即地震反射系数不仅与入射角有关, 而且随频率变化。而常规的AVO反演技术没有考虑地震波在传播过程中的能量衰减和速度频散, 忽略了频率因素。为了更好地利用AVO属性进行油气检测, SMITH等[5]首次提出了流体因子的概念, 将纵横波速度组合起来作为流体预测因子。CASTAGNA等[6]逐步发展了AVO属性交会技术, 用其识别岩性和油气异常。CONNOLLY[7]提出了利用弹性阻抗识别流体的方法。GRAY[8]基于AVO弹性参数反演进行了储层岩性和流体描述, WHITCOMBE等[9]提出了横波弹性阻抗和扩展的弹性阻抗概念。目前弹性阻抗反演的应用已经很成熟, 敏感流体因子的构建对流体识别起着重要的作用。
流体识别因子多数是基于岩石的弹性参数提出的。RUSSELL等[10]基于多孔弹性介质岩石物理理论, 提出了可以反映孔隙流体弹性效应的Russell流体因子和Gassmann流体项, 具有更敏感的流体识别能力。宁忠华等[11]、王栋等[12]提出了高灵敏度的Russell流体识别因子, 一定程度上提高了流体识别的精度。张玉洁等[13]基于喷流效应对Russell流体因子进行了推广和应用。李超等[14]实现了直接反演Gassmann流体项的流体识别方法。但地震波的反射系数与频率之间关系非常密切, 地震波经过油气储层后出现强吸收衰减、速度频散等异常现象, 表现出反射系数的频率依赖特性, 因此, 流体识别因子的构建应该考虑对流体敏感的频散效应。WILSON等[15]、吴小羊[16]将时频分析技术与传统的AVO技术结合起来(称为依赖频率的AVO分析技术), 初步研究了与频散相关的流体识别可能性。张世鑫等[17]研究了纵波速度频散属性反演方法。程冰洁等[18]利用纵横波速度频散属性提出了频变AVO含气性识别技术。CHEN等[19]利用依赖频率的AVO数值模拟方法研究了储层流体流度变化所致的地震响应异常。高刚[20]对含流体孔隙介质的地震响应特征进行了详细分析并提出了利用纵横波频散属性进行流体识别的方法。张震等[21]在纵横波频散属性反演的基础上实现了基于Russell反射系数的频变AVO反演。刘喜武等[22]对裂缝性孔隙介质进行了频变AVAZ反演方法研究, 但该方法对实际地震数据的反演还存在很多问题。
本文在前人研究的基础上, 基于Gray提出的反射系数公式, 考虑了频率因素, 通过依赖频率的AVO反演方法, 构建了新的频散属性Iλ和Iμ, 并将该频散属性作为一种流体识别因子进行流体识别, 分析了不同频散因子对流体的敏感性。
1 方法原理 1.1 依赖频率的AVO响应数值计算方法利用与频率、时间尺度因子等参数有关的弹性张量, 计算出依赖频率的纵横波速度参数vP(ω)和vS(ω), 基于WIGGINS等[23]提出的AVO三项线性近似公式, 将其拓展至入射角度-频率域, 可建立依赖频率的AVO反射系数分布公式[19]:
| $ {R_{\rm{P}}}\left( {\omega ,\theta } \right) = A\left( \omega \right) + B\left( \omega \right){\sin ^2}\theta + C\left( \omega \right){\tan ^2}\theta {\sin ^2}\theta $ | (1) |
其中,
| $ \left\{ \begin{array}{l} A\left( \omega \right) = \frac{1}{2}\left[ {\frac{{\Delta {v_{\rm{P}}}\left( \omega \right)}}{{{v_{\rm{P}}}\left( \omega \right)}} + \frac{{\Delta \rho }}{\rho }} \right]\\ B\left( \omega \right) = \frac{1}{2}\frac{{\Delta {v_{\rm{P}}}\left( \omega \right)}}{{{v_{\rm{P}}}\left( \omega \right)}} - 4{\left[ {\frac{{{v_{\rm{S}}}\left( \omega \right)}}{{{v_{\rm{P}}}\left( \omega \right)}}} \right]^2}\frac{{\Delta {v_{\rm{S}}}\left( \omega \right)}}{{{v_{\rm{S}}}\left( \omega \right)}} - \\ \;\;\;\;\;\;\;\;\;\;\;2{\left[ {\frac{{{v_{\rm{S}}}\left( \omega \right)}}{{{v_{\rm{P}}}\left( \omega \right)}}} \right]^2}\frac{{\Delta \rho }}{\rho }\\ C\left( \omega \right) = \frac{1}{2}\frac{{\Delta {v_{\rm{P}}}\left( \omega \right)}}{{{v_{\rm{P}}}\left( \omega \right)}} \end{array} \right. $ | (2) |
式中:vP(ω)和vS(ω)分别为上下两层介质依赖频率的纵横波速度的平均, ΔvP(ω)和ΔvS(ω)分别是上下两层介质依赖频率的纵横波速度之差; ρ为上下两层介质密度的平均, Δρ为上下两层介质密度之差。
由上述公式可以得到依赖频率的反射系数, 结合计算出的依赖频率的速度, 由相移法波动方程正演模拟方法可得到依赖频率的合成角度道集。在此采用一维波动方程:
| $ \frac{{{\partial ^2}u}}{{\partial {t^2}}} - {v^2}\frac{{{\partial ^2}u}}{{\partial {z^2}}} = 0 $ | (3) |
其中, u为介质的标量位移, v为依赖频率的纵波速度。对于平面波有:
| $ u = {{\rm{e}}^{ - {\rm{i}}{k_z}z}}{{\rm{e}}^{{\rm{i}}\omega t}} $ | (4) |
将(4)式代入(3)式, 并对t做傅氏变换, 可得到与依赖频率的速度v(ω)相关的垂直波数表达式:
| $ {k_z}\left( \omega \right) = \frac{\omega }{{v\left( \omega \right)}} $ | (5) |
利用频率-波数域相移法[20]进行波场延拓, 即可获得依赖频率的AVO响应。相移式表示为:
| $ u\left( {z + \Delta z,\omega } \right) = u\left( {z,\omega } \right){{\rm{e}}^{{\rm{i}}{k_z}\left( \omega \right)\Delta z}} $ | (6) |
当地下有一个反射界面时, 假设界面两侧介质纵横波速度与密度参数分别为vP1, vS1, ρ1和vP2, vS2, ρ2, 则有Aki-Richards近似表达式为:
| $ \begin{array}{l} R\left( \theta \right) = \frac{1}{2}\left( {\frac{{\Delta {v_{\rm{P}}}}}{{{v_{\rm{P}}}}} + \frac{{\Delta \rho }}{\rho }} \right) - 2\frac{{v_{\rm{S}}^2}}{{v_{\rm{P}}^2}}\left( {2\frac{{\Delta {v_{\rm{S}}}}}{{{v_{\rm{S}}}}} + \frac{{\Delta \rho }}{\rho }} \right) \cdot \\ \;\;\;\;\;\;\;\;\;\;\;{\sin ^2}\theta + \frac{1}{2}\frac{{\Delta {v_{\rm{P}}}}}{{{v_{\rm{P}}}}}{\tan ^2}\theta \end{array} $ | (7) |
式中:
GRAY[8]在Aki近似的基础上, 推导了λ-μ-ρ的纵波线性近似方程:
| $ \begin{array}{*{20}{c}} {R\left( \theta \right) = \left[ {\left( {\frac{1}{4} - \frac{1}{{2\gamma _{{\rm{sat}}}^2}}} \right){{\sec }^2}\theta } \right]\frac{{\Delta \lambda }}{\lambda } + \left[ {\frac{1}{{2\gamma _{{\rm{sat}}}^2}}{{\sec }^2}\theta - } \right.}\\ {\left. {\frac{2}{{\gamma _{{\rm{sat}}}^2}}{{\sin }^2}\theta } \right]\frac{{\Delta \mu }}{\mu } + \left[ {\frac{1}{2} - \frac{{{{\sec }^2}\theta }}{4}} \right]\frac{{\Delta \rho }}{\rho }} \end{array} $ | (8) |
Russell等[10]提出了基于f-μ-ρ的AVO反射系数近似表达式:
| $ \begin{array}{*{20}{c}} {R\left( \theta \right) = \left[ {\left( {\frac{1}{4} - \frac{{\gamma _{{\rm{dry}}}^2}}{{4\gamma _{{\rm{sat}}}^2}}} \right)\frac{{{{\sec }^2}\theta }}{4}} \right]\frac{{\Delta f}}{f} + \left[ {\frac{{\gamma _{{\rm{dry}}}^2}}{{4\gamma _{{\rm{sat}}}^2}}{{\sec }^2}\theta - } \right.}\\ {\left. {\frac{2}{{\gamma _{{\rm{sat}}}^2}}{{\sin }^2}\theta } \right]\frac{{\Delta \mu }}{\mu } + \left[ {\frac{1}{2} - \frac{{{{\sec }^2}\theta }}{4}} \right]\frac{{\Delta \rho }}{\rho }} \end{array} $ | (9) |
式中:λ, μ和ρ分别为界面两侧介质的拉梅系数、剪切模量和密度; γsat2和γdry2分别为界面两侧饱和岩石和岩石骨架纵横波速度比的平方, 此处忽略密度项。由公式(9)可知, 反射系数受γdry2的影响大。由于γdry2的大小受岩性的影响较大(不同岩性的γdry2有所不同, 大小一般在1.33~4.00, 不同的工区需要根据岩性类型测定γdry2的大小), 因此, 公式(9)不具有对所有实际资料的普遍适用性。本文主要基于λ-μ-ρ反射系数公式(8)进行依赖频率的AVO反演, 并将得到的频散属性与公式(9)得到的频散属性If进行对比。其中,
| $ \gamma _{{\rm{dry}}}^2 = \left( {\frac{{{v_{\rm{P}}}}}{{{v_{\rm{S}}}}}} \right)_{{\rm{dry}}}^2\;\;\;\;\gamma _{{\rm{sat}}}^2 = \left( {\frac{{{v_{\rm{P}}}}}{{{v_{\rm{S}}}}}} \right)_{{\rm{sat}}}^2 $ | (10) |
| $ \begin{array}{l} \lambda = \rho v_{\rm{P}}^2 - 2\rho v_{\rm{S}}^2 = \rho v_{\rm{P}}^2\left( {1 - \frac{2}{{\gamma _{{\rm{sat}}}^2}}} \right)\\ \mu = \rho v_{\rm{S}}^2 \end{array} $ | (11) |
则有:
| $ \frac{{\Delta \lambda }}{\lambda } = \left( {\frac{{\partial \lambda }}{{\partial {v_{\rm{P}}}}} + \frac{{\partial \lambda }}{{\partial \rho }}\rho } \right)/\left[ {\left( {1 - \frac{2}{{\gamma _{{\rm{sat}}}^2}}} \right)\rho v_{\rm{P}}^2} \right] = \frac{{\Delta \rho }}{\rho } + 2\frac{{\Delta {v_{\rm{P}}}}}{{{v_{\rm{P}}}}} $ | (12) |
| $ \frac{{\Delta \mu }}{\mu }{\rm{ = }}\frac{{\frac{{\partial \mu }}{\mu }\Delta {v_{\rm{S}}} + \frac{{\partial \mu }}{{\partial \rho }}\rho }}{{\left( {v_{\rm{S}}^2\rho } \right)}} = \frac{{\Delta \rho }}{\rho } + 2\frac{{\Delta {v_{\rm{S}}}}}{{{v_{\rm{S}}}}} $ | (13) |
令:
| $ \begin{array}{l} A\left( \theta \right) = \left( {\frac{1}{4} - \frac{1}{{2\gamma _{{\rm{sat}}}^2}}} \right){\sec ^2}\theta \\ B\left( \theta \right) = \left( {\frac{1}{{2\gamma _{{\rm{sat}}}^2}}{{\sec }^2}\theta - \frac{2}{{\gamma _{{\rm{sat}}}^2}}{{\sin }^2}\theta } \right) \end{array} $ | (14) |
由于vP和vS与频率有关, ΔvP/vP和ΔvS/vS也与频率有关, 因此, Δλ/λ和Δμ/μ与频率有关。由于含流体储层的地震反射存在频散效应, 纵横波速度均与频率相关, 为了得到与频率相关的AVO表达式, 将其扩展到频率域, 将反射系数看成是随频率和入射角变化的函数。由于密度的变化相对于弹性参数λ和μ的变化很小, 此处忽略密度项, 将(8)式与依赖频率的速度频散结合起来, 形成依赖频率的AVO反演公式:
| $ R\left( {{\theta _i},{\omega _j}} \right) \approx A\left( {{\theta _i}} \right)\frac{{\Delta \lambda }}{\lambda }\left( {{\omega _j}} \right) + B\left( {{\theta _i}} \right)\frac{{\Delta \mu }}{\mu }\left( {{\omega _j}} \right) $ | (15) |
对公式(15)中的
| $ \begin{array}{*{20}{c}} {R\left( {{\theta _i},{\omega _j}} \right) \approx A\left( {{\theta _i}} \right)\frac{{\Delta \lambda }}{\lambda }\left( {{\omega _0}} \right) + \left( {{\omega _j} - {\omega _0}} \right)A\left( {{\theta _i}} \right)\frac{\partial }{{\partial \omega }} \cdot }\\ {\left( {\frac{{\Delta \lambda }}{\lambda }} \right) + B\left( {{\theta _i}} \right)\frac{{\Delta \mu }}{\mu }\left( {{\omega _0}} \right) + \left( {{\omega _j} - {\omega _0}} \right)B\left( {{\theta _i}} \right)\frac{\partial }{{\partial \omega }}\left( {\frac{{\Delta \mu }}{\mu }} \right)} \end{array} $ | (16) |
其中,
| $ \begin{array}{l} {I_\lambda } = \frac{\partial }{{\partial \omega }}\left( {\frac{{\Delta \lambda }}{\lambda }} \right)\\ {I_\mu } = \frac{\partial }{{\partial \omega }}\left( {\frac{{\Delta \mu }}{\mu }} \right) \end{array} $ | (17) |
分别定义为拉梅系数λ和剪切模量μ的频散程度。
为了计算Iλ和Iμ, 将(16)式重写为:
| $ \begin{array}{*{20}{c}} {R\left( {{\theta _i},{\omega _j}} \right) - A\left( {{\theta _i}} \right)\frac{{\Delta \lambda }}{\lambda }\left( {{\omega _0}} \right) - B\left( {{\theta _i}} \right)\frac{{\Delta \mu }}{\mu }\left( {{\omega _0}} \right) \approx }\\ {\left( {{\omega _j} - {\omega _0}} \right)A\left( {{\theta _i}} \right){I_\lambda } + \left( {{\omega _j} - {\omega _0}} \right)B\left( {{\theta _i}} \right){I_\mu }} \end{array} $ | (18) |
进一步改写为如下形式:
| $ \begin{array}{l} R\left( {{\theta _i},{\omega _j}} \right) - A\left( {{\theta _i}} \right)\frac{{\Delta \lambda }}{\lambda }\left( {{\omega _0}} \right) - B\left( {{\theta _i}} \right)\frac{{\Delta \mu }}{\mu }\left( {{\omega _0}} \right) \approx \\ \;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} {\left( {{\omega _j} - {\omega _0}} \right)A\left( {{\theta _i}} \right)}&{\left( {{\omega _j} - {\omega _0}} \right)B\left( {{\theta _i}} \right)} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{I_\lambda }}\\ {{I_\mu }} \end{array}} \right] \end{array} $ | (19) |
考虑到m个频率ω1, ω2, …, ωm的情况, 将R(θi, ωj)- A(θi)
| $ \begin{array}{l} \mathit{\boldsymbol{r}} = \\ \left[ {\begin{array}{*{20}{c}} {R\left( {t,1,{\omega _1}} \right) - A\left( {t,1} \right)\frac{{\Delta \lambda }}{\lambda }\left( {t,{\omega _0}} \right) - B\left( {t,1} \right)\frac{{\Delta \mu }}{\mu }\left( {t,{\omega _0}} \right)}\\ \vdots \\ {R\left( {t,1,{\omega _m}} \right) - A\left( {t,1} \right)\frac{{\Delta \lambda }}{\lambda }\left( {t,{\omega _0}} \right) - B\left( {t,1} \right)\frac{{\Delta \mu }}{\mu }\left( {t,{\omega _0}} \right)}\\ \vdots \\ {R\left( {t,n,{\omega _1}} \right) - A\left( {t,n} \right)\frac{{\Delta \lambda }}{\lambda }\left( {t,{\omega _0}} \right) - B\left( {t,n} \right)\frac{{\Delta \mu }}{\mu }\left( {t,{\omega _0}} \right)}\\ \vdots \\ {R\left( {t,n,{\omega _n}} \right) - A\left( {t,n} \right)\frac{{\Delta \lambda }}{\lambda }\left( {t,{\omega _0}} \right) - B\left( {t,n} \right)\frac{{\Delta \mu }}{\mu }\left( {t,{\omega _0}} \right)} \end{array}} \right] \end{array} $ | (20) |
[(ωj-ω0)A(θi) (ωj-ω0)B(θi)]定义为m×n行、2列的矩阵:
| $ \mathit{\boldsymbol{e}} = \left[ {\begin{array}{*{20}{c}} {\left( {{\omega _1} - {\omega _0}} \right)A\left( {t,1} \right)}&{\left( {{\omega _1} - {\omega _0}} \right)B\left( {t,1} \right)}\\ \vdots&\vdots \\ {\left( {{\omega _m} - {\omega _0}} \right)A\left( {t,1} \right)}&{\left( {{\omega _m} - {\omega _0}} \right)B\left( {t,1} \right)}\\ \vdots&\vdots \\ {\left( {{\omega _1} - {\omega _0}} \right)A\left( {t,n} \right)}&{\left( {{\omega _1} - {\omega _0}} \right)B\left( {t,n} \right)}\\ \vdots&\vdots \\ {\left( {{\omega _m} - {\omega _0}} \right)A\left( {t,n} \right)}&{\left( {{\omega _m} - {\omega _0}} \right)B\left( {t,n} \right)} \end{array}} \right] $ | (21) |
将(20)式、(21)式代入(19)式, 可得到:
| $ \mathit{\boldsymbol{r}} \approx \mathit{\boldsymbol{e}}\left[ {\begin{array}{*{20}{c}} {{I_\lambda }}\\ {{I_\mu }} \end{array}} \right] $ | (22) |
利用依赖频率的AVO反演方法时, 需要保留反射系数随频率变化的原始特征。然而由于地震记录可以看成是地震子波与反射系数的褶积, 而且褶积运算本身相当于一个滤波过程, 因此, 接收到的地震数据相当于是对反射系数进行了一次滤波, 导致原有的反射能量受到子波的影响在主频位置能量最大, 而在主频位置两侧能量减小, 即各个频率的能量分布不均衡。因此, 在进行依赖频率的AVO反演时, 需要消除这种由于子波效应导致的能量不均衡现象。这里我们采用广义S变换(Generalized S-transform, GST)[24]进行时频谱分析。
GST定义式为:
| $ \begin{array}{l} S\left( {f,\tau } \right) = \int_{ - \infty }^{ + \infty } {x\left( t \right)\frac{{\left| \beta \right|{{\left| f \right|}^p}}}{{\sqrt {2{\rm{ \mathsf{ π} }}} }} \cdot } \\ \;\;\;\;\;\exp \left[ { - \frac{{{\beta ^2}{{\left( {t - \tau } \right)}^2}{f^{2p}}}}{2}} \right]\exp \left( { - {\rm{i}}2{\rm{ \mathsf{ π} }}f} \right){\rm{d}}t \end{array} $ | (23) |
假设叠前AVO道集的地震道数为n, 采样时间为t, 则可将其写为矩阵形式s(t, n)。对该矩阵利用广义S变换进行时频谱分析, 可得到分解之后不同频率ωi的振幅谱形式为:
| $ s\left( {t,n} \right) \to {S_{\omega i}}\left( {t,n} \right) $ | (24) |
用谱均衡的方法对所有的频率成分进行加权求和, 求取瞬时谱的加权因子, 其表达式为:
| $ w\left( {{\omega _i},n} \right) = \frac{{\max \left[ {{S_{\omega 0}}\left( n \right)} \right]}}{{\max \left[ {{S_{\omega i}}\left( n \right)} \right]}} $ | (25) |
式中:Sω0(n)为第n个接收道参考频率ω0的瞬时振幅谱, Sωi(n)为第n个接收道参考频率ωi的瞬时振幅谱。其中, 参考频率的选择非常关键, 一般选择地震子波的主频, 它的选择正确与否会直接影响反演的结果。许迪[25]提出了一种通过交会分析确定参考频率的方法, 该方法可以根据实际资料的情况准确地确定参考频率, 进而提高反演的准确性。利用(25)式得到加权函数后, 对叠前AVO道集的瞬时谱进行谱均衡处理:
| $ {{S'}_{\omega i}}\left( {t,n} \right) = {S_{\omega i}}\left( {t,n} \right)w\left( {{\omega _i},n} \right) $ | (26) |
为了验证公式(15)中依赖频率的AVO反演方法的准确性和可靠性, 设计了两层“亮点”型储层模型, 模型参数如表 1所示。第一层为页岩, 不发生频散, 厚度500 m, 纵横波速度分别为2 743 m/s, 1 394 m/s, 岩石密度为2.06 g/cm3; 第二层为砂岩, 发生速度频散, 厚度300 m, 孔隙度为15%, 裂缝密度为5%, 在初始饱和含水状态下, 纵波速度为2 835 m/s, 横波速度为1 472 m/s, 密度为2.08 g/cm3, 在填充气的情况下密度为2.04 g/cm3。由于该模型第二层的波阻抗低于第一层的波阻抗, 所以反射系数都为负值, 其绝对值随入射角度的增大而增大, 在叠加剖面上表现为强振幅同相轴。
| 表 1 两层模型参数 |
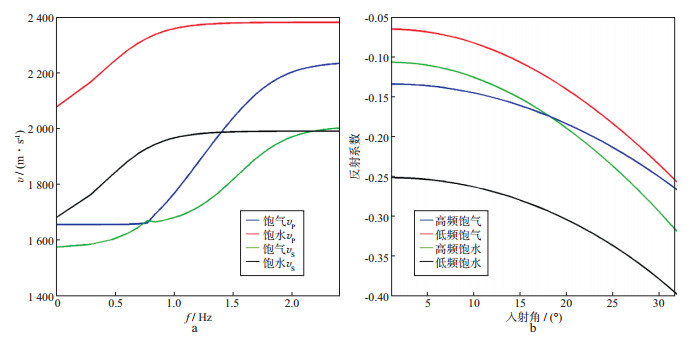
假设水的体积模量为2 GPa, 时间尺度因子τ=5×10-2 s, 气的体积模量为0.2 GPa, 时间尺度因子τ= 4×10-3 s。利用Chapman动态等效介质理论[4]计算饱气与饱水情况下砂岩流体替换时的纵横波速度随频率的变化特征, 如图 1a所示, 频率由0~250 Hz变化, 图中以对数显示。总体来说, 频散饱气的速度低于频散饱水的速度, 且随频率的变化增大。图 1b为高低频限的反射系数随入射角的变化关系, 可以看出不同频率反射系数随入射角变化的趋势不同, 水置换为气时, 高低频限的差距变大, 其频散程度更严重。
|
图 1 纵横波速度随频率的变化(a)与高低频限反射系数随入射角的变化(b) |
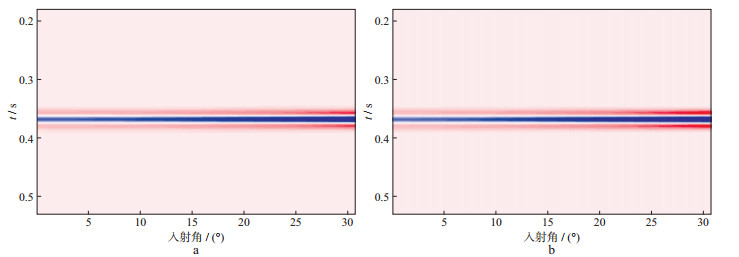
由相移法波动方程正演模拟方法可得到依赖频率的合成角度道集, 如图 2所示。图 2a为频散饱气状态下依赖频率的AVO地震响应, 图 2b为频散饱水状态下依赖频率的AVO地震响应。
|
图 2 两层模型叠前合成地震记录 a 饱气; b 饱水 |
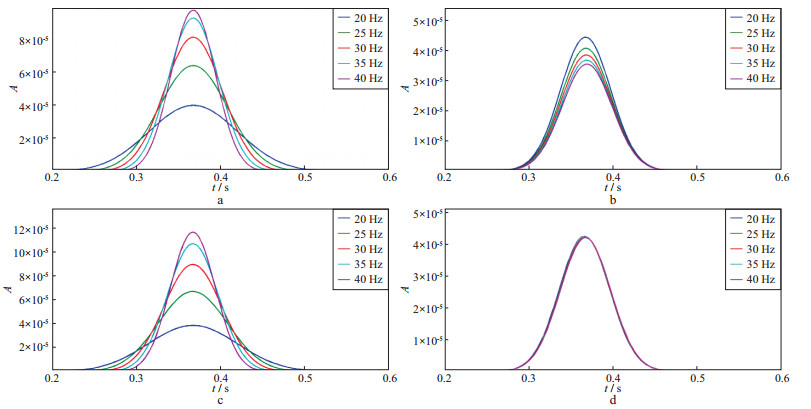
本文选用弹性介质合成记录作为谱均衡的参考振幅谱。选择参考频率为40 Hz, 对频谱分解后频率为20, 25, 30, 35, 40 Hz的振幅谱进行谱均衡处理。图 3对比了饱气和饱水模型零炮检距地震道谱均衡处理前后不同频率的振幅谱, 经过谱均衡处理后, 频散饱气模型在反射界面处仍然保留了频率对振幅产生的作用, 而频散饱水模型各个频率均与40 Hz弹性模型介质振幅一致, 基本消除了频率对振幅产生的影响。
|
图 3 零炮检距地震道谱均衡处理前后不同频率的振幅谱对比 a 饱气谱均衡前; b 饱气谱均衡后; c 饱水谱均衡前; d 饱水谱均衡后 |
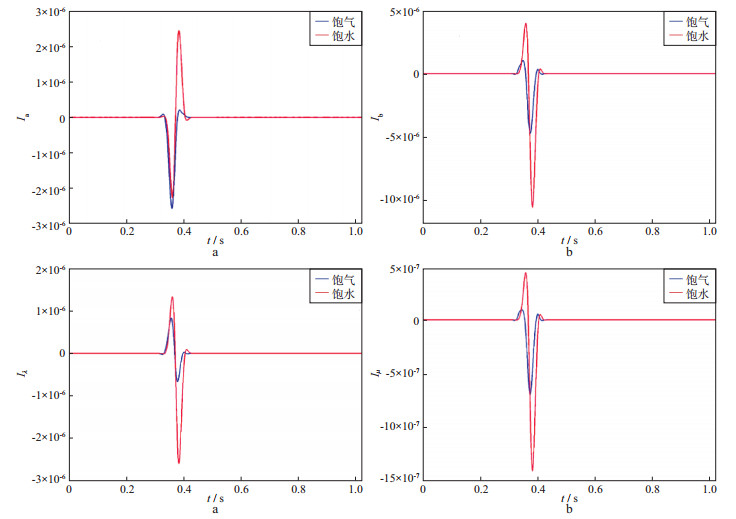
对饱气和饱水两个模型分别进行纵横波频散属性和拉梅系数频散属性依赖频率的AVO反演, 选取35 Hz为参考频率, 反演频率为20, 25, 30, 35, 40 Hz, 结果如图 4所示。可以看出, 饱气和饱水的频散属性在反射界面处均有非常明显的异常, 但敏感性存在差异。当储层饱气和饱水时, 纵波频散属性敏感程度相当, 因此, 难以区分流体类型, 横波频散属性和λ频散属性的敏感程度有一定差异, 且两者特征趋势基本一致; λ的频散属性对不同流体的敏感性差异很大, 而且λ的频散属性值数量级高于μ的频散属性值, 说明λ的频散属性对流体的敏感性更强, 可以更好地指示饱含流体的反射界面位置。因此, 综合利用不同频散属性作为流体识别因子为含流体储层识别提供了更有效的途径。
|
图 4 依赖频率的AVO反演结果 a 纵波频散属性Ia; b 横波频散属性Ib; c λ的频散属性Iλ; d Iμ的频散属性 |
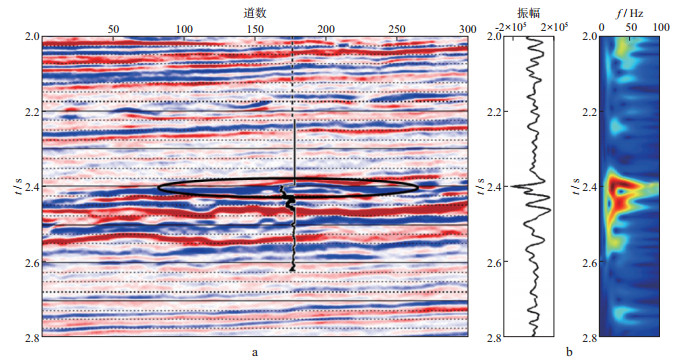
图 5a为某工区叠后地震剖面。由于含气饱和度的差异, 该工区主要存在气层、气水同层、水层三种不同类型的流体, 准确地识别出高含气饱和度的含气储层是研究难点, 其中含流体储层位于图 5a中黑色椭圆所圈位置, 时间延续范围在2.38~2.42 s。抽取储层位置第177道(井旁道)数据进行时频分析, 结果如图 5b所示, 可以看出, 在2.38~2.60 s之间, 振幅能量较强, 气层的主频在20~50 Hz。
|
图 5 某工区叠后地震剖面(a)及其第177道的时频分析结果(b) |
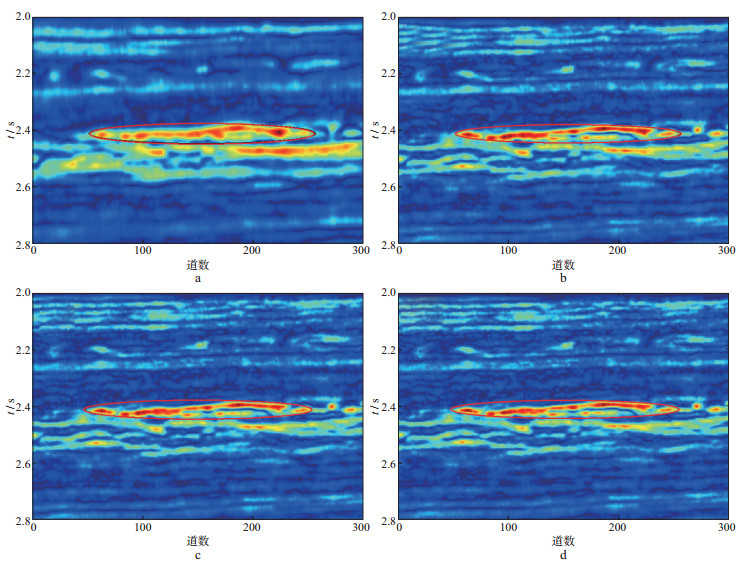
为了解地震波的振幅、衰减等特征信息随频率变化的规律和趋势, 并与叠前数据反演出的频散属性剖面进行对比, 利用广义S变换时频分析方法对研究区叠后地震剖面各道做频谱分解处理, 抽取频率为20, 40, 80, 100 Hz的振幅谱剖面, 如图 6所示。可以看出, 瞬时频率剖面也可以一定程度上刻画出包含流体的储层位置, 但周围背景干扰较大, 且随着频率的增大, 可识别的储层厚度也逐渐变小。
|
图 6 瞬时频率剖面 a 20 Hz; b 40 Hz; c 80 Hz; d 100 Hz |
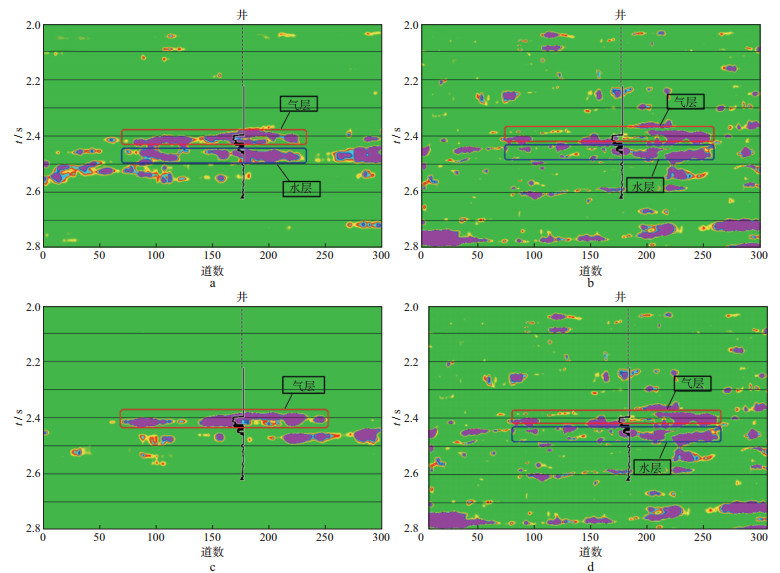
在进行频散属性反演前, 分析资料的实际情况认为地震记录的主频在25 Hz左右, 因此确定以25 Hz为最优参考频率。反演的过程中共选12个频率, 分别为10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65 Hz。在进行谱均衡时, 我们根据资料的情况追踪并提取了t=2.27 s所对应的强反射地震层位作为参考层。图 7为反演的纵横波频散属性以及λ和μ的频散属性剖面, 可以看出:频散程度较强的位置与含流体储层的位置对应很好, 纵波频散属性可以较好地识别出气层和水层, 但难以区分其流体类型; 横波频散属性和剪切模量μ的频散属性难以准确区分出含气储层位置, 受周围背景干扰大; 而λ的频散属性对含气储层的敏感性很强, 可以很好地刻画含气储层的位置, 并且受背景干扰小。综合分析结果可以更好地反映出含气储层的位置所在。
|
图 7 频散属性反演结果对比 a 纵波频散属性; b 横波频散属性; c λ的频散属性; d μ的频散属性 |
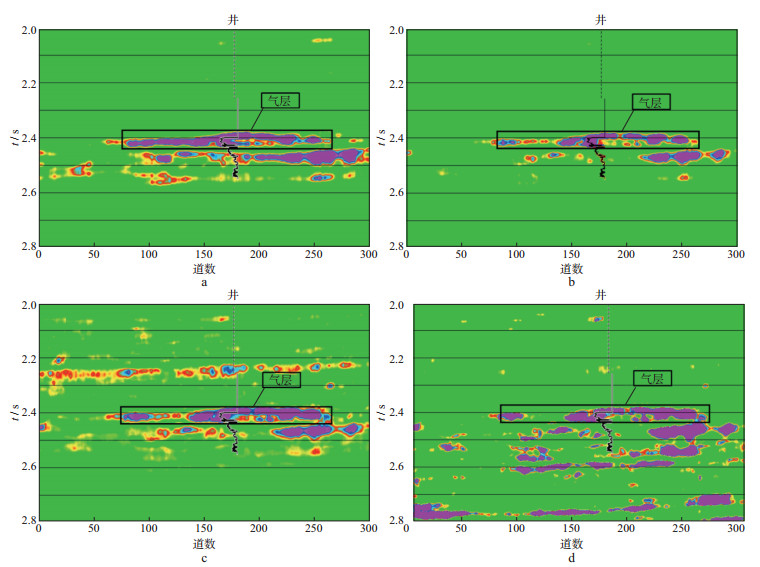
为了说明λ的频散属性识别高含气饱和度储层的有效性, 进一步利用张震等[21]提出的Gassmann流体项f的频散属性If进行了对比分析。基于RUSSELL等[10]提出的f-μ-ρ反射系数公式反演求得的频散属性If受γdry2的影响大(γdry2的大小受储层岩性的影响一般在1.33~4.00之间), 因此对不同γdry2下得到的If进行了对比分析, 如图 8所示。当γdry2为1.33, 2.33, 3.00, 4.00时, If频散剖面对含流体储层的识别效果不同, 但对气层都有一定程度的识别效果。只有当γdry2为2左右时, If频散剖面才具有接近于Iλ的识别效果, 但仍然不如λ的频散因子对含流体储层的敏感性高。而频散属性Iλ不受岩性的影响, 对含气储层的敏感性很高, 因此, 基于λ-μ-ρ反射系数的频变AVO反演更具有普遍适用性。
|
图 8 Gassmann流体项f的频散属性 a γdry2=1.33; b γdry2=2.33; c γdry2=3.00; d γdry2=4.00 |
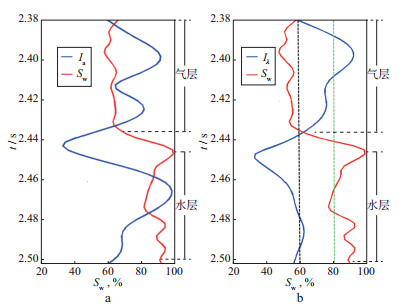
为了更清楚地对比分析Iλ和纵波频散属性Ia识别高含气饱和度储层的效果, 我们抽取第177道(井旁道)Iλ与Ia的频散数据曲线并分别与含水饱和度曲线Sw进行了对比分析, 如图 9所示。可以看出, Iλ对含水饱和度的敏感性更高, 可以更好地区分出流体类型, Sw小于60%时, 主要为气层, 频散异常较强, Sw大于80%时主要为水层, 频散异常较弱;而Ia对流体的敏感性较差, 难以区分出流体类型。因此, λ的频散属性可以更好地识别出高含气饱和度有效储层。
|
图 9 第177道(井旁道)纵波频散属性(a)和λ的频散属性(b)与含水饱和度曲线对比 |
本文基于Gray反射系数公式, 通过依赖频率的AVO反演方法, 构建了拉梅系数λ和剪切模量μ的频散属性, 通过谱均衡方法进行反演优化, 提高了反演精度, 为利用拉梅系数λ和剪切模量μ的频散属性进行储层预测和流体识别提供了一条新的途径。λ的频散属性对含气储层的敏感性很高, 且受背景干扰小, 可以优于纵横波频散属性更为精确地识别出含气储层所在位置, 为进一步区分流体类型提供一定参考。
| [1] | OSTRANDER W J. Plane-wave reflection coefficients for gas sands at non-normal angles of incidence[J]. Geophysics, 1984, 49(10): 1637-1648 DOI:10.1190/1.1441571 |
| [2] | CHAPMAN M, ZATSEPIN S V, CRAMPIN S. Derivation of a microstructural poroelastic model[J]. Geophysical Journal International, 2002, 151(2): 427-451 DOI:10.1046/j.1365-246X.2002.01769.x |
| [3] | CHAPMAN M, LIU E, LI X Y. The influence of abnormally high reservoir attenuation on the AVO signature[J]. The Leading Edge, 2005, 24(11): 1120-1125 DOI:10.1190/1.2135103 |
| [4] | CHAPMAN M, LIU E, LI X Y. The influence of fluid-sensitive dispersion and attenuation on AVO analysis[J]. Geophysical Journal International, 2006, 167(1): 89-105 DOI:10.1111/gji.2006.167.issue-1 |
| [5] | SMITH G C, GIDLOW P M. Weighted stacking for rock property estimation and detection of gas[J]. Geophysics Prospecting, 1987, 35(9): 993-1014 DOI:10.1111/gpr.1987.35.issue-9 |
| [6] | CASTAGNA J P, SWAN H W, FOSTER J D. Framework for AVO gradient and intercept interpretation[J]. Geophysics, 1998, 63(3): 948-956 DOI:10.1190/1.1444406 |
| [7] | CONNOLLY P. Elastic impedance[J]. The Leading Edge, 1999, 18(4): 438-452 DOI:10.1190/1.1438307 |
| [8] | GRAY D. Elastic inversion for Lame parameters[J]. Expanded Abstracts of 72nd Annual Internat SEG Mtg, 2002: 197-200 |
| [9] | WHITCOMBE D N, CONNOLLY P A, REAGAN R L. Extended elastic impedance for fluid and lithology prediction[J]. Geophysics, 2002, 67(1): 63-67 DOI:10.1190/1.1451337 |
| [10] | RUSSELL B H, HEDLIN K, HILTERMAN F J. Fluid-property discrimination with AVO:a Biot-Gassmann perspective[J]. Geophysics, 2003, 68(1): 128-138 |
| [11] |
宁忠华, 贺振华, 黄德济. 基于地震资料的高灵敏流体识别因子[J].
石油物探, 2006, 45(3): 239-241 NING Z H, HE Z H, HUANG D J. High sensitive fluid identification based on seismic data[J]. Geophysical Prospecting for Petroleum, 2006, 45(3): 239-241 |
| [12] |
王栋, 贺振华, 黄德济. 新流体识别因子的构建与应用分析[J].
石油物探, 2009, 48(2): 141-145 WANG D, HE Z H, HUANG D J. Construction of a new fluid identification factor and analysis on its application[J]. Geophysical Prospecting for Petroleum, 2009, 48(2): 141-145 |
| [13] |
张玉洁, 刘洪, 崔栋, 等. 基于挤喷流效应的Russell流体因子推广及应用[J].
地球物理学报, 2016, 59(10): 3091-3097 ZHANG Y J, LIU H, CUI D, et al. Construction and application of the Russell fluid factor with squirt flow effect[J]. Chinese Journal of Geophysics, 2016, 59(10): 3091-3097 |
| [14] |
李超, 张金淼, 朱振宇. 深部储层流体因子直接反演方法[J].
石油物探, 2017, 56(6): 827-833 LI C, ZHANG J M, ZHU Z Y. Direct inversion for fluid factor of deep reservoirs[J]. Geophysical Prospecting for Petroleum, 2017, 56(6): 827-833 |
| [15] | WILSON A, CHAPMAN M, LI X Y. Frequency-dependent AVO inversion[J]. Expanded Abstracts of 79th Annual Internat SEG Mtg, 2009, 28(1): 341-345 |
| [16] |
吴小羊. 基于频谱分析技术的频散AVO反演研究[D]. 北京: 中国地质大学(北京), 2010
WU X Y. Frequency dependent AVO inversion using spectral decomposition techniques[D]. Beijing: China University of Geosciences(Beijing), 2010 http://cdmd.cnki.com.cn/Article/CDMD-10491-2010250478.htm |
| [17] |
张世鑫, 印兴耀, 张广智, 等. 纵波速度频散属性反演方法研究[J].
石油物探, 2011, 50(3): 219-224 ZHANG S X, YIN X Y, ZHANG G Z, et al. Inversion method for the velocity dispersion-dependent attribute of P-wave[J]. Geophysical Prospecting for Petroleum, 2011, 50(3): 219-224 |
| [18] |
程冰洁, 徐天吉, 李曙光. 频变AVO含气性识别技术研究与应用[J].
地球物理学报, 2012, 55(2): 608-613 CHENG B J, XU T G, Li S G. Research and application of frequency dependent AVO analysis for gas recognition[J]. Chinese Journal of Geophysics, 2012, 55(2): 608-613 |
| [19] | CHEN X H, HE Z H, GAO G, et al. A fast combined method for fluid flow related frequency-dependent AVO modeling[J]. Expanded Abstracts of 83rd Annual Internat SEG Mtg, 2013: 3454-3459 |
| [20] |
高刚. 含流体孔隙介质地震响应特征分析及流体识别方法[D]. 成都: 成都理工大学, 2013
GAO G. Analysis of seismic response characteristics in fluid-saturated porous media and study on fluid identification method[D]. Chengdu: Chengdu University of Technology, 2013 |
| [21] |
张震, 印兴耀, 郝前勇. 基于AVO反演的频变流体识别方法[J].
地球物理学报, 2014, 57(12): 4171-4183 ZHANG Z, YIN X Y, HAO Q Y. Frequency-dependent fluid identification method based on AVO inversion[J]. Chinese Journal of Geophysics, 2014, 57(12): 4171-4183 |
| [22] |
刘喜武, 董宁, 刘宇巍. 裂缝性孔隙介质频变AVAZ反演方法研究进展[J].
石油物探, 2015, 54(2): 210-217 LIU X W, DONG N, LIU Y W. Progress on frequency-dependent AVAZ inversion for characterization of fractured porous media[J]. Geophysical Prospecting for Petroleum, 2015, 54(2): 210-217 |
| [23] | WIGGINS R, KENNY G S, MCCLURE C D. Method for determining and displaying the shear wave reflectivities of a geologic formation: European0113944[P]. 1983-01-17 |
| [24] |
陈学华, 贺振华, 黄德济. 广义S变换及其时频滤波[J].
信号处理, 2008, 24(1): 28-31 CHEN X H, HE Z H, HUANG D J. Generalized S transform and its time-frequency filtering[J]. Signal Processing, 2008, 24(1): 28-31 |
| [25] |
许迪. 基于叠前数据反演的流体识别方法[D]. 成都: 成都理工大学, 2015
XU D. The new inversion method for fluid identification based on pre-stack seismic data[D]. Chengdu: Chengdu University of Technology, 2015 http://cdmd.cnki.com.cn/Article/CDMD-10616-1015312670.htm |




