2. 阿美远东(北京)商业服务有限公司国际研发中心, 北京 100102;
3. 中海石油研究中心, 北京 100027
2. International Research and Development Center, Aramco Far East Business Services Company Limited, Beijing 100013, China;
3. CNOOC Research Center, Beijing 100027, China
立体层析反演是层析反演类速度建模方法中极具特色的一种方法。立体层析将一个局部相干同相轴在炮道集与检波点道集内的射线参数水平分量(Psx, Prx, 以下简称地表观测P参数)纳入到数据空间之中, 不仅使得数据空间的准备相比传统反射层析更为简便, 也使得立体层析成为运动学层析反演方法中唯一一种可以同时反演速度结构与反射点位置的方法[1-4]。李振伟等[5]将该方法首次应用于中国南海实际二维地震数据处理, 获得了可靠的反演结果。反演得到的速度模型能够满足叠前深度偏移的需要。王宇翔等[6]利用高效率的结构张量实现了在叠前数据域提取P参数的快速算法, 使得基于结构张量的二维高密度立体层析反演成为现实。杨锴等[7]基于非降阶汉密尔顿在直角坐标系下实现了三维立体层析反演。XING等[8]将该算法首次用于南海某三维实际数据反演, 同样利用结构张量获取三维立体层析数据空间, 获得了理想的速度建模效果。
在实践中我们体会到, 立体层析数据空间的正确提取是保证其反演成功的最关键因素。在BILLETTE等[3]和李振伟等[5]的工作中, 立体层析数据空间提取通过倾斜叠加能量谱的交互分析拾取获得, 这是一种稳健但效率较低的数据空间提取方式。该提取方式在二维数据中还可以使用, 但对于三维数据其应用潜力十分有限。此外, BILLETTE等[1]认为单次反射与单次绕射都可以用于立体层析反演。这个观点值得商榷。我们认为, 绕射波不适用于基于运动学信息的绝大多数层析成像算法, 至少对立体层析而言, 真正有用的仅是一次反射波的运动学信息。这一观点在本文的数值算例中得到了证实。因此, 在提取立体层析数据空间时应尽量避开非一次反射波(如绕射波、多次波和侧面反射)的干扰, 保证提取到的运动学信息都来自一次反射波。
然而, 无论是基于倾斜叠加能量谱的交互拾取还是基于结构张量的自动拾取, 都无法完全避开上述非一次反射波的干扰, 例如:基于倾斜叠加能量谱的交互拾取对多次波的识别或许有效, 但是对绕射波与侧面波则无能为力; 基于结构张量的自动拾取尽管效率十分令人满意, 但对于绕射波、多次波和侧面反射均无法自动识别。总之, 无论使用何种快速算法, 直接从叠前数据体中提取数据空间必然遇到无法辨识多次波、绕射波以及侧面反射的问题; 其次, 由于信噪比和能量强度的原因, 自动拾取往往导致浅层的数据点获取密度很高, 但是深层的数据点信息则大幅减少, 无法保证数据空间的均匀性。这对于中深部目标体的反演相当不利。
CHAURIS等[9]揭示了偏移速度分析中地下成像域运动学信息与地表观测P参数之间的定量关系, 给出了在速度不正确的情况下, 基于叠前成像空间中提取的运动学属性参数(它们分别是共偏移距成像剖面上的构造倾角与共偏移距成像点道集内的剩余曲率), 通过特定的修正公式, 计算得到正确的地表观测P参数。基于上述思想, GUILLAUME等[10]提出了通过“运动学反偏移+校正”获得立体层析数据空间的流程, 这个工作的意义在于, 即便对于不正确的初始速度获得的不正确的成像结果, 通过高效的运动学信息提取和有效的校正手段, 依然可以获得准确的地表观测P参数。这个流程的应用价值在于它提供了一个在成像域确定数据点位置的选择。也就是说, 我们可以根据初始成像道集, 结合自己的地质认识, 避开原始数据上可能存在的绕射、多次波、侧面波等各种非一次反射波的干扰, 优选出最重要、最关键的数据点, 服务于后续的斜率层析或者其它需要P参数的各种快速成像算法[11-12]。需要指出的是, 基于叠前数据体的高效结构张量自动拾取与利用反偏移重建数据空间并不矛盾, 这恰恰构成了立体层析在实际应用过程的两步法:先通过结构张量算法在数据域自动拾取获得初始数据空间, 基于初始数据空间反演得到一个很好的初始速度模型; 然后在观察初始成像数据体后, 通过人工识别去除与绕射波、多次波、侧面反射有关的数据点, 提炼出更为合理的数据空间, 使得立体层析反演精度得到进一步提升。
值得注意的是, 当射线参数水平分量和射线出射到地表的坐标也被纳入到数据空间后, 会导致层析反演有多种可能的实现路径。本文首先分析了立体层析的理论基础——反射地震学中重要的“走时一一映射”条件, 针对立体层析数据空间的特点分析了各种可能的实现策略, 并指出本文的实现策略与所有这些可能策略的关系; 然后详细介绍结构张量以及“运动学反偏移+校正”获得立体层析数据空间的方法原理; 最后利用一个典型的深水理论数据验证了上述算法设计与实现策略的正确性, 证实其可以获得更可靠的数据空间, 获得更合理的反演结果。
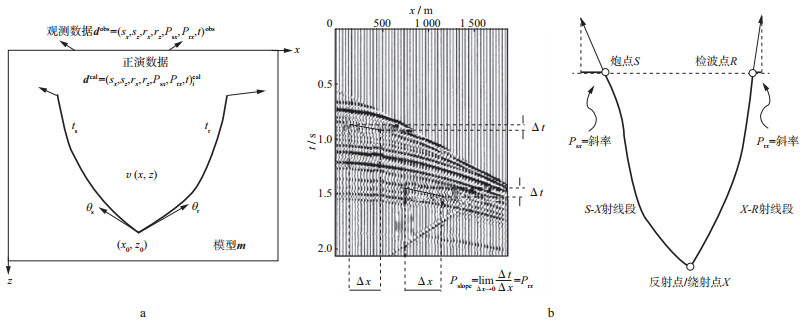
1 立体层析的数据空间、模型空间以及“走时一一映射条件”首先以二维情况为例介绍立体层析反演的模型空间与数据空间。如图 1a所示, 反射射线可以认为是从反射点出发, 分别以不同的散射角θs, θr向炮点位置和检波点位置出射两根射线构成的。当射线到达观测面时, 两条透射射线的出射方向、走时之和以及炮点和检波点位置构成立体层析数据空间。二维立体层析的数据分量(d)和模型分量(m)为:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{d}} = {{\left( {s,r,{P_{{\rm{s}}x}},{P_{{\rm{r}}x}},t} \right)}_i}}\\ {i = 1,2, \cdots ,{n_{{\rm{data}}}}} \end{array} $ | (1a) |
| $ \mathit{\boldsymbol{m}} = \left[ {{{\left( {{x_0},{z_0},{\theta _{\rm{s}}},{\theta _{\rm{r}}}} \right)}_i},i = 1,2, \cdots ,{n_{{\rm{data}}}};v\left( {x,z} \right)} \right] $ | (1b) |
|
图 1 二维立体层析的模型与数据分量 a立体层析的模型与数据分量; b同相轴斜率与慢度矢量之间的关系 |
式中:s, r分别为炮点和检波点横坐标; t为双程走时; x0, z0分别为反射点的横、纵坐标; θs, θr分别为炮点和检波点两侧的散射角; v(x, z)为模型空间中的速度信息。
公式(1a)表达了拾取到的ndata个数据点, 每个数据点对应于一个反射过程。公式(1b)则表达了模型空间信息。
立体层析数据空间中最重要的数据分量是射线参数水平分量(或慢度矢量水平分量)。图 1中所示Psx可在共检波点道集内搜索局部同相轴斜率得到, Prx可在共炮点道集内搜索局部同相轴斜率得到。当考察在图 1b所显示的炮记录中某一局部同相轴时, 由几何关系及射线参数水平分量的定义可得:
| $ {P_{{\rm{slope}}}} = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\Delta t}}{{\Delta x}} = {P_{{\rm{r}}x}} $ | (2) |
式中:Pslope为局部同相轴的斜率; Prx为检波点处射线参数水平分量。公式(2)表明共炮记录内同相轴斜率必对应于检波点处慢度矢量水平分量Prx。由炮检互易原理可知, 共检波记录内同相轴斜率必对应于炮点处慢度矢量的水平分量Psx。只要能够正确提取P参数, 其对应的旅行时和坐标信息均可轻易得到。
对应于二维立体层析的Fréchet偏导数矩阵为:
| $ \mathit{\boldsymbol{F}} = \left[ {\begin{array}{*{20}{c}} {\frac{1}{{{\sigma _T}}}\frac{{\partial T}}{{\partial {x_0}}}}&{\frac{1}{{{\sigma _T}}}\frac{{\partial T}}{{\partial {z_0}}}}&{\frac{1}{{{\sigma _T}}}\frac{{\partial T}}{{\partial {\theta _{\rm{s}}}}}}&{\frac{1}{{{\sigma _T}}}\frac{{\partial T}}{{\partial {\theta _{\rm{r}}}}}}&{\frac{1}{{{\sigma _T}}}\frac{{\partial T}}{{\partial v}}}\\ {\frac{1}{{{\sigma _S}}}\frac{{\partial {S_x}}}{{\partial {x_0}}}}&{\frac{1}{{{\sigma _S}}}\frac{{\partial {S_x}}}{{\partial {z_0}}}}&{\frac{1}{{{\sigma _S}}}\frac{{\partial {S_x}}}{{\partial {\theta _{\rm{s}}}}}}&{\frac{1}{{{\sigma _S}}}\frac{{\partial {S_x}}}{{\partial {\theta _{\rm{r}}}}}}&{\frac{1}{{{\sigma _S}}}\frac{{\partial {S_x}}}{{\partial v}}}\\ {\frac{1}{{{\sigma _R}}}\frac{{\partial {R_x}}}{{\partial {x_0}}}}&{\frac{1}{{{\sigma _R}}}\frac{{\partial {R_x}}}{{\partial {z_0}}}}&{\frac{1}{{{\sigma _R}}}\frac{{\partial {R_x}}}{{\partial {\theta _{\rm{s}}}}}}&{\frac{1}{{{\sigma _R}}}\frac{{\partial {R_x}}}{{\partial {\theta _{\rm{r}}}}}}&{\frac{1}{{{\sigma _R}}}\frac{{\partial {R_x}}}{{\partial v}}}\\ {\frac{1}{{{\sigma _{{P_{{\rm{s}}x}}}}}}\frac{{\partial {P_{{\rm{s}}x}}}}{{\partial {x_0}}}}&{\frac{1}{{{\sigma _{{P_{{\rm{s}}x}}}}}}\frac{{\partial {P_{{\rm{s}}x}}}}{{\partial {z_0}}}}&{\frac{1}{{{\sigma _{{P_{{\rm{s}}x}}}}}}\frac{{\partial {P_{{\rm{s}}x}}}}{{\partial {\theta _{\rm{s}}}}}}&{\frac{1}{{{\sigma _{{P_{{\rm{s}}x}}}}}}\frac{{\partial {P_{{\rm{s}}x}}}}{{\partial {\theta _{\rm{r}}}}}}&{\frac{1}{{{\sigma _{{P_{{\rm{s}}x}}}}}}\frac{{\partial {P_{{\rm{s}}x}}}}{{\partial v}}}\\ {\frac{1}{{{\sigma _{{P_{{\rm{r}}x}}}}}}\frac{{\partial {P_{{\rm{r}}x}}}}{{\partial {x_0}}}}&{\frac{1}{{{\sigma _{{P_{{\rm{r}}x}}}}}}\frac{{\partial {P_{{\rm{r}}x}}}}{{\partial {z_0}}}}&{\frac{1}{{{\sigma _{{P_{{\rm{r}}x}}}}}}\frac{{\partial {P_{{\rm{r}}x}}}}{{\partial {\theta _{\rm{s}}}}}}&{\frac{1}{{{\sigma _{{P_{{\rm{r}}x}}}}}}\frac{{\partial {P_{{\rm{r}}x}}}}{{\partial {\theta _{\rm{r}}}}}}&{\frac{1}{{{\sigma _{{P_{{\rm{r}}x}}}}}}\frac{{\partial {P_{{\rm{r}}x}}}}{{\partial v}}} \end{array}} \right] $ | (3) |
式中:σ为层析矩阵每一行物理量的数量级不同设置的均衡系数; Sx,Rx分别为地表出射炮点和检波点位置; T为总旅行时。可以看到, 常规的旅行时层析由于其模型空间仅包含速度v, 其数据空间仅包含走时, 因此, 其Fréchet偏导数矩阵仅相当于公式(3)中右上角的子矩阵。立体层析Fréchet偏导数矩阵通过在背景介质中进行动力学射线追踪, 然后利用射线扰动理论[13]建立数据空间残差各分量与模型空间残差各分量之间的线性关系后计算得到。
注意, 图 1a表达了反射地震学成像理论中的一个非常重要的成像条件:走时一一映射条件。事实上走时一一映射条件是立体层析与共角度域成像共同的理论基础。该条件由TEN KROODE等[13]通过傅里叶积分算子理论予以严格证明。其物理意义是:地震数据中任意一个局部相干的同相轴, 可以由炮点坐标、检波点坐标、同相轴在两坐标处的局部斜率以及同相轴的局部走时来描述, 它严格对应于从反射点出发、到达炮检点的一个射线对。在速度模型正确的前提下, 记录到的一个局部相干的地震数据同相轴将成像于地下唯一的一个深度点。在反射地震学观测中, 违反这个条件的几率几乎为零。因此该条件有广泛的适用范围。XU等[14]以此条件为准则审视地震数据中的各种道集, 发现共炮道集、共偏移距道集均违反此条件的要求, 只有共角度道集才满足这个条件。在获得这个认识后, 最终在最小二乘Kirchhoff真振幅反演成像框架下导出了输出真振幅角度域成像道集的成像条件。
走时一一映射条件的重要性不仅在于正确的理解角度域成像道集, 还在于它同时揭示了对层析成像而言一些非常重要的事实:①既然炮检点处出射方向确定的一个射线对, 唯一对应于地下的一个反射点, 那么在层析反演中, 就可以将反射问题转化为透射问题, 从而回避传统反射层析中反射层深度与速度耦合性; ②方向信息可以更好地约束射线对, 减少其模糊性。方向信息明确的射线对可以给速度分析提供额外的约束信息, 使得在复杂地质结构下的层析成像成为可能。正是这些重要的认识促使BILLETTE等[1]提出了一种充分利用地震波场所有运动学信息的全新层析方法, 即立体层析反演。
体现这些优势的关键在于同相轴的斜率信息(即P参数)必须进入层析反演的数据空间。通过一个简单的概念实验即可说明同相轴斜率对速度模型的约束作用。如图 1b所示, 当地表炮点位置(S)、检波点位置(R)、炮点处的慢度矢量水平分量(Psx)和检波点处的慢度矢量水平分量(Prx)已知时, 由炮点至检波点的反射过程S→X(反射点)→R唯一确定。分别根据Psx, Prx于炮点、检波点反向朝地下出射射线至两条射线相交时停止, 当速度模型正确时, 两条射线相交在正确的反射点, 反之当速度模型不正确时, 两条射线的交点为错误的反射点。那么如何判断两条射线是否相交在正确的位置呢?走时信息提供了另外的约束条件, 即射线在正确的速度模型上传播时, 两条射线的走时之和恰与反射走时相等, 反之则会出现残差。
显然, 共炮点、共检波点道集上同相轴的斜率为层析反演提供了除走时外的新的运动学约束信息, 即数据空间可以由更加丰富的运动学波场属性参数来刻画, 可以认为立体层析反演的优势主要得益于同相轴斜率的引入, 使得数据空间和模型空间都得到了合理的扩展。
2 基于立体层析数据空间的反演算法设计与实现策略分析从上一节中的概念出发, 即可对基于P参数的层析反演进行归纳和总结。当我们除了拥有旅行时和坐标信息, 同时拥有炮点和检波点处的P参数信息时, 反演方案将会有很多。从残差所属域的角度来看:数据域有旅行时差、P参数差、炮检点坐标差; 成像域残差则体现为剩余曲率(RMO)不为零, 即所谓的不聚焦现象。数据残差的多样性决定了反演时可以有多种策略供选择。注意无论使用哪种算法, 其数据残差各分量与模型残差各分量之间的一阶扰动关系, 都可以通过文献[13]中的射线扰动理论来建立。图 2显示了联合P参数与旅行时的各种层析反演策略。
|
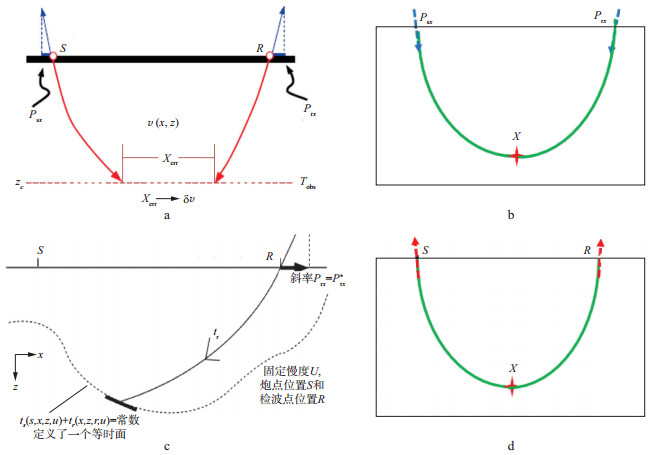
图 2 联合P参数与旅行时的各种层析反演策略分析示意 1第1种方案(利用坐标残差Xerr来反演速度); b第2种方案(用P参数成像, 而后利用数据域旅行时残差信息反演背景速度); c第3种方案(利用数据域δPsx残差信息反演背景速度); d第4种方案(利用P参数与旅行时残差信息反演背景速度) |
第1种方案如图 2a所示:先根据炮点和检波点的P参数信息进行运动学偏移, 即利用Psx和Prx分别从炮检点往下追射线, 当ts+tr=Tobs时射线追踪停止(Tobs为初至旅行时)。由于速度模型错误, 射线追踪停止时必然发生欠聚焦现象, 即两个射线终点水平方向有坐标差Xerr。这时即可利用坐标差Xerr来反演速度。这种方法的实质是, 用P参数和走时一起成像, 利用成像域欠聚焦信息反演背景速度。这正是SWORD[16]最早的基于同相轴斜率信息反演背景速度的思路。
第2种方案如图 2b所示:先根据炮点和检波点处的P参数信息进行反向射线追踪, 直到两支射线在地下相交。相当于完全用P参数成像(即利用P参数确定反射点的位置), 因为速度还不准确, 这时ts+tr必然不等于Tobs, 于是就可以用旅行时差反演速度。这种方法的实质是, 用P参数成像, 而后利用数据域旅行时残差信息反演背景速度。熊凯[17]对这种算法进行了测试, 在简单层状模型时反演效果较为理想, 但是, 当模型趋于复杂时必须排除两根射线夹角过小的情况, 否则会出现由于旅行时差计算不准而导致速度更新量发生异常的情况。
第3种方案如图 2c所示:先分别计算炮点和检波点的旅行时表, 找到地下的等Tobs旅行时面, 再从检波点按Prx出射射线找到地下反射点, 再反追到炮点端, 通过射线正演获得的Psx与实际观测到的Psx*必然有残差δPsx。这时即可利用δPsx更新背景速度。这种方法的特点是, 用检波点端的P参数和旅行时Tobs联合成像, 利用数据域δPsx残差信息反演背景速度。这个实现思路由CHAURIS等[9]首先提出。后面要介绍的“运动学反偏移+校正”就是基于这个想法获得的。
第4种方案如图 2d所示:以初始速度的运动学偏移(即向地下出射射线)初始化地下反射点位置, 从地下反射点往地表出射射线, 找到炮点和检波点, 建立δPsx, δPrx, δT与δv, δx0, δz0之间的扰动关系, 从而更新背景速度和反射点的位置。这种方法的特点是, 运动学偏移初始化反射点后确定地下反射点与地表的局部同相轴的关系, 再反偏移到地表得到数据域残差δPsx, δPrx, δT来更新背景速度和反射点位置。
第5种方案如图 1a所示:通过运动学偏移初始化地下反射的位置和出射角, 根据地下出射角从地下点往地表出射射线, 不追求找到正确的炮点与检波点坐标, 因此射线出射到地表后会有δPsx, δPrx, δT, δSx, δRx 5种数据残差。这种方法的特点是, 运动学偏移获得初始反射点位置后, 即可确定地下反射点与地表的局部同相轴的关系, 反偏移到地表得到数据域残差δPsx, δPrx, δT, δSx, δRx, 然后利用这些数据残差更新背景速度模型。这其实就是传统立体层析的实现思路。
本文的思路是将第3种方案略作调整后与第5种方案相结合。CHAURIS等[9]提出基于炮道集推导的P参数校正公式, 同时指出, 在共偏移距成像道集内有等价的校正公式。由于Kirchhoff偏移算法输出共偏移距成像道集是最常规选项, 因此在共偏移距成像域实现“运动学反偏移+P参数校正”是一个更为自然的选择。我们在共偏移距域推导了相应的运动学反偏移与校正公式。此外, 在实施校正后获得了正确的P参数之后, 原则上认为坐标残差和旅行时残差不需要再进入数据空间, 但考虑到实际数据中运动学反偏移的精度问题以及反演的稳定性问题, 我们依然将所有的数据残差即δPsx, δPrx, δT, δSx, δRx都纳入到数据空间用于反演。我们认为对实际数据而言这是最为稳妥的处理方案。
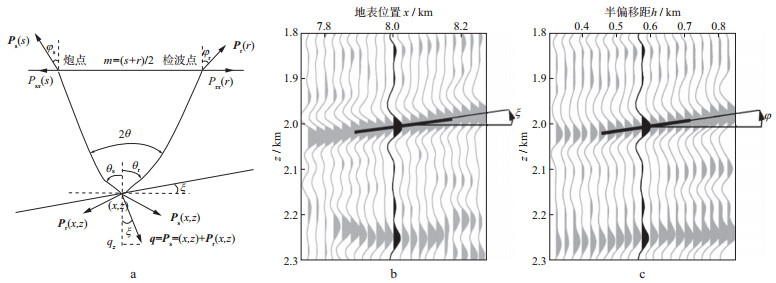
3 “运动学反偏移+P参数校正”的算法原理及其实现流程本节对CHAURIS等[9]提出的“运动学反偏移+P参数校正”的推导过程做一详细介绍。不同于原文基于共炮道集的公式推导, 本文基于同样的思想, 直接利用共偏移距域与共中心点域的P参数(Pmx和Phx)导出适用于共偏移距成像剖面与共偏移距成像道集的“运动学反偏移+P参数校正”公式, 更易于为读者所理解。图 3为运动学反偏移示意图。
|
图 3 运动学反偏移示意 a地下模型信息与地表数据信息的几何关系; b共偏移距成像剖面(在其上拾取构造倾角ξ); c偏移距域共成像点道集(在其上拾取剩余曲率的斜率tan φ) |
在Kirchhoff偏移中, 成像条件满足这样的等时曲线:
| $ {t_{\rm{s}}}\left( {s,x,z,u} \right) + {t_{\rm{r}}}\left( {s,x,z,u} \right) = {t^ * }\left( {h,m} \right) $ | (4) |
式中:u是地下速度; ts, tr分别是地下成像点(x, z)到炮点、检波点的单程走时; h=(s-r)/2是半偏移距; m=(s+r)/2是炮点、检波点的中点; t*(h, m)对应于一根射线从炮点S出发、经过地下某点反射回到地表检波点R的总旅行时。
固定横向位置x和速度模型u, 基于公式(4)对深度z, 半偏移距h和中点m做全微分可得:
| $ \begin{array}{*{20}{c}} {\left( {\frac{{\partial {t_{\rm{s}}}}}{{\partial z}}\left| {_{s,x,u}} \right. + \frac{{\partial {t_{\rm{r}}}}}{{\partial z}}\left| {_{x,r,u}} \right.} \right){\rm{ \mathsf{ δ} }}z + \frac{{\partial {t_{\rm{s}}}}}{{\partial h}}\left| {_{x,z,u}} \right.{\rm{ \mathsf{ δ} }}h + \frac{{\partial {t_{\rm{r}}}}}{{\partial h}}\left| {_{x,z,u}} \right. \cdot }\\ {{\rm{ \mathsf{ δ} }}h + \frac{{\partial \left( {{t_{\rm{s}}} + {t_{\rm{r}}}} \right)}}{{\partial m}}{\rm{ \mathsf{ δ} }}m = \frac{{\partial {t^ * }}}{{\partial m}}{\rm{ \mathsf{ δ} }}m + \frac{{\partial {t^ * }}}{{\partial h}}{\rm{ \mathsf{ δ} }}h} \end{array} $ | (5) |
根据半偏移距h的定义h=(s-r)/2和中点m的定义m=(s+r)/2, 有:
| $ \begin{array}{l} \frac{{\partial s}}{{\partial h}} = 1\\ \frac{{\partial r}}{{\partial h}} = - 1 \end{array} $ | (6) |
由此可得(具体推导见附录A):
| $ \begin{array}{l} {P_{hx}} = {P_{{\rm{s}}x}} - {P_{{\rm{r}}x}}\\ {P_{mx}} = {P_{{\rm{s}}x}} + {P_{{\rm{r}}x}} \end{array} $ | (7a) |
| $ \begin{array}{l} P_{hx}^ * = P_{{\rm{s}}x}^ * - P_{{\rm{r}}x}^ * \\ P_{mx}^ * = P_{{\rm{s}}x}^ * + P_{{\rm{r}}x}^ * \end{array} $ | (7b) |
式中:Psx*, Prx*代表正确的射线出射到地表的P参数信息; Psx, Prx代表以初始速度模型, 从构造倾角ξ出发, 向地表出射射线获得的视射线出射信息。将(6)式代入(5)式, 可得到:
| $ \begin{array}{*{20}{c}} {\left( {\frac{{\partial {t_{\rm{s}}}}}{{\partial z}}\left| {_{s,x,u}} \right. + \frac{{\partial {t_{\rm{r}}}}}{{\partial z}}\left| {_{x,r,u}} \right.} \right){\rm{ \mathsf{ δ} }}z + {P_{{\rm{s}}x}}{\rm{ \mathsf{ δ} }}h - {P_{{\rm{r}}x}}{\rm{ \mathsf{ δ} }}h + }\\ {\frac{{\partial \left( {{t_{\rm{s}}} + {t_{\rm{r}}}} \right)}}{{\partial m}}{\rm{ \mathsf{ δ} }}m = \frac{{\partial {t^ * }}}{{\partial m}}{\rm{ \mathsf{ δ} }}m + \frac{{\partial {t^ * }}}{{\partial h}}{\rm{ \mathsf{ δ} }}h} \end{array} $ | (8) |
因为:
| $ \frac{{\partial \left( {{t_{\rm{s}}} + {t_{\rm{r}}}} \right)}}{{\partial m}}\left| {_{x,z,h,u}} \right. = \frac{{\partial {t^ * }}}{{\partial m}}\left| {_h} \right. $ | (9) |
| $ \left( {\frac{{\partial {t_{\rm{s}}}}}{{\partial z}}\left| {_{s,x,u}} \right. + \frac{{\partial {t_{\rm{r}}}}}{{\partial z}}\left| {_{x,r,u}} \right.} \right){\rm{ \mathsf{ δ} }}z + \left( {{P_{{\rm{s}}x}} - {P_{{\rm{r}}x}}} \right){\rm{ \mathsf{ δ} }}h = P_{hx}^ * {\rm{ \mathsf{ δ} }}h $ | (10) |
将(7a)式代入(10)式, 得到:
| $ \left( {\frac{{\partial {t_{\rm{s}}}}}{{\partial z}}\left| {_{s,x,u}} \right. + \frac{{\partial {t_{\rm{r}}}}}{{\partial z}}\left| {_{x,r,u}} \right.} \right){\rm{ \mathsf{ δ} }}z = P_{hx}^ * {\rm{ \mathsf{ δ} }}h - {P_{hx}}{\rm{ \mathsf{ δ} }}h $ | (11) |
如图 3a所示, 根据慢度矢量的定义有:
| $ \begin{array}{l} \frac{{\partial {t_{\rm{s}}}}}{{\partial z}}\left| {_{s,x,u}} \right. = u\left( {x,z} \right)\cos {\theta _{\rm{s}}}\\ \frac{{\partial {t_{\rm{r}}}}}{{\partial z}}\left| {_{x,r,u}} \right. = u\left( {x,z} \right)\cos {\theta _{\rm{r}}} \end{array} $ | (12) |
式中:θs, θr是射线与垂向的夹角。
| $ \cos {\theta _{\rm{s}}} + \cos {\theta _{\rm{r}}} = 3\cos \beta \cos \xi $ | (13) |
式中:β是反射角, 即射线与反射界面法向的夹角; ξ是构造倾角。
根据(12)式和(13)式, 得到:
| $ \frac{{\partial {t_{\rm{s}}}}}{{\partial z}}\left| {_{s,x,u}} \right. + \frac{{\partial {t_{\rm{r}}}}}{{\partial z}}\left| {_{x,r,u}} \right. = 2u\left( {x,z} \right)\cos \beta \cos \xi $ | (14) |
令α=2ucosβcosξ, 将(14)式代入(8)式, 得:
| $ P_{hx}^ * - {P_{hx}} = \alpha \tan \varphi $ | (15) |
根据(9)式, 得到:
| $ P_{mx}^ * - {P_{mx}} = 0 $ | (16) |
将(7b)式代入(15)式和(16)式, 得到:
| $ \left( {P_{{\rm{s}}x}^ * - {P_{{\rm{s}}x}}} \right) + \left( {P_{{\rm{r}}x}^ * - {P_{{\rm{r}}x}}} \right) = 0 $ | (17a) |
| $ \left( {P_{{\rm{s}}x}^ * - {P_{{\rm{s}}x}}} \right) - \left( {P_{{\rm{r}}x}^ * - {P_{{\rm{r}}x}}} \right) = \alpha \tan \varphi $ | (17b) |
公式(17)将时间域射线的出射斜率信息与成像域共成像点道集内的运动学信息建立了联系, 同时也证明了立体层析中拟合出射斜率与成像域速度分析拉平道集内同相轴等价。
从(4)式出发亦可推导出成像剖面倾角的公式, 固定s, r, u, 基于公式(4)对x, z求全微分, 得:
| $ \begin{array}{l} \left( {\frac{{\partial {t_{\rm{s}}}}}{{\partial z}}\left| {_{s,x,u}} \right. + \frac{{\partial {t_{\rm{r}}}}}{{\partial z}}\left| {_{x,r,u}} \right.} \right){\rm{ \mathsf{ δ} }}z + \\ \;\;\;\;\;\;\;\left( {\frac{{\partial {t_{\rm{s}}}}}{{\partial z}}\left| {_{s,z,u}} \right. + \frac{{\partial {t_{\rm{r}}}}}{{\partial z}}\left| {_{z,r,u}} \right.} \right){\rm{ \mathsf{ δ} }}x = 0 \end{array} $ | (18) |
化简(18)式得到:
| $ \frac{{{\rm{ \mathsf{ δ} }}z}}{{{\rm{ \mathsf{ δ} }}x}} = - \frac{{{{P'}_{{\rm{s}}x}} + {{P'}_{{\rm{r}}x}}}}{{{{P'}_{{\rm{s}}z}} + {{P'}_{{\rm{r}}z}}}} = - \tan \xi $ | (19) |
式中:P′sx, P′sz代表炮点端的射线向下传播到反射点时的慢度分量; P′rx, P′rz代表检波点端的射线向下传播到反射点时的慢度分量。可以看出, 共偏移距成像剖面的构造倾角与成像点道集内RMO无关, 需要单独搜索。
从公式(17)可以看出, 当速度错误时, Psx, Prx信息不可能与Psx*, Prx*一致。但是, 我们可以通过公式(17)从错误的构造倾角ξ以及在共偏移距成像点道集(CIG)上拾取的剩余曲率φ出发, 将Psx, Prx校正为正确的射线参数水平分量Psx*, Prx*的校正公式。GUILLAUME等[10]将这种从成像空间发射射线到地表, 并实施校正得到正确地表观测P参数的过程命名为运动学反偏移。
公式(17)的应用价值在于, 利用不正确的初始速度模型和不正确的构造成像信息, 依然有可能获得正确的立体层析数据空间。毕竟用于叠前深度偏移的初始速度信息不可能完全正确, 因此相应的初始深度成像结果也不可能完美。但是初始成像结果依然有两个优点:①大部分绕射波得到了收敛归位; ②侧面反射与多次波的能量将聚焦到不合理的位置上。此时, 处理人员结合自己的地质认识即可从共偏移距成像剖面上识别出比较可靠的、同时在横向和深度上分布也比较均匀的一次反射波的成像位置, 然后利用结构张量算法提取这些位置处的构造倾角与剩余深度差信息, 通过公式(7)实施运动学反偏移即可获得可靠的、均匀分布的立体层析数据空间。这时再实施立体层析反演将会获得更为可靠的反演结果。
需要强调的是, 运动学反偏移对初始速度模型有一定要求。如果初始速度模型品质不够好, 无论在共偏移距成像点道集内提取RMO或在共偏移距成像剖面内提取构造倾角都将难以进行, 那么后续的反偏移和校正也都失去了前提。不过好在生产中的初始深度模型一般来自于叠前时间偏移速度分析的时深转换或者初至波层析。就本文而言, 我们的初始模型来自全自动拾取的数据域立体层析, 无论通过何种方式获取初始模型其品质都不会差, 基于该模型的初始成像能够满足结构张量算法的拾取要求。
根据上述算法原理即可确定运动学反偏移+P参数校正的实现过程。运动学反偏移的实施需要在偏移后的叠前道集内实施。首先, 在半偏移距h成像剖面内, 拾取感兴趣的反射点位置(x, z, h), 接着搜索构造倾角ξ; 然后, 在共偏移距方向上搜索剩余曲率的斜率tanφ; 根据构造倾角ξ, 即可在初始速度模型上做射线追踪到地表, 拟合地表偏移距2h, 此时即可得到地表出射炮检点位置Sx, Rx, 出射斜率信息Psx, Prx, 地表出射走时ts, tr。由于速度不正确, 需要根据公式(17)进行校正。校正后即可获得正确的地表出射斜率Psx*, Prx*。由于炮检点坐标Sx, Rx及地表出射走时T在校正之前就已经获得, 至此立体层析所需的数据空间已经全部准备就绪。
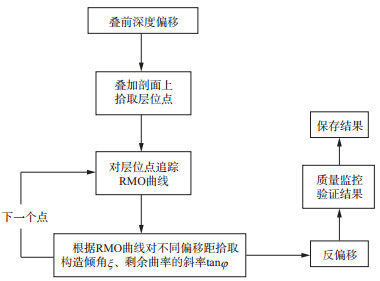
上述实现过程可以总结为如图 4所示的技术流程, 可简述为:根据初始速度模型进行共偏移距Kirchhoff叠前深度偏移; 对小偏移距剖面进行叠加得到成像剖面, 在成像剖面上人工选取立体层析所需的数据点位置; 根据这些位置利用搜索到的RMO信息追踪出大偏移距剖面内的数据点位置, 然后基于这些位置即可利用结构张量开展搜索, 分别获得该位置处的构造倾角与RMO曲线斜率信息; 基于构造倾角和偏移距信息即可向地表出射射线找到对应的炮点和检波点, 获得Psx, Prx; 此时公式(17)所需的输入信息已全部得到, 校正后就可获得正确的慢度水平分量(即同相轴斜率)Psx*, Prx*。
|
图 4 运动学反偏移拾取参数流程 |
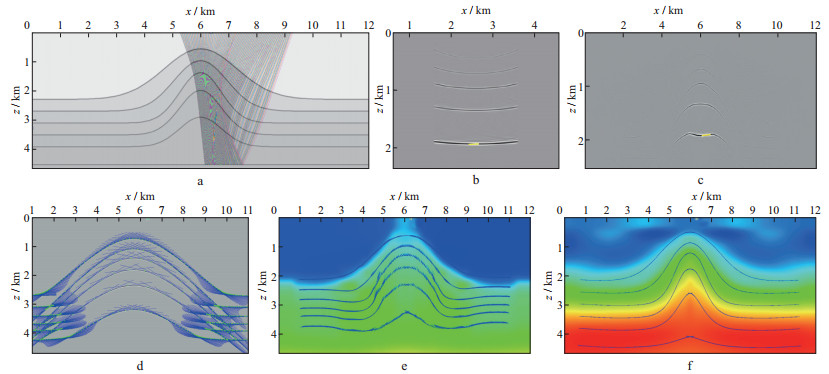
图 5显示了“运动学反偏移+校正”在一个相对简单的6层背斜模型上的测试结果, 主要测试了算法的校正精度。图 5a展示了真实模型以及模拟某一炮的反射射线信息。基于该模型共正演模拟401炮, 每炮401道, 炮间距20m, 道间距10m, 记录时间为4s。图 5b展示了基于该模型模拟获得的多炮正演记录中的一炮反射射线信息。将真实模型乘以0.9, 并略做光滑后实施Kirchhoff叠前深度偏移(PSDM)后、6.2km处的CIG和2.0km共偏移距成像剖面分别如图 5b和图 5c所示, 可以看到, 由于速度偏小, 出现明显的欠偏移现象。图 5d展示了将运动学反偏移+P参数校正后得到的数据点位置与斜率信息贴合到对应的2.0km共偏移距同相轴上后的质量监控显示结果, 可以看出, 其贴合效果相当不错。当然, 仅从视觉上判断其校正精度是不够的, 必须有相应的反演结果才更有说服力。图 5e和图 5f分别显示了利用未做校正的数据空间实施反演的结果和利用校正后的数据空间实施反演的结果, 可以看出, 反演结果差别很大, 显示了校正公式(17)的正确性和实施这种校正的必要性。
|
图 5 运动学反偏移+P参数校正在简单理论数据上的精度测试 a真实模型及某一炮的反射射线信息; b真实模型乘以0.9后实施PSDM后的CIG(6.2km处); c真实模型乘以0.9后实施PSDM的2.0km共偏移距成像剖面; d基于真实模型乘以0.9后实施PSDM的2.0km共偏移距成像剖面实施反偏移+P参数校正后获得的正确反射点位置以及P参数信息; e利用未做校正的数据空间实施反演的结果; f利用校正后的数据空间实施反演的结果 |
如前所述, 立体层析数据空间的提取可以在数据域直接进行, 也可以在成像域提取构造倾角和RMO信息后再实施“运动学反偏移+校正”后换算得到, 因此, 有一个高效率、高精度的运动学信息提取方法至关重要。梯度平方结构张量是图像处理的一种高效的边缘检测算法[18]。如果将地震数据视为一张图像, 结构张量算法是一个用于检测地震数据局部同相轴倾角的极好方法。
二维梯度平方结构张量算法原理可概括如下。对于一张二维图像, 为了检测其边缘, 须首先计算出每一个样点处x, y方向的梯度gx, gy。对于低信噪比图像, 为了提高方向预测的稳定性, 避免梯度矢量在图像边缘两侧互相抵消, 引入梯度平方张量矩阵, 使得同一走向但是方向相反的梯度矢量不至于相互抵消, 反而可以相互增强。实际二维地震资料可以视为一个低信噪比图像, 这是梯度平方张量算法适用于地震数据同相轴检测的重要原因。
对二维图像中某一样点而言, 其梯度平方张量矩阵定义如下:
| $ \mathit{\boldsymbol{G}} = \left( {\begin{array}{*{20}{c}} {g_x^2}&{{g_x}{g_y}}\\ {{g_x}{g_y}}&{g_y^2} \end{array}} \right) $ | (20) |
式中:gx, gy分别表示该样点处的梯度水平分量与梯度垂直分量。梯度平方张量的含义是图像中某一样点处, 对应于单一走向的梯度方向。为提高低信噪比图像中走向信息预测的稳定性, 在该样点附近的邻域内, 比如一个4样点×4样点区域内统计16个这样的梯度平方张量, 并将它们加权叠加得到一个光滑的梯度平方张量矩阵G′将有助于获得该样点位置处比较稳定的走向信息。权系数可以设置为本区域内定义的一个高斯函数, 或可以简单设为1即平均权值, 视具体的搜索效果而定。不妨将G′写为:
| $ \mathit{\boldsymbol{G'}} = \left( {\begin{array}{*{20}{c}} {\left\langle {g_x^2} \right\rangle }&{\left\langle {{g_x}{g_y}} \right\rangle }\\ {\left\langle {{g_x}{g_y}} \right\rangle }&{\left\langle {g_y^2} \right\rangle } \end{array}} \right) $ | (21) |
式中:〈·〉代表光滑后的梯度平方。获得光滑的梯度平方张量矩阵G′之后, 针对半正定矩阵G′, 通过求解特征方程|G′-λI|=0可求得其特征值与特征向量:
| $ \mathit{\boldsymbol{G'}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{v}}_1}}&{{\mathit{\boldsymbol{v}}_2}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\lambda _1}}&0\\ 0&{{\lambda _2}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{v}}_1^{\rm{T}}}&{\mathit{\boldsymbol{v}}_2^{\rm{T}}} \end{array}} \right] $ | (22) |
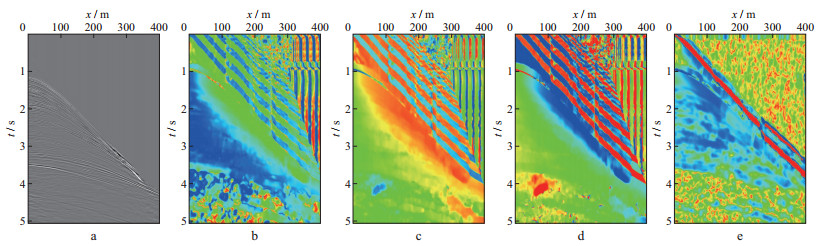
式中:λ1为最大特征值, 对应于张量在特征张量方向v1的能量; λ2为最小特征值, 对应于张量在特征张量方向v2的能量。(λ1-λ2)/λ1表示线性度, 反映局部方向的一致性。对于地震数据而言, 线性度的含义等价于同相性。特征向量描述了图像局部线性结构的方向性。特征向量v1正交于图像的主结构方向, 特征向量v2平行于图像的主结构方向。图 6显示了南海某实际单炮记录以及应用梯度平方结构张量算法提取的属性参数剖面。其中, 图 6e所示的线性度剖面其实就是地震学家所说的同相性剖面, 可以看到, 线性度剖面(图 6e)和图 6a所示的炮数据同相轴有很好的对应关系。注意, 这个线性度的计算完全依赖于之前计算的特征值和特征向量, 因此, 如果图 6b, 图 6c和图 6d的计算有误, 那么线性度将和同相轴失去对应关系, 由此可以看出, 梯度平方结构张量算法稳定, 完全可以用于实际地震数据的局部同相轴斜率估计。
|
图 6 梯度平方张量算法在某单炮记录上的应用效果 a输入实际炮记录(图像); b特征值λ1; c特征值λ2; d局部走向; e线性度(同相性) |
王宇翔等[6]对比了梯度平方结构张量与常规的倾斜叠加及平面波摧毁算法的计算成本, 结果表明, 结构张量算法的计算效率高于平面波摧毁近一个数量级, 高于局部倾斜叠加两个数量级。因此, 该算法用于立体层析数据空间的准备是一个自然的选择。本文数值实验中涉及的地表观测P参数提取以及成像域中的构造倾角与RMO信息的提取, 都是应用梯度平方结构张量算法实现的。图 7a和图 7b分别显示了结构张量算法在共成像点道集(CIG)上搜索RMO以及在共偏移距成像剖面上搜索构造倾角的结果, 可以看出, 搜索到的位置与同相轴的波峰叠合非常一致, 表现出该算法的优秀性能。

|
图 7 梯度平方结构张量算法在叠前成像域的应用效果 a在共成像点道集(CIG)上搜索RMO; b在共偏移距成像剖面上搜索构造倾角 |
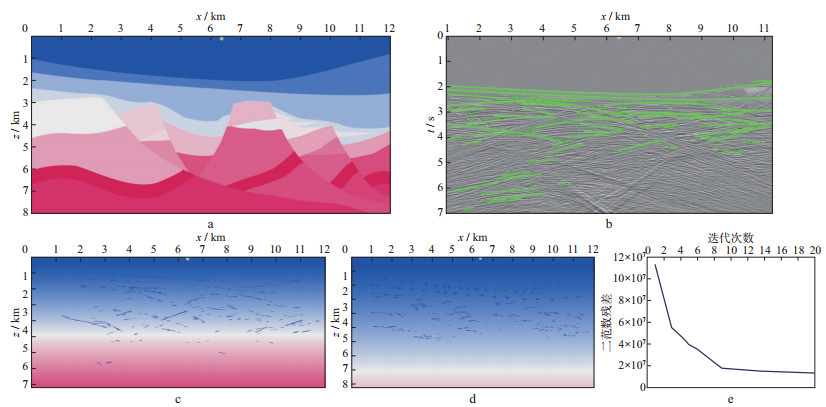
二维理论数据基于图 8a所示的理论模型得到。该模型针对南海深水某工区的复杂断陷模型设计。基于该模型正演共计401炮, 每炮401道, 道间距10m, 炮间距20m, 正演数据通过高阶有限差分声波模拟计算得到。反演之前首先利用结构张量算法自动搜索出相干性比较好的同相轴斜率信息, 再结合王宇翔等[6]提出的波峰判断准则和线性度准则筛出地震记录上的有效数据点。我们在这个理论数据上每隔200m偏移距做一次拾取, 共获得2.2×104个数据点。图 8b显示了1km偏移距剖面内搜索到的数据点信息, 可以看到, 尽管使用了比较高的线性度门槛, 4.5s以下依然有不少数据点信息, 这些数据点大多来自于绕射波。绕射是立体层析中的射线正演无法表达的波现象, 数据空间中存在绕射波的运动学信息使得反演难以正常收敛。图 8c显示了第1次迭代后的结果, 可以看出, 这时倾角反演结果已有异常发生。图 8d显示了第20次迭代的结果, 深部甚至出现了接近90°倾角的垂直构造, 显然不正常。图 8e显示了20次迭代的二范数目标泛函下降曲线, 可以看到, 这个结果无法令人满意。
|
图 8 在数据域直接搜索数据空间获得的反演结果(基于中海油复杂断陷模型理论数据) a真实模型; b共偏移距剖面内通过结构张量自动拾取获得的数据点信息; c第1次迭代后结果; d第20次迭代后结果; e目标泛函下降曲线 |
在初次反演的基础上采用运动学反偏移+校正的方法对数据空间进行提炼, 这样的实施策略有很明确的优点。尽管初始叠前深度偏移(PSDM)成像剖面并不是最好的成像结果, 但是已经可以辨识出大部分断点的位置。图 9显示了运动学反偏移+校正后的数据点的反演结果。图 9a是基于图 8d所示模型实施PSDM后, 用一部分小偏移距剖面叠加获得的初始成像结果。尽管成像结果不是很理想, 但是在人工拾取数据点的过程中, 通过人工辨识依然可以避开绝大多数的对应于绕射波的成像点, 因此, 第2次选择的数据点都无一例外落在了反射界面上。对于实际应用而言, 非一次反射波的信息除了绕射波外还可能包含多次波甚至侧面波, 因此, 这种人工拾取更有意义。
|
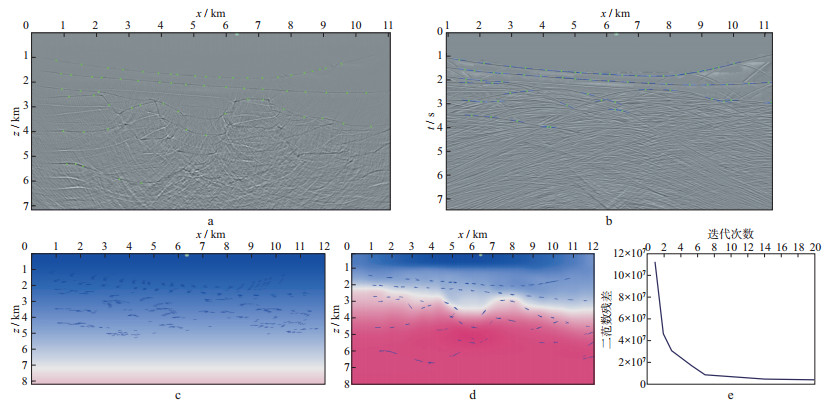
图 9 基于运动学反偏移+校正后的反演结果 a基于初始成像拾取的反射点; b将反射点信息反偏移到时间域的新数据点信息; c第1次迭代后结果; d第20次迭代后结果; e目标泛函下降曲线 |
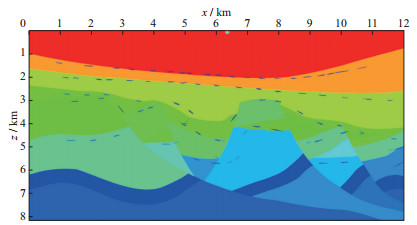
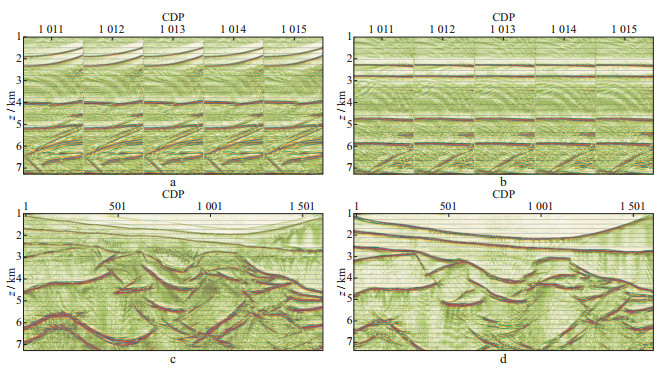
图 9b显示了对图 9a所示的数据点实施运动学反偏移到共偏移距剖面后的质量控制结果, 可以看出, 其绝对数量相比图 8b有明显减少, 事实上, 反偏移+校正后仅获得5000个左右的数据点, 但是后续的反演中证明, 这些数据点反而能提供更为合理的反演结果。图 9c和图 9d显示了第1次和第20次迭代后的反演结果。与图 8d相比, 图 9d中无论是速度反演还是倾角反演结果都要稳定得多。图 9e显示了20次迭代后的二范数目标泛函下降曲线, 可以看到, 随着迭代次数的增多, 二范数目标泛函会非常稳定地下降, 收敛结果明显优于图 8e。图 10是将图 9反演中获得的倾角信息重叠在真实模型上的质量控制显示, 可以看到, 倾角信息和浅中部的主要构造界面叠合得非常一致。图 11显示了基于初始反演速度和新反演速度的PSDM结果, 可以看到, 应用新模型获得的CIG相比用初始模型获得的CIG有更好的聚焦效果, 同时新模型对应的最终成像剖面的分辨率更好, 充分体现了反偏移后获得的数据点更为合理。如果基于图 11所示的偏移结果再挖掘出一些深部构造的数据点, 重复上述流程, 可以进一步提高对应于深部构造的反演精度, 提高深层构造的成像品质。
|
图 10 将新反演结果中倾角信息叠合到真实模型 |
|
图 11 基于初始反演速度的PSDM结果与基于新反演速度的PSDM结果对比 a基于初始反演速度PSDM得到的CIG; b基于新反演速度PSDM得到的CIG; c基于初始反演速度实施PSDM得到的成像剖面; d基于新反演速度实施PSDM得到的成像剖面 |
当射线参数水平分量和射线出射坐标都被纳入到数据空间后, 会导致层析反演有多种可能的实现路径。本文深入分析了基于立体数据空间实现层析反演的多种可能性, 设计了一种首先在数据域获取初始数据空间并实施初步立体层析, 而后在初始成像体内搜索运动学信息、实施运动学反偏移+校正获取更可靠的数据空间的两步法策略。该方法应用于断陷模型理论数据的结果证明了这种策略的优势。
虽然初始模型并非完美, 但是通过初始成像体上的运动学信息, 利用运动学反偏移+校正可以获得在地表观测得到的正确射线参数水平分量信息。这些信息正是立体层析所需的数据空间。运动学反偏移+校正获得数据空间的优势在于:通过在初始成像剖面上人工选择数据点, 可以避开原始数据上可能存在的绕射波、多次波、侧面波等各种非一次反射波的干扰。需要指出, 基于叠前数据体的高效结构张量自动拾取与利用反偏移+校正重建数据空间并不矛盾, 这恰恰体现了两步法的优势:先通过高效率的结构张量算法实施自动拾取获得初始数据空间, 基于初始数据空间反演得到一个较为理想的初始速度模型; 然后在此基础上通过运动学反偏移去除与绕射波、多次波、侧面反射波有关的数据点, 提炼出更合理的数据空间, 使得立体层析反演精度得到进一步提高。
在两步法策略中, 结构张量始终扮演着重要的角色。无论是第1步的数据域初始搜索还是第2步的成像域搜索都是基于高效率的结构张量算法实现, 尤其是第2步在初始最小偏移距成像数据体内人工拾取出比较可靠的数据点位置后, 这些数据点的位置对应于一次反射波的关键反射层, 这些位置需要沿着成像点道集内的同相轴延拓到大偏移距剖面去, 这时结构张量事先在成像点道集内搜索到的同相性非常重要。在数据点位置的延拓完成后, 依然需要使用结构张量搜索出构造倾角, 否则运动学反偏移将无从谈起。本文在典型理论数据的严格测试证实了结构张量的稳定和高效, 为后续实际应用奠定了基础。
附录A 共偏移距、共中心点剖面内Pmx, Phx参数与共炮点、共检波点道集内Psx, Prx参数之间的定量关系对原始数据集, 可看做炮域数据和共偏移距域数据, 有如下关系:
| $ \mathit{t}\left( \mathit{s}\rm{,}\mathit{r} \right)\rm{=}\mathit{t}\left( \mathit{m}\rm{,}\mathit{h} \right) $ | (A1) |
基于公式(A1)对炮点、检波点求导, 得:
| $ \frac{\partial \mathit{t}\left( \mathit{s}\rm{,}\mathit{r} \right)}{\partial \mathit{s}}\rm{=}\frac{\partial \mathit{t}\left( \mathit{m}\rm{,}\mathit{h} \right)}{\partial \mathit{s}}\\ \frac{\partial \mathit{t}\left( \mathit{s}\rm{,}\mathit{r} \right)}{\partial \mathit{r}}\rm{=}\frac{\partial \mathit{t}\left( \mathit{m}\rm{,}\mathit{h} \right)}{\partial \mathit{r}} $ | (A2) |
化简得到:
| $ \begin{align} & {{\mathit{P}}_{\rm{s}\mathit{x}}}\rm{=}\frac{\partial \mathit{t}\left( \mathit{m}\rm{,}\mathit{h} \right)}{\partial \mathit{m}}\frac{\partial \mathit{m}}{\partial \mathit{s}}\rm{+}\frac{\partial \mathit{t}\left( \mathit{m}\rm{,}\mathit{h} \right)}{\partial \mathit{h}}\frac{\partial \mathit{h}}{\partial \mathit{s}} \\ & {{\mathit{P}}_{\rm{r}\mathit{x}}}\rm{=}\frac{\partial \mathit{t}\left( \mathit{m}\rm{,}\mathit{h} \right)}{\partial \mathit{m}}\frac{\partial \mathit{m}}{\partial \mathit{r}}\rm{+}\frac{\partial \mathit{t}\left( \mathit{m}\rm{,}\mathit{h} \right)}{\partial \mathit{h}}\frac{\partial \mathit{h}}{\partial r} \\ \end{align} $ | (A3) |
根据半偏移距h的定义h=(s-r)/2和中点m的定义m=(s+r)/2, 有:
| $ \begin{align} & \frac{\partial \mathit{h}}{\partial \mathit{s}}\rm{=+}\frac{1}{2}\ \ \ \frac{\partial \mathit{m}}{\partial \mathit{s}}\rm{=+}\frac{1}{2} \\ & \frac{\partial \mathit{h}}{\partial \mathit{r}}\rm{=-}\frac{1}{2}\ \ \ \frac{\partial \mathit{m}}{\partial \mathit{r}}\rm{=+}\frac{1}{2} \\ \end{align} $ | (A4) |
即:
| $ \begin{align} & {{\mathit{P}}_{\rm{s}\mathit{x}}}\rm{=}\frac{1}{2}{{\mathit{P}}_{\mathit{mx}}}\rm{+}\frac{1}{2}{{\mathit{P}}_{\mathit{hx}}} \\ & {{\mathit{P}}_{\rm{r}\mathit{x}}}\rm{=}\frac{1}{2}{{\mathit{P}}_{\mathit{mx}}}\rm{-}\frac{1}{2}{{\mathit{P}}_{\mathit{hx}}} \\ \end{align} $ | (A5) |
得到:
| $ \begin{align} & {{\mathit{P}}_{\mathit{mx}}}\rm{=}{{\mathit{P}}_{\rm{s}\mathit{x}}}\rm{+}{{\mathit{P}}_{\rm{r}\mathit{x}}} \\ & {{\mathit{P}}_{\mathit{hx}}}\rm{=}{{\mathit{P}}_{\rm{s}\mathit{x}}}\rm{-}{{\mathit{P}}_{\rm{r}\mathit{x}}} \\ \end{align} $ | (A6) |
| [1] | BILLETTE F, LAMBARÉ G. Velocity macro-model estimation by stereotomography[J]. Geophysical Journal International, 1998, 135(2): 671-680 DOI:10.1046/j.1365-246X.1998.00632.x |
| [2] | LAMBARÉ G. Stereotomgraphy[J]. Geophysics, 2008, 73(5): VE25-VE34 DOI:10.1190/1.2952039 |
| [3] | BILLETTE F, LE BÉGAT S, PODVIN P, et al. Practical aspects and applications of 2D stereotomography[J]. Geophysics, 2003, 68(3): 1008-1021 DOI:10.1190/1.1581072 |
| [4] |
倪瑶, 杨锴, 陈宝书. 立体层析反演方法理论分析与应用测试[J].
石油物探, 2013, 52(2): 121-130 NI Y, YANG K, CHEN B S. Stereotomography inversion method:theory and application testing[J]. Geophysical Prospecting for Petroleum, 2013, 52(2): 121-130 |
| [5] |
李振伟, 杨锴, 倪瑶, 等. 基于立体层析反演的偏移速度建模应用研究[J].
石油物探, 2014, 53(4): 444-452 LI Z W, YANG K, NI Y, et al. Migration velocity analysis with stereo-tomography inversion[J]. Geophysical Prospecting for Petroleum, 2014, 53(4): 444-452 |
| [6] |
王宇翔, 杨锴, 汪小将, 等. 基于梯度平方结构张量算法的高密度二维立体层析反演[J].
地球物理学报, 2016, 59(1): 263-276 WANG Y X, YANG K, WANG X J, et al. A high-density stereo-tomography method based on the gradient square structure tensors algorithm[J]. Chinese Journal of Geophysics, 2016, 59(1): 263-276 DOI:10.6038/cjg20160122 |
| [7] |
杨锴, 邢逢源, 李振伟, 等. 基于非降阶汉密尔顿算子的三维立体层析反演[J].
地球物理学报, 2016, 59(9): 3366-3378 YANG K, XING F Y, LI Z W, et al. 3D stereo-tomography based on the non-reduced Hamiltonian[J]. Chinese Journal of Geophysics, 2016, 59(9): 3366-3378 DOI:10.6038/cjg20160920 |
| [8] | XING F X, YANG K, XUE D, et al. 3D stereotomography applied to the deep-sea data acquired in the South China Sea, part Ⅱ:the real case study[J]. Expanded Abstracts of 86th Annual Internat SEG Mtg, 2016: 3788-3793 |
| [9] | CHAURIS H, NOBLE M S, LAMBARÉ G, et al. Migration velocity analysis from locally coherent events in 2-D laterally heterogeneous media, Part Ⅰ:theoretical aspects[J]. Geophysics, 2002, 67(4): 1202-1212 DOI:10.1190/1.1500382 |
| [10] | GUILLAUME P, LAMBARÉ G, LEBLANC O, et al. Kinematic invariants:an efficient and flexible approach for velocity model building[J]. Expanded Abstracts of 78th Annual Internat SEG Mtg, 2008: 3687-3692 |
| [11] |
王华忠, 冯波, 刘少勇, 等. 叠前地震数据特征波场分解、偏移成像与层析反演[J].
地球物理学报, 2015, 58(6): 2024-2034 WANG H Z, FENG B, LIU S Y, et al. Characteristic wavefield decomposition, imaging and inversion with prestack seismic data[J]. Chinese Journal of Geophysics, 2015, 58(6): 2024-2034 DOI:10.6038/cjg20150617 |
| [12] |
刘少勇, 蔡杰雄, 王华忠, 等. 山前带地震数据射线(束)叠前成像方法研究与应用[J].
石油物探, 2012, 51(6): 598-605 LIU S Y, CAI J X, WANG H Z, et al. Technology and application of beam ray prestack imaging method in foothill areas[J]. Geophysical Prospecting for Petroleum, 2012, 51(6): 598-605 |
| [13] | TEN KROODE A P E, SMIT D J, VERDEL A R. A micro local analysis of migration[J]. Wave Motion, 1998, 28(2): 149-172 DOI:10.1016/S0165-2125(98)00004-3 |
| [14] | XU S, CHAURIS H, LAMBARÉ G, et al. Common angle migration:a strategy for imaging complex media[J]. Geophysics, 2001, 66(6): 1877-1894 DOI:10.1190/1.1487131 |
| [15] | FARRA V, MADARIAGA R. Seismic waveform modeling in heterogeneous media by ray perturbation theory[J]. Journal of Geophysical Research Solid Earth, 1987, 92(B3): 2697-2712 DOI:10.1029/JB092iB03p02697 |
| [16] | SWORD C. Tomographic determination of interval velocities from picked reflection seismic data[J]. Expanded Abstracts of 56th Annual Internat SEG Mtg, 1986: 657-660 |
| [17] |
熊凯. 特征波框架下的背景速度与角度反射系数反演[D]. 上海: 同济大学, 2017
XIONG K.Background velocity and angle reflectivity inversion based on the characteristic wave theory[D]. Shanghai:Tongji University, 2017 |
| [18] | VAN VlIET L J, Verbeek P W.Estimators for orientation and anisotropy in digitized images[R]. Tubingen:Proceeding of First Conference of the Advanced School for Computing & Imaging, 1995:442-450 |



