压缩感知理论近年来在各研究领域都得到了广泛的应用,例如医学成像、CT断层扫描、机器学习等。2006年Candès等[1]指出:当信号具有稀疏特性时,可以通过远小于信号长度的少量观测值来精确地重构稀疏信号。但是一般的自然信号s本身并不是稀疏的,需要在某种稀疏基上进行稀疏表示。不妨给定有限长离散信号s,信号稀疏度为k(即含有k个非零值),则s可以表示成一组正交基的线性组合:
| $ \mathit{\boldsymbol{s}} = \sum\limits_{i = 1}^n {{\psi _i}{x_i}} = {\mathit{\boldsymbol{\psi }}^\rm{T}}\mathit{\boldsymbol{x}} $ | (1) |
其中ψ=[ψ1, ψ2, …, ψn]是一组正交基。
Candès等[2]指出若压缩感知矩阵A满足有限等距性(Restricted Isometry Property, RIP)条件,并且x为稀疏度为k的信号,那么可以通过求解下面的l0范数最小化问题便可以精确地恢复x:
| $ \left\{ \begin{array}{l} \min {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\left\| \mathit{\boldsymbol{x}} \right\|_0}\\ {\rm{s}}{\rm{.t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{Ax}} = \mathit{\boldsymbol{b}} \end{array} \right. $ | (2) |
其中:‖x‖0指的是非零元素的个数,A是传感矩阵。
压缩感知主要包括信号的稀疏表示、观测矩阵的设计以及稀疏信号恢复三个方面[3],主要是通过非线性的重构算法(最优化方法)来恢复信号。

|
图 1 压缩感知理论框架 Figure 1 Theoretical framework of compressive sensing |
由于Ax=b是欠定的,‖·‖0是非凸不可微函数,并且问题(2) 是NP难的,因此通常采用l1范数来替代l0范数,那么重构稀疏信号的问题即变成了求解优化问题(3):
| $ \left\{ \begin{array}{l} \min {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\left\| \mathit{\boldsymbol{x}} \right\|_1}\\ {\rm{s}}{\rm{.t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{Ax}} = \mathit{\boldsymbol{b}} \end{array} \right. $ | (3) |
定义1 定义测量矩阵A的RIP参数δk满足下式的最小值δ:
| $ {\kern 1pt} {\kern 1pt} (1 - {\delta _k}{\kern 1pt} )\left\| \mathit{\boldsymbol{x}} \right\|_2^2 \leqslant \left\| {\mathit{\boldsymbol{Ax}}} \right\|_2^2 \leqslant (1 + {\delta _k})\left\| \mathit{\boldsymbol{x}} \right\|_2^2 $ |
其中x为k阶稀疏信号。
若δk < 1,则称测量矩阵A满足k阶RIP。特别地,当δ2k <
一般有两大类算法对问题(3) 进行近似求解,即贪婪追踪法和凸松弛法,文献[5-9]提出利用匹配追踪算法(Matching Pursuit, MP)和正交追踪算法(Orthogonal Matching Pursuit, OMP)来求解l0最小范数问题,大大地提高了计算速度,且易于实现,但是恢复能力不强。由于传统贪婪算法在抗噪方面不是很强,文献[10]提出了具有较强鲁棒性的压缩采样匹配追踪(Compressive Sampling Matching Pursuit, CoSaMP),但由于CoSaMP算法需要已知信号的稀疏度k,而实际应用中信号的稀疏度k往往是未知的。因此CoSaMP算法在解决稀疏信号重构问题上存在一些问题。MP算法来源于贪婪追踪算法,特点是计算复杂度低,但需要较多的观测值,重构精度低;而OMP算法和CoSaMP算法具有良好的稳定性和理论保证,但仅针对大规模的问题恢复率较高。凸松弛算法,这类方法通过将非凸问题转化为凸问题求解找到信号的逼近,其中最常用的方法就是基追踪(Basis Pursuit, BP)[11],该方法提出利用l1范数替代l0范数来解决最优化问题。这两大类算法在较高的稀疏度下或在较低的观测度下,都很难对高斯信号进行高效重构。
1 反馈神经网络算法 1.1 反馈神经网络鉴于上述算法所存在的弊端,本文采用神经网络算法来解决压缩感知理论中的信号恢复问题。主要从以下几个方面展开工作:第一部分是建立非线性等式约束优化问题相应的反馈神经网络(Recurrent Neural Network, RNN),为便于研究,接着选取合适的凸函数f(x)来逼近‖x‖1, 随后根据梯度下降思想建立神经动力学方程;第二部分探讨所建立的反馈神经网络的稳定性、收敛性和收敛速度与步长的关系等因素;第三部分给出网络的停时条件以及算法具体步骤;第四部分是随机生成离散信号,利用神经网络重构离散信号,并且与已有的重构算法进行对比,从而说明反馈神经网络算法的有效性和准确性。
不论是l0范数最小化还是l1范数最小化问题都可以归结为带约束的优化问题。其中一类通过设计一系列反馈神经网络求解带约束的优化问题的方法统称为神经动力学优化方法。以下是一个非线性等式约束优化问题:
| $\left\{ \begin{array}{l} \min\ f(\mathit{\boldsymbol{x}})\\ {\rm{s}}{\rm{.t}}{\rm{.}} \ h(\mathit{\boldsymbol{x}}) = 0 \end{array} \right. $ | (4) |
其中:x∈Rn,f:Rn → R是目标函数,h:Rn → Rm(m < n)是等式约束条件,假设f是二次可微凸函数,h是Rn上的线性函数。假设问题(4) 至少有一个可行解,由Weierstrass定理知,(4) 至少有一个最小值点。通过Matlab平台,可以利用反馈神经网络求解此类问题。
假设x*是问题(4) 的一个最优解,M1是目标函数f(x)的一个下界,即M1≤f(x*)。函数[5]:
| $ \begin{array}{l} F(\mathit{\boldsymbol{x}}, {M_1}) = {[{(f(\mathit{\boldsymbol{x}})-{M_1})^ + }]^2} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left\{ \begin{array}{l} \frac{1}{2}{(f(\mathit{\boldsymbol{x}}) - {M_1})^2},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} f(\mathit{\boldsymbol{x}}) \geqslant {M_1}\\ 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} f(\mathit{\boldsymbol{x}}) < {M_1} \end{array} \right. \end{array} $ |
由于F(x, M1)是连续可微的非减凸函数,并且:
| $ \nabla F(\mathit{\boldsymbol{x}}, {M_1}) = \left\{ \begin{array}{l} (f(\mathit{\boldsymbol{x}}) - {M_1})\nabla f(\mathit{\boldsymbol{x}}),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} f(\mathit{\boldsymbol{x}}) \geqslant {M_1}\\ 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} f(\mathit{\boldsymbol{x}}) < {M_1} \end{array} \right. $ |
作能量函数:
考虑凸优化问题:
| $ \min \ E(\mathit{\boldsymbol{x}}, {{M}_{1}})=F(\mathit{\boldsymbol{x}}, {{M}_{1}})+\frac{1}{2}h{{(\mathit{\boldsymbol{x}})}^{\rm{T}}}h(\mathit{\boldsymbol{x}}) $ | (5) |
根据梯度下降法,可以建立求解问题(5) 的神经网络:
| $ \left\{ \begin{align} & \frac{\rm{d}\mathit{\boldsymbol{x}}}{\rm{d}\mathit{t}}=-\nabla E(\mathit{\boldsymbol{x}}, {{M}_{1}}) \\ & \mathit{\boldsymbol{x}}({{t}_{0}})={{\mathit{\boldsymbol{x}}}_{0}} \\ \end{align} \right. $ | (6) |
如果神经网络系统(6) 是稳定的,那么其平衡点就是优化问题(5) 的最优解。设系统(6) 的存在平衡点x1*,则E(x1*, M1)≤E(x*, M1),因为x*是问题(4) 的一个最优解,所以有E(x*, M1)=[(f(x*)-M1)+]2。因为M1是目标函数f(x)的一个下界,又不等式:
| $ \sqrt{E(\mathit{\boldsymbol{x}}_{1}^{*}, {{M}_{1}})}\leqslant \sqrt{E({{\mathit{\boldsymbol{x}}}^{*}}, {{M}_{1}})}=\frac{1}{2}(f({{\mathit{\boldsymbol{x}}}^{*}})-{{M}_{1}}) $ |
令
类似地,再次作能量函数:
| $ E(\mathit{\boldsymbol{x}}, {{M}_{2}})={{[{{(f(\mathit{\boldsymbol{x}})-{{M}_{2}})}^{+}}]}^{2}}+\frac{1}{2}\mathit{h}{{(\mathit{\boldsymbol{x}})}^{\rm{T}}}\mathit{h}(\mathit{\boldsymbol{x}}) $ | (7) |
得到相应问题(7) 的子凸优化问题:
| $ \min \ E(\mathit{\boldsymbol{x}}, {{M}_{2}}) $ | (8) |
此时以x1*作为初始点,建立优化问题(8) 的神经网络:
| $ \left\{ \begin{align} & \frac{\rm{d}\mathit{\boldsymbol{x}}}{\rm{d}\mathit{t}}=-\nabla E(\mathit{\boldsymbol{x}}, {{M}_{2}}) \\ & \mathit{\boldsymbol{x}}({{t}_{0}})=\mathit{\boldsymbol{x}}_{1}^{\rm{*}} \\ \end{align} \right.;k=0, 1, \cdots $ | (9) |
基于逐步迭代连续近似的思想,令:
| $ {{M}_{k+1}}={{M}_{k}}+2\sqrt{E(\mathit{\boldsymbol{x}}_{k}^{*}, {{M}_{k}})} $ |
其中xk*是凸优化问题(10) 的最优解:
| $ \min \ E(\mathit{\boldsymbol{x}}, {{M}_{k}}) $ | (10) |
再用xk*作为初始点,构造一系列子凸优化问题:
| $ \min \ E(\mathit{\boldsymbol{x}}, {{M}_{k+1}}) $ | (11) |
相应的神经子网络模型:
| $ \left\{ \begin{align} & \frac{\rm{d}\mathit{\boldsymbol{x}}}{\rm{d}\mathit{t}}=-\nabla E(\mathit{\boldsymbol{x}}, {{M}_{k+1}}) \\ & \mathit{\boldsymbol{x}}({{t}_{0}})=\mathit{\boldsymbol{x}}_\mathit{k}^{\rm{*}} \\ \end{align} \right.;k=0, 1, \cdots $ | (12) |
此神经网络的特点是用前一个子优化问题对应的神经网络的平衡点xk*构造新的能量函数E(x, Mk+1),并建立初值为xk*子神经网络(12)。这一系列神经网络称为反馈神经网络(RNN)。
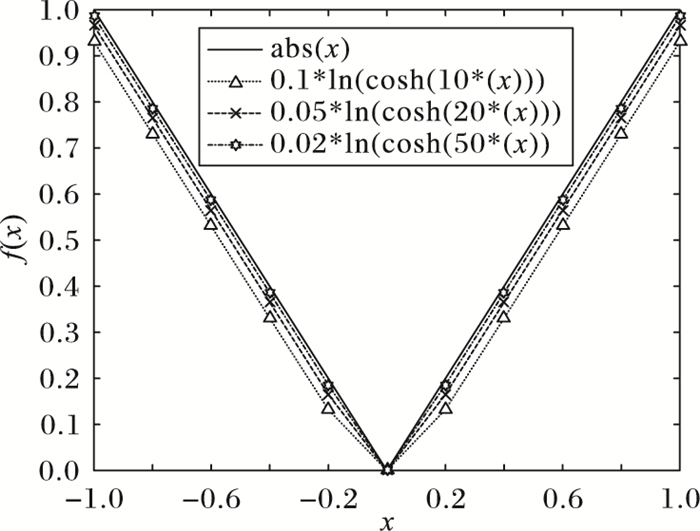
1.2 稀疏信号的恢复结合式(3) 和式(4),考虑建立反馈神经网络来解决问题(3),由于算子‖·‖1在xi=0处不可微,因此不妨考虑凸函数f(xi)=ln(cosh(axi))/a(其中a > 1) 来近似逼近‖x‖1,从图 2可以看出a越大,该近似效果越精确:
| $ {{\left\| \mathit{\boldsymbol{x}} \right\|}_{1}}\approx f(\mathit{\boldsymbol{x}})=\sum\limits_{i=1}^{n}{\frac{\rm{ln}(\rm{cosh}(\mathit{a}{{\mathit{x}}_{\mathit{i}}}))}{a}} $ |
|
图 2 目标函数(n=1时) Figure 2 Objective function (n=1) |
|
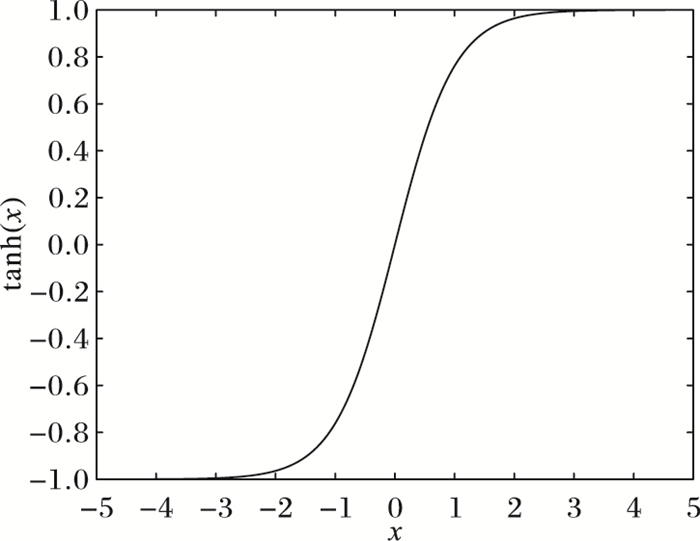
图 3 激活函数y′=tanh(x) Figure 3 Activation function y′=tanh(x) |
对于函数y=ln(cosh(ax))/a,有y′=tanh(ax),并且双曲正切函数是严格单调增函数。
值得注意的是,双曲正切函数在神经网络中经常被当作激活函数使用。此时问题(3) 变成了:
| $ \left\{ \begin{align} & \min \frac{1}{a}\sum\limits_{i=1}^{n}{\ln (\cosh (\mathit{a}{{\mathit{x}}_{\mathit{i}}}))} \\ & \rm{s}\rm{.t}\rm{.}\ \ \ \ \mathit{\boldsymbol{b}}\rm{-}\mathit{\boldsymbol{Ax}}=0 \\ \end{align} \right. $ | (13) |
其中:目标函数是凸函数,约束函数b-Ax是连续函数,因此由凸分析理论知,优化问题(13) 的局部最优解即是全局最优解。相应可建立问题(13) 的Hopfield能量函数:
| $ F(\mathit{\boldsymbol{x}}, {{M}_{1}})=\frac{1}{2}f{{(\mathit{\boldsymbol{x}})}^{2}} $ |
所以
易知E(x, M1)≥0是凸函数,则:
| $ \nabla E(\mathit{\boldsymbol{x}}, {{M}_{1}})=f(\mathit{\boldsymbol{x}})\nabla f(\mathit{\boldsymbol{x}})+{{(\mathit{\boldsymbol{Ax}}-\mathit{\boldsymbol{b}})}^{\rm{T}}}\mathit{\boldsymbol{A}} $ |
那么对于凸优化问题:min E(x, M1)
根据梯度下降法,建立神经动力学方程:
| $ \left\{ \begin{align} & \frac{\rm{d}\mathit{\boldsymbol{x}}}{\rm{d}\mathit{t}}=-f(\mathit{\boldsymbol{x}})\nabla f(\mathit{\boldsymbol{x}})-{{(\mathit{\boldsymbol{Ax}}-\mathit{\boldsymbol{b}})}^{\rm{T}}}\mathit{\boldsymbol{A}} \\ & {\mathit{\boldsymbol{x}}}({{t}_{0}})={{\mathit{\boldsymbol{x}}}_{0}} \\ \end{align} \right. $ | (14) |
为了探讨RNN的稳定性与收敛性能,下面给出两个定理并证明:
定理1 对任何初值x0∈Rn,神经网络(14) 存在唯一最优解x*的充分必要条件是[9]:
定理2 设x*是问题(13) 的一个最优解,M是问题(13) 的一个下界,即M≤f(x*),定义一个能量函数序列
证明 设x*是问题(13) 的一个最优解,
1) 先证f(xk*)≤f(x*)。
因为
| $ \begin{align} & f({{\mathit{\boldsymbol{x}}}^{*}})\geqslant {{M}_{k+1}}={{M}_{k}}+2\sqrt{E(\mathit{\boldsymbol{x}}_{k}^{*}, {{M}_{k}})}\geqslant \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{M}_{k}}+2{{[f(x_{k}^{*})-{{M}_{k}}]}^{+}} \\ \end{align} $ |
① 当f(xk*)≥Mk时,f(x*)≥Mk+f(xk*)-Mk≥f(xk*)。
② 当f(xk*) < Mk时,f(x*)≥Mk > f(xk*),所以f(xk*)≤f(x*)。
2) 下证序列{xk*}收敛到问题(13) 的一个可行解。
由1) 知,序列{Mk}是单调非减有上界序列,由极限存在定理知,序列{Mk}必存在极限,即存在M*,使得
再对等式
又因为
所以序列f(xk*)收敛到问题(13) 的一个最优值。证毕。
3 停时条件神经网络(14) 的平衡点序列xk*收敛到问题(13) 的一个最优解, 从定理2的证明可看出该系统的停时条件是
重构稀疏信号x的主要思想是通过建立反馈神经网络模型,再由龙格-库塔方法,利用Matlab平台逐步迭代寻找问题(3) 的最优解和最优值,直到满足停时条件。下面给出RNN算法的具体步骤。
步骤1 初始化。设t=0,取初始点x(t0)=x0∈Rn,给定步长Δ > 0和ε∈[10-15, 10-5],k:=1, M1≤f(x*)。
步骤2 计算梯度:u(t)=(f(x)-Mk)∇f(x)+(Ax-b)TA。
步骤3 状态更新:x(t+Δt)=x(t)-Δt·u(t)。
步骤4 计算:
步骤5 递归与停止:若l < ε,则令xk=x(t)并输出xk,停止计算,并输出最优解x(t)和最优值E(xk);否则令k=k+1,t=t+Δt,
通过生成仿真信号,采用神经网络模型(14) 求解状态向量
| $ {\kern 1pt} {R_{{\rm{total}}}} = {\left\| {\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{\hat x}}} \right\|_2}/{\left\| \mathit{\boldsymbol{x}} \right\|_2} $ |
其中:x表示原始稀疏信号向量,
1) 产生k稀疏信号x∈Rn, k个非零元素的位置是随机产生的,满足[1, n]的均匀随机分布。相应的非零元素的大小也是随机产生的。
3) 计算观测向量:b=Ax,其中b∈Rm。
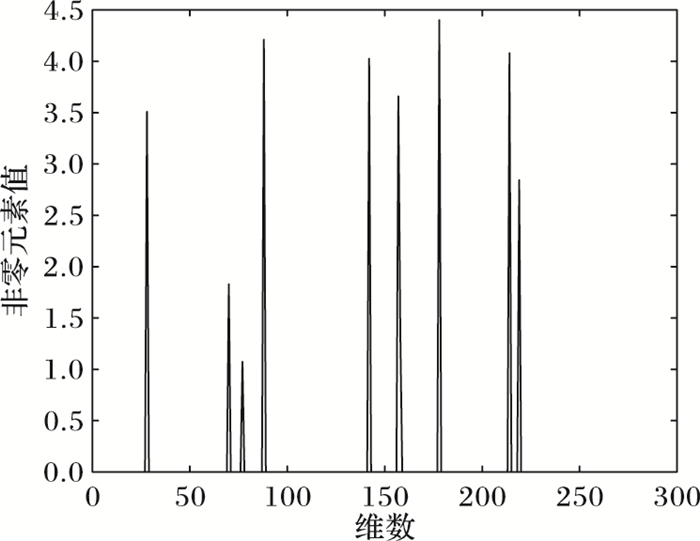
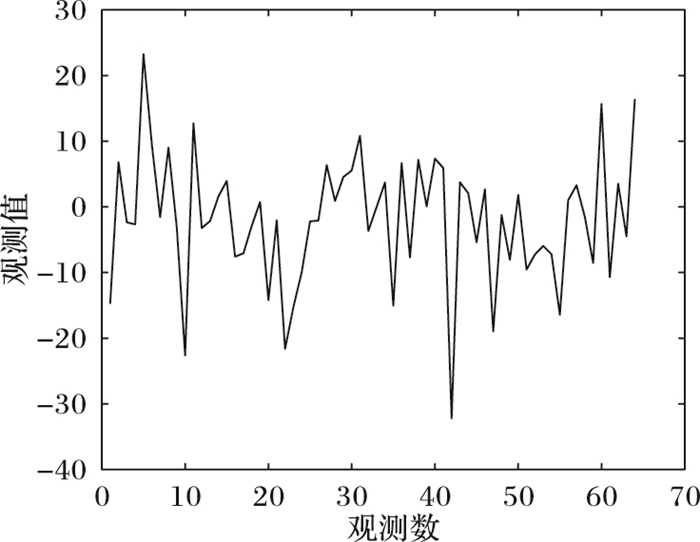
由文献[2]知,当矩阵A满足RIP条件时,精确恢复信号x所需的观测量的数量m满足:m≥Ck log(n/k)即可,其中C是常数,即m只与问题的规模参数组合(n, k)有关。取实验参数为:测量矩阵大小m=64,n=256,原始信号稀疏度k=10。根据上述数据的生成方法,可以产生如图 4和图 5所示的原始稀疏信号和观测向量。
|
图 4 原始稀疏信号 Figure 4 Original sparse signal |
|
图 5 观测向量b Figure 5 Observation vector b |
2) 产生观测矩阵A∈Rm×n,矩阵的所有元素是随机生成的并且服从高斯分布N(0, 1),rank(A)=m。
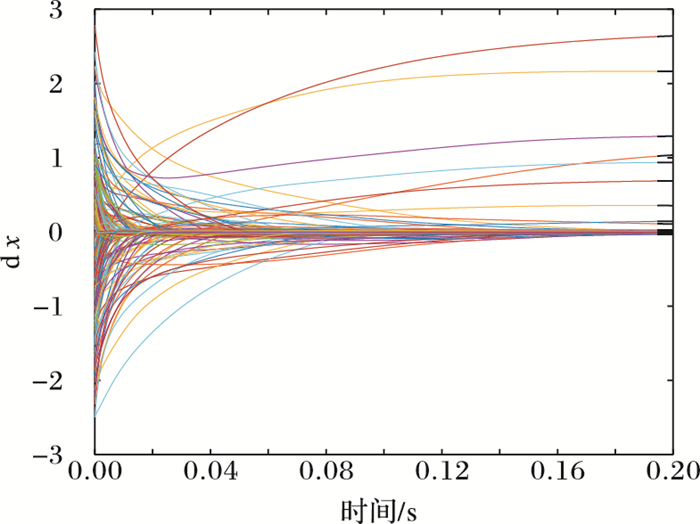
由图 6可知,在b与A给定的情况下,x在神经网络(14) 的不断反馈之下,最终重构并且非零元素均收敛到既定位置上的元素。为了检验不同稀疏度下和观测次数m与正确重构概率的关系,不妨取稀疏度k=[4,12,20,28,36]。
|
图 6 |
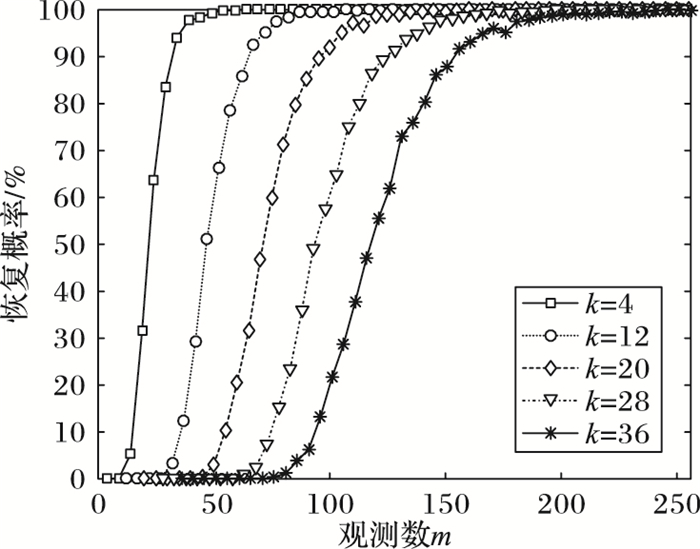
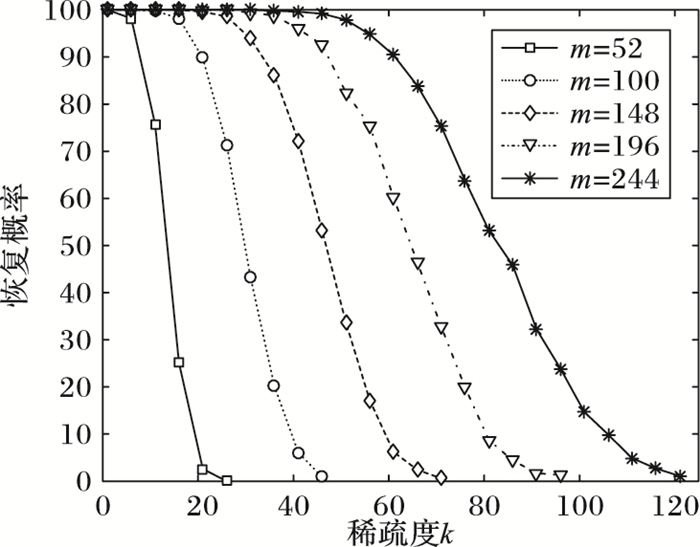
每一组(k, m, n),执行200次随机实验,由图 7可知,对于不同稀疏度k,当观测点数m大于等于110时,RNN方法能正确恢复稀疏信号的概率极高。而由图 8可知,对于不同观测点数的m,当稀疏度k小于等于20时,RNN方法能正确恢复稀疏信号的概率极高。
|
图 7 测量数m与成功恢复的概率关系(n=256) Figure 7 Probability relation between number of measurements and successful recovery (n=256) |
|
图 8 稀疏度k与成功恢复的概率关系(n=256) Figure 8 Probability relation between sparsity k and successful recovery (n=256) |
由表 1知,模型(8) 只需要较少的观测次数就可以正确地恢复稀疏信号,也可以看出,当m大于100时,其他算法也获得较低的恢复误差,说明当观察次数m足够大时,通常适用的算法同样也能获得较精确的恢复效果。
| 表 1 几种算法在不同观测次数下的相对误差 Table 1 Relative error comparison of several algorithms under different observation number |
数据产生之后根据观测向量b通过RNN(14) 进行稀疏信号恢复,选择初始误差容限ε=10-3,为一般性考虑,取随机向量作为初始x0,选取实验参数令k=10,m=64,n=256,经神经网络(14) 不断反馈求解状态向量
本文基于目标函数的性质,设计快速重构稀疏信号的反馈神经网络算法,通过讨论能量函数的梯度,证明该RNN模型最优解的存在性与原问题的近似等价性,讨论了网络的稳定性,并且通过实验验证了算法的有效性;但是该算法也有不足之处,反复实验之下,发现最佳的迭代次数会导致运算量增加,从而稀疏信号重构时间加长,因而该网络需要进一步改进。
| [1] | CANDÈS E J, ROMBERG J K, TAO T. Stable signal recovery from incomplete and inaccurate measurements[J]. Communications on Pure and Applied Mathematics, 2006, 59(8): 1207-1223. DOI:10.1002/(ISSN)1097-0312 |
| [2] | CANDÈS E J, ROMBERG J, TAO T. Robust uncertainty principles:exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509. DOI:10.1109/TIT.2005.862083 |
| [3] | 尹宏鹏, 刘兆栋, 柴毅, 等. 压缩感知综述[J]. 控制与决策, 2013, 28(10): 1441-1445. (YIN H P, LIU Z D, CHAI Y, et al. Survey of compressed sensing[J]. Control and Decision, 2013, 28(10): 1441-1445.) |
| [4] |
FOUCART S, LAI M J. Sparsest solutions of underdetermined linear systems via |
| [5] | BLUMENSATH T, DAVIES M E. Gradient pursuits[J]. IEEE Transactions on Signal Processing, 2008, 56(6): 2370-2382. DOI:10.1109/TSP.2007.916124 |
| [6] | DAI W, MILENKOVIC O. Subspace pursuit for compressive sensing signal reconstruction[J]. IEEE Transactions on Information Theory, 2009, 55(5): 2230-2249. DOI:10.1109/TIT.2009.2016006 |
| [7] | MALLAT S G, ZHANG Z F. Matching pursuits with time-frequency dictionaries[J]. IEEE Transactions on Signal Processing, 1993, 41(12): 3397-3415. DOI:10.1109/78.258082 |
| [8] | FIGUEIREDO M A T, NOWAK R D, WRIGHT S J. Gradient projection for sparse reconstruction:application to compressed sensing and other inverse problems[J]. IEEE Journal of Selected Topics in Signal Processing, 2007, 1(4): 586-597. DOI:10.1109/JSTSP.2007.910281 |
| [9] | CHEN S S, DONOHO D L, SAUNDERS M A. Atomic decomposition by basis pursuit[J]. SIAM Journal on Scientific Computing, 1998, 20(1): 33-61. DOI:10.1137/S1064827596304010 |
| [10] | NEEDELL D, TROPP J A. CaSaMP:iterative signal recovery from incomplete and inaccurate samples[J]. Applied and Computational Harmonic Analysis, 2008, 26(3): 301-321. |
| [11] | 李珅, 马彩文, 李艳, 等. 压缩感知重构算法综述[J]. 红外与激光工程, 2013, 42(S1): 225-232. (LI S, MA C W, LI Y, et al. Survey on reconstruction algorithm based on compressive sensing[J]. Infrared and Laser Engineering, 2013, 42(S1): 225-232.) |
| [12] | BOGACKI P, SHAMPINE L F. A 3(2) pair of Runge-Kutta formulas[J]. Applied Mathematics Letters, 1989, 2(4): 321-325. DOI:10.1016/0893-9659(89)90079-7 |
| [13] | 李国成, 宋士吉, 吴澄. 解决非可微凸优化问题的次梯度反馈神经网络[J]. 中国科学(E辑), 2006, 36(8): 811-824. (LI G C, SONG S J, WU C. Sub-gradient feedback neural network for solving non-differentiable convex optimization[J]. SCIENCE CHINA Sev. E Information Sciences, 2006, 36(8): 811-824.) |
| [14] | 曾喆昭. 神经网络优化方法及其在信息处理中的应用研究[D]. 长沙: 湖南大学, 2008: 62-73. (ZENG Z Z. Neural network optimization method and its application in information processing[D]. Changsha:Hunan University, 2008:62-73.) http://cdmd.cnki.com.cn/Article/CDMD-10532-2009083750.htm |
| [15] | XIA Y, FENG G, WANG J. A novel recurrent neural network for solving nonlinear optimization problems with inequality constraints[J]. IEEE Transactions on Neural Networks, 2008, 19(8): 1340-1353. DOI:10.1109/TNN.2008.2000273 |
| [16] | LIU Q, WANG J. A one-layer recurrent neural network with a discontinuous hard-limiting activation function for quadratic programming[J]. IEEE Transactions on Neural Networks, 2008, 19(4): 558-570. DOI:10.1109/TNN.2007.910736 |
| [17] | LEUNG C S, SUM J, CONSTANTINIDES A G. Recurrent networks for compressive sampling[J]. Neurocomputing, 2014, 129: 298-305. DOI:10.1016/j.neucom.2013.09.028 |
| [18] | LIU Q, WANG J. A one-layer recurrent neural network with a discontinuous activation function for linear programming[J]. Neural Computation, 2008, 20(5): 1366-1383. DOI:10.1162/neco.2007.03-07-488 |




