粒子群优化(Particle Swarm Optimization, PSO)算法[1]是在1995年由Eberhart和Kennedy提出的一种群体智能优化算法。该算法以其实现简便、精度高、收敛快等特点一直以来受到学术界的广泛关注,并在解决科学研究以及理论计算等方面展示了其优越性。但是标准PSO算法在寻优中很容易出现早熟问题,因此对于PSO算法收敛性能的改进研究成为一个重要的发展趋势。文献[2]在PSO算法中引入反向学习与自适应逃逸策略,并将改进算法应用于函数优化问题中,提高了收敛速度与性能;文献[3]在PSO算法寻优中增加粒子群离散多样性评价策略,改善PSO算法寻优后期粒子群的离散多样性特征,提高了算法的收敛性能;文献[4]为增强PSO算法跳出局部最优的能力,结合模拟退火与粒子群算法的优点,提出一种基于动态概率分布的混合粒子群算法,并应用于散乱点与曲面的图像匹配中,提高了匹配的准确率。然而这些改进算法并没有从根本上解决早熟收敛的问题,同时也不能避免粒子群重复搜索同一区域而导致寻优性能降低的问题。
本文结合梯度下降法[5]快速收敛的思想,提出一种基于二次搜索的改进粒子群优化(Twice Search Particle Swarm Optimization, TSPSO)算法。该算法的基本思想是当全局极值保持相同的次数超过最大预设值时,判断相应的粒子落入极值“陷阱”中,利用梯度下降法对该粒子进行二次搜索,并以最终寻优极值点为中心、某一确定长度为“半径”设定禁忌区域,当其他粒子搜索到禁忌区域边界时,对粒子的速度进行反射操作,防止粒子重复搜索同一区域,提高寻优效率;并将落入极值陷阱中的粒子淘汰,依据种群多样性准则,生成新粒子进行接下来的寻优过程。
1 二次搜索粒子群算法 1.1 PSO算法的基本原理PSO中,每个粒子由位置信息与速度信息组成,并且所有粒子由统一的目标函数来决定其相应的适应度值,然后粒子就追随当前的个体及全局最优值进行搜索。
假设有N个粒子构成一个种群S,其中Xi表示D维搜索空间中的一个元素:
| ${\mathit{\boldsymbol{X}}_i} = ({x_{i1}},{x_{i2}}, \cdots ,{x_{iD}});\;\;i = 1,2, \cdots ,N$ | (1) |
Vi表示第i个粒子的“飞行”速度,记为:
| ${\mathit{\boldsymbol{V}}_i} = ({v_{i1}},{v_{i2}}, \cdots ,{v_{iD}});\quad i = 1,2, \cdots ,N$ | (2) |
Xi当前搜索到的最优适应度值所对应的位置称为个体极值:
| ${\mathit{\boldsymbol{P}}_i} = ({p_{i1}},{p_{i2}}, \cdots ,{p_{iD}});\quad i = 1,2, \cdots ,N$ | (3) |
种群S当前搜索到的最优位置称为全局极值:
| ${\mathit{\boldsymbol{p}}_g} = ({p_{g1}},{p_{g2}}, \cdots ,{p_{gD}})$ | (4) |
接下来所有粒子按照如下公式来更新速度及位置信息:
| ${v_{id}} = w * {v_{id}} + {c_1}{r_1}({p_{id}} - {x_{id}}) + {c_2}{r_2}({p_{gd}} - {x_{id}})$ | (5) |
| ${x_{id}} = {x_{id}} + {v_{id}}$ | (6) |
式(5) 中,w表示惯性权重;c1、c2表示学习速率;r1、r2表示满足[0, 1]范围内均匀分布的随机数。
1.2 TSPSO算法的基本原理梯度下降法是一种无约束最优化算法,具有计算过程简单、初始收敛较快等特点,因此经常作为其他算法的核心[6-7],其基本思想是某一质点沿着函数f(p)(p为D维向量)上梯度下降方向可以快速滑落至函数的极值点处,主要由两部分组成:
1) 计算搜索方向:按照下式计算负梯度,即最佳搜索方向。
| ${\mathit{\boldsymbol{d}}^k} = - \nabla f({\mathit{\boldsymbol{p}}^k}) = - \left( {\frac{{\partial f({\mathit{\boldsymbol{p}}^k})}}{{\partial \mathit{\boldsymbol{p}}_1^k}},\frac{{\partial f({\mathit{\boldsymbol{p}}^k})}}{{\partial \mathit{\boldsymbol{p}}_2^k}}, \cdots ,\frac{{\partial f({\mathit{\boldsymbol{p}}^k})}}{{\partial \mathit{\boldsymbol{p}}_D^k}}} \right)$ | (7) |
2) 计算搜索步长:λk取最优步长必须满足式(8) :
| $f({\mathit{\boldsymbol{p}}^k} + {\lambda _k}{\mathit{\boldsymbol{d}}^k}) = \mathop {{\rm{min}}}\limits_\lambda f({\mathit{\boldsymbol{p}}^k} + {\lambda _k}{\mathit{\boldsymbol{d}}^k})$ | (8) |
针对PSO算法中全局极值Pg在若干次迭代后保持不变,造成粒子群体的多样性降低、陷入局部最优的问题,在TSPSO算法中,引入极值陷阱和禁忌区域两个定义。
定义1 极值陷阱。
对于给定的D维空间中的某一曲面方程S(x)=1(x为D维向量),在其中非平坦区域(梯度为非零向量)中存在某一粒子x0∈RD,当x0可以朝着负梯度的方向迅速收敛至陷阱的谷点(极值点)时,x0此刻所处的区域称为极值陷阱。
定义2 禁忌区域。
当处于极值陷阱中的粒子,通过朝着负梯度方向收敛到极值点,为防止其他粒子重复搜索该“陷阱”从而增加时间开销而设定的以该极值点为中心,某一定长为“半径”的D维“圆域”空间称为禁忌区域。
TSPSO算法的基本原理是当全局极值保持的次数超过最大预设值Nmax时,此时判断与全局极值对应的粒子Xi落入极值陷阱之中;利用梯度下降法对该粒子进行二次搜索,最终得到更优的全局极值Pg′;以Pg′为中心、某一确定长度R为“半径”构成“圆域”ΩR(pg′),即禁忌区域,当粒子Xj(j=1, 2, …, N且j≠i)搜索到ΩR(pg′)边界时,令Vj反射,从而防止粒子重复搜索ΩR(pg′)区域,避免陷入局部最优,提高寻优效率;由于粒子Xi在采用梯度下降法进一步寻优时,最终落入谷点,不再适合作为粒子群中的个体继续寻优,因此该粒子将被淘汰,此时依据粒子群多样性准则,在搜索空间之内、禁忌区域ΩR(pg′)之外生成新的粒子替换已被淘汰的粒子。
2 TSPSO算法的实现TSPSO算法与标准PSO算法及其他改进算法相比增加了判断极值陷阱、二次搜索寻优、设定禁忌区域、粒子淘汰与生成四个部分,用来提高算法的搜索效率和寻优性能。
2.1 判断极值陷阱从文献[8]有关PSO算法参数的设置中分析得出粒子搜索后期的寻优轨迹方程为:
| $\mathop {\lim }\limits_{t \to + \infty } {\mathit{\boldsymbol{X}}_i}(t) = \frac{{{c_1}{r_1}{\mathit{\boldsymbol{p}}_i} + {c_2}{r_2}{\mathit{\boldsymbol{p}}_g}}}{{{c_1}{r_1} + {c_2}{r_2}}}$ | (9) |
r1、r2表示满足[0, 1]范围内均匀分布的随机变量,对式(9) 两边求期望得:
| $\mathop {\lim }\limits_{t \to + \infty } E({\mathit{\boldsymbol{X}}_i}(t)) = E(\frac{{{c_1}{r_1}{\mathit{\boldsymbol{p}}_i} + {c_2}{r_2}{\mathit{\boldsymbol{p}}_g}}}{{{c_1}{r_1} + {c_2}{r_2}}}) = \frac{{{c_1}{\mathit{\boldsymbol{p}}_i}}}{{{c_1} + {c_2}}} + \frac{{{c_2}{\mathit{\boldsymbol{p}}_g}}}{{{c_1} + {c_2}}}$ | (10) |
从式(10) 中分析得出:粒子Xi最终搜索的期望为个体极值pi与全局极值pg的加权平均数。
对于一般的粒子Xi,全局极值pg处的适应度值要优于个体极值pi处的适应度值,因此粒子在寻优中受全局极值pg的影响相对较大。当粒子群经过若干次迭代寻优后,全局极值pg保持不变,并且与pg处的极值陷阱对应的全局极值pg′并不是真正的全局最优值时,就会错误地引导其他粒子朝着pg方向移动,致使越来越偏离真正的全局最优值,最终陷入局部最优。
TSPSO算法的优点就是经过若干次迭代后,当全局极值pg一直保持不变时,判断pg处于极值陷阱中,此时对pg进行二次搜索,并记录最终寻优结果后将其淘汰,同时依据群体多样性的准则生成新的粒子。这样就避免了pg长时间对其他粒子的错误引导而导致的局部最优。
2.2 二次搜索寻优二次搜索是指当全局极值pg处于极值陷阱中时,为了防止pg对其他粒子错误引导而导致局部最优,需要对pg进行进一步的独立寻优搜索过程。为了兼顾效率与性能,本文选择梯度下降法进行二次搜索寻优。
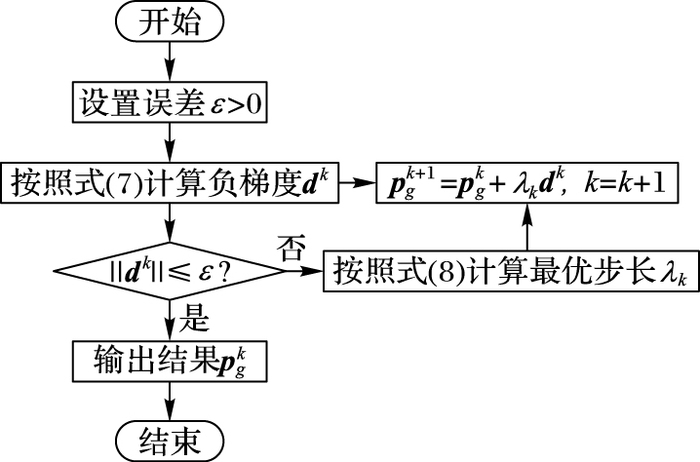
假设对每一个粒子都有一个固定的评价函数,即算法的适应度函数f(Xi),并且函数f(·)在第i(i=1, 2, …, D)维的偏导数存在,那么二次寻优的流程如图 1。
|
图 1 二次寻优流程 Figure 1 Flow chart of twice search optimization |
二次寻优的优势是不仅在一定程度上减小了粒子受全局极值pg的误导影响,同时利用梯度下降算法提高了搜索的精度,而且还可以将粒子群搜索寻优与二次寻优进行独立操作,采用并行处理模式,有效提高寻优的效率。
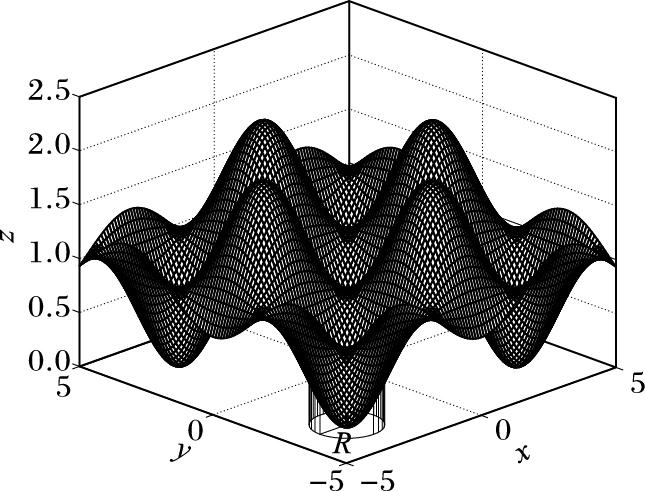
2.3 设定禁忌区域禁忌区域是指以极值陷阱的谷点pg′为中心、某一具体长度R为“半径”所构成的“圆域”空间ΩR(pg′)。例如,函数
| $F(x,y) = \frac{{{x^2} + {y^2}}}{{4000}} - \cos (x)\cos (y) + 1$ | (11) |
在三维空间中的曲面图如图 2所示。
|
图 2 函数F三维曲面 Figure 2 Three-dimensional shaded surface of F |
图 2中的o点即为极值陷阱的谷点,也就是全局极值pg经过二次寻优后的全局极值pg′;坐标面xoy上的投影区域,即表示以pg′为中心、R为半径的“圆域”ΩR(pg′)。假设某一粒子Xi再次搜索到ΩR(pg′)边缘时,即满足如下关系式:
| $\sqrt {\sum\limits_{j = 1}^D {{{({x_{ij}} - p_{gj}^\prime )}^2}} } \le R$ | (12) |
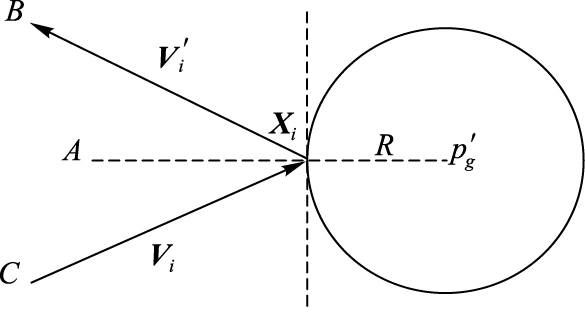
此时为了防止粒子Xi重复搜索ΩR(pg′)区域,提高寻优的效率,需要对粒子的搜索方向进行反射操作,如图 3所示。
|
图 3 粒子Xi反射示意图 Figure 3 Reflection map of Xi |
其中,以R为半径的圆域ΩR(pg′)即为禁忌区域;Vi、Vi′分别表示粒子Xi的“入射”向量与“反射”向量。由光的反射定理可得:
| $\left\{ \begin{array}{l} \angle A{X_i}C = \angle A{X_i}B\\ \left\| {{\mathit{\boldsymbol{V}}_i}} \right\| = \left\| {\mathit{\boldsymbol{V}}_i^\prime } \right\| \end{array} \right.$ | (13) |
即向量Vi与向量Vi′的和向量与向量Xipg′垂直。通过余弦定理可以求得:
| $\begin{array}{l} \cos (\angle A{X_i}C) = \frac{{{\mathit{\boldsymbol{V}}_i}({\mathit{\boldsymbol{X}}_i} - \mathit{\boldsymbol{p}}_g^\prime )}}{{2\left\| {{\mathit{\boldsymbol{V}}_i}} \right\|\left\| {({\mathit{\boldsymbol{X}}_i} - \mathit{\boldsymbol{p}}_g^\prime )} \right\|}} =\\ \;\; \frac{{\sum\limits_{j = 1}^D {{v_{ij}}({x_{ij}} - p_{gj}^\prime )} }}{{2\sqrt {\sum\limits_{j = 1}^D {{v_{ij}}^2} } \sqrt {\sum\limits_{j = 1}^D {{{({x_{ij}} - p_{gj}^\prime )}^2}} } }} \end{array}$ | (14) |
| $V_i^\prime = 2\left\| {{\mathit{\boldsymbol{V}}_i}} \right\|\cos (\angle A{X_i}C)\frac{{({\mathit{\boldsymbol{X}}_i} - \mathit{\boldsymbol{p}}_g^\prime )}}{{\left\| {{\mathit{\boldsymbol{X}}_i} - \mathit{\boldsymbol{p}}_g^\prime } \right\|}} + {\mathit{\boldsymbol{V}}_i}$ | (15) |
将式(14) 代入式(15) 得到Xi经反射后的方向向量Vi′为:
| $\begin{align} & \mathit{\boldsymbol{V}}_{i}^{\prime }=2\left\| {{\mathit{\boldsymbol{V}}}_{i}} \right\|\cos (\angle A{{X}_{i}}C)\frac{{{\mathit{\boldsymbol{X}}}_{i}}-\mathit{\boldsymbol{p}}_{g}^{\prime }}{\left\| {{\mathit{\boldsymbol{X}}}_{i}}-\mathit{\boldsymbol{p}}_{g}^{\prime } \right\|}+{{\mathit{\boldsymbol{V}}}_{i}}= \\ & 2\sqrt{\sum\limits_{j=1}^{D}{v_{ij}^{2}}}\frac{\sum\limits_{j=1}^{D}{{{v}_{ij}}({{x}_{ij}}-p_{gj}^{\prime })}}{2\sqrt{\sum\limits_{j=1}^{D}{{{v}_{ij}}^{2}}}\sqrt{\sum\limits_{j=1}^{D}{{{({{x}_{ij}}-p_{gj}^{\prime })}^{2}}}}}\times \\ & \frac{({{\mathit{\boldsymbol{X}}}_{i}}-\mathit{\boldsymbol{p}}_{g}^{'})}{\sqrt{\sum\limits_{j=1}^{D}{{{({{x}_{ij}}-p_{gj}^{\prime })}^{2}}}}}+{{\mathit{\boldsymbol{V}}}_{i}}=\frac{\sum\limits_{j=1}^{D}{{{v}_{ij}}({{x}_{ij}}-p_{gj}^{\prime })}}{\sum\limits_{j=1}^{D}{{{({{x}_{ij}}-p_{gj}^{\prime })}^{2}}}}\times \\ & ({{\mathit{\boldsymbol{X}}}_{i}}-\mathit{\boldsymbol{p}}_{g}^{\prime })+{{\mathit{\boldsymbol{V}}}_{i}} \\ \end{align}$ | (16) |
通过对粒子速度方向进行反射操作,可以避免粒子重复搜索某一相同区域,有效提高算法的搜索效率。
2.4 粒子淘汰与生成当某一粒子Xi经过若干次迭代后进入极值陷阱中,为防止该粒子对其他粒子的误导影响,需要对Xi进行单独的二次搜索寻优处理。为防止局部最优,Xi已不再适合接下来的寻优搜索过程,因此需将该粒子淘汰,并根据一定的准则生成新的粒子。文献[9]中关于种群S多样性的计算函数式为:
| $Diversity(S)=\frac{1}{N\cdot {{L}_{\max }}}\sum\limits_{i=1}^{N}{\sqrt{\sum\limits_{j=1}^{D}{{{({{x}_{ij}}-{{{\bar{z}}}_{j}})}^{2}}}}}$ | (17) |
其中:N表示粒子群的规模大小;D表示搜索空间的维度;Lmax表示D维搜索空间中的最长搜索半径;zj(j=1, 2, …, D)表示粒子群S在第j维的平均值。由式(17) 分析得出,当粒子的规模N取值较大时,个别粒子(如已淘汰的粒子)对zj的影响较小,甚至可以忽略。要想使新生成的粒子不影响整个粒子群的多样性,必满足D维向量(xi-z)的二范数值尽可能大。因此,要求生成的粒子Xi必须尽可能地远离重心z,即生成粒子的概率密度函数值越偏离越大,如下式所示:
| $f({{x}_{i1}},{{x}_{i2}},...,{{x}_{iD}})=\zeta \cdot \sum\limits_{j=1}^{D}{{{({{x}_{ij}}-{{{\bar{z}}}_{j}})}^{2}}}$ | (18) |
其中,ζ为常数,使得:
| $\int{\int{...\int{\zeta \cdot \sum\limits_{j=1}^{D}{{{({{x}_{ij}}-{{{\bar{z}}}_{j}})}^{2}}}}}}\text{d}{{x}_{i1}}\text{d}{{x}_{i2}}\cdots \text{d}{{x}_{iD}}=1$ | (19) |
式(19) 表示在搜索区域S的D重积分,且S即为该积分区域。
2.5 TSPSO算法流程基于梯度下降法的二次搜索粒子群算法流程如下:
步骤1 确定惯性权重w,学习速率c1、c2,检测极值陷阱的最大迭代次数MI以及粒子群体个数N;
步骤2 在给定范围内,随机生成N个粒子位置xi、速度vi(i=1, 2, …, N)信息;
步骤3 计算xi的适应度值fi,经判断若满足终止条件,则输出结果,否则继续;
步骤4 更新个体极值pi和全局极值pg,依据式(5)、(6) 更新粒子速度和位置信息;
步骤5 判断全局极值pg保持不变的次数是否超过预设最大值,满足则跳至步骤6,否则返回步骤3;
步骤6 判断全局极值pg处于极值陷阱中,采用梯度下降法进行二次搜索寻优,并用寻优结果pg′更新pg(pg=pg′);
步骤7 将与全局极值pg对应的粒子淘汰,并依据种群多样性准则生成新粒子进行替换,返回步骤3。
3 仿真分析 3.1 测试环境软件环境:Microsoft Windows 7操作系统,Matlab 7.8仿真平台。
硬件环境:Intel core i5-3470,主频3.20 GHz处理器,4 GB内存,联想机型。
本文选择4种近几年比较有代表性的改进粒子群算法进行对照仿真实验:线性递减权重粒子群优化(Linearly Decreasing Weight Particle Swarm Optimization, LDWPSO)算法[10]、杂交粒子群优化(Hybrid Particle Swarm Optimization, HPSO)算法[11]、自然选择粒子群优化(Natural Selection Particle Swarm Optimization, NSPSO)算法[12]、免疫粒子群优化(Immune Particle Swarm Optimization, IPSO)算法[13]。
表 1中,Sphere为单极值函数,当x为全0向量时f1(x)取到最优值0;Griewank为单极值函数,但是在极值点的附近存在若干个背离极值点方向上的陡峭峡谷,容易陷入局部极值点之中,当x为全1向量时f2(x)取到最优值0;Rastrigrin与Griewank函数都存在多个极值点,同样容易陷入局部极值点中,当x为全0向量时均取到最优值0。四种测试函数的优化目标是在相应搜索空间内取得最小值。
| 表 1 四种典型测试函数(维数=n) Table 1 Four typical test functions (Dimension=n) |
为验证TSPSO算法的收敛性能,本文通过对相关参考文献的研究,选取文献[14]中四种典型的测试函数进行优化实验,各个测试函数的基本信息如表 1所示。
3.3 算法参数设置TSPSO算法中,检测极值陷阱的最大迭代次数MI取值10;LDWPSO算法中,设置惯性权重w变化范围0.8~0.2;HPSO算法中,杂交概率bc取值0.8,杂交池的大小比例bs取值0.1;IPSO算法中,检测免疫的迭代次数DS取值8,免疫替换概率preplace取值0.5,精度eps取值10-10,粒子间最小距离取值10-10。四种改进PSO算法的惯性权重w、认知项权重c1和社会项权重c2分别取值0.8、2和2;粒子个数N取值50;迭代次数M分别取值1 000、2 000和3 000;搜索空间维数D分别取值10、20和30。
3.4 仿真结果与分析通过Matlab 7.8仿真平台对上述五种改进粒子群优化算法进行仿真实验,所得仿真结果如表 2和图 4所示。
| 表 2 5种PSO算法对4种测试函数仿真结果 Table 2 Simulation result of five PSO algorithms to four test functions |
|
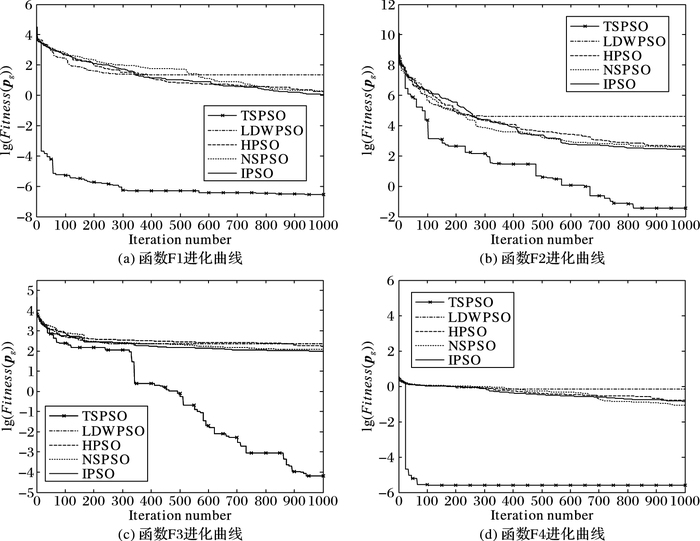
图 4 5种PSO算法对四种测试函数的全局极值进化曲线 Figure 4 Global extremum evolution curves of five PSO algorithms to four test functions |
从表 2中分析得出:总体上,本文提出的TSPSO算法在四种测试函数上的收敛精度均优于LDWPSO、HPSO、NSPSO、IPSO四种算法。对于某一具体测试函数(尤其F2),随着空间维度的增加,TSPSO算法的收敛精度保持相对稳定,而其他四种对照算法收敛精度则急剧降低,因此TSPSO算法更适合应用于高维空间的函数优化问题中。
图 4是在测试函数维度均为30,且5种PSO算法迭代次数均为1 000时的实验结果(横轴表示迭代次数,纵轴表示全局极值取10为底的对数后的结果)。从中分析得出:TSPSO算法的收敛速度和精度均优于四种对照PSO算法。
为验证TSPSO算法较其他四种改进PSO算法的寻优效率,本文针对不同算法对同一测试函数收敛到相同精度的花费时长进行比较。结果如表 3所示。
| 表 3 5种PSO算法对四种测试函数花费时长比较 Table 3 Spent time comparison of five PSO algorithms to four test functions |
表 3中各收敛精度以5种改进PSO算法中最低的精度为基准进行比较,从结果中分析得出:对于函数F1,在不同维度且收敛到相同精度条件下,TSPSO算法与其他4种改进PSO算法相比花费时长更短;对于函数F2,在维度为20和30且收敛到相同精度条件下,TSPSO算法与其他4种改进PSO算法相比花费时长更短;对于函数F3,在维度为30且收敛到相同精度条件下,TSPSO算法与其他4种改进PSO算法相比花费时长更短;对于函数F4,在维度为10且收敛到相同精度条件下,TSPSO算法与其他4种改进PSO算法相比花费时长更短。对于其他情况,TSPSO算法的花费时长与其他算法相比虽然不是最短,但相差很小,从算法的收敛精度方面考虑,可以忽略。因此TSPSO算法的寻优效率总体上较优。
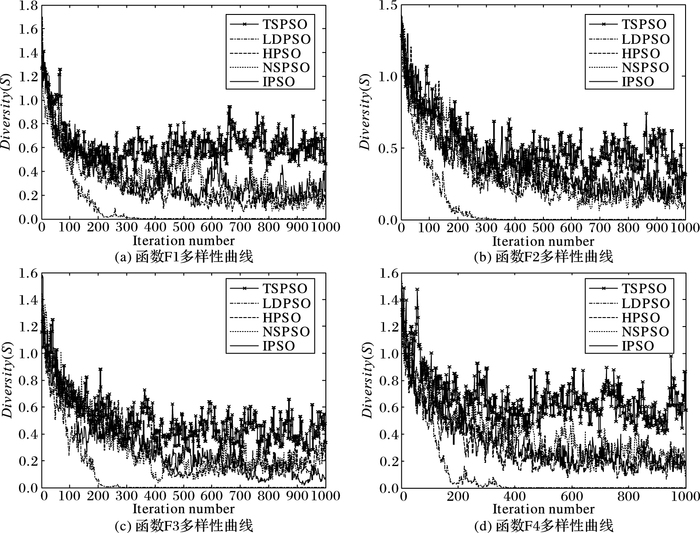
3.5 种群多样性讨论PSO算法中,种群多样性指粒子群两两个体间的总体差异情况,表现在搜索空间中的离散分布程度,即种群多样性越好,粒子群的离散程度越高,搜索范围越广,因此也就更容易寻找到全局最优值。图 5给出了5种改进PSO算法按照式(17) 中的种群多样性公式计算得出的变化曲线,从中分析得出:LDWPSO算法在寻优过程中种群多样性保持能力最差,种群多样性逐渐丧失,容易陷入局部最优;HPSO、NSPSO、IPSO以及本文所提TSPSO四种算法在寻优过程中种群多样性基本保持在一定范围内波动,并且TSPSO算法的种群多样性相对较优,更容易寻找全局最优值。
|
图 5 5种PSO算法对四种测试函数的种群多样性进化曲线 Figure 5 Diversity evolution curves of five PSO algorithms to four test functions |
本文通过对标准PSO算法以及相关的改进算法进行研究分析,针对目前改进PSO算法的研究中存在的缺陷与不足,并结合梯度下降法的快速寻优特点,提出了一种基于二次搜索的粒子群优化(TSPSO)算法。该算法中首次提出二次搜索、极值陷阱、禁忌区域等概念,并通过对四种测试函数与其他改进PSO算法进行对照仿真实验,结果表明TSPSO算法具有更快的收敛速度和更优的寻优性能。最后对TSPSO算法的种群多样性进行讨论,进一步验证了改进算法的有效性与可靠性。然而本文也存在不足,例如如何确定禁忌区域的最长半径R没有确定的计算方法,需要进一步研究。
| [1] | KENNEDY J, EBERHART R. Particle swarm optimization[C]//Proceedings of the IEEE International Conference on Neural Networks. Piscataway, NJ:IEEE, 1995, 4:1942-1948. |
| [2] | 吕莉, 赵嘉, 孙辉. 具有反向学习和自适应逃逸功能的粒子群优化算法[J]. 计算机应用, 2015, 35(5): 1336-1341. (LYU L, ZHAO J, SUN H. Particle swarm optimization algorithm using opposition-based learning and adaption escape[J]. Journal of Computer Applications, 2015, 35(5): 1336-1341. DOI:10.11772/j.issn.1001-9081.2015.05.1336) |
| [3] | 汤可宗, 肖绚, 贾建华, 等. 基于离散式多样性评价策略的自适应粒子群优化算法[J]. 南京理工大学学报, 2013, 37(3): 344-349. (TANG K Z, XIAO X, JIA J H, et al. Adaptive particle swarm optimization algorithm based on discrete estimate strategy of diversity[J]. Journal of Nanjing University of Science and Technology, 2013, 37(3): 344-349.) |
| [4] | 罗磊, 陈恳, 杜峰坡, 等. 基于改进型粒子群算法的曲面匹配与位姿获取[J]. 清华大学学报(自然科学版), 2015, 55(10): 1061-1066. (LUO L, CHEN K, DU F P, et al. Surface fitting and position-pose measurements based on an improved SA-PSO algorithm[J]. Journal of Tsinghua University (Science and Technology), 2015, 55(10): 1061-1066.) |
| [5] | LU C, SHENG W, HAN Y, et al. Phase-only pattern synthesis based on gradient-descent optimization[J]. Journal of Systems Engineering and Electronics, 2016, 27(2): 297-307. DOI:10.1109/JSEE.2016.00030 |
| [6] | 许少华, 宋美玲, 许辰, 等. 一种基于混合误差梯度下降算法的过程神经网络训练[J]. 东北石油大学学报, 2014, 38(4): 92-96. (XU S H, SONG M L, XU C, et al. Training algorithm of process neural networks based on hybrid error gradient descent[J]. Journal of Northeast Petroleum University, 2014, 38(4): 92-96.) |
| [7] | 韩文花, 徐俊, 沈晓晖, 等. 自学习粒子群与梯度下降混杂的漏磁反演方法[J]. 火力与指挥控制, 2015, 40(1): 88-91. (HAN W H, XU J, SHEN X H, et al. Hybrid of self-learning particle swarm optimization and gradient descent based magnetic flux leakage lnversion[J]. Fire Control & Command Control, 2015, 40(1): 88-91.) |
| [8] | 汤可宗, 李慧颖, 李娟, 等. 一种求解复杂优化问题的改进粒子群优化算法[J]. 南京理工大学学报, 2015, 39(4): 386-391. (TANG K Z, LI H Y, LI J, et al. Improved particle swarm optimization algorithm for solving complex optimization problems[J]. Journal of Nanjing University of Science and Technology, 2015, 39(4): 386-391.) |
| [9] | RIGET R, VESTERSTRØM J S. A diversity-guided particle swarm optimizer-the ARPSO[R]. Aarhus, Denmark:University of Aarhus, 2002. |
| [10] | 汤可宗. 遗传算法与粒子群优化算法的改进及应用研究[D]. 南京: 南京理工大学, 2011. (TANG K Z. Improvement and application of genetic algorithm and particle swarm algorithm research[D]. Nanjing:Nanjing University of Technology Institute of Computer Science and Engineering, 2011.) http://cdmd.cnki.com.cn/Article/CDMD-10288-1012320955.htm |
| [11] | 周利军, 彭卫, 曾小强, 等. 基于杂交变异的动态粒子群优化算法[J]. 计算机科学, 2013, 40(11A): 143-146. (ZHOU L J, PENG W, ZENG X Q, et al. Dynamic particle swarm optimization based on hybrid variable[J]. Computer Science, 2013, 40(11A): 143-146.) |
| [12] | 白俊强, 尹戈玲, 孙智伟, 等. 基于二阶振荡及自然选择的随机权重混合粒子群算法[J]. 控制与决策, 2012, 27(10): 1459-1464. (BAI J Q, YIN G L, SUN Z W, et al. Random weighted hybrid particle swarm optimization algorithm based on second order oscillation and natural selection[J]. Control and Decision, 2012, 27(10): 1459-1464.) |
| [13] | 魏建香, 孙越泓, 苏新宁. 一种基于免疫选择的粒子群优化算法[J]. 南京大学学报(自然科学版), 2010, 46(1): 1-9. (WEI J X, SUN Y H, SU X N. A novel particle swarm optimization based on immune selection[J]. Journal of Nanjing University (Natural Sciences), 2010, 46(1): 1-9.) |
| [14] | ZHAN Z H, ZHANG J, LI Y, et al. Adaptive particle swarm optimization[J]. IEEE Transactions on Systems, Man, and Cybernetics-Part B:Cybernetics, 2009, 39(6): 1362-1381. DOI:10.1109/TSMCB.2009.2015956 |
| [15] | 温正. 精通MATLAB智能算法[M]. 北京: 清华大学出版社, 2015: 106-192. |




