随着互联网的发展,大量的WWW(World Wide Web)页面、XML(eXtensible Markup Language)文档等具有半结构化特征的数据不断涌现,对这些数据用无序树建模,并利用频繁子树挖掘技术能够有效挖掘隐藏在其结构中的信息。目前,许多频繁子树挖掘算法已经被提出,比如算法FP-Tree(Frequent Pattern Tree)[1]和PFP-Tree(Projection Frequent Pattern Tree)[2]采用基于投影的思想来挖掘频繁子树,算法EvoMiner[3]、MCFP-Tree(Mining Compressed Frequent Pattern Tree)[4]和FRESTM(Frequent Restrictedly Embedded SubTree Miner)[5]采用基于Apriori的思想进行频繁子树挖掘。但这些算法会输出大规模且带有冗余信息的频繁子树集合,大规模的频繁子树输出会影响后续的操作效率,为了减小频繁子树输出规模、提高后续操作效率,挖掘频繁闭树的FBMiner(Frequent Closed Miner)[6]和极大频繁子树MFTM(Maximal Frequent Tree Mining)[7]两种算法已经被提出,这两种算法虽然能够有效减小频繁子树的输出规模,但却丢失了大量频繁子树的信息。
针对传统方法的不足,本文提出了一种挖掘覆盖模式(Mining CoveRage Pattern, MCRP)算法。该算法采用宽度孩子数编码,该编码方式记录了每个节点与其孩子节点的位置关系,提高了后续子树支持度计算的效率。在宽度孩子数编码的基础上,算法采用了一种基于最大前缀编码序列的边扩展方式生成了所有的候选子树,确保能够找出所有的频繁子树,避免了信息的遗漏。此外,在δ′-覆盖[8]概念的基础上提出了一种新的δ′-覆盖概念,在生成频繁子树的时候同时判断该子树是否满足δ′-覆盖条件,若满足,算法将输出该覆盖模式。
1 度孩子数编码定义1 树的支持度和频繁子树。
D={T1, T2, …, Tn}是树数据集,T是树模式,
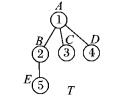
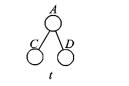
为了提高子树支持度计算效率,在传统字符串编码[9]的基础上优化了一种宽度孩子数编码。在宽度孩子数编码中,树的每个节点用(index(v), range(v), tag(v))三元组表示,其中index(v)表示节点v在树的宽度优先序列中的位置,range(v)表示节点v孩子的位置范围,tag(v)表示节点v的标签。按照宽度优先遍历得到的三元组序列就是宽度孩子数编码。由于无序树中兄弟节点间是无序的,为了使宽度孩子数编码更加规范,对于兄弟关系的树节点按照其标签tag(v)的字典顺序进行排序。如图 1,T的宽度孩子数编码为:code(T)=(1, (2-4), A)-(2, (5), B)-(3, (), C)-(4, (), D)-(5, (), E)。在计算子树支持度时首先要统计子树的频数,例如,统计图 2中树t的频数时可以先在code(T)中找到节点A,然后直接在range(A)范围内查找C、D节点是否存在,避免了从头到尾逐一查找,节约了时间。
|
图 1 树T实例 Figure 1 Example of tree T |
|
图 2 树t实例 Figure 2 Example of tree t |
定义2 最大前缀编码。
一棵无序树按宽度孩子数编码,去掉最后一个节点后剩余节点的编码,称为该树的最大前缀编码。
定义3 δ′-覆盖。
设T和T′是频繁树模式,若T⊆T′,T与T′之间的Jaccard距离[10]小于δ′,H(T′)≤H(T)+1且W(T′)≤W(T)+1,则称T′ δ′-覆盖T。其中,H(T)、W(T)分别表示T的高度和宽度。
该算法主要分为两大核心步骤:第一步使用基于最大前缀编码的边扩展方式生成候选子树并判断候选子树是否为频繁子树;第二步在频繁子树的基础上输出满足δ′-覆盖条件的覆盖树模式。
2.1 基于最大前缀编码的边扩展生成候选子树一般采用边扩展方式,传统的基于最右路径扩展[11]的方法在每次生成候选子树的时候要事先找到最右路径,降低了挖掘效率。基于最大前缀编码的边扩展规定只有具有相同的最大前缀编码的两棵子树才能够进行合并扩展生成候选子树,该方法弥补了上述方法的不足,在时间效率上有所提升,同时能够生成所有的候选子树,减少了信息的遗漏。最大前缀编码相同的两棵树拓扑结构可能相同也可能不同。下面分别讨论这两种情况下候选子树的生成方法。
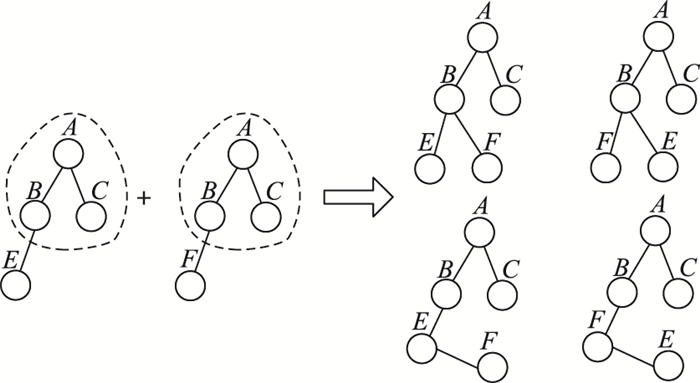
2.1.1 拓扑结构相同拓扑结构相同的两棵待合并树的编码中的最后一个节点一定位于同一层且它们的父亲节点的标签一定相同,此时合并扩展生成的候选子树的编码中最后两个节点可能是兄弟关系节点,也可能是双亲孩子关系节点,如图 3所示。
|
图 3 相同拓扑结构的两棵树合并操作 Figure 3 Merging process of two trees with same topology |
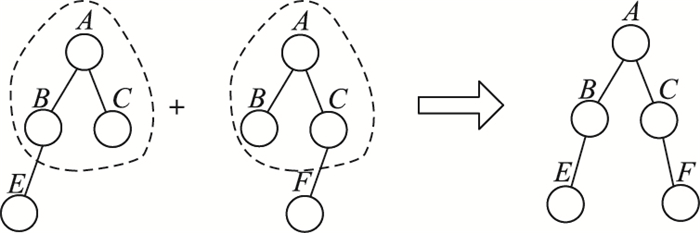
拓扑结构不同的两棵待合并树的编码中的最后一个节点可能在同一层也可能不在同一层,此时直接将两棵树的最大前缀编码重叠,剩下的节点位置不变即可,如图 4所示。
|
图 4 不同拓扑结构的两棵树合并操作 Figure 4 Merging process of two trees with different topology |
生成越多的候选子树意味着保留了越多的原始数据信息,对于某些要求精确结果的子树挖掘应用来说,生成所有的候选子树是很有意义的,基于最大前缀编码的边扩展能够生成所有的候选子树,下面给出理论证明。
证明 设两棵m(m≥2) 叉n(n≥2) 阶频繁树通过穷举法能够生成的候选子树数量为M(n),基于最大前缀编码的边扩展方法能够生成候选子树数量为H(n),式(1) 中h表示两棵最大前缀编码相同的m叉n阶树中每棵树的逻辑结构数。通过穷举法发现M(n)与m、n之间具有如下关系:(
| $ \begin{array}{l} M\left( n \right) = h*\left( {h + 3} \right);\\ h = \left\{ \begin{array}{l} n-\lfloor n/m\rfloor, \;\;\;\;\;n\% m = 0, 1\\ n-\lfloor n/m\rfloor-1\;, n\% m = 2, 3, \cdots, m - 1 \end{array} \right. \end{array} $ | (1) |
接下来采用双层嵌套的数学归纳法来证明上式的正确性。首先固定m的取值,采用数学归纳法证明M(n)与n的关系式成立,接下来假设m=g(g>2) 时公式任然成立,最后推理出m=g+1时公式成立。
1) 当m=2时,式(1) 化简为式(2)。
| $ M\left( n \right) = \left\{ \begin{array}{l} {n^2}/4 + 3n/2, \;\;\;\;\;\;\;n为偶数\\ {n^2}/4 + 2n + 7/4, \;\;n为奇数 \end{array} \right. $ | (2) |
① 当n=2时,M(n)=4,通过穷举法可以验证结果正确。
② 假设当n=k时,式(2) 仍然成立,即式(3) 成立:
| $ M\left( k \right) = \left\{ \begin{array}{l} {k^2}/4 + 3k/2, \;\;\;\;\;\;\;k为偶数\\ {k^2}/4 + 2k + 7/4, \;\;k为奇数 \end{array} \right. $ | (3) |
③ 下面证明当n=k+1时,式(3) 成立。
a)当k为偶数时,k+1为奇数,此时h=k+1-
b)当k为奇数时,k+1为偶数,此时时h=k+1-
综上,式(3) 成立,进而可得m=2时,式(1) 成立。
2) 假设m=g(g>2) 时,式(1) 仍然成立。
3) 接下来证明当m=g+1时,式(1) 成立。
因为n为大于2的任意正整数,由h=n-
综上所述,式(1) 得证。
上述已经证明两棵m(m≥2) 叉n(n≥2) 阶频繁树通过穷举法能够生成的候选子树数量为M(n),接下来证明基于最大前缀编码的边扩展方法生成候选子树数量H(n)的公式。
通过基于最大前缀编码的边扩展方法不难发现,拓扑结构相同的情况下可以生成4h棵子树,拓扑结构不同的情况下可生成h(h-1) 棵子树,进而得:
| $ \begin{array}{l} H\left( n \right) = 4h + h\left( {h-1} \right);\\ h = \left\{ \begin{array}{l} \left( {\left( {m-1} \right)/m} \right)*n, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;n\% m = 0\\ \left( {\left( {m-1} \right)/m} \right)*\left( {n + 1} \right) - 1, \;\;\;\;\;\;\;\;n\% m = m - 1\\ \left( {\left( {m - 1} \right)/m} \right)*\left( {n + 2} \right) - 2, \;\;\;\;\;\;\;n\% m = m - 2\\ \vdots \\ \left( {\left( {m - 1} \right)/m} \right)*\left( {n + \left( {m - 2} \right)} \right) - \left( {m - 2} \right), \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;n\% m = 2\\ \left( {\left( {m - 1} \right)/m} \right)*\left( {n + \left( {m - 1} \right)} \right) - \left( {m - 2} \right), \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;n\% m = 1 \end{array} \right. \end{array} $ | (4) |
将M(n)中h表达式去下限符号后进一步整理发现M(n)=H(n)。至此,基于最大前缀编码的边扩展方法能够生成所有的候选子树得到了证明。
2.2 输出覆盖模式为了减小频繁子树输出规模,提高后续操作效率,用一个小的覆盖模式集合来概括所有的频繁子树模式,领域专家只需要分析这个小的覆盖模式集合就可以了解数据集中的所有信息。若树T被树T′ δ′-覆盖,MCRP将只会输出T′而不会输出T。
覆盖模式建立在δ′-覆盖概念的基础上,为了尽可能使覆盖模式与其对应的被覆盖模式的结构相似,规定覆盖模式与其对应的被覆盖模式阶数差的绝对值不能超过1。当T′比T的高度大1时,在输出T′的时候在其编码的最前面加上标号H,表示T′覆盖了一个高度比自己小1的频繁树,领域专家通过去掉T′最后一层的最后一个节点就可以还原出未被输出的频繁树T;当T′比T宽度大1时,在输出T′的时候在其编码的最前面加上标号W,表示T′覆盖了一个宽度比自己小1的频繁树,领域专家通过去掉T′最右边的节点就可以还原出未被输出的频繁树T;同样的道理,当T′的宽度和高度均比T大1时,本文在T′编码的最前边加上标号HW。理论和实验证明算法保留了原始频繁子树几乎所有的信息,并且大大降低了频繁子树的输出规模。
2.3 MCRP算法伪代码MCRP算法首先采用宽度孩子数编码对树进行编码,然后通过基于最大前缀编码序列的边扩展方式生成所有的候选子树。接下来计算候选子树的支持度,找出频繁子树。由于本文对树采用了宽度孩子数编码,因此在线性时间复杂度内可以完成候选子树支持度的计算。最后在频繁子树集和δ′-覆盖概念的基础上输出覆盖模式集。MCRP算法伪代码如下。
MCRP(D, min_sup, δ′)
输入:数据集D,min_sup,Jaccard距离阈值δ′;
输出:频繁子树的覆盖模式集合CS。
//Sk表示k阶频繁子树集合
//L(Sk)表示集合Sk的大小
//Sk(i)表示集合Sk中第i棵树
//函数countNum(T)用于统计T的频数
1) 遍历数据集D,统计每个节点的频度,D中树的最大阶数M,并将频繁的节点存放在S1中
2) For(int i=0;i<L(S1)-1;i++)
3) For(int j=i; j<L(S1)-1; j++)
4) S1(i)与S1(j)合并扩展所得候选子树T;
5) If(countNum(T)/|D|≥min_sup)
6) Sk ← T;
7) End for
8) End for
9) For(int i=2;i≤M; i++)
10) CS ← GenerateCorageTree(Si, δ′);
11) Return CS;
函数GenerateCorageTree(Sk, δ′)
1) If(L(Sk)≥2)
2) For(int i=0;i<L(Sk)-1;i++)
3) For(int j=i+1; j<L(Sk); j++)
4) If(Sk(i)与Sk(j)最大前缀编码相同)
5) If(Sk(i)与Sk(j)拓扑结构相同)
6) T=合并扩展Sk(i)与Sk(j);
7) Else
8) T将Sk(i)与Sk(j)最大前缀编码重叠;
9) End if
10) If(countNum(T)/|D|≥min_sup)
11) Sk+1←T;
12) If(1-|{Tr|(T⊆Tr) & (Sk(e)⊆Tr),
Tr∈D}|/|{Tr|(T⊆Tr)|(Sk(e)⊆Tr),
Tr∈D}|≥δ′) //e=i,j
13) If(H(T)>H(Sk(e)))
//Tag(“H”, T)表示在code(T)的前面加上标号H
14) CSK ← Tag(“H”, T);
15) Else if(W(T)>W(Sk(e)))
16) CSK ← Tag(“W”, T);
17) Else if(H(T)>H(Sk(e)) & & W(T)>W(Sk(e)))
18) CSK ← Tag(“HW”, T);
19) End if
20) End for
21) End for
22) Return CSK;
2.4 算法时间复杂度分析函数GenerateCorageTree(Si, δ′)在生成k+1阶候选子树的时候需要遍历频繁k阶子树集合,以保证频繁k阶子树集合中任意两棵子树都有机会被判断是否有生成k+1阶候选子树的可能,最坏的情况下任意两棵k阶子树都能生成k+1阶候选子树,此时的时间复杂度为O(L(Sk)2)。当生成一棵候选子树的时候需要计算该子树的频数,这一步需要的时间近似为O(k),所以函数GenerateCorageTree(Si, δ′)的时间复杂度为O(k*L(Sk)2)。函数GenerateCorageTree(Si, δ′)只是输出某一阶频繁子树的覆盖模式,MCRP算法需要输出所有覆盖模式,其时间复杂度为O(k*L(Sk)2*|M|)。在实际情况中MCRP算法的运行时间远远小于本文得出的时间复杂度,因为并不是任意的两棵k阶子树都能满足条件生成k+1阶候选子树,并且实际生成的频繁子树的最大阶数要远小于|M|。
FBMiner算法是频繁闭树模式挖掘中最经典且挖掘效率最高的几个算法之一。该算法采用基于最右路径的边扩展的思想生成候选子树。在生成k+1阶候选子树之前,首先需要遍历k阶频繁子树集合找到每一棵k阶频繁子树的最右路径,这一步的时间复杂度为O(k*L(Sk))。接着在k阶频繁子树的最右路径上的任意一个节点上扩展一条边生成k+1阶候选子树,这一步的时间复杂度为O(m),其中m为最右路径上的节点个数。然后计算候选子树的支持度,这一步的时间复杂度近似为O((k+1)*L(Sk+1))。综上,FBMiner算法的时间复杂度为O(m*k2*L(Sk)*L(Sk+1)*|M|)。
MFTM算法是极大频繁树模式挖掘中的代表性算法。其挖掘流程大致与FBMiner算法相同,不同的是在计算候选子树支持度的时候,其时间复杂度为O(L(Sk+1)2),通常情况下L(Sk+1)远远大于k+1。综上,MFTM算法的时间复杂度近似为O(m*k2*L(Sk+1)2*|M|)。
3 实验设置与分析 3.1 实验设置MCRP算法用于减少频繁子树的输出数量,降低输出频繁子树的冗余性,进而提高候选领域专家的分析效率。与MCRP算法类似,为了减小频繁子树的输出规模,FBMiner和MFTM算法同样只输出部分具有代表性的频繁子树。为了验证MCRP算法可行性,本实验将MCRP算法与频繁闭树挖掘领域中的经典算法FBMiner和极大频繁子树挖掘领域中的代表性算法MFTM在真实实验数据集NI-AGARA (http://research.cs.wisc.edu/niag-ara/data/)上进行实验对比。该数据包含400多个XML文档,每个文档表示好莱坞某个演员的相关信息,以及其出演电影的相关信息。实验采用算法执行时间和输出频繁子树的数量作为衡量算法性能的两个指标。算法执行时间越短表示算法的时间效率越高,算法输出频繁子树的数量越少表示算法的去冗余能力越强。本实验的实验环境如表 1所示。
| 表 1 实验环境 Table 1 Experimental environment |
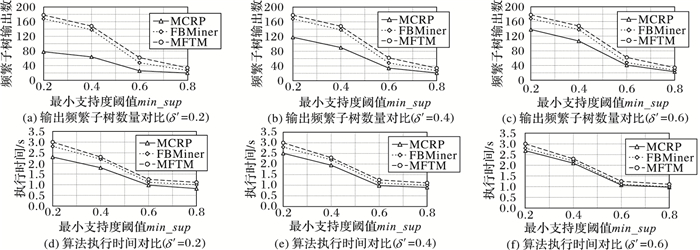
如图 5所示,图中第一行分别表示Jaccard距离阈值δ′分别为0.2、0.4和0.6时MCRP、FBMiner和MFTM算法在不同支持度阈值min_sup的情况下输出的频繁子树的数量。图中第二行分别对应不同δ′值时三个算法的执行时间。由实验图可知,MCRP算法输出的频繁子树数量和算法执行时间都要比算法FBMiner和MFTM输出的频繁子树数量和执行时间少。实验表明,MCRP时间效率优于FBMiner和MFTM,并且能在不丢失频繁子树信息的情况下比FBMiner和MFTM输出更少的频繁子树。
|
图 5 三种算法在δ′=0.2, 0.4, 0.Ⅵ时频繁子树输出数和执行时间与支持度阈值的关系 Figure 5 Number of output frequent subtrees and execution time vs. min_sup for different algorithms when δ′=0.2, 0.4, 0.Ⅵ |
本文探讨了无序树的频繁子树挖掘问题。首先,改进了一种宽度孩子数编码方式,该编码方式保留了节点及其孩子节点的位置信息,使得在计算子树支持度的时间效率得到了提升;然后,在宽度孩子数编码基础上,提出了基于最大前缀编码的边扩展方式用于生成所有的候选子树,避免了频繁子树信息的遗漏;最后,在δ′-覆盖概念的基础上输出覆盖模式,避免输出大规模的频繁子树影响后续操作的效率。实验结果表明MCRP算法在频繁子树降低输出规模以及时间开销上是有效的。频繁子树挖掘中生成候选子树一直以来都是效率瓶颈之一,基于投影的思想挖掘频繁子树虽然不用生成候选子树,但需要消耗大量内存空间,如何弥补该方式的缺陷以及如何应对海量数据的挑战将是后续研究的主要内容。
| [1] | YAKOP M A M, MUTALIB S, ABDUL-RAHMAN S. Data projection effects in frequent itemsets mining[M]//Soft Computing in Data Science. Berlin:Springer, 2015:23-32. https://link.springer.com/chapter/10.1007/978-981-287-936-3_3 |
| [2] | MALVIYA J, SINGH A, SINGH D. An FP tree based approach for extracting frequent pattern from large database by applying parallel and partition projection[J]. International Journal of Computer Applications, 2015, 114(18): 1-5. DOI:10.5120/20075-2077 |
| [3] | DEEPAK A, FERNÁNDEZ-BACA D, TIRTHAPURA S, et al. EvoMiner:frequent subtree mining in phylogenetic databases[J]. Knowledge and Information Systems, 2014, 41(3): 559-590. DOI:10.1007/s10115-013-0676-0 |
| [4] | 吴倩, 罗健旭. 压缩FP-Tree的改进搜索算法[J]. 计算机工程与设计, 2015, 36(7): 1771-1777. (WU Q, LUO J X. Improved search algorithm of compressed FP-Tree[J]. Computer Engineering and Design, 2015, 36(7): 1771-1777.) |
| [5] | ZHANG S, DU Z, WANG J T. New techniques for mining frequent patterns in unordered trees[J]. IEEE Transactions on Cybernetics, 2015, 45(6): 1113-1125. DOI:10.1109/TCYB.2014.2345579 |
| [6] | FENG B, XU Y, ZHAO N, et al. A new method of mining frequent closed trees in data streams[C]//Proceedings of the 20107th International Conference on Fuzzy Systems and Knowledge Discovery. Piscataway, NJ:IEEE, 2010:2245-2249. |
| [7] | 杨沛, 谭琦. 极大频繁子树挖掘及其应用[J]. 计算机科学, 2008, 35(2): 150-153. (YAN P, TAN Q. Maximal frequent subtree mining and its application[J]. Computer Science, 2008, 35(2): 150-153.) |
| [8] | XIN D, HAN J, YAN X, et al. Mining compressed frequent-pattern sets[C]//Proceedings of the 31st International Conference on Very Large Data Bases. Trondheim, Norway:VLDB Endowment, 2005:709-720. |
| [9] | LIU L, LIU J. Mining frequent embedded subtree from tree-like databases[C]//Proceedings of the 2011 International Conference on Internet Computing and Information Services. Washington, DC:IEEE Computer Society, 2011:3-7. |
| [10] | JAIN A K, DUBES R C. Algorithms for Clustering Data[M]. Upper Saddle River, NJ: Prentice-Hall, Inc., 1988: 67-73. |
| [11] | HAN K, LV W, YIN B, et al. Constrained frequent subtree mining method[C]//Proceedings of the 20145th International Conference on Digital Home. Washington, DC:IEEE Computer Society, 2014:287-292. |




