辽宁工程技术大学 电子与信息工程学院, 辽宁 葫芦岛 125105
收稿日期:2017-01-17;修回日期:2017-03-04
基金项目:国家自然科学基金资助项目(61372058);辽宁省高校重点实验室项目(LJZS007)
作者简介:南敬昌(1971-), 男, 河南滑县人, 教授, 博士, 主要研究方向:射频电路与系统、电路系统与电磁仿真、信号处理与信息编码;
崔洪艳(1993-), 女, 辽宁抚顺人, 硕士研究生, 主要研究方向:射频功放非线性分析、射频电路设计
Modeling of power amplifier based on dynamic X-parameter of new two-dimensional kernel function
School of Electronic and Information Engineering, Liaoning Technical University, Huludao Liaoning 125105, China
Foundation Item: This work is partially supported by the National Natural Science Foundation of China (61372058), the Key Laboratory Project of Higher Education of Liaoning Province (LJZS007)
Author introduction: NAN Jingchang, born in 1971, Ph. D., professor. His research interests include RF circuit and system, circuit system and electromagnetic simulation, signal processing and information coding;
CUI Hongyan, born in 1993, M. S. candidate. Her research interests include RF power amplifier nonlinear analysis, RF circuit design
0 引言
随着无线通信系统的不断升级,在面对更大带宽、更高峰均比的调制信号情况下,射频功放固有的非线性和记忆效应严重影响通信质量。射频功放在不同的宽带信号下所呈现的非线性特性并不相同,无记忆功放模型在这样情况下难以满足设计要求,导致器件建模变得更加困难和复杂。在对射频微波电路的非线性行为模型研究中,急待攻克的难题主要是如何对具有记忆效应的非线性功放进行精确的动态建模,并方便地应用于系统级仿真,来获得功放更优的性能。为了评估以及降低功放的记忆非线性效应对通信系统造成的影响,功放器件的非线性建模方法成为当前无线通信领域中的一个重要课题。
功放行为模型建模是利用功放输入及输出数据建立描述功放行为特性的数学模型技术[1]。目前表征带有记忆效应的功放行为模型主要有Volterra级数模型、神经网络模型、动态X参数模型。基于Volterra理论及其多项式的功放模型被认为是最能够准确描述功放特性的模型[2],然而这种近似随着功放非线性增强以及记忆效应加深,使Volterra级数模型的参数辨识变得非常复杂,限制了其对强记忆及强非线性功放的建模。神经网络模型拥有很强的学习能力和逼近能力,但模型泛化能力不强,难以由硬件实现。安捷伦提出了基于测量的X参数模型理论及基于非线性矢量网络分析仪(Nonlinear Vector Network Analyzer,NVNA)平台的测试系统[3-4],作为一种集测量、建模和设计非线性器件的新方法,受到了广泛关注。Jan Verspecht博士在文献[5]中首次提出动态X参数模型,引入了表征长期记忆效应的三维核函数,而三维核函数的提取及验证都极为困难;而后该团队在文献[6-7]针对该模型将记忆效应核函数简化成二维的核函数,一定程度上简化了模型及参数辨识过程,但是模型精度不高。文献[8]提出基于反馈(FeedBack,FB)结构的动态X参数模型,提出一种表征功放记忆效应的新方法,但模型仅考虑功放的长期记忆效应,参数辨识困难且普适性差。文献[9]中提出利用前馈(FeedForward, FF)结构构建动态X参数模型,同时考虑两种记忆效应在建模中的影响,在模型的精度和提取速度上有了一定提高,但是仅仅将两种记忆效应简单叠加,不符合功放记忆效应的产生机制,模型泛化能力不强,模型的精度以及应用范围受到限制。
基于以上的研究,本文提出一种利用新型FB结构的动态X参数模型建模方法。该方法将模型分为静态部分与动态部分。静态部分的核函数为多谐波失真(Poly Harmonic Distortion,PHD)模型,以保证模型对强非线性的正确表征;考虑短期记忆(Short-Term Memory,STM)效应以及长期记忆(Long-Term Memory,LTM)效应相互作用关系,利用双记忆路径模型提取表征记忆效应的非线性函数,替换动态核函数,以提高模型精度;采用将输出信号分为双变量的新型FB结构,引入时变频率变量将三维动态核函数简化为二维核函数,以简化动态核函数的提取过程,降低模型的复杂度。经过实验验证,新的动态X参数模型比静态X参数模型、传统动态X参数模型以及FF结构的动态X参数模型精度更高,仿真速度与已有两种动态模型相当。
1 模型分析
1.1 静态X参数模型
对于一个被测件而言,假定所研究的信号包含一系列离散的基波和谐波频谱分量,X参数[10]就是使用谐波叠加的概念来描述大信号入射波A的所有频率分量Aqn与反射波B的所有频谱分量Bpm之间的关系,如式(1) 所示。p和q是端口数,m和n是谐波次数;XpmF描述器件产生谐波的能力,Xpq, mnS及Xpq, mnT描述器件频率变换的能力。
|
$
\begin{array}{l}
{B_{pm}}{\rm{ = }}X_{pm}^{\rm{F}}(\left| {{A_{11}}} \right|) + \sum\limits_{q, n \ne 1} {X_{pq, mn}^{\rm{S}}(\left| {{A_{11}}} \right|)} {P^{m-n}}{A_{qn}}{\kern 1pt} + \\
\;\;\;\;\;\;\sum\limits_{q, n \ne 1} {X_{pq, mn}^{\rm{T}}(\left| {{A_{11}}} \right|)} {P^{m + n}}A_{qn}^*
\end{array}
$
|
(1) |
1.2 传统动态X参数模型
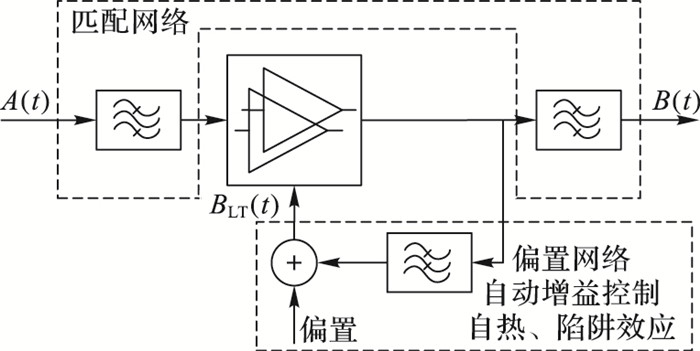
按照产生信号失真的强弱,将记忆效应分为STM效应和LTM效应[11]。STM效应主要由匹配电路、晶体管内的运转时间引起;LTM效应主要由偏置电路、自动增益控制电路、晶体管自热以及陷阱效应引起。这种双记忆效应相互作用的关系如图 1所示。
传统动态X参数模型引入了功放LTM效应对功放模型的影响,输出谐波表达式如式(2) 所示。它是由当前输入|A(t)|、过去输入|A(t-τ)|及时间跨度τ构成的具有三维核函数的动态X参数模型。
|
$
\begin{array}{l}
B\left( t \right) = {X_m}\left( {\left| {A\left( t \right)} \right|} \right) \cdot \mathit{\Phi} \left( t \right) + \\
\int_0^\infty {G\left( {\left| {A\left( t \right)} \right|, \left| {A\left( {t-\tau } \right)} \right|, \tau } \right)} {\rm{d}}u \cdot \mathit{\Phi} \left( t \right)
\end{array}
$
|
(2) |
整个模型是由静态非线性部分及动态非线性部分叠加得到,Xm(·)表征静态核函数,G(·)表征动态核函数,Φ(t)=exp [jφ(A(t))]代表输入信号的相位函数。
1.3 FB结构模型
假设功放的输入信号是一个带通调制信号,如下所示:
|
$
x\left( t \right) = {\rm{Re}}(\left| {A\left( t \right)} \right| \cdot {{\rm{e}}^{{\rm{j}}\omega t}})
$
|
(3) |
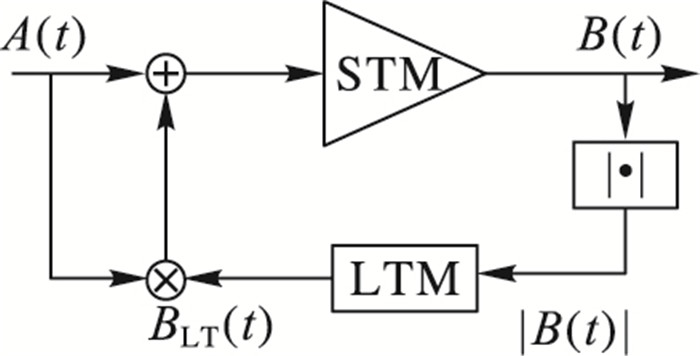
其中:|A(t)|为输入调制信号的包络,ω为输入信号的载波频率。对于功放模型,需要确认包络输入|A(t)|以及输出包络|B(t)|,则基于FB拓扑结构[12]的模型如图 2所示。
根据功放的电路结构建立双记忆路径模型。模型结构中STM路径的作用是捕获功放主动态,担当着放大以及滤波的作用。当一个时变包络信号通过这条路径时,STM路径的短期非线性作用将会产生一个低频信号反馈到LTM路径中,LTM路径本身是动态非线性,进而影响STM路径。
根据这样的结构,得到双记忆路径模型表达式如下:
|
$
B\left( t \right) = \alpha \left( {\left| {A\left( t \right)} \right|, t} \right) \cdot \left( {1 + {B_{{\rm{LT}}}}\left( t \right)} \right) \cdot \left| {A\left( t \right)} \right|
$
|
(4) |
|
$
{B_{{\rm{LT}}}}\left( t \right) = \beta \left( {\left| {A\left( t \right)} \right|, t} \right) \cdot \left| {B\left( t \right)} \right|
$
|
(5) |
其中:α(|A(t)|, t)代表功放的增益,β(|A(t)|, t)代表反馈系数。当单独考虑STM及LTM路径的效应时,用以下非线性积分[13]表示:
|
$
{B_{{\rm{ST}}}}\left( t \right) = \int_0^\infty {{{\hat h}_{{\rm{ST}}}}(\left| {A(t-\tau )} \right|, \tau )} A(t-\tau ){\rm{d}}\tau
$
|
(6) |
|
$
{B_{{\rm{LT}}}}\left( t \right) = \int_0^\infty {{{\hat h}_{{\rm{LT}}}}(\left| {A(t-\tau )} \right|, \tau )} \left| {A(t-\tau )} \right|{\rm{d}}\tau
$
|
(7) |
则输出包络信号可以表示为:
|
$
\begin{array}{l}
B\left( t \right) = \int_0^\infty {{{\hat h}_{{\rm{ST}}}}(\left| {\left[{1 + {B_{{\rm{LT}}}}(t-\tau )} \right] \cdot A(t - \tau )} \right|, \tau ){\kern 1pt} \cdot } \\
{\kern 1pt} \;\;\;\;\;\;\;\;\;\;\left[{1 + {B_{{\rm{LT}}}}(t-\tau )} \right] \cdot A(t -\tau ){\rm{d}}\tau
\end{array}
$
|
(8) |
2 二维核函数模型
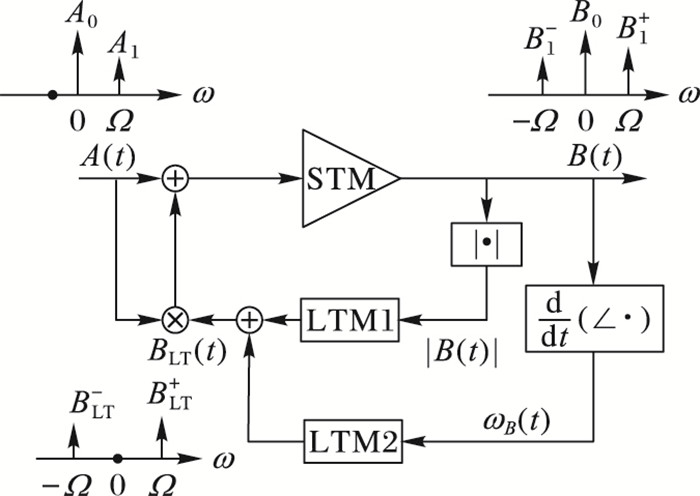
传统功放模型的核函数只是关于当前及过去输入信号幅度的函数,为了提高模型精度,在核函数中引入了新的变量——时变频率,同时将X参数的动态核函数简化成为只与输入信号包络幅度和时变频率相关的二维核函数。在上述的传统FB结构中,在求解核函数时需要求解一个不对称方程,难以得到精确的核函数,因此结合时变频率变量,改进FB模型的拓扑结构,将模型输出包络信号分解为幅度与频率的二维变量,分别提取对应的LTM效应核函数,新的拓扑结构如图 3所示。
考虑信号变化节点,改进的FB结构模型表达式如下所示:
|
$
\begin{array}{l}
B(t) = \int_0^\infty {{{\hat h}_{{\rm{ST}}}}(\left| {\left[{1 + {B_{{\rm{LT}}}}(t-\tau )} \right] \cdot A(t - \tau )} \right|, \tau )} {\kern 1pt} \cdot \\
\;\;\;\;\;\;\;\;\;\;\left[{1 + {B_{{\rm{LT}}}}(t-\tau )} \right] \cdot A(t -\tau ){\rm{d}}\tau
\end{array}
$
|
(9) |
式中:
|
$
{B_{{\rm{ST}}}}\left( t \right) = \int_0^\infty {{{\hat h}_{{\rm{ST}}}}(\left| {A\left( {t-\tau } \right)} \right|, \tau )} A\left( {t-\tau } \right){\rm{d}}\tau
$
|
(10) |
|
$
\begin{array}{l}
{B_{{\rm{LT}}}}\left( t \right) = \int_0^\infty {{{\hat h}_{{\rm{LT1}}}}(\left| {A\left( {t-\tau } \right)} \right|, \tau )} \left| {B\left( {t-\tau } \right)} \right|{\rm{d}}\tau + \\
\;\;\;\;\;\;\;\;\;\;\;\;\int_0^\infty {{{\hat h}_{{\rm{LT}}2}}(\left| {A\left( {t-\tau } \right)} \right|, \tau ){\omega _{{B}}}} \left( {t - \tau } \right){\rm{d}}\tau
\end{array}
$
|
(11) |
|
$
{\omega _B}\left( t \right) = \frac{{d{\varphi _B}\left( t \right)}}{{{\rm{d}}t}}
$
|
(12) |
|
$
{\varphi _B}\left( t \right) = {\rm{ta}}{{\rm{n}}^{- 1}}\left[{-{\rm{j}}\frac{{B\left( t \right)-B{{\left( t \right)}^*}}}{{B\left( t \right) + B{{\left( t \right)}^*}}}} \right]
$
|
(13) |
为了简化核函数,引入时变频率核替换式(9) 中的非线性脉冲响应函数,如式(14)~(16) 所示:
|
$
{H_{{\rm{ST}}}}\left( {\left| {A\left( t \right)} \right|, \mathit{\Omega} } \right) = \int_0^\infty {{{\hat h}_{{\rm{ST}}}}\left( {\left| {A\left( t \right)} \right|, \tau } \right){{\rm{e}}^{-{\rm{j}}\mathit{\Omega} \tau }}} {\rm{d}}\tau
$
|
(14) |
|
$
{H_{{\rm{LT1}}}}\left( {\left| {A\left( t \right)} \right|, \mathit{\Omega} } \right) = \int_0^\infty {{{\hat h}_{{\rm{LT1}}}}\left( {\left| {A\left( t \right)} \right|, \tau } \right){{\rm{e}}^{-{\rm{j}}\mathit{\Omega} \tau }}} {\rm{d}}\tau
$
|
(15) |
|
$
\begin{array}{l}
\\
{H_{{\rm{LT2}}}}\left( {\left| {A\left( t \right)} \right|, \mathit{\Omega} } \right) = \int_0^\infty {{{\hat h}_{{\rm{LT2}}}}\left( {\left| {A\left( t \right)} \right|, \tau } \right){{\rm{e}}^{-{\rm{j}}\mathit{\Omega} \tau }}} {\rm{d}}\tau
\end{array}
$
|
(16) |
新的动态X参数模型如式(17),在其静态部分采用PHD模型表征功放强非线性的特性,动态部分采用提出的新动态核函数模型表征功放STM效应和LTM效应的特性。
|
$
B(t) = {X_m}\left( {\left| {A\left( t \right)} \right|} \right)\mathit{\Phi} \left( t \right) + \int_0^\infty {G\left( {\left| {A\left( t \right)} \right|, \mathit{\Omega} } \right)} {\rm{d}}u
$
|
(17) |
其中:
|
$
G\left( {\left| {A\left( t \right)} \right|, \mathit{\Omega} } \right) = {H_{{\rm{ST}}}}\left( {\left| {A\left( t \right)} \right|, \mathit{\Omega} } \right) \cdot \left( {1 + {H_{{\rm{LT}}}}\left( {\left| {A\left( t \right)} \right|, \mathit{\Omega} } \right)} \right)
$
|
(18) |
|
$
{H_{{\rm{LT}}}}\left( {\left| {A\left( t \right)} \right|, \mathit{\Omega} } \right) = {H_{{\rm{LT1}}}}\left( {\left| {A\left( t \right)} \right|, \mathit{\Omega} } \right) + {H_{{\rm{LT2}}}}\left( {\left| {A\left( t \right)} \right|, \mathit{\Omega} } \right)
$
|
(19) |
3 提取模型动态核函数
3.1 STM核函数
根据记忆效应的原理,当输入信号的幅度不变时,在任何时间输出信号包络的变化都是源于STM效应的影响。因此,STM核函数容易通过包络恒定的调制信号进行测量,这时LTM路径效应为零。假设功放输入信号一个幅度固定为常数的单音连续信号:
|
$
A\left( t \right) = {\rm{Re}}({A_0} \cdot {{\rm{e}}^{{\rm{j}}\left( {\omega + \mathit{\Omega} } \right)t}})
$
|
(20) |
这时输入信号的包络可以由式(21) 表示:
|
$
\tilde A\left( t \right) = {A_0}{{\rm{e}}^{{\rm{j}}\mathit{\Omega} t}}
$
|
(21) |
则输出信号的包络显然是关于输入信号包络幅度及频率的函数,可以由式(22) 表示:
|
$
B\left( t \right) = {B_0}\left( {\left| {{A_0}} \right|, \mathit{\Omega} } \right){{\rm{e}}^{{\rm{j}}\mathit{\Omega} t}}
$
|
(22) |
将式(21) 及式(22) 代入到式(9) 中,得到输出信号:
|
$
{B_0}\left( {{A_0}, \mathit{\Omega} } \right){{\rm{e}}^{{\rm{j}}\mathit{\Omega} t}} = \left( {1 + {H_{{\rm{LT}}}}\left( {\left| {{A_0}} \right|, 0} \right)} \right){\kern 1pt} {\kern 1pt} \cdot {H_{{\rm{ST}}}}\left( {\left| {{A_0}} \right|, \mathit{\Omega} } \right){A_0}{{\rm{e}}^{{\rm{j}}\mathit{\Omega} t}}
$
|
(23) |
整理后发现:
|
$
\frac{{{B_0}\left( {\left| {{A_0}} \right|, \mathit{\Omega} } \right)}}{{{A_0}}} = \left( {1 + {H_{{\rm{LT}}}}\left( {\left| {{A_0}} \right|, 0} \right)} \right) \cdot {H_{{\rm{ST}}}}\left( {\left| {{A_0}} \right|, \mathit{\Omega} } \right)
$
|
(24) |
根据LTM效应的产生机理可知输入恒定包络的信号时,HLT(|A0|, 0) 应该为零,因此得到STM核函数为式(25):
|
$
{H_{{\rm{ST}}}}\left( {\left| {{A_0}} \right|, \mathit{\Omega} } \right) = \frac{{{B_0}\left( {\left| {{A_0}} \right|, \mathit{\Omega} } \right)}}{{{A_0}}}
$
|
(25) |
3.2 LTM核函数
使用双音信号激发功放的LTM效应用以提取LTM核函数。输入信号如式(26) 所示,为一个恒定包络的大信号A0与变包络的小信号A1的叠加。
|
$
A\left( t \right) = {\rm{Re}}({A_0} \cdot {{\rm{e}}^{{\rm{j}}\omega t}} + {A_1} \cdot {{\rm{e}}^{{\rm{j}}\left( {\omega + \mathit{\Omega} } \right)t}})
$
|
(26) |
输入信号的包络为:
|
$
\tilde A\left( t \right) = {A_0} + {A_1}{{\rm{e}}^{{\rm{j}}\mathit{\Omega} t}}
$
|
(27) |
当输入双音信号时,输出端得到一个三音信号,而在LTM核函数处将得到一个双音反馈信号,如图 3所示。得到节点信号如下:
|
$
\begin{array}{l}
B\left( t \right) = {B_0}\left( {\left| {{A_0}} \right|, 0} \right) + B_1^ + \left( {\left| {{A_0}} \right|, \mathit{\Omega} } \right){{\rm{e}}^{{\rm{j}}\mathit{\Omega} t}} + \\
\;\;\;\;\;\;\;\;\;\;B_1^-\left( {\left| {{A_0}} \right|, \mathit{\Omega} } \right){{\rm{e}}^{-{\rm{j}}\mathit{\Omega} t}}
\end{array}
$
|
(28) |
|
$
{\omega _B}\left( t \right) = \mathit{\Omega} \frac{{\varphi \left( {\left| {{A_0}} \right|, \mathit{\Omega} } \right)}}{2}{{\rm{e}}^{{\rm{j}}\mathit{\Omega} t}} + \mathit{\Omega} \frac{{{\varphi ^*}\left( {\left| {{A_0}} \right|, \mathit{\Omega} } \right)}}{2}{{\rm{e}}^{-{\rm{j}}\mathit{\Omega} t}}
$
|
(29) |
|
$
{B_{{\rm{LT}}}}\left( t \right) = B_{{\rm{LT}}}^ + \left( {\left| {{A_0}} \right|, \mathit{\Omega} } \right){{\rm{e}}^{{\rm{j}}\mathit{\Omega} t}} + B_{{\rm{LT}}}^-\left( {\left| {{A_0}} \right|, \mathit{\Omega} } \right){{\rm{e}}^{-{\rm{j}}\mathit{\Omega} t}}
$
|
(30) |
通过实验测量可以直接获得输出信号B(t)和频率ωB(t)。将输入包络信号代入式(9),并考虑STM效应影响,得到输出包络:
|
$
B\left( t \right) = \int_0^\infty {{{\hat h}_{{\rm{ST}}}}\left( {\omega \left( {t-\tau } \right), \tau } \right) \cdot z\left( {t-\tau } \right)} {\rm{d}}\tau
$
|
(31) |
|
$
\hat \omega \left( t \right) = {A_0} + {W_1}{{\rm{e}}^{{\rm{j}}\mathit{\Omega} t}} + W_1^*{{\rm{e}}^{-{\rm{j}}\mathit{\Omega} t}}
$
|
(32) |
|
$
{W_1} = \frac{1}{2}\left( {{A_1} + B_{{\rm{LT}}}^ + \left( {\left| {{A_0}} \right|, \mathit{\Omega} } \right) + B_{{\rm{LT}}}^{-* }\left( {\left| {{A_0}} \right|, \mathit{\Omega} } \right)} \right)
$
|
(33) |
|
$
z\left( t \right) = {A_0} + \left( {{A_1} + B_{{\rm{LT}}}^ + \left( {\left| {{A_0}} \right|, \mathit{\Omega} } \right)} \right){{\rm{e}}^{{\rm{j}}\mathit{\Omega} t}} + B_{{\rm{LT}}}^-\left( {\left| {{A_0}} \right|, \mathit{\Omega} } \right){{\rm{e}}^{{\rm{j}}\mathit{\Omega} t}}
$
|
(34) |
将$ {\hat h_{{\rm{ST}}}}\left( {\omega \left( {t-\tau } \right), \tau } \right) $在A0点一阶展开,BLT(t)可以通过式(35) 计算:
|
$
\begin{array}{l}
B\left( t \right) = {H_{{\rm{ST}}}}\left( {\left| {{A_0}} \right|, \mathit{\Omega} } \right){A_0} + \left( {{d_{11}}\left[{{A_1} + B_{{\rm{LT}}}^ + \left( {\left| {{A_0}} \right|, \mathit{\Omega} } \right)} \right] + {d_{12}}B_{{\rm{LT}}}^{ - * }\left( {\left| {{A_0}} \right|, \mathit{\Omega} } \right)} \right){{\rm{e}}^{{\rm{j}}\mathit{\Omega} t}}\\
+ \left( {d_{21}^ * \left[{A_1^ * + B_{{\rm{LT}}}^{ + * }\left( {\left| {{A_0}} \right|, \mathit{\Omega} } \right)} \right] + d_{22}^ * B_{{\rm{LT}}}^ -\left( {\left| {{A_0}} \right|, \mathit{\Omega} } \right)} \right){{\rm{e}}^{ -{\rm{j}}\mathit{\Omega} t}}
\end{array}
$
|
(35) |
其中:
|
$
{d_{11}} = {H_{{\rm{ST}}}}\left( {\left| {{A_0}} \right|, \mathit{\Omega} } \right) + \frac{1}{2}\frac{{\partial {H_{{\rm{ST}}}}\left( {\left| {{A_0}} \right|, \mathit{\Omega} } \right)}}{{\partial {A_0}}}{A_0}
$
|
(36) |
|
$
{d_{12}} = \frac{1}{2}\frac{{\partial {H_{{\rm{ST}}}}\left( {\left| {{A_0}} \right|, \mathit{\Omega} } \right)}}{{\partial {A_0}}}{A_0}
$
|
(37) |
|
$
{d_{21}} = \frac{1}{2}\frac{{\partial H_{_{{\rm{ST}}}}^*\left( {\left| {{A_0}} \right|, -\mathit{\Omega} } \right)}}{{\partial {A_0}}}{A_0}
$
|
(38) |
|
$
{d_{22}} = H_{_{{\rm{ST}}}}^*\left( {\left| {{A_0}} \right|, -\mathit{\Omega} } \right) + \frac{1}{2}\frac{{\partial H_{_{{\rm{ST}}}}^*\left( {\left| {{A_0}} \right|, -\mathit{\Omega} } \right)}}{{\partial {A_0}}}{A_0}
$
|
(39) |
将式(28) 及(29) 代入到式(11),并且考虑A(t)在A0点展开得到两个LTM核函数HLT1(|A0|, Ω)、HLT2(|A0|, Ω)与BLT+(|A0|, ±Ω)、BLT-(|A0|, ±Ω)之间的关系如下:
|
$
\begin{array}{l}
\frac{{2B_{{\rm{LT}}}^ + \left( {\left| {{A_0}} \right|, \mathit{\Omega} } \right)}}{{{A_1}}} = {M_1}\left( {\left| {{A_0}} \right|, \mathit{\Omega} } \right) \cdot {H_{{\rm{LT}}1}}\left( {\left| {{A_0}} \right|, \mathit{\Omega} } \right) + \\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left| {{B_0}} \right| \cdot \frac{{\partial {H_{{\rm{LT1}}}}\left( {\left| {{A_0}} \right|, \mathit{\Omega} } \right)}}{{\partial {A_0}}} + \mathit{\Omega} {M_2}\left| {{A_0}} \right| \cdot {H_{{\rm{LT2}}}}\left( {\left| {{A_0}} \right|, \mathit{\Omega} } \right)
\end{array}
$
|
(40) |
|
$
\begin{array}{l}
\frac{{2B_{{\rm{LT}}}^-\left( {\left| {{A_0}} \right|, \mathit{\Omega} } \right)}}{{{A_1}}} = M_1^*\left( {\left| {{A_0}} \right|, \mathit{\Omega} } \right) \cdot {H_{{\rm{LT}}1}}\left( {\left| {{A_0}} \right|, -\mathit{\Omega} } \right) + \\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\kern 1pt} \left| {{B_0}} \right| \cdot \frac{{\partial {H_{{\rm{LT}}1}}\left( {\left| {{A_0}} \right|, -\mathit{\Omega} } \right)}}{{\partial {A_0}}} + {\kern 1pt} \mathit{\Omega} M_2^*\left( {\left| {{A_0}} \right|, \mathit{\Omega} } \right) \cdot {H_{{\rm{LT2}}}}\left( {\left| {{A_0}} \right|, - \mathit{\Omega} } \right)
\end{array}
$
|
(41) |
|
$
\begin{array}{l}
\frac{{B_{{\rm{LT}}}^ + \left( {\left| {{A_0}} \right|, -\mathit{\Omega} } \right)}}{{2{A_1}}} = {M_1}\left( {\left| {{A_0}} \right|, -\mathit{\Omega} } \right) \cdot {H_{{\rm{LT}}1}}\left( {\left| {{A_0}} \right|, -\mathit{\Omega} } \right) + \\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left| {{B_0}} \right| \cdot \frac{{\partial {H_{{\rm{LT}}1}}\left( {\left| {{A_0}} \right|, - \mathit{\Omega} } \right)}}{{\partial {A_0}}} - \\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\Omega} {M_2}\left( {\left| {{A_0}} \right|, - \mathit{\Omega} } \right) \cdot {H_{{\rm{LT}}2}}\left( {\left| {{A_0}} \right|, - \mathit{\Omega} } \right)
\end{array}
$
|
(42) |
|
$
\begin{array}{l}
\frac{{B_{{\rm{LT}}}^-\left( {\left| {{A_0}} \right|, -\mathit{\Omega} } \right)}}{{2{A_1}}} = {M_1}\left( {\left| {{A_0}} \right|, -\mathit{\Omega} } \right) \cdot {H_{{\rm{LT}}1}}\left( {\left| {{A_0}} \right|, \mathit{\Omega} } \right) + \\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left| {{B_0}} \right| \cdot \frac{{\partial {H_{{\rm{LT}}1}}\left( {\left| {{A_0}} \right|, \mathit{\Omega} } \right)}}{{\partial {A_0}}} - \\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\Omega} M_2^*\left( {\left| {{A_0}} \right|, - \mathit{\Omega} } \right) \cdot {H_{{\rm{LT}}2}}\left( {\left| {{A_0}} \right|, \mathit{\Omega} } \right)
\end{array}
$
|
(43) |
其中:
|
$
{M_1}\left( {\left| {{A_0}} \right|, \mathit{\Omega} } \right){\rm{ = }}\left( {\frac{{B_1^ + \left( {\left| {{A_0}} \right|, \mathit{\Omega} } \right)}}{{{B_0}}} + \frac{{B{{_1^ + }^*}\left( {\left| {{A_0}} \right|, \mathit{\Omega} } \right)}}{{B_0^*}}} \right) \cdot \frac{{\left| {{B_0}} \right|}}{{{A_1}}}
$
|
(44) |
|
$
{M_2}\left( {\left| {{A_0}} \right|, \mathit{\Omega} } \right) = \frac{{\varphi \left( {\left| {{A_0}} \right|, \mathit{\Omega} } \right)}}{{\left| {{A_1}} \right|}}
$
|
(45) |
|
$
{B_0} = {B_0}\left( {{A_0}, 0} \right)
$
|
(46) |
通过以上推导得到HLT1(|A0|, Ω)、HLT2(|A0|, Ω)两个LTM核函数。由式(40)~(43) 可以看出LTM效应的输出分
量分别与输出包络信号的幅度及时变频率相关,故使用新结构求解动态核函数更为快捷方便,符合记忆效应对功放影响的机理。
4 模型实现和验证
新动态X参数模型中有四个核函数需要确定。静态部分Xm(|A(t)|)可以借助经典PHD模型理论[2],利用安捷伦的ADS (Advanced Design System)软件提取静态X参数模型,同时通过瞬时包络仿真及谐波平衡仿真获取功放输入输出包络及频率信息。为了使动态核函数能够方便地应用于仿真软件及电路实现, 将核函数表征为幅度与频率的矩阵(Ĥ|A|), Ω),可以利用文献[14]中提出的正交表分解法,将二维核函数转化成两个一维变量的形式,如式(47)。使用奇异值算法及三次样条函数构建正交基求出xp(|A|),通过最小二乘法得到yp(Ω),通过时域矢量拟合[15]将式(9) 中的卷积转换为简单的迭代算法,这个方法能够很好地满足动态X参数模型拟合精度和仿真速度。
|
$
\mathit{\boldsymbol{\hat H}}\left( {\left| A \right|, \mathit{\Omega} } \right) = \sum\limits_{p = 1}^P {{x_p}\left( {\left| A \right|} \right)} {y_p}\left( \mathit{\Omega} \right)
$
|
(47) |
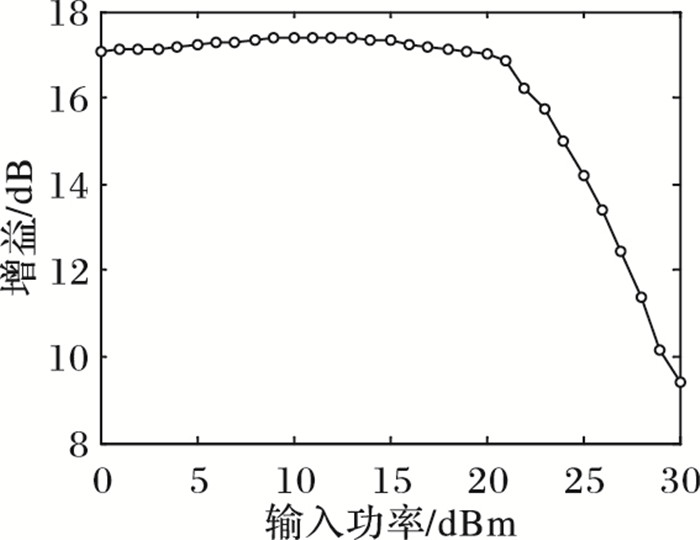
使用恩智浦公司的MW6S010N晶体管设计一款单级功放,其工作的中心频率为850 MHz,工作带宽为30 MHz。使用双向负载牵引方法完成电路匹配设计,设计好的电路增益仿真如图 4所示。功放在输入功率达到约22 dBm时进入非线性区,随着输入功率增大而出现增益压缩。
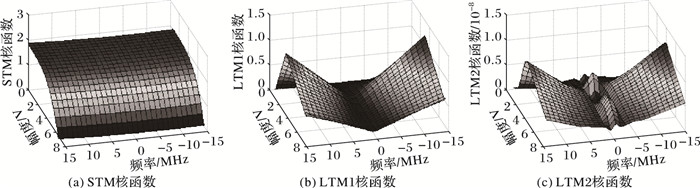
利用ADS产生如式(20) 及式(26) 的大信号激励功放,式中A0取值范围为0~7.103 V,A1取值范围0~1.529 V。当A0和A1均取最大值时输入信号功率为25 dBm,如图 4所示,这时功放约有3 dB增益压缩。在功放整个带宽选择30个频点,每个频点取20个幅度值,用以构建核函数。提取输入输出数据,分别提取STM及LTM核函数并在Matlab中进行建模并仿真,核函数提取结果如图 5所示。
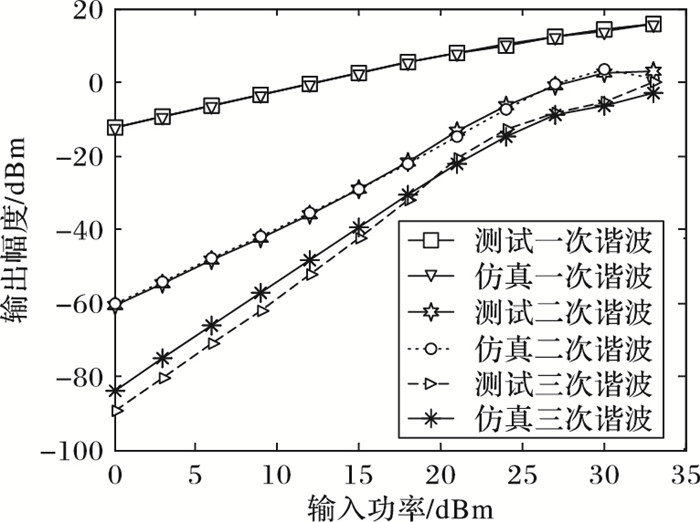
使用单音大信号激励功放及功放模型,测量输出端口各次谐波幅度值,如图 6所示。随着功放非线性增强,二次谐波及三次谐波急剧上升,新模型能够很好地预测功放强非线性失真。
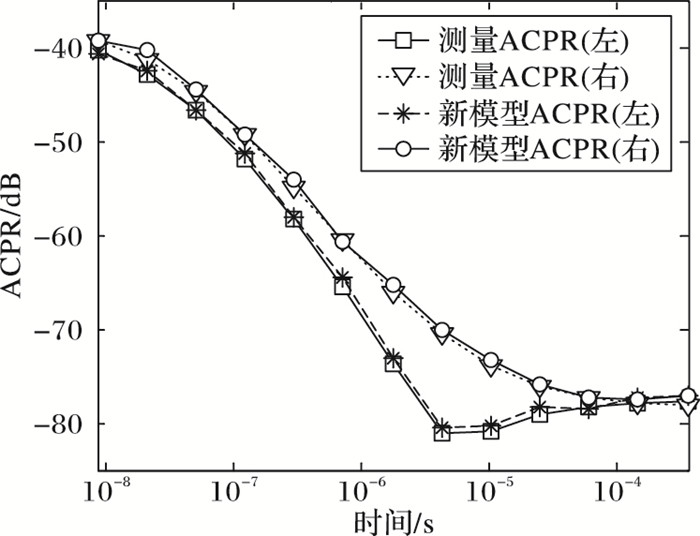
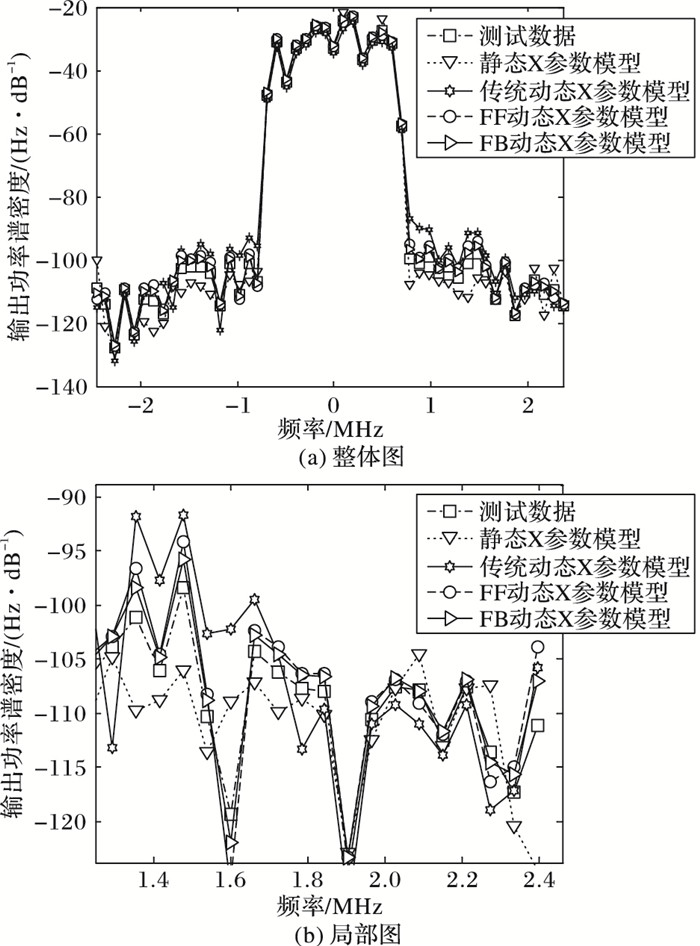
利用ADS产生带宽为1.5 MHz的IS-95码分多址(Code Division Multiple Access, CDMA)信号激励功放模型,对功放进行邻信道功率比(Adjacent Channel Power Ratio,ACPR)分析,可见由于记忆效应引起左、右ACRP数值不对称,如图 7所示,新模型与测量获得数据具有良好一致性。如式(48) 及式(49),通过对输出信号的自相关函数R(τ)进行傅里叶变换得到功率谱密度P(f)。将新模型与四种已有的X参数模型输出功率谱进行比较,如图 8所示,图 8(b)为局部放大图。由图 8可知静态模型在预测记忆效应引起的功放非线性失真时误差较大;在三种动态X参数模型中,新模型较传统动态X参数模型及FF结构的动态X参数模型能更精确地模拟功率放大器特性,准确预测功放的带内失真及带外频谱再生。
|
$
R\left( \tau \right) = \mathop {\lim }\limits_{T \to \infty } \frac{1}{T}\int_{-T/2}^{T/2} {B\left( t \right)} B\left( {t + \tau } \right){\rm{d}}t
$
|
(48) |
|
$
P\left( f \right) = \int_{-\infty }^\infty {R\left( \tau \right){{\rm{e}}^{-{\rm{j}}2{\rm{\pi }}f\tau }}{\rm{d}}\tau }
$
|
(49) |
利用归一化均方误差(Normalized Mean Square Error,NMSE)分析对四种模型的时域性能进行分析,并对仿真时间进行比较。NMSE可以表示为:
|
$
NMSE{\rm{ = }}10\lg \frac{{\sum\limits_{n = 1}^N {{{\left| {B\left( n \right)-\hat B\left( n \right)} \right|}^2}} }}{{\sum\limits_{n = 1}^N {{{\left| {B\left( n \right)} \right|}^2}} }}
$
|
(50) |
其中:B(n)为模型输出,$ \hat B\left( n \right) $为测试输出。经计算,新模型的NMSE比静态X参数模型减少8.0 dB,模型误差大大减少,但由于新模型复杂度提高而使模型仿真时间比静态X参数模型更长;新模型的NMSE比传统动态X参数模型及FF结构X参数模型减少6.3 dB、2.5 dB,模型更加精确,但与已有两种动态X参数模型仿真耗时相近,也就是说,新的功放建模方法在使用二维核函数降低模型复杂度的基础上,考虑功放两种记忆效应作用以提高模型精度。
表 1
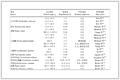
表 1 模型特性比较
Table 1 Comparison of model characteristics
| 模型 |
NMSE/dB |
仿真时间/s |
| FB结构动态X参数模型 |
-32.1 |
62.2 |
| 静态X参数模型 |
-24.1 |
35.3 |
| 传统动态X参数模型 |
-25.8 |
59.6 |
| FF结构动态X参数模型 |
-29.6 |
64.6 |
|
表 1 模型特性比较
Table 1 Comparison of model characteristics
|
5 结语
考虑功放记忆效应的特点,本文在传统双记忆路径表征功放记忆效应的基础上,通过改进FB结构并结合动态X参数进一步简化动态核函数,提出与输入信号幅度及频率相关的二维核函数,建立具有记忆效应的非线性射频功放模型。通过仿真验证,该模型精确度高,且易实现,为下一步研究系统级仿真以及缩短功放开发提供了一种可能性,但该模型在谐波失配情况下仍需进一步改进。