多智能体系统(Multi-Agent System, MAS)被广泛应用于飞船探测、灾难调查、网络传感器等实际生活中,也因此多智能体的分布式控制在近年来一直是研究热点。在对于多智能体分布式控制的研究中,一个最核心的问题就是如何利用好自身和近邻智能体的信息来设计分布式控制策略,使得智能体的所有状态可以达到一致,即大家所熟知的一致性问题。依据不同的控制目标可以将控制多智能体的方法分为两类:第一类的控制目标是使MAS的位置收敛到一个常值[1-2];第二类[3]是使MAS的位置和速度都收敛到一个常值(这个常值一般都不为零)。依据控制对象可以分为一阶[4-6]和二阶模型[7-8]两类。国内的研究人员在针对多智能体编队的控制问题上,常常考虑到现实应用中的一些限制条件,其中主要有MAS在编队过程中的拓扑结构的变换需求以及智能体之间的通信时延和输入时延等[9-12]。其中:文献[9]研究了在固定拓扑和变换拓扑结构下,具有通信时延的MAS的H∞一致性问题;文献[10]考虑到在现实应用中通信时延可能只是随机出现,所以讨论了随机时延下的智能体一致性问题;文献[11]分别设计了线性控制器和非线性控制器使得MAS能够达到加权平均一致性;文献[12]利用广义Nyquist判据推导出使得系统达到一致的充分条件。进行一致性设计的过程中,有效的控制算法可以有效提升系统的一致性性能,而收敛速度是判断一致性协议性能优劣的重要参数,经过多年的研究,已经有一些常见方法可以提高系统的收敛速度。第一种方法是在拓扑结构改变的情况下,将方程平均一致的收敛速度界离散更新,以此得到收敛时间的上界[13-14];第二种方法是通过对局部的节点进行预测来提高收敛速度[15-16];第三种方法则是彻底推翻以前的控制方法,重新设计新的控制方法来提高收敛速度。第四种方法是通过对加权矩阵进行优化来加速一致性协议[17-19]。
本文通过引入绝对位置和相对速度以及二层邻居信息来设计二阶一致性协议,并在此基础上设计了多智能体的编队控制方法。本文提出的一致性控制方法可以使多个智能体的状态最终达到到预置的常值,而且与文献[8]中的二阶一致性控制协议相比,本文的编队控制方法实现编队控制的时间更短。该控制方法既不实质改变MAS的通信拓扑,又提高了状态收敛速度,进而优化了一致性表现性能。最后对基于改进一致性协议的编队控制方法进行了仿真,结果也表明本文提出的控制方法更加高效。
1 一致性问题陈述考虑有m个智能体在一个平面上移动,编号为1, 2, …, m。本文假设每个智能体的机械结构都是相同的,并且每个智能体的动力学模型都可以描述为:
| $ \left\{ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot r}} = \mathit{\boldsymbol{v}}}\\ {\mathit{\boldsymbol{\dot v}} = {\mathit{\boldsymbol{u}}_i}} \end{array}} \right. $ | (1) |
其中:ri∈IRm,vi∈IRm分别表示智能体的位移和速度;ui∈IRm是控制律。
在有向图(N, ε)中的m个节点分别代表m个智能体[20]。这里N表示有限非空点集;ε∈N2是有序节点对,表示边。如果节点υi到节点υj存在一条有向边,那么υi就是这条有向边的父节点,υj就是这条有向边的子节点。在有向图中,有向路径就是(υi1, υi2), (υi2, υi3), …这样的有序边的序列。其中υij∈N。如果有向图不同节点之间都存在一条有向路径,有向图就是强连通的。有向树是有向图中所有的有向连接边形成的。如果一个图存在由图的子集组成的树,则称该图存在一个(有向)生成树。
针对本文中的智能体动力学模型,所提出的一致性协议基于智能体自身的状态信息和它近邻智能体传递过来的相关位置速度信息,使得位移和速度可以和期望的位移和速度达到一致,即:
| $ \left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{r}}_i} \to {\mathit{\boldsymbol{r}}_j} \to {\mathit{\boldsymbol{r}}^d}}\\ {{\mathit{\boldsymbol{v}}_i} \to {\mathit{\boldsymbol{v}}_j} \to {\mathit{\boldsymbol{v}}^d}} \end{array}} \right. $ |
为了推导控制方法渐近稳定所需满足的条件,下面给出推导过程中所需要的两个引理:
引理1 若给定矩阵A=[aij]∈Mn(IR), 这里aii≤0,aij≥0,∀i≠j, 并且对于每一个智能体都有
引理2 令Re(·)和lm(·)分别表示一个数字的实部和虚部,并且一个矩阵的特征值有如下形式:
| $ {\lambda _ \pm } = \frac{{\gamma \mu - \alpha \pm \sqrt {{{(\gamma \mu - \alpha )}^2} - 4\mu } }}{2} $ |
这里λ, μ∈C。如果α≥0, Re(μ)<0, 并且
| $ \gamma > \sqrt {\frac{2}{{\left| \mu \right|\cos (\frac{\pi }{2} - {{\tan }^{ - 1}}\frac{{ - {\mathop{\rm Re}\nolimits} (\mu )}}{{{\mathop{\rm lm}\nolimits} (\mu )}})}}} $ |
那么就有Re(λ±)<0。
证明 令a=γμ,
| $ \begin{array}{l} {s_1} = {\gamma ^2}({A^2} - {B^2}) + 2AB{\gamma ^2}i\\ {s_3} = {\gamma ^2}({A^2} - {B^2}) + 4A + (2AB{\gamma ^2} + 4B)i \end{array} $ |
想要|s1|>|s3|, 就有:
| $ \begin{array}{l} \sqrt {{\gamma ^4}{{({A^2} - {B^2})}^2} + 4{A^2}{B^2}{\gamma ^4}} > \\ \sqrt {{{({\gamma ^2}({A^2} - {B^2}) + 4A)}^2} + {{(2AB{\gamma ^2} + 4B)}^2}} \end{array} $ |
自然可以得到:
| $ \begin{array}{l} 8A{\gamma ^2}({A^2} + {B^2}) + 16({A^2} + {B^2}) < 0\\ \gamma > \sqrt {\frac{2}{{ - {\mathop{\rm Re}\nolimits} (\mu )}}} \end{array} $ |
再通过简单的转换,可以得到:
| $ \gamma > \sqrt {\frac{2}{{\left| \mu \right|\cos (\frac{\pi }{2} - {{\tan }^{ - 1}}\frac{{ - {\mathop{\rm Re}\nolimits} (\mu )}}{{{\mathop{\rm lm}\nolimits} (\mu )}})}}} $ |
所以当满足引理2的条件时,可以得到|s1|>|s3|。对于由s1、s2、s3组成的三角形,通过余弦定理有η1>η3, 这里ηi表示的是由s1、s2、s3组成的三角形对应边si的内角。在极坐标系中,分别用(r1, θ1),(r2, θ2)来表示γμ和γμ-α, 因为坐落在复平面第三象限的μ是坐落在第二象限的μ的共轭复数,所以这里只需要考虑μ坐落在复平面的第二象限里, 令θi∈(π/2, π], 这里i=1, 2。那么(γμ)2和(γμ-α)2在极坐标系中可以用坐标的形式表示为(r12, 2θ1)和(r22, 2θ2),这里考虑另一个由q1、q2、q3组成的三角形,其内角由ϕi表示。注意到(θ2>θ1), 通过比较这两个分别由si与qi组成的三角形,可以得出ϕ1>η1和ϕ3<η3, 这也就意味着ϕ1>ϕ3, 再次通过余弦定理可以得知|(γμi-α)2|>|(γμi-α)2+4μi|, 由此得证Re(λ±)<0。
2 一致性协议文献[8]提出的一致性协议如下:
| $ {\mathit{\boldsymbol{u}}_i} = {\mathit{\boldsymbol{\dot v}}^d} - \alpha ({\mathit{\boldsymbol{v}}_i} - {\mathit{\boldsymbol{v}}^d}) - \sum\limits_{j = 1}^n {{g_{ij}}{k_{ij}}({\mathit{\boldsymbol{r}}_i} - {\mathit{\boldsymbol{r}}_j})} $ | (2) |
其中: ri∈IRm; vi∈IRm; vd∈IRm; α>0;kij>0;并且如果智能体j的状态信息能够传递给智能体i, 那么gij=1, 否则gij=0。在这个一致性协议中,第二项α(vi-vd)表示智能体实际速度与标准速度追踪值之间的偏移,第三项
很明显可以看出上面的一致性协议仅仅考虑了绝对速度偏移和相对位置偏移,这样并没有充分利用智能体自身的状态信息。为了提高收敛速度以及编队效率,在不实际改变MAS网络拓扑的前提下,本文将二层邻居信息引入到一致性协议中,并且考虑标准位置偏移和相对速度偏移,提出一种改进的一致性协议:
| $ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\dot r}}}_i} = {\mathit{\boldsymbol{v}}_i}\\ {{\mathit{\boldsymbol{\dot v}}}_i} = {\mathit{\boldsymbol{u}}_i}\\ {\mathit{\boldsymbol{u}}_i} = {{\mathit{\boldsymbol{\dot v}}}^d} - \alpha ({\mathit{\boldsymbol{v}}_i} - {\mathit{\boldsymbol{v}}^d}) - \beta ({\mathit{\boldsymbol{r}}_i} - {\mathit{\boldsymbol{r}}^d})-\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \sum\limits_{j = 1}^n {{g_{ij}}{k_{ij}}[\gamma ({\mathit{\boldsymbol{v}}_i}-{\mathit{\boldsymbol{v}}_j}) + \gamma \sum\limits_{j = 1}^n {{g_{jk}}({\mathit{\boldsymbol{v}}_i}-{\mathit{v}_k})]} } \end{array} \right. $ | (3) |
其中:vd是标准速度追踪信号,rd是标准位置追踪信号。在本文提出的这个二阶一致性协议中,每个智能体向近邻智能体发送的信息不仅包括自身的速度信息,而且包括自己邻点集的状态信息。这就相当于在自己邻点集与近邻机体之间有了虚拟连接,而虚拟连接构成的虚拟拓扑结构由
A和L是原通信拓扑图的虚拟矩阵和拉普拉斯矩阵,有:
| $ {\mathit{l}_{ij}} = \left\{ {\begin{array}{*{20}{c}} {\sum\limits_{j = 1, j \ne i}^N {{a_{ij}}, i \ne j} }\\ { - {a_{ij}}, i = j} \end{array}} \right. $ | (4) |
引入二层邻居信息之后,
| $ {\tilde a_{ik}} = \sum\limits_{j = 1}^N {{a_{ij}}{a_{jk}}} $ | (5) |
| $ {\mathit{\tilde l}_{ik}} = \left\{ {\begin{array}{*{20}{c}} {\sum\limits_{k = 1, k \ne i}^N {{{\tilde a}_{ik}}, i \ne k} }\\ { - {{\tilde a}_{ik}}, \;\;\;\;\;i = k} \end{array}} \right. $ | (6) |
针对一致性协议(3) 可以指出虚拟邻接矩阵
| $ {\tilde g_{ik}} = \left\{ \begin{array}{l} \sum\limits_{j \in V} {{g_{ij}}{g_{jk}}, ({\upsilon _i}, {\upsilon _k}) \in \tilde {\cal E}} \\ 0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{其他}} \end{array} \right. $ |
对协议(3) 进行简单的变换,可以得到:
| $ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\dot r}}}_i} = {\mathit{\boldsymbol{v}}_i}\\ {{\mathit{\boldsymbol{\dot v}}}_i} = {\mathit{\boldsymbol{u}}_i}\\ {\mathit{\boldsymbol{u}}_i} = {{\mathit{\boldsymbol{\dot v}}}^d} - \alpha ({\mathit{\boldsymbol{v}}_i} - {\mathit{\boldsymbol{v}}^d}) - \beta ({\mathit{\boldsymbol{r}}_i} - {\mathit{\boldsymbol{r}}^d})-\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \sum\limits_{j = 1}^n {{g_{ij}}{k_{ij}}\gamma ({\mathit{\boldsymbol{v}}_i} - {\mathit{\boldsymbol{v}}_j}) - \gamma \sum\limits_{j = 1}^n {{g_{ij}}{g_{jk}}{k_{ij}}({\mathit{\boldsymbol{v}}_i} - {\mathit{\boldsymbol{v}}_k})} } \end{array} \right. $ | (7) |
为了将一致性协议(7) 写成矩阵的形式,这里令智能体位移和速度都转化为向量形式r=[r1, r2, …, rn]T,v=[v1, v2, …, vn]T,
| $ \left[\begin{matrix} {\mathit{\boldsymbol{\dot{\tilde{r}}}}} \\ {\mathit{\boldsymbol{\dot{\tilde{v}}}}} \\ \end{matrix} \right]=\left[\begin{matrix} {{\bf{0}}_{n\times n}} & {{\mathit{\boldsymbol{I}}}_{n}} \\ -\beta {{\mathit{\boldsymbol{I}}}_{n}} &-\alpha {{\mathit{\boldsymbol{I}}}_{n}}-\gamma \mathit{\boldsymbol{\bar{L}}} \\ \end{matrix} \right]\left[\begin{matrix} {\mathit{\boldsymbol{\tilde{r}}}} \\ {\mathit{\boldsymbol{\tilde{v}}}} \\ \end{matrix} \right] $ | (8) |
式中
| $ \mathit{\boldsymbol{ \boldsymbol{\varSigma} }} = \left[{\begin{array}{*{20}{c}} {{{\bf{0}}_{n \times n}}} & {{\mathit{\boldsymbol{I}}_n}}\\ {-\beta {\mathit{\boldsymbol{I}}_n}} & {-\alpha {\mathit{\boldsymbol{I}}_n}-\gamma \mathit{\boldsymbol{\bar L}}} \end{array}} \right] $ |
这里通过求解det(λI2n-Σ)=0得到Σ的特征值:
| $ \begin{array}{l} \det (\lambda {\mathit{\boldsymbol{I}}_{2n}} - \mathit{\boldsymbol{ \boldsymbol{\varSigma} }}) = \det \left( {\left[{\begin{array}{*{20}{c}} {{{\bf{0}}_{n \times n}}} & {{\mathit{\boldsymbol{I}}_n}}\\ {-\beta {\mathit{\boldsymbol{I}}_n}} & {-\alpha {\mathit{\boldsymbol{I}}_n}-\gamma \mathit{\boldsymbol{\bar L}}} \end{array}} \right]} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\det (({\lambda ^2} + \alpha \lambda + \beta ){\mathit{\boldsymbol{I}}_n} + \gamma \lambda \mathit{\boldsymbol{\bar L}}) \end{array} $ | (9) |
由于:
| $ \det (\lambda {\mathit{\boldsymbol{I}}_n} + \mathit{\boldsymbol{\bar L}}) = \prod\limits_{i = 1}^n {(\lambda - {\mathit{u}_i})} $ | (10) |
这里ui是矩阵-L的第i个特征值。
通过比较式(9) 和式(10),式(9) 可以转变为下面的方程:
| $ \begin{array}{l} \det (({\lambda ^2} + \alpha \lambda + \beta ){\mathit{\boldsymbol{I}}_n} + \gamma \lambda \mathit{\boldsymbol{\bar L}}) = \\ \;\;\det (({\lambda ^2} + \alpha \lambda + \beta ) + \gamma \lambda {u_i}) \end{array} $ |
可以进一步得到:
| $ \begin{array}{l} {\lambda ^2} + \alpha \lambda + \beta = \gamma \lambda {\mu _i}\\ {\lambda ^2} + (\alpha - \gamma {\mu _i})\lambda + \beta = 0 \end{array} $ |
因此矩阵Σ的特征值如下:
| $ {\lambda _{i \pm }} = \frac{{\gamma {\mu _i} - \alpha \pm \sqrt {{{(\gamma {\mu _i} - \alpha )}^2} - 4\beta } }}{2} $ |
上式结果表明矩阵Σ的特征值λi±与μi密切相关。
基于引理1和2,下面给出一致性协议(7) 达到状态一致的充分条件。
定理1 一致性协议(7) 可以使得ri→rj→rd,vi→vj→vd,∀i, 即位移和速度都可以渐进地趋近给定的追踪值的条件是多智能体的通信拓扑有生成树,并且满足:
| $ \left\{ \begin{array}{l} \alpha > 0\\ \beta > 0\\ \gamma > \begin{array}{*{20}{c}} {\max }\\ {i = 2, \cdots n} \end{array}\sqrt {\frac{2}{{|{\mu _i}|\cos (\frac{\pi }{2} - {{\tan }^{ - 1}}\frac{{ - {\mathop{\rm Re}\nolimits} ({\mu _i})}}{{{\mathop{\rm lm}\nolimits} ({\mu _i})}})}}} \end{array} \right. $ |
这里μi(i=2, 3, …, n)表示的是-L的非零特征值,并且Re(·)和lm(·)分别表示一个数字的实部和虚部。
证明 如果MAS的通信拓扑有生成树,则由引理1可以得到其拉普拉斯矩阵有一个零特征值,其余的特征值实部都小于零。为了不失一般性,这里令μ1=0,Re(μi)<0(i=2, 3, …, n)。当μ1=0时,也就意味着
为了将一致性协议(7) 应用在多智能体编队控制上,需要对式(7) 进行变形,目的在于使MAS可以实现:ri-rj→δid和vi→vj→vd。不同于一般的编队控制,编队依赖于智能体之间的位置信息交换,使得智能体间的相对位移达到期望位移,这里δid表示的是智能体i与标准位移之间的期望绝对位移,也意味着智能体编队依赖的是自身的位置信息,这样既降低了编队收到通信因素影响的可能,又减轻了智能体的负荷。这里令δi∈IRm, 是一个常数。控制输入设计为:
| $ \begin{array}{l} {\mathit{\boldsymbol{u}}_i} = {{\mathit{\boldsymbol{\dot v}}}^d} - \alpha ({\mathit{\boldsymbol{v}}_i} - {\mathit{\boldsymbol{v}}^d}) - \beta ({\mathit{\boldsymbol{r}}_i} - {\mathit{\boldsymbol{r}}^d} - {\mathit{\boldsymbol{\delta }}_{id}}) - \\ \;\;\;\;\;\;\;\;\;\;\;\sum\limits_{j = 1}^n {{g_{ij}}{k_{ij}}\gamma ({\mathit{\boldsymbol{v}}_i} - {\mathit{\boldsymbol{v}}_j}) - \gamma \sum\limits_{j = 1}^n {{g_{ij}}{g_{jk}}{k_{ij}}({\mathit{\boldsymbol{v}}_i} - {\mathit{\boldsymbol{v}}_k})} } \end{array} $ | (11) |
这样将一致性协议(7) 变形后,就得到了基于绝对位移、绝对速度以及相对速度的多智能体编队控制输入,这样充分利用智能体自身的状态信息达到编队飞行的目的,提高MAS编队控制的效率。
4 仿真与分析 4.1 一致性仿真将本文提出的改进的一致性协议应用在两自由度的含有六个智能体的MAS中。原系统的通信拓扑图如图 1所示。
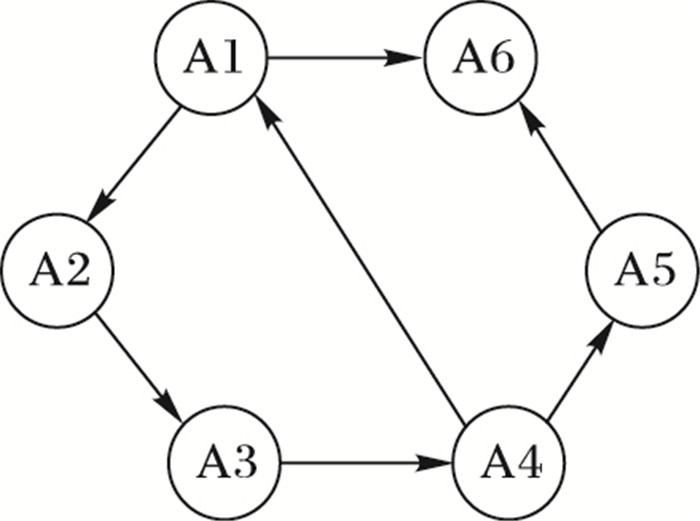
|
图 1 六个智能体的拓扑图 Figure 1 Topology of six Agents |
将“二层邻居”的虚拟通信结构加入到通信拓扑图中,每个智能体获得的状态信息更加丰富,邻居智能体集中的机体数量更加庞大,此时的系统通信拓扑图如图 2所示。
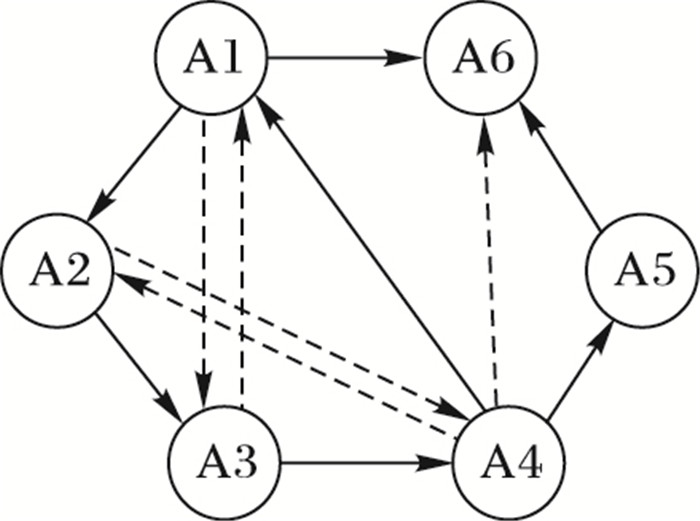
|
图 2 加入二层邻居信息之后的拓扑图 Figure 2 Topology with second-order information |
相应的原图 1的拉普拉斯矩阵为:
| $ \left[{\begin{array}{*{20}{c}} 1&0&0&{-1}&0&0\\ {-1}&1&0&0&0&0\\ 0&{-1}&1&0&0&0\\ 0&0&{ - 1}&1&0&0\\ 0&0&0&{ - 1}&1&0\\ { - 1}&0&0&0&{ - 1}&2 \end{array}} \right] $ |
加入二层邻居信息之后的拉普拉斯矩阵L为:
| $ \left[{\begin{array}{*{20}{c}} 2&0&{-1}&{-1}&0&0\\ {-1}&2&0&{ - 1}&0&0\\ { - 1}&{ - 1}&2&0&0&0\\ 0&{ - 1}&{ - 1}&2&0&0\\ 0&0&{ - 1}&{ - 1}&2&0\\ { - 1}&0&0&{ - 1}&{ - 1}&3 \end{array}} \right] $ |
一致性协议(7) 的仿真结果由图 3和图 4给出。图 3、4中的仿真结果表明,随着时间的推进,六智能体系统中的所有机体的位移与标准位移之间的误差趋近于零,以及所有的机体的速度与标准速度之间的误差趋近于零。这就标示着所有机体的位移可以追随给定的标准位移,可以形成并维持指定的编队队形。
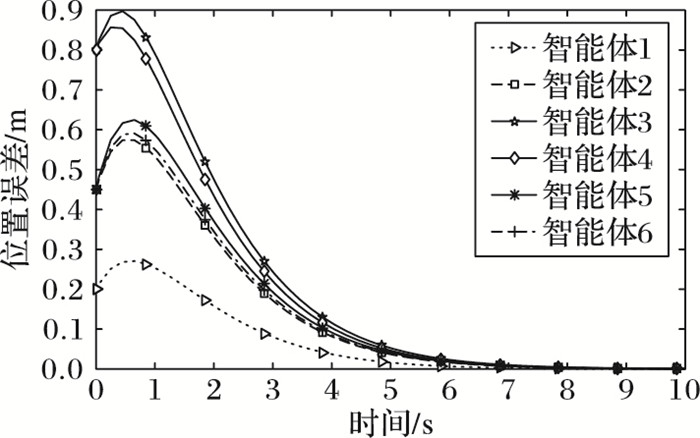
|
图 3 智能体位置误差 Figure 3 Location error of Agents |
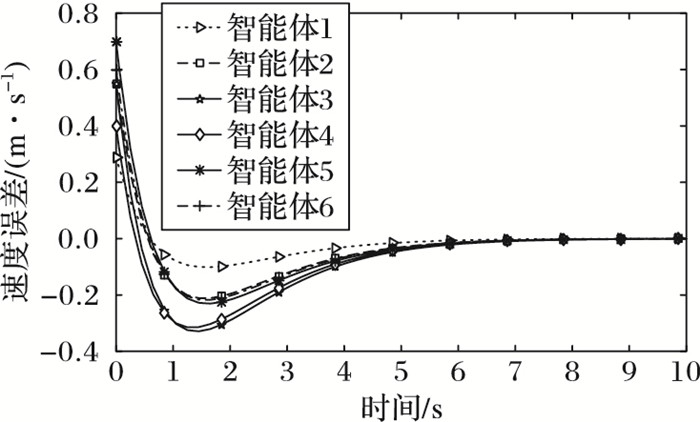
|
图 4 智能体的速度一致性 Figure 4 Speed consistency of Agents |
仿真结果表明本文改进的一致性协议(7) 可以使得每个智能体的状态趋于一致,收敛到给定的追踪值,这也意味着形成编队队形之后,六智能体系统可以保持给定的速度,维持指定队形前进。即:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{r}}_i} \to {\mathit{\boldsymbol{r}}_j} \to {\mathit{\boldsymbol{r}}^d}}\\ {{\mathit{\boldsymbol{v}}_i} \to {\mathit{\boldsymbol{v}}_j} \to {\mathit{\boldsymbol{v}}^d}} \end{array} $ |
要基于本文改进的一致性算法设计编队控制就需要对一致性协议(7) 进行变形,使得MAS在实际编队飞行时可以避免碰撞,并且可以保持队形。为了突显本文编队控制方法的优势,分别对文献[8]中基于式(2) 的编队控制和本文中基于式(11) 的编队控制进行仿真。
首先为了将一致性协议(2) 应用到多智能体编队控制中,需要对式(2) 进行简单变形,在控制律(2) 中引入智能体之间的相对位移,在编队飞行时避免碰触,并且以此来确定编队队形,变形结果如下:
| $ {\mathit{\boldsymbol{u}}_i} = {\mathit{\boldsymbol{\dot v}}^d} - \alpha ({\mathit{\boldsymbol{v}}_i} - {\mathit{\boldsymbol{v}}^d}) - \sum\limits_{j = 1}^n {{g_{ij}}{k_{ij}}[({\mathit{\boldsymbol{r}}_i}-{\mathit{\boldsymbol{\delta }}_j})-({\mathit{\boldsymbol{r}}_j}-{\mathit{\boldsymbol{\delta }}_j})]} $ |
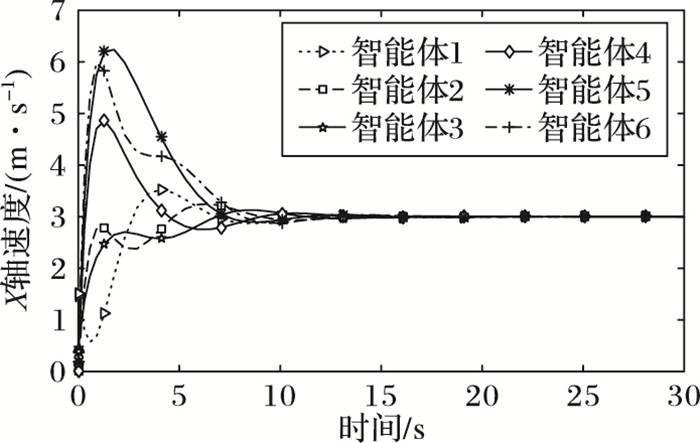
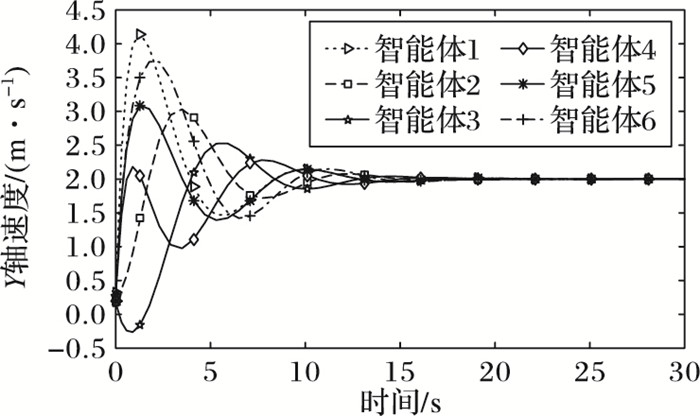
接下来对上面的由控制律(2) 演变而来的编队控制方法进行仿真实验,并且设置vd=(3, 2)。图 5和图 6分别表示的是智能体在编队飞行过程中X和Y轴方向上的速度。从图中可以看出,从控制律(2) 变形而来的控制方法可以使得六智能体在编队飞行时,当时间到达接近18 s时,智能体系统在X轴方向上的速度收敛并将保持在3 m/s,在Y轴方向上的速度会收敛并且保持在2 m/s,收敛到给定的标准值。
|
图 5 X方向上智能体的速度变化(文献[8]方法) Figure 5 Speed variation of Agents at X direction (method of literature [8]) |
|
图 6 Y方向上智能体的速度变化(文献[8]方法) Figure 6 Speed variation of Agents at Y direction (method of literature [8]) |
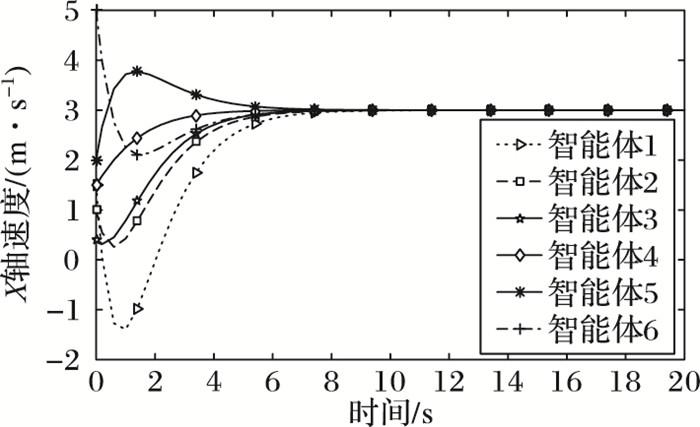
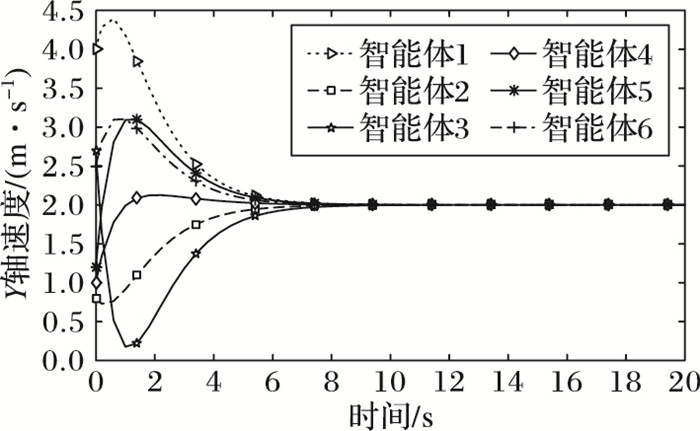
然后将本文中的编队控制策略(11) 应用到六智能体编队飞行中,与上面的仿真实验一致,设置vd=(3, 2), 图 7、8是此编队控制方法的仿真实验结果。从图可以看到,无论是在X轴方向上面的速度Vx, 还是在Y轴方向上面的速度Vy, 都在接近8 s时趋近于设定的期望速度vd=(3, 2), 并且此后会保持这个期望速度继续编队飞行。
|
图 7 X方向上智能体的速度变化(本文方法) Figure 7 Speed variation of Agents at X direction (the proposed method) |
|
图 8 Y方向上智能体的速度变化(本文方法) Figure 8 Speed variation of Agents at Y direction (the proposed method) |
通过图 5~8这四个仿真结果的两两对比,从时间消耗上面分析,以控制律(2) 演变而来的编队控制方法控制的智能体系统的速度收敛并保持期望值的时间是18 s,而以本文的编队控制方法(11) 所需的时间是8 s,由此可以简单得出结论,本文中的编队控制方法的收敛速度更快,编队效率更高。
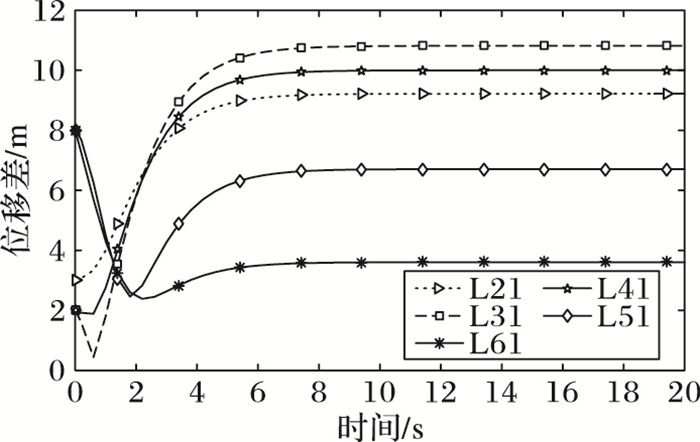
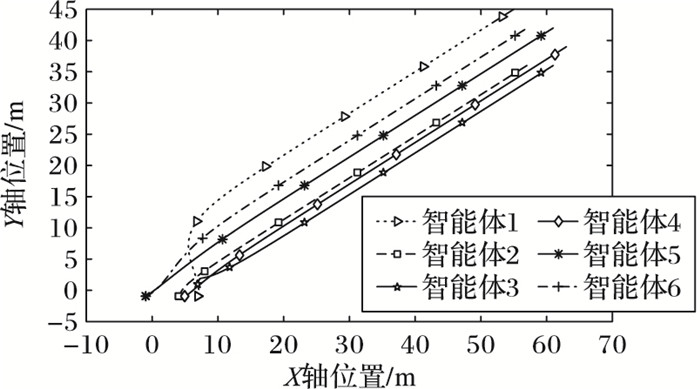
下面进行六智能体系统在编队过程中的位置仿真,首先给出编队控制方法(11) 中的智能体与标准位移之间的期望位移差:δ1d=(-4, 6),δ2d=(-2, -3),δ3d=(2, -3),δ4d=(4, 0),δ5d=(2, 3),δ6d=(-2, 3)。在仿真实验中,以智能体1为基准,以其他智能体与智能体1之间的位移差为输出,得到的仿真结果如图 9所示;图 10表示的是六个智能体编队飞行轨迹。通过这两个仿真结果可以清晰看出六智能体之间的相对位置渐渐趋于稳定,将在收敛到期望值之后按照预置的智能体之间的相对位移保持编队队形继续飞行。
|
图 9 智能体1与其他智能体的相对距离 Figure 9 Relative distance between Agent 1 and others |
|
图 10 编队轨迹 Figure 10 Formation trajectory |
本文主要研究了在不改变实际给定的通信拓扑的情况下,努力提高MAS收敛速度,提高多智能体编队表现性能。在原本的一致性协议基础上引入了标准位置偏移和相对速度偏移,并且将二层邻居信息融入到一致性协议之中,充分利用信息交互提高收敛效率。仿真实验的结果表明本文改进的一致性协议比原协议有更高的收敛速度,并且基于此协议的编队控制方法能使智能体系统更快地达到期望编队队形,这在现实应用中有很大意义。
| [1] | CHOPRA N, SPONG M W. Passivity-based control of multi-Agent systems[M]//Advances in Robot Control:From Everyday Physics to Human-Like Movements. Berlin:Springer-Verlag, 2006:107-134. |
| [2] | CHUNG S-J, SLOTINE J-J E. Cooperative robot control and concurrent synchronization of lagrangian systems[J]. IEEE Transactions on Robotics, 2009, 25(3): 686-700. DOI:10.1109/TRO.2009.2014125 |
| [3] | WANG H. Flocking of networked uncertain Euler-Lagrange systems on directed graphs[J]. Automatica, 2013, 49(9): 2774-2779. DOI:10.1016/j.automatica.2013.05.029 |
| [4] | OLFATISABER R, MURRAY R M. Consensus problems in networks of Agents with switching topology and time-delays[J]. IEEE Transactions on Automatic Control, 2004, 49(9): 1520-1533. DOI:10.1109/TAC.2004.834113 |
| [5] | OLFATI-SABER R, FAX J A, MURRAY R M. Consensus and cooperation in networked multi-Agent systems[J]. Proceedings of the IEEE, 2007, 95(1): 215-233. DOI:10.1109/JPROC.2006.887293 |
| [6] | REN W. Multi-vehicle consensus with a time-varying reference state[J]. Systems & Control Letters, 2007, 56(7/8): 474-483. |
| [7] | CAO M, XIAO F, WANG L. Event-based second-order consensus control for multi-Agent systems via synchronous periodic event detection[J]. IEEE Transactions on Automatic Control, 2015, 60(9): 2452-2457. DOI:10.1109/TAC.2015.2390553 |
| [8] | JIE Q, JIANG G. A simple second-order consensus and formation control for multi-vehicle systems[C]//Proceedings of the 201433rd Chinese Control Conference. Piscataway, NJ:IEEE, 2014:1333-1337. |
| [9] | 刘学良, 胥布工. 具有多个通信时延的多智能体系统分布式H∞一致性控制[J]. 控制与决策, 2012, 27(4): 494-500. (LIU X L, XU B G. Distributed H∞ consensus control for multiple-Agent systems with communication delays[J]. Control and Decision, 2012, 27(4): 494-500.) |
| [10] | 宗鑫, 崔艳. 具有随机通信时延的二阶多智能体系统的一致性控制[J]. 计算机应用, 2015, 35(5): 1358-1360. (ZONG X, CUI Y. Consensus of the second-order multi-Agent systems with random time-delays[J]. Journal of Computer Applications, 2015, 35(5): 1358-1360. DOI:10.11772/j.issn.1001-9081.2015.05.1358) |
| [11] | 俞辉, 蹇继贵, 王永骥. 多智能体时滞网络的加权平均一致性[J]. 控制与决策, 2007, 22(5): 558-561. (XU H, JIAN J G, WANG Y J. Weighted average-consensus for networks of multi-Agent with time-delays[J]. Control and Decision, 2007, 22(5): 558-561.) |
| [12] | 杨洪勇, 张嗣瀛. 离散时间系统的多智能体的一致性[J]. 控制与决策, 2009, 24(3): 413-416. (YANG H Y, ZHANG S Y. Consensus of multi-Agent system with discrete-time[J]. Control and Decision, 2009, 24(3): 413-416.) |
| [13] | OLSHEVSKY A, TSITSIKLIS J N. Convergence rates in distributed consensus and averaging[C]//Proceedings of the 200645th IEEE Conference on Decision and Control. Piscataway, NJ:IEEE, 2007:3387-3392. |
| [14] | ANGELI D, BLIMAN PIERRE-ALEXANDRE. Convergence speed of distributed consensus and topology of the associated information spread[C]//Proceedings of the 200746th IEEE Conference on Decision and Control. Piscataway, NJ:IEEE, 2007:300-305. |
| [15] | AYSAL T C, ORESHKIN B N, COATES M J. Accelerated distrib-uted average consensus via localized node state prediction[J]. IEEE Transactions on Signal Processing, 2009, 57(4): 1563-1576. DOI:10.1109/TSP.2008.2010376 |
| [16] | ZHANG H-T, CHEN M Z Q, STAN G-B. Fast consensus via predictive pinning control[J]. IEEE Transactions on Circuits & Systems Ⅰ:Regular Papers, 2011, 58(9): 2247-2258. |
| [17] | XIAO L, BOYD S. Fast linear iterations for distributed averaging[J]. Systems & Control Letters, 2004, 53(1): 65-78. |
| [18] | XIAO L, BOYD S, LALL S. A scheme for robust distributed sensor fusion based on average consensus[C]//IPSN 2005:Proceedings of the Fourth International Symposium on Information Processing in Sensor Networks. Piscataway, NJ:IEEE, 2005:63-70. |
| [19] | BOYD S, GHOSH A, PRABHAKAR B, et al. Randomized gossip algorithms[J]. IEEE Transactions on Information Theory, Special issue of IEEE Transactions on Information Theory and IEEE ACM Transactions on Networking, 2006, 52(6): 2508-2530. |
| [20] | GODSIL C, ROYLE G. Algebraic Graph Theory[M]. Berlin: Springer-Verlag, 1975: 298. |
| [21] | REN W, BEARD R W. Consensus seeking in multiagent systems under dynamically changing interaction topologies[J]. IEEE Transactions on Automatic Control, 2005, 50(5): 655-661. DOI:10.1109/TAC.2005.846556 |
| [22] | HORN R A, JOHNSON C R. Matrix analysis[J]. Graduate Texts in Mathematics, 2005, 169(8): 1-17. |




