随着科学技术的不断发展,卫星导航系统的应用越来越广泛,而二进制偏移载波(Binary Offset Carrier, BOC)调制技术也在最新的导航系统中得到广泛应用。BOC信号[1]因其独特且良好的频谱分裂特性而被大量应用在各国的导航系统中,并且随着日益增长的技术要求和研究的不断深入,先后出现了许多衍生的BOC调制技术,如:多重二进制偏移载波(Multiplexed Binary Offset Carrier, MBOC)调制[2]和时分数据调制二进制偏移载波(Time Division Data Modulation-Binary Offset Carrier, TDDM-BOC)调制[3]。引入时分数据调制方式产生的TDDM-BOC信号遵循“奇调偶不调”的原则,具有较强的抗干扰能力,能在一定程度上提高信号的捕获跟踪程度,目前被广泛应用于最新一代的Galileo、GPS以及我国的北斗导航系统中。因此,对该信号的一些特征进行深入研究具有重要的意义。
目前,针对TDDM-BOC信号的研究文献多集中在跟踪捕获与参数估计上。文献[4]中针对该信号利用了一种改进的基于奇异值分解(Singular Value Decompositio, SVD)的方法对TDDM-BOC信号实现了组合码序列的估计,但该方法不可避免地具有收敛速度较慢、计算复杂度较高等不足,当序列较长时方法变得缺乏可行性。而主分量神经网络因其自适应地进行模式识别[5]和特征提取[6-7],被广泛应用在音频噪声消噪[8]等方面。如文献[9]中采用通过主分量分析实现自适应特征提取的在线无监督学习神经网络(online unsupervised LEArning neural network for adaptive feature extraction via Principle component analysis, LEAP)对直接序列码分多址(Direct Sequence Code Division Multiple Access, DS-CDMA)信号进行伪码序列估计。
本文提出采用Sanger神经网络(Sanger NN, 一种多主分量神经网络)[10]对TDDM-BOC信号进行组合码序列的盲估计。该方法需已知伪码周期,而文献[11]已求得TDDM-BOC信号的伪码周期。首先将TDDM-BOC信号通过多次输入达到反复训练权值向量的目的,直至逼近信号的组合码序列,并通过重建各个权值向量的符号函数来实现信号的组合码序列盲估计;最后通过理论分析对比Sanger NN、SVD、LEAP的复杂度,并结合仿真实验将同为多主分量神经网络的LEAP和Sanger进行详细分析与对比。
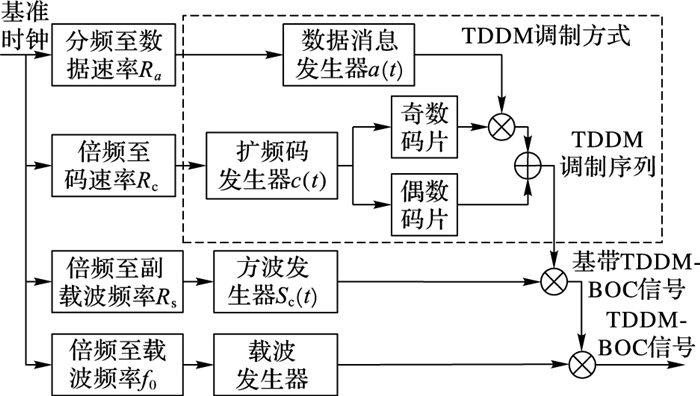
1 TDDM-BOC信号模型TDDM-BOC中的时分数据调制技术不同于以往常规的数据调制处理,实现了不同信号可以叠加在同一频率下,允许同时存在有数据信息部分和无数据信息部分[12]。该信号是在BOC信号的基础上衍生而来的,可以看成是一种特殊的BOC信号,其信号的产生框图与BOC信号的产生框图大致相似,如图 1所示[11]。
|
图 1 TDDM-BOC信号模型 Figure 1 TDDM-BOC modulated signal model |
TDDM-BOC信号为:
| $ \begin{array}{l} S(t)\;\; = \;\;A \times {S_{\rm{B}}}(t) \times {\rm{cos}}(2{\rm{ \mathsf{ π} }}{f_0}t + {\varphi _0}) = \\ \;\;\;\;\;\;\;\;\;\;\;{S_{{\rm{TDDM}}}}(t) \times {S_{\rm{c}}}(t) \times {\rm{cos}}(2{\rm{ \mathsf{ π} }}{f_0}t + {\varphi _0}) \end{array} $ | (1) |
其中:A表示载波信号的幅度;SB(t)表示基带TDDM-BOC信号;Sc(t)表示方波副载波,可以是正弦相位副载波,也可以是余弦相位副载波;f0表示载波频率;φ0表示载波初始相位;STDDM(t)是伪码序列和信息序列经时分数据调制后产生的已调波形,其表达式为
| $ {S_{{\rm{TDDM}}}}(t) = \sum\limits_{n = 0}^\infty {{d_{\rm{n}}}{u_{{T_{\rm{c}}}}}(t - n{T_{\rm{c}}})} $ | (2) |
其中:uTc(t)是幅度值为1的矩形脉冲且持续时间为Tc,Tc表示伪码码元宽度;dn为已调序列,且其范围为dn∈{+1, -1}。
本文采用短码调制信号,即信息码码元宽度Tb等于扩频伪码码片宽度Tc,即一个周期的扩频伪码调制一位信息码。TDDM-BOC信号遵循的原则为“奇调偶不调”:即只有伪码序列中的奇数位码片才和信息序列进行异或处理,其相当于用伪随机序列对信息序列进行扩频; 相反,偶数码片的伪码序列直接输出。
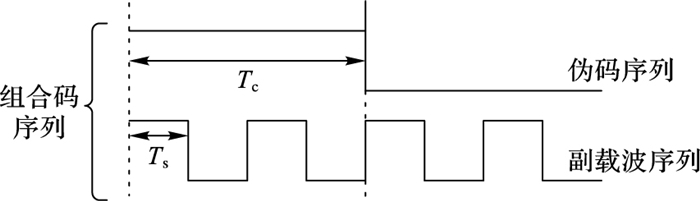
本文主要以TDDM-BOC(10,5) 为例,将信号中的副载波序列与伪码序列相乘并看作一个整体,则称这个整体为组合码序列[13]。下面主要利用Sanger神经网络(Sanger Neural Network, NN)对这个整体序列进行估计。图 2是TDDM-BOC(10,5) 信号的组合码序列示意图。
|
图 2 组合码序列示意图 Figure 2 Schemetic diagram of combination code sequence |
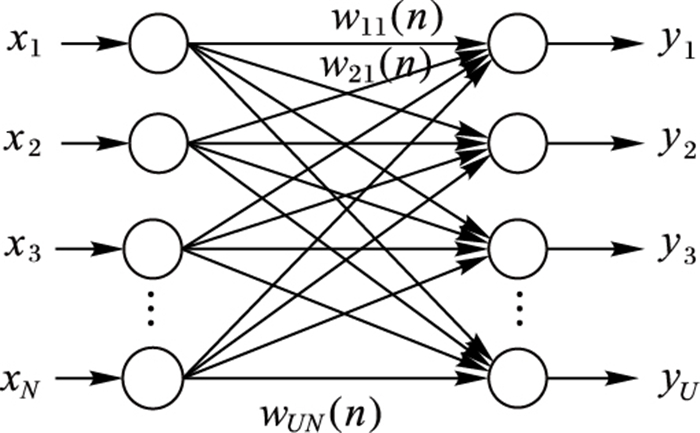
Sanger NN是基于Oja学习规则和Hebbian学习规则提出的一种多主分量神经网络,本文主要参考文献[10]中的具体结构,如图 3所示。
|
图 3 Sanger神经网络 Figure 3 Sanger neural network |
图 3为一个用于主分量分析(Principal Component Analysis, PCA)的双层Sanger NN[10],网络中各单元均为线性的,N个输入和U个输出,且N > U。由图 3可知输出为:
| $ {y_i}(n) = \sum\limits_{j = 1}^N {{w_{ij}}(n){x_j}(n)} {\rm{; }}i = 1, 2, \cdot \cdot \cdot, U $ | (3) |
其中:yi(n)表示第i个输出;wij(n)表示神经元中从第j个输入到第i个输出的前馈连接权值;xj(n)表示神经网络中第j个输入。
式(3) 用向量形式表示为:
| $ {y_i}(n) = \mathit{\boldsymbol{w}}_i^{\rm{T}}(n)\mathit{\boldsymbol{x}}(n) $ | (4) |
则权值向量
基于Hebbian学习规则,wi随着训练过程而不断地发生着变化,由文献[10]可知权值更新公式为:
| $ {\mathit{\boldsymbol{w}}_i}(n + 1) = {\mathit{\boldsymbol{w}}_i}(n) + \mathit{\boldsymbol{\eta }}{y_i}(n)[\mathit{\boldsymbol{x'}}(n)-{y_i}(n){\mathit{\boldsymbol{w}}_i}(n)] $ | (5) |
其中:η为步长,x′(n)表示为
| $ \mathit{\boldsymbol{x'}}(n) = \mathit{\boldsymbol{x}}(n) -\sum\limits_{k = 1}^{j -1} {{y_k}(n){w_k}(n)} $ | (6) |
图 3中,当j=1时,x′(n)= x(n),等价于单个神经元的情况,即x(n)为最大主分量。当j=2,
在Sanger NN中,η的选择与R的特征值有一定的关系。因此,引入自适应变步长学习算法,使其得到较好的收敛效果。
由递归最小二乘算法(Recursive Least-Square, RLS)可推导出最优变步长学习速率,算法的代价函数构建为:
| $ {G_j}(n) = \sum\limits_{l = 0}^n {{r^{n - l}}{{\left| {x(l) - {y_i}(l){w_i}(l)} \right|}^2}} $ | (7) |
其中r∈(0, 1]为遗忘因子,确保系统一直工作在平稳状态下。由代价函数可推得更新公式为:
| $ \begin{array}{l} {w_j}(n) = {w_j}(n - 1) + \\ {\rm{ }}\;\;\;\;\;\;\;\;\;{\left[{\sum\limits_l^n {{r^{n-l}}y_j^2} } \right]^{ - 1}}{y_j}(n)\left[{x(n)-{y_j}(n){w_j}(n-1)} \right] \end{array} $ | (8) |
因此,Sanger NN在RLS下的最优变步长学习速率为:
| $ \eta (n) = {\left[{\sum\limits_{l = 0}^n {{r^{n-l}}y_i^2(l)} } \right]^{ - 1}} $ | (9) |
基带TDDM-BOC信号和基带直扩信号产生原理相似,其中最大的不同仅在于TDDM-BOC信号中伪码序列和信息序列需要先经过时分数据调制,再调制到副载波上加以实现。因此,TDDM-BOC信号可以建模成一般的直扩信号。
本文接收到的TDDM-BOC信号为:
| $ x(t) = s(t - {t_\Delta }) + n(t) $ | (10) |
其中:n(t)为均值为0、方差为δn2的高斯白噪声;tΔ∈[0, T0]且服从均匀分布。由于本文采用短码调制,则T0既是信息码码元宽度,也是伪码周期。
首先对接收的信号进行采样,假设一个码片的宽度就是一个采样周期,则有:
| $ \mathit{\boldsymbol{x'}}(t) = {\left[{{x_1}(t), {x_2}(t), \cdot \cdot \cdot, {x_N}(t)} \right]^{\rm{T}}} $ | (11) |
x′(t)先进行归一化处理后再输入到神经网络中,保证主特征向量可以以鲁棒的形式被估计出。文中采用式(9) 的最优变步长学习速率,可以很好地改善Sanger NN的收敛性。
接下来参考文献[14-15]的相关内容对算法收敛性进行证明。假设TDDM-BOC信号和噪声之间相互独立,则自相关矩阵为:
| $ {\mathit{\boldsymbol{R}}_1} = E\left\{ {\mathit{\boldsymbol{x}}{\mathit{\boldsymbol{x}}^{\rm{T}}}} \right\} $ | (12) |
在现实计算中,假如存在一个足够大的正整数和一个足够小的正整数,可得:
| $ \mathit{\boldsymbol{R}} \approx \frac{1}{M}\sum\limits_{j = n}^{n + M} {\mathit{\boldsymbol{x}}(j){\mathit{\boldsymbol{x}}^{\rm{T}}}(j)} $ | (13) |
| $ {\mathit{\boldsymbol{w}}_i}(n) \approx \frac{1}{M}\sum\limits_{j = n}^{n + M} {{\mathit{\boldsymbol{w}}_i}(n + j)} $ | (14) |
因此,wi(n)的变化速度远远慢于x(n),可得以下的数学模型:
| $ \begin{array}{l} {\mathit{\boldsymbol{w}}_i}(n + M) - {\mathit{\boldsymbol{w}}_i}(n) \approx \\ {\rm{ }}\;\;\;\;\;\beta \left[{\sum\limits_{l = 0}^{M-1} {\mathit{\boldsymbol{x}}(n + l){\mathit{\boldsymbol{w}}_i}(n){\mathit{\boldsymbol{x}}^{\rm{T}}}(n + l)-My_i^2} (n){\mathit{\boldsymbol{w}}_i}(n)} \right] \approx \\ \;\;\;\;\;M\beta \left[{\mathit{\boldsymbol{R}}{\mathit{\boldsymbol{w}}_i}(n)-{\mathit{\boldsymbol{w}}_i}(n)\mathit{\boldsymbol{w}}_i^{\rm{T}}(n)\mathit{\boldsymbol{R}}{\mathit{\boldsymbol{w}}_i}(n)} \right] \end{array} $ | (15) |
| $ \begin{array}{l} \frac{1}{M}\sum\limits_{l = 0}^M {y_i^2} (n + l) \approx \frac{1}{M}\sum\limits_{l = 0}^M {\mathit{\boldsymbol{w}}_i^{\rm{T}}} (n)\mathit{\boldsymbol{x}}(n + l){\mathit{\boldsymbol{x}}^{\rm{T}}}(n + l){\mathit{\boldsymbol{w}}_i}(n) = \\ \;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{w}}_i^T(n){\mathit{\boldsymbol{R}}_M}{\mathit{\boldsymbol{w}}_i}(n) \approx \mathit{\boldsymbol{w}}_i^{\rm{T}}(n)\mathit{\boldsymbol{R}}{\mathit{\boldsymbol{w}}_i}(n) \end{array} $ | (16) |
其中遗忘因子r=Mβ。由上述等价可将原方程近似为非线性、自治确定性方程,也就意味着两个系统的渐进轨迹是等效的,即一个系统收敛,则另一个系统也同样收敛。
用{n, n+1, n+2, …}替代式(16) 中的{n, n+M, n+2M},即Sanger NN非自治随机系统的自治确定性系统数学等价模型化简后为:
| $ \begin{array}{l} {\mathit{\boldsymbol{w}}_i}(n + 1) - {\mathit{\boldsymbol{w}}_i}(n) = \\ \;\;\;\;r\left[{\mathit{\boldsymbol{R}}{\mathit{\boldsymbol{w}}_i}(n)-{\mathit{\boldsymbol{w}}_i}(n)\mathit{\boldsymbol{w}}_i^{\rm{T}}(n)\mathit{\boldsymbol{R}}{\mathit{\boldsymbol{w}}_i}(n)} \right] \end{array} $ | (17) |
对于Sanger NN收敛性的证明可利用已推导出的数学等价模型,证明时应分为i=1和i≠1的两种情况分别讨论。
情况一 当i=1时存在:
| $ \begin{array}{l} {\mathit{\boldsymbol{w}}_1}(n + 1) - {\mathit{\boldsymbol{w}}_1}(n) = \\ \;\;\;\;r\left[{\mathit{\boldsymbol{R}}{\mathit{\boldsymbol{w}}_1}(n)-{\mathit{\boldsymbol{w}}_1}(n)\mathit{\boldsymbol{w}}_1^{\rm{T}}(n)\mathit{\boldsymbol{R}}{\mathit{\boldsymbol{w}}_1}(n)} \right] \end{array} $ | (18) |
| $ {\mathit{\boldsymbol{w}}_1}(n) = \sum\limits_{i = 1}^N {{\theta _{1i}}(n)} {\mathit{\boldsymbol{e}}_i} $ | (19) |
其中: ei是自相关矩阵R中特征值对应的特征向量;θ1i(n)为时变系数,则
| $ {\theta _{1i}}(n + 1) = \left[{1 + \gamma ({\lambda _i}-{\delta _1}(n))} \right]{\theta _{1i}}(n) $ | (20) |
由文献[16]中存在定理1可知,已知:
| $ \left\{ \begin{array}{l} {\rm{A}}1:\lambda > {\lambda _2} > \cdot \cdot \cdot {\lambda _U} > \cdot \cdot \cdot > {\lambda _N} > 0\\ {\rm{A}}2:0 < \left| {{\theta _{1i}}(0)} \right| \le 1\\ {\rm{A}}3:\left| {{\theta _{1i}}(0)} \right| \le 1, i = 2, 3 \cdot \cdot \cdot, N\\ {\rm{A}}4:0 < \gamma < 1\\ {\rm{A}}5:{\theta _{1i}}(n + 1) = \left[{1 + \gamma ({\lambda _i}-\delta (n))} \right]{\theta _i}(n), \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i = 1, 2, \cdot \cdot \cdot, U \end{array} \right. $ | (21) |
当存在
| $ {\delta _1}(n) = \sum\limits_{i = 1}^N {{\lambda _i}\theta _{1i}^2(n)} $ | (22) |
则有
| $ \left\{ \begin{array}{l} \left| {{\theta _i}(n)} \right| \to \left\{ \begin{array}{l} 1, \;\;{\rm{ }}i = 1\\ 0, \;\;\;{\rm{ }}i = 2, \cdot \cdot \cdot N, n \to \infty \end{array} \right.\\ {\delta _1}(n) \to {\mathit{\lambda }_1} \end{array} \right. $ | (23) |
可推得当n→∞,存在w1(n)→e1,δ1(n)→λ1和δ1(n)= w1T(n)Rw1(n)。以上推导可证明i=1的收敛性。
情况二 当i≠1,采用归纳法。首先假设前I-1个输出神经元已经完全收敛并达到稳定状态,接下来只需证明第I个神经元收敛即可,则:
| $ \mathit{\boldsymbol{x'}}(n) = \mathit{\boldsymbol{x}}(n) - \sum\limits_{j = 1}^{i - 1} {{y_j}(n){\mathit{\boldsymbol{w}}_i}(n) = \mathit{\boldsymbol{x}}(n)} $ | (24) |
由于Sanger NN是主分量提取算法中的串行形式,等同于Sanger NN中减去前I-1个神经元,从第I个神经元开始工作,此时收敛性相当于i=1的情况。
4 算法实现与复杂度分析 4.1 算法步骤综上所述,自适应变步长学习算法应用于自组织无监督神经网络来估计TDDM-BOC信号的组合码序列,其步骤简述如下:
1) 网络初始化,神经网络权值随机赋且初始值满足:
| $ \left\| {{\mathit{\boldsymbol{w}}_j}(0)} \right\| = \sqrt {\mathit{\boldsymbol{w}}_j^{\rm{T}}(0){\mathit{\boldsymbol{w}}_j}(0)} \;\; \le \;{2^{ - 1}}j = 1, 2 \cdot \cdot \cdot, l $ | (25) |
2) 设置循环终止条件,即允许有最小误码率的存在。
3) 对于时刻n,输入新的数据向量x(n)。
4) 按式(3) 和式(8) 计算输出yj(n)和估计并修正连接权值,直至其完全收敛并达到稳定状态,方可准确估计出原组合码序列。
本文是在已知组合码周期的前提下实现的组合码序列盲估计。对接收信号进行采样,其采样频率为fs,输入一周期为T0长度的观测数据向量x(t),利用Sanger NN不断输入信号来反复训练权值向量直至收敛。因此,TDDM-BOC信号的组合码序列可以利用各权值向量得以重建。
4.2 复杂度分析算法的复杂度是指算法在实现的过程中的加法次数和乘法次数,本文中将Sanger NN和SVD、LEAP进行复杂度的分析与比较。LEAP[9]是在Sanger NN的基础上将矩阵的形式引入权值更新公式中,网络模型参考Sanger NN,则权值更新公式为:
| $ \begin{array}{l} {\mathit{\boldsymbol{w}}_i}(n + 1) = {\mathit{\boldsymbol{w}}_i}(n) + \beta \left\{ {{\mathit{\boldsymbol{B}}_i}(n)\left[{{y_i}(n)\mathit{\boldsymbol{x}}(n)-} \right.} \right.\\ \left. {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;y_i^2(n){\mathit{\boldsymbol{w}}_i}(n)-\left. {{\mathit{\boldsymbol{A}}_{\bf{i}}}(n){\mathit{\boldsymbol{w}}_i}(n)} \right\}} \right] \end{array} $ | (26) |
其中:
| $ {\mathit{\boldsymbol{A}}_i}(n) = \left\{ \begin{array}{l} 0{\rm{, }}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{ }}i = 1\\ \sum\limits_{j = 1}^{i - 1} {{\mathit{\boldsymbol{w}}_j}(n)\mathit{\boldsymbol{w}}_j^{\rm{T}}(n), \;\;} {\rm{ }}i = 2, 3, \cdot \cdot \cdot, U \end{array} \right. $ | (27) |
| $ {\mathit{\boldsymbol{B}}_i}(n) = \mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{A}}_i}(n){\rm{; }}i = 1, 2, \cdot \cdot \cdot, U $ | (28) |
其中,I为单位矩阵。
本文中信号的伪码序列长度为N,算法达到收敛状态时所需要的信息码元数为M,用户数为U。Sanger NN加法次数为U(U+5)MN/2,乘法次数为U(U+7)MN/2;LEAP的加法次数为(U-1)(U+6)MN2/2+(2U+1)MN,乘法次数为(U-3)(U+4)MN2/2+4UMN;文献[4]中可知奇异值分解法加法次数为N3+(M-1)N2,乘法次数为N3+MN2。
通过上述分析,由于LEAP结构中包含矩阵运算,且N≥U,则Sanger NN的复杂度明显低于LEAP和SVD。
5 仿真实验及分析实验1 验证Sanger NN估计TDDM-BOC信号组合码序列的可行性。本实验采用TDDM-BOC(10, 5) 信号,伪码速率Rc=1.023 MHz,信噪比为-5 dB,采样率Sa=8,令Tx=0。在同步的情况下,选取已分段的一周期四阶TDDM-BOC信号,伪码长度为63,则组合码的周期为63×4=252,进行200次蒙特卡洛仿真。
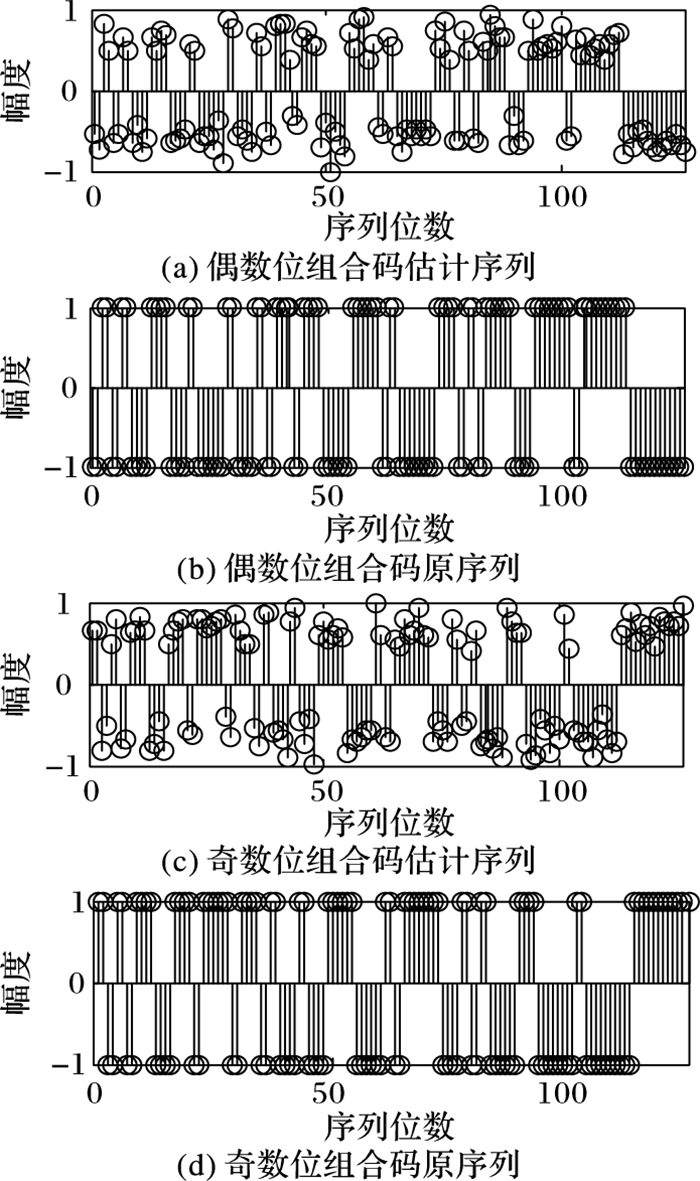
由于TDDM-BOC信号“奇调偶不调”的原则,为避免出现不收敛的情况,将信号送入神经网络前对信号的奇数位和偶数位进行判断,分别估计信号的组合码序列,仿真如图 4所示。
|
图 4 原始组合码序列和权值形成序列 Figure 4 Sequences of original combination code sequences and weights |
实验2 本实验中选取已分段的两周期信号,除Tx≠0外其余参数的选取和实验1相同,验证时延存在时方法的可行性。由于TDDM-BOC信号中偶数位并不含有信息序列,在本实验中只需验证奇数位的组合码序列估计情况。
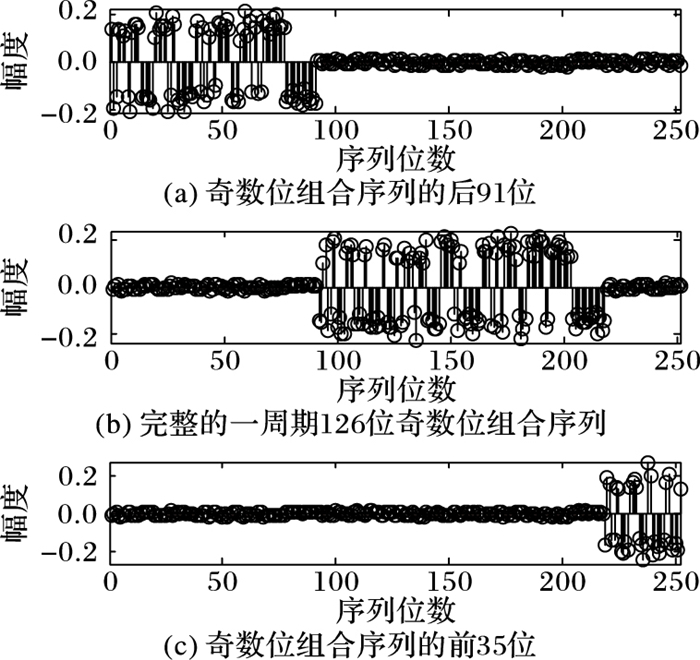
图 5为Tx≠0时输入为两周期信号x(k)所估计的实验结果,分别为奇数位组合码序列的后91位,完整的一周期126位奇数位组合码序列以及奇数位组合码序列的前35位。
|
图 5 奇数位组合码估计序列 Figure 5 Estimation sequence of odd digit of combination code |
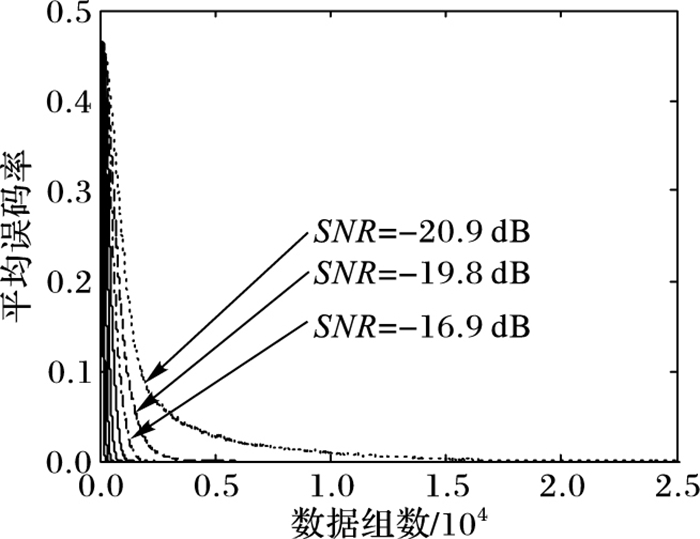
实验3 Sanger NN性能验证。本实验首先验证了TDDM-BOC信号的在信噪比为-20.9~0 dB的性能(如图 6所示);其次为了更清晰地展示各变量之间对比效果,图 7~10还特选取-15.6~0 dB的性能进行对比。
|
图 6 各信噪比下学习收敛曲线 Figure 6 Learning convergence curve under different SNR |
|
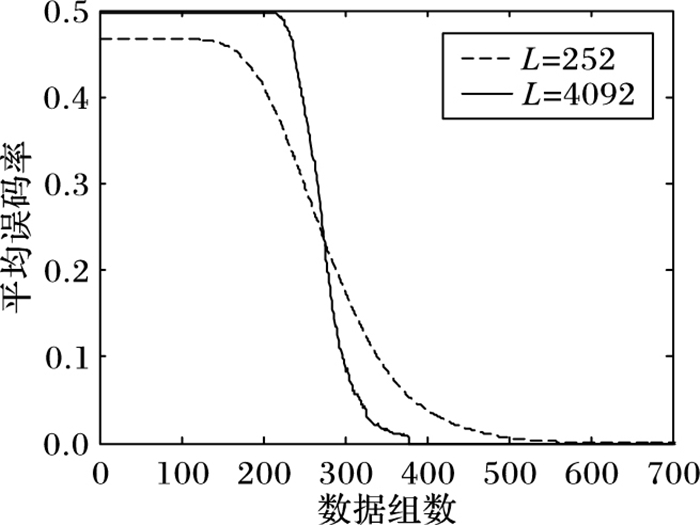
图 7 不同伪码序列长度下的学习收敛曲线 Figure 7 Learning convergence curve under different N |
|
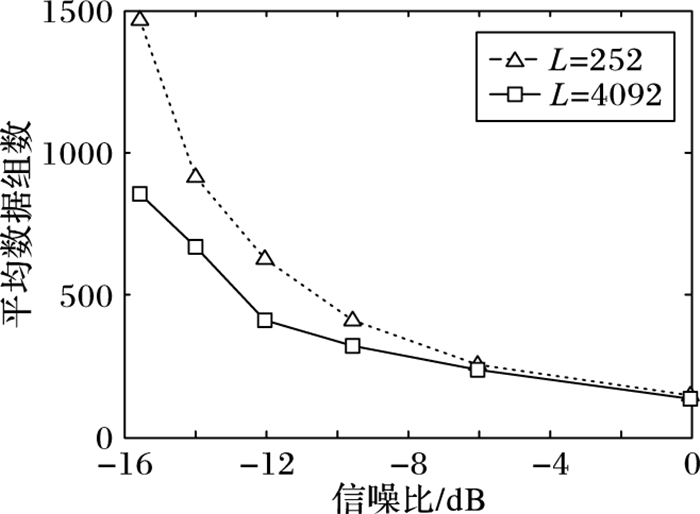
图 8 不同伪码序列长度下的数据组数均值变化 Figure 8 Average number of data group under different N |
|
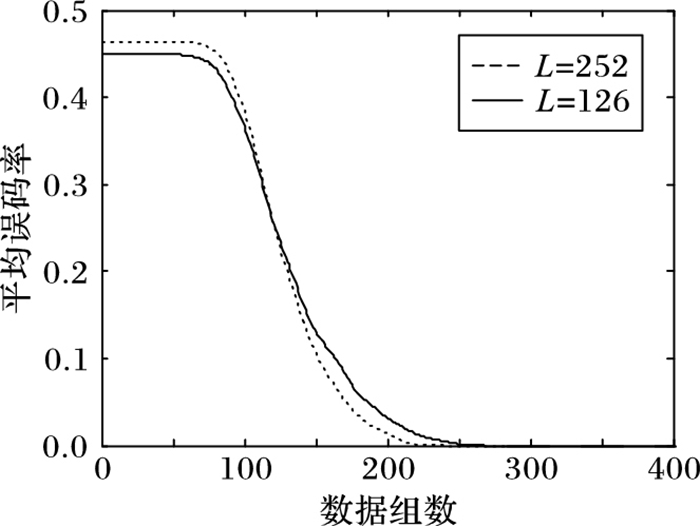
图 9 不同副载波长度下的学习收敛曲线 Figure 9 Learning convergence curve under different subcarrier length |
|
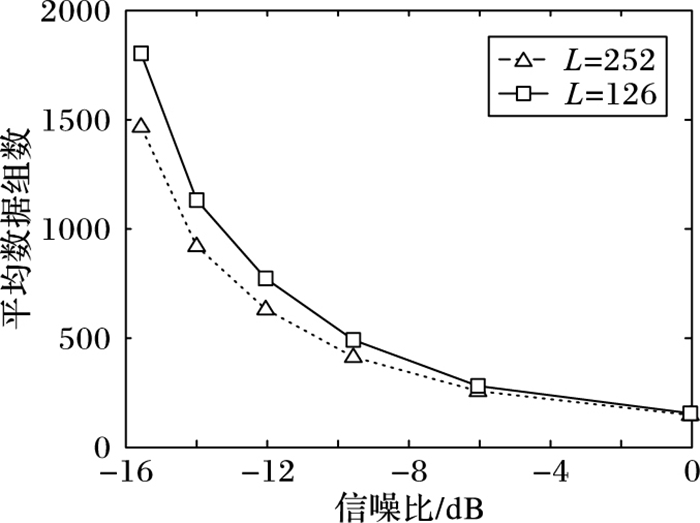
图 10 不同副载波长度下的数据组数均值变化 Figure 10 Average number of data group under different subcarrier length |
由图 6可以看出当组合码的周期为63×4=252时,信噪比SNR为-20.9~0 dB的情况下,随着输入数据不断地输入,组合码估计误差也在不断变化,即该神经网络的学习收敛曲线。在组合码长度、取样率取值相同时,信噪比越高,算法收敛所需数组数越少。
由于组合码由伪码序列和副载波序列组成,则分别改变伪码序列的长度N和副载波的长度,验证各变量对算法性能的影响。在图 7和图 8中,其他取值相同,只改变伪码序列长度,则组合码周期分别为63×4=252和1 023×4=4 092。在图 9和图 10中,其他取值相同,只改变副载波长度,则组合码周期分别为63×4=252和63×2=126。由图 7~10可知,在利用Sanger NN估计组合码序列时,由于伪码长度或副载波长度的不同,导致组合码长度不同时,算法完全收敛所需数组数也在变化,仿真结果表明组合码序列越长,算法收敛所需的数组数越少。
实验4 Sanger NN与LEAP的性能对比。这里将Sanger NN与多主分量神经网络中的LEAP进行对比,取SNR=-14 dB,Sa=8,组合码长度为63×4=252,通过改变算法中变步长初值,观察Sanger NN完全收敛所需的平均数据组数与平均时间,其次在不同信噪比下观察Sanger NN的性能。
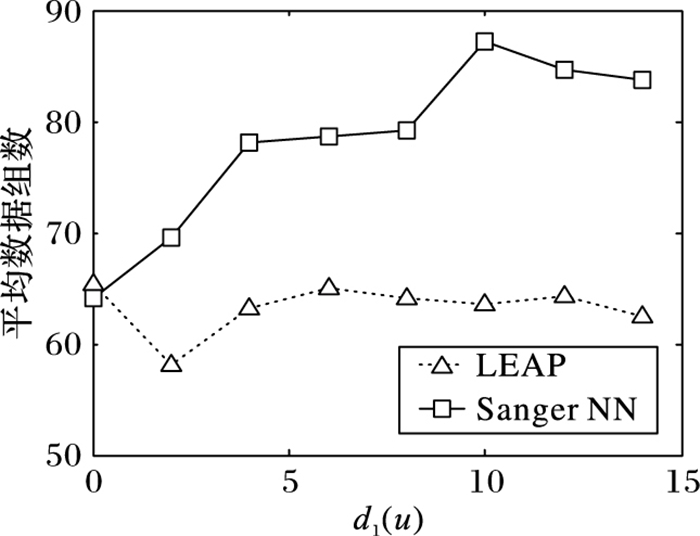
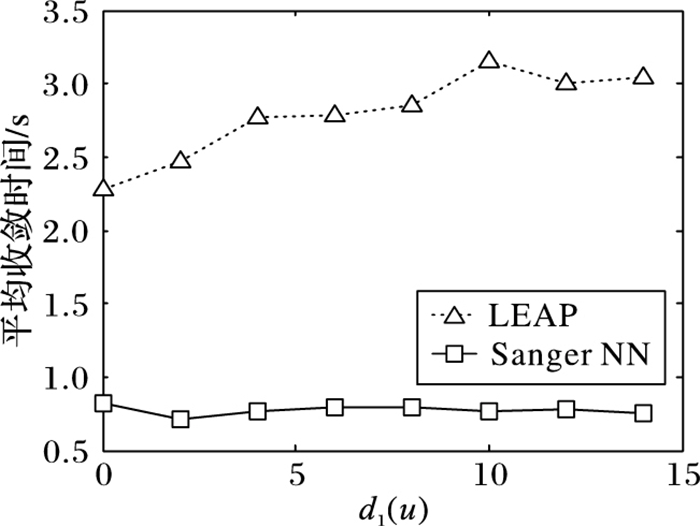
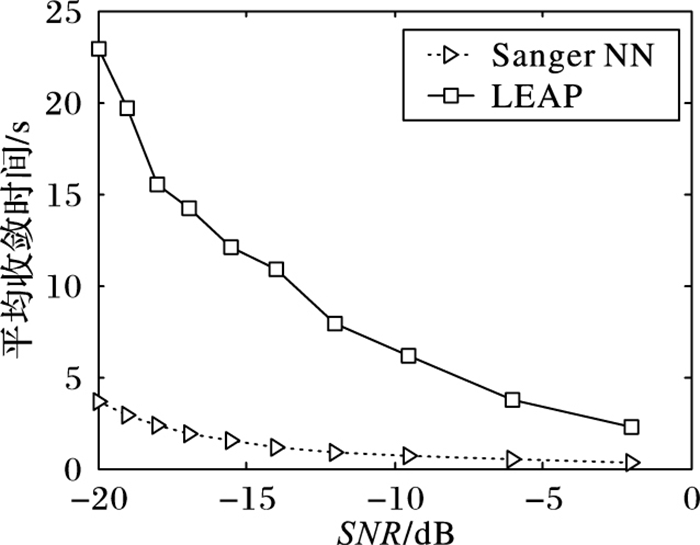
由图 11和图 12可以观察到,以算法中的初值d1(u)为横坐标,通过初值的变化来对比Sanger NN和LEAP的优劣性。仿真结果表明就算法达到完全收敛所需的数据组数而言,Sanger NN所需的数据组数大于LEAP;就算法达到收敛时所需的平均时间,Sanger NN所需时间明显少于LEAP。这是由于LEAP将矩阵引入权值更新公式中,使得算法计算复杂度和运算量增加,并且在处理组合码序列较长时对内存要求高于Sanger NN,因此Sanger NN所需收敛时间比LEAP少。通过对图 13不同信噪比下所需收敛时间的观察可知,信噪比越低,算法完全收敛所需的时间越少,且Sanger NN所需时间明显少于LEAP。
|
图 11 Sanger NN与LEAP收敛数据组数对比 Figure 11 Comparison of convergence number of data group between Sanger NN and LEAP |
|
图 12 Sanger NN与LEAP收敛所需时间对比 Figure 12 Comparison of convergence time between Sanger NN and LEAP |
|
图 13 各信噪比下收敛时间变化 Figure 13 Change of convergence time under different SNR |
本文将扩频码与副载波的组合看作组合码,采用多主分量神经网络(Sanger)的方法,利用权值向量的符号函数来重建TDDM-BOC调制信号的组合码序列,实现了较低信噪比下TDDM-BOC信号组合码序列的盲估计。本文提供了一种基于RLS下的最优变步长收敛模型,很大程度上提高了算法的收敛速度。理论分析表明Sanger NN相较于传统奇异值分解的方法,具有盲估计时的复杂程度低、存储环境要求合理等优点。仿真结果表明Sanger NN收敛所需数据组数大于LEAP,但Sanger NN完全收敛时所需的时间明显少于LEAP,算法复杂度明显低于LEAP。然而,本文算法仍有一定的不足,下一步的研究重点可以放在以下两个方面:提高收敛速度并进一步优化神经网络;尝试估计信号中的副载波,实现低信噪比下TDDM-BOC信号的伪码序列准确估计。
| [1] | LIU Z, HUANG Y, TANG X, et al. Unambiguous s-curve shaping for multipath mitigation for BOC(1, 1) modulated signals in GNSS[J]. IEICE Transactions on Communications, 2015, E98.B(9): 1924-1930. DOI:10.1587/transcom.E98.B.1924 |
| [2] | LIM D W, CHO D J, CHOI H H, et al. A simple and efficient code discriminator for a MBOC signal tracking[J]. IEEE Communications Letters, 2013, 17(6): 1088-1091. DOI:10.1109/LCOMM.2013.040913.122050 |
| [3] | 张洪帅. TDDM的BOC调制信号伪码同步算法的研究[D]. 沈阳: 沈阳理工大学, 2012: 12-22. (ZHANG H S. Research on detection technology of TDDM-BOC modulation signal[D]. Shenyang:Shenyang Ligong University, 2012:12-22.) http://ic.sia.cn/CN/abstract/abstract9905.shtml |
| [4] | 陈昌川, 周杨, 张天骐. TDDM-BOC信号组合码序列及信息序列盲估计[J]. 电子与信息学报, 2016, 38(11): 2760-2766. (CHEN C C, ZHOU Y, ZHANG T Q. Blind estimation of the combination code sequence and information sequence for TDDM-BOC signal[J]. Journal of Electronics & Information Technology, 2016, 38(11): 2760-2766.) |
| [5] | 郭志波, 严云洋, 庞成. 一类多频带主分量分析方法[J]. 数据采集与处理, 2016, 31(1): 139-144. (GUO Z B, YAN Y Y, PANG C. Multi-band principal component analysis method[J]. Journal of Data Acquisition and Processing, 2016, 31(1): 139-144.) |
| [6] | MESSAOUD M A, BOUZID A, ELLOUZE N. Speech enhancement based on wavelet packet of an improved principal component analysis[J]. Computer Speech and Language, 2016, 35: 58-72. DOI:10.1016/j.csl.2015.06.001 |
| [7] | BAI D, LIMING W, CHAN W, et al. Sparse principal component analysis for feature selection of multiple physiological signals from flight task[C]//ICCAS 2015:Proceeding of 201515th IEEE International Conference on Control Automation and Systems. Piscataway, NJ:IEEE, 2015:627-631. |
| [8] | 聂振国, 赵学智. PCA与SVD信号处理效果相似性与机理分析[J]. 振动与冲击, 2016, 35(2): 12-17. (NIE Z G, ZHAO X Z. Similarity of signal processing effect between PCA and SVD and its mechanism analysis[J]. Journal of Vibration and Shock, 2016, 35(2): 12-17.) |
| [9] | ZHANG T Q, DAI S S, LI X S, et al. A neural network method to adaptive feature extraction of weak DS-CDMA signals[C]//CISP' 08:Proceedings of the 2008 Congress on Image and Signal Processing. Washington, DC:IEEE Computer Society, 2008, 5:385-389. |
| [10] | 张天骐. 直扩信号的盲处理[M]. 北京: 国防工业出版社, 2012: 186-206. (ZHANG T Q. Blind Processing for Signal of Direct Sequence Spread Spectrum[M]. Beijing: National Defense Industry Press, 2012: 186-206.) |
| [11] | 周杨, 张天骐, 钱文瑞. 多径环境下TDDM-BOC信号伪码周期估计[J]. 电讯技术, 2015, 55(6): 651-657. (ZHOU Y, ZHANG T Q, QIAN W R. Period estimation of PN sequence for TDDM-BOC Signal in multipath environment[J]. Telecommunication Engineering, 2015, 55(6): 651-657.) |
| [12] | QIAN B, DONG B, LI R, et al. The research of acquiring TDDM-BOC signal base on sub-sampling[C]//ICINIS' 10:Proceedings of the 2010 Third International Conference on Intelligent Networks and Intelligent Systems. Washington, DC:IEEE Computer Society, 2010:193-196. |
| [13] | 阳锐, 张天骐, 石穗, 等. BOC信号的伪码周期和组合码盲估计[J]. 电讯技术, 2014, 54(6): 759-764. (YANG R, ZHANG T Q, SHI S, et al. Blind estimation of pseudo code periodic and combination code for BOC signals[J]. Telecommunication Engineering, 2014, 54(6): 759-764.) |
| [14] | 赵军桃, 张天骐, 江晓磊, 等. 基于LEAP NN的同步DS-CDMA伪码序列盲估计[J]. 计算机应用研究, 2017, 34(2): 552-556. (ZHAO J T, ZHANG T Q, JIANG X L, et al. Blind estimate of the PN sequence synchronous DS-CDMA based on LEAP neural network[J]. Application Research of Computers, 2017, 34(2): 552-556.) |
| [15] | 张天骐, 赵军桃, 江晓磊. 基于多主分量神经网络的同步DS-CDMA伪码盲估计[J]. 系统工程与电子技术, 2016, 38(11): 2638-2647. (ZHANG T Q, ZHAO J T, JIANG X L. PN sequence blind estimate of synchronous DS-CDMA based on multi-principal component neural network[J]. Systems Engineering and Electronics, 2016, 38(11): 2638-2647. DOI:10.3969/j.issn.1001-506X.2016.11.27) |
| [16] | CHEN H, LIN R-W. An on-line unsupervised learning machine for adaptive feature extraction[J]. IEEE Transactions on Circuits and Systems Ⅱ:Analog and Digital Signal Processing, 1994, 41(2): 87-98. DOI:10.1109/82.281840 |



 ,
,