随着无线传感器网络(Wireless Sensor Network,WSN)的广泛运用,作为WSN关键技术之一的时钟同步依然是研究的热点[1-3]。WSN中的数据融合、协作传输、能量管理和节点定位等过程[4-5]都需要精确的时钟同步技术作为支撑。然而, 节点的时钟由廉价的晶体振荡器(简称晶振)提供,由于晶体振荡器制造工艺存在一定差异,并且节点的晶振在工作过程中容易受到温度、电压等多方面外部环境的影响,每个节点的晶振频率很难保持一致,这使得节点的时钟拥有不同的变化速率,即使当前时刻所有节点的时钟都相等,一段时间后节点的时钟便不再相等,因此必须执行时钟同步算法(或协议)才能使时钟再次同步。由于WSN节点体积较小、成本低廉,往往使得节点的能量受到限制,所以研究一种能够满足实际需求、高效节能且无需频繁进行同步操作的时钟同步算法显得非常有必要。
到目前为止,各种时钟同步协议被提出,其中最具有代表性的时钟同步协议有:参考广播同步(Reference-Broadcast Synchronization, RBS)协议[6]和传感器网络定时同步协议(Timing-sync Protocol for Sensor Network, TPSN)[7];还有很多相似的协议如:防洪时间同步协议(Flooding Time Synchronization Protocol, FTSP)[8]和低复杂度时间同步(Lightweight Time Synchronization, LTS)协议[9]。此外,其他的一些同步协议或多或少都是对以上经典协议的改进优化,如文献[10-12]是对TPSN时钟同步协议的改进,其中文献[12]在TPSN的基础上进行改进降低了TPSN算法的复杂度,但是收敛时间比较慢。以上时钟同步协议需要大量的能量去维持分层网络拓扑结构,而且离参考节点越远,累积同步误差就会越来越大。针对以上同步协议的不足,很多研究者提出了各种具有鲁棒性和可扩展性的分布式时钟同步协议,其中较为典型的有RFA(Reachback Firefly Algorithm)[13],但是它只补偿了时钟偏移,没有对时钟偏斜进行补偿;文献[14]提出了既补偿时钟偏斜又补偿时钟偏移的分布式时钟同步协议, 但是计算复杂度高,增加了计算和存储的负担;文献[15]提出了ATS(Average Time Synchronization)算法,该算法同时补偿偏移和偏斜,但是未能考虑信息交换时的时延影响,导致该算法的同步精度未能得到很大提高;文献[16-17]运用一致性理论实现了时钟同步,但是只对节点读数进行补偿而没有考虑对时钟参数进行补偿,导致了需要频繁进行时钟同步,增大了节点能量的消耗。
在分析了当前时钟同步研究现状后,本文提出了基于分布式卡尔曼滤波估计的一致性补偿时钟同步算法DKFCC(Distributed Kalman Filter and Consistency Compensation)。该算法采用双向信息交换机制以及分布式卡尔曼滤波(Distributed Kalman Filter,DKF)算法实现时钟偏斜和偏移两个参数的追踪和最优估计,然后采用一致性补偿实现节点的时钟同步。DKF算法仅要求节点和它直接相连的邻居节点进行有限的信息交换,因此该方法是能量高效的,并且对网络规模具有可扩展性,对网络拓扑的改变具有鲁棒性。本文的DKFCC同步算法对影响时钟读数的两个本质参数偏斜和偏移分别进行了一致性补偿,相比仅实现时钟读数补偿控制的异步一致性同步(Asynchronous Consensus-based time synchronization,AC)算法[17]来说,DKFCC同步算法无需频繁进行时钟同步,是一种高效节能的时钟同步算法。DKFCC同步算法包含邻居一致性补偿和虚拟全局一致性补偿两种方式,其中采用虚拟全局一致性补偿方式的DKFCC同步算法具有同步精度高、适用于大规模网络等特点。
1 时钟参数状态空间模型建立 1.1 时钟参数状态更新模型WSN是一种分布式系统,每个传感器节点都拥有自己的一个本地时钟,文献[16, 18]将节点的时钟读数建模为积分模型,如式(1) 所示:
| $ c\left( t \right) = \int_0^t {\beta \left( \tau \right)} {\rm{d}}\tau + {\theta ^0} $ | (1) |
其中:β是节点的时钟偏斜,表示时钟变化的速率; θ0是节点的初始时钟偏移,表示节点初始的本地时钟与当前标准时钟的差值。
文献[19]根据传感器节点振荡器得到一个模拟时钟的特性:ρi(t)=cosΦi(t),进而得到时钟读数的晶振模型如式(2)。
| $ \begin{array}{l} {c_i}(t)\;\; = \;\;\frac{{{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_i}(t)}}{{2{\rm{ \mathsf{ π} }}{f_0}}} = \frac{{{f_0} + \Delta f}}{{{f_0}}}t + \frac{{{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_i}(0)}}{{2{\rm{ \mathsf{ π} }}{f_0}}} + \frac{{{\zeta _i}(t)}}{{2{\rm{ \mathsf{ π} }}{f_0}}} = \\ \;\;\;\;\;\;\;\;\;\;{\xi _i}t + \theta _i^0 + \sqrt {{p_i}} B(t) \end{array} $ | (2) |
其中:Φi(t)是节点Si的瞬时相位;f0表示晶体振荡器的中心频率;Δf是由于硬件的不完美而引起的频率偏移;Φi(0) 表示初始相位;ζi(t)表示模拟相位噪声的随机过程;ξi是标准化频率;θi0是节点Si的初始时钟偏移;pi是晶振的质量参数;B(t)是标准的维纳过程[20]。通过联立式(1) 和式(2) 可得
| $ {\beta _i}\left( t \right) = {\xi _i} + \sqrt {{p_i}} B'\left( t \right) $ | (3) |
对式(3) 以采样周期τ0进行采样得到:
| $ {\beta _i}\left( l \right) = {\beta _i}\left( {l - 1} \right) + {\delta _i}\left( l \right) $ | (4) |
其中:
对式(1) 以同样的采样周期τ0进行采样得到:
| $ \begin{array}{l} {c_i}\left( l \right) = \sum\limits_{m = 1}^{l - 1} {{\beta _i}} \left( m \right){\tau _0} + {\beta _i}\left( l \right){\tau _0} + \theta _i^0 = \\ \;\;\;\;\;\;\;\;\;\;\left( {l - 1} \right){\tau _0} + \sum\limits_{m = 1}^{l - 1} {\left[{{\beta _i}\left( m \right)-1} \right]} \;{\tau _0} + {\beta _i}\left( l \right){\tau _0} + \theta _i^0 = \\ \;\;\;\;\;\;\;\;\;\;l{\tau _0} + \underbrace {\sum\limits_{m = 1}^{l - 1} {\left[{{\beta _i}\left( m \right)-1} \right]} \;{\tau _0} + \theta _i^0}_{{\theta _i}\left( {l - 1} \right)} + \left[{{\beta _i}\left( l \right)-1} \right]{\tau _0} = \\ \;\;\;\;\;\;\;\;\;\;l{\tau _0} + {\vartheta _i}\left( {l - 1} \right) + \left[{{\beta _i}\left( l \right)-1} \right]{\tau _0} \end{array} $ | (5) |
由式(5) 得到累积时钟偏移的递归关系:
| $ {\vartheta _i}\left( l \right) = {\vartheta _i}\left( {l - 1} \right) + \left( {{\beta _i}\left( l \right) - 1} \right){\tau _0} $ | (6) |
将式(4) 代入式(6) 中,得到:
| $ {\vartheta _i}\left( l \right) = {\vartheta _i}\left( {l - 1} \right) + {\beta _i}\left( {l - 1} \right){\tau _0} + {\delta _i}\left( l \right){\tau _0} - {\tau _0} $ | (7) |
定义
| $ {\mathit{\boldsymbol{x}}_i}\left( l \right) = {\mathit{\boldsymbol{A}}_i}{\mathit{\boldsymbol{x}}_i}\left( {l - 1} \right) + {\mathit{\boldsymbol{w}}_i}\left( l \right) + {\mathit{\boldsymbol{b}}_i} $ | (8) |
其中:
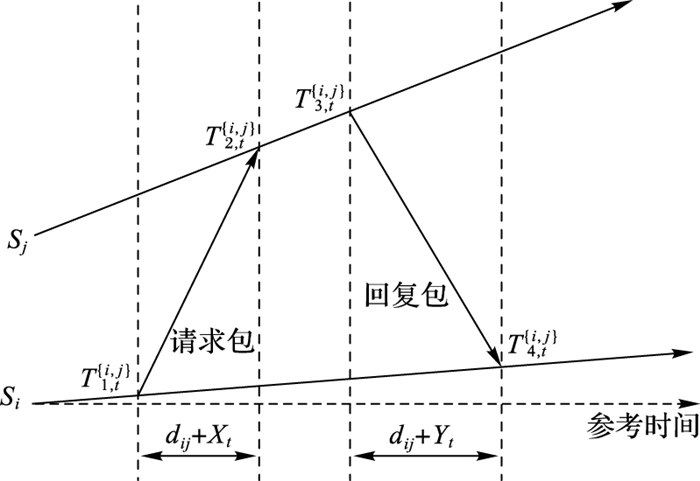
由于节点时钟参数的状态无法直接获得,但是节点的时间戳比较易获得,因此采用WSN中最为经典的基于发送方与接受方的双向信息交换时钟同步机制,建立节点Si和它邻居节点Sj之间的时间戳交换模型[4],如图 1所示。
|
图 1 标准时间t下节点Si和Sj双向时间戳交换 Figure 1 Two-way time-stamp exchange between nodes Si and Sj at standard time t |
现在将式(1) 的时钟模型用参考时间和累积时钟偏移的形式表示如下:
| $ \begin{array}{l} {c_i}\left( t \right) = \int_0^t {{\beta _i}\left( \tau \right)} {\rm{d}}\tau {\rm{ + }}\theta _i^0 = t + \int_0^t {\left[{{\beta _i}\left( \tau \right)-1} \right]} {\rm{d}}\tau {\rm{ + }}\theta _i^0 = \\ \;\;\;\;\;\;\;\;\;\;\;t + {\theta _i}\left( t \right) \end{array} $ | (9) |
因此,可将图 1的时间戳的交换过程建模为:
| $ T_{2, t}^{\left\{ {i, j} \right\}} - {\vartheta _j}\left( t \right) = T_{1, t}^{\left\{ {i, j} \right\}} - {\vartheta _i}\left( t \right) + {d_{ij}} + X_t^{\left\{ {i, j} \right\}} $ | (10) |
| $ T_{3, t}^{\left\{ {i, j} \right\}} - {\vartheta _j}\left( t \right) = T_{4, t}^{\left\{ {i, j} \right\}} - {\vartheta _i}\left( t \right) - {d_{ij}} - Y_t^{\left\{ {i, j} \right\}} $ | (11) |
其中:dij代表节点Si和Sj之间的固定时延部分;Xt{i, j}和Yt{i, j}表示节点Si和Sj之间的随机时延部分,考虑Xt{i, j}和Yt{i, j}是无数个独立的随机过程,所以假设Xt{i, j}和Yt{i, j}是独立同方分布的Gaussian随机变量,且服从均值为0、方差为σ2的高斯分布,该假设已经在文献[21]被证实。
将式(10) 和式(11) 相加,得到了采样之后离散的本地量测模型:
| $ T_{r, l}^{\left\{ {i, j} \right\}} -T_{s, l}^{\left\{ {i, j} \right\}} = 2{\vartheta _j}\left( l \right) -2{\vartheta _i}\left( l \right) + V_l^{\left\{ {i, j} \right\}} $ | (12) |
其中:Sj为节点Si的邻居节点,记为j∈Ni(j);Vt{i, j}=Xt{i, j}-Yt{i, j};Ts, t{i, j}=T1, t{i, j}+T4, t{i, j},Tr, t{i, j}=T2, t{i, j}+T3, t{i, j}。因此,对于节点Si的所有邻居节点,堆叠式(12) 之后,得到:
| $ {\mathit{\boldsymbol{z}}_{i, l}} = {\mathit{\boldsymbol{C}}_{i, l}}\mathit{\boldsymbol{x}}\left( l \right) + {\mathit{\boldsymbol{v}}_i}\left( l \right) $ | (13) |
其中:zi, l(j)=Tr, l{i, Ni(j)}-Ts, l{i, Ni(j)},且j∈{1, 2, …, λi}(λi= | Ni |是节点Si的邻居节点的数量);x(l)=x2T(l) x3T(l) … xNT(l)]T(除标准参考节点外);υi(l)是量测噪声且其均值为零,协方差为Ri=E[υi(l)υiT(l)]=2σ2Ιλi;Ci, l∈Rλi×2(N-1),其相应元素表示如式(14) 所示。
| $ {{\bf{C}}_{i, l}}(j, n) = \left\{ \begin{array}{l} - 2, \;\;\;\;\;n = 2i - 2\\ 2, \;\;\;\;\;\;\;n = 2{N_i}(j) - 2\\ 0, \;\;\;\;\;\;\;其他 \end{array} \right. $ | (14) |
其中:
式(13) 的量测模型也可以被描述为本地子系统状态向量的形式,如下:
| $ {\mathit{\boldsymbol{z}}_{i, l}} = {\mathit{\boldsymbol{\tilde C}}_{i, l}}{\mathit{\boldsymbol{x}}_{{N_{\left[i \right]}}}}\left( l \right) + {\mathit{\boldsymbol{v}}_i}\left( l \right) $ | (15) |
其中:
由式(8) 和式(15) 便建立了分布式时钟参数状态空间模型,如下:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{x}}_i}\left( l \right) = {\mathit{\boldsymbol{A}}_i}{\mathit{\boldsymbol{x}}_i}\left( {l - 1} \right) + {\mathit{\boldsymbol{w}}_i}(l) + {\mathit{\boldsymbol{b}}_i}\\ {\mathit{\boldsymbol{z}}_{i, l}} = {{\mathit{\boldsymbol{\tilde C}}}_{i, l}}{\mathit{\boldsymbol{x}}_{{N_{[i]}}}}(l) + {\mathit{\boldsymbol{\upsilon }}_i}(l) \end{array} \right. $ | (16) |
由于节点的时钟偏移和偏斜是时变的,且这两个参数的真实值不易获得。文献[22]通过全局最优的方式得到一种分布式卡尔曼滤波实现时钟参数的追踪和最优估计,在此本文提出局部最优方式下的一种分布式的卡尔曼滤波算法用于实现时钟参数的追踪和最优估计。现假设以抽样时间间隔τ0的Δ倍执行一次滤波,因此定义lk=Δk,则式(16) 变成如下形式:
| $ \left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{x}}_i}({l_k}) = {\mathit{\boldsymbol{A}}_i}{\mathit{\boldsymbol{x}}_i}({l_{k - 1}}) + {\mathit{\boldsymbol{w}}_i}({l_k}) + {\mathit{\boldsymbol{b}}_i}}\\ {{\mathit{\boldsymbol{z}}_{i, {l_k}}} = {{\mathit{\boldsymbol{\tilde C}}}_{i, {l_k}}}{\mathit{\boldsymbol{x}}_{{N_{[i]}}}}({l_k}) + {\mathit{\boldsymbol{\upsilon }}_i}({l_k})\;\;\;\;\;\;\;} \end{array}} \right. $ | (17) |
其中:
基于式(17) 的分布式时钟参数状态空间模型,网络任意节点Si的时钟参数状态xi(lk)的最优估计
1) 滤波预测步:
预测步估计:
| $ {{\mathit{\boldsymbol{\hat x}}}_i}({l_k}|{l_{k - 1}}) = {\mathit{\boldsymbol{A}}_i}{{\mathit{\boldsymbol{\hat x}}}_i}({l_{k - 1}}|{l_{k - 1}}) + {\mathit{\boldsymbol{b}}_i} $ | (18) |
预测步估计误差:
| $ {\mathit{\boldsymbol{e}}_i}({l_k}|{l_{k - 1}}) = {{\mathit{\boldsymbol{\hat x}}}_i}({l_k}|{l_{k - 1}}) - {{\mathit{\boldsymbol{\hat x}}}_i}({l_k}) $ | (19) |
预测步估计误差协方差:
| $ {\mathit{\boldsymbol{P}}_i}({l_k}|{l_{k - 1}}) = {\mathit{\boldsymbol{A}}_i}{\mathit{\boldsymbol{P}}_i}({l_{k - 1}}|{l_{k - 1}}){\mathit{\boldsymbol{A}}_i}^{\rm{T}} + {\mathit{\boldsymbol{Q}}_i}({l_k}) $ | (20) |
2) 滤波更新步:
更新步最优估计:
| $ \begin{array}{l} {{\mathit{\boldsymbol{\hat x}}}_i}({l_k}|{l_k})\;\; = \;\;{{\mathit{\boldsymbol{\hat x}}}_i}({l_k}|{l_{k - 1}}) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{K}}_i}({l_k})\left( {{\mathit{\boldsymbol{z}}_{i, {l_k}}} - {{\mathit{\boldsymbol{\tilde C}}}_{i, {l_k}}}{{\mathit{\boldsymbol{\hat x}}}_{{N_{[i]}}}}({l_k}|{l_{k - 1}})} \right) \end{array} $ | (21) |
更新步估计误差:
| $ {\mathit{\boldsymbol{e}}_i}({l_k}) = {{\mathit{\boldsymbol{\hat x}}}_i}({l_k}|{l_k}) - {\mathit{\boldsymbol{x}}_i}({l_k}) $ | (22) |
更新步估计误差协方差:
| $ \begin{array}{l} {\mathit{\boldsymbol{P}}_i}({l_k})\;\; = \;\;{\rm{E}}\left[{{\mathit{\boldsymbol{e}}_i}({l_k}){\mathit{\boldsymbol{e}}_i}{{({l_k})}^{\rm{T}}}} \right] = \\ \;\;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{P}}_i}({l_k}|{l_{k - 1}}) - {\mathit{\boldsymbol{p}}_{[i]}}({l_k}|{l_{k - 1}}){{\mathit{\boldsymbol{\tilde C}}}_{i, {l_k}}}^{\rm{T}}{\mathit{\boldsymbol{K}}_i}{({l_k})^{\rm{T}}} - \\ \;\;\;\;\;\;\;\;\;\;\;\;{\left[{{\mathit{\boldsymbol{p}}_{[i]}}({l_k}|{l_{k -1}}){{\mathit{\boldsymbol{\tilde C}}}_{i, {l_k}}}^{\rm{T}}{\mathit{\boldsymbol{K}}_i}{{({l_k})}^{\rm{T}}}} \right]^{\rm{T}}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{K}}_i}({l_k}){\mathit{\boldsymbol{R}}_i}({l_k}){\mathit{\boldsymbol{K}}_i}{({l_k})^{\rm{T}}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{K}}_i}({l_k}){{\mathit{\boldsymbol{\tilde C}}}_{i, {l_k}}}{\mathit{\boldsymbol{P}}_{{N_{[i]}}}}({l_k}|{l_{k -1}}){{\mathit{\boldsymbol{\tilde C}}}_{i, {l_k}}}^{\rm{T}}{\mathit{\boldsymbol{K}}_i}{({l_k})^{\rm{T}}} \end{array} $ | (23) |
为了得到滤波的最优增益,求Pi(lk)的迹Tr[Pi(lk)],然后对Tr[Pi(lk)]关于Ki(lk)微分求解得到:
| $ \begin{array}{l} \frac{{{\rm{d}}{\mathop{\rm Tr}\nolimits} {\mathit{\boldsymbol{P}}_i}({l_k})}}{{{\rm{d}}{\mathop{\rm vec}\nolimits} \left[{{\mathit{\boldsymbol{K}}_i}({l_k})} \right]}}\;\; = \;\; - 2{\mathit{\boldsymbol{p}}_{[i]}}({l_k}|{l_{k - 1}}){{\mathit{\boldsymbol{\tilde C}}}_{i, {l_k}}}^{\rm{T}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;2{\mathit{\boldsymbol{K}}_i}({l_k}){{\mathit{\boldsymbol{\tilde C}}}_{i, {l_k}}}{\mathit{\boldsymbol{P}}_{{N_{[i]}}}}({l_k}|{l_{k - 1}}){{\mathit{\boldsymbol{\tilde C}}}_{i, {l_k}}}^{\rm{T}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;2{\mathit{\boldsymbol{K}}_i}({l_k}){\mathit{\boldsymbol{R}}_i}({l_k}) \end{array} $ | (24) |
最后,根据极值最小原理,令
| $ \begin{array}{l} {\mathit{\boldsymbol{K}}_i}({l_k}) = \left[{{\mathit{\boldsymbol{p}}_{[i]}}({l_k}|{l_{k -1}}){{\mathit{\boldsymbol{\tilde C}}}_{i, {l_k}}}^\rm{T}} \right] \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;{\left[{{{\mathit{\boldsymbol{\tilde C}}}_{i, {l_k}}}{\mathit{\boldsymbol{P}}_{{N_{[i]}}}}({l_k}|{l_{k -1}}){{\mathit{\boldsymbol{\tilde C}}}_{i, {l_k}}}^\rm{T} + {\mathit{\boldsymbol{R}}_i}({l_k})} \right]^{ - 1}} \end{array} $ | (25) |
其中:
至此,DKF滤波算法推导完成。节点Si进行DKF算法一次迭代过程的计算时间复杂度主要产生于三个计算过程:协方差预测阶段的
基于分布式卡尔曼滤波得到时钟参数的最优估计值后,分别对时钟偏斜和时钟偏移进行一致性补偿,使得节点从时钟参数层面实现时钟的本质同步。本文提出的DKFCC同步算法的一致性补偿部分可以采用两种方式:邻居一致性补偿和虚拟全局一致性补偿。
3.1 邻居一致性补偿通过上文提到的分布式卡尔曼滤波估计方法,节点可以得到自身时钟参数的最优估计值,然后将自身时钟参数的最优估计值广播给邻居节点。针对网络任意局部的本地子系统
时钟偏斜的一致性补偿过程为:
| $ \begin{array}{l} {\beta _i}({l_k})\begin{array}{*{20}{c}} = \end{array}{\beta _i}({l_{k{\rm{ - }}1}}) + {\delta _i}({l_k}) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{{\left| {{N_i}} \right|}}\sum\limits_{j = 1, j \ne i}^{\left| {{N_{[i]}}} \right|} {\left[{\frac{{{{\hat \beta }_j}({l_{k{\rm{-}}1}})-{{\hat \beta }_i}({l_{k{\rm{-}}1}})}}{2}} \right]} \end{array} $ | (26) |
时钟偏移的一致性补偿过程为:
| $ \begin{array}{l} {\vartheta _i}({l_k}) = {\vartheta _i}({l_{k{\rm{ - }}1}}) + {\tau _0}{\beta _i}({l_k}) - {\tau _0} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{{\left| {{N_i}} \right|}}\sum\limits_{j = 1, j \ne i}^{\left| {{N_{[i]}}} \right|} {\left[{\frac{{{{\hat \vartheta }_j}({l_{k{\rm{-}}1}})-{{\hat \vartheta }_i}({l_{k{\rm{-}}1}})}}{2}} \right]} \end{array} $ | (27) |
定义
| $ \begin{array}{l} {\mathit{\boldsymbol{x}}_i}({l_k})\;\; = \;\;{\mathit{\boldsymbol{A}}_i}{\mathit{\boldsymbol{x}}_i}({l_{k{\rm{ - }}1}}) + {\mathit{\boldsymbol{\omega }}_i}({l_k}) + {\mathit{\boldsymbol{b}}_i} + \\ \;\;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{A}}_i}\frac{1}{{\left| {{N_i}} \right|}}\sum\limits_{j = 1, j \ne i}^{\left| {{N_{[i]}}} \right|} {\left[{\frac{{{{\mathit{\boldsymbol{\hat x}}}_j}({l_{k{\rm{-}}1}})-{{\mathit{\boldsymbol{\hat x}}}_i}({l_{k{\rm{-}}1}})}}{2}} \right]} \end{array} $ | (28) |
其中:| Ni |表示节点Si的邻居节点个数,| N[i] |是包含中心节点Si和它邻居节点的总节点个数。邻居一致性补偿项为:
由于大多数的WSN应用并不要求节点的时钟同步到物理真实时钟,而只要求节点的本地时钟读数相等即可,至于最终同步到哪个具体值并不关心,所以可以构造一个虚拟全局时钟,并假设待同步节点最终都同步到虚拟全局时钟[23]。因此,采用节点时钟参数的最优估计值与虚拟全局时钟参数的差值作为补偿量可有效实现节点的同步,该算法复杂度低,且无需频繁进行同步操作,从而高效节能。现定义虚拟全局时钟CV=at+b,则虚拟全局时钟参数状态为xV=[a b]T。一般地,可令a=1,b=0。现将节点时钟参数的虚拟全局一致性补偿过程描述如下:
时钟偏斜的一致性补偿过程为:
| $ {\beta _i}({l_k})\begin{array}{*{20}{c}} = \end{array}{\beta _i}({l_{k{\rm{ - }}1}}) + {\delta _i}({l_k}) + \left[{a-{{\hat \beta }_i}({l_k})} \right] $ | (29) |
时钟偏移的一致性补偿过程为:
| $ {\vartheta _i}({l_k}) = {\vartheta _i}({l_{k{\rm{ - }}1}}) + {\tau _0}{\beta _i}({l_k}) - {\tau _0} + \left[{b-{{\hat \vartheta }_i}({l_k})} \right] $ | (30) |
定义
| $ {\mathit{\boldsymbol{x}}_i}({l_k}) = {\mathit{\boldsymbol{A}}_i}{\mathit{\boldsymbol{x}}_i}({l_{k{\rm{ - }}1}}) + {\mathit{\boldsymbol{\omega }}_i}({l_k}) + {\mathit{\boldsymbol{b}}_i} + {\mathit{\boldsymbol{A}}_i}\left( {{\mathit{\boldsymbol{x}}_v} - {{\mathit{\boldsymbol{\hat x}}}_i}({l_k})} \right) $ | (31) |
由于
| $ {{\mathit{\boldsymbol{\hat x}}}_i}({l_k}) = {\mathit{\boldsymbol{A}}_i}{{\mathit{\boldsymbol{\hat x}}}_i}({l_{k{\rm{ - }}1}}) + {\mathit{\boldsymbol{\omega }}_i}({l_k}) + {\mathit{\boldsymbol{b}}_i} + {\mathit{\boldsymbol{A}}_i}\left( {{\mathit{\boldsymbol{x}}_v} - {{\mathit{\boldsymbol{\hat x}}}_i}({l_k})} \right) $ |
上式变换之后得到:
| $ {{\mathit{\boldsymbol{\hat x}}}_i}({l_k}) = {(\mathit{\boldsymbol{I}} + {\mathit{\boldsymbol{A}}_i})^{ - 1}}\left[{{\mathit{\boldsymbol{A}}_i}{{\mathit{\boldsymbol{\hat x}}}_i}({l_{k{\rm{-}}1}}) + {\mathit{\boldsymbol{\omega }}_i}({l_k}) + {\mathit{\boldsymbol{b}}_i} + {\mathit{\boldsymbol{A}}_i}{\mathit{\boldsymbol{x}}_v}} \right] $ |
将上式代入式(31) 得到:
| $ \begin{array}{l} {\mathit{\boldsymbol{x}}_i}({l_k}) = {\mathit{\boldsymbol{A}}_i}{\mathit{\boldsymbol{x}}_i}({l_{k{\rm{ - }}1}}) + {\mathit{\boldsymbol{\omega }}_i}({l_k}) + {\mathit{\boldsymbol{b}}_i} + {\mathit{\boldsymbol{A}}_i}\left[{{\mathit{\boldsymbol{x}}_v}- } \right.\\ \left. {\;\;\;\;\;\;\;\;\;\;\;\;{{(\mathit{\boldsymbol{I}} + {\mathit{\boldsymbol{A}}_i})}^{- 1}}\left[{{\mathit{\boldsymbol{A}}_i}{{\mathit{\boldsymbol{\hat x}}}_i}({l_{k{\rm{-}}1}}) + {\mathit{\boldsymbol{\omega }}_i}({l_k}) + {\mathit{\boldsymbol{b}}_i} + {\mathit{\boldsymbol{A}}_i}{\mathit{\boldsymbol{x}}_v}} \right]} \right] \end{array} $ | (32) |
其中,虚拟全局一致性补偿项为:
| $ {\mathit{\boldsymbol{A}}_i}\left[{{\mathit{\boldsymbol{x}}_v}- {{(\mathit{\boldsymbol{I}} + {\mathit{\boldsymbol{A}}_i})}^{- 1}}\left[{{\mathit{\boldsymbol{A}}_i}{{\mathit{\boldsymbol{\hat x}}}_i}({l_{k{\rm{-}}1}}) + {\mathit{\boldsymbol{\omega }}_i}({l_k}) + {\mathit{\boldsymbol{b}}_i} + {\mathit{\boldsymbol{A}}_i}{\mathit{\boldsymbol{x}}_v}} \right]} \right] $ |
通过该补偿项可以有效实现节点的时钟同步。由于邻居一致性补偿和虚拟全局一致性补偿都是基于DKF滤波算法,因此两种补偿方式时间复杂度主要体现在补偿项,虚拟全局一致性补偿项计算时间复杂度为O(1)。
4 仿真结果与分析本文提出的DKFCC同步算法是在分布式卡尔曼滤波得到时钟参数最优估计的基础上,通过一致性补偿来实现时钟同步的,因此将分别对时钟参数滤波估计性能和加入一致性补偿后时钟同步性能进行仿真分析。
本文考虑在一定区域随机部署100个节点组成无规则的WSN,对该WSN分别采用DKFCC同步算法和文献[17]设计的控制输入的AC算法实现节点的同步,其网络的拓扑结构如图 2所示。实验采用Matlab 2015b仿真工具进行仿真,相关参数见表 1。
|
图 2 网络节点的拓扑结构 Figure 2 Topology structure of network nodes |
| 表 1 仿真参数 Table 1 Simulation parameters |
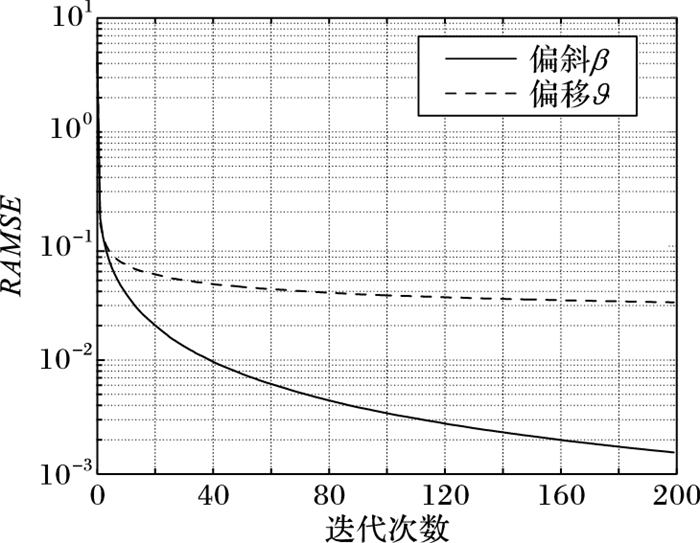
为了评估采用DKF算法对时钟参数最优估计的性能,本文采用根均方误差(Root Average Mean Squared Error, RAMSE)准则[22]对DKF算法进行评估。定义RAMSE如下:
| $ RAMSE(\zeta ({l_k})) = \sqrt {\frac{1}{{N - 1}}\sum\limits_{i = 2}^N {{{({{\hat \zeta }_i}({l_k}) - {\zeta _i}({l_k}))}^2}} } $ | (33) |
其中:
|
图 3 时钟参数的根均方误差值 Figure 3 RAMSE of clock parameters |
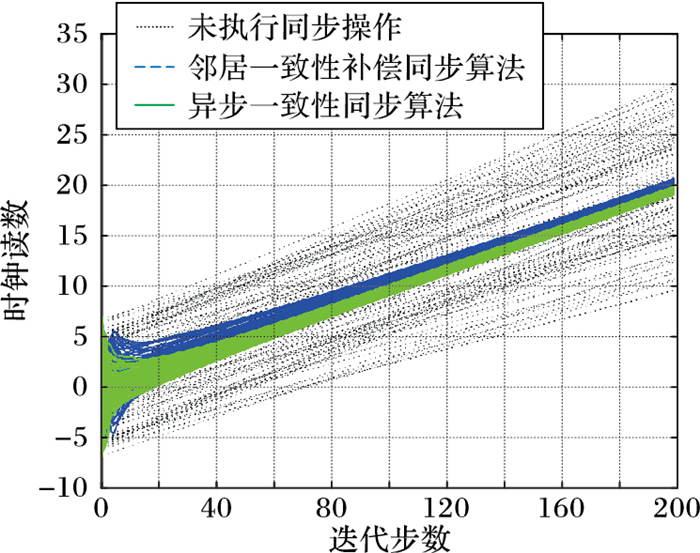
当得到时钟参数的最优估计之后,根据式(5) 和式(28) 可以得到邻居一致性补偿后的时钟读数曲线。根据式(5) 和式(32) 可以得到虚拟全局一致性补偿后的时钟读数曲线。由于现实中节点的初始时刻真实时钟偏斜和偏移都是未知的,但是偏斜和偏移肯定是存在一个值的,因此仿真实验中在某区间任意随机取值用于模拟初始时刻节点的真实时钟偏斜和偏移,再结合式(5) 便可以模拟出真实时钟读数曲线。为了直观地对比分析三种时钟同步算法的性能,通过仿真实验得到图 4~6。
|
图 4 异步与邻居一致性补偿实现时钟同步对比 Figure 4 Comparison of asynchronous consensus-based method and neighbour consistency compensation method for achieving clock synchronization |
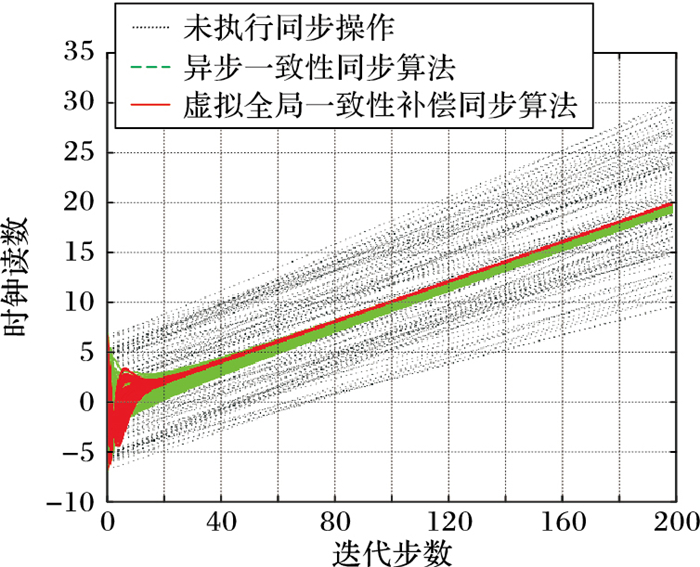
|
图 5 异步与虚拟全局一致性补偿实现时钟同步对比 Figure 5 Comparison of asynchronous consensus-based method and virtual global consistency compensation method for achieving clock synchronization |
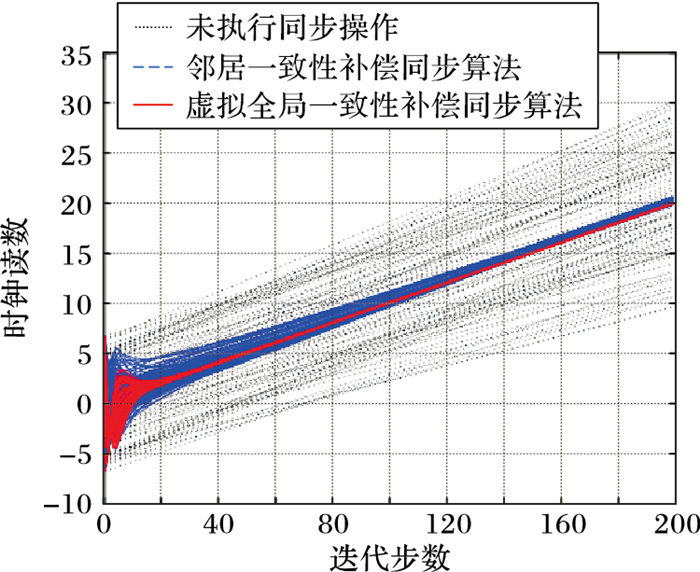
|
图 6 两种一致性补偿方式实现时钟同步的对比 Figure 6 Comparison of two consistency compensation methods for achieving clock synchronization |
所谓时钟同步,从直观的角度看即节点的时钟读数相等,图 4~6中体现为时钟读数曲线的“靠拢”。事实上,具有较高时钟同步精度的网络,网络中的节点时钟读数曲线越靠拢、越接近。对比分析图 4~6可以明显发现,虚拟全局一致性补偿方式的DKFCC同步算法使得100个节点的时钟读数曲线在算法迭代步数为20时就非常“靠拢”,而AC算法和邻居一致性补偿方式的同步算法需要将近140次迭代。
为了定量分析两种一致性补偿方式实现时钟同步的精度和收敛速度等性能,本文采用同步根均方误差(Synchronization Root Average Mean Squared Error, SRAMSE)来对这三种同步算法的性能进行评估,定义SRAMSE如下:
| $ \begin{array}{l} SRAMSE\left( {c({l_k})} \right) = \\ \;\;\;\;\;\sqrt {\frac{1}{{N - 1}}\sum\limits_{i = 2}^N {{{\left( {{c_i}({l_k}) - \frac{1}{{N - 1}}\sum\limits_{i = 2}^N {{c_i}({l_k})} } \right)}^2}} } \end{array} $ |
其中:c(lk)表示节点在时刻lk的读数,
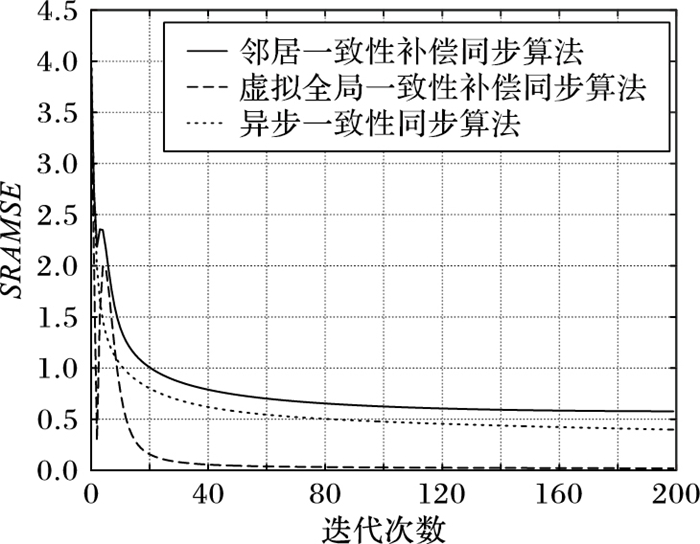
|
图 7 三种时钟同步算法的同步根均方误差对比 Figure 7 SRAMSE comparison of three kinds of clock synchronization algorithms |
从图 7可以看出,随着迭代次数的增加,在DKF算法对时钟参数滤波估计准确后,采用虚拟全局一致性补偿方式的DKFCC同步算法在迭代次数为10以后,比另外两种同步算法的同步根均方误差值要小,因此同步精度更高。通过Matlab计算最后5次迭代的三种同步算法SRAMSE的平均值数据,得到AC算法、邻居一致性方式的DKFCC同步算法、虚拟全局一致性方式的DKFCC同步算法的SRAMSE平均值分别为0.43、0.56和0.02,分析该数据发现采用虚拟全局一致性方式的DKFCC同步算法比AC算法的SRAMSE平均值降低了约95%,因此具有较高的同步精度。为了从量化的角度分析三种同步算法收敛后的同步根均方误差,本文考虑定义一个随机过程。从图 7可以看出,N步以后,同步根均方误差收敛于一个较小的范围δ以内,因此定义同步根均方误差的收敛均值如下:
| $ \overline {SRAMSE} \left( {c({l_k})} \right) = \frac{1}{{L - N + 1}}\sum\limits_{{l_k}{\rm{ = }}N}^L {SRAMSE\left( {c({l_k})} \right)} $ |
其中:L表示一次抽样过程中时钟同步迭代的总次数,也即时钟同步的同步次数。因此,
图 8所示为三种时钟同步算法的同步根均方误差收敛均值对比。图 8表示M=100次随机过程
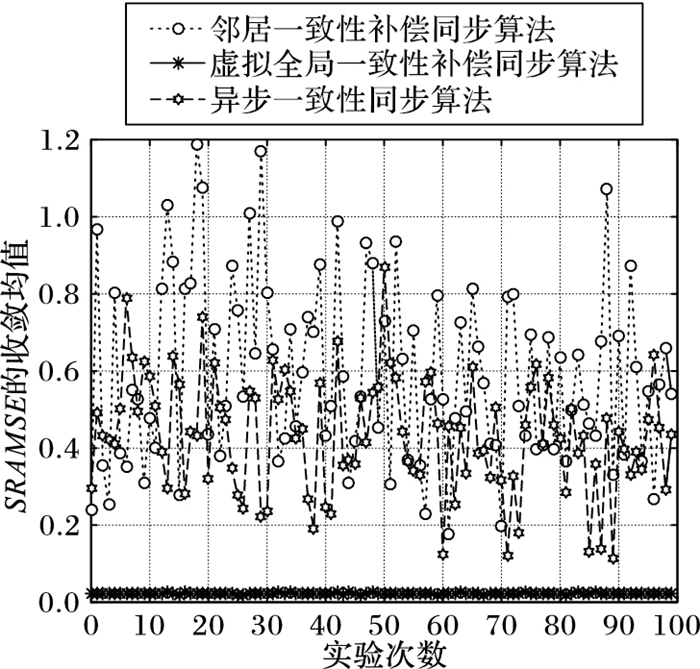
|
图 8 同步根均方误差收敛均值的对比 Figure 8 Comparison of convergence mean of SRAMSE |
通过分析图 7和图 8的实验结果可知,采用虚拟全局一致性方式的DKFCC同步算法具有较高的同步精度,而邻居一致性补偿方式的DKFCC同步算法的同步精度要比AC算法略低,但是从节能角度来讲,两种方式的DKFCC同步算法都是从不易获得的时钟参数层面进行补偿,相比仅仅实现时钟读数补偿控制方式的AC算法更节能。同时,通过对两种方式的DKFCC同步算法一致性补偿项分析,可以发现邻居一致性补偿需要参考不同的邻居节点时钟参数的最优估计值,而虚拟全局一致补偿只需要知道自己时钟参数的最优估计值就可以,因此邻居一致性补偿方式的DKFCC同步算法对网络规模不具有扩展性,适用于小规模的WSN,例如智能家庭网络;而虚拟全局一致性补偿方式的DKFCC同步算法对网络规模具有扩展性,相比AC算法,SRAMSE值不会随着网络规模扩大而显著增大,因此它适用于大规模的WSN,比如大面积森林环境监测的WSN。
5 结语为了尽量降低时钟同步操作的频率,本文考虑对时钟偏斜和偏移两个参数分别进行补偿控制,而针对真实时钟偏斜和偏移两个参数不易获得的问题,本文利用双向信息交换机制及DKF算法实现时钟偏斜和偏移两个参数的最优估计,基于该最优估计值提出了两种一致性补偿方式的DKFCC同步算法,其中虚拟全局一致性补偿方式的DKFCC同步算法具有网络规模扩张性,具有较高的同步精度。在未来的研究中,将分析双向信息交换过程丢包现象对DKF算法估计精度以及同步精度的影响;另外,根据网络的特性和同步的目标,设计不同的补偿策略或控制策略以满足不同WSN应用对时钟同步精度以及节能的要求。
| [1] | 王慧强, 温秀秀, 林俊宇, 等. 基于移动模型的水下传感器网络时间同步算法[J]. 通信学报, 2016, 37(1): 2016001. (WANG H Q, WEN X X, LIN J Y, et al. Time synchronization algorithm based on mobility model for underwater sensor networks[J]. Journal on Communications, 2016, 37(1): 2016001.) |
| [2] | 曾培, 陈伟. 基于控制角度的无线传感器网络时钟同步优化算法[J]. 计算机应用, 2015, 35(10): 2852-2857. (ZENG P, CHEN W. Improved algorithm of time synchronization based on control perspective of wireless sensor network[J]. Journal of Computer Applications, 2015, 35(10): 2852-2857.) |
| [3] | 蒋智鹰, 陈勇, 胡冰, 等. 无线传感器网络时间同步算法研究[J]. 计算机工程与应用, 2017, 53(1): 1-8. (JIANG Z Y, CHEN Y, HU B, et al. Research on time synchronization algorithm for wireless sensor networks[J]. Computer Engineering and Applications, 2017, 53(1): 1-8.) |
| [4] | WU Y-C, CHAUDHARI Q, SERPEDIN E. Clock synchronization of wireless sensor networks[J]. IEEE Signal Processing Magazine, 2011, 28(1): 124-138. DOI:10.1109/MSP.2010.938757 |
| [5] | LIAO C, BAROOAH P. DiSync:Accurate distributed clock synchronization in mobile Ad-Hoc networks from noisy difference measurements[C]//ACC 2013:Proceedings of American Control Conference. Piscataway, NJ:IEEE, 2013:3332-3337. |
| [6] | 李文锋, 王汝传, 孙力娟. 基于RBS的无线传感器网络时间同步算法[J]. 通信学报, 2008, 29(6): 82-86. (LI W F, WANG R C, SUN L J. Proved wireless sensor networks time synchronization algorithm based on RBS[J]. Journal on Communications, 2008, 29(6): 82-86.) |
| [7] | GANERIWAL S, KUMAR R, SRIVASTAVA M B. Timing-sync protocol for sensor networks[C]//SenSys' 03:Proceedings of the 1st International Conference on Embedded Networked Sensor Systems. New York:ACM, 2003:138-149. |
| [8] | MARÓTI M, KUSY B, SIMON G, et al. The flooding time synchronization protocol[C]//SenSys' 04:Proceedings of the 2nd International Conference on Embedded Networked Sensor Systems. New York:ACM, 2004:39-49. |
| [9] | VAN GREUNEN J, RABAEY J. Lightweight time synchronization for sensor networks[C]//WSNA' 03:Proceedings of the 2nd ACM International Conference on Wireless Sensor Networks and Applications. New York:ACM, 2003:11-19. |
| [10] | 陶志勇, 胡明. 基于等级层次结构的TPSN算法改进[J]. 传感技术学报, 2012, 25(5): 691-695. (TAO Z Y, HU M. Improvement based on the hierarchical levels structure of the TPSN algorithm[J]. Chinese Journal of Sensors and Actuators, 2012, 25(5): 691-695.) |
| [11] | 姜帆, 郑霖. 无线传感器网络TPSN-RBS联合时间同步算法[J]. 传感器与微系统, 2016, 35(1): 149-152. (JIANG F, ZHENG L. TPSN-RBS joint time synchronization algorithm for wireless sensor networks[J]. Transducer and Microsystem Technologies, 2016, 35(1): 149-152.) |
| [12] | SICHITIU M L, VEERARITTIPHAN C. Simple, accurate time synchronization for wireless sensor networks[C]//WCNC 2003:Proceedings of the 2003 IEEE Wireless Communications and Networking. Piscataway, NJ:IEEE, 2003:1266-1273. |
| [13] | WERNER-ALLEN G, TEWARI G, PATEL A, et al. Firefly-inspired sensor network synchronicity with realistic radio effects[C]//SenSys' 05:Proceedings of the 3rd International Conference on Embedded Networked Sensor Systems. New York:ACM, 2005:142-153. |
| [14] | SOLIS R, BORKAR V S, KUMAR P R. A new distributed time synchronization protocol for multihop wireless networks[C]//Proceedings of the 45th IEEE Conference on Decision and Control. Piscataway, NJ:IEEE, 2006:2734-2739. |
| [15] | SCHENATO L, FIORENTIN F. Average TimeSynch:a consensus-based protocol for clock synchronization in wireless sensor networks[J]. Automatica, 2011, 47(9): 1878-1886. DOI:10.1016/j.automatica.2011.06.012 |
| [16] | MAGGS M K, O'KEEFE S G, THIEL D V. Consensus clock synchronization for wireless sensor networks[J]. IEEE Sensors Journal, 2012, 12(6): 2269-2277. DOI:10.1109/JSEN.2011.2182045 |
| [17] | AHMED S, XIAO F, CHEN T. Asynchronous consensus-based time synchronisation in wireless sensor networks using unreliable communication links[J]. IET Control Theory & Applications, 2014, 8(12): 1083-1090. |
| [18] | HUA MIAO MIAO, DONG LI DA. A closed-loop adjusting strategy for wireless HART time synchronization[C]//Proceedings of 201111th International Symposium on Communications and Information Technologies. Piscataway, NJ:IEEE, 2011:131-135. |
| [19] | SIMEONE O, SPAGNOLINI U, BAR-NESS Y, et al. Distributed synchronization in wireless networks[J]. IEEE Signal Processing Magazine, 2008, 25(5): 81-97. DOI:10.1109/MSP.2008.926661 |
| [20] | DEMIR A, MEHROTRA A, ROYCHOWDHURY J. Phase noise in oscillators:a unifying theory and numerical methods for characterization[J]. IEEE Transactions on Circuits and Systems Ⅰ:Fundamental Theory and Applications, 2000, 47(5): 655-674. DOI:10.1109/81.847872 |
| [21] | ELSON J, GIROD L, ESTRIN D. Fine-grained network time synchronization using reference broadcasts[J]. ACM SIGOPS Operating Systems Review-OSDI' 02:Proceedings of the 5th Symposium on Operating Systems Design and Implementation, 2002, 36(SI): 147-163. |
| [22] | LUO B, WU Y C. Distributed clock parameters tracking in wireless sensor network[J]. IEEE Transactions on Wireless Communications, 2013, 12(12): 6464-6475. DOI:10.1109/TWC.2013.103013.130811 |
| [23] | LIN L, MA S, MA M. A group neighborhood average clock synchronization protocol for wireless sensor networks[J]. Sensors, 2014, 14(8): 14744-64. DOI:10.3390/s140814744 |



 ,
,