0 引言

路径规划是无人艇自主导航的关键技术之一，路径规划已在移动机器人技术中得到广泛研究。路径规划是指在有障碍物的工作环境中，利用一定的算法或某些优化准则使移动机器人能从起始点绕开障碍物到达目标点，在此过程中尽量优化机器人运动轨迹^[1-3]。

路径规划算法已得到广泛关注和研究，由于真实环境的复杂性，及路径规划的自身困难，至今路径规划仍然是移动机器人自主导航的研究热点之一。现已提出多种路径规划算法。A^*算法是一种典型的启发式搜索算法^[4]，最早由Nilsson等^[5]提出。A^*算法在路径规划研究中得到广泛应用和发展，考虑真实环境中各种因素的影响，在评价函数中加入描述真实环境的各种参量。例如吴天羿等^[6]考虑坡度及路面粗糙度等因素的影响对越野车路径规划研究；Guinness等^[7]研究了浮冰水域船舶路径规划问题。

考虑动力学和运动学约束时，路径规划将朝向运动规划发展。运动规划的最简单形式是一个纯几何问题，给定机器人形状和障碍物分布，计算其无碰路径^[8]。运动规划中需要考虑无人艇的运动学约束，如旋回半径、无人艇的操纵方程等。运动规划已经不仅仅是在位置坐标(地图)上进行路径规划，而是在包含运动状态的位姿空间中搜索合适的运动轨迹及其运动状态。运动规划常用的算法是基于随机采样的路图或者树状图算法，如随机路图法(Probabilistic Roadmap Method, PRM)^[8-9]、快速搜索随机树(Rapidly-exploring Random Tree, RRT)^[10-11]。但这些基于随机采样的方法已被证明是概率完备但结果不最优的。Dubins路径采用圆弧—直线—圆弧的形式构造轨迹路线，其中圆弧部分可以作为无人艇转向形成的旋回圈，直线部分可以作为无人艇直行的轨迹，因此本文选取Dubins路径作为无人艇的基本路径，进行路径规划。

基于Dubins路径的路径规划方法的理论依据是已经证明了满足曲率限制的最短曲线是圆弧与直线构成的^[12]。在此基础上，研究者尝试通过设计各种曲线连接构成满足运动约束的规划路径，如文献[12]中设计的回旋曲线。Dubins路径的计算常用的方法是通过建立方程组进行求解，如文献[13]中通过角度和位置变化等约束建立方程组进行计算。本文设计一种利用纯几何的方法进行Dubins路径的计算，该方法直接易行，没有出现解方程组的运算。

1 问题描述

无人艇状态矢量s=(x, y, cos θ, sin θ, v)^T，其中包含无人艇位置坐标P(x, y)和速度方向向量v_dire=(cos θ, sin θ)^T及速度大小v。无人艇运动规划可以描述成计算由起始状态矢量s_start至目标状态矢量s_target的满足无人艇运动约束的无碰最短路径。

无人艇以一定速度转向时，转向半径需要大于在此速度下的极小半径。基于Dubins路径的路径规划方法可以有效解决此问题。Dubins路径是由起始转向圆弧与目标转向圆弧通过公共切线相连构成，其中，起始转向圆弧半径R_vstart和目标转向圆弧半径R_vtarget需要满足无人艇运动约束，因此，在获取无人艇起始状态矢量s_start和目标状态矢量s_target后，计算Dubins路径是路径规划的一个核心问题。

下面通过理论分析设计一种完全利用几何方法计算Dubins路径的运动规划算法。

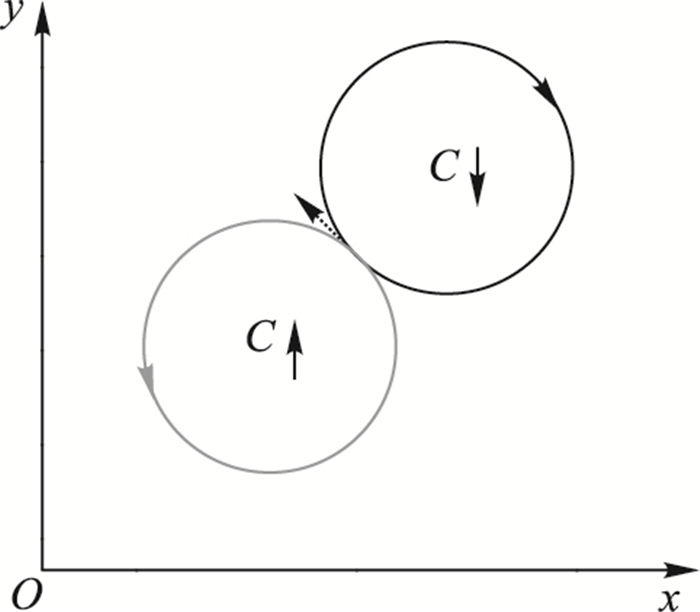
2 理论分析 2.1 转向圆计算

无人艇状态矢量s=(x, y, cos θ, sin θ, v)^T以半径R_v转向，其转向圆可以有两种选择。按右手法则，逆时针转向标记为↑，顺时针转向记为↓。

由于${\overrightarrow {\mathit{\boldsymbol{CP}}} _{{\rm{dire}}}} \bot {\mathit{\boldsymbol{v}}_{{\rm{dire}}}}$，圆心C坐标计算式如下：

$ {\overrightarrow {\mathit{\boldsymbol{CP}}} _{{\rm{dire}}}} = \pm {{\rm{(}} - {\rm{sin}}\theta {\rm{, cos}}\theta {\rm{)}}^{\rm{T}}} $

(1)

$ \overrightarrow {\mathit{\boldsymbol{OC}}} = \overrightarrow {\mathit{\boldsymbol{OP}}} - {R_v}{\overrightarrow {\mathit{\boldsymbol{CP}}} _{{\rm{dire}}}} $

(2)

若${\overrightarrow {\mathit{\boldsymbol{CP}}} _{{\rm{dire}}}} \times {\mathit{\boldsymbol{v}}_{{\rm{dire}}}}$ =(0, 0, 1)^T，则记为圆C_↑，反之记为圆C_↓，如图 1所示。无人艇由起始状态调整至目标状态所经过的路径是经计算选择的一个起始转向圆与一个目标转向圆之间通过合适的公切线相连得到的有向曲线，此有向曲线即是一条Dubins路径。

2.2 公切线计算

两个外离圆之间的公切线有4条，分别为两条外公切线和两条内公切线，但可以按方向连接两个外离有向圆的公切线仅有1条，且若两有向圆的转向相同，连接两圆的公切线是一条外公切线；若两有向圆的转向相反，连接两圆的公切线是一条内公切线。此结论可利用下面定理证明。

定理1  平面上不同两点A、B，且点C、D不在直线AB上：1) 若点C、D在直线AB同侧，则$\overrightarrow {\mathit{\boldsymbol{CA}}} \times \overrightarrow {\mathit{\boldsymbol{AB}}} $与$\overrightarrow {\mathit{\boldsymbol{DB}}} \times \overrightarrow {\mathit{\boldsymbol{AB}}} $所得两矢量同向；2) 若点C、D在直线AB异侧，则$\overrightarrow {\mathit{\boldsymbol{CA}}} \times \overrightarrow {\mathit{\boldsymbol{AB}}} $与$\overrightarrow {\mathit{\boldsymbol{DB}}} \times \overrightarrow {\mathit{\boldsymbol{AB}}} $所得两矢量反向。

外离两圆的Dubins路径计算方法如下：

1) 两圆同向，两圆通过外公切线相连。

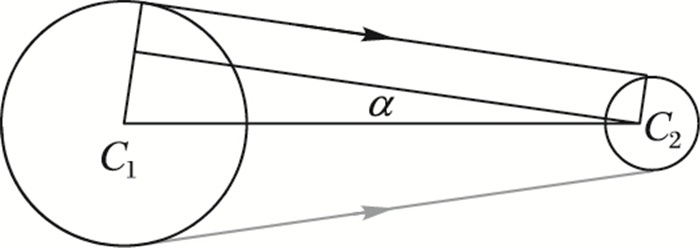
如图 2所示，连心线C₁C₂与外切线的夹角α按式(3) 求得：

$ \alpha {\rm{ = arcsin}}\left( {|{r_1} - {r_2}|/|{C_1}{C_2}|} \right) $

(3)

若圆C₁与圆C₂的转向方向为↑, 则切线为图 2中灰色直线所示，两切点按下面公式计算：

$ {\mathit{\boldsymbol{e}}_R} = {\rm{rotation(}}{\mathit{\boldsymbol{e}}_{\overrightarrow {{\mathit{\boldsymbol{C}}_1}{\mathit{\boldsymbol{C}}_2}} }}{\rm{, }}\alpha - \pi /2{\rm{)}} $

(4)

$ 切点1:\overrightarrow {\mathit{\boldsymbol{O}}{\mathit{\boldsymbol{C}}_1}} + {r_1}{\mathit{\boldsymbol{e}}_R} $

(5)

$ 切点2:\overrightarrow {\mathit{\boldsymbol{O}}{\mathit{\boldsymbol{C}}_2}} + {r_2}{\mathit{\boldsymbol{e}}_R} $

(6)

其中，${{\mathit{\boldsymbol{e}}}_{\overrightarrow{{{C}_{1}}{{C}_{2}}}}}$是矢量$\overrightarrow{{{\mathit{\boldsymbol{C}}}_{1}}{{\mathit{\boldsymbol{C}}}_{2}}}$的单位矢量；函数rotation是矢量旋转函数，按式(7) 计算，即逆时针旋转为正。

$ {\rm{rotation}}\left( {\left[{\begin{array}{*{20}{c}} x\\ y \end{array}} \right], \theta } \right) = \left[{\begin{array}{*{20}{c}} {{\rm{cos}}\theta }&{-{\rm{sin}}\theta }\\ {{\rm{sin}}\theta }&{{\rm{cos}}\theta } \end{array}} \right]\left[{\begin{array}{*{20}{c}} x\\ y \end{array}} \right] $

(7)

若圆C₁与圆C₂的转向方向为↓则切线为图 2中黑色直线所示，由式(8) 计算得到e_R后，两切点仍按式(5)~(6) 计算。

$ {\mathit{\boldsymbol{e}}_R} = {\rm{rotation(}}{\mathit{\boldsymbol{e}}_{\overrightarrow {{\mathit{\boldsymbol{C}}_1}{\mathit{\boldsymbol{C}}_2}} }}{\rm{, \mathsf{ π} }}/2 - \alpha {\rm{)}} $

(8)

2) 两圆异向，两圆通过内公切线相连。

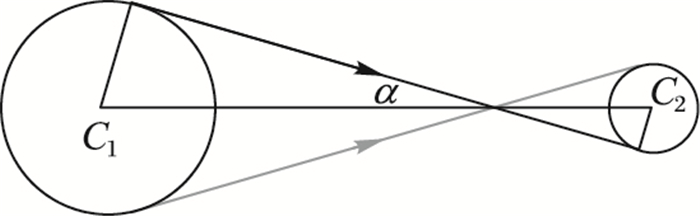
如图 3所示，连心线C₁C₂与内切线的夹角α按式(9) 求得：

$ \alpha {\rm{ = arcsin}}\left( {\left( {{r_1} + {r_2}} \right)/|{C_1}{C_2}|} \right) $

(9)

若圆C₁的转向为↑而圆C₂的转向方向为↓, 则切线为图 3中灰色直线所示，两切点按下面公式计算:

$ {\mathit{\boldsymbol{e}}_R} = {\rm{rotation(}}{\mathit{\boldsymbol{e}}_{\overrightarrow {{\mathit{\boldsymbol{C}}_1}{\mathit{\boldsymbol{C}}_2}} }}{\rm{, }}\alpha - \pi /2{\rm{)}} $

(10)

$ 切点1:\overrightarrow {\mathit{\boldsymbol{O}}{\mathit{\boldsymbol{C}}_1}} + {r_1}{\mathit{\boldsymbol{e}}_R} $

(11)

$ 切点2:\overrightarrow {\mathit{\boldsymbol{O}}{\mathit{\boldsymbol{C}}_2}} + {r_2}{\mathit{\boldsymbol{e}}_R} $

(12)

其中，${{\mathit{\boldsymbol{e}}}_{\overrightarrow{{{C}_{1}}{{C}_{2}}}}}$是矢量$\overrightarrow{{{\mathit{\boldsymbol{C}}}_{1}}{{\mathit{\boldsymbol{C}}}_{2}}}$的单位矢量；函数rotation是矢量旋转函数。

若圆C₁的转向为↓而圆C₂的转向方向为↑，则切线为图 3中黑色直线所示，由式(13) 计算得到e_R后，两切点仍按式(11)~(12) 计算。

$ {\mathit{\boldsymbol{e}}_R} = {\rm{rotation(}}{\mathit{\boldsymbol{e}}_{\overrightarrow {{\mathit{\boldsymbol{C}}_1}{\mathit{\boldsymbol{C}}_2}} }}{\rm{, }}\pi /2 - \alpha $

(13)

两圆的位置关系分为外离、外切、相交、内切、内含五种类型。外切和相交时，外公切线依然存有两条，与外离时一样，此时若两圆的转向相同，Dubins路径计算方法与外离时一致。内切时，两条外公切线退化成一条，同向圆间的Dubins路径中公切线部分退化成两圆的切点。内含时，已不存在外公切线。对于内公切线，两圆外切时已经退化成一条，反向两圆间的Dubins路径中内公切线部分退化成两圆的切点。相交、内切、内含已不存在内公切线。上述结论可总结为表 1。

由以上分析可得，Dubins路径的计算步骤可归纳为以下3步：

1) 分别计算起始状态和目标状态的转向圆，各↑↓两个；

2) 分别选择起始转向圆与目标转向圆，按上面计算方法依次计算连接两转向圆的公切线。接着计算路径长度，由起始点按方向经起始转向圆至公切线切点，然后沿着公切线至目标转向圆切点，按方向经目标转向圆至目标点的路径长度。

3) 在计算得到的Dubins路径(共4条或少于4条)中，选择最短路径并输出。

根据以上分析得到的结论，可以设计下面的Dubins路径计算算法。

3 算法设计 3.1 数据结构

由理论分析，根据问题特点，定义以下三种结构体数据类型：1) 无人艇状态数据类型；2) 圆数据类型；3) 路径数据类型。

这样算法中主要包含：起始状态、目标状态两个状态数据；两个旋转方向相反的起始圆和两个旋转方向相反的目标圆共4个圆数组数据；一个存放4条Dubins路径点的路径数据。

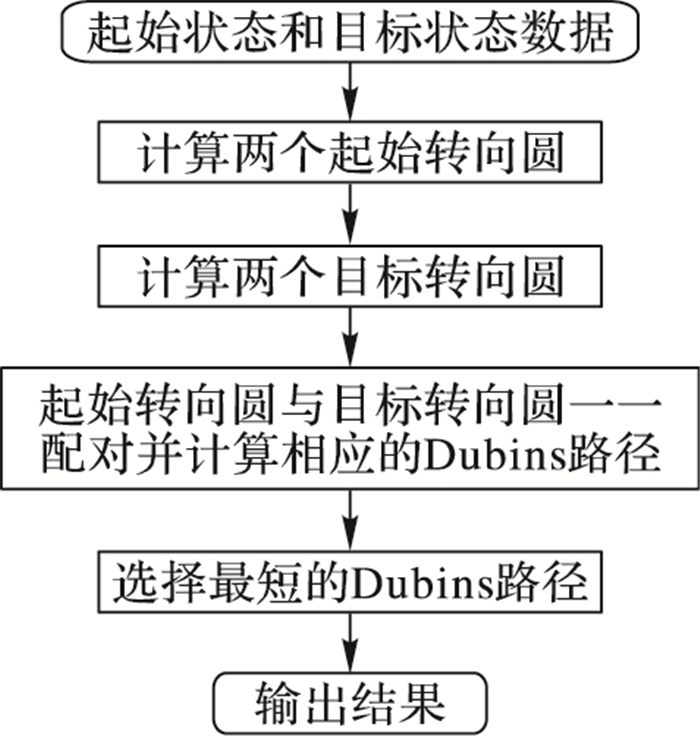
3.2 算法流程

本文提出的基于Dubins路径的路径规划算法流程如图 4所示。

本文提出的计算Dubins路径的算法完全使用几何方法求解，算法简易实用。下面通过仿真实验验证此算法的有效性，仿真实验中设计5个算例，其中4个分别验证外离、外切、内切、内含四种圆的位置关系的Dubins路径计算，最后给出一个无人艇运动状态调整的仿真实验。

4 仿真实验

仿真实验分为两部分：一部分是验证本文所提算法可以计算两圆各种位置关系下的Dubins路径；另一部分是使用Dubins路径完成无人艇运动状态调整。

4.1 Dubins路径计算

本节使用4个算例，如表 2所示，分别验证外离、外切、内切、内含四种圆的位置关系的Dubins路径计算。

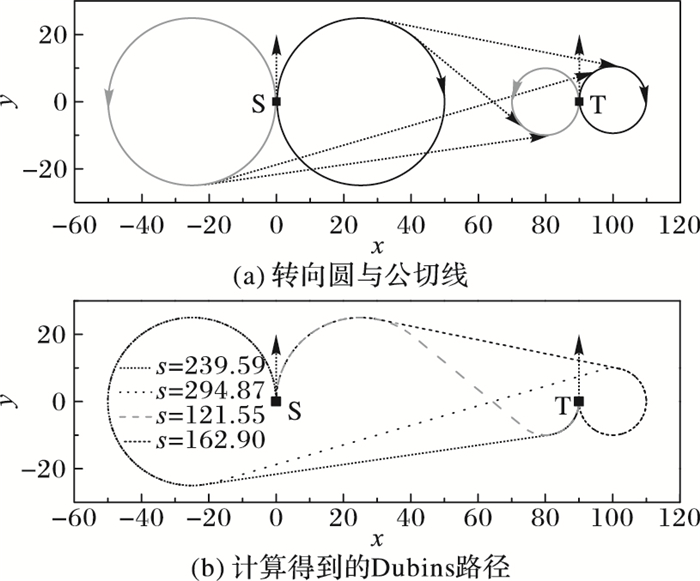
算例1数值实验结果如图 5所示，此算例中起始转向圆与目标转向圆的位置关系均是外离，由起始状态至目标状态的Dubins路径存有4条。图 5(a)给出由起始转向圆连接至目标转向圆间的公切线，图 5(b)给出4条Dubins路径，其中灰色曲线长度为s=121.55，是最短的一条路径，即最终输出的规划路径。

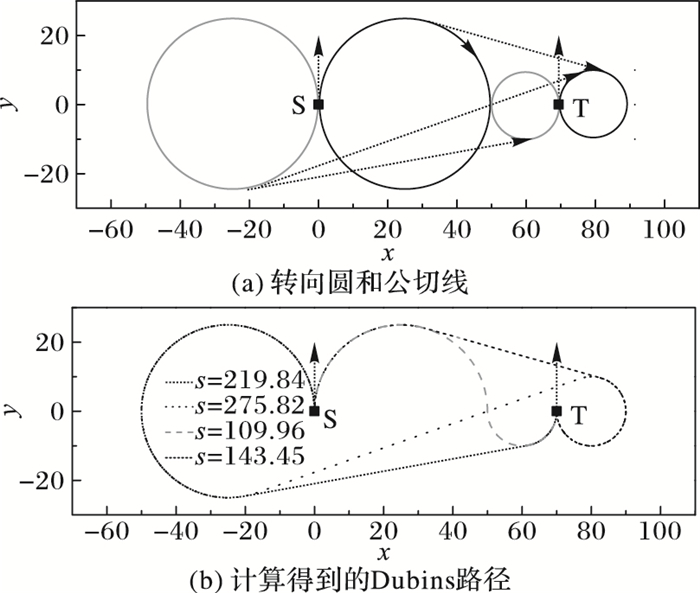
算例2数值实验结果如图 6所示，此算例中起始转向圆与目标转向圆的位置关系有两种：外离和外切。圆C_S↑与圆C_T↓之间的位置关系是外切，Dubins路径中内公切线退化成切点，这样由起始状态至目标状态的Dubins路径仍存有4条，如图 6(b)所示，其中灰色曲线长度s=109.96，为最短的一条，即最终输出的规划路径。

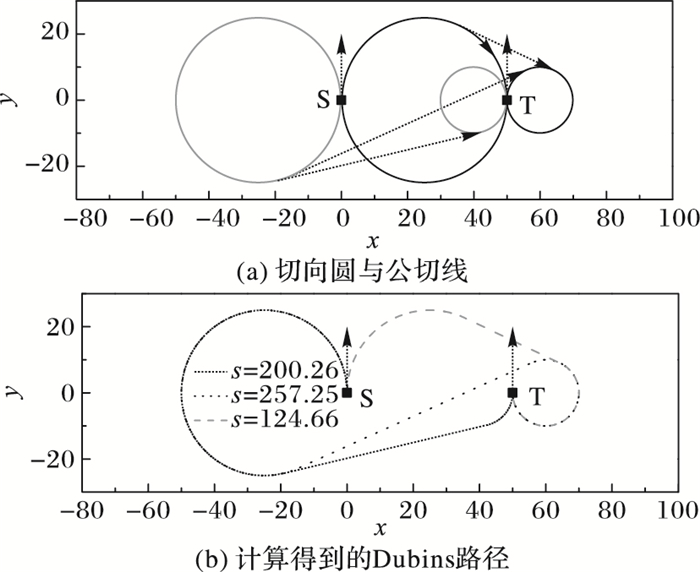
算例3数值实验结果如图 7所示，此算例中起始转向圆与目标转向圆的位置关系有三种：外离、外切及内切。圆C_S↑与圆C_T↓之间的位置关系是内切，圆C_S↑与圆C_T↓之间不存在内公切线，即此两圆之间不存有Dubins路径。圆C_S↑与圆C_T↑之间的位置关系是外切，两圆通过外公切线连接成Dubins路径，如图 7(a)所示。这样由起始状态至目标状态的Dubins路径仅存有3条，如图 7(b)所示，其中灰色曲线长度s=124.66，为最短的一条，即最终输出的规划路径。

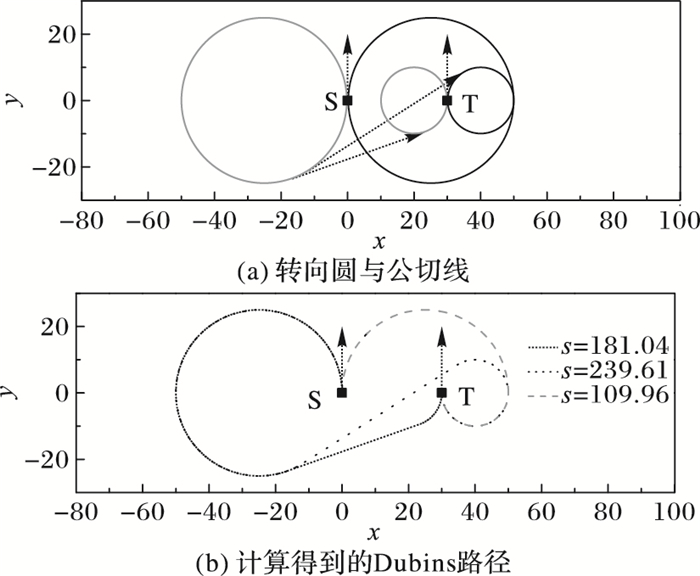
算例4数值实验结果如图 8所示，此算例中起始转向圆与目标转向圆的位置关系有三种：外离、内切及内含。圆C_S↑与圆C_T↓之间的位置关系是内含，圆C_S↑与圆C_T↓不存有Dubins路径。圆C_S↑与圆C_T↑之间的位置关系是内切，

两圆之间的外公切线退化成切点，但仍存有Dubins路径。这样由起始状态至目标状态的Dubins路径仅存有3条，如图 8(b)所示，其中灰色曲线长度s=109.96，为最短的一条，即最终输出的规划路径。

通过4组算例的数值实验可以看出，本文算法对两圆各种位置关系的Dubins路径计算均能得到正确的结果，这充分验证了该算法的有效性。该算法中完全使用几何方法进行计算，计算量较小，适合应用于在线路径规划。

4.2 无人艇运动状态调整

本节是仿真实验中的第5个算例，使用Dubins路径作无人艇运动状态调整。无人艇运动响应模型为：

$ \psi ''{\rm{ + }}\psi '/T{\rm{ = }}K\delta /T $

(14)

其中：ψ为船艏向; δ为舵角。数值实验中取K=0.285，T=0.275。

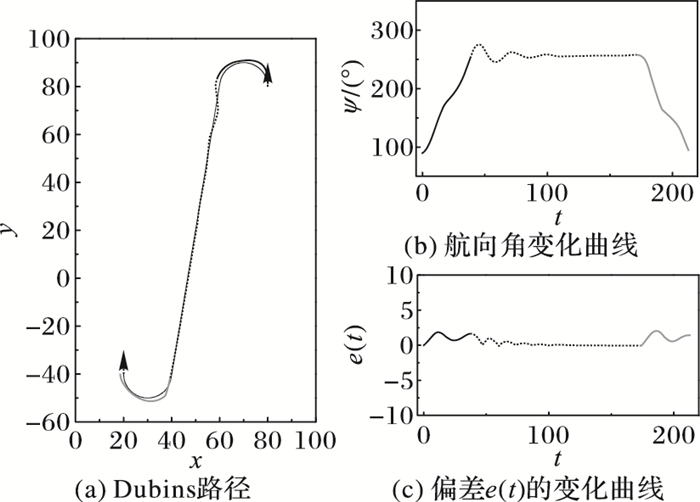
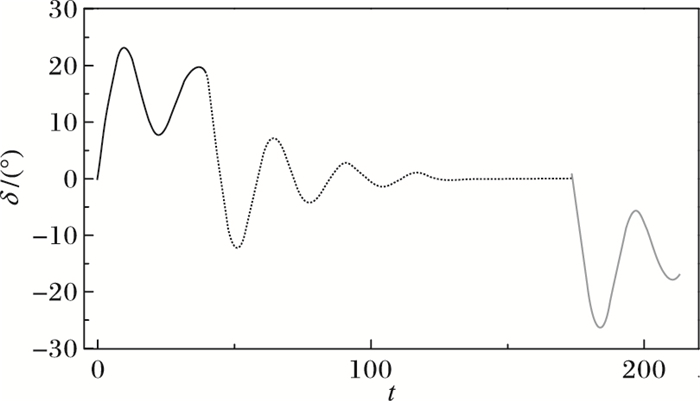
航迹跟踪使用比例-积分-微分(Proportion-Integration-Differentiation, PID)控制，定义偏差e(t)为船当前位置与预设航迹之间的距离。仿真结果如图 9所示，图中分别给出无人船航迹与预设航迹对比图及航向角、偏差函数e(t)的变化曲线。图 10给出仿真实验中的舵角操纵过程。仿真结果表明，无人艇按照预设航迹进行航行，航向角的变化较平滑没有出现过多的超调。航迹偏差维持在2.5m范围内，舵角的操纵在左右30°舵以内，操舵过程也较合理。

5 结语

本文提出一种基于纯粹几何理论的Dubins路径计算方法。对于Dubins路径计算可能出现的各种情况，该方法均能够进行计算。仿真结果表明所提方法的Dubins路径计算直接有效，基于Dubins路径的无人艇运动规划算法用于无人艇的运动状态调整是可行的。接下来将利用文中所提算法对无人艇自主路径规划和自主靠泊等方向作进一步的研究。