0 引言

编码作为遗传算法(Genetic Algorithm, GA)设计中的首要环节，决定着遗传算法的精度和效率，是算法能否解决问题的前提。随着GA研究和应用的日益深入，编码方法也在不断地改进，目前已有多种编码方式，常用的有二进制编码、实数编码、矩阵编码、树型编码和量子编码等^[1-3]。自Holland^[4]提出GA以来，二进制编码成为应用最早和最广的编码方式，具有简单、符合最小符号集编码原则和模式定理的优点，但对于一些多维、高精度连续函数优化问题，二进编码又存在不能直接反映问题的固有结构和个体编码长度大等不足。针对二进制编码的缺陷，Michalewicz等^[5]提出了实数编码，实数编码精度高，适合复杂大空间搜索，对多参数连续函数优化问题具有更好的性能。矩阵编码尤其适用于求解大规模复杂问题、高维数值优化问题和多目标优化问题，例如文献[6]和[7]分别采用矩阵编码的遗传算法实现试题库自动组卷和模拟集成电路模块布局。树型编码也是一种有效的编码方式，主要适用于求解能用树或图表示的优化问题，如Web服务选择^[8]、配电网优化规划^[9]等。量子编码是将染色体用量子的态矢量表示，使算法能够在较小的种群规模下求得最优解，被广泛应用于组合优化、信号处理和自动控制等方面^[10]。

由此可见，不同编码方式有其自身的优缺点和适用场合，事实上，关于该如何设计编码策略长期以来存在许多争议。传统的观点认为，进化的本质主要在于交叉而非变异，从最大化隐并行性的角度出发，建议采用最小字符集编码，例如二进制编码，以便获得尽可能多的模式^[11]，但该原则未能得到一致认同，一方面由于对于相当多的搜索和优化问题，二进制编码不符合问题本身的结构特点，实现起来并不方便^[12]；另一方面，有的研究结果也表明，最小字符集的编码原则并不一定合理。例如，Antonisse等^[13]发现，即使是为了最大化算法的隐并行性，只要从不同的角度解释无关符的作用，就可得到完全相反的结论，即应采用大的编码字符集而非小字符集。而以Fogel等^[14]为代表的研究者对进化的本质持相反的观点，认为其主要在于变异而非交叉，因而置疑隐并行性的意义和最小字符集的编码原则。Fogel等^[15]指出，仅需满足一些一般性的假设条件，即可对任意两种编码字符集设计出功能等效的两类进化算法。此外，即使不考虑最小字符原则，对应该采用二进制编码还是格雷码同样存在争议^[16]。这些争议以及近年来对NFL(No Free Lunch)定理^[17]等关于优化算法的一般性定理的研究^[18-19]表明：通用又高效的编码方式是不存在的，不同类型的适应度函数应采用不同的编码。解决编码策略选择问题的一个可行出路是将通用编码方式的研究转为探寻编码与适应度函数特性之间的通用依赖关系。

在前期研究中，为揭示适应度函数的周期性特点与编码元数之间的关联特性，以可展开为分立周期的正弦函数分量线性组合而成的适应度函数为研究对象，采用一阶积木块数量作为编码性能的评价方法，发现对频率为正整数m的整数次幂的正弦函数为基函数线性组合构成的适应度函数，采用m元整数编码时性能优于其他编码^[20-21]。

然而，一阶积木块是以模式定理为依据的，即认为较优的模式在遗传算法的迭代过程中将按指数规律增长，如果在多个基因座上存在一阶积木块，则在这些基因座上，全局最优串的搜索可以转化为在这些基因座上的并行搜索，故而GA可较快找到较优值，但事实上模式定理在某些情况下不一定成立，GA欺骗、超平面不一致性和同步等现象可能会导致GA向错误的方向搜索^[22]，这时将不能保证积木块数量与优化性能之间的正相关关系。

基于此，本文希望找到一种更合理的编码性能评价方法来进一步验证适应度函数的周期性特点与编码元数之间的关联特性。编码方式影响到GA的很多方面，如积木块数量、连锁^[23]和适应度分布^[24]等，所有这些因素又最终影响到GA进化的难易程度，在其他参数相同的情况下，不同编码下GA进化的难易程度是编码性能最直观的体现。在判断进化算法的难易程度时，运行时间是使用最广泛、最可靠的性能指标^[25-26]，文献[27]指出，逃脱概率(Escape Probability，EP)反映了当前个体进化到更优个体的概率，其大小与期望运行时间成反相关，因此，EP可以有效反映进化算法的难易程度；在EP基础上得到的累积逃脱概率(Accumulated Escape Probability，AEP)实现了进化难易程度数值化，可用于比较不同算法之间的性能。本文提出以AEP作为编码性能的评价指标。

1 研究对象 1.1 适应度函数

选取形如$G\left(x \right){\rm{ = }}\sum\limits_{i = 1}^{{n_B}} {{a_i}\sin (2\pi {m^{i -1}}x + {\varphi _i}) + c} $的适应度函数为研究对象，探讨编码与适应度函数周期之间的关联性；其中n_B, m为正整数，且m>1；a_i≥0，φ_i∈[0, 2π)，c为常数，且G(x)≥0。实际问题的求解精度总是有限的，可将任意待优化问题的定义域以一定精度映射到单变量整数集合，用有限长度的整数或者浮点数为各个体编码，因此可不失一般性限定适应度函数定义域为x∈[0, 1]。

1.2 广义整数编码

常用的二进制编码、十进制编码等均属于线性加权整数编码，现一般性地讨论m进制整数编码。当采用串长为l、编码元数为m的整数编码时，个体x可以表示为$x = \sum\limits_{h = 1}^l {{x_h}{m^{h -l -1}}} $，其中x_h∈{0, 1, …, m－1}，二进制编码和十进制编码分别对应m=2和m=10，当以m=3为编码元数时，$x = \sum\limits_{h = 1}^l {{x_h}{3^{h -l -1}}} $, 其中x_h∈{0, 1, 2}。

对形如G(x)的适应度函数，当单基因座上取值变化时，m元整数编码遗传算法对于搜索空间的搜索呈周期采样的特点，且其采样周期为m^－i[21]。例如，对3进制编码$x = \sum\limits_{h = 1}^4 {{x_h}{3^{h -5}}} $，将最右边基因座记为1，若基因座1、2、3上取值均为0，基因座4上取值由0变到2，可相应得到个体串0000，1000，2000，其对应解码后点的序列为0.000，0.333，0.666，将该过程视为对搜索空间的采样，则采样周期为3^－1。同理，基因座1、2、3上取值的变化对应的采样周期分别为3^－4、3^－3和3^－2。显然，采样周期决定于基因座序号h和编码元数m，因此，适应度函数的周期性和编码之间可建立起明确的关系。本文通过AEP对m元整数编码与其他编码元数的性能进行比较。

2 基于逃脱概率的编码选择方法 2.1 AEP定义

文献[27]在逃脱概率的基础上给出了AEP的定义。给定G(x)，在其搜索空间进行采样，并将所得结果按适应度大小分为L级，得适应度集合为F={f₀, f₁, …, f_L|f₀ < f₁ < … < f_L}，其中，第i级适应度f_i为适应度落于该级的所有采样点的适应度均值。记S_i为处于第i级适应度f_i的个体升至更高适应度级所需的平均变异次数，则逃脱概率P(f_i)定义为：

$ P({f_i}) = 1/{S_i} $

(1)

对于特定的f_i，逃脱概率越大表示越容易获得比当前值更高的适应度。将逃脱概率的定义扩展到适应度集合，P_i表示所有大于等于f_i的适应度的逃脱概率平均值，定义如下：

$ {P_i} = \left( {\sum\limits_{{f_i} \in {C_i}} {P({f_i})} } \right)/\left| {{C_i}} \right| $

(2)

其中C_i={f_j|j>i}。进一步定义适应度概率云(Fitness-Probability Cloud，FPC)为：

$ FPC = \{ ({f_0},{P_0}),({f_1},{P_1}),...,({f_L},{P_L})\} $

(3)

由FPC，得到累积逃脱概率AEP为:

$ AEP = \left( {\sum\limits_{{f_i} \in F} {{P_i}} } \right)/\left| F \right| $

(4)

AEP实际上是集合F中P_i的平均值。由逃脱概率P(f_i)和P_i的定义可知，AEP越大，则表示适应度函数进化难度越小。

2.2 AEP计算方法

根据AEP的定义，本文实现AEP的计算步骤如下：

1) 采样。本文研究对象为连续适应度函数，为了得到离散的适应度集合F={f₀, f₁, …, f_L|f₀ < f₁ < … < f_L}，采用Metropolis-Hastings采样方法^[28]。记φ为φ(x, y)=min(1, y/x)，f(s_k)为个体s_k的适应度，Metropolis-Hastings采样方法得到个体集合{s₁, s₂, …, s_n}的伪代码如下：

开始

随机生成个体s₁

for i:=2 to n do

1) 随机生成个体α;

2) 在(0, 1) 范围等概率随机生成一实数k;

3) 若(k≤φ(f(s_i－1), f(α)))

则s_k:=α

否则跳转至1)

4) i:=i+1

end for

结束

2) 计算每个样本点的适应度函数，按从小到大排序(根据适应度的取值范围，本文中若两个样本点适应度之差小10^－6，则认为这两个样本点适应度位于同一级)。计算所有适应度处于第i级的个体的适应度均值作为f_i)，得到适应度集合F={f₀, f₁, …, f_L|f₀ < f₁ < … < f_L}。

3) 计算每个样本点的逃脱概率。对每个采样点，采用交叉和位变异操作获得若干个邻域点，以大于该样本适应度的邻域点数与总邻域点数的比值近似计算逃脱概率P(f_i)。

由于采样点没有现成的个体与之进行交叉，本文通过以下步骤近似实现交叉操作：按交叉率决定是否需要进行交叉，若是，则随机选择样本个体串上一个点，分别对该点之前的所有位和之后的所有位按一定概率变异，得到两个新的个体，取适应度较大的个体作为交叉的结果。

4) 由式(3) 计算得到FPC。

5) 由式(4) 计算得到AEP。

为了提高准确率，对每个适应度函数样本重复计算AEP 10次，取10次结果的均值作为最终的AEP值。

2.3 不同编码的AEP比较

对$G\left(x \right){\rm{ = }}\sum\limits_{i = 1}^{{n_B}} {{a_i}\sin (2\pi {m^{i -1}}x + {\varphi _i}) + c} $，选择(m=2，n_B=22)、(m=3，n_B=14)、(m=4，n_B=11)、(m=5，n_B=10) 和(m=6，n_B=9) 五组适应度函数，每组适应度函数随机生成系数a_1i~a_5i和φ_1i~φ_5i得到1 000个样本，总共5 000个适应度函数样本，具体如表 1所示。

为了保证适应度非负，取${c_j}{\rm{ = }}\sum\limits_{i = 1}^{{n_B}} {{a_{ji}}} $。每个适应度函数样本分别采用编码元数为m、n和k的整数编码，其中n，k不等于m。当编码元数为m时，简记为base-m编码。为了使不同编码下的计算精度近似一致，base-2、base-3、base-4、base-5、base-6编码的串长分别设置为33，21，17，15，13。

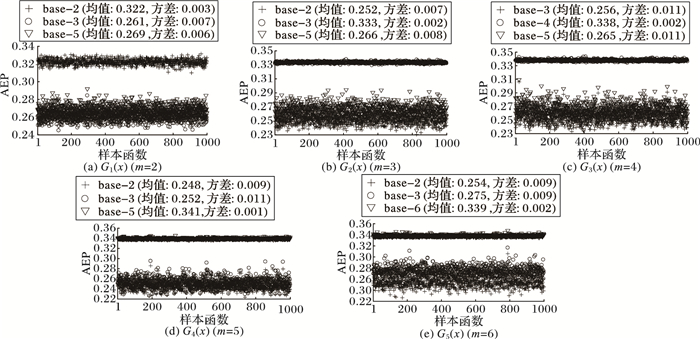
按以上步骤计算AEP，其中样本点数、邻域点数和变异率分别取10 000，50和0.3，每组适应度函数的1 000个函数样本在不同编码下的AEP分别如图 1所示。

由图 1可见，当m=2时，1 000个G₁(x)样本在base-2编码下AEP的均值为0.322，base-3和base-5编码对应AEP均值分别为0.261和0.269，base-2对应的AEP明显大于base-3和base-5编码；当m为3，4，5和6时，分别是base-3，base-4，base-5和base-6编码对应的AEP值最大。图 1的结果表明，对于适应度函数G(x)，base-m编码对应的AEP明显大于另外两种编码，反映了base-m编码的GA进化难度较小，即在相同条件下，base-m编码将期望获得优于另外两种编码的性能。

3 GA仿真

为了验证AEP的结论，采用两种方式对不同编码的性能进行比较，第一种是最终优化结果比较，第二种是群体平均适应度的上升时间比较，适应度的最终优化结果越大、群体适应度均值上升到一定值时所需的进化代数越小则表示编码的性能越好。

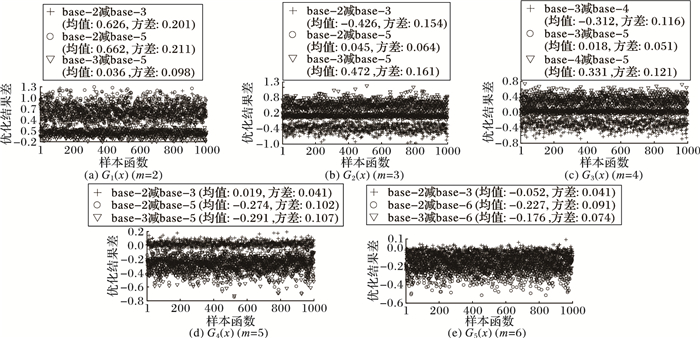
3.1 最终优化结果比较

采用传统GA对表 1中的5组适应度函数共5 000个样本进行优化仿真。仿真参数设置如表 2所示。每个函数重复运算20次，取这20个最优值的均值得到平均适应度作为最终的优化结果。为了方便比较，对不同编码下的优化结果取差值。5组函数在不同编码下的优化结果差分别如图 2所示。

由图 2可见，当m=2时, 1 000个G₁(x)样本采用base-2编码与base-3和base-5的优化结果差的均值分别为0.626和0.662，base-2的优化结果明显优于其他两种编码；当m为3，4，5和6时，分别是base-3、base-4、base-5和base-6编码对应的优化结果最优。由此可见，对G(x)，base-m编码的性能明显优于码元非m的整数编码，与AEP的结论一致。

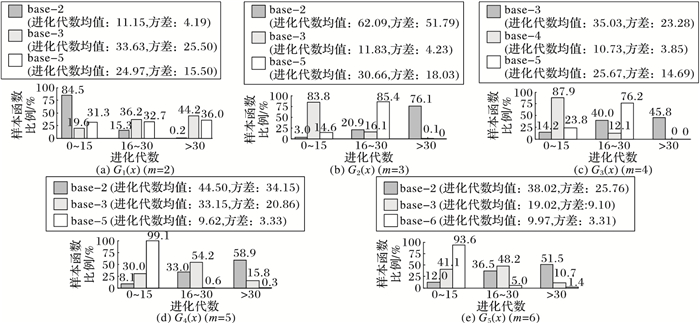
3.2 群体平均适应度上升时间比较

对表 1中的5组适应度函数，以10^-6为步长，通过穷举搜索法得到每个样本函数适应度的全局极大值，然后计算不同编码下每个样本函数群体适应度的均值上升到全局极大值70%时所需要的进化代数，最大进化代数设500，其他参数与表 2相同。将所需进化代数划分为(0~15)、(16~30) 和(>30)3组，统计每组进化代数的样本函数比例，结果如图 3所示。由图 3可见，对5组适应度函数，当采用base-m编码时，最少83.8%以上的样本函数在15代以内群体平均适应度上升到全局极大值的70%，所需进化代数的均值和方差都明显小于其他两种编码，反映了该类适应度函数采用base-m编码更容易进化，与AEP的结论一致。

4 结语

本文以频率为正整数m的整数次幂的正弦函数为基函数线性组合构成的适应度函数为研究对象，采用AEP作为编码性能指标，分析比较了该类适应度函数在不同码元整数编码下的AEP，发现该类适应度函数采用base-m编码时进化难度小于其他码元非m编码。5 000个适应度函数样本的仿真结果表明，该类函数采用base-m编码时，最终优化结果和群体平均适应度的上升速度明显优于其他非m码元编码，验证了AEP对编码性能评价的有效性。

本文结果再次确认了对于该类适应度函数m元整数编码优于非m元整数编码的结论，可为GA的编码设计提供借鉴。另外，AEP反映了进化的难易程度，可推广应用于适应度函数的设计和操作算子的选择，如设计不同的适应度函数通过AEP选择较容易进化的一个，以及选择有利于进化的选择算子、交叉率和变异率等。