0 引言

在分布式存储系统中节点失效成为常态的情况下，设计分布式存储系统时必须考虑到合适的容错机制。目前广泛使用的容错机制有复制备份和纠删码两种。复制备份方案简单易行，数据恢复高效；但存储空间浪费明显，常用的3副本备份机制需要将同一数据块存储3份，额外使用了两倍的存储空间，而且存在副本一致性难以维护的问题。相比之下，基于纠删码^[1]的编码冗余方案不仅能保证高可靠性，同时可取得高存储空间利用率，在数据量日趋增大的情况下，在很大程度上降低了存储成本，故而受到了Facebook^[2]、Google^[3]、Microsoft^[4]等公司的重视及广泛应用。其中应用最为广泛的当属里德索罗门(Reed-Solomon, RS)码^[5]等具有极大距离可分(Maximum Distance Separable, MDS)性质的纠删码，可以达到最优存储效率。以(n, k)RS码为例，它首先将原始数据文件分成k个块，并根据编码算法生成共n块数据(n>k)，然后将n个数据块存储在不同的节点上，可以保证不丢失超过n-k个数据块时，均可由剩余的块根据译码算法恢复出原始的数据文件，但是这种简单的修复方案在节点失效时，为维持系统冗余度需要生成丢失节点存储的数据，就要从k个节点传输足够的数据量从而成功译码出原始数据文件，再编码生成丢失节点的数据块，整个过程产生大量的网络带宽(这里及后文的修复带宽指传输数据量)，从而会严重影响现有数据的读取速度^[6]，因此，设计一种能有效降低修复带宽的存储编码方法对实际的大规模存储系统来说至关重要。

针对纠删码的高修复带宽问题，Dimakis等^[7]将网络编码^[8]的思想应用于分布式存储中，提出了再生码的概念。它通过在每个节点多存储一定量的数据，并将数据传送至失效节点前先在本地进行编码，可以显著地减少节点修复过程中需要传输的数据量，降低了网络带宽消耗。但是Dimakis等^[7]仅从理论上证明了再生码可以达到存储开销和修复带宽的均衡，且其所给出的线性随机网络编码方案^[9]完全基于有限域GF(q)上元素的运算：一方面计算开销大，实现复杂，另一方面修复后的数据与原节点的数据不一致，只是保证了全部编码块整体的冗余能力，故而实际用途并不大。Suh等^[10]基于干扰对齐的思想提出了精确修复再生码的构造方法，但构造过程整体上复杂；Rashmi等^[11]基于乘积矩阵的通用性框架给出了可以精确修复失效节点数据的方案，其中给出的基于范德蒙矩阵或柯西矩阵的乘积矩阵方案，直观紧凑，容易实现；但是基于GF(q)上的运算，需要比较大的有限域规模，从而影响了计算效率，不能适应实际中的使用。

为了提高再生码的运算效率，摆脱有限域GF(q)上的运算，本文应用陈亮等^[12]提出的基于GF(2) 上部分随机矩阵的随机二元可扩展码(Random Binary Extensive Code, RBEC)，并结合文献[11]中给出的乘积矩阵思想，提出了一种再生码的构造方案。实验结果表明，该方案虽然是概率型的，但其成功概率完全可控(付出一定的冗余将获得稳定的失效恢复的高概率)，在保证失效恢复高概率成功的基础上，相比文献[11]中被认为是基准的基于范德蒙编码矩阵的再生码方案，有更高的编码速度和失效恢复速度，从而更加方便了再生码在大规模存储系统中的实际应用。

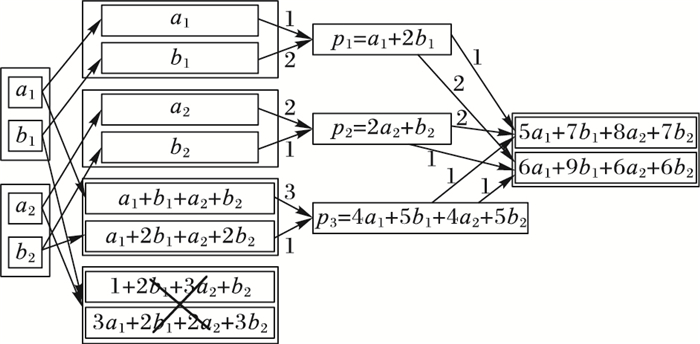
1 再生码的基本原理

Dimakis等^[7]将分布式存储系统的数据存储和失效节点数据修复抽象成经典图论中的信息流图，利用网络编码中信息关联和信息分散存储的思想，提出了可以降低节点修复带宽的再生码方案。下面结合Dimakis文中所举的(4, 2) 再生码为例，来说明再生码的基本思想。图 1中待编码的原始文件大小为2 MB，使用任意一种(4, 2) MDS纠删码将原文件分成2块，再编码成4块，存储在不同的节点上。假设最后一个节点失效导致其存储的数据丢失，那么需要立即启用一个新的节点来恢复丢失的数据。具体的恢复过程如下：剩余存活的3个节点分别将自己所存的1 MB大小的数据通过随机选择编码参数，先在本节点内部编码成大小为0.5 MB的编码块，再发送至新启用的节点，新启用的节点再根据接收到的3个编码块，译码恢复出失效节点丢失的数据块。在这个简单的例子中，总共只需要传输1.5 MB的数据即可完成失效节点的修复，同时文中也指出这是理论上的最小值。当然，这个简单例子给出的是一种功能性修复方案^[13]，修复后的节点数据和原始数据不一致，后文主要给出的是准确修复方案，保证准确恢复出丢失的数据。

事实上，文献[10]中指出针对(n, k)再生码，每个节点的存储数据量α和单节点的失效修复带宽γ之间存在反比关系。当一个节点失效时，新节点需要从剩余存活的节点中选择d(k≤d≤n－1) 个，并从每个节点中传输β大小的数据块，所以总修复带宽γ=dβ。故而再生码的构造参数为：(n, k, d, α, γ, M)，其中M为原文件大小。文献[14]指出再生码的参数应满足条件${M \le \sum\limits_{i = 0}^{k -1} {\min \left\{ {\alpha, \left({d -i} \right)\beta } \right\}} }$，这实质上意味着节点存储数据块大小α和单节点失效时的修复带宽β不可能同时达到最小。此外，文献[7]中给出了存储容量最小时和修复带宽最小时的两种特殊码字最小带宽再生(Minimum Bandwidth Regenerating, MBR)码和最小存储再生(Minimum Storage Regenerating, MSR)码的单节点存储数据块大小和失效修复带宽值。计算式如下：

$ ({\alpha _{\rm {MBR}}},{\gamma _{\rm {MBR}}}) = (\frac{{2Md}}{{2kd - {k^2} + k}},\frac{{2Md}}{{2kd - {k^2} + k}}) $

(1)

$ ({\alpha _{\rm {MSR}}},{\gamma _{\rm {MSR}}}) = (\frac{M}{k},\frac{{Md}}{{k(d - k + 1)}}) $

(2)

其中，MSR码本质上仍是一种实现比RS码的修复方案更低修复带宽的MDS纠删码，每个节点存储的数据块大小和MDS纠删码编码后的每个数据块大小相同，主要通过增加参与修复的节点个数以及在每个参与修复节点本地预先编码数据块来降低修复带宽。MBR码在每个节点存储的数据块大小大于一般MDS纠删码生成的编码块，MBR码通过在每个节点多存储一定量的数据，并在参与修复的节点上预先编码数据块来降低修复带宽。此外，Rashmi等^[15]证明了在准确地恢复出失效节点数据的情况下，除MBR和MSR两种情况外的其他参数的码字构造都是不能实现的，因此，本文主要针对的是MBR和MSR两种码字的构造方案。

2 RBEC码的随机编码矩阵

对于在域GF(2) 上的纯随机矩阵A_n×n，其矩阵中的每个元素a_ij(i=1, 2, …, n, j=1, 2, …, n)取0或1的概率均为1/2。统计意义上来看构造出来的矩阵的稀疏度在50%左右。针对完全随机方阵A_n×n，Cooper^[16]证明了它满秩的概率渐进趋近于常数C₂≈0.288 79。与完全随机矩阵不同，文献[12]中的编码矩阵采用的是一种上单位阵下完全随机阵、整体上稀疏的随机矩阵，即编码矩阵${\boldsymbol{G}_{n \times k}} = \left[ \begin{array}{l} {\boldsymbol{I}_{k \times k}}\\ {\boldsymbol{R}_{\left({\delta + t} \right) \times k}} \end{array} \right]$，其中n=k+δ+t，矩阵R_(δ+t)×k中的每个元素是随机地取0或1。文献[12]中指出并证明了从G中任意删除t行，剩余的子矩阵G′列满秩的概率大于1－1/2^δ，在δ=20时，列满秩概率将超过0.999 999。这也就保证了虽然矩阵的构造包含随机性，但是实际译码时失效的概率可控，并且可以保持在非常低的范围内。整体上，RBEC码的编译码过程只涉及数据块的异或运算，并且编码矩阵具有包含的1个数少的低密度特性，因此，编译码过程中异或次数少，效率高。

3 基于稀疏随机矩阵的MBR和MSR构造

再生码针对MBR和MSR两种码字的一个关键构造参数是参与节点修复的存活节点数d。根据前面给出的γ的公式不难看出，随着d的增加，修复带宽γ不断下降，在d=n－1时降至最小，当然此时需要其余n－1个节点全部存活，这也就相应地降低了码字的容错能力。不失一般性，下面根据文献[14]给出β=1时的MBR和MSR稀疏随机矩阵构造方案。当β>1时，编码和译码可简单地通过多次重复β=1时的方案来实现。两种方案下采用的编码矩阵均是RBEC码使用的稀疏随机编码矩阵，关键的不同之处在于乘积矩阵方案中数据块矩阵的布局方式，数据块矩阵中的每个元素可以认为是一个个大小相等的数据块，后文可以看到数据块矩阵的特殊布局方式对于节点的成功失效恢复至关重要。编码过程中，根据编码矩阵中0和1的分布，将数据块矩阵中相应的行数据块进行异或即可得出每个节点要存储的编码块。

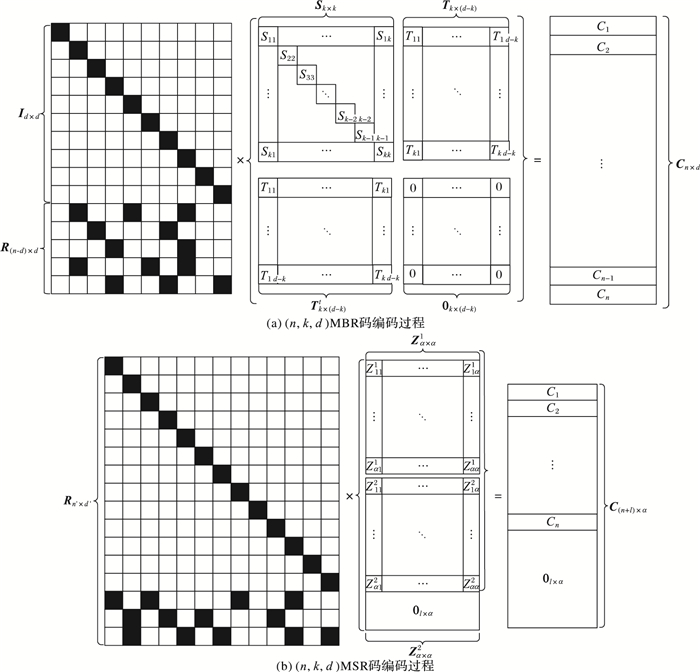
3.1 稀疏随机矩阵MBR构造方案

在β=1时，α_MBR=d，|M_MBR|=(2kd－k²+k)/2，γ_MBR=d。编码矩阵的规模为n×d，数据块矩阵的布局为${{\boldsymbol{M}}_{\rm {MBR}}} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{S}}_{k \times k}}}&{{{\boldsymbol{T}}_{k \times (d -k)}}}\\ {{\boldsymbol{T}}_{k \times (d -k)}^t}&{{{\boldsymbol{0}}_{(d -k) \times (d -k)}}} \end{array}} \right]$。其中：S_k×k是对称矩阵，和T_k×(d－k)一起用来存放原始数据，0_{(d－k)×(d－k)}中存放的是全零数据块，这里特殊的数据块排布方式保证了M_MBR是对称矩阵。此外，参数d在满足k≤d≤n－1时，MBR码都能实现最小带宽情况下的单节点失效修复。此处特殊构造的数据块矩阵相比RS码编码时的数据块矩阵多存储了一定的冗余数据，并且浪费了一些存储空间，使得最终每个节点也相应地多存储一定量的数据。MBR码具体编码过程如图 2(a)所示(左侧编码矩阵中黑色方块代表 1，白色方块代表 0，下同)。

3.2 稀疏随机矩阵MSR构造方案

在β=1时，α_MSR=d－k+1，|M_MSR|=k(d－k+1)，γ_MSR=d。Rashmi等^[11]指出在不进行符号扩展时，必须满足d≥2k－3才能构造出线性准确修复MSR码。同时，参数为(n, k, d)(2k－2≤d≤n－1) 的MSR子码C可由参数为(n′=n+l, k′=k+l, d′=d+l)(d′=2k′－2，l=d－2k+2) 的MSR母码C′构造出来。针对母码，原始数据大小M′=M+lα=α(α+1)，每个节点存储的数据量仍是α=k′－1=d－k+1，只是在数据矩阵尾部添加了大小l×α的全零矩阵。此外，子码C的译码恢复过程也都需要通过母码来完成。MSR母码C′的编码矩阵为G_n′×d′=R_n′×d′，R_n′×d′是上述提到的随机矩阵。消息矩阵的构造为M′_MSR=[Z₁ Z₂]^T，Z₁和Z₂都是大小为α×α的对称矩阵，恰好和M′大小相等。编码过程如图 2(b)所示。

4 基于稀疏随机矩阵的MBR和MSR恢复

在编码操作完成后，每个节点存储的数据量α和对应的编码向量g_j(j=1, 2, …, n)已经确定。假设失效的节点编号是f，其对应的编码行向量为g_f。为了恢复节点f的数据，需要剩余存活节点发送数据至替代f的新节点f′来帮助恢复。这里假设参与恢复的节点数目为L(L≥d+δ，δ为某个正整数)，编号为h_i(1≤h_i≤d, i≠f, i=1, 2, …, L)，则每个节点在本地计算r_i=g_hiMg_f^T，这相当于用失效节点的编码向量对所有帮助恢复的节点本地的数据块进行编码，接着再传送r_ι至新的替代节点f′。这样做避免了直接传送帮助恢复节点的本地数据块，使得单次传送的总数据量仅为L，从而显著地降低了修复带宽。此时，f′可以通过求解方程组来计算出节点f的原始数据块g_fM，方程组形式如下：

$ {{\boldsymbol{G}}_{L \times d}}{{\boldsymbol{M}}_{d \times \alpha }}{\boldsymbol{g}}_f^{\rm T} = {\left[ {\begin{array}{*{20}{c}} {{\boldsymbol{r}_1}}&{{\boldsymbol{r}_2}}& \cdots &{{\boldsymbol{r}_L}} \end{array}} \right]^{\rm{T}}} $

(3)

其中G_L×d=[g_h1 g_h1 … g_hL]^T。

针对MBR码，这里由于数据块矩阵M_MBR是对称矩阵，则(M_MBRg_f^T)^T(即等于g_fM_MBR^T)即为节点f原始存储的数据，故此时的恢复过程就等价于求上述广义上超定方程组的解。

同理，针对MSR码，可解方程得到：

$ {{\boldsymbol{M}}_{MSR}}{\boldsymbol{g}}_{fi}^{\rm T} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{Z}}_1}}\\ {{{\boldsymbol{Z}}_2}} \end{array}} \right]{\boldsymbol{g}}_{fi}^{\rm T} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{Z}}_1}{\boldsymbol{g}}_{fi}^{\rm T}}\\ {{{\boldsymbol{Z}}_2}{\boldsymbol{g}}_{fi}^{\rm T}} \end{array}} \right];\;i = 1,2 $

这里的g_fi(i=1, 2) 是编码向量g_f的前后两个长度相等的子向量。由于Z₁和Z₂都是对称矩阵，所以Z_ig_fi^T=g_fiZ_i。故而通过计算g_f1Z₁+g_f2Z₂即得到节点f原始存储的数据。每个帮助恢复的节点需要在本地计算g_hiMg_f1^T和g_hiMg_f2^T，因此这里总共需要发送2L大小的数据量至f′，接着再通过求解两个方程组来恢复出原始数据。

此外，因为构造MBR码和MSR码时采用的编码矩阵是稀疏随机矩阵，为了保证方程组存在唯一解，这里需要保证其系数矩阵G_L×d列满秩。如第2章所述，可以通过控制δ的取值保证G_L×d以任意高的概率列满秩，也就保证了方程组可解，从而能成功地恢复出丢失的数据。同时由于方程组的系数矩阵稀疏，故而实际求解时涉及到数据块矩阵中数据块的异或运算次数就相应少，从而可以保证方程组能高效求解。实质上，从上面的恢复过程可以看出，这里给出的是δ近似MBR和δ近似MSR的恢复过程，这里δ近似的意思是相对于标准的再生码参数，需要额外的δ个节点参与恢复过程。当然，这实际上牺牲了标准再生码的一些容错能力，但是在再生码的参数取值较大时，这几乎可以忽略不计，不会带来太大的额外开销。

5 稀疏随机矩阵再生码的性能分析

本章主要从数学角度来分析稀疏随机矩阵再生码的存储开销和编译码效率。

5.1 存储开销

矩阵G_L×d的列满秩与否直接关系着能否译码成功。在这里，L=d+δ，因此n需要满足n>d+δ，那么码率r=k/n < k/(d+δ)。文献[12]中指出δ决定了G_L×d满秩的概率下界，其满秩概率大于1－1/2^δ。针对MBR码，参数d可取值的范围是k≤d≤n－1，因此存储开销为n/k>1+δ/d，这里通常d>δ。针对MSR码，参数d可取值的范围是2k－2≤d≤n－1，因此，存储开销为n/k>2+2(δ－2)/(d+2)>2，因此，MSR码通常比MBR码有更高的存储开销。

5.2 编译码效率

基于稀疏随机矩阵的再生码的编码过程只涉及到数据块之间的异或运算，因此，编码效率取决于生成校验块需要的异或次数，而异或次数又取决于编码矩阵下半部分中1的个数，这里1的个数平均为(n－d)×d/2，因此时间复杂度为O(nd)。译码过程涉及到矩阵的求逆和数据块之间的异或运算，时间复杂度为O(d³)。在MBR和MSR的参数d的取值范围下，时间复杂度为O(k³)。

6 实验结果与分析

为了验证本文给出的基于稀疏随机矩阵的再生码方案的优越性，本文选取了不同大小的原数据文件和多组编码参数(n, k, l)，其中L=d+δ, δ=16。首先，对MBR码、MSR码和RS码修复方案(这里的RS码修复方案即为引言中提到的方案)的修复带宽进行了比较；然后，对比了基于RBEC码的稀疏随机编码矩阵构造的稀疏随机最小带宽再生(Sparse Random-Minimum Bandwidth Regenerating，SR-MBR)码、稀疏随机最小存储再生(Sparse Random-Minimum Storage Regenerating, SR-MSR)码和基于范德蒙矩阵构造的范德蒙最小带宽再生(Vandermonde-Minimum Bandwidth Regenerating, Van-MBR)码、范德蒙最小存储再生(Vandermonde-Minimum Storage Regenerating, Van-MSR)码的编码速率和失效恢复速率。本章实验的硬件环境为Intel Core i3 3.07 GHz CPU、4 GB RAM；软件环境为Ubuntu 14.04 64位、Jerasure 2.0、GF-Complete。

6.1 修复带宽

本节中选取的原文件的大小为20 MB和60 MB。针对再生码选取了不同的参与修复节点数L={56, 116}来显示L其对再生码修复带宽的影响。

从表 1中可以看出，针对20 MB大小的原始文件，参数为(60, 40, 56) 的MBR码单节点数据修复带宽仅为0.77 MB，远远小于RS码修复方案修复时的20 MB。针对60 MB大小的原文件，(128, 100, 116) MBR码修复带宽仅为1.1 MB，大约为RS码修复方案的1/60。针对实际使用的分布式存储系统，在文件大小达到更大的量级时，将更加体现出MBR码的低修复带宽优势。

表 2给出了不同参数MSR码和RS码修复方案的单节点修复带宽比较结果，可以看出针对20 MB大小的原始文件，(90, 36, 86) MSR码的修复带宽仅为2.73 MB，大约为RS码修复方案的1/10，(180, 70, 154) MSR码修复带宽为3.83 MB，大约为传统修复方法的1/16。这体现了近似MSR码在获得近似MDS性质的同时，带来相对RS码修复方案明显的低修复带宽优势。

6.2 编码和恢复速率

本节中选取大小为20 MB、60 MB、100 MB、140 MB的原数据文件，比较了在相同编码参数(n, k)下基于稀疏随机矩阵的再生码和基于范德蒙矩阵的再生码的编码速率和单节点失效时的数据恢复速率。

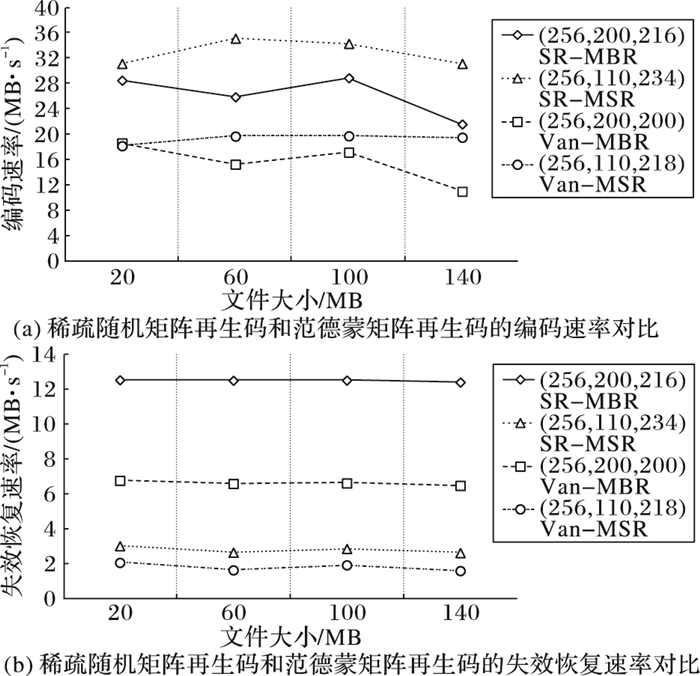
图 3(a)中给出了编码速率的对比结果。从中可以看出，在100 MB文件大小时，(256, 200, 216) SR-MBR码，编码速率约为29 MB/s，(256, 200, 200) Van-MBR码编码速率约为17 MB/s，提升了大约70%；(256, 110, 234) SR-MSR码编码速率约为34 MB/s，(256, 110, 218) Van-MSR码编码速率约为20 MB/s，提升了大约70%。

图 3(b)给出了单节点失效恢复速率的对比结果。从中可以看出，针对100 MB大小的文件，(256, 200, 216) SR-MBR码恢复速率约为12.5 MB/s，(256, 200, 200) Van-MBR码恢复速率约为6.5 MB/s，提升了大约一倍；(256, 110, 234) SR-MSR码恢复速率约为3 MB/s，(256, 110, 218) Van-MSR码恢复速率约为2 MB/s，提升了大约50%，因此，SR-MBR码相比Van-MBR码以及SR-MSR码相比Van-MSR码都有明显的恢复速度优势。

从图 3中可以看出，在再生码的参数(n, k, d)达到中等规模大小时，稀疏随机矩阵再生码相比范德蒙矩阵再生码在编码速率和节点失效恢复速率上有明显的优势。

7 结语

本文提出的将RBEC码的稀疏随机矩阵和乘积矩阵方案相结合的一种再生码构造方案既能保证大幅度降低节点失效修复带宽，同时相比基于传统范德蒙编码矩阵的乘积矩阵方案有更高的编码速度和失效译码恢复速度。此外，虽然本文提出的再生码方案的预期执行结果是概率型的，但其成功的高概率完全可控。进一步说，真实的存储系统中节点失效的出现情况本来就是随机性的，因此本文这种方案的机制在本质上是符合现实情况的，并且其数据恢复在实际使用中的失败概率完全可以控制在非常小的范围内，由此保证实用中的可行性和高效性。

本文提出的MBR码和MSR码构造方案目前仅考虑了单节点的失效修复问题，多个节点的失效修复在技术上可以通过多次单节点失效修复过程的重复来完成。尽管如此，修复过程的循环重复还是会占用多余的网络传输带宽，从而增加修复时间，因此，探索针对多节点失效修复的更加直接、更加高效的实现方案就成了下一步的重要工作方向。