随着数据量的爆炸式增长,传统的存储服务已无法满足用户的日常需求。为节约成本,越来越多的公司和用户选择将数据外包给云服务商(Cloud Service Provider, CSP)进行管理和存储[1]。为使利益最大化,CSP可能不按照服务等级协议的约定存储数据,使用户数据面临极大的风险[2]。为保证数据的高可用性,CSP通常将数据分成多个副本进行存储,所以用户需要强有力的证据表明CSP完整无误地存储着所有数据且所有副本都与用户最近一次修改保持一致[3]。
Ateniese等[4]最早提出可证明数据持有(Provable Data Possession,PDP)方案,该方案引入“挑战—应答”协议,支持公开审计但计算开销较大。之后他们提出改进的可扩展数据持有性(Scalable Provable Data Possession,SPDP)证明方案[5],增加了部分动态更新功能,但方案验证次数有限。Erway等[6]基于跳表(Skip List)结构提出支持全动态更新的PDP方案。Juels等[7]首次提出可恢复性证明(Proofs Of Retrievability,POR)方案,该方案能恢复部分受损数据,但不支持公开验证和数据动态更新。Schacham等[8]在随后提出支持公开验证的POR机制,验证次数没有限制但通信开销较大且不支持动态更新。Wang等[9]提出一种基于Merkel哈希树(Merkel Hash Tree, MHT)的验证方案,该方案支持公开审计和数据动态更新,但计算开销较大。李勇等[10]提出一种基于多分支路径树的完整性验证方案,简化了动态更新过程但产生辅助信息过多,导致通信开销较大。Wang[11]引入第三方审计者(Third Party Auditor,TPA)协助用户验证数据完整性,该方案减少了用户负担,但CSP计算开销较大。Chen[12]提出一种基于代数签名的验证方案,支持用户无限次验证,但不支持动态操作。
为解决现有方案计算开销大、不能较好地支持全动态更新的问题,本文提出一种基于B+树的数据持有性证明方案,通过引入数据版本表以支持数据块级的全动态更新;通过优化系统模型并引入节点检索值,能识别定位错误数据并提高TPA的验证效率。
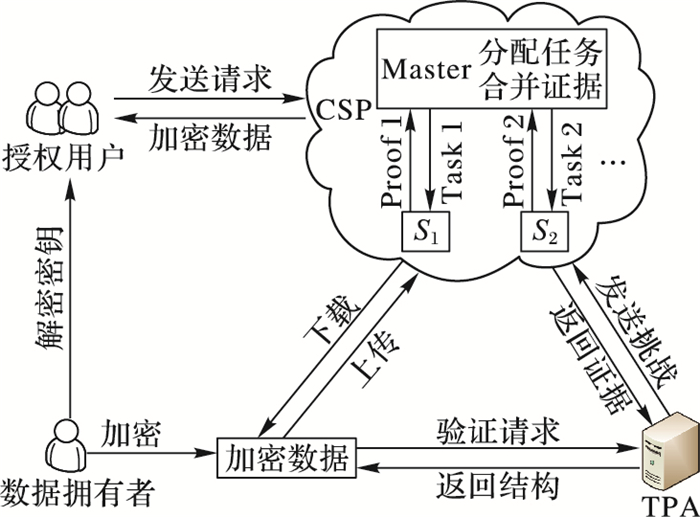
1 相关知识 1.1 系统模型方案模型如图 1所示,由4类实体组成。
|
图 1 系统模型 Figure 1 System model |
1) 数据拥有者。指有存储需求的用户,与远程CSP建立通信,并将加密数据上传至云存储服务器中。
2) 授权用户。经过数据拥有者授权的其他用户,与数据拥有者共享数据解密密钥,可以远程访问数据并进行更新操作。
3) CSP。包括一个主服务器Master和若干个存储服务器Slaves。为提高验证效率,本方案设计由Master负责分配证据生成任务,并收集结果返回给TPA;Slave根据指令为被挑战的数据生成证据,并返回给Master。
4) TPA。第三方审计者,拥有强大的计算能力,代替数据拥有者对CSP发起挑战,并对返回的证据进行验证,将最终结果通知数据拥有者。
1.2 安全模型用户数据的完整性面临以下威胁:
1) CSP为获取最大利益并保持公司声誉,可能隐瞒数据损坏、丢失的情况,还可能删除用户访问频率较低的数据以节省存储空间。
2) CSP可能存储比服务协议更少的副本数量,并欺骗用户,让用户以为所有数据被正确完整地存储。
3) 为节省计算资源,CSP可能忽略用户的更新请求,或只更新部分数据,从而导致多个备份副本数据不一致。
1.3 B+树和双线性对B+树是一种n叉平衡树,其每个非叶子节点可以拥有大量叶子节点。一棵深度为h、存储索引值为b的n阶B+树应满足以下特性[13]。
1) 一棵B+树由三部分组成:根节点、内部节点和叶子节点。
2) 所有叶子节点的深度相同,数据索引值存储在叶子节点中。
3) 一棵B+树中能够存储的最小数据量为:
4) 进行数据查找、插入和删除数据的时间复杂度均为O(log nb)。
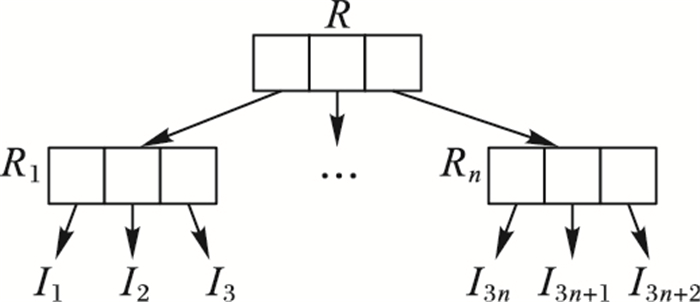
图 2为B+树结构的一种实例,其中每个叶子节点存储一个数据块索引Ii,根节点R的索引链接可表示为Hash函数:H(R1‖R2‖…‖Rn)。叶子节点Ri的索引链接为:H(I1‖I2‖…‖In)。
|
图 2 B+树结构 Figure 2 B+ tree structure |
双线性对 假设G1和G2是阶为素数P的循环群。g1,g2是G1和G2的生成元。定义双线性映射e:G1×G2→GT,满足以下性质[14]。
1) 可计算性。存在有效算法能够计算e。
2) 双线性性。对所有的u∈G1,v∈G2和a, b∈Zp,有e(ua, vb)=e(u, v)ab。
3) 非退化性。e(g1, g2)≠1。
计算性Diffie-Hellman(CDH)问题给定e(g1, g2)≠1,其中x, y∈Zp,计算gxy。
2 B+树动态数据持有性证明方案 2.1 数据版本表本文方案支持对外包数据进行动态更新,由于CSP是不可信的,所以需要对已更新数据块进行验证,以确保所有数据与用户最近一次修改相一致。此外,TPA应该知道数据块的索引值,以保证能够验证CSP是否在用户所请求的特定数据块位置执行相应的操作。由此引入数据版本表(Data Version Table,DVT),DVT是一种小型元数据信息,由3部分组成。
1) 数据块索引号(IN)。IN是数据块的索引值,它存储着数据块的具体物理地址。
2) 数据块编号(BN)。BN是数据块的逻辑编号,它存储着数据块的逻辑地址。
3) 数据块版本号(VN)。VN是当前数据块的版本号,初始设定值为1,每更新一次,VN值增加1。
本文方案中TPA只需存储一份DVT,对于n个大小为|F|的数据副本,CSP的存储空间开销为O(n|F|),而TPA的存储开销仅为o(m),m为数据块的个数。由于DVT以链接列表形式,数据块按照顺序依次排列,对于实际实现,IN不需要存储在表中,因此每个表项中仅包含BN和VN(8 Bytes),DVT大小为8m Bytes。在理论分析中,DVT的大小与数据大小呈线性相关,但经过实验发现,前者通常小好几个数量级。例如,分块大小为16 KB的1 GB数据文件,TPA存储的DVT大小仅为512 KB,小于文件大小的0.05%。
2.2 方案步骤为方便描述,符号定义如表 1所示。
| 表 1 符号定义 Table 1 Symbol definition |
本文方案包含8个多项式时间算法,如下所示。
1) KeyGen→(pk, sk)。假设e:G1×G2→GT是一个双线性映射,g是G2的生成元。用户运行该算法生成用户私钥sk∈Zp和公钥pk=gx∈G2。
2) GenB+tree。该算法在用户端构造B+树,每个叶子节点对应一个数据块检索值,映射完成后对B+树的根节点签名得到SignB+tree(H(R))=H(R)x。签名后和随后生成的数据块标签一起发送给CSP,CSP端由Master节点构造与用户相同的B+树。
3) GenTag→δ。用户将文件f划分成m个数据块,即f=(bi)1≤i≤m,对于n个备份副本来说,将副本编号值j与数据块链接表示为f=(bij)1≤i≤m,使用具有强扩散性的加密算法Ek()加密得到数据块bij=Ek(j‖bi)。用户随机挑选s个元素(u1, u2, …, us),为每个数据块生成一个标签
4) PreUpdate(D, UpdateInfo)。用户需要插入、修改或删除数据时,在数据块级进行细粒度操作。首先由用户发送请求(IDf|BlockO|i|bi′|δi′),其中IDf是文件标识码,BlockO代表用户请求的操作类型,如块插入、块删除等,i代表请求更新的数据块索引,bi′代表新的数据块值,δi′代表新的标签集合。
① 数据块修改。对于数据文件f=(b1, b2, …, bm),用户需要将其中某块bi修改为bi′,执行如下算法:
a)在DVT中更新版本号,VN=VN+1;
b)生成n个不同的数据块b′ij并加密得到b′ij=Ek(j‖bi),1≤j≤n;
c)为每个数据块生成新的标签
d)向CSP发送修改请求(IDf|Modify||i|b′ij|δ′)。
② 数据块插入。假设用户需要在文件f的第i个数据块后插入新的数据块b′,构造新的文件f=(b1, b2, …, bi, b′, …, bm+1)。由于本文方案的数据块索引号不包含在数据块标签中,故不必计算插入新块后移位的数据块的标签值。用户执行如下算法:
a)在DVT中第i个数据块后添加新表项(IN|BN|VN)=(i+1|BNmax|1);
b)生成n个不同的数据块b′i并加密得到b′i=Ek(i║b);
c)为新数据块计算标签δ′ij=(H′(IDf|BNmax+1|1)·ukb′i)x,BN值加1,版本号为1,然后生成新标签集合
d)向CSP发送请求(IDf|Insert|i|b′i|δ′)。
③ 数据块删除。分为两种情况,删除最后一块和删除其他位置的数据块。这里主要讨论第二种情况。假设用户删除第i块,执行算法如下:
a)用户删除DVT中的第i个表项,第i项后的所有表项IN减1,其余值不变;
b)向CSP发送(IDf|Delete|i|Null|Null)。
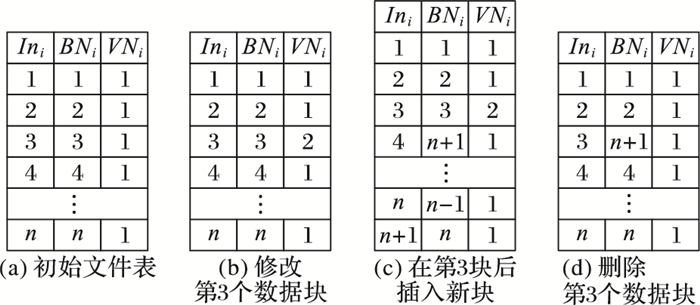
图 3对动态更新过程中DVT的变化进行了举例。假设初始文件f的DVT如图 3(a)所示,INi=BNi,VNi=1,1≤i≤n;当修改第3块时,VN3加1,其余值不变,如图 3(b)所示;如果在第3块后插入新的数据块,新块的IN4=4,BN4=n+1, VN4=1,如图 3(c)所示;删除第3块,DVT变化如图 3(d)所示。
|
图 3 DVT在动态操作时的变化 Figure 3 DVT change with dynamic operation |
5) ExecUpdate。CSP收到更新请求后,执行下列算法。
① 数据块修改。CSP收到数据块修改请求后,执行下列操作:
a)用新块b′ij代替原数据块bij,生成新的副本文件f ′;
b)用新的数据标签δ′ij代替原标签δij,生成新的标签集合δ′。
② 数据块插入。CSP收到数据块插入请求后,执行下列操作:
a)将新块b′i插入到数据块bi之后,并生成新的副本文件f ′;
b)将新的数据标签δ′i插入到DVT中,并生成新的标签集合δ′。
③ 数据块删除。CSP收到数据块删除请求,执行下列操作:
a)删除第i个数据块,生成新的文件副本f ′;
b)删除数据标签δi,生成新的标签集合δ′。
6) Chal→(ω, πkey(k1), ψkey(k2))。TPA随机抽取若干个数据块进行挑战。需要生成ω,πkey(k1),ψkey(k2),ω代表需要挑战的文件编号,πkey(k1)代表伪随机置换,ψkey(k2)代表伪随机函数。将其组合成挑战信息Chal=(ω, πkey(k1), ψkey(k2))发送给CSP。
7) GenProof→(μ, δ)。CSP收到挑战信息后,Master节点对任务进行分配,每个Slave节点进行下列计算:
| $ {{\mu _i} = \prod\limits_{i = 1}^\omega {{\pi _{{\rm{key}}}}\left( {{k_1}} \right){\psi _{{\rm{key}}}}\left( {{k_2}} \right)H{{\left( R \right)}^x}} } $ | (1) |
| $ {{\delta _i} = {{\left( {H\left( {I{D_f}\left| {B{N_i}} \right|V{N_i}} \right)\cdot\prod\limits_{k = 1}^\omega {u_k^{{b_i}}} } \right)}^x}} $ | (2) |
计算完成后将结果返回给Master进行组合,计算
8) Verify→(0, 1)。TPA验证CSP返回的B+树根节点签名Sign′B+tree(H(R))与本地签名值是否相等,相等则继续验证下列公式是否成立:
| $ e\left( {\delta ,g} \right)\underline{\underline ?} e\left\{ {{{\left[ {\prod\limits_{i = 1}^\omega {H(I{N_i},B{N_i},V{N_i})} } \right]}^n} \times \prod\limits_{i = 1}^\omega {u_I^{\prod\limits_{i = 1}^\omega {{\delta _i}} },g} } \right\} $ | (3) |
TPA由DVT可得数据块逻辑号和版本号并对证据进行计算,如果等式成立,则输出1,代表验证成功;否则为0。最终,TPA将检测结果发送给用户。
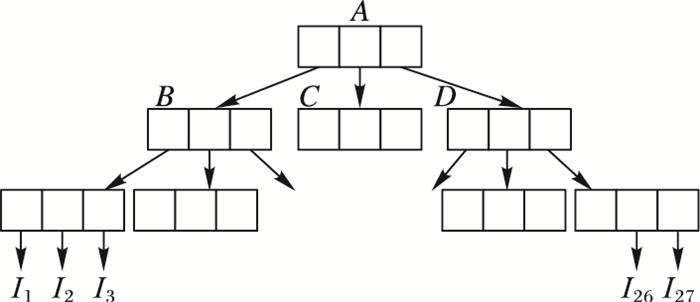
2.3 识别损坏副本本文方案在B+tree中加入节点检索值(Retrieved Value,RV),能有效识别并定位错误数据块。RV的定义如下:从当前节点向下检索,能够检索到的叶子节点的总数。图 4中的B+树深度为3,叶子节点对应的数据块索引值用Hash函数表示:hA=h(hB|hC|hD),RVA=27,hB=h(hI1|hI2|hI3),RVB=9,hi=h(Ii)1≤i≤9。
|
图 4 3阶B+树结构 Figure 4 3-order B+ tree structure |
不同存储服务器返回的证据不同说明用户数据遭到破坏。假设TPA在验证时检测出不同存储服务器返回的同一数据块的Hash值hI3不同,需要检测i=3的叶子节点,判断哪个存储服务器出现问题,利用RV可快速识别定位错误数据,具体算法如下:
1) 比较i和RVA的值。如果RVA < i,返回False,停止计算;否则令x=i。
2) 比较x和RVB的值,如果X≤RVB,则对此节点的子节点进行检索。如果X>RVB,则令x=x-RVB,比较x和RVC的大小,如果X≤RVC,则从此节点向下检索;否则继续重复该步骤,直到确定继续向下检索的节点。本例中x=i=3,可确定继续检索第一个子树。
3) 加入当前节点到该数据块的认证路径中。
重复步骤2)~3),直到x=1,检索到对应的叶子节点。在B+树结构中使用本算法能较快地检索到出现问题的节点,减少TPA的验证开销。
3 安全性分析定理 如果本文提出的B+ tree签名不可伪造,且CDH问题在双线性群中是难解的,那么TPA在检测数据完整性时,没有攻击者能够欺骗TPA,除非返回的证据是正确的。
证明 TPA期望CSP返回正确的证据P=(μ, δ, SignB+tree)。假设攻击者返回证据P′=(μ′, δ′, Sign′B+tree),通过验证e(Sign′B+tree, g)和用户本地的e(SignB+tree, g)值是否相等来验证证据的正确性。因为
将本文方案与现有两类方案进行对比,结果如表 2所示,其中n表示数据块的数量。通过对比,可以看出本文方案的TPA验证开销和通信开销较小,具有实用性。
| 表 2 3种方案性能对比 Table 2 Performance comparison of three schemes |
为更好地评估方案性能,将本文方案与基于MHT的方案[9]进行对比。实验在Hadoop 2.7.3框架下的Spark平台上使用Python语言编程实现,双线性对运算和哈希运算分别在OpenSSL库和PBC库中实现。设群阶的大小为160 bit,获得80 bit的安全参数。随机生成数据文件2000个,分块大小为64 KB,数据文件的大小为2 GB,DVT为1 MB,实验取10次结果的平均值。
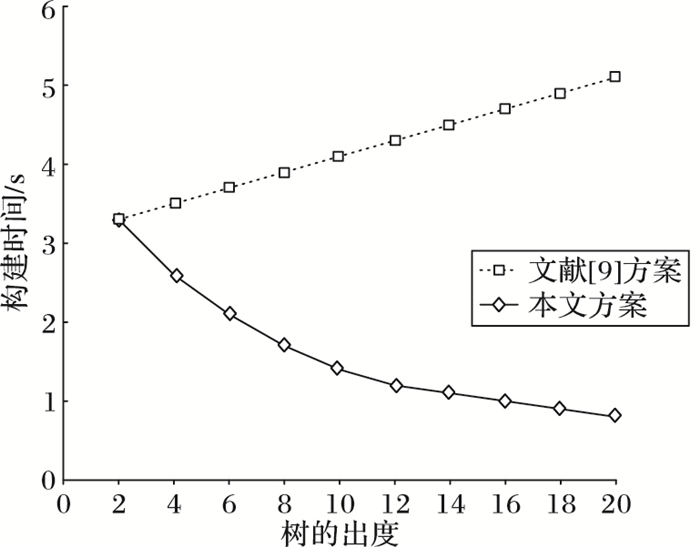
首先,通过计算用户和CSP构建B+树、MHT树的时间,比较本文方案与文献[9]方案的性能。MHT树是二叉树结构,假设数据被分为n块,则至少需要建立深度为1+lb n的二叉树,树的深度随数据块n呈线性增加。相较于B+树结构,构造MHT的计算开销较大。生成不同认证树结构的时间如图 5所示,可以看到构建B+树的时间与构建MHT树的时间在树的出度为2时相同,随着出度的增加,构建MHT树的时间逐渐增加,而构建B+树的时间大大减少,说明本文方案能够有效地降低构建数据结构的计算开销。
|
图 5 不同出度树的构建时间对比 Figure 5 Construction time comparison of different out-degree trees |
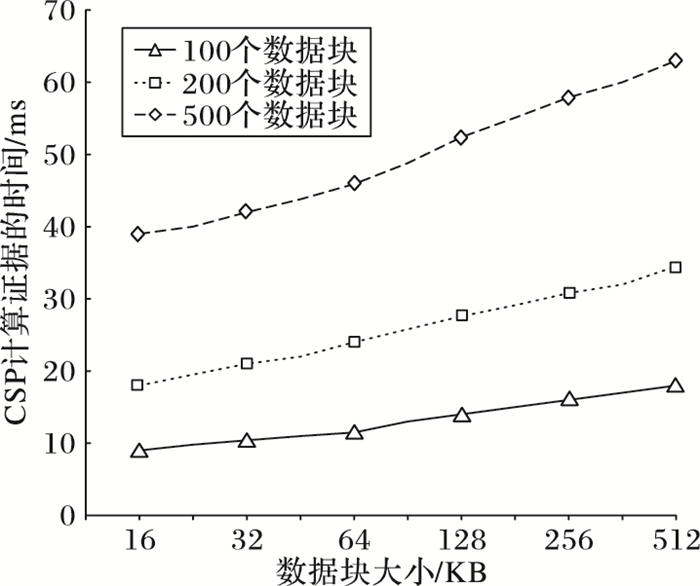
为进一步分析方案性能,对CSP计算证据的时间开销进行分析。运行程序后输入不同的数据块数量,得到计算证据的时间如图 6所示。可以看出随着数据块大小的增加,CSP计算证据的时间都会逐渐增加;每次验证的数据块数量越多,CSP计算证据所花费的时间也越多,CSP的计算开销越大。
|
图 6 CSP计算证据的时间开销 Figure 6 Proof time cost generated by CSP |
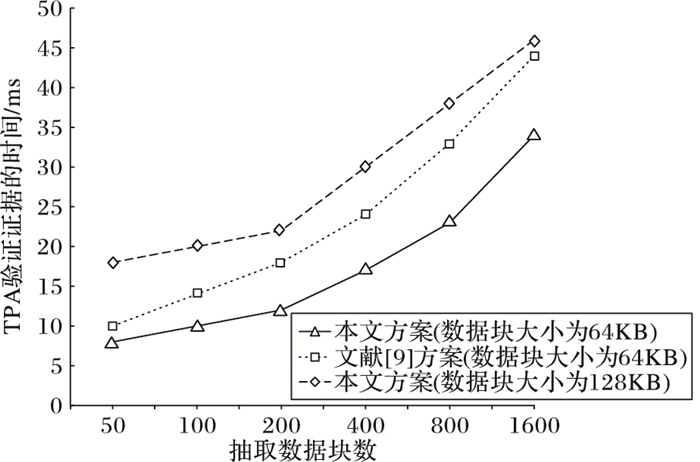
最后对TPA的验证时间开销进行分析。以数据块大小作为输入,程序最终输出TPA相应的验证时间。选取数据块大小分别为64 KB和128 KB两种情况,实验结果如图 7所示。通过实验对比,可以发现在数据块大小均为64 KB时,两种方案的TPA验证时间在数据块数量较少时较为相近;但随着抽取数据块的数量不断增加,本文方案的验证时间开销明显低于文献[9]方案的时间开销。当设定本文方案数据块大小为128 KB时,TPA验证时间与数据块大小为64 KB的文献[9]方案的时间相近。
|
图 7 TPA验证时间 Figure 7 Verification time of TPA |
通过上述实验可知,相比文献[9]方案,本文方案使用B+树认证结构能够有效降低用户和CSP构建数据结构的计算开销,减少TPA的验证时间,提高数据完整性验证效率。
5 结语为解决传统数据持有性证明方案计算开销大、验证时间较长等问题,提出基于B+树的数据持有性证明方案。在B+树认证结构中引入数据版本表和节点检索值,有效支持数据动态更新和错误数据识别。实验证明:本文方案能有效降低模型中各实体的计算开销,提高TPA的验证效率。由于本文方案假设TPA是完全可信的,审计过程中用户数据可能遭到TPA和CSP的共谋攻击而泄露,下一步将对如何保护用户数据隐私展开研究。
| [1] | 俞能海, 郝卓, 徐甲甲, 等. 云安全研究进展综述[J]. 电子学报, 2013, 41(2): 371-381. (YU N H, HE Z, XU J J, et al. Review of cloud computing security[J]. Acta Electronica Sinica, 2013, 41(2): 371-381.) |
| [2] | 李晖, 孙文海, 李凤华, 等. 公共云存储服务数据安全及隐私保护技术综述[J]. 计算机研究与发展, 2014, 51(7): 1397-1409. (LI H, SUN W H, LI F H, et al. Secure and privacy-preserving data storage service in public cloud[J]. Journal of Computer Research and Development, 2014, 51(7): 1397-1409. DOI:10.7544/issn1000-1239.2014.20140115) |
| [3] | BARSOUM A F, HASAN M A. Provable multicopy dynamic data possession in cloud computing systems[J]. IEEE Transactions on Information Forensics & Security, 2015, 10(3): 485-497. |
| [4] | ATENIESE G, BURNS R, CURTMOLA R, et al. Provable data possession at untrusted stores[C]//Proceedings of the 2007 ACM Conference on Computer and Communications Security. New York:ACM, 2007:598-609. |
| [5] | ATENIESE G, PIETRO R D, MANCINI L V, et al. Scalable and efficient provable data possession[C]//Proceedings of the 4th International Conference on Security and Privacy in Communication Networks. New York:ACM, 2008:Article No. 9. |
| [6] | ERWAY C C, PAPAMANTHOU C, TAMASSIA R. Dynamic provable data possession[J]. ACM Transactions on Information & System Security, 2009, 17(4): 213-222. |
| [7] | JUELS A, KALISKI B S. PORs:proofs of retrievability for large files[C]//Proceedings of the 2007 ACM Conference on Computer and Communications Security. New York:ACM, 2007:584-597. |
| [8] | SHACHAM H, WATERS B. Compact proofs of retrievability[C]//ASIACRYPT'08:Proceedings of the 14th International Conference on the Theory and Application of Cryptology and Information Security:Advances in Cryptology. Berlin:Springer, 2008:90-107. |
| [9] | WANG Q, WANG C, REN K, et al. Enabling public auditability and data dynamics for storage security in cloud computing[J]. IEEE Transactions on Parallel & Distributed Systems, 2011, 22(5): 847-859. |
| [10] | 李勇, 姚戈, 雷丽楠, 等. 基于多分支路径树的云存储数据完整性验证机制[J]. 清华大学学报(自然科学版), 2016, 56(5): 504-510. (LI Y, YAO G, LEI L N, et al. LBT-based cloud data integrity verification scheme[J]. Journal of Tsinghua University (Science and Technology), 2016, 56(5): 504-510.) |
| [11] | WANG H. Identity-based distributed provable data possession in multicloud Storage[J]. IEEE Transactions on Services Computing, 2015, 8(2): 328-340. DOI:10.1109/TSC.2014.1 |
| [12] | CHEN L. Using algebraic signatures to check data possession in cloud storage[J]. Future Generation Computer Systems, 2013, 29(7): 1709-1715. DOI:10.1016/j.future.2012.01.004 |
| [13] | JENSEN C S, LIN D, OOI B C. Query and update efficient B+-tree based indexing of moving objects[C]//Proceedings of the Thirtieth International Conference on Very Large Data Bases. Amsterdam:Elsevier, 2004:768-779. |
| [14] | VAPNIK V N. The Nature of Statistical Learning Theory[M]. Berlin: Springer, 2000: 988-999. |
| [15] | WANG H, ZHANG Y. On the knowledge soundness of a cooperative provable data possession scheme in multicloud storage[J]. IEEE Transactions on Parallel & Distributed Systems, 2014, 25(1): 264-267. |
| [16] | BARSOUM A F, HASAN M A. Provable multicopy dynamic data possession in cloud computing systems[J]. IEEE Transactions on Information Forensics & Security, 2015, 10(3): 485-497. |




