2. 贵州工程应用技术学院 信息工程学院, 贵州 毕节 551700
2. School of Information Engineering, Guizhou University of Engineering Science, Bijie Guizhou 551700, China
大数据时代,数据挖掘已展现出其魅力,如何使用数理统计模型从海量数据中挖掘有效信息越来越受到业界的关注。在建立模型初期,一般会选择尽可能多的自变量(属性集)减小因缺少重要自变量而出现的模型偏差,但建模过程中需要寻找对结果变量解释力最强的自变量集合,即通过对自变量选择来提高模型的预测精度与准确度[1]。统计学中常用的模型之一是线性回归模型,而对线性回归模型而言, 模型的准确性主要取决于变量的选择和回归系数的取值。在Frank等[2]提出的Ridge Regression算法和Bireman[3]提出的Nonnegative Garrote算法的启发下,Tibshirani[4]提出了一种称之为最小绝对收缩和选择算子(Least absolute shrinkage and selection operator, Lasso)的新的变量选择方法。该算法通过构造一个惩罚函数来压缩系数,在回归系数的绝对值之和小于一个常数的约束条件下,使残差的平方最小化,Lasso方法作为一种压缩估计,具有较高的检测精度和较好的参数收敛一致性。进一步,Efron等[5]提出最小角回归(Least Angle Regression, LARS)算法来支撑Lasso问题的解法,并进一步提出了修正的LARS算法,该算法通过消除了回归系数β异号的情况来得到Lasso问题的解。修正的LARS算法采用逐步回归,每一步路径都保持当前的残差与所有入选变量的相关性都相同,同时满足Lasso解与当前逼近保持同向的要求,保证最优结果,降低算法复杂度[6-7]。但LARS算法在求解过程中,利用了自变量的均分的“角分线”方向对解向量进行逼近,并没有考虑到不同变量对最终解的权重影响。
因此本文提出了采用多维权重的方式计算变量的权重,考虑到不是所有属性项(变量)都影响着检测结果,每个回归变量在回归模型中所占权重不同,即此属性变量在整体评价中的相对重要程度不同,因此,在LARS算法计算“角分线”时,将各回归变量与剩余变量的联合相关度纳入考虑,用来区分不同属性变量对检测结果的影响。实验通过Pima Indians Diabetes数据集,两组评价指标对本文提出的方法进行了讨论,其结果表明加入多维权重的LARS对Lasso问题的解答具有更高的准确性能。
1 Lasso问题及LARS算法 1.1 Lasso问题描述存在多维自变量设Xj∈Rn(j=1, 2, …, m),因变量y∈Rn,且每组自变量Xj都有对应的因变量y,用自变量Xj对因变量y进行线性回归,在限定回归系数β的L1范数小于t的情况下,求使得残差平方和最小的回归系数β的估值。因此,线性Lasso回归模型可以表示为:
| $ \boldsymbol{y} = \boldsymbol{X\beta} + \boldsymbol{e} $ | (1) |
其中:β是j维列向量,为待估参数; 误差向量e满足E(e)=0,且Var(e)=σ2。并且假定E(y|X)=β1x1+β2x2+…+βjxj。注意该模型是稀疏模型,即β1, β2, …, βj中有很多系数为零。变量选择的目的就是根据获取的数据来识别模型中哪些系数为零,并估计其他非零参数,即寻找构建稀疏模型的参数。需要求解的问题写成矩阵表达式为:
| $ \left( {\boldsymbol{\alpha, \beta }} \right){\text{ }} = {\text{ arg}}\;{\text{min}}{\left\| {\boldsymbol{y}-\boldsymbol{X\beta}-\boldsymbol{\alpha} } \right\|_2};\;\;\;{\text{ }}{\left\| \boldsymbol{\beta} \right\|_1} \leqslant t $ | (2) |
LARS算法很好地解决了Lasso问题,其建立在前向选择算法和前向梯度算法的基础上,逐步前进步长适中,降低计算复杂度的同时又尽可能地保留了信息相关性。LARS算法的基本步骤如下:
1) LARS算法判断自变量xK与y的相关度,用相关度最大的xK对y进行逼近。
2) 直到另一个xP具有相同的对y的相关度,即rxKy=rxPy,此时开始从xK与xP的“角分线”方向xU逼近y。
3) 同样的,当出现第三个xT对y相关度与xU相同时,将xT纳入到逼近队列中,选择三个向量共同的“角分线”方向xU进行新一轮逼近,此时“角分线”表示高维空间中各向量的平分线。
4) 逐步逼近直到残差小于某个阈值或所有自变量都参与进逼近,算法结束。
图 1中,两个自变量x1与x2与因变量y相关度rx1y>rx2y,用x1进行逼近,直至β1x1与y的残差和x1、x2的相关度相同,即残差处于x1与x2的角平分线上,此后用x1与x2的角平分线方向逼近因变量y。
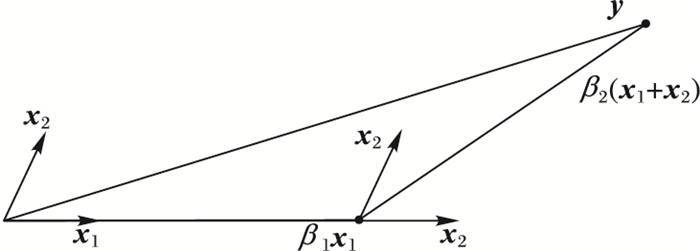
|
图 1 LARS算法求解步骤 Figure 1 Solving process of LARS algorithm |
在LARS逐步回归过程中,将所有入选变量视为同等重要进行角回归,每次逼近选择与y最大相关度xj,考虑到每个回归变量xj在回归模型中所占权重不同,即此指标在整体评价中的相对重要程度不同,将自变量xj与剩余变量的联合相关度纳入考虑。每一次逼近,将xj与y的相关度及Xj在整体指标中所占重要程度同时作为选择逼近特征的条件。
对于x1、x2,原LARS选择对y逼近变量的条件是回归变量对y的相关度,此时由rx1y>rx2y,将x1作为第一逼近变量;我们将自变量xj对整个系统的贡献率作为逼近条件之一,此时新的相关度为:
| $ {\boldsymbol{R}_{{X_i}y}} = \left. {{r_{{X_i}y}} * {W_{{X_j}}}} \right|_v^u $ | (3) |
其中:WXj为自变量xj对系统的贡献率,计算方法将在下面详细描述;u、v为常数。将自变量对y相关度与对系统的贡献率的乘积作为逼近条件,必然会增加判断条件的值域,为了保留系统逼近的稳定性,将乘积限制在某个值域范围内,即规定在[v, u]内。
经过变换后,可能使自变量xj的被选入性增加,如x2变换后向y靠近θ2,到达新的向量位x′2;x1变换后向y靠近θ1,到达新的向量位x′1。也可能使自变量被选入性减小,如x1变换后向y偏移θ3,到达新的向量位x″1,如图 2所示。
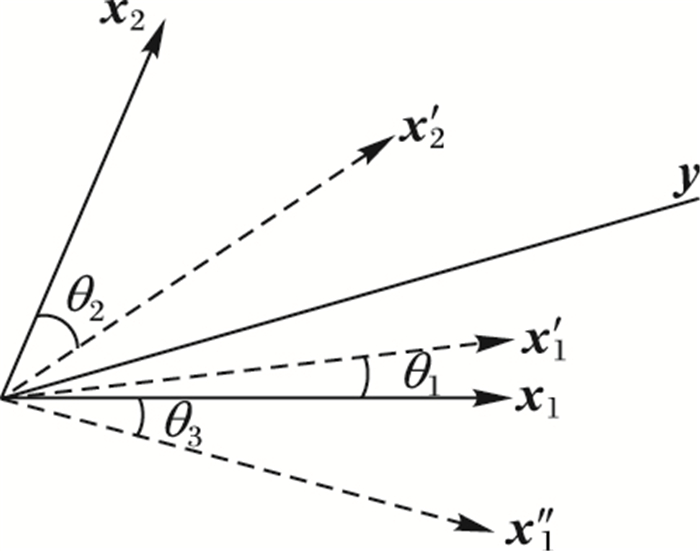
|
图 2 加入多维权重后X与y的相关性变化 Figure 2 Correlation change of X and y after joining multi-dimensional weight |
在图 2的基础上,采用新的相关度会对系统的逼近过程有较大的改变。如图 3所示,原初始逼近自变量为x1,前进至β1x1位置时,出现与残差e=y-β1x1相关度相同的变量x2,逼近方向改为x1和x2的角分线,再前进β2(x1+x2),完成逼近过程。采用新的逼近条件后,逼近过程有了较大改变:此时两个自变量被选入性改变,初始逼近自变量变为x′2,前进至β′1x′2位置时,x′1与残差e=y-β′1x′2相关度相同,逼近方向改为x′1和x′2的角分线,再前进β′2(x′1+x′2),完成逼近过程。可以看出,逼近路径改变,回归变量β1和β2也随着改变,得到改进回归方法下的新的回归变量组β。
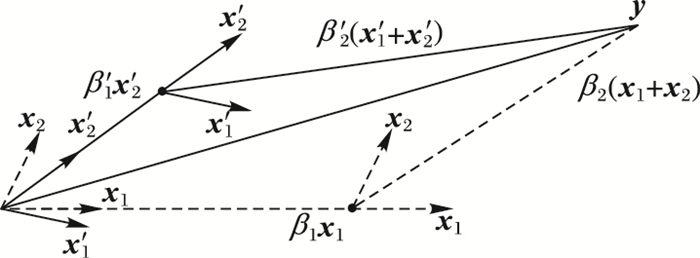
|
图 3 加入多维权重后的X前进方向 Figure 3 Approaching direction for X after joining multi-dimensional weight |
将上述过程应用到多维高阶系统,将m个特性指标及n个对象用矩阵表示为:
| $ {{\boldsymbol{X}}_{n \times m}} = \left[\begin{gathered} {x_{11}}\;\;{x_{12}}\;\;...\;\;{x_{1j}}\;\;...\;\;{x_{1m}} \hfill \\ {x_{21}}\;\;{x_{21}}\;\;...\;\;{x_{2j}}\;\;...\;\;{x_{2m}} \hfill \\ \; \vdots \;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\; \vdots \hfill \\ {x_{i1}}\;\;{x_{i2}}\;\;...\;\;\;{x_{ij}}\;\;...\;\;\;{x_{im}} \hfill \\ \vdots \;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\; \vdots \hfill \\ {x_{n1}}\;\;{x_{n2}}\;\;...\;\;{x_{nj}}\;\;...\;\;{x_{nm}} \hfill \\ \end{gathered} \right] $ | (4) |
或者表示为:
| $ \boldsymbol{X} = \left[{{\boldsymbol{X}_1}\;\;{\boldsymbol{X}_2}\;\;...\;\;{\boldsymbol{X}_j}\;\;...\;\;{\boldsymbol{X}_m}} \right] $ | (5) |
则应变量Y用矩阵表示为:
| $ \boldsymbol{Y} = {\left[{{\boldsymbol{y}_1}\;\;{\boldsymbol{y}_2}\;\;...\;\;{\boldsymbol{y}_i}\;\;...\;\;{\boldsymbol{y}_n}} \right]^{\text{T}}} $ | (6) |
回归过程中,WXi有多种计算方法,本文采用以下三种权重确定方法来控制回归过程。
1) 主成分分析法。
统计学中,主成分分析(Principle Component Analysis, PCA)借用正交变换进行降维[8-9],将数据变换到一个新的坐标系统中,使数据投影的最大方差处于第一坐标(称为第一主成分),第二方差处于第二坐标(称为第二主成分),依此类推。变换后,保留了数据集的低阶主成分,忽略高阶主成分,确定起支配作用的因素,通常保留总体信息利用率高于85%的前m个主成分。借用主成分分析法的思想,同时保留所有成分的评价值,确定每个成分的方差贡献率,算法步骤如下:
对样本进行如下标准化变换:
| $ {Z_{ij}} = \frac{{{x_{ij}}-{{\bar x}_j}}}{{{s_j}}};\;\;i = 1, 2, ..., n;j = 1, 2, ..., m $ | (7) |
其中:
| $ \left\{ \begin{gathered} {{\bar x}_j} = \sum\limits_{i = 1}^n {{x_{ij}}} /n \hfill \\ s_j^2 = \sum\limits_{i = 1}^n {{{\left( {{x_{ij}}-{{\bar x}_j}} \right)}^2}/\left( {n-1} \right)} \hfill \\ \end{gathered} \right. $ | (8) |
将相关系数矩阵R作为每个特征的信息利用率:
| $ \boldsymbol{R} = {[{r_{ij}}]_{n \times m}} = {\boldsymbol{Z}^{\text{T}}}\boldsymbol{Z}/\left( {n -1} \right) $ | (9) |
其中:
| $ {r_{ij}} = \sum {{z_{ij}} \cdot {z_{ij}}/\left( {n-1} \right)} $ | (10) |
2) 独立性权数法。
利用数据统计学中的多元回归方法,对特征的复相关系数进行排序,复相关系数越大,所重复的信息越多,信息利用率响应越小,权重越小。计算方式如下:
| $ {R'_j} = \frac{{\sum {\left( {{\boldsymbol{X}_j}-\boldsymbol{\bar X}} \right)\left( {\boldsymbol{\tilde X}-\boldsymbol{\bar X}} \right)} }}{{\sqrt {\sum {{{\left( {{\boldsymbol{X}_j}-\boldsymbol{\bar X}} \right)}^2}\sum {{{\left( {\boldsymbol{\tilde X} - \boldsymbol{\bar X}} \right)}^2}} } } }};\;j = 1, 2, ..., m $ | (11) |
其中:
| $ \boldsymbol{\bar X} = {\text{mean}}\left( \boldsymbol{X} \right) $ | (12) |
由R与权重为负比例关系,取复相关系数的倒数作为评分,经归一化处理得到权重系数,最终的权重表示为:
| $ \boldsymbol{R} = \left[{\begin{array}{*{20}{c}} {\frac{1}{{{{R'}_1}}}\;\;\frac{1}{{{{R'}_2}}}}& \cdots &{\frac{1}{{{{R'}_j}}}}& \cdots &{\frac{1}{{{{R'}_m}}}} \end{array}} \right];\;\;j = 1, 2, ..., m $ | (13) |
3) CRITIC法。
在独立权数法的基础上,更进一步,基于Intercriteria相关性的指标的重要度评价法(CRiteria Importance Though Intercriteria Correlation, CRITIC)是由Diakoulaki[10]提出的一种客观权重赋权法,它以确定指标的客观权数来评价指标间的对比强度和冲突性为基础。标准差的大小表明在同一指标内,各方案取值差距的大小,可用标准差表现对比强度;各指标间的冲突性是以指标之间的相关性为基础,可用相关度表示冲突性[11]。计算步骤如下:
第j个指标与其他指标的冲突性量化指标为:
| $ \sum\limits_{t = 1}^m {\left( {1-{r_{tj}}} \right)} $ | (14) |
其中,rtj表示评价指标Xt和Xj之间的相关系数:
| $ {r_t}_j = \frac{{\sum {\left( {{{\boldsymbol{X}}_t}-{\boldsymbol{\bar X}}} \right)\left( {{{\boldsymbol{X}}_j}-{\boldsymbol{\bar X}}} \right)} }}{{\sqrt {\sum {{{\left( {{{\boldsymbol{X}}_t}-{\boldsymbol{\bar X}}} \right)}^2}\sum {{{\left( {{{\boldsymbol{X}}_j} - {\boldsymbol{\bar X}}} \right)}^2}} } } }} $ | (15) |
Cj表示第j个指标所包含的信息量:
| $ {C_j} = {\sigma _j}\sum\limits_{t = 1}^m {\left( {1-{r_{tj}}} \right)} ;j = 1, 2, ..., m $ | (16) |
Cj越大,表示j个评价指标所包含的信息量越大[12-13],该指标的重要性也就越大,则第j个指标的客观权重表示为:
| $ {R_j} = {C_j}/\sum\limits_{j = 1}^m {{C_j}} ;\;\;j = 1, 2, ..., m $ | (17) |
以上所述三个方法得到权重后,将权重Rj集中化后表示权重对前进方向的影响:
| $ {R'_j} = centralization({R_j}) $ | (18) |
为获得稳定的数值解,对式(2) 进行预处理和归一化,消去常数α,并使结果向量y和自变量向量Xj(j=1, 2, …, m)零均值且l2范数归一。
定义指标集A={sj1xj1, sj2xj2, …, sjlxjl, …, sjkxjk}⊆{1, 2, …, m},存在从X中选出的满足指标集A的列向量XA,使其与y同向。
| $ {\boldsymbol{X}_A} = \left[{{s_{j1}}{x_{j1}}, {s_{j2}}{x_{j2}}, ..., {s_{jl}}{x_{jl}}, ..., {s_{jk}}{x_{jk}}} \right] \in {\boldsymbol{{\text{R}}}^{n \times k}} $ | (19) |
其中sjl为符号变量:
| $ {s_{jl}} = \left\{ {\begin{array}{*{20}{c}} {1, }&{\left\langle {{x_{jl}}, \boldsymbol{y}} \right\rangle > 0} \\ {0, }&{\left\langle {{x_{jl}}, \boldsymbol{y}} \right\rangle = 0} \\ {-1, }&{\left\langle {{x_{jl}}, \boldsymbol{y}} \right\rangle < 0} \end{array}} \right. $ | (20) |
定义XA中向量的“角分线”uA:
| $ \left\{ \begin{gathered} {\boldsymbol{G_A}} = \boldsymbol{X}_\boldsymbol{A}^{\text{T}}{\boldsymbol{X}_\boldsymbol{A}} \hfill \\ {\boldsymbol{A_A}} = {\left( {1_\boldsymbol{A}^T\boldsymbol{G}_\boldsymbol{A}^{-1}{1_\boldsymbol{A}}} \right)^{-\frac{1}{2}}} \hfill \\ {\boldsymbol{w}_\boldsymbol{A}} = {\boldsymbol{A_A}}\boldsymbol{G_A}^{-1}{1_\boldsymbol{A}} \hfill \\ {\boldsymbol{u}_\boldsymbol{A}} = {\boldsymbol{X_A}}{\boldsymbol{w_A}} \hfill \\ \end{gathered} \right. $ | (21) |
其中:1A为长度为|A|0所有元素为1的列向量;uA是角分线上的单位矢量;wA可理解为选中的变量集XA中每个属性Xl对角分线的贡献度。为改变前进方向与前进变量的选择,对wA进行加权处理。
进一步具体描述,初始逼近方向u0=0,且每次逼近产生新的u,假设上一步结束时算法的估计是
| $ \boldsymbol{c} = {\boldsymbol{X}^{\text{T}}}\left( {\boldsymbol{y}-{{\boldsymbol{\tilde u}}_\boldsymbol{A}}} \right)或{c_j} = \boldsymbol{\langle {x}_j}, \boldsymbol{y}-{\boldsymbol{\tilde u_A}}\rangle $ | (22) |
取
| $ {s_j} = {\text{sign}}\left\{ C \right\};\;\;j \in \boldsymbol{A} $ | (23) |
| $ \boldsymbol{a} = {\boldsymbol{X}^{\text{T}}}{\boldsymbol{u_A}}或{a_j} = \langle {\boldsymbol{x}_j}, {\boldsymbol{u_A}}\rangle $ | (24) |
此时算法沿uA方向前进的长度为:
| $ \gamma = \min _{j \notin A}^ + \left\{ {\frac{{C - {c_j}}}{{{A_A} - {a_j}}}, \frac{{C + {c_j}}}{{{A_A} + {a_j}}}} \right\} $ | (25) |
式中min上面的加号表示在此轮逼近中,只计算集合中正数的最小值。每个A中的自变向量相应增加γwA,同时加入权重控制逼近方向:
| $ \boldsymbol{w}' = \boldsymbol{w} \times {\boldsymbol{R}_{\tilde j}} $ | (26) |
| $ {\boldsymbol{\beta _A}} = {\boldsymbol{\beta _A}} + \gamma \boldsymbol{w}' $ | (27) |
其中
| $ {\boldsymbol{\tilde u_{A + }}} = {\boldsymbol{\tilde u_A}} + \boldsymbol{\gamma {u_A}}{\boldsymbol{R}_{\tilde j}} $ | (28) |
之后需要引入新的元素:
| $ {\boldsymbol{A}_ + } = \boldsymbol{A} \cup \left\{ {j'} \right\} $ | (29) |
其中j′是为式(25) 取最小值的j,为了符合Lasso解要求与当前逼近保持同向,在最早出现异号的步长为:
| $ \tilde \gamma {\text{ = }}\min _{j \notin A}^ + \left\{ {-{\beta _j}/w_j} \right\} $ | (30) |
当
输入 自变量集X,因变量集Y,误差项ε;
输出 式(2) 中的回归系数β。
1) 程序准备;
2) 数据预处理,对X、Y归一化;
3) 初始化:逼近方向u= 0, 残差
4)
5)
6)
7) Rweight=PCA(X)或Rweight=IW(X)或Rweight=CRITIC(X)
8) 集中化Rweight;
9) 当
10) LARS循环中
| $ \begin{gathered} rate = {\boldsymbol{R}_{{\text{weight}}}}\left( {1:row(w), :} \right); \hfill \\ \boldsymbol{w}' = \boldsymbol{w}*rate; \hfill \\ \end{gathered} $ |
11) 循环结束;
12) 返回回归系数β。
算法加入权重分析,增加了计算步骤,使得计算时间增加,但统计模型中各自变向量与因变向量的前进机制不变,空间复杂度与原算法保持一致。
3 实验结果与分析 3.1 数据集数据集采用美国约翰·霍普金斯大学应用物理实验室(Applied Physics Laboratory, The Johns Hopkins University)提供的皮马印第安人糖尿病数据集(Pima Indians Diabetes Data Set)[14]。该数据记录了768个体征性能描述与糖尿病阴阳性样本,包括8个属性变量和一个分类值,分类值中“1”表示检测结果为阳性,“0”表示检测结果为阴性。将8个不同属性值作为输入自变量Xj,是否患病作为输出因变量Y验证算法,检测目标是在原LARS算法结果上对检测结果准确度加以改进。
3.2 验证条件为了更直观地对本文提出的方法性能进行评估比较,本文采用ROC曲线展示结果。参与者糖尿病检测阴阳性为二元分类问题,检测的结果有以下四种类型:
1) 真阳性(True Positive, TP):检测为阳性,实际上也为阳性。2) 伪阳性(False Positive, FP):检测为阳性,实际却为阴性。3) 真阴性(True Negative, TN):检测为阴性,实际上也为阴性。4) 伪阴性(False Negative, FN):检测为阴性,实际却为阳性。
通过ROC空间四个基础类型统计,P表示正例,N表示负例,采用以下三个性质作为检查标准:
1) 准确度(ACCuracy, ACC):
| $ ACC = \left( {TP + TN} \right)/\left( {P + N} \right) $ |
2) 真阴性率(True Positive Ratio, TPR):
| $ TPR = TP/P = TP/\left( {TP + FN} \right) $ |
3) 阴性预测值(Negative Predictive Value, NPV):
| $ NPV = TN/\left( {TN + FN} \right) $ |
对于阈值t,从0开始以0.01为步长进行增加至1,以阴阳性为因变量,8个属性特征性能值为自变量,绘出准确度、阳性预测值、真阴性率的变化曲线。
图 4展示了在Pima Indians Diabetes数据集下,Lasso算法每轮循环后准确度以及Lasso算法每轮循环后的三项检查指标的综合最优值。
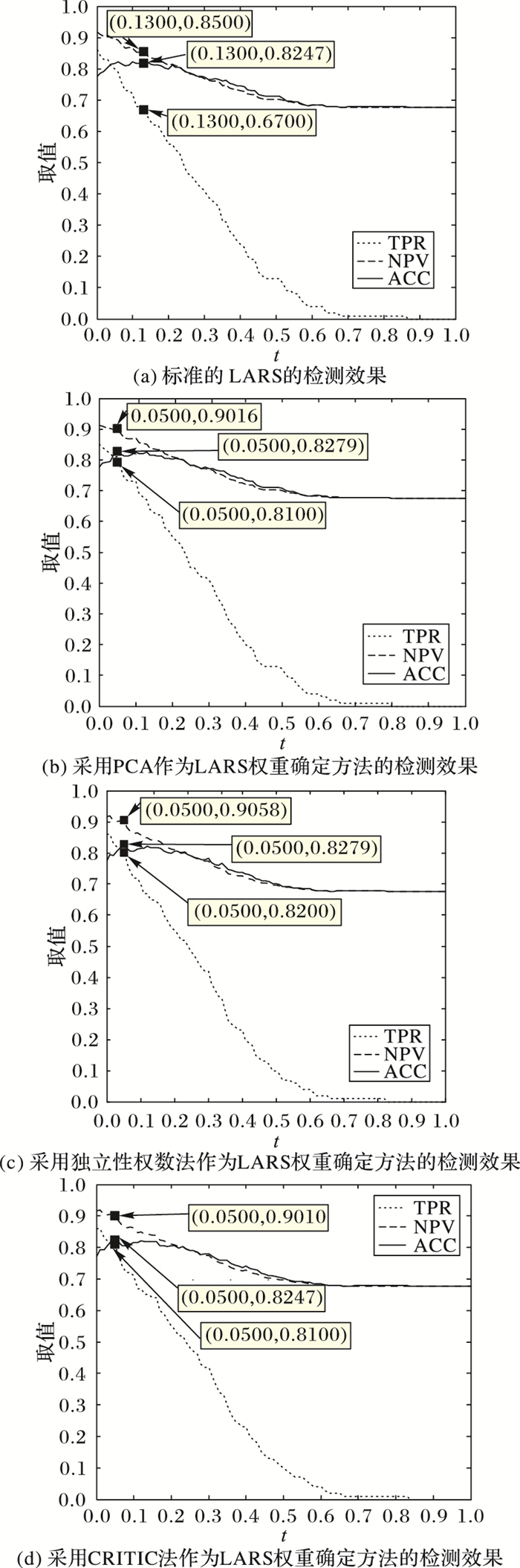
|
图 4 不同检测标准曲线 Figure 4 Curves of different detection standards |
NPV表示检测为阳性的人中实际为阳性即检测正确的比例,图 4中显示,加入权重后Lasso解法的NPV均有所提高,其中,加入主成分分析后NPV提高5.16个百分点,采用独立权数法NPV提高5.58个百分点,采用CRITIC法NPV提高5.1个百分点。
与NPV相比较,真阴性率(TPR)又称命中率,表示检测为阳性的人中检测正确的比例。图 4中显示,PCA对算法前进方向的改变使得TPR提高13个百分点,独立权数法使TPR提高14个百分点,CRITIC使TPR提高13个百分点。
准确度(ACC)表示在因变量阳性和阴性的总和中,经Lasso求解判断正确的个体点的个数,即检测为阳性、实际也阳性与检测为阴性、实际也为阴性的人数的总和,可以看出,加入主成分分析使得ACC增加了0.32个百分点,加入CRITIC法对ACC无影响,加入独立权数法后的Lasso解法使得ACC提高了0.32个百分点,三个方法都使ACC保持不变或有所提高。
综合以上三个指标,可以发现加入多维度权重的前进方向后,系统最优解的阈值减小,代表系统回归系数绝对值之和小于某一更小的阈值,即在更苛刻的阈值范围内满足要求。
图 5展示了在Pima Indians Diabetes数据集下,Lasso算法每轮循环因变量与角分线方向的残量的平方和(Sum of Squared Residuals, SSR),而SSR平稳的转折点就对应了Lasso在Pima Indians Diabetes数据集中进行回归的最佳自变量系数。
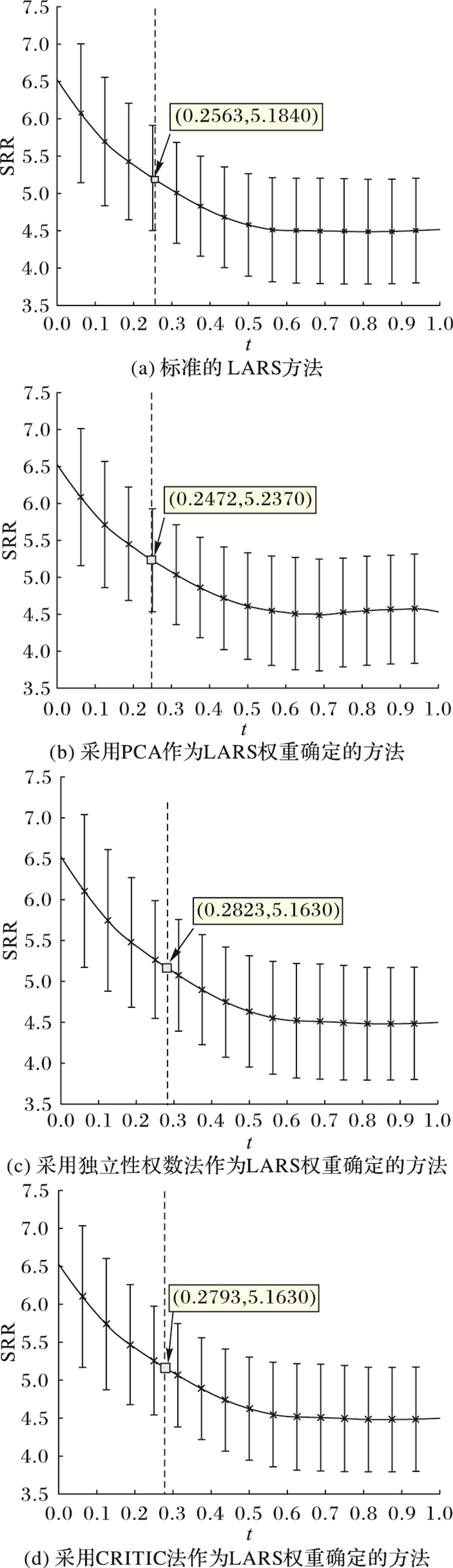
|
图 5 因变量与角分线方向的残量的平方曲线 Figure 5 Curve of the sum of squared residuals for dependent variable and angle bisector direction |
由图 5可以看出,加入不同权重判定后,SSR的整体走向完全一致,且最佳系数处对应的残量基本保持一致,加入权重后不会改变Lasso解法原有的优点。最佳自变量系数有明显的增大,此时所对应的因变量与角分线方向的残量有所变化,其中:加入主成分分析法的Lasso解法增加了5.1个百分点的残量,加入独立权数法降低了2.1个百分点的残量,加入CRITIC法降低了2.1个百分点的残量,即加入独立权数法和CRITIC法后最后的回归结果更接近真实因变量。
综合以上指标,加入独立权数法后Lasso解的准确性最高,其次是CRITIC法和主成分分析法。加入权重通过改变回归系数方向提高解准确性,表 1展示了原始的回归系数β以及加入主成分分析法后的β-PCA,加入独立权数法后的β-IW,加入CRITIC法后的β-CRITIC。从表 1中可以看出,β-IW对应的回归系数相对于原始回归系数有一定减小,取值区间变窄,但其收敛性没有改变,而且从图 5中可以看出,其回归结果更加准确。
| 表 1 不同方法回归系数 Table 1 Regression coefficients of different methods |
本文针对Lasso问题的解法即LARS算法的选择变量与前进方向过程,提出了基于多维权重的LARS算法,提高了Lasso问题解的准确性,并且保持原Lasso的参数估计具有稳定的回归系数、较少参数数量的同时具有较好的参数收敛一致性,并采用Pima Indians Diabetes数据集验证算法的有效性。由于自变量集维数较大,计算权重的准确度存在瑕疵,因此以后研究中需要进一步优化嵌入的确定权重的算法,以提升回归算法在利用权重改变前进变量和前进方向选择时的精度和准确度。
| [1] | 马景义, 张辛连, 苏治, 等. 广义线性模型组LASSO路径算法[J]. 中国科学:数学, 2015, 45(10): 1725-1738. ( MA J Y, ZHANG X L, SU Z, et al. An algorithm for the estimation of regularization paths of generalized linear models with group LASSO penalty[J]. SCIENTIA SINICA Mathematica, 2015, 45(10): 1725-1738. ) |
| [2] | FRANK I E, FRIEDMAN J H. A statistical view of some chemometrics regression tools[J]. Technometrics, 1993, 35(2): 109-135. doi: 10.1080/00401706.1993.10485033 |
| [3] | BREIMAN L. Better subset regression using the nonnegative garrote[J]. Technometrics, 1995, 37(4): 373-384. doi: 10.1080/00401706.1995.10484371 |
| [4] | TIBSHIRANI R. Regression shrinkage and selection via the Lasso[J]. Journal of the Royal Statistical Society. Series B (Methodological), 1996, 58(1): 267-288. |
| [5] | EFRON B, HASTIE T, JOHNSTONE I, et al. Least angle regression[J]. The Annals of Statistics, 2004, 32(2): 407-499. doi: 10.1214/009053604000000067 |
| [6] | 李锋, 盖玉洁, 卢一强. 测量误差模型的自适应LASSO变量选择方法研究[J]. 中国科学:数学, 2014, 44(9): 983-1006. ( LI F, GAI Y J, LU Y Q. Adaptive LASSO for measurement error models[J]. SCIENTIA SINICA Mathematica, 2014, 44(9): 983-1006. ) |
| [7] | MARAHIEL M A. Introducing Lasso peptides as a molecular scaffold for drug design[J]. Journal of Peptide Science, 2014, 20: S27-S28. |
| [8] | SHAHBEIG S, POURGHASSEM H. Fast and automatic algorithm for optic disc extraction in retinal images using principle-component-analysis-based preprocessing and curvelet transform[J]. Journal of the Optical Society of America A-Optics Image Science and Vision, 2013, 30(1): 13-21. doi: 10.1364/JOSAA.30.000013 |
| [9] | WANG J, WANG J. Forecasting stock market indexes using principle component analysis and stochastic time effective neural networks[J]. Neurocomputing, 2015, 156: 68-78. doi: 10.1016/j.neucom.2014.12.084 |
| [10] | DIAKOULAKI D, MAVROTAS G, PAPAYANNAKIS L. Determining objective weights in multiple criteria problems:the CRITIC method[J]. Computers & Operations Research, 1995, 22(7): 763-770. |
| [11] | ALHAMZAWI R, YU K M. Bayesian Lasso-mixed quantile regression[J]. Journal of Statistical Computation and Simulation, 2014, 84(4): 868-880. doi: 10.1080/00949655.2012.731689 |
| [12] | KAUL A. Lasso with long memory regression errors[J]. Journal of Statistical Planning and Inference, 2014, 153: 11-26. doi: 10.1016/j.jspi.2014.05.003 |
| [13] | LI L H, MO R. A comprehensive decision-making approach based on hierarchical attribute model for information fusion algorithms' performance evaluation[J]. Mathematical Problems in Engineering, 2014, 2014: 2014:Article ID 124156. |
| [14] | BACHE K, LICHMAN M. UCI machine learning repository[DB/OL]. Irvine, CA:University of California.[2016-09-20]. http://archive.ics.uci.edu/ml. |



 ,
,