微波有源非线性电路的分析与设计一直是微波技术领域的主要工作, 自20世纪80年代以来, 谐波平衡法[1-2]被广泛应用于射频微波电路的非线性分析中。谐波平衡分析中算法求解过程较为耗时且精度不高。拟牛顿算法[3]每次迭代只需通过测量梯度的变换构造一个目标函数模型从而达到超线性收敛特性, 避免了牛顿法中Hessen矩阵的计算, 更适合现实大规模非线性电路的求解;但若初值远离极值点将导致算法不收敛。文献[4]引入伽辽金法以减少谐波分析时采用过采样技术产生的多项式方程, 从而降低求解维度;但在求解过程中计算目标函数一阶导数及Hessen矩阵时增加了算法的计算复杂度。针对以上问题, 文献[5]提出拟牛顿粒子群算法, 可有效避免传统算法对初值的限制, 且无需进行目标函数导数计算, 在一定程度上加快了算法后期收敛, 但粒子群算法易陷入局部最优, 导致求解精度受限; 文献[6]提出的混合蚁群算法虽提高了算法后期收敛速度, 但由于蚁群算法迭代初期信息素匮乏, 算法初期仍存在收敛较慢的问题。针对以上算法的问题和不足, 有必要去探索新型智能、高效的算法来提高收敛速度及求解精度。
人工蜂群 (Artificial Bee Colony, ABC) 算法[7]作为一种新兴的群智能优化技术, 由于其控制参数少、易于实现、计算方便等优点, 近几年备受学者关注。文献[8]受粒子群速度进化公式启发, 在蜜源搜索中引入“自我认知能力”和“社会认知能力”, 提高了算法的寻优能力, 同时加入互斥因子以保证种群的多样性; 文献[9]引入拥挤距离保持种群的多样性, 并根据帕累托最优理论改进跟随蜂选择概率, 在保持种群多样性的同时提高了求解精度; 文献[10]将正交学习策略引入到搜索公式中, 使产生的解更具搜索前景, 增强了局部寻优能力; 文献[11]通过调整递进步长使搜索精度提高, 并引入了最大尝试次数, 从而加快算法收敛。上述文献虽然针对ABC算法的不足提出了多种改进策略, 但在平衡算法探索能力和开发能力方面仍需进行进一步的研究。
本文在标准蜂群算法的基础上, 为克服算法易陷入局部最优、后期收敛速度慢的缺点以及提高算求解精度, 引入动态调整因子ω, 使引领蜂由随机搜索转为向着当前最优解方向搜索, 在保证遍历性的同时减少了算法的迭代次数; 参照文献[5-6]的局部寻优策略, 在收敛后期将BFGS (Broyden-Fleteher-Goldfarl-Shanno) 算法融合到改进的蜂群算法中, 将当前最优解作为BFGS算法的初始值, 利用其快速收敛的优点提高改进算法后期的迭代速度。实验结果表明, 改进算法能有效应用于求解谐波平衡方程。
1 谐波平衡分析方程对于大信号下的射频电路, 去除激励源, 可以把其大信号等效电路分为线性和非线性两部分12, 根据Kirchhoff定律线性与非线性端口电流相等可得到谐波平衡方程, 再采用适当的算法求解, 进而可求出电路中任意元件上的电流和电压值, 且求得的值含有谐波, 可以很好地描述电路中的非线性现象。
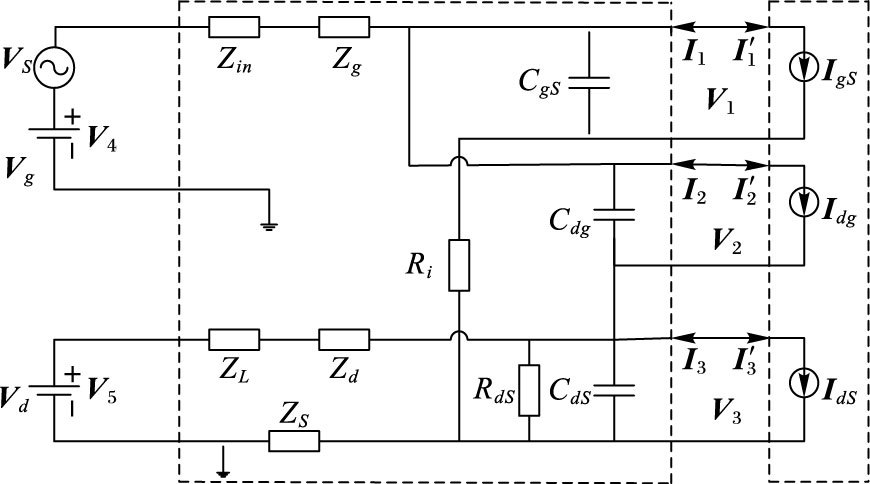
图 1为金属-半导体场效晶体管 (Metal-Semiconductor Field-Effect Transistor, MESFET) 大信号模型电路模型2, 电路中的非线性网络仅包含非线性元件, 分别是压控电流源Igs、Idg和Ids; 线性网络包含电路中所有的线性元件、源端阻抗、负载阻抗以及直流偏置和激励, 其中Zin和ZL分别为输入、输出匹配阻抗。Vs是输入信号, Vg和Vd为栅极和漏极的直流偏置电压。谐波平衡方程的频域表达式如下:
|
图 1 经分解的晶体管大信号电路模型 Figure 1 Decomposed large signal circuit model of the transistor |
| $\mathit{\boldsymbol{f}}\left( \mathit{\boldsymbol{V}} \right)=\left[ \begin{array}{*{35}{l}} {{\mathit{\boldsymbol{I}}}_{1}} \\ {{\mathit{\boldsymbol{I}}}_{2}} \\ {{\mathit{\boldsymbol{I}}}_{3}} \\ \end{array} \right]+\left[ \begin{array}{*{35}{l}} {{\mathit{\boldsymbol{I}}}^{'}}_{1} \\ {{\mathit{\boldsymbol{I}}}^{'}}_{2} \\ {{\mathit{\boldsymbol{I}}}^{'}}_{3} \\ \end{array} \right]=\left[ \begin{array}{*{35}{l}} \bf{0} \\ \bf{0} \\ \bf{0} \\ \end{array} \right]$ | (1) |
其中线性网络电流可表示为:
| $\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{I}}_1}}\\ {{\mathit{\boldsymbol{I}}_2}}\\ {{\mathit{\boldsymbol{I}}_3}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{Y}}_{11}}}&{{\mathit{\boldsymbol{Y}}_{12}}}&{{\mathit{\boldsymbol{Y}}_{13}}}\\ {{\mathit{\boldsymbol{Y}}_{21}}}&{{\mathit{\boldsymbol{Y}}_{22}}}&{{\mathit{\boldsymbol{Y}}_{23}}}\\ {{\mathit{\boldsymbol{Y}}_{31}}}&{{\mathit{\boldsymbol{Y}}_{32}}}&{{\mathit{\boldsymbol{Y}}_{33}}} \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{V}}_1}}\\ {{\mathit{\boldsymbol{V}}_2}}\\ {{\mathit{\boldsymbol{V}}_3}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{Y}}_{14}}}&{{\mathit{\boldsymbol{Y}}_{15}}}\\ {{\mathit{\boldsymbol{Y}}_{24}}}&{{\mathit{\boldsymbol{Y}}_{25}}}\\ {{\mathit{\boldsymbol{Y}}_{34}}}&{{\mathit{\boldsymbol{Y}}_{35}}} \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{V}}_4}}\\ {{\mathit{\boldsymbol{V}}_5}} \end{array}} \right]$ |
V4由直流偏压Vg和基波偏压Vs组成, V5由直流偏压Vd组成。其中,V1、V2、V3即为所求, 在求解算法中需对其进行初值设定。导纳矩阵Y中的元素也都是矩阵形式, 每一个子矩阵都是对角线矩阵形式, 它的元素Ym, n是在每一个基本激励频率ωp的谐波k(k=0, 1, …, K) 上的分量。
| ${\mathit{\boldsymbol{Y}}_{m,n}} = {\rm{diag}}\left[ {{\mathit{\boldsymbol{Y}}_{m,n}}(k{\mathit{\boldsymbol{\omega }}_p})} \right];{\rm{ }}k = 0,1, \cdots ,K$ | (2) |
电流矢量In是第n个端口的电流谐波:
| ${\mathit{\boldsymbol{I}}_n} = {\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{I}}_{n,0}}}&{{\mathit{\boldsymbol{I}}_{n,1}}}& \cdots &{{\mathit{\boldsymbol{I}}_{n,k}}} \end{array}} \right]^{\rm{T}}}$ |
非线性网络中的Igs、Idg和Ids根据经验公式[1]可表达为:
| ${\mathit{\boldsymbol{I}}_{gs}} = {\mathit{\boldsymbol{I}}_{g0}}({e^{{\alpha _f}{V_g}}} - 1)$ | (3) |
| ${\mathit{\boldsymbol{I}}_{dg}} = {\mathit{\boldsymbol{I}}_{b0}}({e^{{\alpha _r}{V_{dg}}}} - 1)$ | (4) |
| ${\mathit{\boldsymbol{I}}_{ds}} = \frac{{\beta {{({\mathit{\boldsymbol{V}}_g} - {\mathit{\boldsymbol{V}}_T})}^2}}}{{1 + b({\mathit{\boldsymbol{V}}_g} - {\mathit{\boldsymbol{V}}_T})}}(1 + \lambda {\mathit{\boldsymbol{V}}_d}){\rm{tanh}}(\alpha {\mathit{\boldsymbol{V}}_d})$ | (5) |
其中:电流Igs受电容Cgs两端的电压Vg控制, Vg即为模型中的1端口电压V1; Idg受电容Cdg两端电压Vdg控制;Vdg为模型中的2端口电压V2; Ids与电压Vg和Vd有关, Vd=Vds-IgRs-Id(Rd+Rs)。式 (3) ~(5) 中的Ig0、Ib0、αf、αr、β、λ、b、VT和α利用MESFET直流特性得到。
最后谐波平衡方程可表达为:
| $\begin{array}{l} \mathit{\boldsymbol{f}}\left( \mathit{\boldsymbol{V}} \right) = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{Y}}_{11}}}&{{\mathit{\boldsymbol{Y}}_{12}}}&{{\mathit{\boldsymbol{Y}}_{13}}}\\ {{\mathit{\boldsymbol{Y}}_{21}}}&{{\mathit{\boldsymbol{Y}}_{22}}}&{{\mathit{\boldsymbol{Y}}_{23}}}\\ {{\mathit{\boldsymbol{Y}}_{31}}}&{{\mathit{\boldsymbol{Y}}_{32}}}&{{\mathit{\boldsymbol{Y}}_{33}}} \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{V}}_1}}\\ {{\mathit{\boldsymbol{V}}_2}}\\ {{\mathit{\boldsymbol{V}}_3}} \end{array}} \right] + \\ \quad \quad \quad \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{Y}}_{14}}}&{{\mathit{\boldsymbol{Y}}_{15}}}\\ {{\mathit{\boldsymbol{Y}}_{24}}}&{{\mathit{\boldsymbol{Y}}_{25}}}\\ {{\mathit{\boldsymbol{Y}}_{34}}}&{{\mathit{\boldsymbol{Y}}_{35}}} \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{V}}_4}}\\ {{\mathit{\boldsymbol{V}}_5}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{I}}_{gs}}}\\ {{\mathit{\boldsymbol{I}}_{dg}}}\\ {{\mathit{\boldsymbol{I}}_{ds}}} \end{array}} \right] = 0 \end{array}$ | (6) |
f(V) 即为电流误差矢量, 在求解过程中作为目标函数。
2 融合BFGS的自适应蜂群算法针对蜂群算法后期收敛速度较慢, 将引领蜂搜索公式进行改进, 使其具有动态自适应性, 在保证算法遍历性的前提下加快局部收敛特性; 同时在算法后期加入BFGS算法, 使其达到快速收敛。
2.1 标准蜂群算法蜂群算法[13-15]通过模拟蜜蜂采蜜机制处理函数优化问题。在求解优化问题时, 食物源的位置即为解空间, 优化问题的可行解的集合称为一个种群, 种群中每个个体 (可行解) 对应一个食物源, 食物源的优劣程度取决于待优化问题的适应度值, 可行解的个数等于引领蜂与跟随蜂之和。谐波平衡方程可以看作是非线性函数最小值问题, 可表示为min f(V), 由式 (1) 得到适应度函数:
| $\mathit{\boldsymbol{fi}}{\mathit{\boldsymbol{t}}_i} = \left| {f\left( {{\mathit{\boldsymbol{V}}_i}} \right)} \right|$ | (7) |
下面对ABC算法求解谐波平衡方程的关键步骤进行介绍:
1) 设置初始进化代数m=0, 最大循环次数mMAX, 标志向量bas(u)=0记录每个个体 (可行解) 出现的次数。在m=0时刻, 算法根据式 (8) 随机生成NP个个体V构成初始种群。
| $\mathit{\boldsymbol{V}}_i^j = \mathit{\boldsymbol{V}}_i^{{\rm{min}}} + {\rm{rand}}\left( {} \right) \times (\mathit{\boldsymbol{V}}_i^{{\rm{max}}} - \mathit{\boldsymbol{V}}_i^{{\rm{min}}});{\rm{ }}i = 1,2 \cdots ,NP$ | (8) |
其中: j∈{1, 2, …, D}, 为D维解向量的某个分量; Vimax和Vimin分别为V取值的上、下限; rand () 为区间[-1, 1]内的随机数。针对目标函数f(V), 待求参量V1、V2、V3组成一个可行解,其中每个电压都为矢量形式,可分为K+1个频率成分电压,并且每个频率成分电压都有实部虚部,故谐波平衡方程中含有2N(K+1) 个变量,K为谐波次数,N为端口数量。因此V1、V2、V3所组成的可行解的维数D=2N(K+1),为了一下算法阐述方便,用j表示维数,j∈{1, 2, …, 2N(K+1) }。V=(V1, V2, …, VNP) 代表一个种群,V(0)表示初始种群。分别计算各解向量的适应度函数值, 将适应度值较小的一半作为初始引领蜂种群V(0)。
2) T=t时刻, 对于第t代的引领蜂V(t), 在其当前位置附近邻域内, 局部搜索新的食物源 (可行解) 搜索公式为:
| $\mathit{\boldsymbol{X}}_i^j = \mathit{\boldsymbol{V}}_i^j + {\rm{rand}}\left( {} \right) \times (\mathit{\boldsymbol{V}}_i^j - \mathit{\boldsymbol{V}}_k^j)$ | (9) |
其中: j∈{1, 2, …, D}; k∈{1, 2, …, NP/2}随机生成; rand () 为区间[0, 1]内的随机数。对引领蜂局部搜索生成的Xi和目标个体Vi进行适应度值计算并比较, 保留适应度值较小的个体, 确保种群在进化方向上不出现退化。
| ${\mathit{\boldsymbol{V}}_i^j = \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{X}}_i^j,}&{fit\left( {\mathit{\boldsymbol{X}}_i^j} \right) \le fit\left( {\mathit{\boldsymbol{V}}_i^j} \right)}\\ {\mathit{\boldsymbol{V}}_i^j,}&{fit(\mathit{\boldsymbol{X}}_i^j) > fit(\mathit{\boldsymbol{V}}_i^j)} \end{array}} \right.}$ | (10) |
3) 跟随蜂根据概率式 (11) 在新的引领蜂种群中选择较优个体Vkj, 个体的概率越小, 其对应的食物源质量就越好。跟随结束后按式 (9) ~(10) 进行搜索择优, 产生新个体Vkj(k∈{NP/2+1, NP/2+2, …, NP}), 形成跟随蜂种群。
| ${{P_i} = \mathit{\boldsymbol{fi}}{\mathit{\boldsymbol{t}}_i}/\sum\limits_{i = 1}^{NP/2} {\mathit{\boldsymbol{fi}}{\mathit{\boldsymbol{t}}_i}} }$ | (11) |
4) 当某一个引领蜂对应的食物源经多次搜索后仍为发现的最优位置, 即bas(u)≥limit(limit为设定的淘汰条件), 对应的个体被淘汰并按式 (8) 搜索产生新个体。此淘汰机制可避免种群多样性丧失, 防止种群陷入局部最优值。
5) 若满足终止条件, 算法停止迭代, 输出最优食物源位置 (最优解);否则跳转至步骤2) 继续执行。
2.2 BFGS自适应蜂群算法 2.2.1 搜索公式改进标准蜂群算法的邻域搜索公式通过随机变量控制邻域食物源位置搜索, 存在很大的盲目性, 从而影响了算法的收敛速度。由于谐波平衡方程呈现非线性, 故在改进搜索公式时考虑引入非线性的动态调整因子。本文将自适应动态调整因子ω代替搜索公式中的随机变量, 在保证算法遍历性的同时加快算法的收敛速度。改进搜索公式如下:
| $\mathit{\boldsymbol{X}}_i^j = \mathit{\boldsymbol{V}}_i^j + \mathit{\boldsymbol{\omega }}\left( {\mathit{\boldsymbol{V}}_i^j - \mathit{\boldsymbol{V}}_k^j} \right)$ | (12) |
| $\mathit{\boldsymbol{\omega }} = \left\{ {\begin{array}{*{20}{l}} {\frac{{{\mathit{\boldsymbol{\omega }}_{{\rm{min}}}} - \left( {{\mathit{\boldsymbol{\omega }}_{{\rm{max}}}} - {\mathit{\boldsymbol{\omega }}_{{\rm{min}}}}} \right)\left( {\mathit{\boldsymbol{fi}}{\mathit{\boldsymbol{t}}_i} - \mathit{\boldsymbol{fi}}{\mathit{\boldsymbol{t}}_{{\rm{min}}}}} \right)}}{{\left( {\mathit{\boldsymbol{fi}}{\mathit{\boldsymbol{t}}_{{\rm{avg}}}} - \mathit{\boldsymbol{fi}}{\mathit{\boldsymbol{t}}_{{\rm{min}}}}} \right)}},}&{\mathit{\boldsymbol{fi}}{\mathit{\boldsymbol{t}}_i} \le \mathit{\boldsymbol{fi}}{\mathit{\boldsymbol{t}}_{{\rm{avg}}}}}\\ {{\mathit{\boldsymbol{\omega }}_{{\rm{max}}}},}&{\mathit{\boldsymbol{fi}}{\mathit{\boldsymbol{t}}_i} > \mathit{\boldsymbol{fi}}{\mathit{\boldsymbol{t}}_{{\rm{avg}}}}} \end{array}} \right.$ |
其中:ωmax、ωmin分别表示自适应动态调整因子ω的最大值和最小值; fiti代表引领蜂当前的适应度值; fitavg表示平均适应度值; fitmin表示最小的适应度值。自适应调整因子随着适应度值而自动改变,因此使得改进的搜索公式具有自适应性。
对于适应度值小于平均适应度值的引领蜂,其对应的自适应调整因子较小,从而保护了这个引领蜂所在蜜源; 反之,对于适应度值大于平均适应度值的引领蜂,其对应的自适应调整因子较大,增大搜索的全局性,使其向较好的蜜源靠拢。
2.2.2 BFGS算法BFGS算法是一种应用最为广泛的拟牛顿算法[16], 不需要计算Hessen矩阵, 同时保存了牛顿算法的超线性收敛特性。为加快蜂群算法的局部搜索特性, 本文将BFGS算法融合到自适应蜂群算法求解中, BFGS算法校正公式如下:
| $\begin{array}{l} {\mathit{\boldsymbol{H}}_{k + 1}} = {\mathit{\boldsymbol{H}}_k} + \frac{{{\mathit{\boldsymbol{S}}_k}{{({\mathit{\boldsymbol{S}}_k})}^{\rm{T}}}}}{{{{({\mathit{\boldsymbol{S}}_k})}^{\rm{T}}}{\mathit{\boldsymbol{y}}_k}}}\left[ {1 + \frac{{{{({\mathit{\boldsymbol{y}}_k})}^{\rm{T}}}{\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{y}}_k}}}{{{{({\mathit{\boldsymbol{S}}_k})}^{\rm{T}}}{\mathit{\boldsymbol{y}}_k}}}} \right] - \\ \quad \quad \frac{1}{{{{({\mathit{\boldsymbol{S}}_k})}^{\rm{T}}}{\mathit{\boldsymbol{y}}_k}}}\left[ {{\mathit{\boldsymbol{S}}_k}{{({\mathit{\boldsymbol{y}}_k})}^{\rm{T}}}{\mathit{\boldsymbol{H}}_k} + {\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{y}}_k}{{({\mathit{\boldsymbol{S}}_k})}^{\rm{T}}}} \right] \end{array}$ |
当蜂群算法运行达到最大的循环次数mMAX时, 将蜂群算法当前最优解作为BFGS算法的初值V(0), 具体步骤如下:
步骤1 给定初值点V(0), 设定H0为I, I为单位矩阵, 精度εMAX。
步骤2 判断f(V(0))≤εMAX, 若成立输出结果V(0);否则令q(k)=-Hk∇f(V(k)), k=0。
步骤3 进行一维搜索求得αk, 使
步骤4 判断f(V(k+1))≤εMAX, 若成立则输出V(k+1),否则转至步骤5。
步骤5 通过校正公式得到Hk+1, 其中Sk=V(k+1)-V(k), yk=∇f(V(k+1))-∇f(V(k)), 令q(k)=-Hk+1∇f(V(k+1)), k=k+1, 转至步骤3。
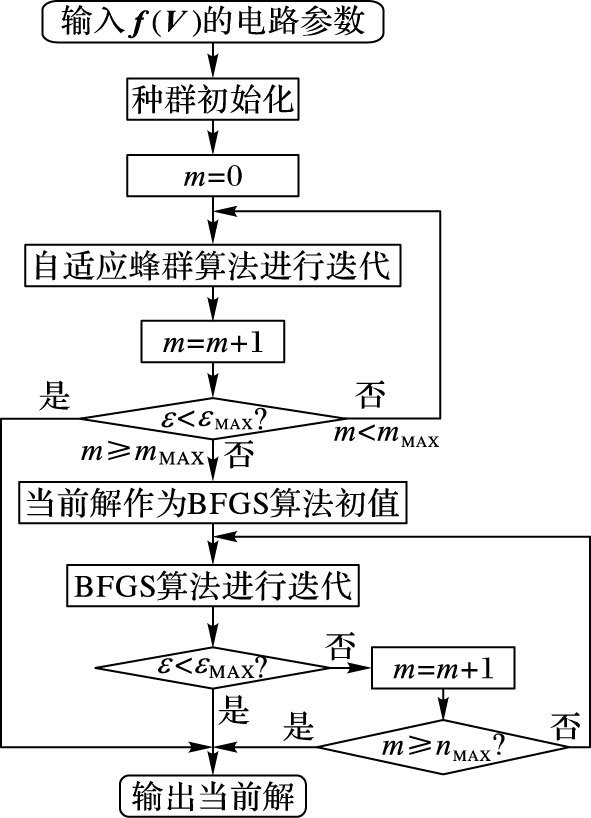
2.2.3 融合BFGS算法的自适应蜂群算法改进算法求解f(V) 的流程如图 2所示。
|
图 2 改进算法流程 Figure 2 Flow chart of improved algorithm |
步骤1 初始化种群, 自适应蜂群算法最大循环次数mMAX, 改进算法全局最大循环次数nMAX, 误差精度εMAX, 初始进化代数m, 标志向量bas(u), 根据式 (8) 生成初始解, 计算每个解的适应度。
步骤2 取适应度值较小的一半个体为引领蜂, 根据式 (11) 进行自适应搜索产生新解X, 并计算各解向量的适应度函数值。
步骤3 根据式 (10) 进行贪婪选择, 若Xi的适应度值小于Vi, 则用Xi代替Vi, 将Xi作为当前最优解;否则保留Vi。
步骤4 计算选择概率Pi, 跟随蜂根据Pi选择食物源, 根据式 (12) 进行邻域搜索产生新解Xi, 并计算各解向量的适应度函数值。
步骤5 对跟随蜂搜索产生新解的适应度函数值与原跟随蜂种群中解的适应度函数值根据式 (10) 进行贪婪选择。
步骤6 判断是否有需要放弃的解, 若bas(u)≥limit, 侦查蜂根据式 (8) 生成一个新解代替原个体。
步骤7 判断是否满足精度εMAX, 若达到精度要求,即ε<εMAX,则输出当前解。反之, 判断是否达到自适应蜂群算法最大的循环次数mMAX, 若m≥mMAX, 转至步骤8;否则转至步骤2。
步骤8 将得到的当前较优解作为BFGS算法的初值V(0), 继续进行迭代, 当满足精度εMAX或达到最大循环次数nMAX时, 算法结束, 输出当前解;若不满足, 继续按步骤8进行迭代。
2.3 时间复杂度分析融合BFGS的自适应蜂群算法与标准蜂群算法在搜索策略和后期迭代方式上均有不同, 因此, 需要对改进蜂群算法的时间复杂度进行分析。设种群大小为NP, 算法 (迭代一次) 的时间复杂度分析如下:引领蜂进行局部搜素的时间复杂度为O(NP), 计算蜜源适应度值和蜜源择优更新的时间复杂度均为O(NP), 跟随蜂采用轮盘赌方式进行跟随的时间复杂度为O(NP2), 之后进行局部搜索和蜜源更新的时间复杂度均为O(NP), 侦查蜂阶段进行蜜源更新的时间复杂度为O(NP)。搜索公式更新后的蜜源的局部搜索时间复杂度仍为O(NP), BFGS算法的时间复杂度为O(NP)。
综上所述融合BFGS的自适应蜂群算法的最差时间复杂度为O(NP2), 同理, 标准蜂群算法的最差时间复杂度为O(NP2), 所以改进蜂群算法并没有增加原始算法的时间复杂度。
3 仿真分析本文选用MRF6S19060N晶体管, 用Matlab软件进行电路建模分析, 建立并计算谐波平衡方程。晶体管漏极直流电压VDS=28 V, 漏极静态电流IDQ=0.632 A, 栅极偏压VGS=2.7 V, 工作频率为1.96 GHz, 输入功率为20 dBm, 源端阻抗和负载阻抗均为50 Ω。改进蜂群算法部分参数设置如下:NP=40,ωmax=0.9,limit=30,ωmin=0.6。
3.1 算法收敛时间分析本次实验选取谐波数目K分别为8和16, mMAX=50, 将误差精度作为算法终止条件, 精度选取如表 1所示, 在每个误差精度下随机进行20次独立实验。为了验证本文算法的性能, 分别与求解谐波平衡的基本算法 (BFGS算法)、改进粒子群算法[5]、混合蚁群算法[6]比较分析。
| 表 1 算法平均收敛时间 Table 1 Average convergence time of the algorithm |
如表 2所示, 本文改进算法相对于BFGS算法, 在求解较高精度解以及高谐波的条件下, 收敛速度明显提高; 较文献[5-6]算法在相同精度和谐波数的情况下, 收敛时间均有不程度的减少。
| 表 2 收敛可靠性对比 % Table 2 Comparison of convergence reliability % |
分别采用BFGS算法、标准蜂群算法和本文改进算法随机进行100次独立实验, 将最大迭代次数100作为算法终止条件。表 2给出了3种算法求解谐波平衡方程的收敛可靠性。
由表 3可以看出, 融合BFGS的自适应蜂群算法收敛可靠性达到100%;标准蜂群算法由于后期收敛速度较慢, 其收敛可靠性仅为21%;拟牛顿算法受初值选取的限制, 收敛可靠性为64%。由此证明改进算法很好地解决了拟牛顿算法的初值依赖问题, 提高了算法的收敛可靠性。
| 表 3 栅、漏极电压谐波 V Table 3 Gate, drain voltage harmonics V |
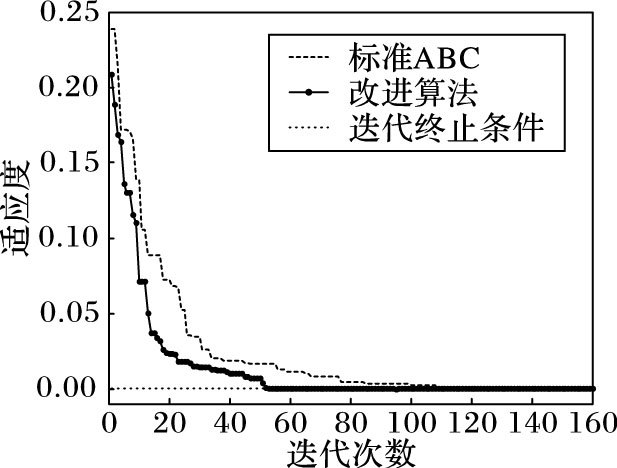
图 3是标准蜂群算法与本文改进算法求解谐波平衡方程的迭代曲线, 标准蜂群算法需迭代108次, 而本文改进算法迭代52次便完成收敛, 相对于标准蜂群算法迭代次数减少51.9%, 可见, 融合BFGS算法的自适应蜂群算法在后期迭代次数明显减少。改进算法迭代曲线始终处于标准蜂群算法迭代曲线下侧, 是由于改进后的搜索方程具有自适应性, 加快了算法整体的迭代速度。
|
图 3 融合BFGS的自适应蜂群算法与标准蜂群算法迭代对比 Figure 3 Iterative comparison of adaptive bee colony algorithm with BFGS and standard bee colony algorithm |
电路仿真中, 由于存在非线性元件, 导致整个电路出现非线性现象, 在工程设计中通常考虑二次、三次谐波对电路的影响, 故表 3给出了计算所得栅极和漏极基波、二次和三次谐波电压。
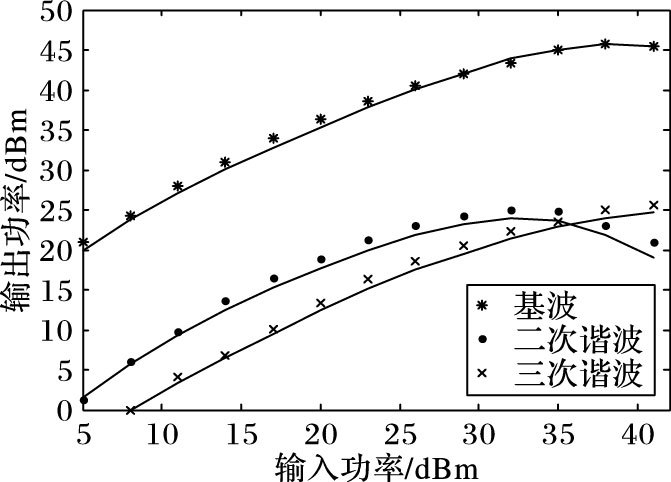
图 4描述了单音输入时的谐波特性, 当输入小于30 dBm时, 随着输入功率的增大, 基波输出功率随之增加, 当输入大于30 dBm时输出功率产生压缩特性, 逐渐趋于饱和, 表现出功放的非线性特点; 二次谐波由于晶体管内部的特性, 增大到一定程度达到饱和, 并逐渐减小; 三次谐波随着输入功率不断增加, 并且输出功率逐渐超过二次谐波。图 4~5中直线表示实测数据, 点表示仿真数据。
|
图 4 单音输入谐波特性 Figure 4 Characteristics of single input harmonic |
|
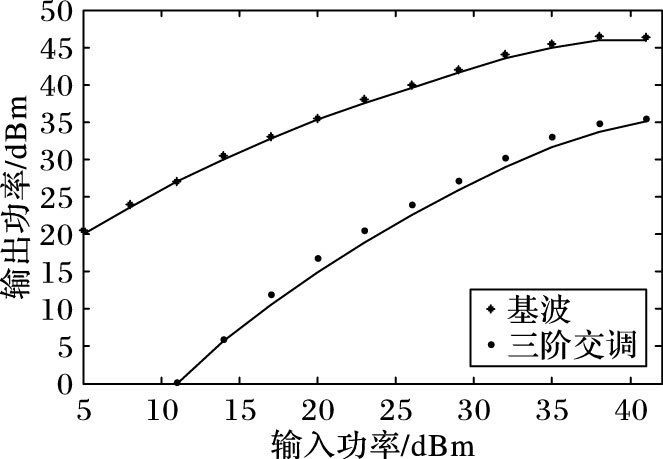
图 5 双音输入谐波特性 Figure 5 Characteristics of two tone input harmonic |
图 5为1 958.75 MHz和1 961.25 MHz双音信号等功率输入的谐波特性曲线图, 基波和三阶交调波的输出功率都随着输入功率的增大而不断增大, 而基波的增大速度逐渐减小。从图 4~5可以看出, 实测曲线与仿真曲线基本吻合, 证明本文改进算法在谐波平衡分析中应用成功。
4 结语本文针对分析射频功率放大器时所建立的谐波平衡方程, 提出一种新的求解算法, 即融合BFGS的自适应蜂群算法。该算法将动态调整因子引入到食物源更新机制中, 加快算法向全局最优值的搜索进程, 后期采用基于BFGS算法的局部寻优策略进行快速求解, 以克服蜂群算法后期收敛速度慢的缺点。仿真结果表明, 本文提出的改进蜂群算法成功应用于谐波平衡分析, 并且可有效减少收敛时间, 提高谐波平衡方程求解效率。
| [1] | 赵世杰. 基于谐波平衡法非线性散射函数仿真技术研究[D]. 西安: 西安电子科技大学, 2010. ( ZHAO S J. The research on simulation technology of nonlinear scattering function based on harmonic balance[D]. Xi'an:Xidian University, 2010. ) |
| [2] | 王家礼, 郝延红, 孙璐. 微波有源电路理论分析及设计[M]. 西安: 西安电子科技大学出版社, 2012 : 182 -185. ( WANG J L, HAO Y H, SNU L. Theoretical Analysis and Design of Microwave Active Circuits[M]. Xi'an: Xidian University Press, 2012 : 182 -185. ) |
| [3] | RIZZOLI V, NERI A. Harmonic-balance analysis of multitone autonomous nonlinear microwave circuits[C]//Proceedings of the 1991 IEEE MTT-S International Microwave Symposium Digest. Piscataway, NJ:IEEE, 1991:107-110. |
| [4] | BIZZARRI F, BRAMBILLA A, CODECASA L. Reduction of harmonic balance equations through Galerkin's method[C]//Proceedings of the 2015 European Conference on Circuit Theory and Design. Piscataway, NJ:IEEE, 2015:1-4. |
| [5] | 李厚儒, 南敬昌. 拟牛顿粒子群算法在非线性电路谐波平衡方程中的应用[J]. 计算机应用与软件, 2013, 30(2): 103-105. ( LI H R, NAN J C. Application of quasi-Newton particle swarm algorithm in nonlinear circuit harmonic balance equation[J]. Computer Applications and Software, 2013, 30(2): 103-105. ) |
| [6] | 刘文进, 从日静, 南敬昌. 混合蚁群算法在非线性谐波平衡分析中的应用[J]. 计算机应用研究, 2015, 32(11): 3341-3344. ( LIU W J, CONG R J, NAN J C. Application of hybrid ant colony algorithm in nonlinear harmonic balance analysis[J]. Application Research of Computers, 2015, 32(11): 3341-3344. doi: 10.3969/j.issn.1001-3695.2015.11.032 ) |
| [7] | EL-HAWARY M E, ABU-MOUTI F S. Overview of Artificial Bee Colony (ABC) algorithm and its applications[C]//Proceedings of the 2012 IEEE International Systems Conference. Piscataway, NJ:IEEE, 2012:1-6. |
| [8] | 谢娟, 邱剑锋, 闵杰, 等. 具有双重认知能力的人工蜂群算法及性能分析[J]. 计算机科学, 2014, 41(11): 269-272. ( XIE J, QIU J F, MIN J, et al. Improved artificial bee colony algorithm with dual cognitive abilities and performance analysis[J]. Computer Science, 2014, 41(11): 269-272. doi: 10.11896/j.issn.1002-137X.2014.11.052 ) |
| [9] | MOHAMMADI S A, DERAKHSHI M R F, AKBARI R. An adaptive multi-objective artificial bee colony with crowding distance mechanism[C]//Proceedings of the 201216th CSI International Symposium on Artificial Intelligence and Signal Processing. Piscataway, NJ:IEEE, 2012:68-73. |
| [10] | GAO W-F, LIU S-Y, HUANG L-L. A novel artificial bee colony algorithm based on modified search equation and orthogonal learning[J]. IEEE Transactions on Cybernetics, 2013, 43(3): 1011-1024. doi: 10.1109/TSMCB.2012.2222373 |
| [11] | 许爱军. 改进ABC算法优化LSSVM的网络流量预测模型[J]. 计算机应用与软件, 2015, 23(1): 323-326. ( XU A J. Network traffic edication based on optimising LSSVM by improved[J]. Computer Applications and Software, 2015, 23(1): 323-326. ) |
| [12] | 吴龙胜, 刘佑宝. 功率MESFET大信号非线性等效电路的谐波平衡分析[J]. 电力电子术, 2002, 36(6): 76-78. ( WU L S, LIU Y B. Analysis of large-signal nonlinear model of power MESFET by harmonic balance method[J]. Power Electronics, 2002, 36(6): 76-78. ) |
| [13] | REKABY A, YOUSSIF A A, ELDIN A S. Introducing adaptive artificial bee colony algorithm and using it in solving traveling salesman problem[C]//Proceedings of the 2013 Science and Information Conference. Piscataway, NJ:IEEE, 2013:502-506. |
| [14] | XU H, JIANG M, XU K. Archimedean copula estimation of distribution algorithm based on artificial bee colony algorithm[J]. Journal of Systems Engineering and Electronics, 2015, 26(2): 388-396. doi: 10.1109/JSEE.2015.00045 |
| [15] | LI M, ZHAO H, WENG X, et al. Artificial bee colony algorithm with comprehensive search mechanism for numerical optimization[J]. Journal of Systems Engineering and Electronics, 2015, 26(3): 603-617. doi: 10.1109/JSEE.2015.00068 |
| [16] | 潘学. 求解非线性方程组的蛙跳和BFGS混合算法[J]. 计算机与现代化, 2013, 12(9): 9-13. ( PAN X. Shuffled frog leaping algorithm based on BFGS for solving systems of nonlinear functions[J]. Computer and Modern, 2013, 12(9): 9-13. ) |




