2. 光电测试技术北京市重点实验室 (北京信息科技大学), 北京 100192
2. Beijing Key Laboratory of Optoelectronics Measurement Technology (Beijing Information Science & Technology University), Beijing 100192, China
近年来,随着科学技术的迅猛发展,机器人已经逐步进入我们的社会生活中,如在柔性装配、智能服务、自主导航、逆向工程、焊接工程等领域得到了广泛应用[1-2]。机器人手眼标定作为机器人视觉的关键技术之一,一直以来都是机器视觉领域中的研究热点,为了提高手眼标定的精度,从而使机器人更好地为人类服务,国内外研究学者作了大量工作。
1989年,Tsai等[3]和Shiu等[4]首次提出手眼标定问题,并提出了基于轴角变换的手眼标定闭环线性解法,以后关于手眼标定的研究多是以此数学模型为基础。受他们二人的启发,Horaud等[5]、Daniilidis[6]、Andreff等[7]在Tsai和Shiu的研究基础上分别提出了基于单位四元数、对偶四元数、矩阵直积的线性闭环解法,但这些参数化方法在通常情况下并不满足标定矩阵的正交和单位特性,需要对其再加入正交和单位约束,从而影响了闭环求解精度的稳定性。2001年,文献[8]以机器人视觉伺服系统为背景,提出利用运动恢复结构 (Structure from Motion,SfM) 算法求解相机的方位信息,虽然摆脱了手眼标定过程中对靶标的依赖,扩展了手眼标定的应用场景,但其标定精度并不高。2008年,考虑到标定数据的选择同样会影响手眼变换矩阵的求解精度,Schmidt等[9]在Tsai建立的标定误差数学模型基础上,提出利用矢量化编码技术构建手眼标定数据筛选机制,提高了手眼变换矩阵的求解精度的稳定性,但求解效率较低。此后,文献[10-13]又提出了采用分支定界法和L2范数理论来解决手眼标定过程中的全局优化问题,在一定程度上提高了计算结果的准确性,但在实际应用中需要调整许多参数,并且需要有针对性地对算法进行设计,才能提高算法的执行效率。在国内,2011年,王君臣等[14]提出一种基于最大似然估计的手眼标定非线性优化算法。2015年,王金桥等[15]提出利用遗传算法解决关节臂视觉检测系统中的手眼标定问题,然而,当误差存在的情况下这些优化算法都容易出现过早收敛的问题,影响求解精度的稳定性。综上,不管是国内和国外,综合考虑标定方程的求解算法及误差影响因素的研究还比较少,而事实上,标定数据的筛选和标定方程的求解算法都会直接影响手眼变换矩阵的求解精度,因此有必要综合在一起进行研究。
针对上述机器人手眼标定问题中存在的关键问题,本文首先利用标定方程中旋转矩阵的误差模型,结合随机抽样一致性 (Random Sample Consensus, RANSAC) 算法对标定数据中旋转轴之间的夹角进行预筛选;然后,鉴于目前非线性优化算法的局限性,提出一种基于线性矩阵不等式 (Linear Matrix Inequality, LMI) 松弛技术的凸松弛全局优化手眼标定算法;最后,通过实验分析,验证了本文算法较之非线性优化算法的优越性。
1 基于四元数的手眼标定问题描述 1.1 标定方程四元数解法参照Tsai等[3]的定义方式,A1、A2表示靶标世界坐标系到两个不同姿态的摄像机坐标系的变换矩阵,B1、B2表示为两次不同姿态的机械手末端执行器坐标系到机械手基坐标系的变换矩阵,X表示摄像机坐标系到机械手末端执行器坐标系的变换矩阵,则手眼关系可以表示为式 (1):
| $\mathit{\boldsymbol{AX}} = \mathit{\boldsymbol{XB}}$ | (1) |
其中:A、B、X都为4×4的矩阵,可以表示为:
| $\begin{array}{l} \mathit{\boldsymbol{X}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{R}}_x}} & {{\mathit{\boldsymbol{t}}_x}}\\ {{\mathit{\boldsymbol{0}}^T}} & 1 \end{array}} \right]\;\;\\ \mathit{\boldsymbol{A}} = {\mathit{\boldsymbol{A}}_2}\mathit{\boldsymbol{A}}_1^{ - 1} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{R}}_A}} & {{\mathit{\boldsymbol{t}}_A}}\\ {{\mathit{\boldsymbol{0}}^T}} & 1 \end{array}} \right]\;\\ \;\mathit{\boldsymbol{B}} = \mathit{\boldsymbol{B}}_2^{ - 1}{\mathit{\boldsymbol{B}}_1} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{R}}_B}} & {{\mathit{\boldsymbol{t}}_B}}\\ {{\mathit{\boldsymbol{0}}^T}} & 1 \end{array}} \right] \end{array}$ |
将上式代入式 (1) 展开,表示成只含有旋转矩阵和平移向量的方程形式为:
| ${\mathit{\boldsymbol{R}}_A}{\mathit{\boldsymbol{R}}_X} = {\mathit{\boldsymbol{R}}_X}{\mathit{\boldsymbol{R}}_B}$ | (2) |
| $({\mathit{\boldsymbol{R}}_A} - {\mathit{\boldsymbol{I}}_3}){\mathit{\boldsymbol{t}}_X} = {\mathit{\boldsymbol{R}}_X}{\mathit{\boldsymbol{t}}_B} - {\mathit{\boldsymbol{t}}_A}$ | (3) |
根据式 (2) 和 (3) 可知,至少需要两次旋转轴非平行的相对位姿变换才可以唯一确定手眼关系X。文献[5]给出上述标定方程的四元数解法,求解步骤如下:
首先,利用四元数法参数化手眼标定式 (2) 和 (3),建立目标函数f如式 (4) 所示,定义nA、nB分别为旋转矩阵RA、RB特征值为1时所对应的单位特征向量,qx为Rx的单位四元数法表示,qx为qx的共轭四元数,则有:
| $\left\{ {\begin{array}{*{20}{l}} f\left( {{\mathit{\boldsymbol{q}}_x},{\mathit{\boldsymbol{t}}_x}} \right) = \mathop {{\rm{min}}}\limits_{q,t} \left[ {{\lambda _1}{f_1}\left( {{\mathit{\boldsymbol{q}}_x}} \right) + {\lambda _2}{f_2}\left( {{\mathit{\boldsymbol{q}}_x},{\mathit{\boldsymbol{t}}_x}} \right) + \lambda {{\left( {1 - \mathit{\boldsymbol{q}}_x^{\rm{T}}{\mathit{\boldsymbol{q}}_x}} \right)}^2}} \right]\\ {f_1}\left( {{\mathit{\boldsymbol{q}}_x}} \right) = {\sum\limits_{i = 1}^n {\left\| {\mathit{\boldsymbol{n}}_A^i - {\mathit{\boldsymbol{q}}_x} * \mathit{\boldsymbol{n}}_B^i * {{\mathit{\boldsymbol{\bar q}}}_x}} \right\|} ^2}\\ {f_2}\left( {{\mathit{\boldsymbol{q}}_x},{\mathit{\boldsymbol{t}}_x}} \right) = {\sum\limits_{i = 1}^N {\left\| {{\mathit{\boldsymbol{q}}_x} * \mathit{\boldsymbol{t}}_B^i * {{\mathit{\boldsymbol{\bar q}}}_x} - \left( {\mathit{\boldsymbol{R}}_A^i - {\mathit{\boldsymbol{I}}_3}} \right){\mathit{\boldsymbol{t}}_x} - \mathit{\boldsymbol{t}}_A^i} \right\|} ^2} \end{array}} \right.$ | (4) |
然后,利用Levenberg-Marquardt非线性优化算法求解式 (4),即可得到手眼变换矩阵X中的旋转平移关系Rx和tx。为了保证参量qx的单位性质,求解过程中取λ1=λ2=1,λ=106。
1.2 标定方程的误差模型Tsai等[3]利用一系列引理给出标定方程中旋转矩阵的误差模型,并对影响手眼标定方程的求解精度关键因素进行了仿真实验。假定机械手和摄像机两次相对运动变换矩阵A,B中R的标定误差为ΔR,表示为式 (5):
| $\left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{A}}_{\Delta \mathit{\boldsymbol{RR}}}} = {\mathit{\boldsymbol{A}}_{\Delta \mathit{\boldsymbol{R}}}} + {\mathit{\boldsymbol{A}}_\mathit{\boldsymbol{R}}}\;}\\ {{\mathit{\boldsymbol{B}}_{\Delta \mathit{\boldsymbol{RR}}}} = {\mathit{\boldsymbol{B}}_{\Delta \mathit{\boldsymbol{R}}}} + {\mathit{\boldsymbol{B}}_\mathit{\boldsymbol{R}}}} \end{array}} \right.$ | (5) |
将式 (5) 代入式 (1),则可以得到手眼变换矩阵X中旋转矩阵R的均方根误差,表示为σR,以三位姿情况为例,旋转矩阵的均方根误差σRAB可以表示为:
| $\begin{array}{l} {\sigma _{{R_{{\rm{AB}}}}}} = \frac{1}{{\sin (\angle ({\mathit{\boldsymbol{r}}_{B12}},{\mathit{\boldsymbol{r}}_{B23}}))}} \cdot \\ \sqrt {\frac{2}{3}(\sigma _{{R_{A12}}}^2 + \sigma _{{R_{B12}}}^2) \cdot \left[ {\frac{1}{{{{({\theta _{{B_{12}}}})}^2}}} + \frac{1}{{{{({\theta _{{B_{23}}}})}^2}}}} \right]} \end{array}$ | (6) |
其中:
设W(x) 为x=(x1, x2, …, xn)∈Cn上的标量多元多项式,则多元多项式的优化问题通常可以描述为:
| $\min \;{W_0}\left( x \right)$ | (7) |
s.t. Wi(x)≥0,i=1, 2, …, k
其中x=(x1, x2, …, xn)T∈Cn
由于上述非凸多项式优化问题的极值点不唯一,因此极小值并不一定是最小值,而通过初等微积分数学概念寻找上述多元多项式优化问题的全局最优解是一个NP问题。为了很好地解决此类问题,Lasserre利用Putinar定理[16],把原多项式优化问题松弛为半正定规划问题求解。通过LMI对非凸函数在可行域Cn内进行凸松弛,经过多次松弛逼近多元多项式函数全局最优解,使得多极值非凸优化问题松弛为凸函数优化问题。虽然蒙特卡罗采样法、神经网络、禁忌搜索以及模拟退火等都是具有通用性的启发式全局优化算法,但在实际应用中需要调整许多参数,并且需要有针对性地对算法进行设计,才能提高算法的执行效率,而基于LMI松弛技术的优化方法是专门针对多项式优化问题的方法,从理论上讲,LMI方法与其他确定性全局优化算法相比更具有可靠性,可以最大限度地保证计算结果优化到全局最优值。
定义vt(x) 为t次多项式W(x) 的典范基,t∈N,设s(2t) 是vt(x) 的维数,表示为:
| ${\mathit{\boldsymbol{v}}_t}(\mathit{\boldsymbol{x}}) = \left\{ {1,{x_1},{x_2},...,{x_n},x_1^2,{x_1}{x_2},...,{x_1}{x_n},{x_2}{x_3},...,x_n^2,...,x_1^t,...,x_n^t} \right\}$ | (8) |
即vt(x) 为x中的元素xi互乘得到的次数不高于t的所有单项式和常量1构成的集合。
定义标量多元多项式W(x) 表示为:
| $W(\mathit{\boldsymbol{x}}) = \sum\limits_\alpha {{\mathit{\boldsymbol{p}}_\alpha }{\mathit{\boldsymbol{x}}^\alpha }} \;\;;{\mathit{\boldsymbol{x}}^\alpha } = {x_1}^{{\alpha _1}}{x_2}^{{\alpha _2}} \cdot \cdot \cdot {x_n}^{{\alpha _n}}\;\;\sum\limits_i {{\alpha _i} \le t} $ |
其中pα为多项式W(x) 以式 (8) vt(x) 为空间基的系数向量。
定义s(2t) 维向量y={yα},且y0, 0, …, 0 =1,则半定矩阵Mt(y) 可以表示成分块矩阵{Mi, j(y)}0≤i, j≤2t形式,其行列系数由基vt(x) 顺序确定,表示为:
| ${\mathit{\boldsymbol{M}}_{i,j}}\left( \mathit{\boldsymbol{y}} \right) = \;\left( {\begin{array}{*{20}{c}} {{y_{i + j,0}}} & {{y_{i + j - 1,1}}} & { \cdot \cdot \cdot } & {{y_{i,j}}}\\ {{y_{i + j - 1,1}}} & {{y_{i + j - 2,2}}} & { \cdot \cdot \cdot } & {{y_{i - 1,j + 1}}}\\ { \cdot \cdot \cdot } & { \cdot \cdot \cdot } & { \cdot \cdot \cdot } & { \cdot \cdot \cdot }\\ {{y_{j,i}}} & {{y_{i + j - 1,1}}} & { \cdot \cdot \cdot } & {{y_{0,i + j}}} \end{array}} \right)$ | (9) |
例如,当n=2,t=2时,式 (9) 可以表示为:
| ${\mathit{\boldsymbol{M}}_2}\left( \mathit{\boldsymbol{y}} \right) = \;\left( {\begin{array}{*{20}{c}} 1 & {{y_{10}}} & {{y_{01}}} & {{y_{20}}} & {{y_{11}}} & {{y_{02}}}\\ {{y_{10}}} & {{y_{20}}} & {{y_{11}}} & {{y_{30}}} & {{y_{21}}} & {{y_{12}}}\\ {{y_{01}}} & {{y_{11}}} & {{y_{02}}} & {{y_{21}}} & {{y_{12}}} & {{y_{03}}}\\ {{y_{20}}} & {{y_{30}}} & {{y_{21}}} & {{y_{40}}} & {{y_{30}}} & {{y_{22}}}\\ {{y_{11}}} & {{y_{21}}} & {{y_{12}}} & {{y_{31}}} & {{y_{22}}} & {{y_{13}}}\\ {{y_{02}}} & {{y_{12}}} & {{y_{03}}} & {{y_{22}}} & {{y_{13}}} & {{y_{04}}} \end{array}} \right)$ |
最后,根据文献[17]中4.3节给出的矩阵秩相等条件确定最优解,如果定义y*为式 (7) 的最优解,则存在:
| ${\rm{rank}}({\mathit{\boldsymbol{M}}_t}({\mathit{\boldsymbol{y}}^*})){\rm{ = rank(}}{\mathit{\boldsymbol{M}}_{t - d}}({\mathit{\boldsymbol{y}}^*}))$ | (10) |
其中
综上,多项式LMI优化方法一般可以归纳为如下3个步骤:
1) 使用提升变量线性化目标函数和约束项W(x)。使用
2) 添加半正定矩阵约束。按照t次多项式的基vt(x) 的排列顺序,添加半正定矩阵约束Mt(y)≥0,Mt(Wy)≥0。
3) 将凸松弛多项式优化问题转化为半正定规划问题求解。使用对偶内点算法求解由前两步组成的新半正定规划问题,利用式 (10) 秩相等的条件来判别是否收敛到全局最优解。
2.2 基于全局优化算法的手眼变换矩阵估计首先,将手眼变换矩阵X用四元数参数化为如下形式:
| $\mathit{\boldsymbol{X}}\left( {{\mathit{\boldsymbol{q}}_x},{\mathit{\boldsymbol{t}}_x}} \right) = \left( {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{R}}\left( {{\mathit{\boldsymbol{q}}_x}} \right)} & {{\mathit{\boldsymbol{t}}_x}}\\ {{\mathit{\boldsymbol{0}}^{\rm{T}}}} & 1 \end{array}} \right)$ | (11) |
其中,旋转矩阵R(qx) 可以表示为:
| $\begin{array}{l} \mathit{\boldsymbol{R}}\left( {{\mathit{\boldsymbol{q}}_x}} \right) = \\ \left( {\begin{array}{*{20}{c}} {q_0^2 + q_1^2 - q_2^2 - q_3^2} & {2\left( {{q_1}{q_2} - {q_0}{q_3}} \right)} & {2\left( {{q_1}{q_3} + {q_0}{q_2}} \right)}\\ {2\left( {{q_1}{q_2} + {q_0}{q_3}} \right)} & {q_0^2 - q_1^2 + q_2^2 - q_3^2} & {2\left( {{q_2}{q_3} - {q_0}{q_1}} \right)}\\ {2\left( {{q_1}{q_3} - {q_0}{q_2}} \right)} & {2\left( {{q_2}{q_3} + {q_0}{q_1}} \right)} & {q_0^2 - q_1^2 - q_2^2 + q_3^2} \end{array}} \right) \end{array}$ |
然后以最小化标定方程式 (1) 为几何误差目标函数,以单位四元数的性质为约束条件,建立关于式 (11) 的多元多项式优化问题:
| $\begin{array}{l} \quad \min f\left( {{\mathit{\boldsymbol{q}}_x},{\mathit{\boldsymbol{t}}_x}} \right) = \mathop {\min }\limits_{{q_x},{t_x}} {\sum\limits_{i = 1}^n {\left\| {{\mathit{\boldsymbol{A}}_i}\mathit{\boldsymbol{X}}\left( {{\mathit{\boldsymbol{q}}_x},{\mathit{\boldsymbol{t}}_x}} \right) - \mathit{\boldsymbol{X}}\left( {{\mathit{\boldsymbol{q}}_x},{\mathit{\boldsymbol{t}}_x}} \right){\mathit{\boldsymbol{B}}_i}} \right\|} ^2}\\ s.t.\;\;\mathit{\boldsymbol{q}}_x^{\rm{T}}{\mathit{\boldsymbol{q}}_x} = 1\;,{\mathit{\boldsymbol{q}}_x} \ge 0 \end{array}$ |
最后,利用Lasserre非凸函数LMI松弛技术把上述多项式函数优化问题松弛为半正定规划问题求解,图 1是LMI凸松弛优化算法流程。

|
图 1 LMI凸松弛优化算法流程 Figure 1 Flow diagram of LMI convex relaxation optimization |
经计算得知,目标函数f为4次7元的多项式函数,由85个不同的单项式组成,由于求解过程中至少会得到2个全局最优解,因此需要增加约束条件qx≥0,为了提高求解的数值稳定性,可以先将Ai,Bi中平移向量归一化,再根据实际要求对平移向量tx加入线性约束,将平移向量的模限制在有限的空间内 (例如,可设‖tx‖2≤1),从而确保半正定规划的内点法可以高效地进行解算。
具体的计算过程可以采用Henrion发布的GloptiPoly3软件包[18]。Henrion等[18]率先把LMI优化方法引入到计算机视觉中解决多视图几何下的三维重建问题。本文采用此方法计算手眼标定矩阵,LMI全局优化算法的关键在于如何将需要优化的目标函数转化为半正定规划问题求解,基于全局优化算法求解手眼变换矩阵X的部分程序如下所示:
输入:筛选后得到手眼标定数据Ai,Bi;
输出:全局优化后得到的手眼变换矩阵X最优解。
1) 综合考虑求解精度和速度要求,设置迭代停止条件:
pars.eps=1.0E-20; mset (pars)
2) 定义多项式变量,用四元数法参数化未知量X:
mpol (′q0′, ′q1′, ′q2′, ′q3′, ′t1′, ′t2′, ′t3′)
| $\begin{array}{l} \mathit{\boldsymbol{X}} = \\ \left[ {\begin{array}{*{20}{c}} {q_0^2 + q_1^2 - q_2^2 - q_3^2} & {2\left( {{q_1}{q_2} - {q_0}{q_3}} \right)} & {2\left( {{q_1}{q_3} + {q_0}{q_2}} \right)} & {{t_1}}\\ {2\left( {{q_1}{q_2} + {q_0}{q_3}} \right)} & {q_0^2 - q_1^2 + q_2^2 - q_3^2} & {2\left( {{q_2}{q_3} - {q_0}{q_1}} \right)} & {{t_2}}\\ {2\left( {{q_1}{q_3} - {q_0}{q_2}} \right)} & {2\left( {{q_2}{q_3} + {q_0}{q_1}} \right)} & {q_0^2 - q_1^2 - q_2^2 + q_3^2} & {{t_3}}\\ 0 & 0 & 0 & 1 \end{array}} \right] \end{array}$ |
3) 根据标定方程几何误差,创建关于未知量X的目标函数:
| ${f_X} = \sum\limits_{i = 1}^n {{{\left\| {{\mathit{\boldsymbol{A}}_i}\mathit{\boldsymbol{X}} - \mathit{\boldsymbol{X}}{\mathit{\boldsymbol{B}}_i}} \right\|}_2}^2} $ |
4) 根据单位四元数的性质,添加多项式变量约束条件:
| $\begin{array}{*{35}{l}} K\_qx=[q{{0}^{{{\text{ }\!\!\hat{\ }\!\!\text{ }}^{2}}}}+q{{1}^{{{\text{ }\!\!\hat{\ }\!\!\text{ }}^{2}}}}+q{{2}^{{{\text{ }\!\!\hat{\ }\!\!\text{ }}^{2}}}}+q{{3}^{{{\text{ }\!\!\hat{\ }\!\!\text{ }}^{2}}}}==1,q0>=0]; \\ K\_tx=[t{{1}^{{{\text{ }\!\!\hat{\ }\!\!\text{ }}^{2}}}}+t{{2}^{{{\text{ }\!\!\hat{\ }\!\!\text{ }}^{2}}}}+t{{3}^{{{\text{ }\!\!\hat{\ }\!\!\text{ }}^{2}}}}\text{ }=1]; \\ \end{array}$ |
5) 建立2次LMI凸松弛优化问题,将非凸多项式优化问题转化为半定规划问题求解:
P=msdp (min (fX), K_qx, K_tx, 2)
6) 调用求解器,求解极小值,输出手眼变换矩阵X最优解:
msol (P); X=double (qx, tx)
3 实测结果与分析为了进一步验证本文提出的算法精度和鲁棒性,设计实测实验,在Inter Core i5-4590 CPU 3.3 GHz、4 GB内存的PC机上,用Matlab R2014a编程实现手眼标定,并比较分析实验结果。实验中选用日本电裝公司DENSO机械手VS-6577GM,X、Y、Z各方向的重复定位精度为±0.02 mm,选用凯视佳公司UD274M/C型号的CCD工业相机,分辨率为1628×1236 pixel相机,像元尺寸为4.4 μm,选用COMPUTAR 12 mm镜头对11 mm×11 mm棋盘格平面靶标进行相机参数标定,实验前需要先将摄像机固定在机械手末端执行器法兰盘上,搭建的实测实验平台如图 2所示。

|
图 2 手眼标定实测实验平台 Figure 2 Experimental platform for hand-eye calibration |
考虑到机械手末端执行器相对运动旋转轴之间的夹角对标定方程求解精度的影响,为了提高算法的鲁棒性,参照标定方程的误差模型见式 (6),首先利用自适应RANSAC算法预先对标定数据进行角度筛选,然后再用全局优化算法求解手眼变换矩阵。定义rij和rkl分别表示机械手末端执行器从位姿i到位姿j及从位姿k到位姿l的单位旋转轴,θij, kl表示两次相对运动的单位旋转轴的夹角,如下式所示,当θij, kl接近90°或者θt接近0°时,旋转矩阵的误差最小:
θt=‖90-θij, kl‖;θij, kl=∠(rij, rkl)
具体的实验操作步骤如下:
首先,利用机械手带动摄像机每次选取Q个不同位姿对平面靶标拍照成像,两两进行组合可以得到S=Q(Q-1) /2组手眼标定数据集,由于至少需要两组旋转轴非平行的标定数据就可以唯一确定手眼变换矩阵,所以最少数据点mn=2,设定满足角度阈值要求的内点比例初值w0=0.1,K次抽样中所有样本均为坏样本的概率z=0.02,角度阈值初值θ0=5°,终止RANSAC抽样的条件为满足角度阈值的标定数据集CS≥15,采用自适应算法抽样并更新w0和θ0,直到标定数据集CS≥15,记下此时的角度阈值θt,终止抽样。
然后,将筛选出的标定数据集CS代入标定式 (1) 利用不同的算法求解XCS。由于非线性算法在初值选取适当的情况下,与其他手眼标定算法相比可以达到更高的精度,因此本文以文献[6]中的对偶四元数算法作为初值估计,使用文献[5]中的算法进行非线性迭代优化,将本文提出的全局优化算法 (Global Optimization,GO) 与文献[5]中的非线性迭代优化算法 (Nonlinear,OL) 进行比较分析。
最后,采用手眼标定方程的几何误差‖AX-XB‖2作为精度评价方法,评估标定矩阵XCS的求解精度,定义S组手眼标定数据集中手眼变换矩阵XCS的几何误差平均值和标准差为:
| $\begin{array}{l} 平均值\;\bar \mu {\rm{ = }}\frac{1}{S}\sum\limits_{i = 1}^S {{{\left\| {{\mathit{\boldsymbol{A}}_i}{\mathit{\boldsymbol{X}}_{{C^S}}} - {\mathit{\boldsymbol{X}}_{{C^S}}}{\mathit{\boldsymbol{B}}_i}} \right\|}_2}} \\ 标准差\;\delta {\rm{ = }}\sqrt {\frac{1}{S}\sum\limits_{i = 1}^S {{{\left( {{{\left\| {{\mathit{\boldsymbol{A}}_i}{\mathit{\boldsymbol{X}}_{{C^S}}} - {\mathit{\boldsymbol{X}}_{{C^S}}}{\mathit{\boldsymbol{B}}_i}} \right\|}_2} - {{\bar \mu }_X}} \right)}^2}} } \end{array}$ |
为了证明算法的可靠性,每次机械手变换Q=16个不同的位置,进行10组完全独立的重复标定实验,利用Matlab Camera Calibration Toolbox工具箱[19]标定摄像机的内外参数,内参数标定的最大误差均在0.1 pixel内,随机选取10组实验中一组相机标定内参数矩阵T和镜头的径向、切向畸变系数kC为:
| $\begin{array}{l} \mathit{\boldsymbol{T}}{\rm{ = }}\left[ {\begin{array}{*{20}{c}} {{\rm{5466}}{\rm{.51}}} & 0 & {{\rm{1251}}{\rm{.17}}}\\ 0 & {{\rm{5465}}{\rm{.11}}} & {{\rm{1002}}{\rm{.54}}}\\ 0 & 0 & 1 \end{array}} \right]\\ {\mathit{\boldsymbol{k}}_C} = \left[ {\begin{array}{*{20}{c}} {{\rm{ - 0}}{\rm{.072958}}} , {{\rm{0}}{\rm{.094598}}} , {{\rm{ - 0}}{\rm{.001835}}} , {{\rm{ - 0}}{\rm{.001131}}} , 0 \end{array}} \right] \end{array}$ |
以此内参数矩阵求解相机的外参数,在同样的标定数据下,利用本文GO算法和OL算法得到的手眼变换矩阵分别为:
| ${\mathit{\boldsymbol{X}}_{{\rm{GO}}}}{\rm{ = }}\left[ {\begin{array}{*{20}{r}} { - 0.9641} & {0.2611} & {0.0489} & { - 2.3369}\\ { - 0.0351} & {0.0575} & { - 0.9977} & {87.9896}\\ { - 0.2633} & { - 0.9636} & { - 0.0463} & { - 30.9224}\\ 0 & 0 & 0 & {1.0000} \end{array}} \right]$ |
| ${\mathit{\boldsymbol{X}}_{{\rm{OL}}}}{\rm{ = }}\left[ {\begin{array}{*{20}{r}} { - 0.9639} & {0.2615} & {0.0491} & { - 2.2456}\\ { - 0.0354} & {0.0572} & { - 0.9977} & {87.9045}\\ { - 0.2638} & { - 0.9635} & { - 0.0459} & { - 30.8220}\\ 0 & 0 & 0 & {1.0000} \end{array}} \right]$ |
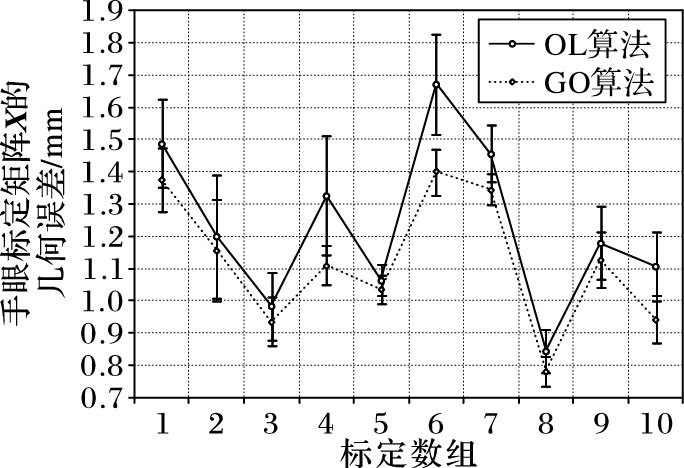
10组完全独立的实测实验全局优化算法 (GO) 与非线性优化算法 (OL) 的手眼标定几何误差的平均值和标准差见图 3和表 1所示,其中图 3为表 1中数据的误差棒图。
| 表 1 GO算法与OL算法手眼标定几何误差平均值μ及标准差δ Table 1 Geometric average error μ and standard deviation δ of hand-eye calibration by GO and OL algorithms |
|
图 3 实测实验手眼标定几何误差棒图 Figure 3 Comparison of geometric error bars for hand-eye calibration experiment |
由图 3可知,从手眼标定几何误差的精度和稳定性上看,GO算法的每组观测误差值均低于OL算法。10组测量数据中:GO算法的手眼变换矩阵误差平均值最大为1.4 mm,标准差小于0.16 mm;而OL算法的手眼变换矩阵误差平均值最大已超过1.6 mm,标准差接近0.2 mm。筛选后标定数据集CS中的最大夹角阈值θt如表 1所示,由表 1可知,针对10组不同的观测数据,经过RANSAC算法筛选后参与计算变换矩阵X的标定数据中两次相对运动的单位旋转轴的夹角θij, kl均接近90°,在83°和97°之间,由式 (6) 可知,此时标定方程中旋转矩阵误差σR接近最小,即标定数据的误差对标定方程求解精度的影响最小。此外,为了比较两种算法的运行效率,将两种算法的运行时间在Matlab R2014a测试平台下进行比较分析,如表 2所示。
| 表 2 GO算法和OL算法的运行时间比较 Table 2 Comparison of calculation time for GO and OL algorithms |
由表 2可知,从计算时间上看,GO算法计算手眼变换矩阵的平均时间为0.51 s,OL算法计算手眼变换矩阵的平均时间为0.025 s,与OL算法相比,GO算法计算耗时较大,因此有必要利用GPU加速技术提升算法的运行速度。
4 结语针对机器人运动学正解及相机的外参数标定偏差对手眼标定方程求解精度的影响,本文利用标定方程中旋转矩阵的误差模型,通过单位旋转轴的夹角建立标定数据筛选机制,减小了标定数据的选择对标定方程求解精度的影响。此外,为了最大限度避免优化结果过早陷入局部最小值,在现有的四元数手眼标定算法的基础上,提出一种基于凸松弛全局优化技术的手眼标定算法,在不需要初值估计的情况下,保证了求解的最优性。实测结果表明,本文提出的全局优化算法较非线性优化手眼标定算法具有较高的精度和鲁棒性,在高精度的机器人视觉系统中具有一定的应用潜力,但计算较为耗时,需要利用GPU并行计算进行加速。下一步将针对全局优化算法的计算耗时问题,应用统一计算设备架构 (Compute Unified Device Architecture, CUDA) 并行架构理念,将本文提出的手眼标定算法中具有并行性的部分应用CUDA架构实现并行处理,提高算法的处理速度,扩展算法的应用范围。
| [1] | 陈锡爱, 徐方. 基于手眼立体视觉的机器人定位系统[J]. 计算机应用, 2005, 25(S1): 302-304. ( CHEN X A, XU F. Robot positioning system based on hand-eye stereo vision[J]. Journal of Computer Applications, 2005, 25(S1): 302-304. ) |
| [2] | 战茜, 屠大维. 移动机器人自主抓取作业[J]. 计算机应用, 2016, 36(S1): 95-98. ( ZHAN X, TU D W. Research on autonomous grasping of mobile robot[J]. Journal of Computer Applications, 2016, 36(S1): 95-98. ) |
| [3] | TSAI R Y, LENZ R K. A new technique for fully autonomous and efficient 3D robotics hand/eye calibration[J]. IEEE Transactions on Robotics and Automation, 1989, 5(3): 345-358. doi: 10.1109/70.34770 |
| [4] | SHIU Y C, AHMAD S. Calibration of wrist-mounted robotic sensors by solving homogeneous transform equations of the form AX=XB[J]. IEEE Transactions on Robotics and Automation, 1989, 5(1): 16-29. doi: 10.1109/70.88014 |
| [5] | HORAUD R, DORNAIKA F. Hand-eye calibration[J]. The International Journal of Robotics Research, 1995, 14(3): 195-210. doi: 10.1177/027836499501400301 |
| [6] | DANⅡLIDIS K. Hand-eye calibration using dual quaternions[J]. The International Journal of Robotics Research, 1999, 18(3): 286-298. doi: 10.1177/02783649922066213 |
| [7] | ANDREFF N, HORAUD R, ESPIAU B. On-line hand-eye calibration[C]//Proceedings of the 2nd International Conference on 3-D Digital Imaging and Modeling. Washington, DC:IEEE Computer Society, 1999:430-436. |
| [8] | ANDREFF N, HORAUD R, ESPIAU B. Robot hand-eye calibration using structure-from-motion[J]. The International Journal of Robotics Research, 2001, 20(3): 228-248. doi: 10.1177/02783640122067372 |
| [9] | SCHMIDT J, NIEMANN H. Data selection for hand-eye calibration:a vector quantization approach[J]. The International Journal of Robotics Research, 2008, 27(9): 1027-1053. doi: 10.1177/0278364908095172 |
| [10] | ZHAO Z. Hand-eye calibration using convex optimization[C]//Proceedings of the 2011 IEEE International Conference on Robotics and Automation. Piscataway, NJ:IEEE, 2011:2947-2952. |
| [11] | HELLER J, HAVLENA M, PAJDLA T. A branch-and-bound algorithm for globally optimal hand-eye calibration[C]//Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway, NJ:IEEE, 2012:1608-1615. |
| [12] | RULAND T, PAJDLA T, KRVGER L. Globally optimal hand-eye calibration[C]//Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway, NJ:IEEE, 2012:1035-1042. |
| [13] | 马腾, 陈庶樵, 张校辉, 等. 基于规则集划分的多决策树报文分类算法[J]. 计算机应用, 2013, 33(9): 2450-2454. ( MA T, CHEN S Q, ZHANG X H, et al. Multiple decision-tree packet classification algorithm based on rule set partitioning[J]. Journal of Computer Applications, 2013, 33(9): 2450-2454. ) |
| [14] | 王君臣, 王田苗, 杨艳, 等. 非线性最优机器人手眼标定[J]. 西安交通大学学报, 2011, 45(9): 15-20. ( WANG J C, WANG T M, YANG Y, et al. Nonlinear optimal robot hand-eye calibration[J]. Journal of Xi'an Jiaotong University, 2011, 45(9): 15-20. doi: 10.7652/xjtuxb201109004 ) |
| [15] | 王金桥, 段发阶, 汪润. 精确标定关节臂视觉检测系统手眼关系[J]. 计算机工程与应用, 2015, 51(21): 225-229. ( WANG J Q, DUAN F J, WANG R. Accurate calibration of AACMM visual detection system hand-eye relationship[J]. Computer Engineering and Applications, 2015, 51(21): 225-229. doi: 10.3778/j.issn.1002-8331.1407-0606 ) |
| [16] | PUTINAR M. Positive polynomials on compact semi-algebraic sets[J]. Indiana University Mathematics Journal, 1993, 42(3): 969-984. doi: 10.1512/iumj.1993.42.42045 |
| [17] | LASSERRE J B. Moments, positive polynomials and their applications[EB/OL].[2016-06-20]. http://www.worldscientific.com/doi/pdf/10.1142/9781848164468_fmatter. |
| [18] | HENRION D, LASSERRE J B, LOFBERG J. GloptiPoly 3:moments, optimization and semidefinite programming[J]. Optimization Methods & Software, 2009, 24(4/5): 761-779. |
| [19] | BOUGUET J Y. Camera calibration toolbox for matlab[EB/OL].[2016-06-20]. http://www.cvg.ethz.ch/teaching/2011spring/3dphoto/Misc/Calib_toolbox_instructions.pdf. |




