人类表情是一种非语言沟通方式,它通过细微的面部特征传达人的心理活动和自身情感,它通常比人的语言表达更具真实性和可靠性。统计表明,人类大部分的沟通交流都是通过表情完成,由此可见,表情在人的行为方式中占有非常重要的地位。近几十年来,表情识别一直是个热门的研究领域,它在现实世界中的应用非常广泛,比如犯罪侦查、安全驾驶和医疗机构病人监控等。然而,表情图像提取特征后产生的高维数据给识别任务带来了巨大的挑战。规模庞大的数据存在无价值的噪声和冗余,不仅会给存储和计算带来很大的开销负担,还会增加学习模型的复杂性,甚至会给分析问题带来负面影响。在这种背景下,降维意义重大。降维可以从丰富的资源中过滤掉无用的信息,挖掘其隐含的、更有意义的低维子空间,从而帮助用户更好地认识和处理数据。
降维通常从数据几何特性的角度出发,寻找转换准则实现数据属性的约减。一般来说,降维可以归结为目标准则优化问题,其关键是找到一个最优投影矩阵,从而在低维空间中获得原始数据的重新表示。例如,主成分分析 (Principal Component Analysis, PCA)[1]和线性判别分析 (Linear Discriminant Analysis, LDA)[2]是两种常用的降维工具。PCA优化的目标是投影空间内样本集合的协方差,LDA目标是最大化投影空间的类间距离和类内距离的比值。研究表明,真实的数据通常是高维非线性的[3-4],PCA和LDA等传统的线性降维技术已经不能满足要求,这使得一些流形学习方法迅速发展起来。流形学习挖掘数据中蕴含的低维局部结构,求出相应的映射机制,实现维数约简或者数据可视化,流形方法比传统的线性方法更能反映数据的内在本质。典型的流形降维方法有等距映射 (ISOmetric Feature MAPping, ISOMAP)[5]、局部线性嵌入 (Locally Linear Embedding, LLE)[6-7]等。ISOMAP的主要思想是利用局部邻域距离近似计算数据点间的流形测地线距离,并通过在原始高维空间和目标低维空间建立测地距离的对等关系完成数据降维。LLE通过最小化样本和其近邻的重构误差来保持数据的流形结构。局部保持投影 (Locality Preserving Projection, LPP)[8]同样是一种有效的流形学习算法,它通过保持降维前后的相对关系不变完成高维数据的低维嵌入。此外还有拉普拉斯特征映射算法 (Laplacian Eigenmaps, LE)[9],局部切空间重排列 (Local Tangent Space Alignment, LTSA)[10]、Hessian特征映射 (Hessian-based Locally Linear Embedding, HLLE)[11]等。
面向识别和分类工作的降维技术,很多文献借助样本间距的思想建立优化模型。间距没有统一的定义,在不同的文献中有不同的含义和计算方式,可以把间距理解为描述事物之间彼此相隔的远近程度的物理量。Qiu等[12]提出了非参数最大间距准则 (Nonparametric Maximum Margin Criterion, NMMC),该方法通过重构类内类间离散矩阵,最大化间距进行降维。Huang等[13]通过对局部间距进行判别分析,有效发现嵌入在高维数据中的低维判别模型。边界Fisher分析 (Marginal Fisher Analysis, MFA)[14-15]通过样本点的同类近邻和异类近邻建立样本间距准则实现低维映射。最大间距准则 (Maximum Margin Criterion, MMC)[16]和前面的方法有相似的优化目标,通过最大化样本间距提高新空间中数据的区分度。MMC是一个全局的降维方法,通过类中心间的距离和类内离散矩阵建立每一类样本整体的间距。NMMC和MFA跟前者不同,这两种方法更加强调数据的局部结构。
MMC和MFA属于两种不同类型的降维方法,虽然已经在很多场合下验证了它们的有效性,但是仍然存在不足之处。本文吸收MMC和MFA的优点,同时注意避免它们的缺点,提出了基于间距的判别投影降维方法——间距判别投影 (Margin Discriminant Projection, MDP)。MDP结合样本的局部和全局信息,使用新的方式构建度量样本类间距的准则。MDP通过最大化类间距使得类内样本尽可能紧靠,类间样本尽可能分离,提高了分类精度。
1 相关算法给定样本矩阵Xd×n=[x1, x2, …, xi, …, xn],xi表示第i个样本,n是样本个数,d是样本维数。l(xi)∈{1, 2, …, c}表示样本xi所属的类别,c是类别总数。一般降维方法的目标是寻找一个投影矩阵P,对任意一个样本xi,进行yi=PTxi的映射变换,得到样本xi在新的特征空间中的表示yi。
1.1 MFAMFA利用图论直观地描述了数据的空间几何关系,是一种有监督的降维方法。它求出样本xi的k1个同类近邻和k2个异类近邻,并分别用集合Nk1w(i) 和Nk2b(i) 表示,然后MFA根据数据点的近邻结构构建本征图和惩罚图。本征图权重矩阵为:
| $ W_{ij}^w = \left\{ {\begin{array}{*{20}{c}} {1, \;\;{{\boldsymbol{x}}_j} \in N_{{k_1}}^w(i)\;{\rm{or}}\;{{\boldsymbol{x}}_i} \in N_{{k_2}}^w(j)}\\ {0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;其他\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;} \end{array}} \right. $ | (1) |
惩罚图权重矩阵:
| $ W_{ij}^b = \left\{ {\begin{array}{*{20}{c}} {1, \;\;\;\;{{\boldsymbol{x}}_j} \in N_{{k_1}}^b(i)\;{\rm{or}}\;{{\boldsymbol{x}}_i} \in N_{{k_2}}^b(j)}\\{0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;其他\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;} \end{array}} \right. $ | (2) |
根据图构造拉普拉斯矩阵L为L=Λ-W,Λ是对角矩阵:
| $ {\mathit{\Lambda} _{ii}} = \sum\limits_j {{W_{ij}}} $ | (3) |
MFA最终优化的目标函数如式 (4) 所示:
| $ {\rm{max}}\;\frac{{{\rm{tr}}\left( {{{\boldsymbol{P}}^{\rm{T}}}{\boldsymbol{X}}{{\boldsymbol{L}}^b}{{\boldsymbol{X}}^{\rm{T}}}{\boldsymbol{P}}} \right)}}{{{\rm{tr}}\left( {{{\boldsymbol{P}}^{\rm{T}}}{\boldsymbol{X}}{{\boldsymbol{L}}^w}{{\boldsymbol{X}}^{\rm{T}}}{\boldsymbol{P}}} \right)}} $ | (4) |
MFA通过最大化间距保持同类近邻在嵌入空间中仍然是相应的近邻关系,同时使异类近邻在嵌入空间中相互分开。MFA充分考虑了样本的局部信息,有利于高维数据的降维,但是MFA需要求出每个样本邻域,计算工作量比较大,而且在只有少量训练样本的条件下,MFA无法有效地发现类内样本的邻域结构。
1.2 MMCMMC的优化目标是最大化投影之后的低维空间中样本的类间散度,同时最小化类内散度,函数模型如下:
| $ \begin{array}{l} {\rm{max}}\;{\rm{tr}}\left( {{{\boldsymbol{P}}^{\rm{T}}}({{\boldsymbol{S}}_b}-{{\boldsymbol{S}}_w}){\boldsymbol{P}}} \right)\\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;\;\;\;{{\boldsymbol{P}}^{\rm{T}}}{\boldsymbol{P}} = {\boldsymbol{I}} \end{array} $ | (5) |
其中, Sb和Sw计算方法如下:
| $ {{\boldsymbol{S}}_b} = \sum\limits_{i = 1}^c {{p_i}({{\boldsymbol{u}}_i}-{\boldsymbol{u}})} {({{\boldsymbol{u}}_i}-{\boldsymbol{u}})^{\rm{T}}} $ | (6) |
| $ {{\boldsymbol{S}}_w} = \sum\limits_{i = 1}^c {{p_i}\sum\limits_{l({{\boldsymbol{x}}_j}) = i} {({{\boldsymbol{x}}_j} - {{\boldsymbol{u}}_i}){{({{\boldsymbol{x}}_j} - {{\boldsymbol{u}}_i})}^{\rm{T}}}} } $ | (7) |
其中:pi是第i类样本的先验概率,u是整体样本均值,ui是第i类样本的均值。
MMC是全局线性降维方法,速度快、实现容易,但MMC忽略了样本的局部结构,丢弃了重要的判别信息,使复杂的数据降维受到很大限制。
2 间距判别投影 2.1 基本思想样本均值是反映数据分布信息的重要指标,它表明样本集中的趋势,本文中第i类样本的均值矢量记为mi。MDP把均值矢量看作是一般的数据点,利用均值的局部近邻结构建立类间离散度矩阵来评价异类样本间的离散程度,同时充分利用每类样本的全局信息建立类内离散度矩阵,最后运用判别分析的思想,MDP获得了衡量样本间距的准则。首先给出下面两个定义:
定义1 把均值矢量mi看作类别为i的普通的样本,求出其p个异类近邻样本的集合记为E(i),表示第i类的边界样本的集合。
定义2 E(i) 中样本的均值称为第i类的边界向量,记为ei:
| $ {{\boldsymbol{e}}_i} = \frac{1}{p}\sum\limits_{{{\boldsymbol{x}}_i} \in E(i)} {{{\boldsymbol{x}}_i}} $ | (8) |
边界向量代表了偏离类中心较近的异类样本的位置,可以表示类的边缘。类边缘通常是样本异类近邻集中在位置,同时,边缘区域也是样本混杂、重叠的区域,处于边缘位置的样本有更高的概率被错误分类。因此,均值与边界向量的关系和样本与其异类近邻的关系是一致的,也就是说,在投影的过程中,如果能使每一个类均值和边界向量远离,就可以达到分离不同类别样本的效果。
利用均值和边界向量的距离表示第i类样本的类间距离sb(i):
| $ {s_b}(i) = {\left\| {{{\boldsymbol{m}}_i} - {{\boldsymbol{e}}_i}} \right\|^2} $ | (9) |
许多研究指出,相似的样本更有可能有相同的类别标签[17-18],因此,类间的局部邻近结构往往包含了具有判别特性的信息。MMC直接使用均值间的欧氏距离计算类间离散程度,考虑的是样本集合的全局信息,同时隐含考虑了异类间非近邻点对之间的关系,并不能准确地表示类间的分离度。本文提出的类间方法是局部的,能更好地把高维数据区分开来。
MFA根据样本的局部近邻关系构造类内离散矩阵,在每类的训练样本比较少情况下,原本相距较远,相似性非常低的样本也会被划分为同类近邻对,这就消弱了MFA模型学习的能力,使它在实际应用中受到很大的局限。在本文中,采用全局的方法度量类内离散度sw(i),sw(i) 的计算方式如式 (10) 所示:
| $ {s_w}(i) = \frac{1}{{{n_i}}}\sum\limits_{l({{\boldsymbol{x}}_j}) = i} {{{\left\| {{{\boldsymbol{x}}_j} - {{\boldsymbol{m}}_i}} \right\|}^2}} $ | (10) |
其中:ni为类别标签为i的样本的总个数;sw(i) 反映了类中的样本到类中心的平均距离,即属于同一类的各样本之间的分散程度。sw(i) 的值越小,类内样本越紧凑,反之亦然。使用式 (11) 计算第i类样本和异类样本间的间距mar:
| $ mar = {s_b}(i) - {s_w}(i) $ | (11) |
在面向分类或识别的降维工作中,一般性目标是增强同类样本的相似性,同时降低异类样本间的相似性。由上述目标作为引导,选择最大化投影后的类间距,则目标函数是:
| $ \begin{array}{l} {\rm{max}}\;\frac{1}{c}\sum\limits_{i = 1}^c {{{\left\| {{{\boldsymbol{P}}^{\rm{T}}}{\rm{(}}{{\boldsymbol{m}}_i}-{{\boldsymbol{e}}_i}{\rm{)}}} \right\|}^2}}-\\ \;\;\;\;\;\frac{1}{c}\sum\limits_{i = 1}^c {\sum\limits_{l({{\boldsymbol{x}}_j}) = i} {\frac{1}{{{n_i}}}{{\left\| {{{\boldsymbol{P}}^{\rm{T}}}{\rm{(}}{{\boldsymbol{x}}_j}-{{\boldsymbol{m}}_i}{\rm{)}}} \right\|}^2}} } \; = \;{\rm{tr}}\left( {{{\boldsymbol{P}}^{\rm{T}}}{\rm{(}}{{\boldsymbol{S}}_b} - {{\boldsymbol{S}}_w}){\boldsymbol{P}}} \right) \end{array} $ | (12) |
其中:Sb是类间离散度矩阵,Sw是类内离散度矩阵:
| $ {{\boldsymbol{S}}_b} = \frac{1}{c}\sum\limits_{i = 1}^c {({{\boldsymbol{m}}_i} - {{\boldsymbol{e}}_i}){{({{\boldsymbol{m}}_i} - {{\boldsymbol{e}}_i})}^{\rm{T}}}} $ | (13) |
| $ {{\boldsymbol{S}}_w} = \frac{1}{c}\sum\limits_{i = 1}^c {\sum\limits_{l({{\boldsymbol{x}}_j}) = i} {\frac{1}{{{n_i}}}({{\boldsymbol{x}}_j} - {{\boldsymbol{m}}_i}){{({{\boldsymbol{x}}_j} - {{\boldsymbol{m}}_i})}^{\rm{T}}}} } $ | (14) |
MFA算法的目标函数是迹商的形式,在真实的求解过程中,通常会遭遇奇异矩阵问题[19],导致不能直接得到投影矩阵,因此,在实现MFA方法之前需要对样本进行降维的预处理。本文算法和MMC类似,目标函数是迹差的形式,如式 (12) 所示,可以很好地避免矩阵的奇异性问题。极大化式 (12) 等价于优化两个目标:使边界向量远离均值从而分离类间样本,同时使类内样本靠近均值从而使得类内样本紧靠。MDP通过优化式 (12) 的目标模型最终达到提高分类精度的目的。
同时,为了保持数据的几何结构,在目标公式中引入正交约束,于是最终目标函数如下:
| $ \begin{array}{l} {\rm{max}}\;{\rm{tr}}\left( {{{\boldsymbol{P}}^{\rm{T}}}({{\boldsymbol{S}}_b} - {{\boldsymbol{S}}_w}){\boldsymbol{P}}} \right)\\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;\;\;\;{{\boldsymbol{P}}^{\rm{T}}}{\boldsymbol{P}} = {\boldsymbol{I}} \end{array} $ | (15) |
式 (15) 求解投影矩阵P的过程可以转化为下面特征值分解问题:
| $ ({{\boldsymbol{S}}_b} - {{\boldsymbol{S}}_w}){\boldsymbol{p}} = \lambda {\boldsymbol{p}} $ | (16) |
至此,只需要求出样本得到类间和类内离散矩阵就可以求出最佳的投影方向。
MDP和MMC、MFA这两种降维方式相比,有以下特点:
1) MDP考虑了类的边缘样本点在模式分类中的作用,充分地利用了样本的局部结构信息,构建了比MMC判别性能更好的类间离散度矩阵。
2) MDP在设计类内离散度矩阵时不涉及近邻关系,避免了MFA在样本数量少的情况下存在缺陷。
3) 在建立目标模型的过程中,MFA需要计算每个样本和剩余样本的距离,MDP只需要计算每一类的均值和全部训练样本的距离,MDP复杂度比MFA相对低。
4) MFA需要设定两个参数,参数间的平衡难度大,MDP中只有一个自定义参数,相对简单。通过上面的对比可以看出,MDP在构建自身的优化模型的过程中吸收了MMC和MFA的优点,兼顾了效率和模型的判别性能,同时MDP很好地解决了MMC和MFA在建立目标函数的过程中存在的影响分类精度的问题,因此MDP降维方法将更有利于后续的表情识别任务。
2.2 算法和复杂度分析 2.2.1 算法的基本步骤MDP的实现步骤如下:
输入 训练样本矩阵X和对应的样本类别标签,测试样本,均值近邻数目p,约减后的维数D。
输出 训练样本的低维表示Y和测试样本的低维表示。
步骤1 根据X和X中样本的标签计算每个类别的均值矢量。
步骤2 求出均值矢量的p个异类近邻。
步骤3 根据式 (8) 计算每个类的边界向量。
步骤4 根据式 (13) 和 (14) 分别计算类间离散矩阵Sb,类内离散矩阵Sw。
步骤5 对矩阵Sb-Sw进行特征值分解,求得的前D个最大的特征值对应的特征向量构成所需的投影矩阵P。
步骤6 计算Y=PT X,获得训练样本投影后的低维数据矩阵Y,同时测试样本经过相同的投影变换得到对应的低维表示。
2.2.2 复杂度分析算法主要的计算量包括均值和其近邻计算、矩阵的运算和特征值分解三个部分:第一部分需要计算每个类中心和均值到异类样本的距离,时间复杂度和样本的个数、样本的维度、样本类别数有关,为O(cdn)。第一部分的工作获得了样本均值的异类近邻关系,在这个基础上,计算类间和类内离散度矩阵只涉及简单的矢量运算,总的时间复杂度O(cd+dn)。矩阵分解特征值的工作比较复杂,目前,比较快速的方法是利用正交三角分解技术[20-21],但是时间复杂度仍然比较高,与样本维数的立方成正比,为O(d3)。因此,算法总的时间复杂度为O(cdn +d3)。
3 实验 3.1 数据集描述本文在JAFFE、Extended Cohn-Kanade (简称为CK+) 这两个广泛应用的数据集上进行表情识别实验,并通过识别精度分析算法的性能,图 1是两个数据集中的部分图像实例。为了方便使用,实验前依据各数据库的实际情况对图像进行不同的处理。

|
图 1 JAFFE和CK+数据集的图片 Figure 1 Images from JAFFE data sets and CK+ data sets |
JAFFE是表情识别中常用的数据集,其中包含了10名日本女性的二百多张人脸表情图像,原始图像大小为256×256。每个人都包含了Neutral、Anger、Disgust、Fear、Happy、Sad、Surprise 7种表情,每种表情包括2~3张图片。进行识别实验时,剔除中性表情,只使用6种基本的表情,同时,把图片裁剪为100×100大小的人脸图像。
CK+发布于2010年,是由早期的Cohn-Kanade (简称为CK) 库扩展而来。CK+数据库解决了CK数据库中存在的一些问题,更加适合研究人员使用。CK+集包括123名志愿者的593组表情序列,除了CK中有的Neutral、Anger、Disgust、Fear、Happy、Sad、Surprise 7种表情外,新增加了Contempt表情序列。CK+数据库中的每一组表情序都完整地展示了从中性面到某一个表情峰值表示的过程。在进行表情识别实验时,使用除了中性表情外的7种基本表情。CK+数据集中,并不是所有的志愿者都有全部的表情,他们可能只有其中的一种或者几种表情,实验使用随机选择的方式获取7个表情子集,即在拥有某一表情序列的全部志愿者中,随机选择18个人的强度最大的6张表情图像加入该表情子集,用这种方法,得到7种类别的表情子集作为实验使用的数据,每一个子集都包含108张表情图像。原始的图像大小为490×460,本文把图像裁剪为100×120的人脸图像以方便使用。
实验使用的数据集的具体信息见表 1。图 2展示了两个数据集中的经过处理的图像示例。
| 表 1 数据集描述 Table 1 Database description |

|
图 2 JAFFE和CK+数据集预处理效果 Figure 2 Preprocessed images from JAFFE and CK+ data sets |
实验中把图像分为测试机和训练集两部分,随机产生每个类别的L幅图像加入训练集,剩余的作为测试样本。MDP建立优化模型的过程中包含有一个自定义参数p,在实验前的预想中,p的值不能过大或过小,过小容易受噪声和孤立点的影响,过大则不能准确反映类别的边缘,并且会增加后续计算的工作量,比较耗时和浪费资源。目前无法从理论层面获得最优的p值,p的值是通过实验进行调整的,最终确定为3。
分别使用MDP、MMC、MFA和PCA对人脸图像进行降维 (维数D的取值是1~50的整数),最后使用K最近邻 (K-Nearest Neighbor, KNN) 分类器进行识别实验,统计10次分类精度的平均值作为最终的结果。在实现MFA前,需要先使用PCA将数据降维克服小样本问题,降维数目根据数据集的不同有一定的差异,具体细节将会在下面每个数据集的实验中介绍。
KNN是一种线性分类器,训练过程不需要太多处理,不涉及复杂的运算,简单高效。KNN测试的过程中只需要计算测试样本和训练样本的距离,因此,使用时只需要对决策类别的近邻数目进行设置。在本文实验中,KNN的近邻参数设置为3。
3.2 在JAFFE数据集上的实验在JAFFE人脸库上的识别实验中,每类训练样本的数目L取值分别为12、14、16、18。MFA实现前用PCA进行预处理,对应不同的L值把样本依次降到70、80、90、100维。
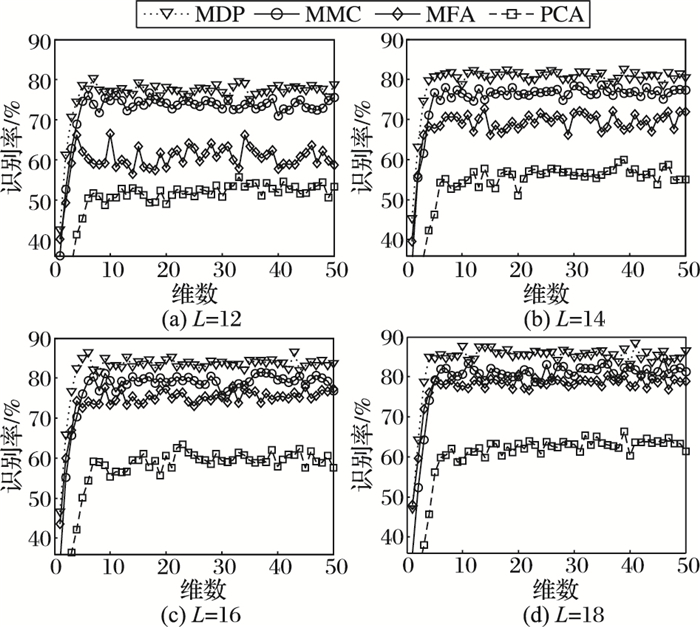
在JAFFE库上的实验结果记录在图 3,分类结果显示识别率随着维数的增加上升,但是这种趋势不是恒定不变的,当维数大于一定的值时,分类结果在一个较小的范围内波动,甚至有下降的可能,这时候,选择更多的维数意义不大。表 2记录了几种算法最好的识别结果。
|
图 3 JAFFE数据集上的识别率曲线 Figure 3 Recognition rate curve of JAFFE data sets |
| 表 2 JAFFE上分类的最高识别率 Table 2 The highest recognition rate on JAFFE |
在训练样本规模比较小时,不同算法之间的效果表现出了很大差别。PCA降维能最大限度地保留数据的主要信息,在去除噪声和冗余方面有着较好的效果,但是,PCA降维的过程中没有使用样本的类别信息,投影在低维空间中的样本可能混杂在一起无法区分,因此,在分类工作中,PCA不占优势。从实验中可以观察到,PCA在几种情况下的识别精度都是最差的,远远低于其他方法。MDP通过间距最大化,提高了类内的相似性,降低了类间的相似性,使得低维空间中的样本具有更高的区分度。MDP在4种情况下的识别率都超过了80%,且总是高于其他算法。在L的值为18,维数是41维时,MDP获得了88.53%的识别精度,是在JAFFE这个数据集上最好的识别结果。MMC的识别效果比较好,但是,它作为一种全局线性方法,有一定的局限性,它的降维效果略差于MDP,在L取值为12、14、16、18时,MDP最高识别率分别比MMC高了3.65、3.99、5.06、3.93个百分点。MFA在每个数据点的邻域结构内,判别分析其间距,从而使类内差异缩小,类间差异加大,但是,当训练样本数目比较小时,MFA不能有效地学习到样本类内的近邻结构,因此,MFA降维后的数据不一定能达到预期效果。从表 2可以看出,MFA的识别效果和MDP比有很大差距,最大识别率分别比MDP低15.97(L=12)、9.85(L=14)、8.56(L=16) 和7.06(L=18) 个百分点。在每类训练样本相对少的情况下,MDP和MFA相比,有很明显的优越性。从图 1中识别率曲线的变化可以看出,随着L的增长,MFA和MDP的差距在不断减小。
3.3 在CK+数据集上识别结果分析在CK+数据集上进行实验时,每类表情分别选择20、30、40、50张图像作为训练数据,同时,PCA作为MFA的预处理工具时,样本维数对应降到180、200、220、240维。
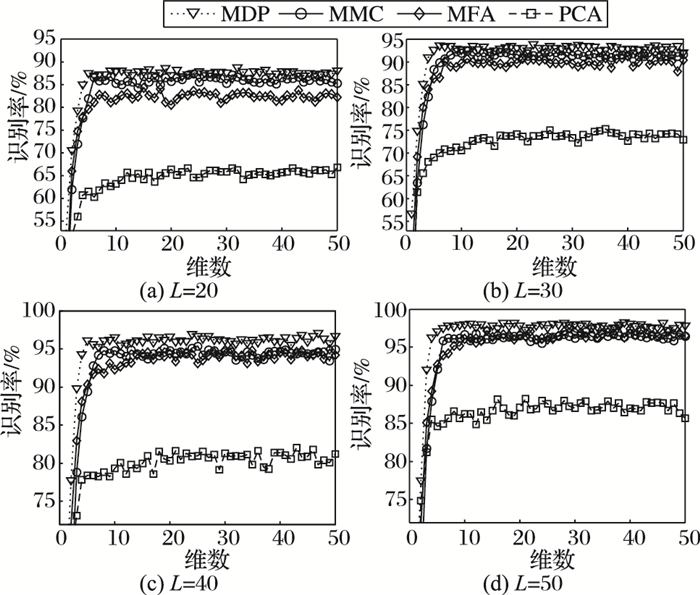
表情识别的识别率随维数变化的曲线如图 4所示,整体上看来,增加样本可以提高分类精度,但是,当样本数目超过一定的数目之后,正确率增提升的空间不大。几种算法在维数超过10之后,识别效果趋于稳定。
|
图 4 CK+数据集上的识别率曲线 Figure 4 Recognition rate curve of CK+ data sets |
表 3是几种方法的最好识别效果。PCA在几种情况下的识别率仍然是最低的。当每类中取50个作为训练样本时,MDP只有很小一部分的表情没有正确分类,这时,最好的准确率达到98.20%,是在CK+上最高的,且对应的维数也比较小。L的取值分别为20、30、40和50时,MDP最好的识别精度对应比MMC高1.29、1.53、1.72和1.24个百分点;同时,MDP比MFA分别高了4.40、2.16和2.14和0.48个百分点。值得注意的是,在CK+数据集中,训练样本比较充足,MFA有效发挥了它的降维功能, 特别是L的值为50时,MFA表现出了和MDP同样优异的识别性能,最高识别率达到了97.72%,和MDP比相差不大,甚至比MMC高0.76个百分点。
| 表 3 CK+上分类的最高识别率 Table 3 The highest recognition rate on CK+ |
降维是克服维数灾难和提高表情识别精度的重要技术,通过降维能减少数据的复杂程度,简化后续的处理过程,有效提高机器学习的效率。本文提出一种基于间距最大化的降维方法,MDP利用样本的全局和局部信息构造了判别性能更好的类间距度量准则,然后MDP极大化类间距以增大类间样本差异、缩小类内样本差异。MFA的分类精度很大程度上受样本规模制约,并且在大样本时候有内存开销大、训练速度慢等,MDP不存在的缺陷。和MMC相比,MDP能更有效地提取出数据的非线性局部结构。在JAFFE和CK+两个数据库上进行表情识别的对比实验,结果表明相较于PCA、MMC和MFA,MDP降维效果更好,分类精度更高。
虽然MDP取得了良好的实验效果,但算法中还存在需要改进的地方。例如,MDP需要自定义均值异类近邻数目p,算法的性能在一定程度上依赖人工干预;另外,分类过程中最好识别结果对应的维数D难以估计。如何自适应地产生最优的p值和D值,是需要进一步深入研究的问题。
| [1] | ABDI H, WILLIAMS L J. Principal component analysis[J]. Wiley Interdisciplinary Reviews Computational Statistics, 2010, 2(4): 433-459. doi: 10.1002/wics.v2:4 |
| [2] | AN L L, XING H J. Linear discriminant analysis based on Zp-norm maximization[C]//Proceedings of the 20142nd International Conference on Information Technology and Electronic Commerce. Piscataway, NJ:IEEE, 2014:88-92. |
| [3] | 甘炎灵, 金聪. SRC最佳鉴别投影及其在人脸识别中的应用[J]. 计算机工程与科学, 2016, 38(11): 139-145. ( GAN Y L, JIN C. SRC optimal discriminate projection and its application in face recognition[J]. Computer Engineering and Science, 2016, 38(11): 139-145. ) |
| [4] | YAN H, LU J, ZHOU X, et al. Multi-feature multi-manifold learning for single-sample face recognition[J]. Neurocomputing, 2014, 143(16): 134-143. |
| [5] | DE SILVA V, TENENBAUM J B. Global versus local methods in nonlinear dimensionality reduction[J]. Advances in Neural Information Processing Systems, 2003, 15: 1959-1966. |
| [6] | CHANG H, YEUNG D Y. Robust locally linear embedding[J]. Pattern Recognition, 2006, 39(6): 1053-1065. doi: 10.1016/j.patcog.2005.07.011 |
| [7] | FANG Y, LI H, MA Y, et al. Dimensionality reduction of hyperspectral images based on robust spatial information using locally linear embedding[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(10): 1712-1716. doi: 10.1109/LGRS.2014.2306689 |
| [8] | ZHANG L, QIAO L, CHEN S. Graph-optimized locality preserving projections[J]. Pattern Recognition, 2010, 43(6): 1993-2002. doi: 10.1016/j.patcog.2009.12.022 |
| [9] | MARTINEZ-DEL-RINCON J, LEWANDOWSKI M, NEBEL J C, et al. Generalized Laplacian eigenmaps for modeling and tracking human motions[J]. IEEE Transactions on Cybernetics, 2014, 44(9): 1646-1660. doi: 10.1109/TCYB.2013.2291497 |
| [10] | KIM K, LEE D. Inductive manifold learning using structured support vector machine[J]. Pattern Recognition, 2014, 47(1): 470-479. doi: 10.1016/j.patcog.2013.07.011 |
| [11] | WANG J. Hessian locally linear embedding[M]. Berlin: Springer, 2012 : 249 -265. |
| [12] | QIU X, WU L. Face recognition by stepwise nonparametric margin maximum criterion[C]//Proceedings of the 10th IEEE International Conference on Computer Vision. Piscataway, NJ:IEEE, 2005:1567-1572. |
| [13] | HUANG P, TANG Z, CHEN C, et al. Local maximal margin discriminant embedding for face recognition[J]. Journal of Visual Communication and Image Representation, 2013, 25(2): 296-305. |
| [14] | YAN S, XU D, ZHANG B, et al. Graph embedding:a general framework for dimensionality reduction[C]//Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Piscataway, NJ:IEEE, 2005:830-837. |
| [15] | YAN S, XU D, ZHANG B, et al. Graph embedding and extensions:a general framework for dimensionality reduction[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2007, 29(1): 40-51. doi: 10.1109/TPAMI.2007.250598 |
| [16] | LI H, JIANG T, ZHANG K. Efficient and robust feature extraction by maximum margin criterion[J]. IEEE Transactions on Neural Networks, 2006, 17(1): 157-165. doi: 10.1109/TNN.2005.860852 |
| [17] | DE CARVALHO F A T, TENÓRIO C P. Fuzzy K-means clustering algorithms for interval-valued data based on adaptive quadratic distances[J]. Fuzzy Sets and Systems, 2010, 161(23): 2978-2999. doi: 10.1016/j.fss.2010.08.003 |
| [18] | ZHU X, GHAHRAMANI Z, LAFFERTY J. Semi-supervised learning using Gaussian fields and harmonic functions[C]//Proceedings of the 20th International Conference on Machine Learning. Washington, DC:AAAI Press, 2003, 3:912-919. |
| [19] | WANG S J, YAN S, YANG J, et al. A general exponential framework for dimensionality reduction[J]. IEEE Transactions on Image Processing, 2014, 23(2): 920-930. doi: 10.1109/TIP.2013.2297020 |
| [20] | 张贤达. 矩阵分析与应用[M]. 北京: 清华大学出版社, 2004 : 229 -243. ( ZHANG X D. Matrix Analysis and Applications[M]. Beijing: Tsinghua University Press, 2004 : 229 -243. ) |
| [21] | GOLUB G H, VAN LOAN C F. Matrix Computations[M]. Baltimore: JHU Press, 2013 : 458 -466. |




